
讨论决策树:什么构成好的分割?
图片由 Editor | ChatGPT 提供
引言
如今,大多数先进的人工智能解决方案,其基础都是强大而复杂的模型,例如 Transformer、扩散模型和其他深度学习架构,这已是公开的秘密。然而,复杂度较低到中等的模型——例如**决策树**和随机森林(它们将多个决策树结合起来执行单一预测任务)——在构建预测系统方面仍然非常流行且有效,尤其是在商业领域。从金融欺诈检测到客户流失预测,再到通过预测产品需求优化供应链,基于决策树的模型已广泛应用于现实世界。
但是,是什么让决策树如此适合各种预测任务?它们在内部使用了什么标准来构建?具体来说,在形成树形结构时,节点是如何被递归分割的?本文将**深入探讨决策树的内部工作原理,重点关注分支是如何通过有目的、数据驱动的分割来创建的**(剧透:这绝不是随机发生的)。
决策树的构建方法
为了初步了解决策树的构建方式,以及因此,包含训练数据样本的节点是如何被分割的,请看下图所示的例子。
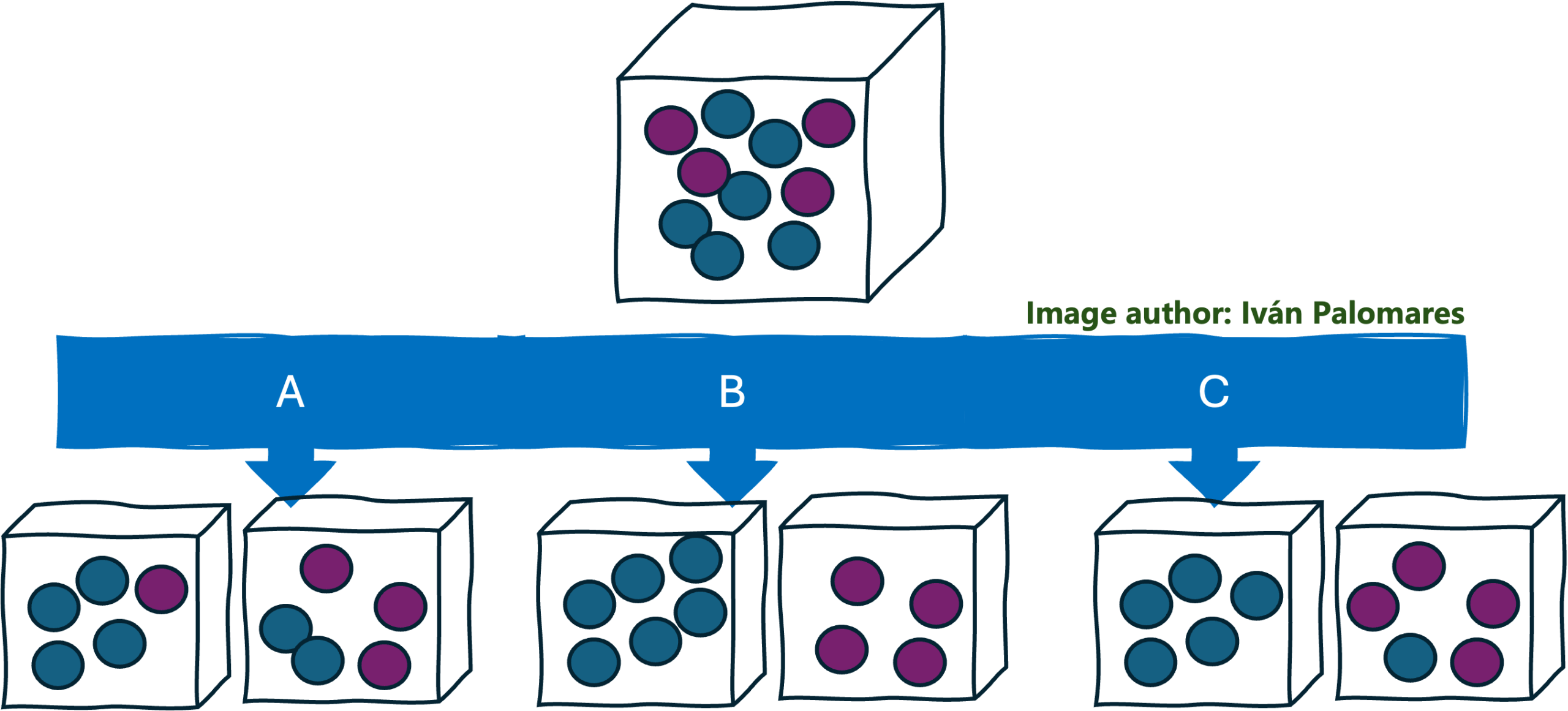
同质性是构建良好决策树的指导原则
作者提供图片
假设我们有一个装有两种不同颜色球的大盒子,我们想把它们分到两个小盒子里。要求是尽量将这组球分成两个尽可能同质的子集;也就是说,混合的颜色越少越好。这里提出了三种选项来对原盒子进行这种“分割”操作,将其分成两个盒子:选项 A、选项 B 和选项 C。你会选择哪一个?
如果你选择了选项 B,那我们就是志同道合的。最重要的是,你已经掌握了决策树构建方式的精髓。
构建或训练决策树的过程始于一个节点,在下图所示的顶部有视觉化表示。就像一个位于顶部的加尔顿板(Galton Board)上的微小豆子一样,初始节点包含了整个训练数据集。例如,如果我们采用流行的鸢尾花数据集,并打算构建一个决策树来将鸢尾花观测值分类到三种可能的物种(类别)之一,训练过程将从顶部节点中包含的 150 个数据集实例开始。
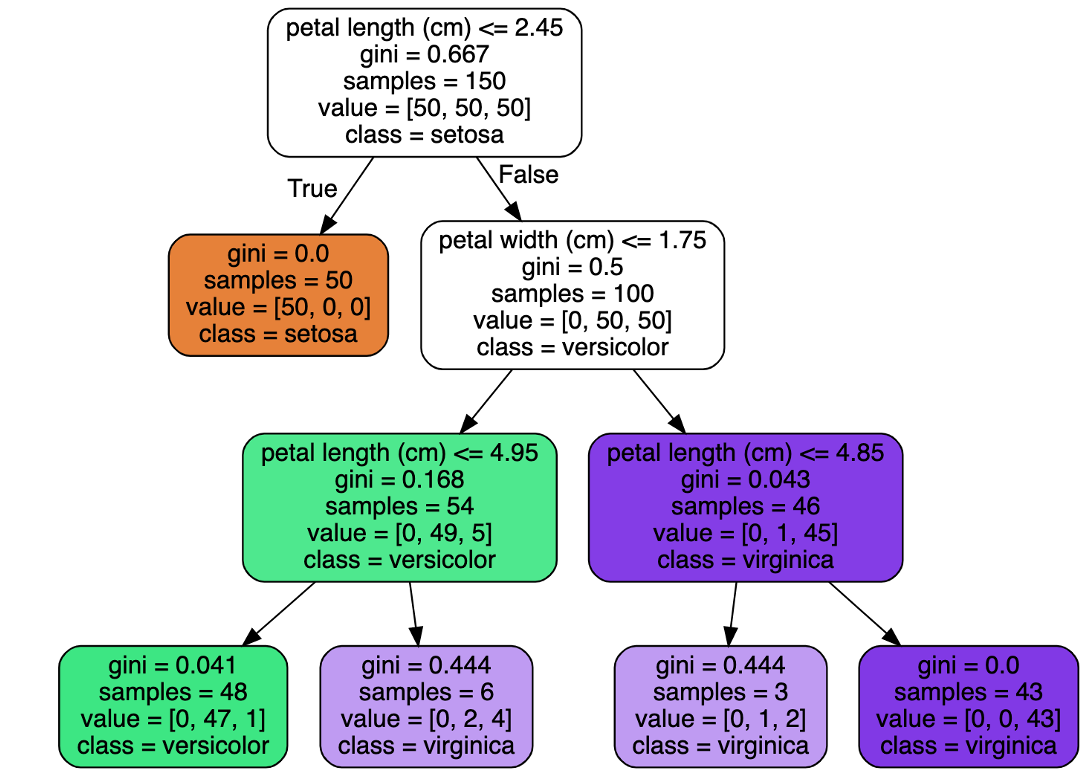
基于鸢尾花数据集构建的示例决策树
作者提供图片
这就是关键所在,也是为什么我们在之前的例子中将选项 B 视为最佳选择的原因:**类别同质性是追求的关键标准**,在分割决策树的根节点并逐步增长它的过程中。我们需要确保数据实例被逐渐分离到尽可能同质的节点中。显然,起点远非同质,初始的完整训练集包含 150 个实例,平均分布在三个类别中,每个类别 50 个实例。
做出良好的分割
那么,我们如何将一个包含,比如说,150 个实例的节点分割成两个“更小的”节点,每个节点包含这些实例的一个子集?这是通过定义一个与数据集中的属性相关的**分割条件**,以及一个阈值来实现的,该阈值根据实例的值将其发送到分割的一侧或另一侧。例如,通过查看根节点顶部的_信息,我们可以观察到条件
这个条件用于分割 150 个实例,使得“花瓣长度”属性值小于或等于 2.45 的实例被发送到一个“子节点”,而花瓣长度大于 2.45 厘米的实例被发送到另一个子节点。这导致了 50 个实例具有比 2.45 厘米更短的花瓣长度,而 100 个实例具有更长的花瓣长度。
我之前说过,“构建决策树时,没有任何事情是随机发生的”,我的意思是:涉及花瓣长度属性和 2.45 阈值的**分割条件不是随意选择的**,而是**应用一个名为 CART(分类和回归树)的决策树构建算法**的结果,该算法搜索并识别一个分割条件,以最大化类别同质性,或者换句话说,最小化节点不纯度。**不纯度**是衡量决策树节点中包含的实例的异质性的度量,有几种度量主要基于信息论来衡量它:熵和基尼指数是最常用的。
像 CART 这样的决策树算法会评估一个大的可能的 [属性 – 阈值] 条件空间,以将树的一个节点分割成两个子节点或子节点,并选择能够最大化不纯度减少的分割;换句话说,“将大盒子里的彩色球分成两个小盒子,哪个条件能最显著地从一个单一的、多样化的盒子转移到两个更同质的盒子?”这就是不纯度减少:在我们通过生长新节点和执行连续分割来构建树的过程中,从不那么同质的节点向更同质的节点移动。
如果你查看前面可视化决策树中每个节点里的**值 = [X, Y, Z]** 列表,这些列表显示了该节点中每个类别的实例分布,你可以看到随着我们向下遍历树,分布变得越来越集中在一个类别周围,这大致是构建树的目标。
最后,并非所有事情都是绝对的,总有一些实际的细微之处需要考虑。例如,在实践中,在树的每个部分追求完全的同质性通常不是一个好主意。事实上,为了实现完全同质性而过度生长一棵树,通常意味着模型正在记忆训练数据,而不是以平衡的方式从中学习。如果你对机器学习相当熟悉,你可能会知道这意味着什么:**过拟合**的风险。因此,尽管分割决策树节点的主要指导原则是追求类别同质性,但这个过程必须谨慎执行,以避免最终的模型因为过度记忆训练数据而无法泛化到未来未见过的数据。
总结
本文探讨了机器学习中基于决策树的模型工作的一个关键方面:分割节点以构建和增长决策树以进行分类和回归等预测任务的过程。我们用通俗易懂的语言,不深入技术细节,揭示了构建能够基于动态定义的规则或条件层次结构做出准确预测的决策树的内幕。




暂无评论。