双退火是一种随机全局优化算法。
它是广义模拟退火算法的一种实现,也是模拟退火的扩展。此外,它还与一种局部搜索算法配对,该算法在模拟退火过程结束时自动执行。
这种有效的全局和局部搜索过程的结合为具有挑战性的非线性优化问题提供了一种强大的算法。
在本教程中,您将了解双退火全局优化算法。
完成本教程后,您将了解:
- 双退火优化是一种全局优化算法,它是模拟退火的修改版本,也使用了局部搜索算法。
- 如何在 Python 中使用双退火优化算法 API。
- 使用双退火解决具有多个最优解的全局优化问题的示例。
通过我的新书《机器学习优化》来启动您的项目,其中包括分步教程和所有示例的 Python 源代码文件。
让我们开始吧。
使用 Python 进行双重退火优化
照片由 Susanne Nilsson 拍摄,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 什么是双退火
- 双退火 API
- 双退火示例
什么是双退火
双退火是一种全局优化算法。
因此,它适用于具有非线性响应曲面的目标函数。它是一种随机优化算法,这意味着它在搜索过程中使用随机性,并且每次搜索运行可能会找到不同的解决方案。
双退火基于模拟退火优化算法。
模拟退火是一种随机爬山算法,其中候选解决方案以随机方式修改,并且修改后的解决方案以概率方式接受以替换当前的候选解决方案。这意味着更差的解决方案可能会替换当前的候选解决方案。这种替换的概率在搜索开始时很高,并随着每次迭代而降低,由“温度”超参数控制。
双退火是经典模拟退火 (CSA) 算法的一种实现。它基于 1997 年论文《广义模拟退火算法及其在 Thomson 模型中的应用》中描述的广义模拟退火 (GSA) 算法。
它结合了“快速模拟退火”(FSA) 的退火调度(温度随算法迭代降低的速度)和另一种统计过程“Tsallis 统计”(以作者命名)的概率接受。
实验结果表明,这种广义模拟退火算法的性能似乎优于与之比较的经典或快速版本的算法。
GSA 不仅比 FSA 和 CSA 收敛更快,而且比 FSA 和 CSA 更容易摆脱局部最小值。
— 用于全局优化的广义模拟退火:GenSA 包,2013 年。
除了这些对模拟退火的修改之外,还可以将局部搜索算法应用于模拟退火搜索找到的解决方案。
这是可取的,因为全局搜索算法通常善于定位最优解决方案的盆地(搜索空间中的区域),但通常不善于在盆地中找到最优解决方案。而局部搜索算法擅长找到盆地的最优解。
将局部搜索与模拟退火过程配对可确保搜索最大程度地利用找到的候选解决方案。
现在我们已经从高层次上熟悉了双退火算法,让我们看一下 Python 中双退火的 API。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
双退火 API
双退火全局优化算法可以通过 dual_annealing() SciPy 函数在 Python 中使用。
该函数以目标函数的名称和每个输入变量的边界作为搜索的最小参数。
|
1 2 3 |
... # 执行双退火搜索 result = dual_annealing(objective, bounds) |
搜索有许多附加超参数,它们具有默认值,尽管您可以配置它们以自定义搜索。
“maxiter”参数指定算法的总迭代次数(而不是函数评估的总次数),默认为 1,000 次迭代。“maxfun”可以根据需要指定以限制函数评估的总次数,默认为 1000 万次。
搜索的初始温度由“initial_temp”参数指定,默认为 5,230。一旦温度达到等于或小于(initial_temp * restart_temp_ratio)的值,退火过程将重新启动。该比率默认为一个非常小的数字 2e-05(即 0.00002),因此重新退火的默认触发温度为(5230 * 0.00002)或 0.1046。
该算法还提供了对基于它的广义模拟退火特定超参数的控制。这包括通过“visit”参数控制搜索过程中可以跳跃的距离,默认为 2.62(优选小于 3 的值),以及通过“accept”参数控制接受新解决方案的可能性,默认为 -5。
使用默认超参数调用 minimize() 函数进行局部搜索。可以通过向“local_search_options”参数提供超参数名称和值的字典来配置局部搜索。
通过将“no_local_search”参数设置为 True,可以禁用搜索的局部搜索组件。
搜索结果是一个 OptimizeResult 对象,其属性可以像字典一样访问。搜索的成功(或不成功)可以通过“success”或“message”键访问。
函数评估的总次数可以通过 ‘nfev’ 访问,搜索找到的最优输入可以通过 ‘x’ 键访问。
现在我们已经熟悉了 Python 中的双退火 API,让我们看一些实际示例。
双退火示例
在本节中,我们将看一个在多模态目标函数上使用双退火算法的示例。
Ackley 函数是多模态目标函数的一个示例,它具有单个全局最优解和多个局部最优解,局部搜索可能会陷入其中。
因此,需要一种全局优化技术。它是一个二维目标函数,在 [0,0] 处有全局最优解,其值为 0.0。
下面的例子实现了 Ackley 函数并创建了一个三维曲面图,显示了全局最优解和多个局部最优解。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# ackley 多峰函数 from numpy import arange from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行该示例会创建 Ackley 函数的曲面图,显示大量的局部最优解。
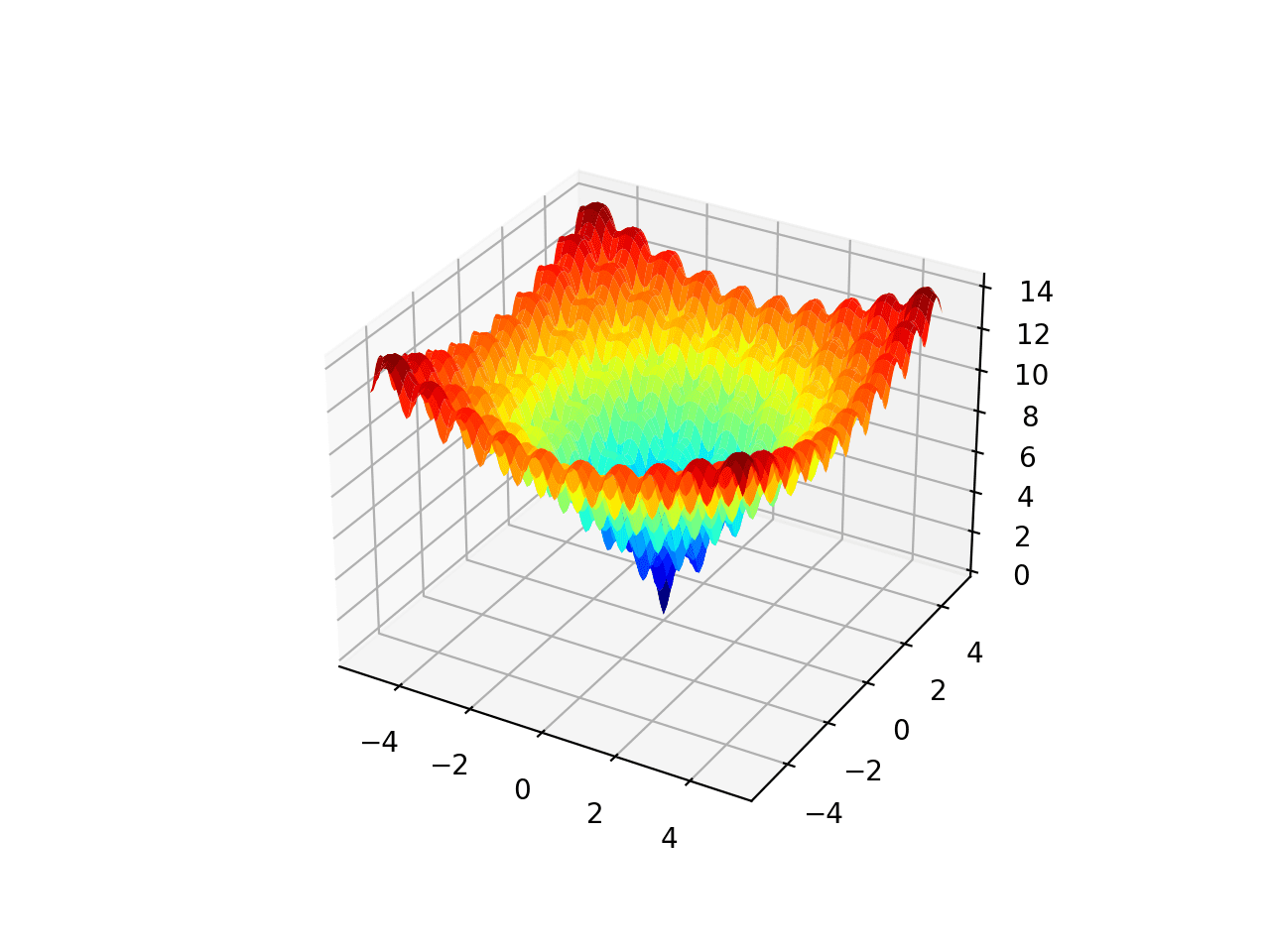
Ackley 多峰函数的三维曲面图
我们可以将双退火算法应用于 Ackley 目标函数。
首先,我们可以将搜索空间的边界定义为每个维度中函数的限制。
|
1 2 3 |
... # 定义搜索的边界 bounds = [[r_min, r_max], [r_min, r_max]] |
然后我们可以通过指定目标函数的名称和搜索边界来应用搜索。
在这种情况下,我们将使用默认超参数。
|
1 2 3 |
... # 执行模拟退火搜索 result = dual_annealing(objective, bounds) |
搜索完成后,它将报告搜索状态和执行的迭代次数,以及找到的最佳结果及其评估。
|
1 2 3 4 5 6 7 8 |
... # 总结结果 print('Status : %s' % result['message']) print('Total Evaluations: %d' % result['nfev']) # 评估解 solution = result['x'] evaluation = objective(solution) print('Solution: f(%s) = %.5f' % (solution, evaluation)) |
综合来看,将双退火应用于 Ackley 目标函数的完整示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# 针对 Ackley 多模态目标函数的双退火全局优化 from scipy.optimize import dual_annealing from numpy.random import rand from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi # 目标函数 def objective(v): x, y = v return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 定义搜索的边界 bounds = [[r_min, r_max], [r_min, r_max]] # 执行双退火搜索 result = dual_annealing(objective, bounds) # 总结结果 print('Status : %s' % result['message']) print('Total Evaluations: %d' % result['nfev']) # 评估解 solution = result['x'] evaluation = objective(solution) print('Solution: f(%s) = %.5f' % (solution, evaluation)) |
运行该示例会执行优化,然后报告结果。
注意:考虑到算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到算法找到了输入非常接近零的最优解,并且目标函数评估实际上为零。
我们可以看到总共执行了 4,136 次函数评估。
|
1 2 3 |
状态:['达到最大迭代次数'] 总评估次数:4136 解决方案:f([-2.26474440e-09 -8.28465933e-09]) = 0.00000 |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 广义模拟退火算法及其在 Thomson 模型中的应用, 1997.
- 广义模拟退火, 1996.
- 用于全局优化的广义模拟退火:GenSA 包, 2013.
API
文章
总结
在本教程中,您了解了双退火全局优化算法。
具体来说,你学到了:
- 双退火优化是一种全局优化算法,它是模拟退火的修改版本,也使用了局部搜索算法。
- 如何在 Python 中使用双退火优化算法 API。
- 使用双退火解决具有多个最优解的全局优化问题的示例。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



请问,您能将它用于房屋数据集吗?
感谢您的建议。
您能否包含具有多维输入/设计变量(超过 3 个)的不等式/等式约束,以实现单一目标优化?
感谢您的建议。
感谢您的教程!我遇到以下错误
TypeError: objective() 缺少 1 个必需的位置参数:'y'
当我运行
result = dual_annealing(objective, bounds)
我没有看到错误。您使用的是哪个版本的 scikit-learn?
嗨,Jason,
这很有帮助。感谢分享!双退火算法是否适用于全局约束?例如,我有 10 种产品,想找到每种产品的最优价格以最大化利润,但又不想让我的销量下降太多。Python 中的 dual_annealing() API 似乎没有约束参数。
嗨 Yw……以下内容可能对您有帮助
https://aicorespot.io/dual-annealing-optimization-with-python/
嗨,Jason,
感谢您的解释。如果您不介意,我有一个问题。终止标准是什么?您提到迭代的默认值为 1000,这是否意味着如果我设置为 10,000,我将有更多的搜索?
我尝试了 maxiter 为 10,000;它搜索得越来越多。如果这是真的,它是如何收敛的?
此致,
Dawit
嗨 Dawit……非常欢迎!以下资源可能对您有帮助
https://lightrun.com/answers/scipy-scipy-enh-stopping-rule-for-dual_annealing-function
谢谢,詹姆斯。你是明星!