评估用于人类活动识别的机器学习算法

作者：Jason Brownlee（于 2020 年 8 月 28 日发布）| 分类：时间序列深度学习 | 评论：34

人类活动识别是指将由专用安全带或智能手机记录的加速度计数据序列分类为已知的、定义明确的运动的问题。

该问题的一些传统方法包括基于固定大小的窗口从时间序列数据中手动提取特征，并训练机器学习模型，例如决策树的集成。困难之处在于这种特征工程需要该领域的深厚专业知识。

最近，循环神经网络和一维卷积神经网络（或 CNN）等深度学习方法已在具有少量或无数据特征工程的具有挑战性的活动识别任务上取得了最先进的结果，而是使用原始数据的特征学习。

在本教程中，您将发现如何评估“使用智能手机进行活动识别”数据集中的各种机器学习算法。

完成本教程后，您将了解：

如何加载和评估用于活动识别数据集的特征工程版本中的非线性与集成机器学习算法。
如何加载和评估用于活动识别数据集的原始信号数据中的机器学习算法。
如何为能够进行特征学习的更复杂的算法（例如深度学习方法）定义预期的性能的合理下限和上限。

开始您的项目，阅读我的新书《时间序列预测深度学习》，其中包含分步教程和所有示例的Python 源代码文件。

让我们开始吧。

How to Evaluate Machine Learning Algorithms for Human Activity Recognition

如何评估用于人类活动识别的机器学习算法
照片作者：Murray Foubister，部分权利保留。

教程概述

本教程分为三个部分；它们是：

使用智能手机数据集进行活动识别
建模特征工程数据
建模原始数据

使用智能手机数据集进行活动识别

人类活动识别，简称HAR，是根据传感器记录的人体运动轨迹预测其正在做什么的问题。

一个标准的人类活动识别数据集是 2012 年发布的“使用智能手机进行活动识别”数据集。

它由意大利热那亚大学的 Davide Anguita 等人准备并发布，并在其 2013 年的论文“使用智能手机进行人类活动识别的公共领域数据集”中得到了全面描述。该数据集已在他们 2012 年的论文“使用多类硬件友好支持向量机进行智能手机上的活动识别”中被机器学习算法建模。

该数据集已发布，可从UCI机器学习库免费下载

使用智能手机数据集进行人类活动识别，UCI 机器学习存储库

这些数据收集自 30 名年龄在 19 至 48 岁之间的受试者，他们在佩戴腰部智能手机记录运动数据时执行六种标准活动之一。记录了每位受试者执行活动的视频，并且根据这些视频手动标记了运动数据。

下面是受试者执行活动并记录运动数据的示例视频。

执行的六项活动如下：

步行
上楼梯
下楼梯
坐着
站立
躺着

记录的运动数据是智能手机（特别是三星 Galaxy S II）的 x、y 和 z 轴加速度计数据（线性加速度）和陀螺仪数据（角速度）。观测值以 50 Hz（即每秒 50 个数据点）的频率记录。每位受试者重复执行活动序列两次，一次设备在左侧，一次设备在右侧。

无法获取原始数据。而是提供了一个预处理版本的数据集。预处理步骤包括

使用噪声滤波器预处理加速度计和陀螺仪。
将数据分割成2.56秒（128个数据点）的固定窗口，重叠率为50%。
将加速度计数据分解为重力（总）和身体运动分量。

对窗口数据应用特征工程，并提供了一份包含这些工程特征的数据副本。

从每个窗口中提取了人类活动识别领域常用的时间和频率特征。结果是生成了一个包含561个元素的特征向量。

数据集根据受试者的数据分为训练集（70%）和测试集（30%），例如21名受试者用于训练，9名受试者用于测试。

针对智能手机（例如定点算术）设计的支持向量机的实验结果在测试数据集上达到了 89% 的预测准确率，与未经修改的 SVM 实现取得了类似的结果。

该数据集可免费从UCI机器学习库下载。

数据以一个大小约为58兆字节的zip文件提供。直接下载链接如下：

UCI HAR Dataset.zip

下载数据集，并将所有文件解压缩到当前工作目录中的一个名为“HARDataset”的新目录中。

时间序列深度学习需要帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

建模特征工程数据

在本节中，我们将开发代码来加载数据集的特征工程版本，并评估一套非线性机器学习算法，包括原始论文中使用的 SVM。

目标是在测试数据集上达到至少 89% 的准确率。

使用该数据集特征工程版本的方法的结果为开发用于该原始数据版本的方法提供了基线。

本节分为五个部分：

加载数据集
定义模型
评估模型
总结结果
完整示例

加载数据集

第一步是加载训练和测试输入 (X) 和输出 (y) 数据。

具体来说，是以下文件

HARDataset/train/X_train.txt
HARDataset/train/y_train.txt
HARDataset/test/X_test.txt
HARDataset/test/y_test.txt

输入数据是 CSV 格式，列之间用空格分隔。这些文件都可以加载为 NumPy 数组。

下面的 `load_file()` 函数加载给定文件路径的数据集，并以 NumPy 数组的形式返回加载的数据。

# load a single file as a numpy array
def load_file(filepath):
	dataframe = read_csv(filepath, header=None, delim_whitespace=True)
	return dataframe.values

# 将单个文件加载为numpy数组

def load_file(filepath):

dataframe = read_csv(filepath, header=None, delim_whitespace=True)

return dataframe.values

我们可以调用此函数来加载给定训练或测试集组的 _X_ 和 _y_ 文件，考虑到目录布局和文件名中的相似性。下面的 `load_dataset_group()` 函数将加载一个组的这两个文件，并以 NumPy 数组的形式返回 X 和 y 元素。然后可以使用此函数加载训练和测试组的 X 和 y 元素。

# load a dataset group, such as train or test
def load_dataset_group(group, prefix=''):
	# load input data
	X = load_file(prefix + group + '/X_'+group+'.txt')
	# load class output
	y = load_file(prefix + group + '/y_'+group+'.txt')
	return X, y

# 加载数据集组，例如训练集或测试集

def load_dataset_group(group, prefix=''):

# 加载输入数据

X = load_file(prefix + group + '/X_'+group+'.txt')

# 加载类别输出

y = load_file(prefix + group + '/y_'+group+'.txt')

return X, y

最后，我们可以加载训练和测试数据集，并将它们作为 NumPy 数组返回，准备好进行拟合和评估机器学习模型。

# load the dataset, returns train and test X and y elements
def load_dataset(prefix=''):
	# load all train
	trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/')
	print(trainX.shape, trainy.shape)
	# load all test
	testX, testy = load_dataset_group('test', prefix + 'HARDataset/')
	print(testX.shape, testy.shape)
	# flatten y
	trainy, testy = trainy[:,0], testy[:,0]
	print(trainX.shape, trainy.shape, testX.shape, testy.shape)
	return trainX, trainy, testX, testy

#加载数据集，返回train和test的X和y元素

def load_dataset(prefix=''):

# 加载所有训练数据

trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/')

print(trainX.shape, trainy.shape)

# 加载所有测试数据

testX, testy = load_dataset_group('test', prefix + 'HARDataset/')

print(testX.shape, testy.shape)

# 展平 y

trainy, testy = trainy[:,0], testy[:,0]

print(trainX.shape, trainy.shape, testX.shape, testy.shape)

return trainX, trainy, testX, testy

我们可以调用此函数加载所有需要的数据；例如：

# load dataset
trainX, trainy, testX, testy = load_dataset()

1 2	# 加载数据集 trainX, trainy, testX, testy = load_dataset()

定义模型

接下来，我们可以定义一个机器学习模型列表来针对此问题进行评估。

我们将使用默认配置来评估这些模型。此时我们不追求这些模型的最佳配置，只是想大致了解一下复杂的模型在使用默认配置时在此问题上的表现。

我们将评估一套多样化的非线性与集成机器学习算法，具体包括：

非线性算法

k-近邻
分类与回归树
支持向量机
朴素贝叶斯

集成算法

装袋决策树
随机森林
额外树
梯度提升机

我们将定义模型并将它们存储在一个字典中，该字典将模型对象映射到一个简短的名称，这有助于分析结果。

下面的 `define_models()` 函数定义了我们将要评估的八个模型。

# create a dict of standard models to evaluate {name:object}
def define_models(models=dict()):
	# nonlinear models
	models['knn'] = KNeighborsClassifier(n_neighbors=7)
	models['cart'] = DecisionTreeClassifier()
	models['svm'] = SVC()
	models['bayes'] = GaussianNB()
	# ensemble models
	models['bag'] = BaggingClassifier(n_estimators=100)
	models['rf'] = RandomForestClassifier(n_estimators=100)
	models['et'] = ExtraTreesClassifier(n_estimators=100)
	models['gbm'] = GradientBoostingClassifier(n_estimators=100)
	print('Defined %d models' % len(models))
	return models

# 创建一个要评估的标准模型字典 {名称:对象}

def define_models(models=dict()):

# 非线性模型

models['knn'] = KNeighborsClassifier(n_neighbors=7)

models['cart'] = DecisionTreeClassifier()

models['svm'] = SVC()

models['bayes'] = GaussianNB()

# 集成模型

models['bag'] = BaggingClassifier(n_estimators=100)

models['rf'] = RandomForestClassifier(n_estimators=100)

models['et'] = ExtraTreesClassifier(n_estimators=100)

models['gbm'] = GradientBoostingClassifier(n_estimators=100)

print('已定义 %d 个模型' % len(models))

返回 models

此函数具有很强的可扩展性，您可以轻松地进行更新以定义您想要的任何机器学习模型或模型配置。

评估模型

下一步是在加载的数据集上评估已定义的模型。

此步骤分为评估单个模型和评估所有模型。

我们将通过首先在训练数据集上拟合模型，在测试数据集上进行预测，然后使用指标评估预测来评估单个模型。在这种情况下，我们将使用分类准确率，它能够捕捉模型在平衡观测值跨六种活动（或类别）时的性能（或错误）。

下面的 `evaluate_model()` 函数实现了此行为，它评估给定的模型并以百分比形式返回分类准确率。

# evaluate a single model
def evaluate_model(trainX, trainy, testX, testy, model):
	# fit the model
	model.fit(trainX, trainy)
	# make predictions
	yhat = model.predict(testX)
	# evaluate predictions
	accuracy = accuracy_score(testy, yhat)
	return accuracy * 100.0

# 评估单个模型

def evaluate_model(trainX, trainy, testX, testy, model):

# 拟合模型

model.fit(trainX, trainy)

# 进行预测

yhat = model.predict(testX)

# 评估预测结果

accuracy = accuracy_score(testy, yhat)

return accuracy * 100.0

我们现在可以为每个已定义的模型重复调用 `evaluate_model()` 函数。

下面的 `evaluate_models()` 函数实现了此行为，它接受已定义模型的字典，并返回一个模型名称与其分类准确率映射的字典。

由于模型评估可能需要几分钟时间，该函数在评估每个模型后会打印其性能，作为一些详细的反馈。

# evaluate a dict of models {name:object}, returns {name:score}
def evaluate_models(trainX, trainy, testX, testy, models):
	results = dict()
	for name, model in models.items():
		# evaluate the model
		results[name] = evaluate_model(trainX, trainy, testX, testy, model)
		# show process
		print('>%s: %.3f' % (name, results[name]))
	return results

# 评估模型字典 {名称:对象}，返回 {名称:分数}

def evaluate_models(trainX, trainy, testX, testy, models):

results = dict()

for name, model in models.items():

# 评估模型

results[name] = evaluate_model(trainX, trainy, testX, testy, model)

# 显示过程

print('>%s: %.3f' % (name, results[name]))

return results

总结结果

最后一步是总结发现。

我们可以按分类准确率降序对所有结果进行排序，因为我们希望最大化准确率。

然后可以打印评估模型的那些结果，清楚地显示每个评估模型的相对排名。

下面的 `summarize_results()` 函数实现了此行为。

# print and plot the results
def summarize_results(results, maximize=True):
	# create a list of (name, mean(scores)) tuples
	mean_scores = [(k,v) for k,v in results.items()]
	# sort tuples by mean score
	mean_scores = sorted(mean_scores, key=lambda x: x[1])
	# reverse for descending order (e.g. for accuracy)
	if maximize:
		mean_scores = list(reversed(mean_scores))
	print()
	for name, score in mean_scores:
		print('Name=%s, Score=%.3f' % (name, score))

# 打印和绘制结果

def summarize_results(results, maximize=True):

# 创建一个 (名称, 平均(分数)) 元组列表

mean_scores = [(k,v) for k,v in results.items()]

# 按平均分数对元组进行排序

mean_scores = sorted(mean_scores, key=lambda x: x[1])

# 反转为降序（例如，对于准确率）

if maximize:

mean_scores = list(reversed(mean_scores))

print()

for name, score in mean_scores:

print('名称=%s, 分数=%.3f' % (name, score))

完整示例

我们知道我们已经具备了所有必要的组成部分。

评估数据集特征工程版本的八个机器学习模型的完整示例如下所示。

# spot check on engineered-features
from pandas import read_csv
from sklearn.metrics import accuracy_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier

# load a single file as a numpy array
def load_file(filepath):
	dataframe = read_csv(filepath, header=None, delim_whitespace=True)
	return dataframe.values

# load a dataset group, such as train or test
def load_dataset_group(group, prefix=''):
	# load input data
	X = load_file(prefix + group + '/X_'+group+'.txt')
	# load class output
	y = load_file(prefix + group + '/y_'+group+'.txt')
	return X, y

# load the dataset, returns train and test X and y elements
def load_dataset(prefix=''):
	# load all train
	trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/')
	print(trainX.shape, trainy.shape)
	# load all test
	testX, testy = load_dataset_group('test', prefix + 'HARDataset/')
	print(testX.shape, testy.shape)
	# flatten y
	trainy, testy = trainy[:,0], testy[:,0]
	print(trainX.shape, trainy.shape, testX.shape, testy.shape)
	return trainX, trainy, testX, testy

# create a dict of standard models to evaluate {name:object}
def define_models(models=dict()):
	# nonlinear models
	models['knn'] = KNeighborsClassifier(n_neighbors=7)
	models['cart'] = DecisionTreeClassifier()
	models['svm'] = SVC()
	models['bayes'] = GaussianNB()
	# ensemble models
	models['bag'] = BaggingClassifier(n_estimators=100)
	models['rf'] = RandomForestClassifier(n_estimators=100)
	models['et'] = ExtraTreesClassifier(n_estimators=100)
	models['gbm'] = GradientBoostingClassifier(n_estimators=100)
	print('Defined %d models' % len(models))
	return models

# evaluate a single model
def evaluate_model(trainX, trainy, testX, testy, model):
	# fit the model
	model.fit(trainX, trainy)
	# make predictions
	yhat = model.predict(testX)
	# evaluate predictions
	accuracy = accuracy_score(testy, yhat)
	return accuracy * 100.0

# evaluate a dict of models {name:object}, returns {name:score}
def evaluate_models(trainX, trainy, testX, testy, models):
	results = dict()
	for name, model in models.items():
		# evaluate the model
		results[name] = evaluate_model(trainX, trainy, testX, testy, model)
		# show process
		print('>%s: %.3f' % (name, results[name]))
	return results

# print and plot the results
def summarize_results(results, maximize=True):
	# create a list of (name, mean(scores)) tuples
	mean_scores = [(k,v) for k,v in results.items()]
	# sort tuples by mean score
	mean_scores = sorted(mean_scores, key=lambda x: x[1])
	# reverse for descending order (e.g. for accuracy)
	if maximize:
		mean_scores = list(reversed(mean_scores))
	print()
	for name, score in mean_scores:
		print('Name=%s, Score=%.3f' % (name, score))

# load dataset
trainX, trainy, testX, testy = load_dataset()
# get model list
models = define_models()
# evaluate models
results = evaluate_models(trainX, trainy, testX, testy, models)
# summarize results
summarize_results(results)

# 对特征工程数据进行抽样检查

from pandas import read_csv

from sklearn.metrics import accuracy_score

from sklearn.neighbors import KNeighborsClassifier

from sklearn.tree import DecisionTreeClassifier

from sklearn.svm import SVC

from sklearn.naive_bayes import GaussianNB

from sklearn.ensemble import BaggingClassifier

from sklearn.ensemble import RandomForestClassifier

from sklearn.ensemble import ExtraTreesClassifier

from sklearn.ensemble import GradientBoostingClassifier

# 将单个文件加载为numpy数组

def load_file(filepath):

dataframe = read_csv(filepath, header=None, delim_whitespace=True)

return dataframe.values

# 加载数据集组，例如训练集或测试集

def load_dataset_group(group, prefix=''):

# 加载输入数据

X = load_file(prefix + group + '/X_'+group+'.txt')

# 加载类别输出

y = load_file(prefix + group + '/y_'+group+'.txt')

返回 X, y

#加载数据集，返回train和test的X和y元素

def load_dataset(prefix=''):

# 加载所有训练数据

trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/')

print(trainX.shape, trainy.shape)

# 加载所有测试数据

testX, testy = load_dataset_group('test', prefix + 'HARDataset/')

print(testX.shape, testy.shape)

# 展平 y

trainy, testy = trainy[:,0], testy[:,0]

print(trainX.shape, trainy.shape, testX.shape, testy.shape)

return trainX, trainy, testX, testy

# 创建一个要评估的标准模型字典 {名称:对象}

def define_models(models=dict()):

# 非线性模型

models['knn'] = KNeighborsClassifier(n_neighbors=7)

models['cart'] = DecisionTreeClassifier()

models['svm'] = SVC()

models['bayes'] = GaussianNB()

# 集成模型

models['bag'] = BaggingClassifier(n_estimators=100)

models['rf'] = RandomForestClassifier(n_estimators=100)

models['et'] = ExtraTreesClassifier(n_estimators=100)

models['gbm'] = GradientBoostingClassifier(n_estimators=100)

print('已定义 %d 个模型' % len(models))

返回模型

# 评估单个模型

def evaluate_model(trainX, trainy, testX, testy, model):

# 拟合模型

model.fit(trainX, trainy)

# 进行预测

yhat = model.predict(testX)

# 评估预测结果

accuracy = accuracy_score(testy, yhat)

return accuracy * 100.0

# 评估模型字典 {名称:对象}，返回 {名称:分数}

def evaluate_models(trainX, trainy, testX, testy, models):

results = dict()

for name, model in models.items():

# 评估模型

results[name] = evaluate_model(trainX, trainy, testX, testy, model)

# 显示过程

print('>%s: %.3f' % (name, results[name]))

return results

# 打印和绘制结果

def summarize_results(results, maximize=True):

# 创建一个 (名称, 平均(分数)) 元组列表

mean_scores = [(k,v) for k,v in results.items()]

# 按平均分数对元组进行排序

mean_scores = sorted(mean_scores, key=lambda x: x[1])

# 反转为降序（例如，对于准确率）

if maximize:

mean_scores = list(reversed(mean_scores))

print()

for name, score in mean_scores:

print('名称=%s, 分数=%.3f' % (name, score))

# 加载数据集

trainX, trainy, testX, testy = load_dataset()

# 获取模型列表

models = define_models()

# 评估模型

results = evaluate_models(trainX, trainy, testX, testy, models)

# 总结结果

summarize_results(results)

运行该示例会首先加载训练和测试数据集，显示输入和输出组件各自的形状。

然后依次评估八个模型，并打印每个模型的性能。

最后，将显示模型在测试集上的性能排名。

注意：由于算法或评估程序的随机性，或数值精度的差异，您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。

我们可以看到，ExtraTrees 集成方法和支持向量机（SVM）非线性方法在测试集上的性能均约为 94% 的准确率。

这是一个很好的结果，超过了原始论文中 SVM 报告的 89%。

(7352, 561) (7352, 1)
(2947, 561) (2947, 1)
(7352, 561) (7352,) (2947, 561) (2947,)
Defined 8 models
>knn: 90.329
>cart: 86.020
>svm: 94.028
>bayes: 77.027
>bag: 89.820
>rf: 92.772
>et: 94.028
>gbm: 93.756

Name=et, Score=94.028
Name=svm, Score=94.028
Name=gbm, Score=93.756
Name=rf, Score=92.772
Name=knn, Score=90.329
Name=bag, Score=89.820
Name=cart, Score=86.020
Name=bayes, Score=77.027

(7352, 561) (7352, 1)

(2947, 561) (2947, 1)

(7352, 561) (7352,) (2947, 561) (2947,)

已定义 8 个模型

>knn: 90.329

>cart: 86.020

>svm: 94.028

>bayes: 77.027

>bag: 89.820

>rf: 92.772

>et: 94.028

>gbm: 93.756

名称=et, 分数=94.028

名称=svm, 分数=94.028

名称=gbm, 分数=93.756

名称=rf, 分数=92.772

名称=knn, 分数=90.329

名称=bag, 分数=89.820

名称=cart, 分数=86.020

名称=bayes, 分数=77.027

这些结果表明，通过在数据准备和特定领域特征工程中运用领域专业知识可以取得何种成果。因此，这些结果可以被视为更高级方法（例如深度学习方法）可以实现的性能上限，这些方法可能能够在模型拟合过程中自动学习特征。

任何此类高级方法都将在派生出工程特征的原始数据上进行拟合和评估。因此，在这些数据上直接评估的机器学习算法的性能可能为任何更高级方法提供的性能下限。

我们将在下一节中探讨这一点。

建模原始数据

我们可以使用相同的框架来评估原始数据上的机器学习模型。

原始数据加载确实需要更多工作。

原始数据中有三种主要的信号类型：总加速度、身体加速度和身体陀螺仪。每种信号都有三个轴的数据。这意味着每个时间步共有九个变量。

此外，每个数据系列都已划分为重叠的窗口，每个窗口持续 2.65 秒的数据，即 128 个时间步。这些数据窗口对应于上一节中工程特征（行）的窗口。

这意味着一行数据包含 128 * 9，即 1,152 个元素。这比上一节中的 561 个元素向量的尺寸大约小一半，并且可能存在一些冗余数据。

信号存储在训练和测试子目录下的 _/Inertial Signals/_ 目录中。每个信号的每个轴都存储在单独的文件中，这意味着训练和测试数据集中的每个数据集都有九个要加载的输入文件和一个要加载的输出文件。鉴于一致的目录结构和文件名约定，我们可以将这些文件的加载分批处理。

首先，我们可以将给定组的所有数据加载到一个单一的三维 NumPy 数组中，数组的维度为 [样本，时间步，特征]。为了更清楚地说明，有 128 个时间步和九个特征，其中样本数是任何给定原始信号数据文件中的行数。

下面的 load_group() 函数实现了此行为。NumPy 的 dstack() 函数允许我们将每个加载的 3D 数组堆叠成一个单一的 3D 数组，其中变量在第三个维度（特征）上分离。

# load a list of files into a 3D array of [samples, timesteps, features]
def load_group(filenames, prefix=''):
	loaded = list()
	for name in filenames:
		data = load_file(prefix + name)
		loaded.append(data)
	# stack group so that features are the 3rd dimension
	loaded = dstack(loaded)
	return loaded

#将一组文件加载到三维数组[样本数、时间步长、特征数]中

def load_group(filenames, prefix=''):

loaded = list()

for name in filenames:

data = load_file(prefix + name)

loaded.append(data)

# 堆叠组，使特征成为第三维度

loaded = dstack(loaded)

return loaded

我们可以使用此函数加载给定组的所有输入信号数据，例如train或test。

下面的 load_dataset_group() 函数使用目录之间一致的命名约定加载单个组的所有输入信号数据和输出数据。

# load a dataset group, such as train or test
def load_dataset_group(group, prefix=''):
	filepath = prefix + group + '/Inertial Signals/'
	# load all 9 files as a single array
	filenames = list()
	# total acceleration
	filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt']
	# body acceleration
	filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt']
	# body gyroscope
	filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt']
	# load input data
	X = load_group(filenames, filepath)
	# load class output
	y = load_file(prefix + group + '/y_'+group+'.txt')
	return X, y

# 加载数据集组，例如训练集或测试集

def load_dataset_group(group, prefix=''):

filepath = prefix + group + '/Inertial Signals/'

# 将所有9个文件加载为单个数组

filenames = list()

# 总加速度

filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt']

# 身体加速度

filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt']

# 身体陀螺仪

filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt']

# 加载输入数据

X = load_group(filenames, filepath)

# 加载类别输出

y = load_file(prefix + group + '/y_'+group+'.txt')

return X, y

最后，我们可以加载每个train和test数据集。

作为准备加载数据的一部分，我们必须将窗口和特征展平成一个长向量。

我们可以使用 NumPy 的 reshape 函数来实现这一点，并将三个维度 [样本，时间步，特征] 转换为两个维度 [样本，时间步 * 特征]。

下面的 load_dataset() 函数实现了此行为，并返回可用于拟合和评估已定义模型的训练和测试 X 和 y 元素。

# load the dataset, returns train and test X and y elements
def load_dataset(prefix=''):
	# load all train
	trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/')
	print(trainX.shape, trainy.shape)
	# load all test
	testX, testy = load_dataset_group('test', prefix + 'HARDataset/')
	print(testX.shape, testy.shape)
	# flatten X
	trainX = trainX.reshape((trainX.shape[0], trainX.shape[1] * trainX.shape[2]))
	testX = testX.reshape((testX.shape[0], testX.shape[1] * testX.shape[2]))
	# flatten y
	trainy, testy = trainy[:,0], testy[:,0]
	print(trainX.shape, trainy.shape, testX.shape, testy.shape)
	return trainX, trainy, testX, testy

#加载数据集，返回train和test的X和y元素

def load_dataset(prefix=''):

# 加载所有训练数据

trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/')

print(trainX.shape, trainy.shape)

# 加载所有测试数据

testX, testy = load_dataset_group('test', prefix + 'HARDataset/')

print(testX.shape, testy.shape)

# 展平 X

trainX = trainX.reshape((trainX.shape[0], trainX.shape[1] * trainX.shape[2]))

testX = testX.reshape((testX.shape[0], testX.shape[1] * testX.shape[2]))

# 展平 y

trainy, testy = trainy[:,0], testy[:,0]

print(trainX.shape, trainy.shape, testX.shape, testy.shape)

return trainX, trainy, testX, testy

综上所述，完整的示例代码如下。

# spot check on raw data
from numpy import dstack
from pandas import read_csv
from sklearn.metrics import accuracy_score
from sklearn.neighbors import KNeighborsClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier

# load a single file as a numpy array
def load_file(filepath):
	dataframe = read_csv(filepath, header=None, delim_whitespace=True)
	return dataframe.values

# load a list of files into a 3D array of [samples, timesteps, features]
def load_group(filenames, prefix=''):
	loaded = list()
	for name in filenames:
		data = load_file(prefix + name)
		loaded.append(data)
	# stack group so that features are the 3rd dimension
	loaded = dstack(loaded)
	return loaded

# load a dataset group, such as train or test
def load_dataset_group(group, prefix=''):
	filepath = prefix + group + '/Inertial Signals/'
	# load all 9 files as a single array
	filenames = list()
	# total acceleration
	filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt']
	# body acceleration
	filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt']
	# body gyroscope
	filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt']
	# load input data
	X = load_group(filenames, filepath)
	# load class output
	y = load_file(prefix + group + '/y_'+group+'.txt')
	return X, y

# load the dataset, returns train and test X and y elements
def load_dataset(prefix=''):
	# load all train
	trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/')
	print(trainX.shape, trainy.shape)
	# load all test
	testX, testy = load_dataset_group('test', prefix + 'HARDataset/')
	print(testX.shape, testy.shape)
	# flatten X
	trainX = trainX.reshape((trainX.shape[0], trainX.shape[1] * trainX.shape[2]))
	testX = testX.reshape((testX.shape[0], testX.shape[1] * testX.shape[2]))
	# flatten y
	trainy, testy = trainy[:,0], testy[:,0]
	print(trainX.shape, trainy.shape, testX.shape, testy.shape)
	return trainX, trainy, testX, testy

# create a dict of standard models to evaluate {name:object}
def define_models(models=dict()):
	# nonlinear models
	models['knn'] = KNeighborsClassifier(n_neighbors=7)
	models['cart'] = DecisionTreeClassifier()
	models['svm'] = SVC()
	models['bayes'] = GaussianNB()
	# ensemble models
	models['bag'] = BaggingClassifier(n_estimators=100)
	models['rf'] = RandomForestClassifier(n_estimators=100)
	models['et'] = ExtraTreesClassifier(n_estimators=100)
	models['gbm'] = GradientBoostingClassifier(n_estimators=100)
	print('Defined %d models' % len(models))
	return models

# evaluate a single model
def evaluate_model(trainX, trainy, testX, testy, model):
	# fit the model
	model.fit(trainX, trainy)
	# make predictions
	yhat = model.predict(testX)
	# evaluate predictions
	accuracy = accuracy_score(testy, yhat)
	return accuracy * 100.0

# evaluate a dict of models {name:object}, returns {name:score}
def evaluate_models(trainX, trainy, testX, testy, models):
	results = dict()
	for name, model in models.items():
		# evaluate the model
		results[name] = evaluate_model(trainX, trainy, testX, testy, model)
		# show process
		print('>%s: %.3f' % (name, results[name]))
	return results

# print and plot the results
def summarize_results(results, maximize=True):
	# create a list of (name, mean(scores)) tuples
	mean_scores = [(k,v) for k,v in results.items()]
	# sort tuples by mean score
	mean_scores = sorted(mean_scores, key=lambda x: x[1])
	# reverse for descending order (e.g. for accuracy)
	if maximize:
		mean_scores = list(reversed(mean_scores))
	print()
	for name, score in mean_scores:
		print('Name=%s, Score=%.3f' % (name, score))

# load dataset
trainX, trainy, testX, testy = load_dataset()
# get model list
models = define_models()
# evaluate models
results = evaluate_models(trainX, trainy, testX, testy, models)
# summarize results
summarize_results(results)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

# 对原始数据进行抽查

from numpy import dstack

from pandas import read_csv

from sklearn.metrics import accuracy_score

from sklearn.neighbors import KNeighborsClassifier

from sklearn.tree import DecisionTreeClassifier

from sklearn.svm import SVC

from sklearn.naive_bayes import GaussianNB

from sklearn.ensemble import BaggingClassifier

from sklearn.ensemble import RandomForestClassifier

from sklearn.ensemble import ExtraTreesClassifier

from sklearn.ensemble import GradientBoostingClassifier

# 将单个文件加载为numpy数组

def load_file(filepath):

dataframe = read_csv(filepath, header=None, delim_whitespace=True)

return dataframe.values

#将一组文件加载到三维数组[样本数、时间步长、特征数]中

def load_group(filenames, prefix=''):

loaded = list()

for name in filenames:

data = load_file(prefix + name)

loaded.append(data)

# 堆叠组，使特征成为第三维度

loaded = dstack(loaded)

return loaded

# 加载数据集组，例如训练集或测试集

def load_dataset_group(group, prefix=''):

filepath = prefix + group + '/Inertial Signals/'

# 将所有9个文件加载为单个数组

filenames = list()

# 总加速度

filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt']

# 身体加速度

filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt']

# 身体陀螺仪

filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt']

# 加载输入数据

X = load_group(filenames, filepath)

# 加载类别输出

y = load_file(prefix + group + '/y_'+group+'.txt')

返回 X, y

#加载数据集，返回train和test的X和y元素

def load_dataset(prefix=''):

# 加载所有训练数据

trainX, trainy = load_dataset_group('train', prefix + 'HARDataset/')

print(trainX.shape, trainy.shape)

# 加载所有测试数据

testX, testy = load_dataset_group('test', prefix + 'HARDataset/')

print(testX.shape, testy.shape)

# 展平 X

trainX = trainX.reshape((trainX.shape[0], trainX.shape[1] * trainX.shape[2]))

testX = testX.reshape((testX.shape[0], testX.shape[1] * testX.shape[2]))

# 展平 y

trainy, testy = trainy[:,0], testy[:,0]

print(trainX.shape, trainy.shape, testX.shape, testy.shape)

return trainX, trainy, testX, testy

# 创建一个要评估的标准模型字典 {名称:对象}

def define_models(models=dict()):

# 非线性模型

models['knn'] = KNeighborsClassifier(n_neighbors=7)

models['cart'] = DecisionTreeClassifier()

models['svm'] = SVC()

models['bayes'] = GaussianNB()

# 集成模型

models['bag'] = BaggingClassifier(n_estimators=100)

models['rf'] = RandomForestClassifier(n_estimators=100)

models['et'] = ExtraTreesClassifier(n_estimators=100)

models['gbm'] = GradientBoostingClassifier(n_estimators=100)

print('已定义 %d 个模型' % len(models))

返回模型

# 评估单个模型

def evaluate_model(trainX, trainy, testX, testy, model):

# 拟合模型

model.fit(trainX, trainy)

# 进行预测

yhat = model.predict(testX)

# 评估预测结果

accuracy = accuracy_score(testy, yhat)

return accuracy * 100.0

# 评估模型字典 {名称:对象}，返回 {名称:分数}

def evaluate_models(trainX, trainy, testX, testy, models):

results = dict()

for name, model in models.items():

# 评估模型

results[name] = evaluate_model(trainX, trainy, testX, testy, model)

# 显示过程

print('>%s: %.3f' % (name, results[name]))

return results

# 打印和绘制结果

def summarize_results(results, maximize=True):

# 创建一个 (名称, 平均(分数)) 元组列表

mean_scores = [(k,v) for k,v in results.items()]

# 按平均分数对元组进行排序

mean_scores = sorted(mean_scores, key=lambda x: x[1])

# 反转为降序（例如，对于准确率）

if maximize:

mean_scores = list(reversed(mean_scores))

print()

for name, score in mean_scores:

print('名称=%s, 分数=%.3f' % (name, score))

# 加载数据集

trainX, trainy, testX, testy = load_dataset()

# 获取模型列表

models = define_models()

# 评估模型

results = evaluate_models(trainX, trainy, testX, testy, models)

# 总结结果

summarize_results(results)

运行示例首先会加载数据集。

我们可以看到，原始的训练集和测试集样本数量与工程特征（分别为 7352 和 2947）相同，并且三维数据已正确加载。我们还可以看到展平后的数据以及将提供给模型的 1152 个输入向量。

接下来将依次评估八个已定义的模型。

注意：由于算法或评估程序的随机性，或数值精度的差异，您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。

最终结果表明，决策树集成模型在原始数据上的表现最佳。梯度提升和随机森林的准确率约为 87% 和 86%，比在特征工程版本数据集上的最佳模型低约七个百分点。

令人鼓舞的是，随机森林集成方法在这两个数据集上都表现良好；这表明它及类似的树集成方法可能适用于该问题，至少在这种简化的框架下。

我们还可以看到 SVM 的准确率下降到大约 72%。

决策树集成模型表现良好可能表明需要进行特征选择，以及集成方法能够选择与预测相关活动最相关的特征。

(7352, 128, 9) (7352, 1)
(2947, 128, 9) (2947, 1)
(7352, 1152) (7352,) (2947, 1152) (2947,)
Defined 8 models
>knn: 61.893
>cart: 72.141
>svm: 76.960
>bayes: 72.480
>bag: 84.527
>rf: 84.662
>et: 86.902
>gbm: 87.615

Name=gbm, Score=87.615
Name=et, Score=86.902
Name=rf, Score=84.662
Name=bag, Score=84.527
Name=svm, Score=76.960
Name=bayes, Score=72.480
Name=cart, Score=72.141
Name=knn, Score=61.893

(7352, 128, 9) (7352, 1)

(2947, 128, 9) (2947, 1)

(7352, 1152) (7352,) (2947, 1152) (2947,)

已定义 8 个模型

> knn: 61.893

> cart: 72.141

> svm: 76.960

> bayes: 72.480

> bag: 84.527

> rf: 84.662

> et: 86.902

> gbm: 87.615

名称=gbm, 分数=87.615

名称=et, 分数=86.902

名称=rf, 分数=84.662

名称=bag, 分数=84.527

名称=svm, 分数=76.960

名称=bayes, 分数=72.480

名称=cart, 分数=72.141

名称=knn, 分数=61.893

如前一节所述，这些结果为任何可能尝试从原始数据中自动学习更高阶特征（例如通过深度学习方法中的特征学习）的更复杂方法提供了准确率的下限。

总之，对于此类方法，在此数据集上的准确率范围从原始数据的 GBM 准确率约 87% 到经过高度处理的数据集的随机森林和 SVM 准确率约 94%（[87% 到 94%]）。

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

更多算法。该问题仅评估了八种机器学习算法；尝试一些线性方法，也许还有一些更非线性和集成方法。
算法调优。没有对机器学习算法进行调优；主要使用了默认配置。选择一种方法，如 SVM、ExtraTrees 或 Gradient Boosting，并对一组不同的超参数配置进行网格搜索，看看是否能进一步提升在该问题上的性能。
数据缩放。数据已经过缩放 [-1,1]，可能是按主体缩放的。探索额外的缩放，如标准化，是否能获得更好的性能，尤其是在对这种缩放敏感的方法（如 kNN）上。

如果您探索了这些扩展中的任何一个，我很想知道。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

论文

文章

总结

在本教程中，您学习了如何评估“利用智能手机识别人类活动”数据集上的各种机器学习算法。

具体来说，你学到了：

如何加载和评估用于活动识别数据集的特征工程版本中的非线性与集成机器学习算法。
如何加载和评估用于活动识别数据集的原始信号数据中的机器学习算法。
如何为能够进行特征学习的更复杂的算法（例如深度学习方法）定义预期的性能的合理下限和上限。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

如何对智能手机数据进行人类活动建模

用于人类活动识别的 1D 卷积神经网络模型

34 条回复关于评估机器学习算法以识别人类活动

David 2018年10月20日 11:17 am #

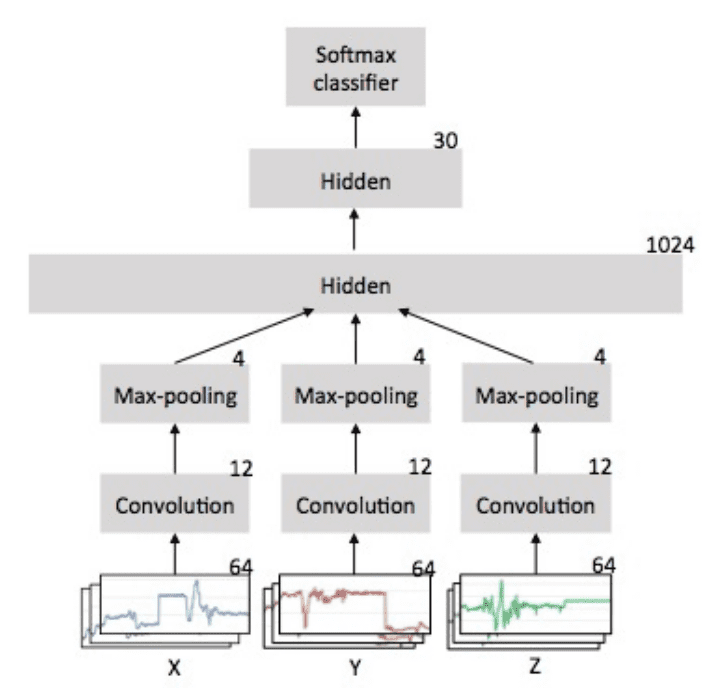
嘿，很棒的教程。对于原始模型，分数较低的原因是

“缝合”数据集以使其尽可能接近特征工程版本是否很困难？或者两者之间是否存在其他根本性差异？

谢谢！

回复
- Jason Brownlee 2018年10月21日 6:10 am #
  
  我认为特征工程会大大提高结果。
  
  回复
  - David Yao 2018年10月22日 1:27 am #
    
    我注意到原始文件的一点是，特征已经标准化了。这基本是主要区别吗？
    
    回复
    - Jason Brownlee 2018年10月22日 6:23 am #
      
      不，我认为使用了更高级的信号处理方法。
      
      回复
didi 2019年2月21日 2:56 am #

很棒的教程！

回复
- Jason Brownlee 2019年2月21日 8:14 am #
  
  谢谢。
  
  回复
jamila 2019年3月4日 6:58 am #

我们可以对半监督学习算法使用相同的想法吗？

回复
- Jason Brownlee 2019年3月4日 7:03 am #
  
  也许可以。
  
  回复
Manisha 2019年4月3日 9:28 am #

先生，您好，

你为什么在这里使用高斯朴素贝叶斯？
难道我们不用高斯 NB 来处理回归类型问题吗？
此外，为什么 NB 的准确率如此之差？有什么直观的解释吗？

回复
- Jason Brownlee 2019年4月3日 4:12 pm #
  
  高斯朴素贝叶斯可用于分类。
  
  也许该算法表现不佳是因为它做出了无益的简化假设。
  
  回复
Manisha 2019年4月29日 3:10 pm #

先生，您好，
为什么基于树的集成模型在原始数据集上的表现优于其他模型？

回复
- Jason Brownlee 2019年4月30日 6:47 am #
  
  我们不知道原因，至少不容易知道。
  
  这是 ML 算法不擅长回答的问题——为什么某些算法对给定数据集效果好而其他算法效果不好。
  
  回复
Manisha 2019年5月1日 3:01 am #

“具体结果可能因算法的随机性而每次运行时略有不同。但是，考虑到数据集的大小，算法性能之间的相对关系应该相当稳定。”

先生，为什么像 knn、svm 等 ML 模型是随机的？

这里我们说 ML 模型运行一次就会稳定，但在深度学习模型中，我们会运行模型多次。为什么会这样？是因为在深度学习模型中，我们最初分配了更多随机参数值，例如权重、批次大小等吗？

回复
- Jason Brownlee 2019年5月1日 7:09 am #
  
  并非所有算法都是随机的，例如 knn，但许多算法是随机的，例如决策树集成。
  
  回复
kit 2019年9月5日 12:43 pm #

你好，我可以用视频来训练一种运动吗？例如推、拉、拳击、开/关门？

回复
- Jason Brownlee 2019年9月5日 1:49 pm #
  
  我认为可以，您需要一个不同的模型。抱歉，我没有关于这方面的教程。
  
  回复
Bushra 2020年4月1日 11:42 pm #

你好，我想基于 Kinetics 数据集识别人类活动……
我想创建我自己的训练模型
您有什么可以帮助我的资源吗？
请帮帮我，我是一名初学者，我想学得更多。

回复
- Jason Brownlee 2020年4月2日 5:56 am #
  
  也许这里的某些教程可以适配您的数据集。
  https://machinelearning.org.cn/start-here/#deep_learning_time_series
  
  回复
Tanveer 2020年4月2日 3:50 am #

我们可以使用逻辑回归吗？

回复
- Jason Brownlee 2020年4月2日 6:03 am #
  
  当然可以。
  
  回复
Tanveer 2020年4月8日 6:52 pm #

谢谢

回复
- Jason Brownlee 2020年4月9日 7:59 am #
  
  不客气。
  
  回复
Mai khaled 2020年9月2日 8:57 am #

我们能否在此示例中计算精确率和召回率？

回复
- Jason Brownlee 2020年9月2日 1:29 pm #
  
  是的，这会有帮助
  https://machinelearning.org.cn/how-to-calculate-precision-recall-f1-and-more-for-deep-learning-models/
  
  回复
Tanveer 2020年9月12日 9:10 pm #

您是如何将时间序列数据转换为离散性质的？请解释一下。

回复
- Jason Brownlee 2020年9月13日 6:03 am #
  
  好问题，也许可以从这里开始
  https://machinelearning.org.cn/time-series-forecasting-supervised-learning/
  
  回复
  - Tanveer 2020年9月13日 7:57 pm #
    
    解释得很棒。
    UCI HAR 数据集已经经过滑动窗口方法的预处理，这意味着您可以直接应用监督学习模型吗？请纠正我。
    但是对于 LSTM，您是如何应用相同的预处理数据的？
    
    回复
    - Jason Brownlee 2020年9月14日 6:46 am #
      
      LSTM 示例使用了原始数据。
      
      回复
Tanveer 2020年9月12日 10:28 pm #

请解释一下特征（有 9 个）和特征变量（有 561 个）。您是如何在集成、监督算法和 LSTM 中使用相同的特征的？

回复
- Jason Brownlee 2020年9月13日 6:05 am #
  
  抱歉，我不明白您的问题，您的意思是什么？
  
  回复
  - Tanveer 2020年9月13日 8:43 pm #
    
    根据以上陈述（结果是一个 561 维的特征向量，
    有 128 个时间步和九个特征）
    亲爱的 Jason，这个数据集中有多少特征？我们可以说特征是 9 个吗？
    
    回复
    - Jason Brownlee 2020年9月14日 6:49 am #
      
      这将帮助您理解数据集。
      https://machinelearning.org.cn/how-to-model-human-activity-from-smartphone-data/
      
      回复
Farjam 2022年4月12日 9:34 pm #

我想了解窗口数据部分是如何进行特征工程的，例如，将数据分割成 2.56 秒的固定窗口。

非常感谢。

回复
- Farjam 2022年5月21日 6:44 pm #
  
  有人能帮帮我吗。
  
  回复

导航

评估用于人类活动识别的机器学习算法

教程概述

使用智能手机数据集进行活动识别

时间序列深度学习需要帮助吗？

建模特征工程数据

加载数据集

定义模型

评估模型

总结结果

完整示例

建模原始数据

扩展

进一步阅读

论文

文章

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

34 条回复关于评估机器学习算法以识别人类活动

留下回复点击此处取消回复。

导航

教程概述

使用智能手机数据集进行活动识别

时间序列深度学习需要帮助吗？

建模特征工程数据

加载数据集

定义模型

评估模型

总结结果

完整示例

建模原始数据

扩展

进一步阅读

论文

文章

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

34 条回复关于 评估机器学习算法以识别人类活动

留下回复 点击此处取消回复。

34 条回复关于评估机器学习算法以识别人类活动

留下回复点击此处取消回复。