最大似然估计是一种通过搜索概率分布及其参数来估计数据集密度的方法。
它是一种通用且有效的方法,是许多机器学习算法的基础,尽管它要求训练数据集是完整的,例如所有相关的相互作用的随机变量都存在。如果存在与数据集中变量相互作用但被隐藏或未观察到的变量(所谓的潜在变量),则最大似然估计将变得难以处理。
期望最大化算法是一种在存在潜在变量的情况下执行最大似然估计的方法。它通过首先估计潜在变量的值,然后优化模型,然后重复这两个步骤直到收敛来实现。它是一种有效且通用的方法,最常用于具有缺失数据的密度估计,例如高斯混合模型之类的聚类算法。
在本帖中,您将了解期望最大化算法。
阅读本文后,你将了解:
- 在存在潜在变量的情况下,最大似然估计在数据上具有挑战性。
- 期望最大化为具有潜在变量的最大似然估计提供了一种迭代解决方案。
- 高斯混合模型是一种密度估计方法,其中分布的参数使用期望最大化算法进行拟合。
开始你的项目,阅读我的新书《机器学习概率》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
- 更新于2019年11月:修复了代码注释中的拼写错误(感谢Daniel)

期望最大化(EM算法)入门指南
照片由 valcker 拍摄,部分权利保留。
概述
本教程分为四个部分;它们是
- 最大似然估计中潜在变量的问题
- 期望最大化算法
- 高斯混合模型与 EM 算法
- 高斯混合模型示例
最大似然估计中潜在变量的问题
一个常见的建模问题是如何估计数据集的联合概率分布。
密度估计涉及选择一个概率分布函数和该分布的参数,以最好地解释观测数据的联合概率分布。
有许多技术可以解决这个问题,尽管一种常见的方法称为最大似然估计,或简称为“最大似然”。
最大似然估计涉及将问题视为优化或搜索问题,我们在其中寻找一组参数,这些参数能使数据样本的联合概率获得最佳拟合。
最大似然估计的一个局限性是它假设数据集是完整的,或完全可观测的。这并不意味着模型可以访问所有数据;相反,它假设所有与问题相关的变量都存在。
情况并非总是如此。可能存在一些数据集,其中只有部分相关变量可以被观测到,而有些则不能,尽管它们会影响数据集中的其他随机变量,但它们仍然是隐藏的。
更一般地说,这些未观测到或隐藏的变量被称为 潜在变量。
许多现实世界的问题都有隐藏变量(有时称为潜在变量),这些变量在可用于学习的数据中是不可观测的。
— 第 816 页,《人工智能:一种现代方法》,第三版,2009。
在存在潜在变量的情况下,传统的最大似然估计效果不佳。
… 如果我们有缺失的数据和/或潜在变量,那么计算[最大似然]估计就会变得困难。
— 第 349 页,《机器学习:概率视角》,2012。
相反,需要一种替代的最大似然公式来在存在潜在变量的情况下搜索适当的模型参数。
期望最大化算法就是这样一种方法。
想学习机器学习概率吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
期望最大化算法
期望最大化算法,简称 EM 算法,是一种在存在潜在变量的情况下进行最大似然估计的方法。
在潜在变量模型中寻找最大似然估计量的一种通用技术是期望最大化(EM)算法。
— 第 424 页,《模式识别与机器学习》,2006。
EM 算法是一种迭代方法,在两个模式之间循环。第一个模式尝试估计缺失或潜在变量,称为估计步骤或 E 步。第二个模式尝试优化模型参数以最好地解释数据,称为最大化步骤或 M 步。
- E 步。估计数据集中缺失的变量。
- M 步。在数据存在的情况下最大化模型的参数。
EM 算法可以广泛应用,尽管在机器学习中它最著名的是用于无监督学习问题,例如密度估计和聚类。
也许 EM 算法最受讨论的应用是用于混合模型的聚类。
高斯混合模型与 EM 算法
一个 混合模型 是由多个概率分布函数的不指定组合组成的模型。
使用统计过程或学习算法来估计概率分布的参数,以最好地拟合给定训练数据的密度。
高斯混合模型(简称 GMM)是一种混合模型,它使用高斯(正态)概率分布的组合,并且需要为每个分布估计均值和标准差参数。
有许多估计 GMM 参数的技术,尽管最大似然估计可能是最常见的。
考虑一种情况,即数据集由许多点组成,这些点恰好由两个不同的过程生成。每个过程的点具有高斯概率分布,但数据混合在一起,并且分布足够相似,以至于不容易确定给定点属于哪个分布。
用于生成数据点的过程代表一个潜在变量,例如过程 0 和过程 1。它影响数据但不可观测。因此,EM 算法是用于估计分布参数的合适方法。
在 EM 算法中,估计步骤将为每个数据点估计过程潜在变量的值,而最大化步骤将优化概率分布的参数,以尝试最好地捕获数据的密度。该过程重复进行,直到获得一组良好的潜在值和适合数据的最大似然。
- E 步。估计每个潜在变量的期望值。
- M 步。使用最大似然估计优化分布的参数。
我们可以想象如何将这种优化过程约束到仅分布均值,或者推广到混合多个不同高斯分布。
高斯混合模型示例
我们可以通过一个实际示例来具体说明 EM 算法在 GMM 中的应用。
首先,让我们构建一个数据集,其中数据点是从两个高斯过程之一生成的。点是一维的,第一个分布的均值为 20,第二个分布的均值为 40,两个分布的标准差均为 5。
我们将从第一个过程抽取 3,000 个点,从第二个过程抽取 7,000 个点并将它们混合在一起。
|
1 2 3 4 5 |
... # 生成样本 X1 = normal(loc=20, scale=5, size=3000) X2 = normal(loc=40, scale=5, size=7000) X = hstack((X1, X2)) |
然后,我们可以绘制点的直方图,以直观地了解数据集。我们期望看到一个双峰分布,每个峰对应于两个分布的均值。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 由两个高斯过程构造的双峰示例 from numpy import hstack from numpy.random import normal from matplotlib import pyplot # 生成样本 X1 = normal(loc=20, scale=5, size=3000) X2 = normal(loc=40, scale=5, size=7000) X = hstack((X1, X2)) # 绘制直方图 pyplot.hist(X, bins=50, density=True) pyplot.show() |
运行该示例将创建数据集,然后为数据点创建直方图。
该图清楚地显示了预期的双峰分布,第一个过程的峰值在 20 左右,第二个过程的峰值在 40 左右。
我们可以看到,对于分布峰值中间的大部分点,它们是从哪个分布中抽取的仍然是模糊的。
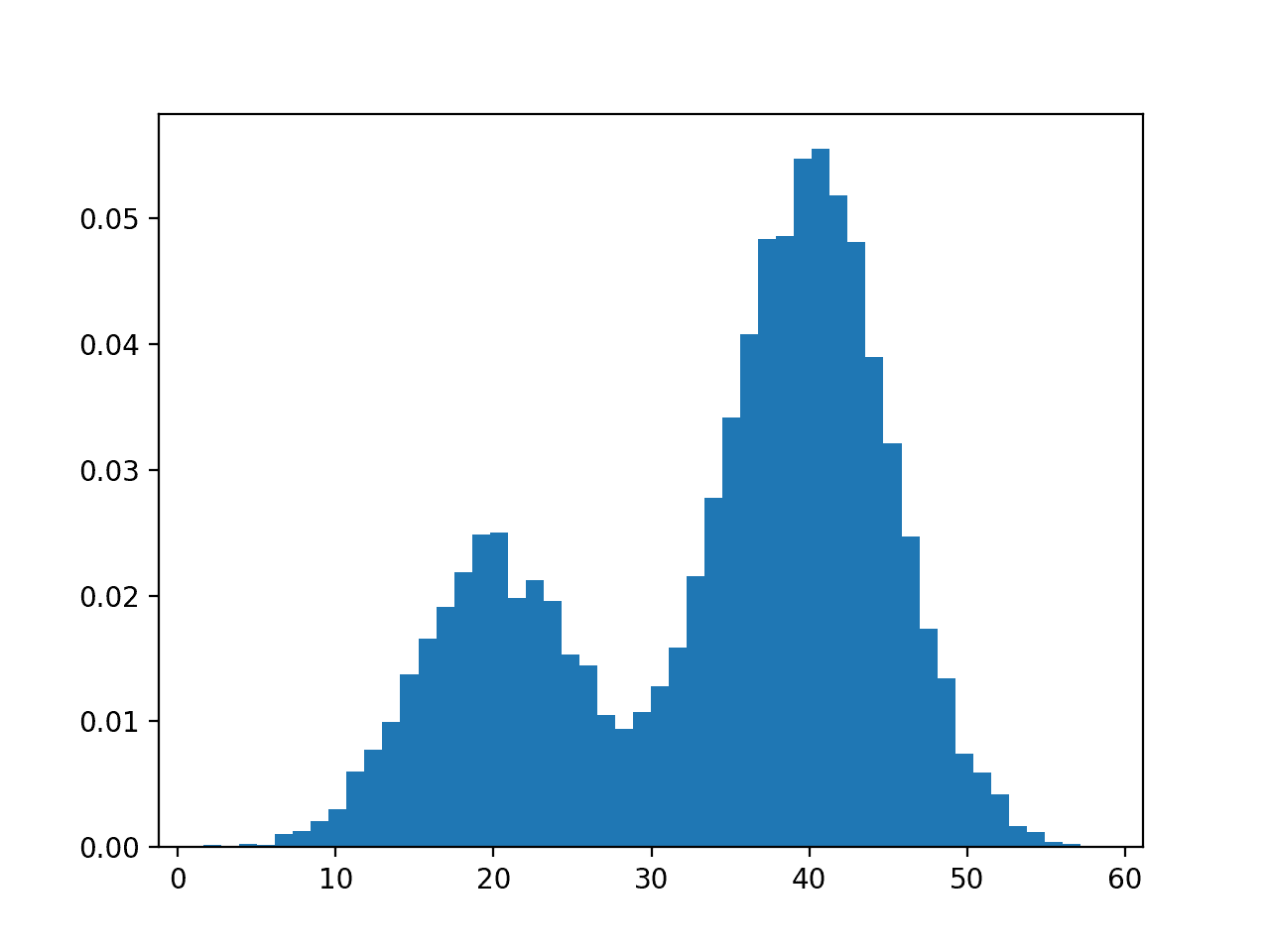
由两个不同高斯过程构建的数据集直方图
我们可以使用高斯混合模型来模拟估计此数据集密度的问题。
scikit-learn 的 GaussianMixture 类可用于模拟此问题,并使用期望最大化算法估计分布的参数。
该类允许我们通过定义模型时的 _n_components_ 参数来指定用于生成数据的潜在过程的数量。我们将此设置为 2,代表两个过程或分布。
如果过程数量未知,可以测试不同数量的组件,并选择拟合最佳的模型,其中可以使用赤池信息准则或贝叶斯信息准则(AIC 或 BIC)等分数来评估模型。
我们还可以通过多种方式配置模型以整合我们可能了解的关于数据的信息,例如如何估计分布的初始值。在这种情况下,我们将通过将 _init_params_ 参数设置为“random”来随机猜测初始参数。
|
1 2 3 4 |
... # 拟合模型 model = GaussianMixture(n_components=2, init_params='random') model.fit(X) |
模型拟合后,我们可以通过模型的参数(如均值、协方差、混合权重等)来访问学习到的参数。
更有用的是,我们可以使用拟合的模型来估计现有和新数据点的潜在参数。
例如,我们可以估计训练数据集中的数据点的潜在变量,我们期望前 3,000 个点属于一个过程(例如,_value=1_),而接下来的 7,000 个数据点属于另一个过程(例如,_value=0_)。
|
1 2 3 4 5 6 7 |
... # 预测潜在值 yhat = model.predict(X) # 检查前几个点处的潜在值 print(yhat[:100]) # 检查最后几个点处的潜在值 print(yhat[-100:]) |
将所有这些联系在一起,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 使用期望最大化拟合高斯混合模型的示例 from numpy import hstack from numpy.random import normal from sklearn.mixture import GaussianMixture # 生成样本 X1 = normal(loc=20, scale=5, size=3000) X2 = normal(loc=40, scale=5, size=7000) X = hstack((X1, X2)) # 重塑为单列的表格 X = X.reshape((len(X), 1)) # 拟合模型 model = GaussianMixture(n_components=2, init_params='random') model.fit(X) # 预测潜在值 yhat = model.predict(X) # 检查前几个点处的潜在值 print(yhat[:100]) # 检查最后几个点处的潜在值 print(yhat[-100:]) |
运行示例使用 EM 算法在准备好的数据集上拟合高斯混合模型。拟合后,使用该模型预测训练数据集中的示例的潜在变量值。
注意:鉴于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。请考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到,至少对于数据集中的前几个和最后几个示例,模型大多能预测出潜在变量的正确值。这是一个普遍具有挑战性的问题,并且期望分布峰值之间的点将保持模糊,并整体分配给一个过程或另一个过程。
|
1 2 3 4 5 6 |
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1] [0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0] |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 第 8.5 节 EM 算法,《统计学习要素》,2016。
- 第 9 章 混合模型和 EM,《模式识别与机器学习》,2006。
- 第 6.12 节 EM 算法,《机器学习》,1997。
- 第 11 章 混合模型和 EM 算法,《机器学习:概率视角》,2012。
- 第 9.3 节 聚类和概率密度估计,《数据挖掘:实用机器学习工具与技术》,第四版,2016。
- 第 20.3 节 带有隐藏变量的学习:EM 算法,《人工智能:一种现代方法》,第三版,2009。
API
文章
总结
在本帖中,您了解了期望最大化算法。
具体来说,你学到了:
- 在存在潜在变量的情况下,最大似然估计在数据上具有挑战性。
- 期望最大化为具有潜在变量的最大似然估计提供了一种迭代解决方案。
- 高斯混合模型是一种密度估计方法,其中分布的参数使用期望最大化算法进行拟合。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






“尽管它(EM)要求训练数据集是完整的”——这部分似乎与其后的内容相矛盾。
哦,它指的是最大似然,算了。
不客气。
你好 Jason,你好吗?希望你一切都好!
我很困惑,第一个输出列表应该是 0 吧?第二个应该是 1,但它们颠倒了。提前感谢!
示例显示了识别出的两个不同过程,例如两个类标签。
期望特定的标签被分配是错误的。我已经更新了它。谢谢!
亲爱的,
我想使用一个带有 EM 算法的库来进行半监督学习。然而,我在 Python 中找不到现有的库。您知道有现存的吗?有很多关于这个主题的论文(Rout et al. 2017, Hassan & Islam 2019)使用 EM 进行半监督学习,但它们的代码不是开源的。
alexander.ligthart@live.com
诚挚的问候
通常 EM 是为另一项任务实现的。
例如:高斯混合模型
https://scikit-learn.cn/stable/modules/mixture.html
你好,
我有两个问题,请
– 如何在数学上计算高斯的中心概率 mu(鉴于它是最高概率)
– 是否有自动探索方法来搜索给定随机过程的高斯数量?
谢谢你
这是 PDF 的作用。提供一个值并获得一个概率。
计算分布的均值并使用 pdf 计算概率。
据我所知,没有。
sklearn 的 BayesianGaussianMixture 类怎么样?
我们能否在时间序列预测中将此 EM 算法用于填充缺失值?
它对于填充缺失值有效吗?如果不是,请为时间序列问题建议一些填充缺失值的方法。
看这里
https://machinelearning.org.cn/handle-missing-timesteps-sequence-prediction-problems-python/
你好。一如既往,这帖子太棒了!很有帮助!谢谢!
在此示例中,您使用了一个特征进行 GMM 聚类。
在我的情况下,我使用了一个多维数据集,其中包含约 50 个特征和 1,000,000 个样本(多参数图像上下文)。
我找不到任何明确的答案来回答是否需要(或更好)缩放特征,例如在 k-means 中使用 z-score。你能帮我吗?
如果您有一些加快计算速度的技巧,那就太好了 🙂
谢谢你。
谢谢。
谢谢。
如果输入变量具有不同的单位,则缩放是一个好主意。如果它们是高斯的,则进行标准化是一个好主意。
抱歉,我暂时没有加快计算速度的建议。
我能获取这篇文章的 PDF 吗?
嗨 Sana…我们不提供帖子的 PDF,但我们有优秀的电子书供您选择:https://machinelearning.org.cn/products/
你好,
如何评估该算法是一些好的方法?我能想到的一种方法是计算算法正确预测的平均数量,将正确分配的数量相加并除以数据点的数量。您对此有何看法,还有其他评估该算法的方法吗?
谢谢
嗯。
如果您将其用于聚类,您可以探索特定于聚类的指标。
https://scikit-learn.cn/stable/modules/classes.html#clustering-metrics
你好 Jason,
如果我的理解正确,则给定示例中的潜在参数是每个峰值的高斯参数?
我猜我们可以通过将适当的函数拟合到直方图数据来实现与本练习类似的目标,对吗?
此致!
更多是定义分布的参数。
我能在金融数学中估计具有状态切换均值回归模型的参数时,获得期望最大化算法的 Python 代码吗?
也许可以先进行 Google 搜索?
引用您的文本
E 步。估计每个潜在变量的期望值。
M 步。使用最大似然估计优化分布的参数。
有人可能会误解您的帖子,只是“插入”潜在变量的期望值,然后认为它们在 M 步是固定的。
EM 的工作方式并非如此。
E 步不涉及计算每个潜在变量的期望值,它涉及通过对潜在变量根据其条件分布(给定观测变量和当前估计值)进行边际化来“计算”边际对数似然。
此外,潜在变量的通常“估计量”是最大后验值,而不是它们的期望值。如果潜在变量的后验分布是对称的(就像您的示例一样),它们是相同的,但通常不是。
谢谢您的留言。
嗨,Jason,
我有一个关于您在高斯混合模型示例中的问题。例如,如果我有三种高斯分布组合。我们训练的数据模型是否仍然用值 0 和 1 估计潜在变量,还是有 3 种可能性,例如:0、1 或 2?非常感谢您的回复。
是的,我认为您可以适应您的示例。
我不理解 EM 算法。以两个高斯为例。您有一系列点——您是随机选择一对高斯,比较它们的性能,然后选择最好的一个吗?然后您随机调整参数吗?这不可能是正在发生的事情,但您没有确切解释这个过程是如何进行的。
不完全是,是个好问题——我需要写一个更完整的算法教程。
作为开始,我建议阅读“进一步阅读”部分中的一些参考文献。