如何为时间序列预测配置多层感知器网络

作者 Jason Brownlee 于 2020年8月28日发布在时间序列深度学习 53

在开始使用神经网络进行新的预测建模项目时，可能会遇到困难。

需要配置的内容太多，而且不知道从哪里入手。

系统化非常重要。您可以打破错误的假设，快速找到有效的配置以及可能带来回报的进一步研究领域。

在本教程中，您将了解如何使用多层感知器（MLP）神经网络的探索性配置来为时间序列预测找到良好的初步模型。

完成本教程后，您将了解：

如何设计一个强大的实验测试框架来评估用于时间序列预测的 MLP 模型。
用于更改时期、神经元和滞后配置的系统化实验设计。
如何解释结果并使用诊断信息来了解表现良好的模型。

通过我的新书《时间序列预测深度学习》启动您的项目，其中包含分步教程和所有示例的Python源代码文件。

让我们开始吧。

更新于 2017 年 7 月：已更改创建模型的函数以使其更具描述性。
2019 年 4 月更新：更新了数据集链接。

Exploratory Configuration of a Multilayer Perceptron Network for Time Series Forecasting

时间序列预测的多层感知器网络的探索性配置
摄影：Lachlan Donald，部分权利保留。

教程概述

本教程分为6个部分。它们是：

洗发水销售数据集
实验测试框架
改变训练时期
改变隐藏层神经元数量
改变隐藏层神经元数量及滞后
结果回顾

环境

本教程假定您已安装 Python SciPy 环境。您可以使用 Python 2 或 3。

本教程假定您已安装 Keras v2.0 或更高版本，并使用 TensorFlow 或 Theano 后端。

本教程还假定您已安装 scikit-learn、Pandas、NumPy 和 Matplotlib。

接下来，让我们看看一个标准的时间序列预测问题，我们可以将其作为本次实验的背景。

如果您需要帮助设置 Python 环境，请参阅此帖子

如何使用 Anaconda 设置用于机器学习和深度学习的 Python 环境

洗发水销售数据集

此数据集描述了 3 年期间洗发水月销量。

单位是销售计数，共有 36 个观测值。原始数据集归功于 Makridakis、Wheelwright 和 Hyndman (1998)。

下载数据集.

以下示例加载并创建加载数据集的图表。

# load and plot dataset
from pandas import read_csv
from pandas import datetime
from matplotlib import pyplot
# load dataset
def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# summarize first few rows
print(series.head())
# line plot
series.plot()
pyplot.show()

# 加载并绘制数据集

from pandas import read_csv

from pandas import datetime

from matplotlib import pyplot

# 加载数据集

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 总结前几行

print(series.head())

# 线图

series.plot()

pyplot.show()

运行该示例将数据集作为 Pandas Series 加载并打印前 5 行。

Month
1901-01-01 266.0
1901-02-01 145.9
1901-03-01 183.1
1901-04-01 119.3
1901-05-01 180.3
Name: Sales, dtype: float64

月份

1901-01-01 266.0

1901-02-01 145.9

1901-03-01 183.1

1901-04-01 119.3

1901-05-01 180.3

名称：销售额，数据类型：float64

然后创建该系列的线图，显示出明显的上升趋势。

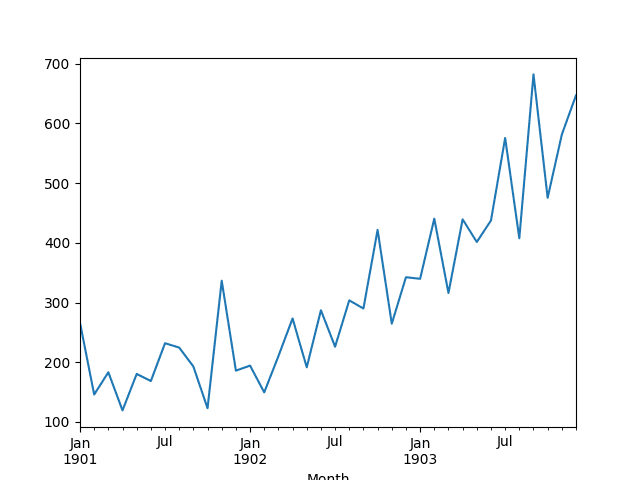
洗发水销售数据集的折线图

接下来，我们将看一下实验中使用的模型配置和测试工具。

实验测试框架

本节将介绍本教程中使用的测试框架。

数据分割

我们将把洗发水销售数据集分为两部分：训练集和测试集。

前两年的数据将用于训练数据集，剩下的一年数据将用于测试集。

模型将使用训练数据集进行开发，并对测试数据集进行预测。

在测试数据集上的持久性预测（朴素预测）实现了136.761个月洗发水销量的误差。这为测试集上的性能提供了一个可接受的较低界限。

模型评估

将使用滚动预测方案，也称为向前验证模型。

测试数据集的每个时间步都将逐一进行。模型将用于预测时间步，然后将从测试集中获取实际期望值，并将其提供给模型用于预测下一个时间步。

这模拟了现实世界场景，其中每个月都会有新的洗发水销售观察值，并用于预测下个月。

这将通过训练和测试数据集的结构进行模拟。

将收集测试数据集上的所有预测，并计算误差分数以总结模型的技能。将使用均方根误差（RMSE），因为它会惩罚较大的误差，并产生与预测数据相同的单位得分，即每月洗发水销量。

数据准备

在我们将 MLP 模型拟合到数据集之前，我们必须转换数据。

在拟合模型和进行预测之前，对数据集执行以下三种数据转换。

转换时间序列数据使其平稳。具体来说，进行 lag=1 的差分以消除数据中不断增长的趋势。
将时间序列转换为监督学习问题。具体来说，将数据组织成输入和输出模式，其中前一个时间步的观测值用于预测当前时间步的观测值。
将观测值缩放到特定范围。具体来说，将数据重新缩放到-1 和 1 之间的值。

在计算误差分数之前，这些转换将被应用于预测中，以将它们恢复到其原始尺度。

MLP 模型

我们将使用一个基础 MLP 模型，它具有 1 个隐藏层、隐藏层神经元的 ReLU 激活函数以及输出层神经元的线性激活函数。

批次大小设置为 4，并尽可能截断训练数据以确保模式数量可被 4 整除。在某些情况下，批次大小为 2。

通常，训练数据集在每个批次或每个时期后都会被打乱，这有助于在分类和回归问题上拟合训练数据集。所有实验都关闭了打乱，因为这似乎能带来更好的性能。还需要更多的研究来确认时间序列预测的这一结果。

模型将使用高效的ADAM优化算法和均方误差损失函数进行拟合。

实验运行

每个实验场景将运行 30 次，并从每次运行的末尾记录测试集上的 RMSE 分数。

让我们开始实验。

时间序列深度学习需要帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

改变训练时期

在第一个实验中，我们将研究一个具有一个隐藏层和一个隐藏层神经元的简单 MLP 的训练时期数量的变化。

我们将使用批次大小为 4，并评估 50、100、500、1000 和 2000 个训练时期。

完整的代码列表如下。

此代码列表将作为所有后续实验的基础，仅在后续部分提供对此代码的更改。

from pandas import DataFrame
from pandas import Series
from pandas import concat
from pandas import read_csv
from pandas import datetime
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense
from math import sqrt
import matplotlib
# be able to save images on server
matplotlib.use('Agg')
from matplotlib import pyplot
import numpy

# date-time parsing function for loading the dataset
def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')

# frame a sequence as a supervised learning problem
def timeseries_to_supervised(data, lag=1):
	df = DataFrame(data)
	columns = [df.shift(i) for i in range(1, lag+1)]
	columns.append(df)
	df = concat(columns, axis=1)
	return df

# create a differenced series
def difference(dataset, interval=1):
	diff = list()
	for i in range(interval, len(dataset)):
		value = dataset[i] - dataset[i - interval]
		diff.append(value)
	return Series(diff)

# invert differenced value
def inverse_difference(history, yhat, interval=1):
	return yhat + history[-interval]

# scale train and test data to [-1, 1]
def scale(train, test):
	# fit scaler
	scaler = MinMaxScaler(feature_range=(-1, 1))
	scaler = scaler.fit(train)
	# transform train
	train = train.reshape(train.shape[0], train.shape[1])
	train_scaled = scaler.transform(train)
	# transform test
	test = test.reshape(test.shape[0], test.shape[1])
	test_scaled = scaler.transform(test)
	return scaler, train_scaled, test_scaled

# inverse scaling for a forecasted value
def invert_scale(scaler, X, yhat):
	new_row = [x for x in X] + [yhat]
	array = numpy.array(new_row)
	array = array.reshape(1, len(array))
	inverted = scaler.inverse_transform(array)
	return inverted[0, -1]

# fit an MLP network to training data
def fit_model(train, batch_size, nb_epoch, neurons):
	X, y = train[:, 0:-1], train[:, -1]
	model = Sequential()
	model.add(Dense(neurons, activation='relu', input_dim=X.shape[1]))
	model.add(Dense(1))
	model.compile(loss='mean_squared_error', optimizer='adam')
	model.fit(X, y, epochs=nb_epoch, batch_size=batch_size, verbose=0, shuffle=False)
	return model

# run a repeated experiment
def experiment(repeats, series, epochs, lag, neurons):
	# transform data to be stationary
	raw_values = series.values
	diff_values = difference(raw_values, 1)
	# transform data to be supervised learning
	supervised = timeseries_to_supervised(diff_values, lag)
	supervised_values = supervised.values[lag:,:]
	# split data into train and test-sets
	train, test = supervised_values[0:-12], supervised_values[-12:]
	# transform the scale of the data
	scaler, train_scaled, test_scaled = scale(train, test)
	# run experiment
	error_scores = list()
	for r in range(repeats):
		# fit the model
		batch_size = 4
		train_trimmed = train_scaled[2:, :]
		model = fit_model(train_trimmed, batch_size, epochs, neurons)
		# forecast test dataset
		test_reshaped = test_scaled[:,0:-1]
		output = model.predict(test_reshaped, batch_size=batch_size)
		predictions = list()
		for i in range(len(output)):
			yhat = output[i,0]
			X = test_scaled[i, 0:-1]
			# invert scaling
			yhat = invert_scale(scaler, X, yhat)
			# invert differencing
			yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)
			# store forecast
			predictions.append(yhat)
		# report performance
		rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))
		print('%d) Test RMSE: %.3f' % (r+1, rmse))
		error_scores.append(rmse)
	return error_scores

# load dataset
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# experiment
repeats = 30
results = DataFrame()
lag = 1
neurons = 1
# vary training epochs
epochs = [50, 100, 500, 1000, 2000]
for e in epochs:
	results[str(e)] = experiment(repeats, series, e, lag, neurons)
# summarize results
print(results.describe())
# save boxplot
results.boxplot()
pyplot.savefig('boxplot_epochs.png')

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

from pandas import DataFrame

from pandas import Series

从 pandas 导入 concat

from pandas import read_csv

from pandas import datetime

from sklearn.metrics import mean_squared_error

从 sklearn.预处理导入 MinMaxScaler

from keras.models import Sequential

from keras.layers import Dense

from math import sqrt

import matplotlib

# 能够在服务器上保存图像

matplotlib.use('Agg')

from matplotlib import pyplot

import numpy

# 用于加载数据集的日期时间解析函数

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

# 将序列构造成监督学习问题

def timeseries_to_supervised(data, lag=1):

df = DataFrame(data)

columns = [df.shift(i) for i in range(1, lag+1)]

columns.append(df)

df = concat(columns, axis=1)

return df

# 创建差分序列

def difference(dataset, interval=1):

diff = list()

for i in range(interval, len(dataset)):

value = dataset[i] - dataset[i - interval]

diff.append(value)

return Series(diff)

# 反转差分值

def inverse_difference(history, yhat, interval=1):

return yhat + history[-interval]

# 将训练和测试数据缩放到 [-1, 1]

def scale(train, test):

# 拟合缩放器

scaler = MinMaxScaler(feature_range=(-1, 1))

scaler = scaler.fit(train)

# 转换训练集

train = train.reshape(train.shape[0], train.shape[1])

train_scaled = scaler.transform(train)

# 转换测试集

test = test.reshape(test.shape[0], test.shape[1])

test_scaled = scaler.transform(test)

return scaler, train_scaled, test_scaled

# 预测值的逆缩放

def invert_scale(scaler, X, yhat):

new_row = [x for x in X] + [yhat]

array = numpy.array(new_row)

array = array.reshape(1, len(array))

inverted = scaler.inverse_transform(array)

return inverted[0, -1]

# fit an MLP network to training data

def fit_model(train, batch_size, nb_epoch, neurons):

X, y = train[:, 0:-1], train[:, -1]

model = Sequential()

model.add(Dense(neurons, activation='relu', input_dim=X.shape[1]))

model.add(Dense(1))

model.compile(loss='mean_squared_error', optimizer='adam')

model.fit(X, y, epochs=nb_epoch, batch_size=batch_size, verbose=0, shuffle=False)

return model

# 运行重复实验

def experiment(repeats, series, epochs, lag, neurons):

# 将数据转换为平稳

raw_values = series.values

diff_values = difference(raw_values, 1)

# 将数据转换为监督学习

supervised = timeseries_to_supervised(diff_values, lag)

supervised_values = supervised.values[lag:,:]

# 将数据分割成训练集和测试集

train, test = supervised_values[0:-12], supervised_values[-12:]

# 转换数据尺度

scaler, train_scaled, test_scaled = scale(train, test)

# 运行实验

error_scores = list()

for r in range(repeats):

# 拟合模型

batch_size = 4

train_trimmed = train_scaled[2:, :]

model = fit_model(train_trimmed, batch_size, epochs, neurons)

# 预测测试数据集

test_reshaped = test_scaled[:,0:-1]

output = model.predict(test_reshaped, batch_size=batch_size)

predictions = list()

for i in range(len(output)):

yhat = output[i,0]

X = test_scaled[i, 0:-1]

# 反转缩放

yhat = invert_scale(scaler, X, yhat)

# 反转差分

yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)

# 存储预测

predictions.append(yhat)

# 报告性能

rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))

print('%d) Test RMSE: %.3f' % (r+1, rmse))

error_scores.append(rmse)

return error_scores

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# experiment

repeats = 30

results = DataFrame()

lag = 1

neurons = 1

# vary training epochs

epochs = [50, 100, 500, 1000, 2000]

for e in epochs:

results[str(e)] = experiment(repeats, series, e, lag, neurons)

# 总结结果

print(results.describe())

# save boxplot

results.boxplot()

pyplot.savefig('boxplot_epochs.png')

运行实验会在每次实验运行结束时打印测试集 RMSE。

所有运行结束后，将提供一个摘要统计表，每行一个统计项，每列一个配置。

注意：由于算法或评估程序的随机性，或者数值精度的差异，您的结果可能有所不同。可以考虑运行几次示例并比较平均结果。

摘要统计数据表明，平均而言，1000 个训练时期能带来更好的性能，并且随着训练时期增加，误差总体呈下降趋势。

               50         100         500        1000        2000
count   30.000000   30.000000   30.000000   30.000000   30.000000
mean   129.660167  129.388944  111.444027  103.821703  107.500301
std     30.926344   28.499592   23.181317   22.138705   24.780781
min     94.598957   94.184903   89.506815   86.511801   86.452041
25%    105.198414  105.722736   90.679930   90.058655   86.457260
50%    129.705407  127.449491   93.508245   90.118331   90.074494
75%    141.420145  149.625816  136.157299  135.510850  135.741340
max    198.716220  198.704352  141.226816  139.994388  142.097747

50 100 500 1000 2000

count 30.000000 30.000000 30.000000 30.000000 30.000000

mean 129.660167 129.388944 111.444027 103.821703 107.500301

std 30.926344 28.499592 23.181317 22.138705 24.780781

min 94.598957 94.184903 89.506815 86.511801 86.452041

25% 105.198414 105.722736 90.679930 90.058655 86.457260

50% 129.705407 127.449491 93.508245 90.118331 90.074494

75% 141.420145 149.625816 136.157299 135.510850 135.741340

max 198.716220 198.704352 141.226816 139.994388 142.097747

还创建了每个配置的测试 RMSE 分布的箱线图，并已保存到文件。

该图显示每个配置都显示了相同的测试 RMSE 分数分布（框），中位数（绿线）随着训练时期数的增加而呈下降趋势。

结果证实，为 1000 个时期配置的 MLP 是此问题的一个良好起点。

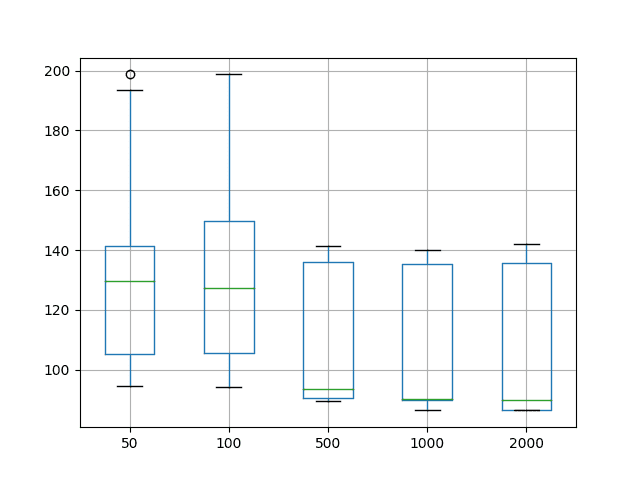
Box and Whisker Plot of Vary Training Epochs for Time Series Forecasting on the Shampoo Sales Dataset

洗发水销量数据集上的时间序列预测训练时期变化箱线图

网络配置的另一个角度是，在模型拟合过程中，它如何随着时间的推移而表现。

我们可以在每个训练时期后在训练和测试数据集上评估模型，以了解该配置是否对问题过拟合或欠拟合。

我们将对每个实验集中的最佳结果采用这种诊断方法。将运行配置的 10 次重复，并将每个训练时期后的训练和测试 RMSE 分数绘制在线图上。

在这种情况下，我们将对拟合 1000 个时期的 MLP 使用此诊断。

完整的诊断代码列表如下。

与之前的代码列表一样，下面的代码列表将作为本教程中所有诊断的基础，并且仅在后续部分提供对此列表的更改。

from pandas import DataFrame
from pandas import Series
from pandas import concat
from pandas import read_csv
from pandas import datetime
from sklearn.metrics import mean_squared_error
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense
from math import sqrt
import matplotlib
# be able to save images on server
matplotlib.use('Agg')
from matplotlib import pyplot
import numpy

# date-time parsing function for loading the dataset
def parser(x):
	return datetime.strptime('190'+x, '%Y-%m')

# frame a sequence as a supervised learning problem
def timeseries_to_supervised(data, lag=1):
	df = DataFrame(data)
	columns = [df.shift(i) for i in range(1, lag+1)]
	columns.append(df)
	df = concat(columns, axis=1)
	df = df.drop(0)
	return df

# create a differenced series
def difference(dataset, interval=1):
	diff = list()
	for i in range(interval, len(dataset)):
		value = dataset[i] - dataset[i - interval]
		diff.append(value)
	return Series(diff)

# scale train and test data to [-1, 1]
def scale(train, test):
	# fit scaler
	scaler = MinMaxScaler(feature_range=(-1, 1))
	scaler = scaler.fit(train)
	# transform train
	train = train.reshape(train.shape[0], train.shape[1])
	train_scaled = scaler.transform(train)
	# transform test
	test = test.reshape(test.shape[0], test.shape[1])
	test_scaled = scaler.transform(test)
	return scaler, train_scaled, test_scaled

# inverse scaling for a forecasted value
def invert_scale(scaler, X, yhat):
	new_row = [x for x in X] + [yhat]
	array = numpy.array(new_row)
	array = array.reshape(1, len(array))
	inverted = scaler.inverse_transform(array)
	return inverted[0, -1]

# evaluate the model on a dataset, returns RMSE in transformed units
def evaluate(model, raw_data, scaled_dataset, scaler, offset, batch_size):
	# separate
	X, y = scaled_dataset[:,0:-1], scaled_dataset[:,-1]
	# forecast dataset
	output = model.predict(X, batch_size=batch_size)
	# invert data transforms on forecast
	predictions = list()
	for i in range(len(output)):
		yhat = output[i,0]
		# invert scaling
		yhat = invert_scale(scaler, X[i], yhat)
		# invert differencing
		yhat = yhat + raw_data[i]
		# store forecast
		predictions.append(yhat)
	# report performance
	rmse = sqrt(mean_squared_error(raw_data[1:], predictions))
	return rmse

# fit an MLP network to training data
def fit(train, test, raw, scaler, batch_size, nb_epoch, neurons):
	X, y = train[:, 0:-1], train[:, -1]
	# prepare model
	model = Sequential()
	model.add(Dense(neurons, activation='relu', input_dim=X.shape[1]))
	model.add(Dense(1))
	model.compile(loss='mean_squared_error', optimizer='adam')
	# fit model
	train_rmse, test_rmse = list(), list()
	for i in range(nb_epoch):
		model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)
		# evaluate model on train data
		raw_train = raw[-(len(train)+len(test)+1):-len(test)]
		train_rmse.append(evaluate(model, raw_train, train, scaler, 0, batch_size))
		# evaluate model on test data
		raw_test = raw[-(len(test)+1):]
		test_rmse.append(evaluate(model, raw_test, test, scaler, 0, batch_size))
	history = DataFrame()
	history['train'], history['test'] = train_rmse, test_rmse
	return history

# run diagnostic experiments
def run():
	# config
	repeats = 10
	n_batch = 4
	n_epochs = 1000
	n_neurons = 1
	n_lag = 1
	# load dataset
	series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
	# transform data to be stationary
	raw_values = series.values
	diff_values = difference(raw_values, 1)
	# transform data to be supervised learning
	supervised = timeseries_to_supervised(diff_values, n_lag)
	supervised_values = supervised.values[n_lag:,:]
	# split data into train and test-sets
	train, test = supervised_values[0:-12], supervised_values[-12:]
	# transform the scale of the data
	scaler, train_scaled, test_scaled = scale(train, test)
	# fit and evaluate model
	train_trimmed = train_scaled[2:, :]
	# run diagnostic tests
	for i in range(repeats):
		history = fit(train_trimmed, test_scaled, raw_values, scaler, n_batch, n_epochs, n_neurons)
		pyplot.plot(history['train'], color='blue')
		pyplot.plot(history['test'], color='orange')
		print('%d) TrainRMSE=%f, TestRMSE=%f' % (i, history['train'].iloc[-1], history['test'].iloc[-1]))
	pyplot.savefig('diagnostic_epochs.png')

# entry point
run()

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

from pandas import DataFrame

from pandas import Series

从 pandas 导入 concat

from pandas import read_csv

from pandas import datetime

from sklearn.metrics import mean_squared_error

从 sklearn.预处理导入 MinMaxScaler

from keras.models import Sequential

from keras.layers import Dense

from math import sqrt

import matplotlib

# 能够在服务器上保存图像

matplotlib.use('Agg')

from matplotlib import pyplot

import numpy

# 用于加载数据集的日期时间解析函数

def parser(x):

return datetime.strptime('190'+x, '%Y-%m')

# 将序列构造成监督学习问题

def timeseries_to_supervised(data, lag=1):

df = DataFrame(data)

columns = [df.shift(i) for i in range(1, lag+1)]

columns.append(df)

df = concat(columns, axis=1)

df = df.drop(0)

return df

# 创建差分序列

def difference(dataset, interval=1):

diff = list()

for i in range(interval, len(dataset)):

value = dataset[i] - dataset[i - interval]

diff.append(value)

return Series(diff)

# 将训练和测试数据缩放到 [-1, 1]

def scale(train, test):

# 拟合缩放器

scaler = MinMaxScaler(feature_range=(-1, 1))

scaler = scaler.fit(train)

# 转换训练集

train = train.reshape(train.shape[0], train.shape[1])

train_scaled = scaler.transform(train)

# 转换测试集

test = test.reshape(test.shape[0], test.shape[1])

test_scaled = scaler.transform(test)

return scaler, train_scaled, test_scaled

# 预测值的逆缩放

def invert_scale(scaler, X, yhat):

new_row = [x for x in X] + [yhat]

array = numpy.array(new_row)

array = array.reshape(1, len(array))

inverted = scaler.inverse_transform(array)

return inverted[0, -1]

# 在数据集上评估模型，返回转换单位的 RMSE

def evaluate(model, raw_data, scaled_dataset, scaler, offset, batch_size):

# 分离

X, y = scaled_dataset[:,0:-1], scaled_dataset[:,-1]

# 预测数据集

output = model.predict(X, batch_size=batch_size)

# 反转预测数据转换

predictions = list()

for i in range(len(output)):

yhat = output[i,0]

# 反转缩放

yhat = invert_scale(scaler, X[i], yhat)

# 反转差分

yhat = yhat + raw_data[i]

# 存储预测

predictions.append(yhat)

# 报告性能

rmse = sqrt(mean_squared_error(raw_data[1:], predictions))

return rmse

# fit an MLP network to training data

def fit(train, test, raw, scaler, batch_size, nb_epoch, neurons):

X, y = train[:, 0:-1], train[:, -1]

# 准备模型

model = Sequential()

model.add(Dense(neurons, activation='relu', input_dim=X.shape[1]))

model.add(Dense(1))

model.compile(loss='mean_squared_error', optimizer='adam')

# 拟合模型

train_rmse, test_rmse = list(), list()

for i in range(nb_epoch):

model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)

# 在训练数据上评估模型

raw_train = raw[-(len(train)+len(test)+1):-len(test)]

train_rmse.append(evaluate(model, raw_train, train, scaler, 0, batch_size))

# 在测试数据上评估模型

raw_test = raw[-(len(test)+1):]

test_rmse.append(evaluate(model, raw_test, test, scaler, 0, batch_size))

history = DataFrame()

history['train'], history['test'] = train_rmse, test_rmse

return history

# 运行诊断实验

def run():

# 配置

repeats = 10

n_batch = 4

n_epochs = 1000

n_neurons = 1

n_lag = 1

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 将数据转换为平稳

raw_values = series.values

diff_values = difference(raw_values, 1)

# 将数据转换为监督学习

supervised = timeseries_to_supervised(diff_values, n_lag)

supervised_values = supervised.values[n_lag:,:]

# 将数据分割成训练集和测试集

train, test = supervised_values[0:-12], supervised_values[-12:]

# 转换数据尺度

scaler, train_scaled, test_scaled = scale(train, test)

# 拟合和评估模型

train_trimmed = train_scaled[2:, :]

# 运行诊断测试

for i in range(repeats):

history = fit(train_trimmed, test_scaled, raw_values, scaler, n_batch, n_epochs, n_neurons)

pyplot.plot(history['train'], color='blue')

pyplot.plot(history['test'], color='orange')

print('%d) TrainRMSE=%f, TestRMSE=%f' % (i, history['train'].iloc[-1], history['test'].iloc[-1]))

pyplot.savefig('diagnostic_epochs.png')

# 入口点

run()

运行诊断程序会打印每次运行的最终训练和测试 RMSE。更有趣的是创建的最终折线图。

折线图显示了每个训练时期后的训练 RMSE（蓝色）和测试 RMSE（橙色）。

在这种情况下，诊断图显示在约 400 个训练时期后，训练和测试 RMSE 之间几乎没有差异。训练和测试性能都趋于平缓，近乎水平线。

这种快速趋于平缓表明模型已达到其容量上限，可能需要更多的滞后观测信息或更多的神经元。

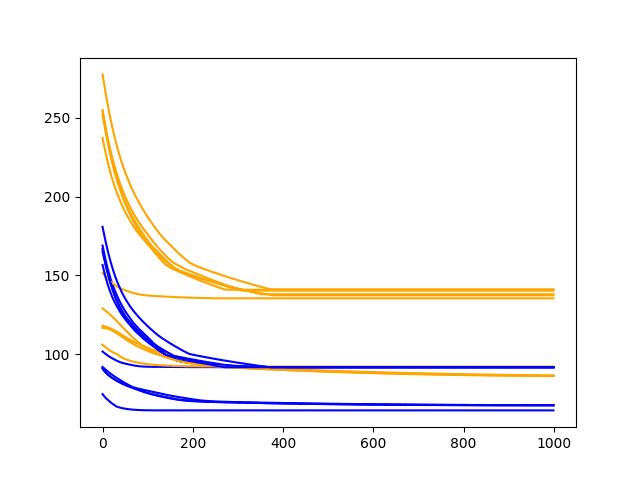
Diagnostic Line Plot of Train and Test Performance of 400 Epochs on the Shampoo Sales Dataset

洗发水销量数据集上 1000 个时期的训练和测试性能诊断折线图

改变隐藏层神经元数量

在本节中，我们将研究增加单个隐藏层中的神经元数量。

增加神经元数量可以提高网络的学习能力，但有使训练数据过拟合的风险。

我们将探索将神经元数量从 1 增加到 5，并训练网络 1000 个时期。

实验脚本中的差异如下所示。

# load dataset
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# experiment
repeats = 30
results = DataFrame()
lag = 1
epochs = 1000
# vary neurons
neurons = [1, 2, 3, 4, 5]
for n in neurons:
	results[str(n)] = experiment(repeats, series, epochs, lag, n)
# summarize results
print(results.describe())
# save boxplot
results.boxplot()
pyplot.savefig('boxplot_neurons.png')

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# experiment

repeats = 30

results = DataFrame()

lag = 1

epochs = 1000

# vary neurons

neurons = [1, 2, 3, 4, 5]

for n in neurons:

results[str(n)] = experiment(repeats, series, epochs, lag, n)

# 总结结果

print(results.describe())

# save boxplot

results.boxplot()

pyplot.savefig('boxplot_neurons.png')

运行实验会为每个配置打印摘要统计数据。

注意：由于算法或评估程序的随机性，或者数值精度的差异，您的结果可能有所不同。可以考虑运行几次示例并比较平均结果。

从平均性能来看，这表明随着隐藏层中神经元数量的增加，测试 RMSE 呈下降趋势。

最佳结果似乎是使用 3 个神经元。

                1           2           3           4           5
count   30.000000   30.000000   30.000000   30.000000   30.000000
mean   105.107026  102.836520   92.675912   94.889952   96.577617
std     23.130824   20.102353   10.266732    9.751318    6.421356
min     86.565630   84.199871   83.388967   84.385293   87.208454
25%     88.035396   89.386670   87.643954   89.154866   89.961809
50%     90.084895   91.488484   90.670565   91.204303   96.717739
75%    136.145248  104.416518   93.117926  100.228730  101.969331
max    143.428154  140.923087  136.883946  135.891663  106.797563

1 2 3 4 5

count 30.000000 30.000000 30.000000 30.000000 30.000000

mean 105.107026 102.836520 92.675912 94.889952 96.577617

std 23.130824 20.102353 10.266732 9.751318 6.421356

min 86.565630 84.199871 83.388967 84.385293 87.208454

25% 88.035396 89.386670 87.643954 89.154866 89.961809

50% 90.084895 91.488484 90.670565 91.204303 96.717739

75% 136.145248 104.416518 93.117926 100.228730 101.969331

max 143.428154 140.923087 136.883946 135.891663 106.797563

还创建了箱线图来总结和比较结果的分布。

该图证实了与其它配置相比，3 个神经元表现良好的说法，并且还表明结果的分布范围也更小。这可能表明配置更稳定。

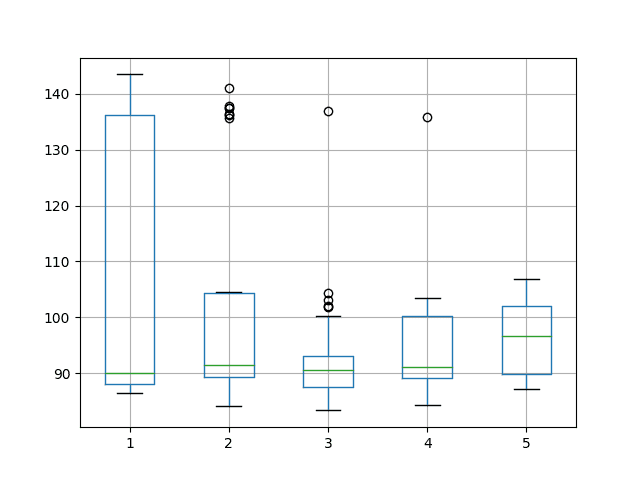
Box and Whisker Plot of Varying Hidden Neurons for Time Series Forecasting on the Shampoo Sales Dataset

洗发水销量数据集上的时间序列预测隐藏神经元变化箱线图

同样，我们可以通过检查 1000 个时期下 3 个神经元配置的诊断信息来深入了解。

诊断脚本的更改仅限于run() 函数，如下所示。

# run diagnostic experiments
def run():
	# config
	repeats = 10
	n_batch = 4
	n_epochs = 1000
	n_neurons = 3
	n_lag = 1
	# load dataset
	series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
	# transform data to be stationary
	raw_values = series.values
	diff_values = difference(raw_values, 1)
	# transform data to be supervised learning
	supervised = timeseries_to_supervised(diff_values, n_lag)
	supervised_values = supervised.values[n_lag:,:]
	# split data into train and test-sets
	train, test = supervised_values[0:-12], supervised_values[-12:]
	# transform the scale of the data
	scaler, train_scaled, test_scaled = scale(train, test)
	# fit and evaluate model
	train_trimmed = train_scaled[2:, :]
	# run diagnostic tests
	for i in range(repeats):
		history = fit(train_trimmed, test_scaled, raw_values, scaler, n_batch, n_epochs, n_neurons)
		pyplot.plot(history['train'], color='blue')
		pyplot.plot(history['test'], color='orange')
		print('%d) TrainRMSE=%f, TestRMSE=%f' % (i, history['train'].iloc[-1], history['test'].iloc[-1]))
	pyplot.savefig('diagnostic_neurons.png')

# 运行诊断实验

def run():

# 配置

repeats = 10

n_batch = 4

n_epochs = 1000

n_neurons = 3

n_lag = 1

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 将数据转换为平稳

raw_values = series.values

diff_values = difference(raw_values, 1)

# 将数据转换为监督学习

supervised = timeseries_to_supervised(diff_values, n_lag)

supervised_values = supervised.values[n_lag:,:]

# 将数据分割成训练集和测试集

train, test = supervised_values[0:-12], supervised_values[-12:]

# 转换数据尺度

scaler, train_scaled, test_scaled = scale(train, test)

# 拟合和评估模型

train_trimmed = train_scaled[2:, :]

# 运行诊断测试

for i in range(repeats):

history = fit(train_trimmed, test_scaled, raw_values, scaler, n_batch, n_epochs, n_neurons)

pyplot.plot(history['train'], color='blue')

pyplot.plot(history['test'], color='orange')

print('%d) TrainRMSE=%f, TestRMSE=%f' % (i, history['train'].iloc[-1], history['test'].iloc[-1]))

pyplot.savefig('diagnostic_neurons.png')

运行诊断脚本会生成一个折线图，显示每个训练时期后的训练和测试 RMSE。

诊断表明模型技能趋于平稳，可能在 400 个时期左右。该图还表明可能存在过拟合的情况，即测试 RMSE 在最后 500 个训练时期略有增加，但训练 RMSE 没有显著增加。

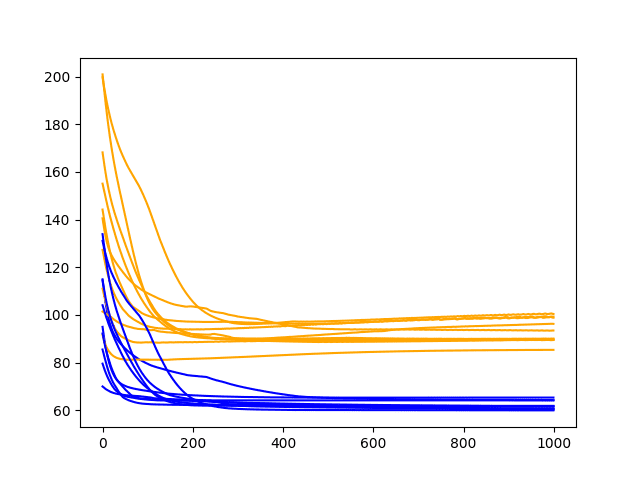
Diagnostic Line Plot of Train and Test Performance of 3 Hidden Neurons on the Shampoo Sales Dataset

洗发水销量数据集上 3 个隐藏神经元训练和测试性能的诊断折线图

改变隐藏层神经元数量及滞后

在本节中，我们将研究增加滞后观测作为输入，同时增加网络的容量。

增加滞后观测会自动调整输入神经元的数量。例如，3 个滞后观测作为输入将产生 3 个输入神经元。

增加的输入需要在网络中增加容量。因此，我们将把隐藏层中的神经元数量与用作输入的滞后观测数量进行匹配。

我们将使用奇数个滞后观测作为输入，从 1、3、5 和 7 开始，并分别使用相同数量的神经元。

输入数量的增加会影响将时间序列数据转换为监督学习问题过程中的训练模式总数。因此，本节所有实验的批次大小从 4 减至 2。

每次实验运行使用总共 1000 个训练时期。

基础实验脚本的更改仅限于experiment() 函数和实验运行，如下所示。

# run a repeated experiment
def experiment(repeats, series, epochs, lag, neurons):
	# transform data to be stationary
	raw_values = series.values
	diff_values = difference(raw_values, 1)
	# transform data to be supervised learning
	supervised = timeseries_to_supervised(diff_values, lag)
	supervised_values = supervised.values[lag:,:]
	# split data into train and test-sets
	train, test = supervised_values[0:-12], supervised_values[-12:]
	# transform the scale of the data
	scaler, train_scaled, test_scaled = scale(train, test)
	# run experiment
	error_scores = list()
	for r in range(repeats):
		# fit the model
		batch_size = 2
		model = fit_model(train_scaled, batch_size, epochs, neurons)
		# forecast test dataset
		test_reshaped = test_scaled[:,0:-1]
		output = model.predict(test_reshaped, batch_size=batch_size)
		predictions = list()
		for i in range(len(output)):
			yhat = output[i,0]
			X = test_scaled[i, 0:-1]
			# invert scaling
			yhat = invert_scale(scaler, X, yhat)
			# invert differencing
			yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)
			# store forecast
			predictions.append(yhat)
		# report performance
		rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))
		print('%d) Test RMSE: %.3f' % (r+1, rmse))
		error_scores.append(rmse)
	return error_scores

# load dataset
series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
# experiment
repeats = 30
results = DataFrame()
epochs = 1000
# vary neurons
neurons = [1, 3, 5, 7]
for n in neurons:
	results[str(n)] = experiment(repeats, series, epochs, n, n)
# summarize results
print(results.describe())
# save boxplot
results.boxplot()
pyplot.savefig('boxplot_neurons_lag.png')

# 运行重复实验

def experiment(repeats, series, epochs, lag, neurons):

# 将数据转换为平稳

raw_values = series.values

diff_values = difference(raw_values, 1)

# 将数据转换为监督学习

supervised = timeseries_to_supervised(diff_values, lag)

supervised_values = supervised.values[lag:,:]

# 将数据分割成训练集和测试集

train, test = supervised_values[0:-12], supervised_values[-12:]

# 转换数据尺度

scaler, train_scaled, test_scaled = scale(train, test)

# 运行实验

error_scores = list()

for r in range(repeats):

# 拟合模型

batch_size = 2

model = fit_model(train_scaled, batch_size, epochs, neurons)

# 预测测试数据集

test_reshaped = test_scaled[:,0:-1]

output = model.predict(test_reshaped, batch_size=batch_size)

predictions = list()

for i in range(len(output)):

yhat = output[i,0]

X = test_scaled[i, 0:-1]

# 反转缩放

yhat = invert_scale(scaler, X, yhat)

# 反转差分

yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i)

# 存储预测

predictions.append(yhat)

# 报告性能

rmse = sqrt(mean_squared_error(raw_values[-12:], predictions))

print('%d) Test RMSE: %.3f' % (r+1, rmse))

error_scores.append(rmse)

return error_scores

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# experiment

repeats = 30

results = DataFrame()

epochs = 1000

# vary neurons

neurons = [1, 3, 5, 7]

for n in neurons:

results[str(n)] = experiment(repeats, series, epochs, n, n)

# 总结结果

print(results.describe())

# save boxplot

results.boxplot()

pyplot.savefig('boxplot_neurons_lag.png')

运行实验会使用描述性统计数据来总结每个配置的结果。

注意：由于算法或评估程序的随机性，或者数值精度的差异，您的结果可能有所不同。可以考虑运行几次示例并比较平均结果。

结果表明，随着滞后输入变量的增加和隐藏神经元的增加，性能有所下降。

值得注意的是 1 个神经元和 1 个输入配置，与上一节的结果相比，其均值和标准差相似。

性能下降可能与较小的批次大小有关，而 1 个神经元/1 个滞后案例的结果不足以揭示这一点。

                1           3           5           7
count   30.000000   30.000000   30.000000   30.000000
mean   105.465038  109.447044  158.894730  147.024776
std     20.827644   15.312300   43.177520   22.717514
min     89.909627   77.426294   88.515319   95.801699
25%     92.187690  102.233491  125.008917  132.335683
50%     92.587411  109.506480  166.438582  145.078842
75%    135.386125  118.635143  189.457325  166.329000
max    139.941789  144.700754  232.962778  186.185471

1 3 5 7

count 30.000000 30.000000 30.000000 30.000000

mean 105.465038 109.447044 158.894730 147.024776

std 20.827644 15.312300 43.177520 22.717514

min 89.909627 77.426294 88.515319 95.801699

25% 92.187690 102.233491 125.008917 132.335683

50% 92.587411 109.506480 166.438582 145.078842

75% 135.386125 118.635143 189.457325 166.329000

max 139.941789 144.700754 232.962778 186.185471

还创建了结果的箱线图，以便比较配置。

有趣的是，3 个神经元和 3 个输入变量的使用显示出比其他配置更紧密的分布。这与上一节中观察到的 3 个神经元和 1 个输入变量的情况相似。

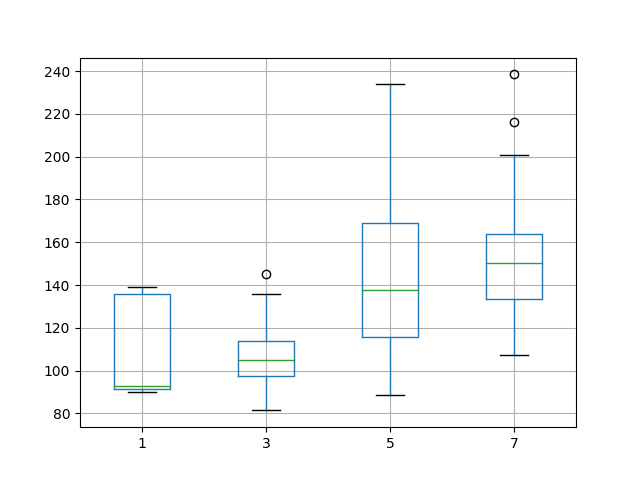
Box and Whisker Plot of Varying Lag Features and Hidden Neurons for Time Series Forecasting on the Shampoo Sales Dataset

洗发水销量数据集上的时间序列预测隐藏神经元和滞后变量变化的箱线图

我们还可以使用诊断信息来深入了解模型在拟合过程中动态如何变化。

3 个滞后/3 个神经元的 3 个滞后/3 个神经元的结果很有趣，我们将进一步研究它们。

诊断脚本的更改仅限于run() 函数。

# run diagnostic experiments
def run():
	# config
	repeats = 10
	n_batch = 2
	n_epochs = 1000
	n_neurons = 3
	n_lag = 3
	# load dataset
	series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
	# transform data to be stationary
	raw_values = series.values
	diff_values = difference(raw_values, 1)
	# transform data to be supervised learning
	supervised = timeseries_to_supervised(diff_values, n_lag)
	supervised_values = supervised.values[n_lag:,:]
	# split data into train and test-sets
	train, test = supervised_values[0:-12], supervised_values[-12:]
	# transform the scale of the data
	scaler, train_scaled, test_scaled = scale(train, test)
	# fit and evaluate model
	train_trimmed = train_scaled[2:, :]
	# run diagnostic tests
	for i in range(repeats):
		history = fit(train_trimmed, test_scaled, raw_values, scaler, n_batch, n_epochs, n_neurons)
		pyplot.plot(history['train'], color='blue')
		pyplot.plot(history['test'], color='orange')
		print('%d) TrainRMSE=%f, TestRMSE=%f' % (i, history['train'].iloc[-1], history['test'].iloc[-1]))
	pyplot.savefig('diagnostic_neurons_lag.png')

# 运行诊断实验

def run():

# 配置

repeats = 10

n_batch = 2

n_epochs = 1000

n_neurons = 3

n_lag = 3

# 加载数据集

series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)

# 将数据转换为平稳

raw_values = series.values

diff_values = difference(raw_values, 1)

# 将数据转换为监督学习

supervised = timeseries_to_supervised(diff_values, n_lag)

supervised_values = supervised.values[n_lag:,:]

# 将数据分割成训练集和测试集

train, test = supervised_values[0:-12], supervised_values[-12:]

# 转换数据尺度

scaler, train_scaled, test_scaled = scale(train, test)

# 拟合和评估模型

train_trimmed = train_scaled[2:, :]

# 运行诊断测试

for i in range(repeats):

history = fit(train_trimmed, test_scaled, raw_values, scaler, n_batch, n_epochs, n_neurons)

pyplot.plot(history['train'], color='blue')

pyplot.plot(history['test'], color='orange')

print('%d) TrainRMSE=%f, TestRMSE=%f' % (i, history['train'].iloc[-1], history['test'].iloc[-1]))

pyplot.savefig('diagnostic_neurons_lag.png')

运行诊断脚本会生成一个折线图，显示 10 次实验运行中每个训练时期的训练和测试 RMSE。

结果表明，在前 500 个时期内学习效果良好，而在剩余时期可能存在过拟合，测试 RMSE 呈上升趋势，训练 RMSE 呈下降趋势。

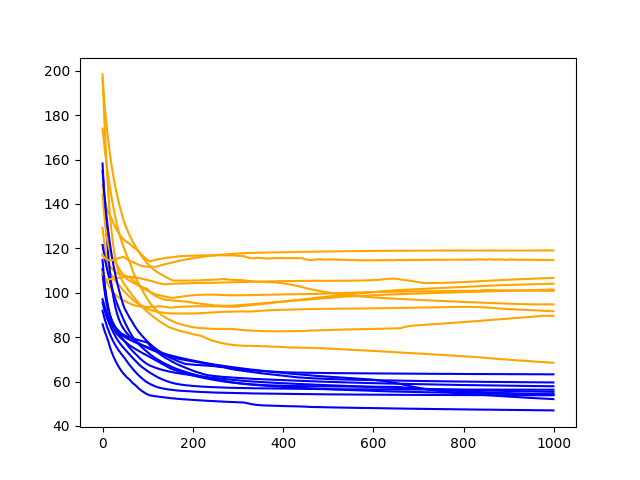
Diagnostic Line Plot of Train and Test Performance of 3 Hidden Neurons and Lag Features on the Shampoo Sales Dataset

洗发水销量数据集上 3 个隐藏神经元和滞后变量的训练和测试性能诊断折线图

结果回顾

我们在本教程中涵盖了很多内容。让我们回顾一下。

时期。我们研究了模型性能如何随训练时期数量的变化而变化，发现 1000 个时期可能是一个不错的起点。
神经元。我们研究了隐藏层中神经元数量的变化，发现 3 个神经元可能是一个不错的配置。
滞后输入。我们研究了滞后观测数量作为输入的变化，同时增加了隐藏层中的神经元数量，发现结果普遍变差，但 3 个隐藏层神经元仍然值得关注。结果不佳可能与批次大小从 4 更改为 2 有关，而与其他实验相比。

结果建议使用 1 个滞后输入、3 个隐藏层神经元，并拟合 1000 个时期作为初步模型配置。

这可以通过多种方式进行改进；下一节列出了一些想法。

扩展

本节列出了您可能想要探索的扩展和后续实验。

打乱 vs. 不打乱。未使用打乱，这是不寻常的。进行实验以比较在为时间序列预测拟合模型时对训练集进行打乱与不打乱。
归一化方法。数据被重新缩放到 -1 到 1，这对于 tanh 激活函数（模型配置未使用）来说是典型的。探索其他重新缩放方法，例如 0-1 归一化和标准化，以及它们对模型性能的影响。
多层。探索使用多个隐藏层来增加网络容量，以学习更复杂的多步模式。
特征工程。探索使用附加特征，例如误差时间序列，甚至日期-时间元素的观测值。

另外，请查看此帖子

如何提升深度学习性能

你尝试过这些扩展吗？
请在下方评论区发布你的结果。

总结

在本教程中，您了解了如何使用系统化实验来探索用于时间序列预测的多层感知器的配置并开发初步模型。

具体来说，你学到了：

如何开发用于评估时间序列预测 MLP 模型的稳健测试框架。
如何系统地评估训练时期、隐藏层神经元和滞后输入。
如何使用诊断信息来帮助解释结果并建议后续实验。

您对本教程有什么疑问吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

时间序列预测状态 LSTM 在线学习的不稳定性

LSTM 网络时间序列预测的 Dropout

对如何配置多层感知器网络进行时间序列预测的 53 条回复

elina 2017 年 4 月 26 日晚上 11:00 #

将观测值缩放到特定范围是什么意思？您能用简单的例子详细解释一下吗？

回复
- Jason Brownlee 2017 年 4 月 27 日上午 8:40 #
  
  是的，将每一列归一化到 0-1 的范围。
  
  回复
Kunpeng Zhang 2017 年 4 月 28 日凌晨 3:12 #

嗨，Jason，
我有一个关于预测结果评估的问题。
在我的代码中，我通过 keras 得到 MSE MAE MAPE 计算如下：
model.compile(loss=’mse’, optimizer=optimizer, metrics=[‘mae’, ‘mape’])
…
第 150 周期/150
0s – loss: 0.0038 – mean_absolute_error: 0.0455 – mean_absolute_percentage_error: 164095.5176
mse=0.003538, mae=0.043654, mape=58238.251235
————————————————————————-
但是当我用代码计算这些值时：
mse = mean_squared_error(test_Y, predicted_output)
rmse = math.sqrt(mse)
mae = mean_absolute_error(test_Y, predicted_output)
mape = np.mean(np.abs(np.divide(np.subtract(test_Y, predicted_output), test_Y))) * 100
RMSE: 14.992
MAE: 10.462
MAPE: 2.208

两个结果之间差异很大。怎么回事？

回复
- Jason Brownlee 2017 年 4 月 28 日上午 7:53 #
  
  这很有趣。我不确定这里发生了什么。
  
  我更相信手动计算的结果。我自己没有遇到过这样的问题，我的时期分数总是与训练后的评估相符。
  
  考虑准备一个小的独立示例并将其作为 bug 发布到 Keras 项目
  https://github.com/fchollet/keras
  
  回复
  - Kunpeng Zhang 2017 年 4 月 29 日晚上 11:46 #
    
    我试了你的例子。
    https://machinelearning.org.cn/time-series-prediction-lstm-recurrent-neural-networks-python-keras/
    
    更改
    model.compile(loss='mean_squared_error', optimizer='adam')
    推广到
    model.compile(loss=’mean_squared_error’, optimizer=’adam’, metrics=[‘mae’, ‘mape’])
    得到了相同的结果。
    0s – loss: 0.0019 – mean_absolute_error: 0.0343 – mean_absolute_percentage_error: 620693.8651
    第96/100个周期
    0s – loss: 0.0020 – mean_absolute_error: 0.0351 – mean_absolute_percentage_error: 326543.9207
    第97/100个周期
    0s – loss: 0.0019 – mean_absolute_error: 0.0345 – mean_absolute_percentage_error: 488762.9108
    第98/100个周期
    0s – loss: 0.0019 – mean_absolute_error: 0.0345 – mean_absolute_percentage_error: 514091.1566
    Epoch 99/100
    0s – loss: 0.0019 – mean_absolute_error: 0.0345 – mean_absolute_percentage_error: 531419.0410
    Epoch 100/100
    0s – loss: 0.0019 – mean_absolute_error: 0.0341 – mean_absolute_percentage_error: 454424.3737
    训练得分：22.34 RMSE
    测试得分：45.66 RMSE
    
    回复
Hans 2017 年 4 月 28 日下午 6:12 #

过拟合最稳健的迹象是什么？

回复
- Jason Brownlee 2017 年 4 月 29 日上午 7:22 #
  
  测试集上的技能比训练集差。
  
  回复
  - Hans 2017 年 4 月 30 日下午 3:50 #
    
    是否有可用的过拟合迹象列表？
    
    替代方案
    
    如果我想准备这样的列表，它应该是什么样的？
    
    1. 测试集上的技能比训练集差。
    2. ?
    3. ?
    4. ?
    5. ?
    
    回复
    - Hans 2017 年 4 月 30 日下午 3:51 #
      
      是否有适用于我们代码的函数可以“警示”过拟合？
      
      回复
      - Hans 2017 年 4 月 30 日下午 4:00 #
        
        我将您的示例的每个结果和多个参数都记录到了 Sqlite 数据库中。
        
        因此，我可以轻松地标记过拟合。
        
        例如，如果测试结果比训练集差。
        
        是否存在更多参数和结果的关系可供监控以防过拟合？
      - Jason Brownlee 2017 年 5 月 1 日上午 5:55 #
        
        过拟合是一个趋势，而不是一个结果一定更差。
        https://en.wikipedia.org/wiki/Overfitting
      - Jason Brownlee 2017 年 5 月 1 日上午 5:54 #
        
        不行。
    - Jason Brownlee 2017 年 5 月 1 日上午 5:54 #
      
      不。第一个就够了。
      
      相反，您需要开发数百种方法来解决过拟合/提前收敛问题。
      
      回复
      - Hans 2017 年 5 月 1 日上午 9:21 #
        
        A)
        “测试集上的技能比训练集差”
        是否意味着 trainRmse 小于 testRmse？
        
        在我的基线测试中，我的 trainRmse 始终为零，而 testRmse 总是更高？这正常吗？
        
        B)
        我们可以说测试值的方差较高是过拟合的指标吗？
      - Jason Brownlee 2017 年 5 月 2 日上午 5:56 #
        
        这篇帖子可能会让您更清楚，Hans。
        https://machinelearning.org.cn/overfitting-and-underfitting-with-machine-learning-algorithms/
Hans 2017 年 4 月 30 日下午 4:52 #

我们是否可以假设，使用此 MLP 设置找到的最佳性能时期、神经元和滞后输入也适用于 LSTM 模型或任何其他模型？

回复
- Jason Brownlee 2017 年 5 月 1 日上午 5:56 #
  
  不，通常发现的结果不能转移到其他问题或其他算法。
  
  回复
Hans 2017 年 5 月 1 日晚上 8:59 #

是否可以将训练好的模型保存在硬盘上，以便以后以更短的时间来预测未见过的数据？

回复
Magnus 2017 年 5 月 12 日晚上 11:22 #

是否可以使用 GridSearchCV 实现与您在另一篇文章中进行的相同研究？或者对于时间序列不可行？

回复
- Jason Brownlee 2017 年 5 月 13 日上午 6:15 #
  
  不，我们必须使用前向验证来正确评估时间序列模型。
  https://machinelearning.org.cn/backtest-machine-learning-models-time-series-forecasting/
  
  回复
Jussi 2017 年 12 月 4 日上午 6:07 #

嗨，Jason，

感谢精彩的教程。

您能否就如何使用 MLP 对多元时间序列进行建模给我一些建议？例如，如果我们像上面的示例一样，使用窗口方法对时间序列（例如能源消耗）进行建模。如何添加/建模其他特征，如日期、温度等，它们也可以是时间序列？

唯一的选择是将所有不同的时间序列一个接一个地创建成一个数组，并希望网络能够学习它们的关系？如果是这样，似乎没有办法指示哪些输入在时间上相互关联……但我猜 LSTM 和其他 RNN 就是为此目的而生的……

回复
- Jason Brownlee 2017 年 12 月 4 日上午 8:00 #
  
  您可以尝试使用单独的网络对每个系列进行建模，然后集成这些模型；您可以尝试一个大型模型来处理所有系列，我建议您进行实验，看看对您的数据最有效的方法。
  
  回复
  - kingsley udeh 2018 年 8 月 2 日晚上 9:21 #
    
    嗨，Jason，
    
    请问您有这方面的例子吗？
    
    “您可以尝试使用单独的网络对每个系列进行建模，然后集成这些模型…”
    
    您能否详细解释一下我们如何组合模型来形成一个集成？
    
    在这种情况下，是否需要一个最终模型？也就是说，用所有可用数据拟合集成模型？
    
    回复
    - Jason Brownlee 2018 年 8 月 3 日上午 6:02 #
      
      没有，抱歉。
      
      回复
Steven 2018 年 2 月 20 日上午 6:13 #

嗨，Jason，

感谢您提供的大量教程。我尝试了 LSTM 示例和这个 MLP 示例。所有这些示例都给了我很好的见解，并帮助我为自己的数据配置模型并进行优化。

时间序列的一个特征是预测（预测）基于历史数据。但在 MLP 示例中，我观察到测试数据用于进行预测
output = model.predict(test_reshaped, batch_size=batch_size)
我认为这本质上是回归问题，而不是时间序列问题。模型只能根据输入值进行预测，而不能仅根据历史数据进行预测。您能评论一下吗？

回复
- Jason Brownlee 2018 年 2 月 21 日上午 6:33 #
  
  这实际上取决于您如何构建您的预测问题，Steven。
  
  通常，测试预测模型的好方法是使用前向验证，该验证在测试时间步之间将测试数据提供给模型进行训练/重新训练。在此了解更多。
  https://machinelearning.org.cn/backtest-machine-learning-models-time-series-forecasting/
  
  回复
Amelie 2018年11月26日晚上11:23 #

感谢您的演示，

请问，NAR和MLP之间有什么区别？
以及MLP如何考虑序列的时间方面？

您能给我一个BPTT（Backpropagation through time，通过时间反向传播）的应用示例吗？

回复
- Jason Brownlee 2018年11月27日凌晨6:35 #
  
  什么是NAR？
  
  在此了解更多关于BPTT的信息
  https://machinelearning.org.cn/gentle-introduction-backpropagation-time/
  
  回复
  - Amelie 2018年11月27日晚上7:31 #
    
    NAR（非线性自回归神经网络）和MLP（多层感知机）的区别
    
    回复
    - Jason Brownlee 2018年11月28日凌晨7:40 #
      
      如果NAR是一个特定的方法，我对此不熟悉，抱歉。
      
      从名字上看，应用于时间序列的MLP将是非线性的（即激活函数），并且是自回归的（将滞后观测值作为输入）。
      
      回复
Ehsan 2018年12月8日凌晨7:04 #

谢谢Jason。我运行了您的代码，得到了您认为重要的信息（神经元数量、训练周期等）。那么现在我该如何使用这些参数来运行模型并绘制未来价格预测图？在Auto ARIMA中，我得到了显示未来值与原始值的图，但在MLP中我不知道如何做到这一点。谢谢！

回复
- Jason Brownlee 2018年12月8日凌晨7:14 #
  
  也许这会有帮助。
  https://machinelearning.org.cn/how-to-make-classification-and-regression-predictions-for-deep-learning-models-in-keras/
  
  回复
mk 2018年12月29日下午4:53 #

MLP模型可以处理多变量输入/输出、多步时间序列吗？

您在这篇帖子中的工作太棒了 https://machinelearning.org.cn/how-to-develop-convolutional-neural-networks-for-multi-step-time-series-forecasting/#comment-460415

多步时间序列、多变量输入和输出对我的工作是必需的。

回复
- Jason Brownlee 2018年12月30日凌晨5:37 #
  
  是的，我有很多例子。也许可以从这里开始
  https://machinelearning.org.cn/how-to-develop-multilayer-perceptron-models-for-time-series-forecasting/
  
  回复
Hala 2019年10月28日晚上10:16 #

如何为具有恒定训练周期的重复范围绘制RMSE箱线图？

回复
- Jason Brownlee 2019年10月29日凌晨5:24 #
  
  抱歉，我不明白，您能详细说明一下吗？
  
  回复
Hala 2019年10月29日晚上8:48 #

您在这里的例子中，绘制了不同训练周期的箱须图。
我想为测试实验的重复次数绘制RMSE误差的箱须图。

回复
- Jason Brownlee 2019年10月30日凌晨6:04 #
  
  听起来很棒。
  
  回复
Pam 2020年4月8日下午4:49 #

您是否有将预测（训练集和测试集）与实际值一起绘制的代码？

回复
- Jason Brownlee 2020年4月9日凌晨7:55 #
  
  是的，请看这里，关于绘图有帮助
  https://machinelearning.org.cn/time-series-data-visualization-with-python/
  
  回复
Carlos 2020年5月16日凌晨2:26 #

亲爱的 Jason,

感谢您的文章。您能否提供有关此解决方案的更多信息？“探索使用附加特征，例如误差时间序列，甚至每个观测值的时间日期元素。”

谢谢你。

回复
- Jason Brownlee 2020年5月16日凌晨6:18 #
  
  当然。这是给您尝试的建议。具体哪里让您感到困惑？
  
  回复
  - Carlos 2020年6月3日凌晨4:36 #
    
    抱歉，Jason，我不明白您的意思，也不知道您如何获得这些特征。您是否在其他文章或您的书中进行了解释？
    
    谢谢你。
    
    回复
    - Jason Brownlee 2020年6月3日凌晨8:04 #
      
      也许这会有帮助。
      https://machinelearning.org.cn/basic-feature-engineering-time-series-data-python/
      
      回复
Lucas 2020年6月8日晚上6:15 #

亲爱的 Jason,

我认为您的方法是配置神经网络的好方法。我唯一的问题是，是否有特定原因先评估训练周期，然后是神经元数量，最后是滞后？例如，训练周期的选择是否不受神经元数量或滞后变化的影响？

我希望能得到您的回复。
卢卡斯

回复
- Jason Brownlee 2020年6月9日凌晨6:00 #
  
  不一定，是的，它们会相互影响。
  
  回复
AA 2021年6月2日凌晨5:48 #

如何使用上面的代码计算MAPE？

谢谢你，

回复
- Jason Brownlee 2021年6月3日凌晨5:26 #
  
  您可以使用此函数
  https://scikit-learn.cn/stable/modules/generated/sklearn.metrics.mean_absolute_percentage_error.html
  
  回复
Alphonse 2021年11月29日凌晨9:44 #

嗨，Jason，
感谢这篇精彩的文章！

我想知道，如果我们想调整以找到隐藏层的数量，可以检查多少层？我理解这取决于数据的大小和耗时，但有多少层可以调整以进行检查？

谢谢

回复
- Adrian Tam 2021年12月2日凌晨12:12 #
  
  很难说，但您可以参考其他成功的模型，它们与您的问题最接近。例如，对于执行MNIST数字分类的完全连接网络，已有报告成功使用5层，呈反金字塔形，具有800-400-200个神经元。如果你的问题相似，可以从这里开始，然后调整为多一层或少一层，神经元数量增加或减少50%，看看哪个效果最好。
  
  回复
  - Alphonse 2021年12月2日凌晨8:52 #
    
    谢谢Adrian
    
    回复
Cotion 2024年4月11日晚上1:44 #

在演示中
# 拟合模型
batch_size = 4
train_trimmed = train_scaled[2:, :]
batch_size是4，为什么train_trimmed是从2开始的？

回复
- James Carmichael 2024年4月12日凌晨8:25 #
  
  你好Cotion…这个例子只是为了缩短训练数据集，但我们建议您尝试更大的数据集。
  
  回复

导航

如何为时间序列预测配置多层感知器网络

教程概述

环境

洗发水销售数据集

实验测试框架

数据分割

模型评估

数据准备

MLP 模型

实验运行

时间序列深度学习需要帮助吗？

改变训练时期

改变隐藏层神经元数量

改变隐藏层神经元数量及滞后

结果回顾

扩展

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

对如何配置多层感知器网络进行时间序列预测的 53 条回复

留下回复点击此处取消回复。

导航

教程概述

环境

洗发水销售数据集

实验测试框架

数据分割

模型评估

数据准备

MLP 模型

实验运行

时间序列深度学习需要帮助吗？

改变训练时期

改变隐藏层神经元数量

改变隐藏层神经元数量及滞后

结果回顾

扩展

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

对如何配置多层感知器网络进行时间序列预测的 53 条回复

留下回复 点击此处取消回复。

留下回复点击此处取消回复。