机器学习的最新进展使得人脸识别不再是一个困难的问题。但在过去,研究人员已经进行了各种尝试并开发了各种技能,以使计算机能够识别个体。其中一个早期尝试且效果适中的方法是 **特征脸** (eigenface),它基于线性代数技术。
在本教程中,我们将了解如何使用一些简单的线性代数技术,例如主成分分析,来构建一个基本的人脸识别系统。
完成本教程后,您将了解:
- 特征脸技术的发展
- 如何使用主成分分析从图像数据集中提取特征图像
- 如何将任何图像表示为特征图像的加权和
- 如何通过主成分的权重来比较图像的相似性
让我们开始吧。

使用主成分分析进行人脸识别
照片作者:Rach Teo,部分版权保留。
教程概述
本教程分为3个部分;它们是
- 图像与人脸识别
- 特征脸概述
- 特征脸的实现
图像与人脸识别
在计算机中,图片被表示为像素矩阵,每个像素的特定颜色都以某种数值进行编码。自然地,我们会问计算机是否能读取图片并理解其中的内容,如果可以,我们是否可以用矩阵数学来描述其中的逻辑。为了降低目标,人们尝试将问题的范围限制在识别人类面孔上。早期人脸识别的尝试是将矩阵视为高维细节,并从中推断出低维信息向量,然后在低维空间中尝试识别人物。这在过去是必要的,因为当时的计算机性能不高且内存量非常有限。然而,通过探索如何 **压缩** 图像到更小的尺寸,我们开发了一种技能,可以比较两张图片是否描绘的是同一个人,即使图片不完全相同。
1987年,Sirovich 和 Kirby 的一篇论文提出了一个想法,即所有人类面部图片都可以表示为少量“关键图片”的加权和。Sirovich 和 Kirby 将这些关键图片称为“特征图片”(eigenpictures),因为它们是人类面部图片减去均值后的协方差矩阵的特征向量。在该论文中,他们确实提供了人脸图片数据集在其矩阵形式下的主成分分析算法。加权和中使用的权重确实对应于人脸图片在每个特征图片上的投影。
1991年,Turk 和 Pentland 的一篇论文创造了“特征脸”(eigenface)一词。他们在此基础上,将权重和特征图片用作识别面部的特征。Turk 和 Pentland 的论文提出了一种内存高效计算特征图片的方法。它还提出了一种算法,说明人脸识别系统如何运行,包括如何更新系统以包含新面孔以及如何将其与视频采集系统结合。同一篇论文还指出,特征脸的概念有助于重建部分遮挡的图片。
特征脸概述
在我们开始编写代码之前,让我们先概述一下使用特征脸进行人脸识别的步骤,并指出一些简单的线性代数技术如何帮助完成这项任务。
假设我们有一堆人类面部的图片,所有图片的像素尺寸都相同(例如,都是 r×c 的灰度图像)。如果我们有 M 张不同的图片,并将每张图片 **向量化** 成 L=r×c 个像素,我们可以将整个数据集表示为一个 L×M 的矩阵(我们称之为矩阵 $A$),其中矩阵的每个元素都是像素的灰度值。
回想一下,主成分分析(PCA)可以应用于任何矩阵,其结果是一组称为 **主成分** 的向量。每个主成分的长度与矩阵的列长度相同。来自同一矩阵的不同主成分相互正交,这意味着任何两个主成分的向量点积都为零。因此,各种主成分构建了一个向量空间,其中矩阵的每一列都可以表示为主成分的线性组合(即加权和)。
实现方式是首先取 $C=A – a$,其中 $a$ 是矩阵 $A$ 的均值向量。所以 $C$ 是一个矩阵,它将 $A$ 的每一列减去均值向量 $a$。然后协方差矩阵是
$$S = C\cdot C^T$$
然后我们从中找到它的特征向量和特征值。主成分就是这些特征向量,按特征值递减排序。因为矩阵 $S$ 是一个 L×L 的矩阵,我们可以考虑寻找一个 M×M 的矩阵 $C^T\cdot C$ 的特征向量,因为 $C^T\cdot C$ 的特征向量 $v$ 可以通过 $u=C\cdot v$ 转化为 $C\cdot C^T$ 的特征向量 $u$,只是我们通常更倾向于将 $u$ 写成归一化向量(即 $u$ 的范数为 1)。
主成分向量的物理意义(或者等同于 $S=C\cdot C^T$ 的特征向量)是,它们是我们可以构建矩阵 $A$ 列的关键方向。不同主成分向量的相对重要性可以从相应的特征值推断出来。特征值越大,主成分向量越有用(即包含 $A$ 的信息越多)。因此,我们只保留前 K 个主成分向量。如果矩阵 $A$ 是人脸图片的训练集,那么前 K 个主成分向量就是最重要的 K 个“人脸图片”。我们称它们为 **特征脸** 图片。
对于给定的任何一张人脸图片,我们可以将其均值减去后的版本通过向量点积投影到特征脸图片上。结果表示这张图片与特征脸的关联程度。如果人脸图片与特征脸完全无关,我们期望其结果为零。对于 K 个特征脸,我们可以为任何给定的人脸图片找到 K 个点积。我们可以将结果表示为这张图片相对于特征脸的 **权重**。权重通常表示为一个向量。
反过来,如果我们有一个权重向量,我们可以将每个特征脸乘以相应的权重并相加,从而重建一张新的人脸。我们用矩阵 $F$ 表示特征脸,它是一个 L×K 的矩阵,权重向量 $w$ 是一个列向量。那么对于任何 $w$,我们可以构建人脸图片如下:
$$z=F\cdot w$$
其中 $z$ 是一个长度为 L 的列向量。因为我们只使用前 K 个主成分向量,我们应该期望生成的人脸图片会有一些失真,但保留了一些面部特征。
由于特征脸矩阵对于数据集是固定的,变化的权重向量 $w$ 意味着变化的脸部图片。因此,我们可以预期同一人的图片会产生相似的权重向量,即使图片不完全相同。因此,我们可以利用两个权重向量之间的距离(例如 L2 范数)作为衡量两张图片相似度的指标。
特征脸的实现
现在我们尝试使用 numpy 和 scikit-learn 来实现特征脸的思想。我们还将利用 OpenCV 读取图片文件。您可能需要使用 pip 命令安装相关包。
|
1 |
pip install opencv-python |
我们使用的数据集是 ORL人脸数据库,这个数据库已经比较老了,但我们可以从Kaggle下载。
该文件是一个约 4MB 的 zip 文件。它包含 40 个人的图片,每个人有 10 张图片,总共 400 张图片。在下面的内容中,我们假设文件已下载到本地目录并命名为 attface.zip。
我们可以解压 zip 文件以获取图片,也可以直接利用 Python 的 zipfile 包读取 zip 文件中的内容。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import cv2 import zipfile import numpy as np faces = {} with zipfile.ZipFile("attface.zip") as facezip: for filename in facezip.namelist(): if not filename.endswith(".pgm"): continue # not a face picture with facezip.open(filename) as image: # If we extracted files from zip, we can use cv2.imread(filename) instead faces[filename] = cv2.imdecode(np.frombuffer(image.read(), np.uint8), cv2.IMREAD_GRAYSCALE) |
以上代码读取 zip 文件中的每个 PGM 文件。PGM 是一种灰度图像文件格式。我们通过 image.read() 将每个 PGM 文件提取为字节字符串,并将其转换为字节的 numpy 数组。然后,我们使用 OpenCV 通过 cv2.imdecode() 将字节字符串解码为像素数组。OpenCV 会自动检测文件格式。我们将每张图片保存到 Python 字典 faces 中以供后续使用。
这里我们可以使用 matplotlib 来看看这些人类面部的图片。
|
1 2 3 4 5 6 7 8 |
... import matplotlib.pyplot as plt fig, axes = plt.subplots(4,4,sharex=True,sharey=True,figsize=(8,10)) faceimages = list(faces.values())[-16:] # take last 16 images for i in range(16): axes[i%4][i//4].imshow(faceimages[i], cmap="gray") plt.show() |

我们还可以查找每张图片的像素尺寸。
|
1 2 3 |
... faceshape = list(faces.values())[0].shape print("Face image shape:", faceshape) |
|
1 |
Face image shape: (112, 92) |
人脸图片通过 Python 字典中的文件名进行标识。我们可以看看这些文件名。
|
1 2 |
... print(list(faces.keys())[:5]) |
|
1 |
['s1/1.pgm', 's1/10.pgm', 's1/2.pgm', 's1/3.pgm', 's1/4.pgm'] |
因此,我们可以将同一人的脸部归为同一类。共有 40 类,总共 400 张图片。
|
1 2 3 4 |
... classes = set(filename.split("/")[0] for filename in faces.keys()) print("Number of classes:", len(classes)) print("Number of pictures:", len(faces)) |
|
1 2 |
Number of classes: 40 Number of pictures: 400 |
为了说明特征脸在识别方面的能力,我们想在生成特征脸之前预留一些图片。我们将一个人的所有图片以及另一个人的一张图片作为我们的测试集。剩余的图片被向量化并转换为一个二维 numpy 数组。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
... # 使用 1-39 类进行特征脸生成,保留整个 40 类以及 # 第 39 类的第 10 张图片作为样本外测试 facematrix = [] facelabel = [] for key,val in faces.items(): if key.startswith("s40/"): continue # this is our test set if key == "s39/10.pgm": continue # this is our test set facematrix.append(val.flatten()) facelabel.append(key.split("/")[0]) # Create facematrix as (n_samples,n_pixels) matrix facematrix = np.array(facematrix) |
现在我们可以对这个数据集矩阵执行主成分分析。我们不按步骤计算 PCA,而是利用 scikit-learn 中的 PCA 函数,这样可以轻松获取所需的所有结果。
|
1 2 3 4 5 |
... # Apply PCA to extract eigenfaces 从 sklearn.分解 导入 PCA pca = PCA().fit(facematrix) |
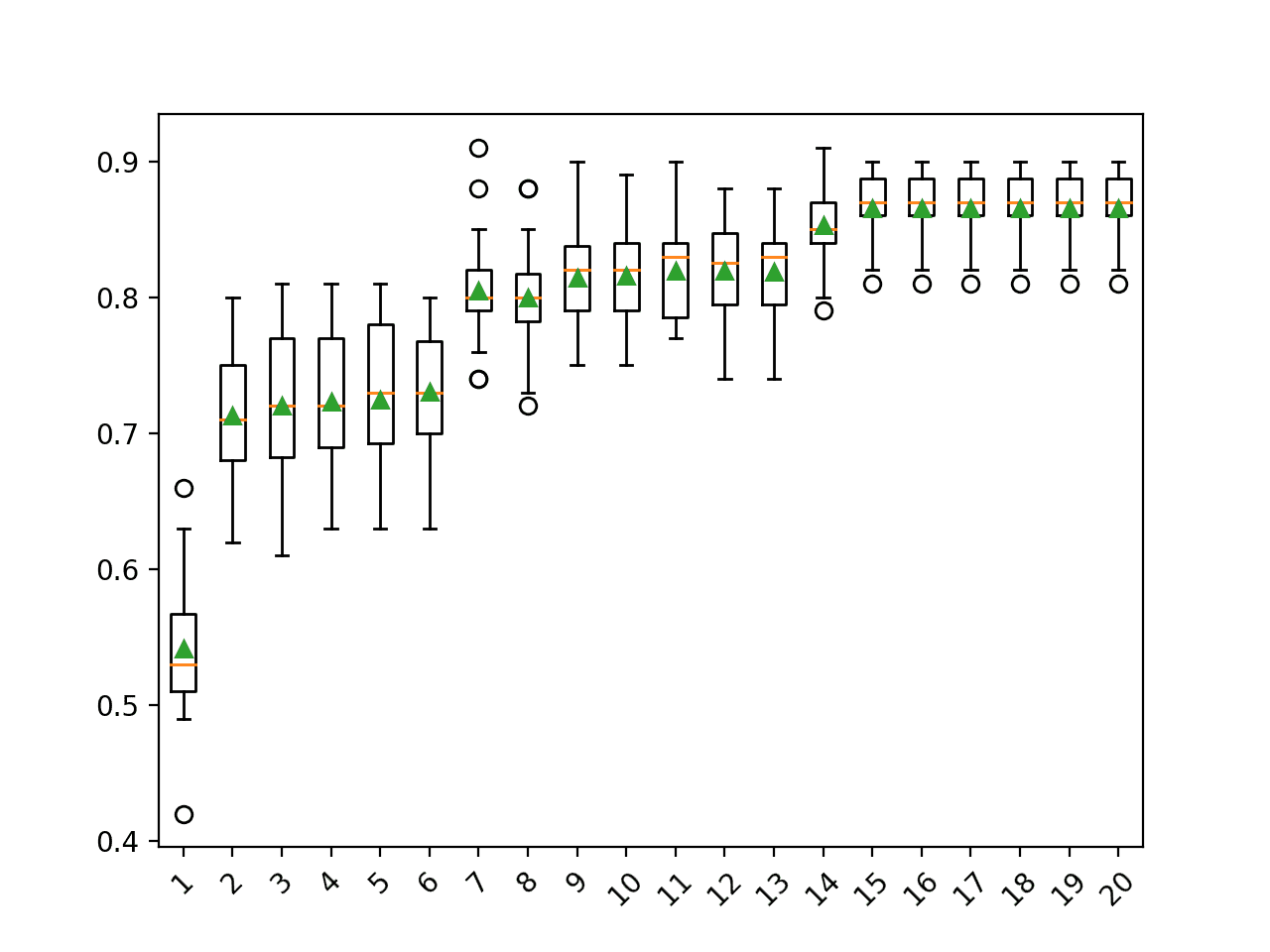
我们可以通过解释方差比来识别每个主成分的重要性。
|
1 2 |
... print(pca.explained_variance_ratio_) |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
[1.77824822e-01 1.29057925e-01 6.67093882e-02 5.63561346e-02 5.13040312e-02 3.39156477e-02 2.47893586e-02 2.27967054e-02 1.95632067e-02 1.82678428e-02 1.45655853e-02 1.38626271e-02 1.13318896e-02 1.07267786e-02 9.68365599e-03 9.17860717e-03 8.60995215e-03 8.21053028e-03 7.36580634e-03 7.01112888e-03 6.69450840e-03 6.40327943e-03 5.98295099e-03 5.49298705e-03 5.36083980e-03 4.99408106e-03 4.84854321e-03 4.77687371e-03 ... 1.12203331e-04 1.11102187e-04 1.08901471e-04 1.06750318e-04 1.05732991e-04 1.01913786e-04 9.98164783e-05 9.85530209e-05 9.51582720e-05 8.95603083e-05 8.71638147e-05 8.44340263e-05 7.95894118e-05 7.77912922e-05 7.06467912e-05 6.77447444e-05 2.21225931e-32] |
或者我们可以随便取一个适中的数字,比如说 50,并将这许多主成分向量作为特征脸。为了方便起见,我们从 PCA 结果中提取特征脸并将其存储为 numpy 数组。请注意,特征脸存储在矩阵的行中。如果需要显示,我们可以将其转换回二维。下面,我们展示一些特征脸,看看它们是什么样的。
|
1 2 3 4 5 6 7 8 9 10 |
... # Take the first K principal components as eigenfaces n_components = 50 eigenfaces = pca.components_[:n_components] # Show the first 16 eigenfaces fig, axes = plt.subplots(4,4,sharex=True,sharey=True,figsize=(8,10)) for i in range(16): axes[i%4][i//4].imshow(eigenfaces[i].reshape(faceshape), cmap="gray") plt.show() |

从这张图中,我们可以看到特征脸是模糊的面孔,但实际上每个特征脸都包含一些面部特征,可用于构建图片。
由于我们的目标是构建一个人脸识别系统,我们首先计算每个输入图片的权重向量。
|
1 2 3 |
... # Generate weights as a KxN matrix where K is the number of eigenfaces and N the number of samples weights = eigenfaces @ (facematrix - pca.mean_).T |
上面的代码使用矩阵乘法来代替循环。它大致等同于以下代码:
|
1 2 3 4 5 6 7 8 |
... weights = [] for i in range(facematrix.shape[0]): weight = [] for j in range(n_components): w = eigenfaces[j] @ (facematrix[i] - pca.mean_) weight.append(w) weights.append(weight) |
到此为止,我们的人脸识别系统已经完成。我们使用了 39 个人的图片来构建我们的特征脸。我们使用属于这 39 个人之一的测试图片(从训练 PCA 模型的矩阵中预留出来的那张),来看看它是否能成功识别出这张脸。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
... # Test on out-of-sample image of existing class query = faces["s39/10.pgm"].reshape(1,-1) query_weight = eigenfaces @ (query - pca.mean_).T euclidean_distance = np.linalg.norm(weights - query_weight, axis=0) best_match = np.argmin(euclidean_distance) print("Best match %s with Euclidean distance %f" % (facelabel[best_match], euclidean_distance[best_match])) # Visualize fig, axes = plt.subplots(1,2,sharex=True,sharey=True,figsize=(8,6)) axes[0].imshow(query.reshape(faceshape), cmap="gray") axes[0].set_title("Query") axes[1].imshow(facematrix[best_match].reshape(faceshape), cmap="gray") axes[1].set_title("Best match") plt.show() |
上面,我们首先用PCA结果中的平均向量减去矢量化图像。然后,我们计算这个均值减去向量到每个特征脸的投影,并将其作为该图片的权重。之后,我们将待识别图片的权重向量与每张现有图片的权重向量进行比较,并找出L2距离最小的作为最佳匹配。我们可以看到,它确实能够成功地在同一类别中找到最接近的匹配。
|
1 |
最佳匹配为 s39,欧氏距离为 1559.997137 |
我们可以通过并排比较最匹配的结果来可视化结果。

我们可以再次尝试使用我们从PCA中排除的第40个人的图片。我们永远无法正确识别它,因为它对我们的模型来说是一个新人。然而,我们想看看它会错得多离谱,以及在距离度量中的数值是多少。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
... # 测试新类别的 out-of-sample 图像 query = faces["s40/1.pgm"].reshape(1,-1) query_weight = eigenfaces @ (query - pca.mean_).T euclidean_distance = np.linalg.norm(weights - query_weight, axis=0) best_match = np.argmin(euclidean_distance) print("Best match %s with Euclidean distance %f" % (facelabel[best_match], euclidean_distance[best_match])) # Visualize fig, axes = plt.subplots(1,2,sharex=True,sharey=True,figsize=(8,6)) axes[0].imshow(query.reshape(faceshape), cmap="gray") axes[0].set_title("Query") axes[1].imshow(facematrix[best_match].reshape(faceshape), cmap="gray") axes[1].set_title("Best match") plt.show() |
我们可以看到,它的最佳匹配具有更大的L2距离。
|
1 |
最佳匹配为 s5,欧氏距离为 2690.209330 |
但我们可以看到,错误的识别结果与待识别的图片有一些相似之处。

在 Turk 和 Pentland 的论文中,他们建议我们为L2距离设置一个阈值。如果最佳匹配的距离小于阈值,我们就认为人脸被识别为同一个人。如果距离大于阈值,我们就声称该图片是某张我们从未见过的人,即使在数值上可以找到最佳匹配。在这种情况下,我们可以考虑将此作为新的人纳入我们的模型,即记住这个新的权重向量。
实际上,我们可以更进一步,使用特征脸生成新的人脸,但结果不是很逼真。下面,我们使用随机权重向量生成一个,并将其与“平均脸”并排展示。
|
1 2 3 4 5 6 7 8 9 10 |
... # 可视化平均脸和随机脸 fig, axes = plt.subplots(1,2,sharex=True,sharey=True,figsize=(8,6)) axes[0].imshow(pca.mean_.reshape(faceshape), cmap="gray") axes[0].set_title("Mean face") random_weights = np.random.randn(n_components) * weights.std() newface = random_weights @ eigenfaces + pca.mean_ axes[1].imshow(newface.reshape(faceshape), cmap="gray") axes[1].set_title("Random face") plt.show() |

特征脸有多好?对于模型的简单性来说,它令人惊讶地表现出色。然而,Turk 和 Pentland 在各种条件下对其进行了测试。他们发现其准确率在“光照变化下平均为 96%,方向变化下为 85%,尺寸变化下为 64%”。因此,作为人脸识别系统,它可能不太实用。毕竟,在放大和缩小后,作为矩阵的图片在主成分域中会发生很大变形。因此,现代的替代方法是使用卷积神经网络,它对各种变换具有更强的容忍性。
把所有东西放在一起,下面是完整的代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 |
import zipfile import cv2 import numpy as np import matplotlib.pyplot as plt from sklearn.decomposition import PCA # 动态读取 zip 文件中的人脸图像 faces = {} with zipfile.ZipFile("attface.zip") as facezip: for filename in facezip.namelist(): if not filename.endswith(".pgm"): continue # not a face picture with facezip.open(filename) as image: # If we extracted files from zip, we can use cv2.imread(filename) instead faces[filename] = cv2.imdecode(np.frombuffer(image.read(), np.uint8), cv2.IMREAD_GRAYSCALE) # 使用 matplotlib 显示样本人脸 fig, axes = plt.subplots(4,4,sharex=True,sharey=True,figsize=(8,10)) faceimages = list(faces.values())[-16:] # take last 16 images for i in range(16): axes[i%4][i//4].imshow(faceimages[i], cmap="gray") print("Showing sample faces") plt.show() # 打印一些细节 faceshape = list(faces.values())[0].shape print("Face image shape:", faceshape) classes = set(filename.split("/")[0] for filename in faces.keys()) print("Number of classes:", len(classes)) print("Number of images:", len(faces)) # 使用 1-39 类进行特征脸生成,保留整个 40 类以及 # 第 39 类的第 10 张图片作为样本外测试 facematrix = [] facelabel = [] for key,val in faces.items(): if key.startswith("s40/"): continue # this is our test set if key == "s39/10.pgm": continue # this is our test set facematrix.append(val.flatten()) facelabel.append(key.split("/")[0]) # 创建一个 NxM 矩阵,其中 N 张图像,每张图像 M 个像素 facematrix = np.array(facematrix) # 应用 PCA 并取前 K 个主成分作为特征脸 pca = PCA().fit(facematrix) n_components = 50 eigenfaces = pca.components_[:n_components] # Show the first 16 eigenfaces fig, axes = plt.subplots(4,4,sharex=True,sharey=True,figsize=(8,10)) for i in range(16): axes[i%4][i//4].imshow(eigenfaces[i].reshape(faceshape), cmap="gray") print("Showing the eigenfaces") plt.show() # Generate weights as a KxN matrix where K is the number of eigenfaces and N the number of samples weights = eigenfaces @ (facematrix - pca.mean_).T print("Shape of the weight matrix:", weights.shape) # Test on out-of-sample image of existing class query = faces["s39/10.pgm"].reshape(1,-1) query_weight = eigenfaces @ (query - pca.mean_).T euclidean_distance = np.linalg.norm(weights - query_weight, axis=0) best_match = np.argmin(euclidean_distance) print("Best match %s with Euclidean distance %f" % (facelabel[best_match], euclidean_distance[best_match])) # Visualize fig, axes = plt.subplots(1,2,sharex=True,sharey=True,figsize=(8,6)) axes[0].imshow(query.reshape(faceshape), cmap="gray") axes[0].set_title("Query") axes[1].imshow(facematrix[best_match].reshape(faceshape), cmap="gray") axes[1].set_title("Best match") plt.show() # 测试新类别的 out-of-sample 图像 query = faces["s40/1.pgm"].reshape(1,-1) query_weight = eigenfaces @ (query - pca.mean_).T euclidean_distance = np.linalg.norm(weights - query_weight, axis=0) best_match = np.argmin(euclidean_distance) print("Best match %s with Euclidean distance %f" % (facelabel[best_match], euclidean_distance[best_match])) # Visualize fig, axes = plt.subplots(1,2,sharex=True,sharey=True,figsize=(8,6)) axes[0].imshow(query.reshape(faceshape), cmap="gray") axes[0].set_title("Query") axes[1].imshow(facematrix[best_match].reshape(faceshape), cmap="gray") axes[1].set_title("Best match") plt.show() |
延伸阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- L. Sirovich 和 M. Kirby (1987)。“用于表征人脸的低维过程”。美国光学学会杂志A。4(3): 519–524。
- M. Turk 和 A. Pentland (1991)。“用于识别的特征脸”。认知神经科学杂志。3(1): 71–86。
书籍
- 线性代数导论,第五版,2016。
API
文章
总结
在本教程中,您学习了如何使用源自主成分分析的特征脸构建人脸识别系统。
具体来说,你学到了:
- 如何使用主成分分析从图像数据集中提取特征图像
- 如何使用特征图像集为任何已见或未见的图像创建权重向量
- 如何使用不同图像的权重向量来衡量它们的相似性,并将此技术应用于人脸识别
- 如何从特征图像生成新的随机图像





我想说,特征脸是特征向量而不是特征值。特征值是标量。
正确。那是笔误。
在 “eigenfaces @ (facematrix – pca.mean_).T” 中的 @ 有什么用?我没见过 @ 运算符。如果这是个愚蠢的问题,请原谅。
这是 Python 3.5 或更高版本中的用法,表示向量点积或矩阵乘法。在此页面上搜索“矩阵乘法”:https://docs.pythonlang.cn/3/library/operator.html
嗨,亲爱的
在实现这段代码时,我在(# 测试现有类别的 out-of-sample 图像)部分遇到了一个错误,
—————————————————————————
ValueError 回溯 (最近一次调用)
C:\Users\NEGINR~1\AppData\Local\Temp/ipykernel_2036/1504760658.py in
3 query = faces[“s40/1.pgm”].reshape(1,-1)
4 query_weight = eigenfaces @ (query – pca.mean_).T
—-> 5 euclidean_distance = np.linalg.norm(weights – query_weight, axis=0)
6 best_match = np.argmin(euclidean_distance)
7 print(“Best match %s with Euclidean distance %f” % (facelabel[best_match], euclidean_distance[best_match]))
ValueError: operands could not be broadcast together with shapes (389,50) (50,1)
我能解决这个错误吗?请帮忙。
嗨 Abazari…以下资源或许能帮助您更好地理解:
https://www.geeksforgeeks.org/how-to-fix-valueerror-operands-could-not-be-broadcast-together-with-shapes/
嗨 Carmichael
非常感谢您提供的信息
解决我的问题
此致
嗨 Abazarii,您能告诉我您是如何解决这个问题的吗,因为我也遇到了同样的问题 :(((
谢谢您的资源,我解决了这些问题。
嗨,亲爱的 Carmichael
谢谢您的回复
我是 Python 初学者
我希望您能告诉我该怎么做
嘿,教程很好,但我遇到了一个问题
ValueError:使用序列设置数组元素。
在
pca = PCA().fit(facematrix) 第 49 行
也许是由 facematrix = np.array(facematrix) 第 46 行引起的
请帮助
嗨 Flo…您可能会对以下内容感兴趣
https://stackoverflow.com/questions/4674473/valueerror-setting-an-array-element-with-a-sequence
嗨,感谢您的快速回复。我明白这个错误的意思,但不知道为什么会发生。只有当我输入 2 张图像时,特征脸才会被计算…
File “C:\Users\Flo\PycharmProjects\\venv\lib\site-packages\sklearn\decomposition\_pca.py”, line 408, in fit
self._fit(X)
File “C:\Users\Flo\PycharmProjects\VA53_ACP\venv\lib\site-packages\sklearn\decomposition\_pca.py”, line 456, in _fit
X = self._validate_data(
File “C:\Users\Flo\PycharmProjects\sklearn\base.py”, line 577, in _validate_data
X = check_array(X, input_name=”X”, **check_params)
File “C:\Users\Flo\PycharmProjects\\venv\lib\site-packages\sklearn\utils\validation.py”, line 856, in check_array
array = np.asarray(array, order=order, dtype=dtype)
ValueError:使用序列设置数组元素。
我需要帮助
我的最佳匹配是 s39,欧氏距离为 1559.997137,但现在显示的是 0.0000000。如何纠正?请回复。
嗨 satwat…请详细说明您是如何实现模型的,这样我们才能更好地帮助您。
我正在学习您的代码,但查询照片和最佳匹配照片是相同的,如何处理?我正在做一个大三下学期的计算机科学专业小项目,所以希望您能帮助我。如果您能帮助我,我将不胜感激。
似乎缺少了什么,我不确定,但测试时我们不应该使用 facematrix,因为 facematrix 包含了所有图像,我们需要将给定图像测试到主成分。
嗨 MR X…请详细说明模型可能表现不足的地方,这样我们才能更好地解决任何潜在问题。