在房地产领域,理解房产特征的细微差别及其对销售价格的影响至关重要。在本研究中,我们将深入探讨艾姆斯住房数据集,揭示各种特征与其销售价格相关性之间的关系。通过利用数据可视化,我们将揭示模式、趋势和见解,这些将指导从房主到房地产开发商的利益相关者。
让我们开始吧。

特征关系 101:来自 Ames Housing 数据的经验
照片来源:Andraz Lazic。部分权利保留。
概述
这篇博文分为三部分;它们是:
- 揭示相关性
- 使用热力图进行可视化
- 通过散点图解析特征关系
揭示相关性
相关性是一种统计衡量标准,它说明了两个变量共同变化的程度。正相关表示一个变量增加时,另一个变量也倾向于增加,反之亦然。相反,负相关意味着一个变量增加时,另一个变量倾向于减少。
|
1 2 3 4 5 6 7 8 9 10 |
# 加载数据集 import pandas as pd Ames = pd.read_csv('Ames.csv') # 计算所有特征与“SalePrice”的相关性 correlations = Ames.corr(numeric_only=True)['SalePrice'].sort_values(ascending=False) # 显示与“SalePrice”相关性最高的 10 个特征 top_correlations = correlations[1:11] print(top_correlations) |
输出如下:
|
1 2 3 4 5 6 7 8 9 10 11 |
OverallQual 0.790661 GrLivArea 0.719980 TotalBsmtSF 0.652268 1stFlrSF 0.642623 GarageCars 0.639017 GarageArea 0.635029 YearBuilt 0.544569 FullBath 0.535175 GarageYrBlt 0.521105 YearRemodAdd 0.514720 Name: SalePrice, dtype: float64 |
根据艾姆斯住房数据集,与住房价格最相关的特征是:
- OverallQual:房屋的整体质量,评分等级从 1(非常差)到 10(非常好)。
- GrLivArea:地上居住面积,以平方英尺为单位。它包括地下室之外的居住面积。
- TotalBsmtSF:地下室总面积,以平方英尺为单位。这包括地下室的装修和未装修的区域。
- 1stFlrSF:一楼面积,表示房屋一楼的大小。
- GarageCars:车库大小(以汽车容量计)。这表示可以停放多少辆汽车的车库。
- GarageArea:车库大小,以平方英尺为单位。它提供了车库总占地面积的概念。
- YearBuilt:原始建造日期,表示房屋主要工程完成的年份。
- FullBath:地上完整浴室数量。这计算了地上(即有水槽、马桶和浴缸或淋浴)而非地下室的完整浴室数量。
- GarageYrBlt:车库建造年份。这表示车库建造的年份。对于没有车库的房屋,此特征可能为空。
- YearRemodAdd:翻新日期。它表示翻新或加建的年份,如果没有翻新或加建,则与建造年份相同。
最相关的特征是具有最佳预测能力的特征。如果您要构建一个预测住房价格的模型,这些就是输入特征中很有可能成功的子集。相关特征也可能由其他一些共同因素引起,这本身就是数据科学中一个您想研究和详细说明的主题。
上面的代码打印了correlations[1:11],因为correlations[0]是 SalesPrice,根据定义它是 1.0。从特征选择的角度来看,您还应该检查correlations[-10:]以获取负相关性最高的特征,它们也可能在解释价格方面非常强大。在此特定数据集中并非如此。
通过我的书《数据科学入门指南》开启您的项目。它提供了带有可运行代码的自学教程。
使用热力图进行可视化
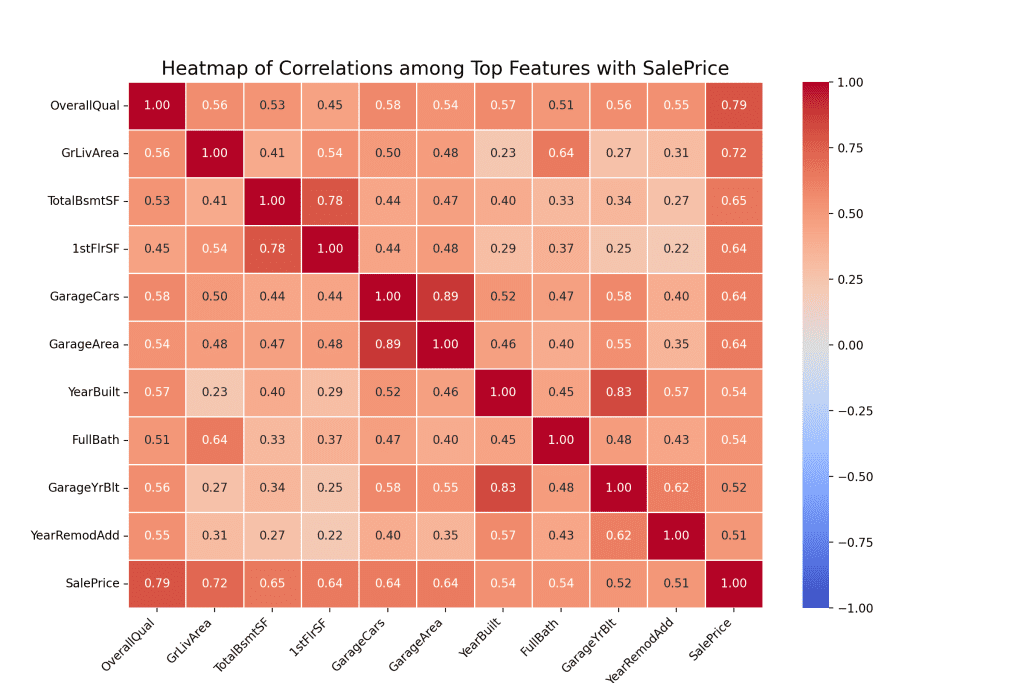
热力图提供了一种强大的二维数据可视化工具,颜色表示幅度或频率。在相关性方面,热力图可以精美地说明多个特征之间关系的强度和方向。让我们深入研究一个展示了与SalePrice最相关的前几个特征之间相关性的热力图。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# 导入所需的库 import seaborn as sns import matplotlib.pyplot as plt # 选择包括 SalePrice 在内的最相关的 10 个特征 selected_features = list(top_correlations.index) + ['SalePrice'] # 计算选定特征的相关性 correlation_matrix = Ames[selected_features].corr() # 设置 matplotlib 图形 plt.figure(figsize=(12, 8)) # 生成热力图 sns.heatmap(correlation_matrix, annot=True, cmap="coolwarm", linewidths=.5, fmt=".2f", vmin=-1, vmax=1) # 标题 plt.title("Heatmap of Correlations among Top Features with SalePrice", fontsize=16) # 显示热力图 plt.show() |
热力图是同时可视化多个变量之间关系强度和方向的绝佳方式。热力图中的每个单元格的颜色强度对应于相关性的幅度,暖色表示正相关,冷色表示负相关。上面的热力图中没有蓝色,因为只考虑了 10 个正相关性最高的列。
在上面的热力图中,我们可以观察到以下几点:
- OverallQual,代表房屋的整体质量,与 SalePrice 的正相关性最强,相关系数约为 0.79。这意味着随着房屋质量的提高,销售价格也趋于上涨。
- GrLivArea 和 TotalBsmtSF,分别代表地上居住面积和地下室总面积,也显示出与销售价格的强正相关性。
- 大多数特征与 SalePrice 存在正相关,这表明随着这些特征的增加或改进,房屋的销售价格也趋于上涨。
- 值得注意的是,有些特征之间也存在相关性。例如,GarageCars 和 GarageArea 具有很强的相关性,这很有道理,因为更大的车库可以停放更多的汽车。
这些见解对于房地产行业的各种利益相关者来说都非常有价值。例如,房地产开发商可以专注于改善房屋的特定特征,以提高其市场价值。
以下是完整的代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
import seaborn as sns import matplotlib.pyplot as plt import pandas as pd # 加载数据集 Ames = pd.read_csv('Ames.csv') # 计算与“SalePrice”相关性最高的 10 个特征 correlations = Ames.corr(numeric_only=True)['SalePrice'].sort_values(ascending=False) top_correlations = correlations[1:11] # 选择包括 SalePrice 在内的最相关的 10 个特征 selected_features = list(top_correlations.index) + ['SalePrice'] # 计算选定特征的相关性 correlation_matrix = Ames[selected_features].corr() # 设置 matplotlib 图形 plt.figure(figsize=(12, 8)) # 生成热力图 sns.heatmap(correlation_matrix, annot=True, cmap="coolwarm", linewidths=.5, fmt=".2f", vmin=-1, vmax=1) plt.title("Heatmap of Correlations among Top Features with SalePrice", fontsize=16) plt.show() |
通过散点图解析特征关系
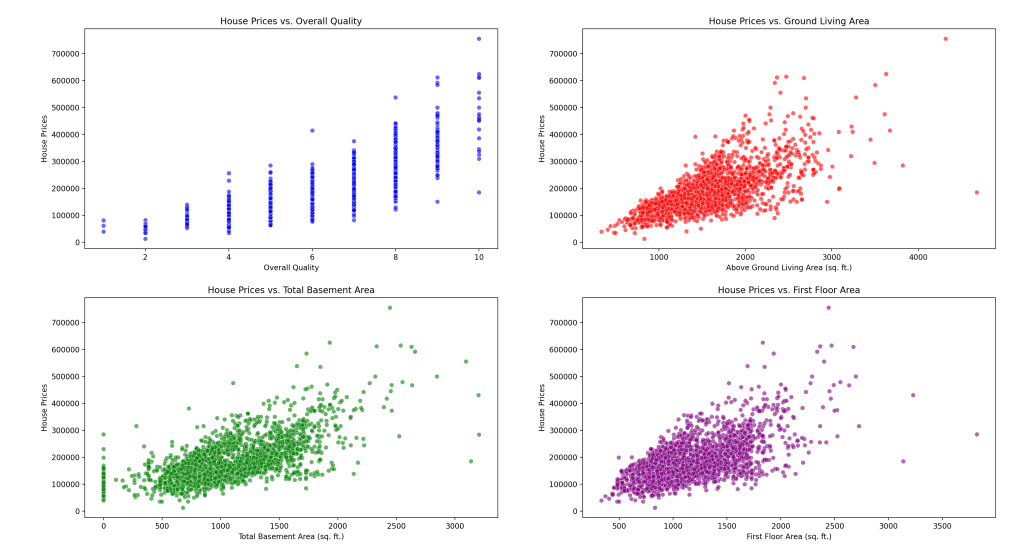
虽然相关性提供了对关系的初步了解,但进一步可视化这些关系至关重要。例如,散点图可以更清晰地描绘两个特征如何相互作用。此外,区分相关性和因果关系也很重要。高度相关性并不一定意味着一个变量导致了另一个变量的变化。它仅仅表示一种关系。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
# 导入所需的库 import pandas as pd import matplotlib.pyplot as plt import seaborn as sns Ames = pd.read_csv('Ames.csv') # 设置图形和轴 fig, ax = plt.subplots(2, 2, figsize=(15, 12)) # SalePrice 与 OverallQual 的散点图 sns.scatterplot(x=Ames['OverallQual'], y=Ames['SalePrice'], ax=ax[0, 0], color='blue', alpha=0.6) ax[0, 0].set_title('House Prices vs. Overall Quality') ax[0, 0].set_ylabel('House Prices') ax[0, 0].set_xlabel('Overall Quality') # SalePrice 与 GrLivArea 的散点图 sns.scatterplot(x=Ames['GrLivArea'], y=Ames['SalePrice'], ax=ax[0, 1], color='red', alpha=0.6) ax[0, 1].set_title('House Prices vs. Ground Living Area') ax[0, 1].set_ylabel('House Prices') ax[0, 1].set_xlabel('Above Ground Living Area (sq. ft.)') # SalePrice 与 TotalBsmtSF 的散点图 sns.scatterplot(x=Ames['TotalBsmtSF'], y=Ames['SalePrice'], ax=ax[1, 0], color='green', alpha=0.6) ax[1, 0].set_title('House Prices vs. Total Basement Area') ax[1, 0].set_ylabel('House Prices') ax[1, 0].set_xlabel('Total Basement Area (sq. ft.)') # SalePrice 与 1stFlrSF 的散点图 sns.scatterplot(x=Ames['1stFlrSF'], y=Ames['SalePrice'], ax=ax[1, 1], color='purple', alpha=0.6) ax[1, 1].set_title('House Prices vs. First Floor Area') ax[1, 1].set_ylabel('House Prices') ax[1, 1].set_xlabel('First Floor Area (sq. ft.)') # 调整布局 plt.tight_layout(pad=3.0) plt.show() |
散点图强调了销售价格与关键特征之间强烈的正相关关系。随着整体质量、地上居住面积、地下室面积和一楼面积的增加,房屋通常能卖出更高的价格。然而,一些例外和异常值表明,其他因素也影响最终的销售价格。一个典型的例子来自上面的“房屋价格与地上居住面积”的散点图:在 2500 平方英尺及以上时,点分散,这表明房屋价格存在很大差异,而面积与此关系不大或未被有效解释。
想开始学习数据科学新手指南吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
进一步阅读
如果您想深入了解此主题,本节提供了更多资源。
资源
总结
在探索艾姆斯住房数据集的过程中,我们踏上了一段旅程,旨在了解各种房产特征及其与销售价格的相关性。通过热力图和散点图,我们揭示了可能对房地产利益相关者产生重大影响的模式和见解。
具体来说,你学到了:
- 相关性及其在理解房产特征与销售价格之间关系中的重要性。
- 热力图在可视化多个特征之间相关性方面的效用。
- 散点图所增加的深度,强调了在相关系数之外,区分单个特征动态的重要性。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。




暂无评论。