
从线性回归到 XGBoost:性能对比
图片由 Editor | ChatGPT 提供
引言
回归无疑是机器学习模型可以解决的最主流的任务之一。有许多类型的机器学习方法可以构建不同的模型,这些模型能够根据一些称为预测变量的特征对目标变量(标签)进行数值预测或估计,这足以证明这一点。本文重点介绍两种广泛使用的回归模型:线性回归和 XGBoost,通过并排的实践比较来突出每种模型的主要特点、优缺点。
线性回归
线性回归模型是参数化的、数学上定义的模型,它们遵循以下线性方程(视觉上等同于一个超平面)来估计目标输出 y(例如房价),基于描述该房屋的几个属性,记为 x1, x2, …, xn
\[
y = \beta_0 + \beta_1 x_1 + \beta_2 x_2 + \dots + \beta_n x_n + \varepsilon
\]
重要的是,给定 n 个预测属性,如房屋大小、房间数量、纬度等,一个线性回归模型由 n + 1 个可学习的参数定义:与属性相关的权重,加上一个偏置项 β₀,这个偏置项对于为不经过坐标原点的数据集构建回归模型是必需的。残差或误差项 ε 表示真实值(例如,如果已知,房屋的真实价格)与模型预测值之间的差异。
在快速回顾了回归模型的样子之后,是时候实现一个了!我们将使用一个简化版的加州住房数据集,你可以从这个仓库免费获取。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import pandas as pd import numpy as np from sklearn.model_selection import train_test_split 来自 sklearn.linear_model 导入 LinearRegression from sklearn.metrics import mean_squared_error, r2_score from sklearn.preprocessing import StandardScaler import xgboost as xgb import matplotlib.pyplot as plt url = "https://raw.githubusercontent.com/gakudo-ai/open-datasets/main/housing.csv" df = pd.read_csv(url) df_numeric = df.select_dtypes(include=[np.number]).dropna() |
上述代码导入了我们在整个实践示例中需要的库,将数据集加载到 Pandas DataFrame 中,并且只选择数值特征,忽略了数据集中的分类特征,如 ocean_proximity。
接下来,我们从其余的数值特征中分离出要预测的标签,即房屋价值,将数据分割成训练集和测试集(这对于后续的模型评估和比较非常重要),并在 scikit-learn 库的帮助下,训练线性回归模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
X = df_numeric.drop(columns=["median_house_value"], errors="ignore") y = df_numeric["median_house_value"] X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42) # 特征缩放是可选的,但在大多数情况下推荐使用,以获得更好的模型性能 scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test) # 训练线性回归模型 lr_model = LinearRegression() lr_model.fit(X_train_scaled, y_train) y_pred_lr = lr_model.predict(X_test_scaled) |
请注意,我们在上面的代码结尾处,还对测试集(占整个数据集的 20%)上获得了一组预测的房价,并将这些预测存储在 y_pred_lr 变量中。
这些预测将与包含在 y_test 中的真实测试标签一起,通过两个误差指标来评估模型的性能。
- 均方根误差 (RMSE):一种误差度量,特别适用于测量与目标变量具有相同量级或单位的误差。其值越低,模型性能越好。
- R2 分数:决定系数是模型可以解释的目标变量中方差的归一化比例。其值越高(越接近 1),性能越好。
让我们看看我们的模型表现如何。
|
1 2 3 |
print("Linear Regression:") print(" RMSE:", np.sqrt(mean_squared_error(y_test, y_pred_lr))) print(" R²:", r2_score(y_test, y_pred_lr)) |
输出
|
1 2 3 |
Linear Regression: RMSE: 70025.94402055633 R²: 0.6377762608657407 |
考虑到数据集中房价的范围在几十万美元左右,RMSE 指示的误差乍一看似乎是中等的:不算太糟,但也不是很好。接近 64% 的 R² 系数也表明了一个相当可接受的表现,可能还有改进的空间。怎么改进?当然是尝试一个不同的模型!
从线性回归到 XGBoost
XGBoost 是一个集成模型;也就是说,它是多个单一模型的组合,这些模型“联手”解决一个单一的预测任务。在预测准确性方面,这些模型通常超越了更简单的、单独训练的模型的界限,在大多数情况下显著提高了性能。
我们现在将构建一个 XGBoost 集成模型,并将其性能与线性回归模型在相同的测试数据上进行比较。
|
1 2 3 |
xgb_model = xgb.XGBRegressor(n_estimators=100, max_depth=4, random_state=42) xgb_model.fit(X_train_scaled, y_train) y_pred_xgb = xgb_model.predict(X_test_scaled) |
使用相同的指标、相同的真实标签和新获得的预测进行模型评估。
|
1 2 3 |
print("\nXGBoost:") print(" RMSE:", np.sqrt(mean_squared_error(y_test, y_pred_xgb))) print(" R²:", r2_score(y_test, y_pred_xgb)) |
输出
|
1 2 3 |
XGBoost: RMSE: 48493.29955250359 R²: 0.8262909540328014 |
虽然还不是完美的,但我们可以看到预测准确性有了显著的提高:RSME 减少了 30%,R² 从 0.64 增加到近 0.83。
我们还可以分析两个模型的特征重要性,如下所示。对于线性回归模型,我们通过访问模型的 coef_ 和 intercept_ 对象属性来获取系数和偏置项的学习值。
|
1 2 3 4 5 6 7 8 9 |
weights = lr_model.coef_ intercept = lr_model.intercept_ print("\nLinear Regression Model Weights (Coefficients):") for feature, weight in zip(X.columns, weights): print(f" {feature}: {weight}") print("\nLinear Regression Model Intercept:") print(f" {intercept}") |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Linear Regression Model Weights (Coefficients): longitude: -86213.51301116456 latitude: -91473.1604053909 housing_median_age: 14408.8614690844 total_rooms: -17846.275216795897 total_bedrooms: 45971.21052309778 population: -43836.303286778704 households: 20362.11026834444 median_income: 76146.2722814509 Linear Regression Model Intercept: 206580.12749296476 |
这里有两点需要注意:
- 负权重并不意味着相关属性的重要性很低,而是表示影响的方向,即它们如何对更高或更低的预测产生反向贡献。关键是观察其大小或绝对值。
- 如果我们希望观察这种特征归因,推荐进行特征缩放。
那么 XGBoost 集成模型呢?在这种情况下,该模型类型提供了一种非常直观的方式来获取甚至可视化特征的相对重要性,这种方式更具解释性和可比性。
|
1 2 3 |
xgb.plot_importance(xgb_model) plt.title("XGBoost Feature Importance") plt.show() |
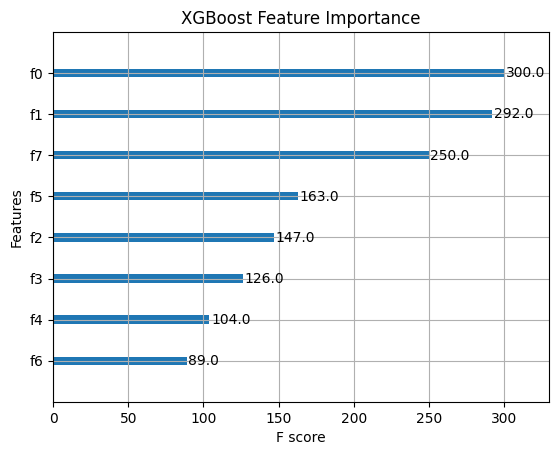
XGBoost 集成模型中的特征重要性
两种模型在赋予相同属性更多重要性方面似乎表现相似,特别是前两个与房屋位置相关的属性(纬度和经度,请参阅数据集链接)。
让我们用一些关于我们刚刚比较的两种模型的一般指导原则和事实来做个总结。
线性回归可以构成一个很好的基线模型,并且由于其简单性和可管理的学习参数数量,通过观察其学习到的权重很容易解释。重要的是,像这样的线性模型在处理主要具有非线性模式的训练数据时可能会受到限制。
XGBoost 在大多数情况下都能显著提高性能,包括本文中使用的住房数据集。由于基于决策树,它具有对复杂、非线性模式和特征之间相互作用进行建模的卓越能力。
结论
本文提供了一个实用的、以示例驱动的比较,比较了构建回归机器学习模型的两种流行选择:线性回归和 XGBoost 集成模型。虽然像线性回归这样的简单模型对于机器学习从业者来说是很好的起点,并且如果数据集足够简单,有时可能足以获得良好的预测,但在大多数情况下,选择一个稍微复杂和灵活的模型,如 XGBoost 集成模型,可能会得到回报,因为它可能产生更优越的结果。




暂无评论。