无论是在机器学习项目、模拟还是其他模型中,您都需要在代码中生成随机数。R 作为一种编程语言,有多种用于生成随机数的函数。在这篇文章中,您将了解它们,并了解它们如何在一个更大的程序中使用。具体来说,您将学习:
- 如何将高斯随机数生成到向量中
- 如何生成均匀随机数
- 如何操作随机向量和随机矩阵
让我们开始吧。

在 R 中生成随机数。
图片由 Kaysha 提供。保留部分权利。
概述
这篇博文分为三部分;它们是:
- 随机数生成器
- 相关多元高斯随机数
- 从均匀分布生成随机数
随机数生成器
随机数是从概率分布中提取的。最著名的分布应该是高斯分布,也称为正态分布。
标准正态分布由其密度函数 $f(x) = (2\pi)^{-1/2} \exp(-x^2/2)$ 定义。它的范围是整个实数,即从负无穷到正无穷。对 $f(x)$ 在此范围内积分结果为 1.0。在数学中,我们有分布函数 $F(x) = \int_{-\infty}^x (2\pi)^{-1/2} \exp(-t^2/2) dt$,定义为在标准正态分布中数字小于 $x$ 的概率。
在 R 中,您不仅有基于标准正态分布的随机数生成函数,还有其他一些辅助函数:
dnorm(x): 密度函数 $f(x)$pnorm(x): 分布函数 $F(x)$qnorm(x): 分位数函数 $F^{-1}(x)$ 作为 $F(x)$ 的反函数rnorm(k): 随机数生成函数
函数 dnorm(x)、pnorm(x)、qnorm(x) 在需要处理其他概率分布的一些项目中会很有用。函数 rnorm(k) 是一个函数,它为您提供一个包含 k 个从标准正态分布中提取的随机值的向量。这是您最常使用的函数。
您可以通过从中获取大量样本并绘制直方图来判断这是生成标准正态分布输出的随机数生成器。
|
1 |
hist(rnorm(10000), breaks=30, freq=FALSE) |
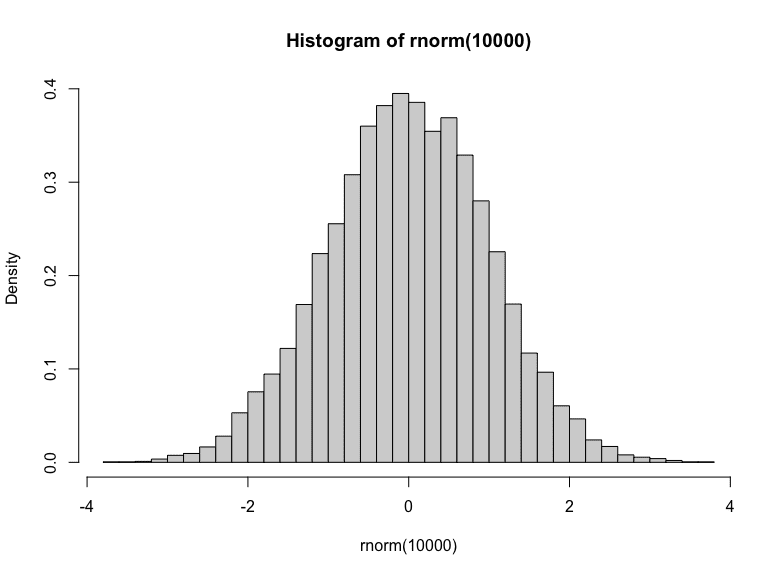
高斯随机数的直方图
您可以在图中看到一个以零为中心的钟形直方图。此外,您还可以看出大部分样本在 -1 到 +1 之间(准确地说,有 68%)。hist() 函数中的 freq=FALSE 参数使 y 轴表示密度而不是频率。因此,您可以将直方图与密度函数进行匹配。
相关多元高斯随机数
标准正态随机数生成器的一个常见用例是创建成对的相关高斯随机数。换句话说,您需要具有非零相关性的二元高斯随机数。
生成这种相关随机数的算法是:
- 首先,生成相同数量的独立标准正态随机数
- 设置协方差矩阵以指定不同随机数之间的关系
- 对协方差矩阵进行 Cholesky 分解
- 将独立标准正态随机数矩阵与 Cholesky 分解矩阵相乘
- 可选地,调整均值
在代码中,它是:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 二元高斯 n_fea <- 2 # 每个观测值的随机值数量 (n) n_obs <- 1000 # 要创建的观测值数量 (k) means <- c(0, 1) # 随机值的均值 vars <- c(1., 1.) # 随机值的方差 corr <- matrix( # 相关矩阵 c(1.0, 0.6, 0.6, 1.0), byrow = TRUE, nrow = 2 ) sd.diag <- diag(sqrt(vars)) cov <- sd.diag %*% corr %*% sd.diag # 协方差矩阵 cholesky <- chol(cov) # Cholesky 分解 obs <- matrix(rnorm(n_fea * n_obs), nrow=n_obs) # n x k 独立同分布高斯随机值矩阵 samples <- (obs %*% cholesky) + rep(means, each=nrow(obs)) print(samples) |
上述代码大部分都很直观。棘手的部分是调整均值:标准高斯随机数以零为中心。从 cholesky <- chol(cov) 行获得的 Cholesky 分解矩阵只能调整协方差,而不能调整均值。要平移均值,您需要对每一列统一添加一个值。在上面,您将向量重复成与随机观测值相同形状的矩阵,以便可以进行加法。
如何判断这是正确的?一种方法是验证统计数据。您可以计算并打印相关矩阵、列均值和列标准差,如下所示:
|
1 2 3 4 5 6 |
... # 验证结果 print(cor(samples)) # 期望与相关矩阵匹配 print(colMeans(samples)) # 期望与样本均值匹配 print(apply(samples, 2, sd)) # 期望与方差匹配 |
这三行应该分别打印经验相关矩阵、均值和标准差。您还可以尝试将随机数绘制成散点图:
|
1 2 3 |
... plot(samples[, 1], samples[, 2]) |
它应该看起来像这样:
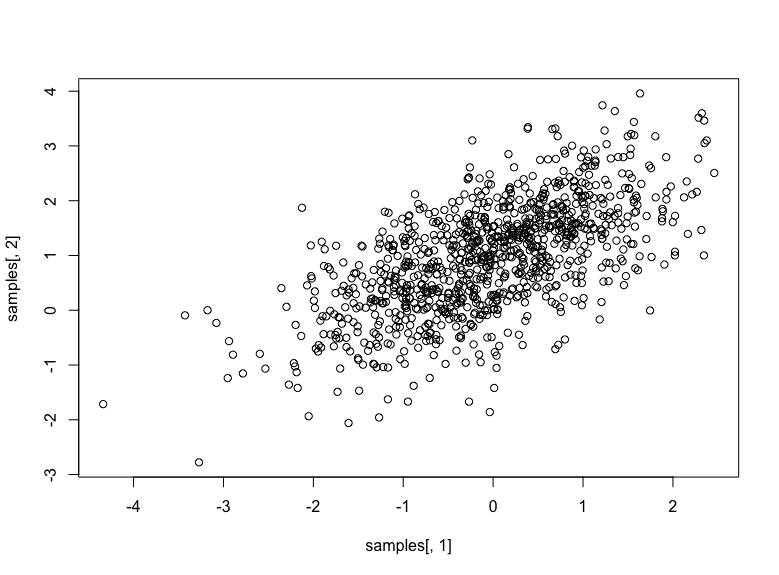
均值在 (0,1) 且相关性为 0.6 的二元高斯随机数
把所有东西放在一起,下面是完整的代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# 二元高斯 n_fea <- 2 # 每个观测值的随机值数量 (n) n_obs <- 1000 # 要创建的观测值数量 (k) means <- c(0, 1) # 随机值的均值 vars <- c(1., 1.) # 随机值的方差 corr <- matrix( # 相关矩阵 c(1.0, 0.6, 0.6, 1.0), byrow = TRUE, nrow = 2 ) sd.diag <- diag(sqrt(vars)) cov <- sd.diag %*% corr %*% sd.diag # 协方差矩阵 chol <- chol(cov) # Cholesky 分解 obs <- matrix(rnorm(n_fea * n_obs), nrow=n_obs) # n x k 独立同分布高斯随机值矩阵 samples <- (obs %*% chol) + rep(means, each=nrow(obs)) print(samples) # 验证结果 print(cor(samples)) # 期望与相关矩阵匹配 print(colMeans(samples)) # 期望与样本均值匹配 print(apply(samples, 2, sd)) # 期望与方差匹配 # 散点图 plot(samples[, 1], samples[, 2]) |
从均匀分布生成随机数
高斯分布是最常用的分布。但有时您会需要不同的分布。一个例子是模拟热线上下一个电话的到达时间。这是指数分布的经典例子。显然,它不是高斯分布,因为高斯随机值可以是负数。
指数分布的密度函数为 $f(x) = \lambda \exp(-\lambda x)$。由于 $x$ 的范围从零到正无穷,分布函数为 $F(x) = 1-\exp(-\lambda x)$。请记住,分布函数的值介于 0 和 1 之间。
对于任意分布函数,您可以使用逆变换采样方法通过均匀分布生成随机数。其思想是您可以将 $F(x)$ 视为标准均匀分布。然后您可以查找 $x$ 的值作为生成的随机数。在这种情况下,您需要定义分布函数 $F(x)$ 的逆函数 $F^{-1}(x)$。
指数分布中的逆函数很简单:设 $y = 1 – exp(-lambda x)$,则 $x = -\log(1-y)/\lambda$。因此 $F^{-1}(x) = -\log(1-y)/\lambda$。在 R 中,您可以按如下方式生成指数分布的随机数:
|
1 2 3 4 5 6 7 8 9 10 |
# 生成遵循指数分布的随机数 lambda <- 2.5 # 参数:到达率 F.inv <- function(x) { return(-log(1-x)/lambda) } n <- 1000 # 要生成的样本数量 x <- runif(n) x <- F.inv(x) print(x) |
在上面,您没有使用 rnorm() 函数,而是使用了 runif() 函数来生成 0 到 1 之间的均匀分布。对于均匀分布,也有一整套函数,例如 dunif() 和 punif()。
如果您从生成的数字绘制直方图,您就会知道生成的数字遵循指数分布:
|
1 |
hist(x, breaks=30, freq=FALSE) |
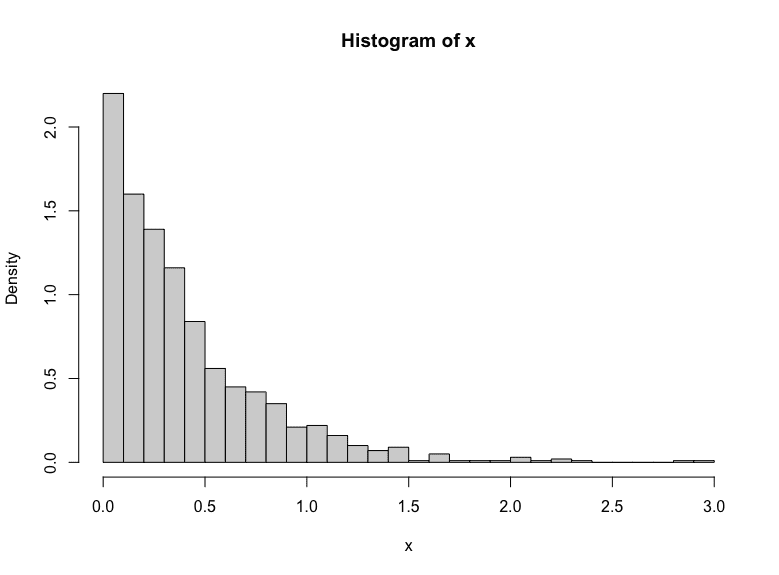
经验生成的指数分布。
当您在 R 中构建离散事件模拟模型时,此技术将非常有用。
进一步阅读
您可以从以下来源了解有关上述主题的更多信息:
网站
总结
在这篇文章中,您学习了如何在 R 中生成随机数。具体来说,您学习了:
- R 中用于概率分布和随机数生成的一系列函数
- 如何创建高斯分布中的随机数
- 如何创建均匀分布中的随机数
- 如何利用随机数生成器创建多元高斯分布或使用逆变换方法创建其他分布。






抱歉,如何在 [0,1]x[0,1] 中生成均匀随机数?