自相关和偏自相关图在时间序列分析和预测中被广泛使用。
这些图表以图形方式总结了时间序列中一个观测值与先前时间步的观测值之间的关系强度。自相关和偏自之间的区别对于时间序列预测的初学者来说可能很难理解和感到困惑。
在本教程中,您将学习如何使用 Python 计算和绘制自相关和偏自相关图。
完成本教程后,您将了解:
- 如何绘制和回顾时间序列的自相关函数。
- 如何绘制和回顾时间序列的偏自相关函数。
- 自相关和偏自相关函数在时间序列分析中的区别。
立即开始您的项目,阅读我的新书 《Python 时间序列预测》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
- 2019 年 4 月更新:更新了数据集链接。
日最低气温数据集
此数据集描述了墨尔本市 10 年(1981-1990 年)的每日最低气温。
单位是摄氏度,共有3650个观测值。数据来源归功于澳大利亚气象局。
下载数据集并将其放在当前工作目录中,文件名为“daily-minimum-temperatures.csv”。
下面的示例将加载最低每日温度数据并绘制时间序列图。
|
1 2 3 4 5 |
from pandas import read_csv from matplotlib import pyplot series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0) series.plot() pyplot.show() |
运行示例将数据集加载为 Pandas Series 并创建时间序列的折线图。
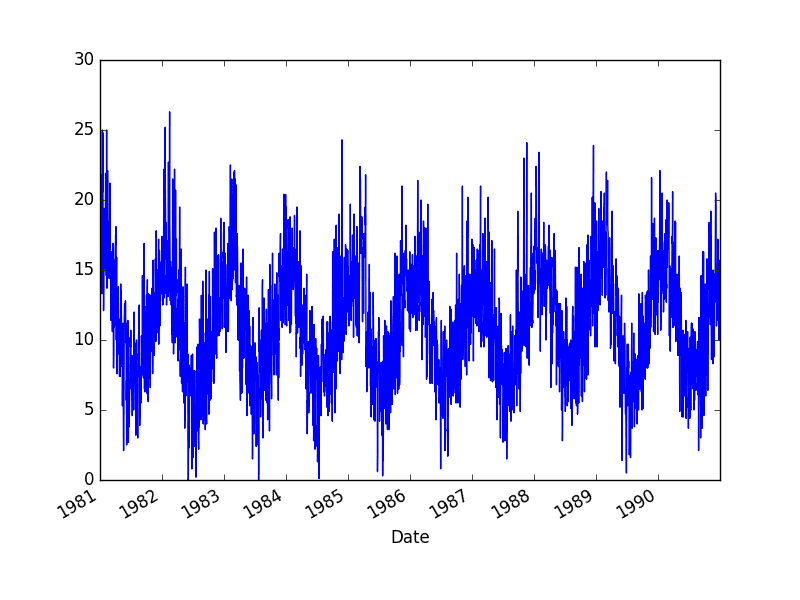
最低每日温度数据集图
停止以**慢速**学习时间序列预测!
参加我的免费7天电子邮件课程,了解如何入门(附带示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
相关性和自相关性
统计相关性总结了两个变量之间关系强度。
我们可以假设每个变量的分布都符合高斯(钟形曲线)分布。如果是这种情况,我们可以使用 Pearson 相关系数来总结变量之间的相关性。
Pearson 相关系数是一个介于 -1 和 1 之间的数值,分别表示负相关或正相关。值为零表示没有相关性。
我们可以计算时间序列观测值与先前时间步的观测值之间的相关性,这被称为滞后。由于时间序列观测值的相关性是与同一序列先前时间的数值计算的,因此这被称为序列相关性,或自相关性。
按滞后绘制的时间序列自相关图称为自相关函数,或缩写 ACF。此图有时称为相关图或自相关图。
下面是使用 statsmodels 库中的 plot_acf() 函数计算和绘制最低每日温度自相关图的示例。
|
1 2 3 4 5 6 |
from pandas import read_csv from matplotlib import pyplot from statsmodels.graphics.tsaplots import plot_acf series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0) plot_acf(series) pyplot.show() |
运行示例将创建一个二维图,显示 x 轴上的滞后值,y 轴上的相关性(介于 -1 和 1 之间)。
置信区间显示为圆锥形。默认情况下,它设置为 95% 的置信区间,这表明超出此范围的相关值很可能表示相关性,而不是统计上的巧合。
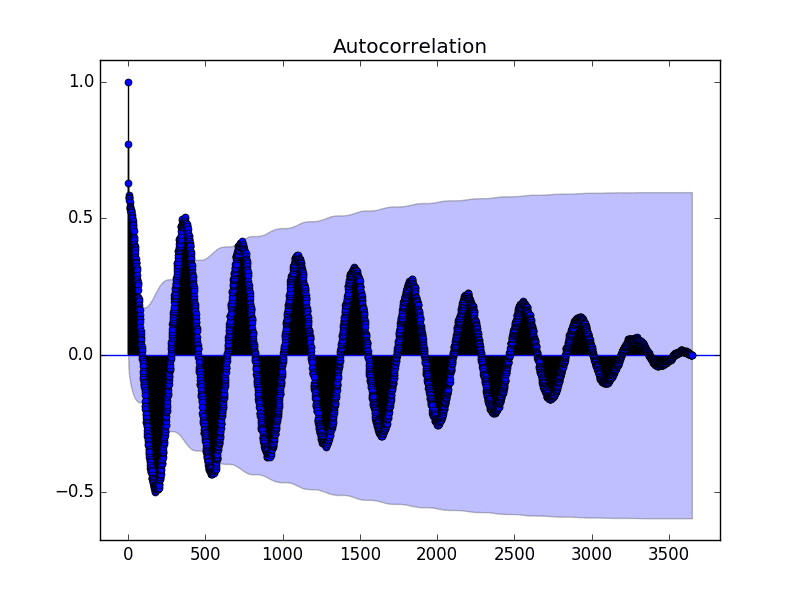
最低每日温度数据集的自相关图
默认情况下,会显示所有滞后值,这会使图表变得混乱。
我们可以将 x 轴上的滞后数限制为 50,以便使图表更易于阅读。
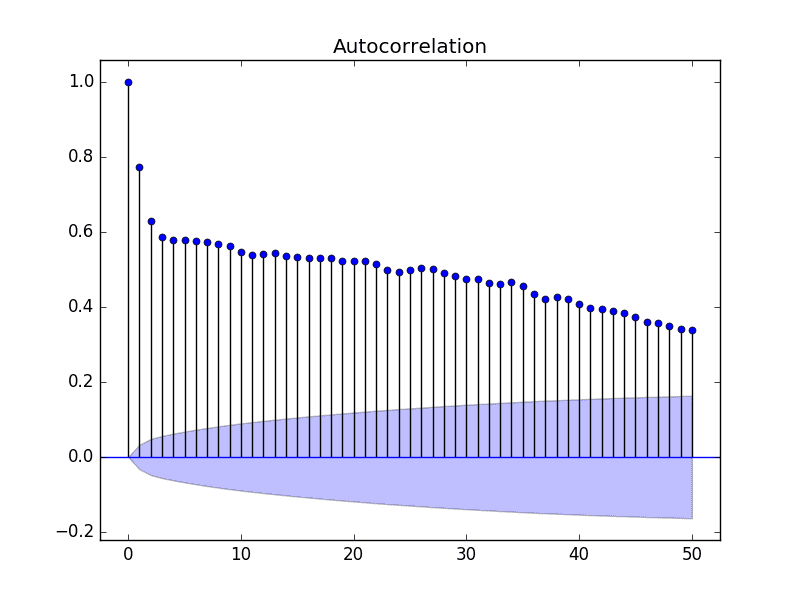
最低每日温度数据集的滞后较少的自相关图
偏自相关函数
偏自相关性是对时间序列中的一个观测值与先前时间步的观测值之间的关系进行的总结,同时消除了中间观测值的影响。
滞后 k 的偏自相关性是消除较短滞后项的任何相关性影响后产生的结果。
— 第 81 页,第 4.5.6 节 偏自相关,《R 语言时间序列入门》。
一个观测值与先前时间步的观测值之间的自相关性包含直接相关性和间接相关性。这些间接相关性是该观测值与中间时间步的观测值之间相关性的线性函数。
正是这些间接相关性是偏自相关函数试图去除的。在不深入数学的情况下,这就是偏自相关的直观理解。
下面的示例使用 statsmodels 库中的 plot_pacf() 函数计算和绘制最低每日温度数据集前 50 个滞后的偏自相关函数图。
|
1 2 3 4 5 6 |
from pandas import read_csv from matplotlib import pyplot from statsmodels.graphics.tsaplots import plot_pacf series = read_csv('daily-minimum-temperatures.csv', header=0, index_col=0) plot_pacf(series, lags=50) pyplot.show() |
运行示例将创建一个显示前 50 个滞后偏自相关性的二维图。
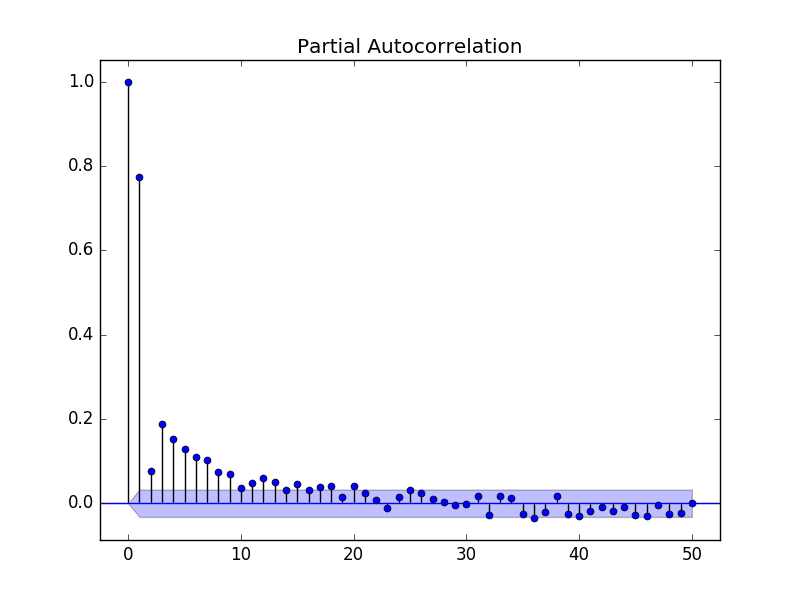
最低每日温度数据集的偏自相关图
ACF 和 PACF 图的直观理解
时间序列的自相关函数和偏自相关函数图讲述了一个非常不同的故事。
我们可以使用上面的 ACF 和 PACF 直观理解来探索一些思想实验。
自回归直观理解
考虑一个由滞后为 k 的自回归 (AR) 过程生成的时间序列。
我们知道 ACF 描述了观测值与先前时间步的观测值之间的自相关性,其中包含直接和间接依赖信息。
这意味着我们预计 AR(k) 时间序列的 ACF 在滞后 k 处会很强,并且这种关系的惯性会持续到后续的滞后值,然后在某个点逐渐减弱,因为效应减弱了。
我们知道 PACF 只描述了观测值与其滞后之间的直接关系。这表明滞后值超过 k 将没有相关性。
这正是 AR(k) 过程的 ACF 和 PACF 图的预期。
移动平均直观理解
考虑一个由滞后为 k 的移动平均 (MA) 过程生成的时间序列。
请记住,移动平均过程是时间序列残差误差的自回归模型,这些误差来自先前的预测。另一种思考移动平均模型的方式是,它会根据近期预测的错误来纠正未来预测。
我们预计 MA(k) 过程的 ACF 在滞后 k 处与近期值会显示出很强的相关性,然后急剧下降至低或无相关性。根据定义,该过程就是这样生成的。
对于 PACF,我们预计该图在滞后处会显示出很强的关系,并且从滞后开始相关性会逐渐下降。
同样,这正是 MA(k) 过程的 ACF 和 PACF 图的预期。
进一步阅读
本节提供了一些有关时间序列自相关和偏自相关的进一步阅读资源。
- Wikipedia 上的相关性和依赖性
- Wikipedia 上的自相关性
- Wikipedia 上的相关图
- Wikipedia 上的偏自相关函数。
- 第 3.2.5 节 偏自相关函数,第 64 页,《时间序列分析:预测与控制》。
总结
在本教程中,您学习了如何使用 Python 为时间序列数据计算自相关和偏自相关图。
具体来说,你学到了:
- 如何计算和创建时间序列数据的自相关图。
- 如何计算和创建时间序列数据的偏自相关图。
- 解释 ACF 和 PACF 图的区别和直观理解。
您对本教程有任何疑问吗?
在下面的评论中提出你的问题,我会尽力回答。







无法下载数据集。抛出错误
抱歉,我已修复链接。
我一点也不喜欢这篇帖子。
您无法或不愿创建一个真实的示例,并说明那些“间接关系”是什么,它们与相关观测值如何相关。一切都完全是抽象的,没有任何切实的、贴近现实的案例。
一个观测值与先前时间步的观测值之间的自相关性包含直接相关性和间接相关性。这些间接相关性是该观测值与中间时间步的观测值之间相关性的线性函数。
如果您无法将其转化为具体的事物,那对我来说毫无意义。
很抱歉让您感到沮丧。
这是一个使用 ACF/PACF 图直接确定 p 和 q 值的示例
https://machinelearning.org.cn/time-series-forecast-study-python-monthly-sales-french-champagne/
我相信还有许多类似的示例,您可以使用博客搜索。
我建议使用网格搜索,它更有效
https://machinelearning.org.cn/grid-search-arima-hyperparameters-with-python/
我在之前的示例中也对此进行了演示。
此外,这本书涵盖了所有这些以及更多内容。
https://machinelearning.org.cn/introduction-to-time-series-forecasting-with-python/
感谢您平静的回复,特别是您提供的第一个链接,我现在就去查看。
顺便说一句,您的书也很棒,所以感谢您(我承认我……是在网上找到的,但请您放心,一旦我找到工作和/或建立起一个有利可图的交易系统,我会买几本 :))。
谢谢。
谢谢 🙂
不客气,Yasha。
我有一个可能很蠢的问题。我正在 Anaconda Prompt 上运行命令。当我输入 `series.plot()` 时,我得到一个错误“数据框中没有整数”。我检查了数据集,它确实包含整数值。我是否遗漏了什么特别之处?
你好,Yasha,
请仔细检查数据文件,用文本编辑器打开并确保没有页脚数据。
另外,查找并删除文件中的“?”字符。
如果仍然出现错误,请告诉我,并在评论中粘贴。
嗨,Jason,
我目前正在使用带有滑动窗口的 MLP 模型来预测时间序列的未来值。一个似乎至关重要的超参数是窗口的大小(网络输入的神经元数量)。我想知道这个值是否必须像通常使用 ARIMA 模型那样,通过研究序列的 ACF/PACF 图来确定?我很难找到明确讨论此超参数的文档。
提前感谢
我建议进行 ACF/PACF 分析。
我也建议对窗口大小进行网格搜索。
我认为这篇帖子/教程中的链接指向了错误的数据集。
https://datamarket.com/data/set/2328/daily-rainfall-in-melbourne-australia-1981-1990#!ds=2328&display=line
你说得对,我已经修复了。
在此处获取数据
https://datamarket.com/data/set/2324/daily-minimum-temperatures-in-melbourne-australia-1981-1990#!ds=2324&display=line
嗨,Jason,
我在您的帖子/教程中搜索了,但我找不到使用降雨历史的示例。您是否有这样的帖子可以进行预测?
我有很多关于如何进行预测的帖子,例如
https://machinelearning.org.cn/make-sample-forecasts-arima-python/
先生,我正在重新发布这个问题,因为我也阅读了这篇博文,但仍然感到困惑。
我正在对我的 CDR 数据集应用 ARIMA 模型。我已通过 Augmented Dickey-Fuller 检验检查出我的数据是非平稳的
ADF 统计量: -1.569036
p 值: 0.499127
临界值
1%: -3.478
10%: -2.578
5%: -2.882
然后我绘制了 ACF,它显示我的前 15 个滞后值的自相关值大于 0.5。所以我设置参数 'p' 为 15(p = 15 正确吗?),'d' 为 1 用于平稳性。您能否指导我如何找到移动平均 MA(q) 参数 q 的值?
我能否通过可视化 ACF 图来确定 'q' 参数的值?
谢谢
是的,查看 PACF 图和 ACF 图,然后阅读“移动平均直观理解”部分。
如果这仍然没有帮助,请尝试网格搜索。
https://machinelearning.org.cn/grid-search-arima-hyperparameters-with-python/
嗨,Jason,
是否可以自动进行 PACF 和 ACF 图的审查?
也许可以。或者,您可以对模型的 p/q 值进行网格搜索(这是我的首选方法)。
你好先生
正如我在上一个问题中告诉您的,我正在对我的 CDR 数据集应用 ARIMA 模型。我已经通过迪基富勒检验确定我的序列是平稳的,
然后我绘制了 ACF 和 PACF。在 ACF 图中,我的前 12 个滞后的 AC 值大于 0.5,而在 PACF 图中,前两个滞后的 PAC 值大于 0.5,前 4 个滞后的 PAC 值大于等于 0.2。因此,我将 'p' 设置为 12,'p' 设置为 4,d 设置为 1 用于平稳性(这些参数值是否正确?)。
其次,当我设置这些值为 ARIMA(12,1,4) 时,我收到以下错误:
“ValueError: computed initial AR coefficients are not stationary
您应该引入平稳性,选择不同的模型顺序,或者您可以
pass your own start_params。”
当我设置 ARIMA(12,1,2) 时,我也收到同样的错误。为什么?
第三,当我使用网格搜索 ARIMA 时,它显示最佳 ARIMA(1,0,1),为什么?
我阅读了您的许多博文,但仍然感到困惑。
您能否指导我?
谢谢
不知道,也许可以尝试一个大的 d?
也许可以尝试手动准备数据?
很棒的解释。谢谢!
很高兴它有帮助。
谢谢!这是一个很好的入门介绍。
最好的,bue
谢谢 Elmar。
好东西!一个简洁的教程。
谢谢。
嗨,Jason,
由于我无法通过 SSMS 显示 Python 图表,我想将 ACF 和 PACF 保存为 png 文件,而不是使用 pyplot.show() 显示它们。
您能否向我展示一下如何做到这一点?提前感谢!🙂
您可以使用
感谢 Jason 的文章。我刚开始接触机器学习,只有基本的统计知识。所以我还不能解释图表。
前两个图表很有意义。但另外两个图表“最低每日温度数据集的自相关图”和“最低每日温度数据集的滞后较少的自相关图”告诉我什么?
提前感谢您的帮助。
也许可以看看标题为“偏自相关函数”的部分。
这有帮助吗?
非常感谢 Jason。
不客气。
非常感谢 Jason。您在博客中展示的内容非常有价值,置信区间代表什么?我不太明白为什么那些超出置信区间的 ACF 值是有意义的!您能解释一下吗?
您可以在这里了解更多关于置信区间的信息。
https://machinelearning.org.cn/confidence-intervals-for-machine-learning/
嗨,Jason,
我想知道为什么置信区间是圆锥形的,而不是“正常的”水平线。
您是否知道这背后的理论依据?
祝好,
Nikos
我猜和你一样。
嗨,Jason,
您能否用更基础的术语解释一下移动平均模型的作用?移动平均模型是如何进行预测的?我之所以问,是因为您说移动平均模型是对预测误差的自回归。
MA 是误差分量的自回归,误差分量来自每个先前的观测值。
你可以在这里了解更多
https://machinelearning.org.cn/model-residual-errors-correct-time-series-forecasts-python/
嗨,Jason,
您能解释一下如何最好地找到 p,q 和 d 吗?
是的,使用网格搜索。
https://machinelearning.org.cn/grid-search-arima-hyperparameters-with-python/
嗨 Jason,感谢您的教程,我只想问一下关于选择 p 系数的问题,我已经显示了我序列的前 50 个滞后,我发现相关性的最大值出现在滞后 47,但当我测试它时,它显示了一个错误消息(
ValueError:计算出的初始 AR 系数不平稳
您应该引入平稳性,选择不同的模型顺序,或者您可以
pass your own start_params.)。
那么选择 p 的最佳方法是什么?以及我们如何构建网格搜索方法的 p 值输入列表?
谢谢你
我推荐网格搜索,这是一个例子。
https://machinelearning.org.cn/grid-search-arima-hyperparameters-with-python/
你好,
当我尝试“手动”计算 Python 中的自相关时
val = pd.DataFrame(series.values)
lag = 2200
shifted = val.shift(lag)
dataframe = pd.concat([shifted, val], axis = 1)
dataframe.columns = [‘t’, ‘t+lag’]
result = dataframe.corr()
print(result)
对于 lag = 2200,我得到的 corr = 0.554,而 plot_acf 或 autocorrelation.plot 的自相关图 1. 随着滞后的增加而减小,2. 在 0.25 的水平。总的来说,我的计算相关性图与 plot_acf 或 autocorrelation.plot 差异很大。
我的计算有什么问题?我只是遵循了您在“Python 时间序列预测”中的代码片段 > p. 190, Listing 22.2
提前感谢您的解释:)
此致,
Andy
区别在于 ACF 计算的是每个示例与 t-1 和 t-2 等的关联。
您只计算了 t-1 的相关性。
感谢这篇帖子,但我仍然没有理解 ACF 和 PACF 的直观概念。
在您考虑的温度示例中(特别是过去 50 天(滞后)),ACF 显示出很强的相关性,而 PACF 立即消失了,这表明间接度量很强,因此 ACF 缓慢消失,而直接度量则不那么强。如果我的理解是正确的,我应该得出什么结论?
我赞扬您进行了非常清晰的解释。
谢谢。
嗨,首先感谢您的所有工作。我未能理解的一点是如何通过 ACF 和 PACF 图来决定 ARMA 模型的阶数?
谢谢你。
我在那里更详细地解释了如何解释它们。
https://machinelearning.org.cn/gentle-introduction-box-jenkins-method-time-series-forecasting/
此外,我在这里展示了如何进行值的网格搜索(可能更可靠)。
https://machinelearning.org.cn/grid-search-arima-hyperparameters-with-python/
我明白了为什么自相关从 1 开始,然后逐渐变为负数,当移动到 182 天时,然后在 365 天的倍数处达到最大值。
但是为什么它会逐渐趋于零?您应该期望两年后的相关性与一年后的相同。
这种模式在正弦波的自相关中也很常见。无论有多少个周期,自相关都会交替出现并趋于零。
发生了什么?代码是否用零填充了未知数据(例如:t-500 对于第一个数据点)?
很好的问题。
3 年后的自相关比 2 年后的自相关差,因为第二年的观测值与第三年的共同点比现在多。这是有道理的。
我们希望消除这种影响,而这正是 PCAF 所能实现的。
为什么 2019 年 4 月 12 日的温度与 2018 年 4 月 12 日的温度比与 2017 年的温度有更多的共同之处?为什么它们与 2009 年 4 月 12 日的温度没有任何共同之处?
更糟糕的是,如果数据集的开头是 1999 年,为什么它们会与 2009 年有更多的共同之处?
感谢您的回复——我非常感谢能与您一起解决这个问题。
很好的问题!
通常在时间序列中,“接近”的观测值之间存在很强的线性依赖关系。对于季节性数据,“接近”意味着一个或多个周期。
从统计学角度来看,大部分依赖关系可以用一两个接近的观测值来解释,而来自更远观测值的贡献则非常小。
这是有道理的,因为我们期望今天的数据比昨天更像昨天,比上周更像上周。去年比前年更像今年。至少平均而言。
这有帮助吗?
我仍然很困惑,但感谢您的耐心。
我明白为什么今天比昨天更像昨天,比上周更像上周。现在是春天,上周天气更冷。
我只是不明白为什么去年的四月会比前一年更相似。对于成千上万年的四月来说,天气似乎大致相同。但时间序列的开头却显示出零相似性。
我通过生成正弦曲线进行了检查,正弦曲线的模式在每个周期都精确地重复——但结果仍然相同。
我错过了一些关于它在做什么的信息。
是的,但一个序列可以在周期内有一般的上升或下降趋势,并且通常会这样做。
同样,我们不是在谈论观测值之间的绝对差异/相似性。相反,我们讨论的是有多少信号可以被解释(或在一个简单的线性模型中依赖)。我们可以用周期中的先前观测值来解释很多,之后的回报会递减。
Mike 和 Jason。这个问题是否与所谓的(我们姑且称之为)直接 1 / n 离散自相关以及另一方面无偏的 1 / (n-k) 自相关有关?我注意到,Mike 似乎也注意到了,即使是纯粹的正弦伪数据,也会发生以下情况:典型的/直接的自相关,对于长时序和较大的滞后值,最终会趋于零。理论上这不应该发生(对于连续情况),所以它必须处理离散估计量的有偏性/无偏性。无偏自相关不会出现这个问题——或者如果会出现,那也会是在比我测试的数据更大、滞后值更大的情况下。对于大的 n 和相对大的滞后 k,很容易看出 1 / (n-k) 可以是 1 / n 的 3、4 倍,甚至 6 倍。因此,它显然会缓解滞后尾部的零化。在 Py 包 statsmodels.tsa.stattools.acf 中,acf 对象可以选择典型版本和无偏版本。希望这能在四个月后回答您的问题!
说得好,感谢分享!
也许我开始明白了?
以正弦周期为例(规律重复,类似于温度但没有噪声),它在自相关中显示出相同的周期逐渐下降到零。
假设自相关只查看无法通过先前观测值解释的信息(这是完全有道理的)。我认为它应该在一个周期(365 天)后降至零。
如果这是重复的,请原谅。我试图理解,因为我相信对这个工具的良好理解将对我正在解决的问题非常有帮助。
先生,您能否告诉我 PACF 图中滞后峰值在置信区间内或不在 95% 置信区间范围内有什么意义?这与查找 p 值有什么关系?
将小于 95%。
在此处了解更多关于 p 值的信息。
https://machinelearning.org.cn/faq/single-faq/how-do-i-interpret-a-p-value
你好 Jason,
在使用 PACF/ACF 之前,是否需要应用任何幂转换(YJ 或 Box-Cox)?谢谢。
是的,在转换之前和之后,以了解转换对您的数据有什么影响。
您说“之后”是什么意思?
如果我们使用 PACF 进行特征选择(滞后选择),是否有必要在选择滞后之前应用 PT?
通常,我喜欢在每次转换之前和之后审阅和建模数据,以确认它增加了预测的技能。
嗨,Jason,
ACF 和 PACF 用于查找 ARIMA 模型的 p 和 q 参数。因此,我开始绘制两者,并发现了两种不同的情况。在 PACF 中,滞后 0 和 1 的值接近 1.0,而其他滞后的值接近 0.05,但从不低于显著线。在这种情况下,我认为很容易选择,所以我取 1 作为 p 项。在 ACF 的情况下,选择起来更困难,因为滞后 0 的值接近 1.0,而其他值线性下降到滞后 350,这是最后一个超过显著线的滞后。
我无法使用迭代方法,因为我的数据量太大。
也许可以尝试处理一小部分数据,并抽查一套模型配置?
嗨,Jason,
感谢这篇文章。我有一个疑问,请您看看能否解答。
我下载了 csv 文件,如附件所示,修改了 Temp 字段的值,其变化类似于正弦波。数值如下
日期
1981-01-01 0
1981-01-02 1
1981-01-03 2
1981-01-04 3
1981-01-05 2
1981-01-06 1
1981-01-07 0
1981-01-08 -1
1981-01-09 -2
1981-01-10 -3
1981-01-11 -2
1981-01-12 -1
1981-01-13 0
1981-01-14 1
1981-01-15 2
1981-01-16 3
1981-01-17 2
1981-01-18 1
1981-01-19 0
1981-01-20 -1
1981-01-21 -2
1981-01-22 -3
1981-01-23 -2
1981-01-24 -1
1981-01-25 0
现在我尝试找出第 12 个滞后的相关性
series = Series.from_csv(‘daily-minimum-temperatures.csv’, header=0)
values = DataFrame(series.values)
values_shift = values.shift(12)
df=concat([values, values_shift], axis=1)
df.columns = [‘t’, ‘t-12’]
print df.corr()
t t-12
t 1.0 1.0
t-12 1.0 1.0
plot_acf(series)
pyplot.show()
但是当我执行 plot_acf 时,它显示第 12 个滞后的值为 0.5。您能否指导我 plot_acf 在这个滞后处如何计算自相关性?
嗨,Json,
我想我明白了。plot_acf 将相关性乘以 %采样数。
correlation*(totalsample-lag)/(totalsamples)
所以在上面的例子中,总采样数为 25。
滞后 12 时的相关性为 1。
所以 plot_acf 计算为 = 1 *(25-12)/25=.5
很高兴听到这个消息。
0.5 的相关性很高。
问题究竟是什么?
嗨,Jason,
我再说一遍这个问题。我下载了“daily_minimum_tempretures.csv”。然后修改了“temp”列中的值,使其从 0 上升到 3,然后从 3 下降到 0,然后从 0 下降到 -3,再从 -3 上升到 0,每隔一年间隔 1 天,从 1981 年 1 月 1 日到 1981 年 12 月 1 日。然后相同的模式重复了另外三年。
现在我们形成了 4 个数据帧,它们分别滞后 0、12、24、36。
series = Series.from_csv(‘daily-minimum-temperatures.csv’, header=0)
values = DataFrame(series.values)
values_shift_12= values.shift(12)
values_shift_24= values.shift(24)
values_shift_36= values.shift(36)
df=concat([values, values_shift_12, values_shift_24, values_shift_36], axis=1)
df.columns = [‘t’, ‘t-12’, ‘t-24’, ‘t-36’]
print df
t t-12 t-24 t-36
0 0 NaN NaN NaN
1 1 NaN NaN NaN
2 2 NaN NaN NaN
3 3 NaN NaN NaN
4 2 NaN NaN NaN
5 1 NaN NaN NaN
6 0 NaN NaN NaN
7 -1 NaN NaN NaN
8 -2 NaN NaN NaN
9 -3 NaN NaN NaN
10 -2 NaN NaN NaN
11 -1 NaN NaN NaN
12 0 0.0 NaN NaN
13 1 1.0 NaN NaN
14 2 2.0 NaN NaN
15 3 3.0 NaN NaN
16 2 2.0 NaN NaN
17 1 1.0 NaN NaN
18 0 0.0 NaN NaN
19 -1 -1.0 NaN NaN
20 -2 -2.0 NaN NaN
21 -3 -3.0 NaN NaN
22 -2 -2.0 NaN NaN
23 -1 -1.0 NaN NaN
24 0 0.0 0.0 NaN
25 1 1.0 1.0 NaN
26 2 2.0 2.0 NaN
27 3 3.0 3.0 NaN
28 2 2.0 2.0 NaN
29 1 1.0 1.0 NaN
30 0 0.0 0.0 NaN
31 -1 -1.0 -1.0 NaN
32 -2 -2.0 -2.0 NaN
33 -3 -3.0 -3.0 NaN
34 -2 -2.0 -2.0 NaN
35 -1 -1.0 -1.0 NaN
36 0 0.0 0.0 0.0
37 1 1.0 1.0 1.0
38 2 2.0 2.0 2.0
39 3 3.0 3.0 3.0
40 2 2.0 2.0 2.0
41 1 1.0 1.0 1.0
42 0 0.0 0.0 0.0
43 -1 -1.0 -1.0 -1.0
44 -2 -2.0 -2.0 -2.0
45 -3 -3.0 -3.0 -3.0
46 -2 -2.0 -2.0 -2.0
47 -1 -1.0 -1.0 -1.0
所以这里我们可以看到,从第 12 行开始,t 和 t-12 列的值在每个区间都相同。对于 t-24 和 t-36 列,从第 24 行和第 36 行开始,情况也一样。换句话说,所有这些列的相关性都是 1。
print df.corr()
t t-12 t-24 t-36
t 1.0 1.0 1.0 1.0
t-12 1.0 1.0 1.0 1.0
t-24 1.0 1.0 1.0 1.0
t-36 1.0 1.0 1.0 1.0
当我们绘制 acf_plot 时
plot_acf(series)
pyplot.show()
我们发现在滞后 12、24 和 36 处的 ACF 值分别为 0.75、0.5 和 0.25。
我最初认为 ACF 在某个滞后处是当前时间与该滞后之间的相关性。但后来我明白了,滞后值在计算 ACF 中也起着重要作用。
在这种情况下
第 n 个滞后的 ACF = (当前时间与第 n 个滞后之间协方差) / 当前时间的方差 * (采样数据数 - n) / 采样数据数
第 0 个滞后的 ACF = 1*(48-0)/48=1
第 12 个滞后的 ACF = 1*(48-12)/48=.75
第 24 个滞后的 ACF = 1*(48-24)/48=.5
第 36 个滞后的 ACF = 1*(48-36)/48=.25
ACF 在第 n 个滞后的实际公式是 = (当前时间数据与第 n 个滞后之间协方差) / 当前时间方差
谢谢,
Sanjeev Patro
谢谢,
Sanjeev patro
干得不错。
我有一个问题——当我从 statsmodels 运行 acf 函数并将 alpha 设置为返回置信区间时,那些值很接近,但与运行 plot_acf 时显示的圆锥不匹配,所以实际上没有一个 acf 值超出了圆锥。您知道差异可能在哪里吗?
暂时不知道,抱歉。
也许可以确认两个情况下的区间是否匹配,例如,它们是否都是 95% 百分位数或其他什么?
事实上,在我评论大约 15 分钟后我就找到了答案,但我找不到我的评论,所以我直到现在才回复。圆锥图中的值实际上是 acf 值减去置信区间(上限或下限),由 acf 函数计算。
很高兴听到这个消息。
很棒的教程。谢谢!!
谢谢,很高兴它帮到了你!
嗨,Jason,我有一个问题,根据上面的 ACF 和 PACF 图,我应该为 ARMA 模型选择什么值,为什么?
也许可以重新阅读上面的帖子,它解释了如何选择合适的 d 和 q 值。
还可以看看其他教程,它们在构建模型时演示了这种分析,例如
https://machinelearning.org.cn/time-series-forecast-study-python-annual-water-usage-baltimore/
好的,非常有帮助,非常感谢。
不客气。
嗨
如何手动计算数据的 acf 的示例。
谢谢你
感谢您的建议。
小的修正:数据文件名为 daily-min-temperatures.csv,但代码调用的是 daily-minimum-temperatures.csv。
谢谢,请注意这一行
“下载数据集并将其放在当前工作目录中,文件名为‘daily-minimum-temperatures.csv’。”
我根据同一产品的认证参考样品的测定值对制造批次的产品进行化学测定。
我是否应该期望一系列制造批次,与相同的参考样品相比,其测定值是自相关的?
如果是,那么制造批次系列的标准差是否会产生偏差?
我不知道,抱歉。
嗨,Jason,
感谢您发布如此有用的博文。我从它们中学到了很多。我对使用的数据有一个疑问。
我在汽车领域工作,拥有离合器温度的测试数据。数据大致描述如下:
采样间隔为 20 毫秒。
值从大约 20 度开始,上升到 200 度,然后下降到大约 50 度(这是执行实验的性质)。
有多个包含此类数据的文件。
现在我需要分析所有这些数据文件以进行 ARIMA 分析。我正在考虑将这些文件合并到一个数据框中,但最大的问题是,一个文件的结束是 50 度,而下一个文件的开始是 20 度,这会产生一个不现实的突然下降。
您能否推荐一种正确合并文件以供使用的方法?或者您认为更好的方法?很抱歉写了这么长的帖子,但我非常期待您的帮助。
此致,
Gopal
也许将其合并为一个时间序列,以便观测值是连续的。
也许进行实验以查看是否确实需要所有数据。
感谢您的回复 Jason。我的快速跟进
“也许将其合并为一个时间序列,以便观测值是连续的。”:您建议如何实现这一点?在文件末尾和下一个文件开头之间进行插值是否有帮助?
“也许进行实验以查看是否确实需要所有数据。”:您能否详细说明?数据文件只是对同一实验执行多次且略有不同的数据。
我不明白您想实现什么,抱歉。不确定我能帮上什么忙。
嗨
虽然我不是专家,但出于好奇,我还是想评论一下!
在您的实验中,离合器温度与时间成正比,其他参数保持不变。温度应持续升高,直到发动机卡死/发动机机油烧干。这意味着第一次实验结束了。
我不确定在实验过程中离合器板的温度如何降至 50 度,除非您更改参数。在这种情况下,下一个实验的数据不能与前一个实验的数据一起视为时间序列。这两个数据集完全不同。
如果这没有意义,请忽略。
此致
维韦克
工作很棒。如果您能告诉我“p”和“q”的值是多少,一切都会变得清晰明了!
它们是 ARIMA 模型的超参数。
https://machinelearning.org.cn/arima-for-time-series-forecasting-with-python/
很棒,非常有用,正是我需要的,谢谢你 man。
谢谢,很高兴能帮到您!
非常感谢您的文章。pandas.plotting.autocorrelation_plot 是否应该显示与本文使用的 statsmodels plot_acf 相同的值?
也许可以,取决于实现是否相同。
感谢您的回复。您所说的实现是指什么?它们似乎为本文中的练习给出了不同的结果。
谢谢 Jason。经过一些调整,我已经让它们一致了。
太棒了!
它们是不同库中的函数,因此它们的实现会有所不同。从而产生不同的结果。
嗨 Jason。感谢您发表这篇很棒的帖子。
我尝试绘制 ACF 和 PACF。ACF 是合理的,但 PACF 显示的值大于 1,例如 4。
您知道为什么我会得到这样的值吗?
是的,ACF/PACF 为您提供了如何配置 ARIMA 模型的 q/p 值的提示。
但我的意思是,它们的值不应该在 -1 和 +1 之间吗?
啊,我明白了。是的,我期望值在这个范围内。也许我错了——请检查该函数的 API 文档。
我们能否将空间自相关纳入机器学习算法,如 xgboost?
我曾对空间数据运行 xgboost 并测试了残差的自相关性(全局 Moran's I)。残差是聚集的。我想知道如何解决这个问题?
也许更适合 CNN-LSTM 等模型,例如时空模型。
是否有办法计算多元时间序列的自相关性?
你好 Panagiota……在这种情况下,您要寻找的是“互相关性”,而不是“自相关性”。
https://www.statology.org/cross-correlation-in-python/
嗨,Jason,
感谢您的教程。我的数据存在自相关问题,所有超出圆锥的滞后都存在。您在教程中遗漏了解释如果您的数据存在自相关怎么办,这是否是一个问题?如果是,如何在给定我将使用 LSTM 来训练我的数据的情况下解决它?
嗨 Keeva……自相关只是“衡量”数量之间相对关系的一种方式。它不是“好”或“坏”。
以下内容可能有助于阐明。
https://www.statisticssolutions.com/dissertation-resources/autocorrelation/
在我的时间序列中,我每天都有一个变量 X 的测量值。我使用过去两个观测值(D 和 D-1)来预测前一天(D+1)。在进行了自相关研究后,我通过 ACF 发现滞后 D-7 和 D-14 比 D 和 D-1 具有更高的相关性(这对我来说是有意义的,因为 D-7 代表一周前的同一天,D-14 代表两周前的同一天)。所以,我将它们作为输入用到我的模型中,但实际上我的预测结果比使用 D 和 D-1 时更差。
有什么想法可能导致这个问题?
嗨 Jason,我是 Vinay。感谢您提供如此直观的理解,但我仍然不清楚我的疑问。我正在处理一个基于传感器的时序数据,我需要预测 OilTemperature,但在我的情况下,在进行预处理和过滤非零 OilTemperature 数据后,我的 ACF 和 PACF 图有两种变体:一种 ACF 恒定且高于阈值线,而另一种则逐渐下降。
在两种情况下如何解释结果?
这是否意味着我的数据在第一种情况下是平稳的,而在第二种情况下是非平稳的?
请帮助我理解这一点。
你好 Vinay……你或许可以考虑将深度学习模型用于此目的。
https://machinelearning.org.cn/start-here/#deep_learning_time_series