梯度下降是一种优化算法,它沿着目标函数的负梯度方向移动,以找到函数的最小值。
梯度下降的一个局限性在于,对于所有输入变量都使用单一的步长(学习率)。梯度下降的扩展,如自适应动量估计(Adam)算法,为每个输入变量使用独立的步长,但可能会导致步长迅速减小到非常小的值。
AMSGrad是梯度下降的Adam版本的扩展,旨在提高算法的收敛性,避免为每个输入变量的学习率发生大的突然变化。
在本教程中,您将了解如何从头开始开发AMSGrad的梯度下降优化。
完成本教程后,您将了解:
- 梯度下降是一种优化算法,它利用目标函数的梯度来导航搜索空间。
- AMSGrad是梯度下降的Adam版本的扩展,旨在加速优化过程。
- 如何从头开始实现AMSGrad优化算法,并将其应用于目标函数并评估结果。
开始您的项目,我的新书机器学习优化,包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
从零开始用AMSGrad实现梯度下降优化
照片来源:Steve Jurvetson,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- 梯度下降
- AMSGrad优化算法
- 带有AMSGrad的梯度下降
- 二维测试问题
- 带有AMSGrad的梯度下降优化
- AMSGrad优化可视化
梯度下降
梯度下降是一种优化算法。
它在技术上被称为一阶优化算法,因为它明确使用了目标函数的一阶导数。
一阶方法依赖梯度信息来帮助指导寻找最小值……
——第69页,《优化算法》,2019年。
一阶导数,或简称为“导数”,是目标函数在特定点(例如,对于特定输入)的变化率或斜率。
如果目标函数有多个输入变量,则称为多元函数,输入变量可以视为一个向量。反过来,多元目标函数的导数也可以视为一个向量,通常称为梯度。
- 梯度:多元目标函数的一阶导数。
导数或梯度指向特定输入处目标函数最陡峭上升的方向。
梯度下降指一种最小化优化算法,它沿着目标函数的负梯度方向“下坡”移动,以找到函数的最小值。
梯度下降算法需要一个正在优化的目标函数和目标函数的导数函数。目标函数*f()*为给定的一组输入返回一个分数,而导数函数*f'()*为给定的输入集提供目标函数的导数。
梯度下降算法需要问题中的一个起点(x),例如输入空间中随机选择的一个点。
然后计算导数,并在输入空间中迈出一步,预计会导致目标函数下坡移动(假设我们正在最小化目标函数)。
通过首先计算在输入空间中移动的距离(计算为步长(称为 alpha 或学习率)乘以梯度),来进行下坡移动。然后将其从当前点减去,确保我们沿着梯度反方向移动,即沿着目标函数的下坡方向。
- x(t) = x(t-1) – step_size * f'(x(t))
给定点处目标函数越陡峭,梯度的幅值越大,反之,在搜索空间中迈出的步长也越大。所迈步长的大小由步长超参数进行缩放。
- 步长:控制算法每次迭代中逆着梯度在搜索空间中移动距离的超参数。
如果步长太小,在搜索空间中的移动会很小,搜索将花费很长时间。如果步长太大,搜索可能会在搜索空间中跳跃并跳过最优解。
现在我们已经熟悉了梯度下降优化算法,让我们来看看AMSGrad算法。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
AMSGrad优化算法
AMSGrad算法是自适应动量估计(Adam)优化算法的扩展。更广泛地说,它是梯度下降优化算法的扩展。
该算法由J. Sashank等人于2018年发表在题为“关于Adam及其后续的收敛性”的论文中。
通常,Adam会自动为优化问题中的每个参数自适应地调整一个独立的步长(学习率)。
Adam的一个局限性在于,它可以在接近最优解时减小步长(这是好的),但在某些情况下也会增加步长(这是坏的)。
AdaGrad 专门解决了这个问题。
… ADAM 大幅度增加了学习率,然而 […] 这可能对算法的整体性能产生不利影响。 […] 相比之下,AMSGRAD 不增加也不减少学习率,而且,它会减小 vt,即使未来迭代中的梯度很大,也可能导致学习率不减小。
— 关于Adam及其后续的收敛性,2018。
AdaGrad是Adam的扩展,它维护了二阶矩向量的最大值,并用它来校正更新参数的梯度,而不是矩向量本身。这有助于防止优化过程过快减慢(例如,过早收敛)。
AMSGRAD与ADAM的关键区别在于,它维护了直到当前时间步的所有 vt 的最大值,并使用此最大值来归一化梯度的运行平均值,而不是ADAM中的vt。
— 关于Adam及其后续的收敛性,2018。
让我们逐步了解算法的每个元素。
首先,我们必须为搜索中要优化的每个参数维护一个一阶矩向量、二阶矩向量以及最大二阶矩向量,分别称为*m*和*v*(希腊字母 nu,但我们将使用 v),以及*vhat*。
它们在搜索开始时初始化为 0.0。
- m = 0
- v = 0
- vhat = 0
算法以迭代方式执行,时间 t 从 t=1 开始,每次迭代都涉及计算一组新的参数值 x,例如从 x(t-1) 到 x(t)。
如果我们将重点放在更新一个参数上,可能会更容易理解该算法,这可以通过向量运算推广到更新所有参数。
首先,计算当前时间步的梯度(偏导数)。
- g(t) = f'(x(t-1))
接下来,使用梯度和超参数*beta1*更新一阶矩向量。
- m(t) = beta1(t) * m(t-1) + (1 – beta1(t)) * g(t)
超参数*beta1*可以保持不变,也可以在搜索过程中呈指数衰减,例如
- beta1(t) = beta1^(t)
或者,或者
- beta1(t) = beta1 / t
使用梯度的平方和超参数*beta2*更新二阶矩向量。
- v(t) = beta2 * v(t-1) + (1 – beta2) * g(t)^2
接下来,更新二阶矩向量的最大值。
- vhat(t) = max(vhat(t-1), v(t))
其中*max()*计算提供的值中的最大值。
然后可以使用计算出的项和步长超参数*alpha*来更新参数值。
- x(t) = x(t-1) – alpha(t) * m(t) / sqrt(vhat(t)))
其中*sqrt()*是平方根函数。
步长也可以保持不变或呈指数衰减。
回顾一下,该算法有三个超参数;它们是
- alpha:初始步长(学习率),典型值为0.002。
- **beta1**:一阶动量的衰减因子,典型值为 0.9。
- **beta2**:无穷范数的衰减因子,典型值为 0.999。
就是这样。
有关Adam算法背景下AMSGrad算法的完整推导,我建议阅读该论文。
- 关于Adam及其后续的收敛性, 2018.
接下来,我们看看如何在Python中从头开始实现该算法。
带有AMSGrad的梯度下降
在本节中,我们将探讨如何实现带有AMSGrad动量的梯度下降优化算法。
二维测试问题
首先,让我们定义一个优化函数。
我们将使用一个简单的二维函数,它将每个维度的输入平方,并将有效输入范围定义为-1.0到1.0。
下面的 objective() 函数实现了这一点。
|
1 2 3 |
# 目标函数 def objective(x, y): return x**2.0 + y**2.0 |
我们可以创建一个数据集的三维图来感受响应曲面的曲率。
下面列出了绘制目标函数的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 绘制测试函数的三维图 from numpy import arange from numpy import meshgrid from matplotlib import pyplot # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 r_min, r_max = -1.0, 1.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
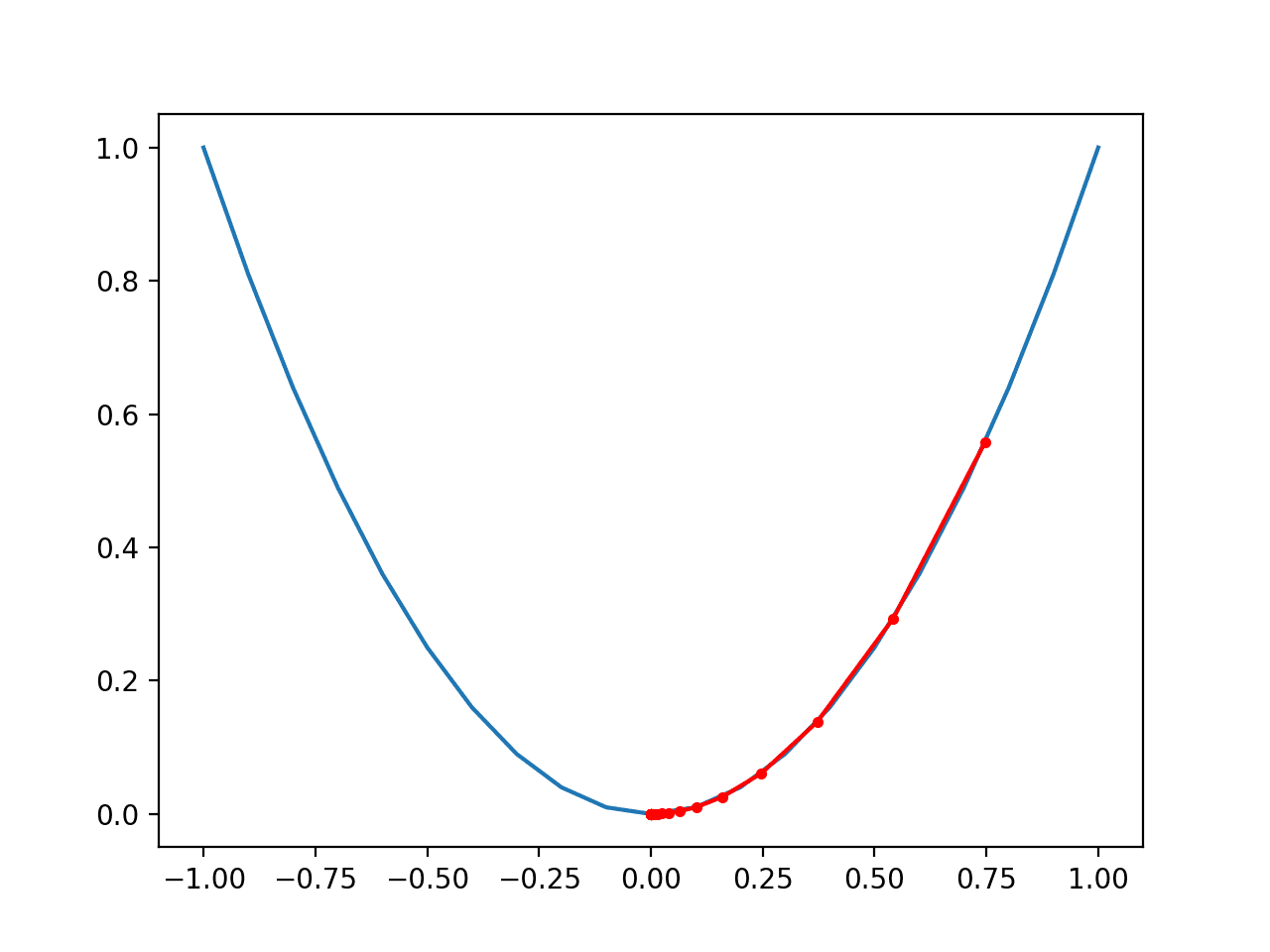
运行示例将创建目标函数的三维曲面图。
我们可以看到熟悉的碗形,全局最小值在 f(0, 0) = 0。
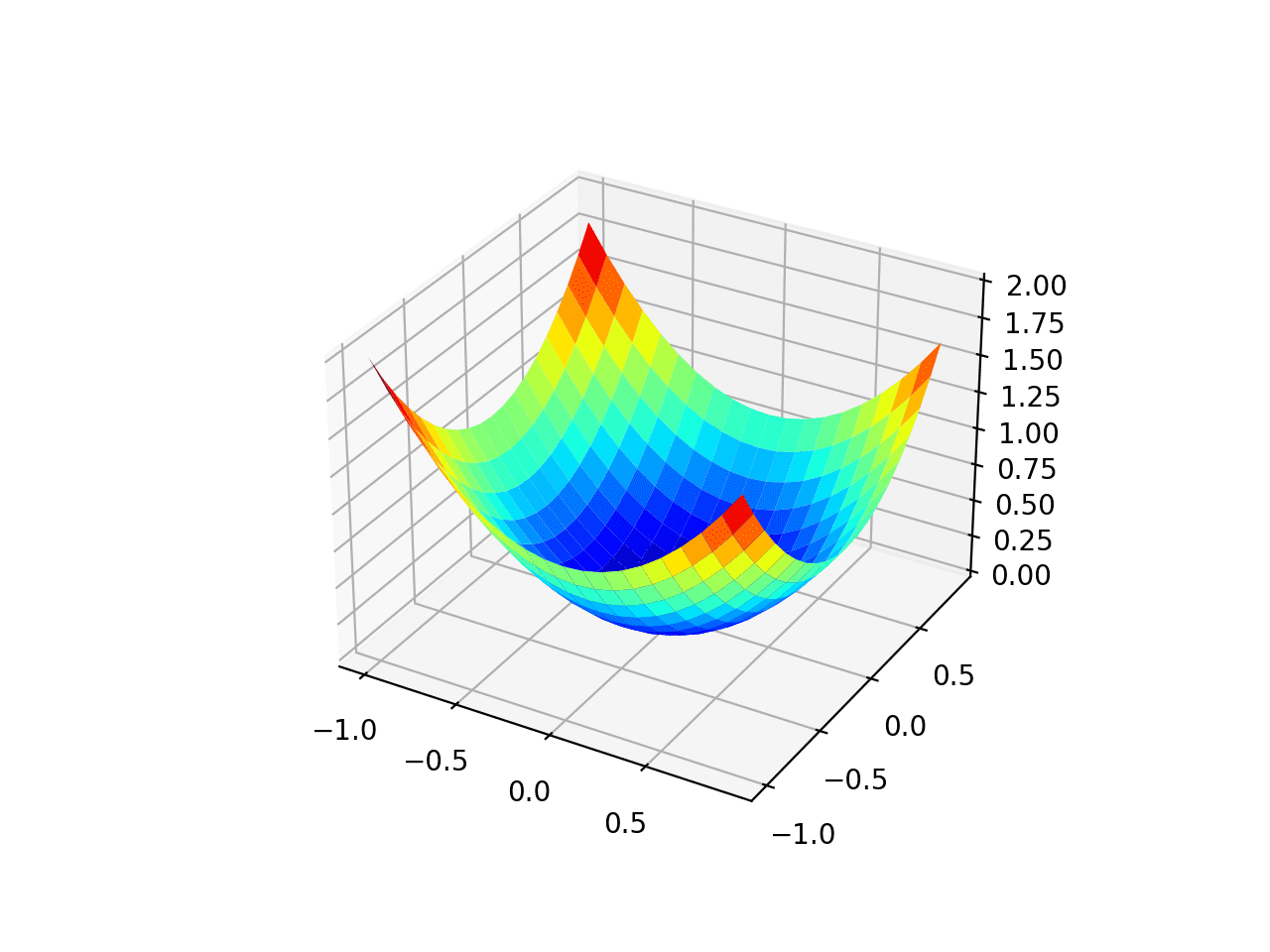
测试目标函数的三维图
我们还可以创建函数的二维图。这将在以后我们想要绘制搜索进度时提供帮助。
以下示例创建了目标函数的等高线图。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 绘制测试函数的等高线图 from numpy import asarray from numpy import arange from numpy import meshgrid from matplotlib import pyplot # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 以 0.1 为增量均匀采样输入范围 xaxis = arange(bounds[0,0], bounds[0,1], 0.1) yaxis = arange(bounds[1,0], bounds[1,1], 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用50个级别和jet颜色方案创建填充等高线图 pyplot.contourf(x, y, results, levels=50, cmap='jet') # 显示绘图 pyplot.show() |
运行示例将创建目标函数的二维等高线图。
我们可以看到碗状被压缩成用颜色梯度显示的等高线。我们将使用这个图来绘制搜索过程中探索的特定点。
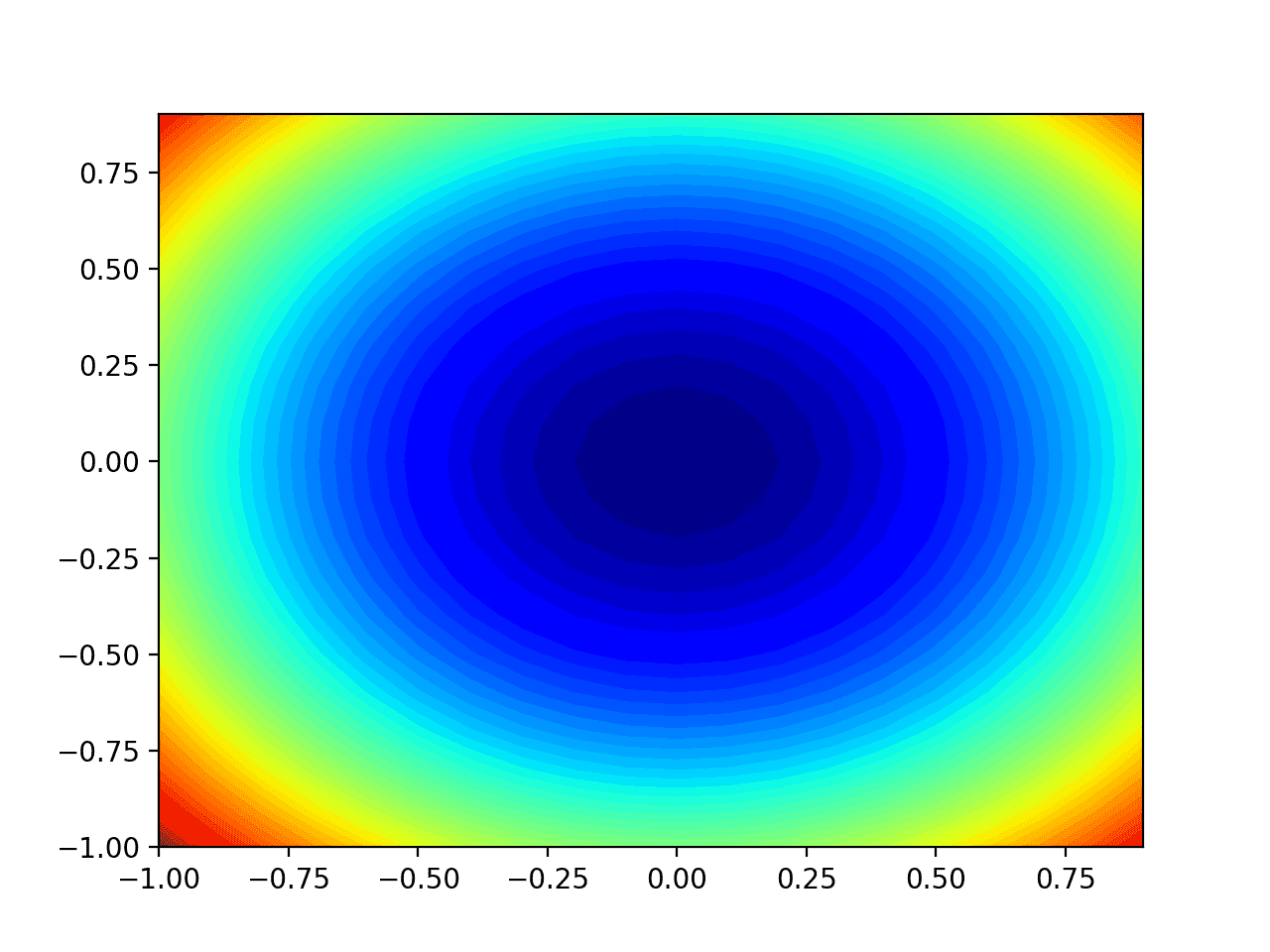
测试目标函数的二维等高线图
现在我们有了测试目标函数,让我们看看如何实现AMSGrad优化算法。
带有AMSGrad的梯度下降优化
我们可以将带有AMSGrad的梯度下降应用于测试问题。
首先,我们需要一个函数来计算此函数的导数。
*x*2的导数是每个维度上的*x* * 2*。
- f(x) = x^2
- f'(x) = x * 2
*derivative()*函数实现如下。
|
1 2 3 |
# 目标函数的导数 def derivative(x, y): return asarray([x * 2.0, y * 2.0]) |
接下来,我们可以实现带有AMSGrad的梯度下降优化。
首先,我们可以在问题的边界内选择一个随机点作为搜索的起点。
这假设我们有一个数组,它定义了搜索的边界,每行一个维度,第一列定义最小值,第二列定义最大值。
|
1 2 3 |
... # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) |
接下来,我们需要初始化矩向量。
|
1 2 3 4 5 |
... # 初始化矩向量 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] vhat = [0.0 for _ in range(bounds.shape[0])] |
然后我们运行由“_n_iter_”超参数定义的固定迭代次数。
|
1 2 3 4 |
... # 运行梯度下降迭代 for t in range(n_iter): ... |
第一步是计算当前参数集的导数。
|
1 2 3 |
... # 计算梯度 g(t) g = derivative(x[0], x[1]) |
接下来,我们需要执行AMSGrad更新计算。我们将使用命令式编程风格,逐个变量地执行这些计算,以提高可读性。
实际上,我建议使用NumPy向量操作以提高效率。
|
1 2 3 4 |
... # 逐个变量构建解 for i in range(x.shape[0]): ... |
首先,我们需要计算一阶矩向量。
|
1 2 3 |
... # m(t) = beta1(t) * m(t-1) + (1 - beta1(t)) * g(t) m[i] = beta1**(t+1) * m[i] + (1.0 - beta1**(t+1)) * g[i] |
接下来,我们需要计算二阶矩向量。
|
1 2 3 |
... # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = (beta2 * v[i]) + (1.0 - beta2) * g[i]**2 |
然后,计算二阶矩向量与上一迭代值和当前值的最大值。
|
1 2 3 |
... # vhat(t) = max(vhat(t-1), v(t)) vhat[i] = max(vhat[i], v[i]) |
最后,我们可以计算变量的新值。
|
1 2 3 |
... # x(t) = x(t-1) - alpha(t) * m(t) / sqrt(vhat(t))) x[i] = x[i] - alpha * m[i] / sqrt(vhat[i]) |
我们可以向分母添加一个很小的值以避免除以零的错误;例如
|
1 2 3 |
... # x(t) = x(t-1) - alpha(t) * m(t) / sqrt(vhat(t))) x[i] = x[i] - alpha * m[i] / (sqrt(vhat[i]) + 1e-8) |
然后对每个要优化的参数重复此操作。
在迭代结束时,我们可以评估新的参数值并报告搜索的性能。
|
1 2 3 4 5 |
... # 评估候选点 score = objective(x[0], x[1]) # 报告进展 print('>%d f(%s) = %.5f' % (t, x, score)) |
我们可以将所有这些内容整合到一个名为*amsgrad()*的函数中,该函数接受目标函数和导数函数的名称以及算法超参数,并在搜索结束时返回找到的最佳解决方案及其评估值。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# 带有AMSGrad的梯度下降算法 def amsgrad(objective, derivative, bounds, n_iter, alpha, beta1, beta2): # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 初始化矩向量 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] vhat = [0.0 for _ in range(bounds.shape[0])] # 运行梯度下降 for t in range(n_iter): # 计算梯度 g(t) g = derivative(x[0], x[1]) # 逐个变量更新 for i in range(x.shape[0]): # m(t) = beta1(t) * m(t-1) + (1 - beta1(t)) * g(t) m[i] = beta1**(t+1) * m[i] + (1.0 - beta1**(t+1)) * g[i] # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = (beta2 * v[i]) + (1.0 - beta2) * g[i]**2 # vhat(t) = max(vhat(t-1), v(t)) vhat[i] = max(vhat[i], v[i]) # x(t) = x(t-1) - alpha(t) * m(t) / sqrt(vhat(t))) x[i] = x[i] - alpha * m[i] / (sqrt(vhat[i]) + 1e-8) # 评估候选点 score = objective(x[0], x[1]) # 报告进度 print('>%d f(%s) = %.5f' % (t, x, score)) return [x, score] |
然后我们可以定义函数的边界和超参数,并调用函数执行优化。
在这种情况下,我们将运行算法100次迭代,初始学习率为0.007,beta为0.9,beta2为0.99,这些值是通过一些试错得出的。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
... # 初始化伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 定义总迭代次数 n_iter = 100 # 步长 alpha = 0.007 # 平均梯度因子 beta1 = 0.9 # 平均梯度平方因子 beta2 = 0.99 # 使用amsgrad执行梯度下降搜索 best, score = amsgrad(objective, derivative, bounds, n_iter, alpha, beta1, beta2) |
在运行结束时,我们将报告找到的最佳解决方案。
|
1 2 3 4 |
... # 总结结果 print('Done!') print('f(%s) = %f' % (best, score)) |
将所有这些内容汇总起来,AMSGrad梯度下降应用于我们测试问题的完整示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
# 适用于二维测试函数的梯度下降优化与amsgrad from math import sqrt from numpy import asarray from numpy.random import rand from numpy.random import seed # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 目标函数的导数 def derivative(x, y): return asarray([x * 2.0, y * 2.0]) # 带有AMSGrad的梯度下降算法 def amsgrad(objective, derivative, bounds, n_iter, alpha, beta1, beta2): # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 初始化矩向量 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] vhat = [0.0 for _ in range(bounds.shape[0])] # 运行梯度下降 for t in range(n_iter): # 计算梯度 g(t) g = derivative(x[0], x[1]) # 逐个变量更新 for i in range(x.shape[0]): # m(t) = beta1(t) * m(t-1) + (1 - beta1(t)) * g(t) m[i] = beta1**(t+1) * m[i] + (1.0 - beta1**(t+1)) * g[i] # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = (beta2 * v[i]) + (1.0 - beta2) * g[i]**2 # vhat(t) = max(vhat(t-1), v(t)) vhat[i] = max(vhat[i], v[i]) # x(t) = x(t-1) - alpha(t) * m(t) / sqrt(vhat(t))) x[i] = x[i] - alpha * m[i] / (sqrt(vhat[i]) + 1e-8) # 评估候选点 score = objective(x[0], x[1]) # 报告进度 print('>%d f(%s) = %.5f' % (t, x, score)) return [x, score] # 初始化伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 定义总迭代次数 n_iter = 100 # 步长 alpha = 0.007 # 平均梯度因子 beta1 = 0.9 # 平均梯度平方因子 beta2 = 0.99 # 使用amsgrad执行梯度下降搜索 best, score = amsgrad(objective, derivative, bounds, n_iter, alpha, beta1, beta2) print('Done!') print('f(%s) = %f' % (best, score)) |
运行示例将AMSGrad优化算法应用于我们的测试问题,并报告算法每次迭代的搜索性能。
注意:鉴于算法或评估过程的随机性,或数值精度的差异,您的结果可能有所不同。请考虑运行几次示例并比较平均结果。
在这种情况下,我们可以看到在搜索大约90次迭代后找到了一个接近最优的解,输入值接近0.0和0.0,评估结果为0.0。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
... >90 f([-5.74880707e-11 2.16227707e-03]) = 0.00000 >91 f([-4.53359947e-11 2.03974264e-03]) = 0.00000 >92 f([-3.57526928e-11 1.92415218e-03]) = 0.00000 >93 f([-2.81951584e-11 1.81511216e-03]) = 0.00000 >94 f([-2.22351711e-11 1.71225138e-03]) = 0.00000 >95 f([-1.75350316e-11 1.61521966e-03]) = 0.00000 >96 f([-1.38284262e-11 1.52368665e-03]) = 0.00000 >97 f([-1.09053366e-11 1.43734076e-03]) = 0.00000 >98 f([-8.60013947e-12 1.35588802e-03]) = 0.00000 >99 f([-6.78222208e-12 1.27905115e-03]) = 0.00000 完成! f([-6.78222208e-12 1.27905115e-03]) = 0.000002 |
AMSGrad优化可视化
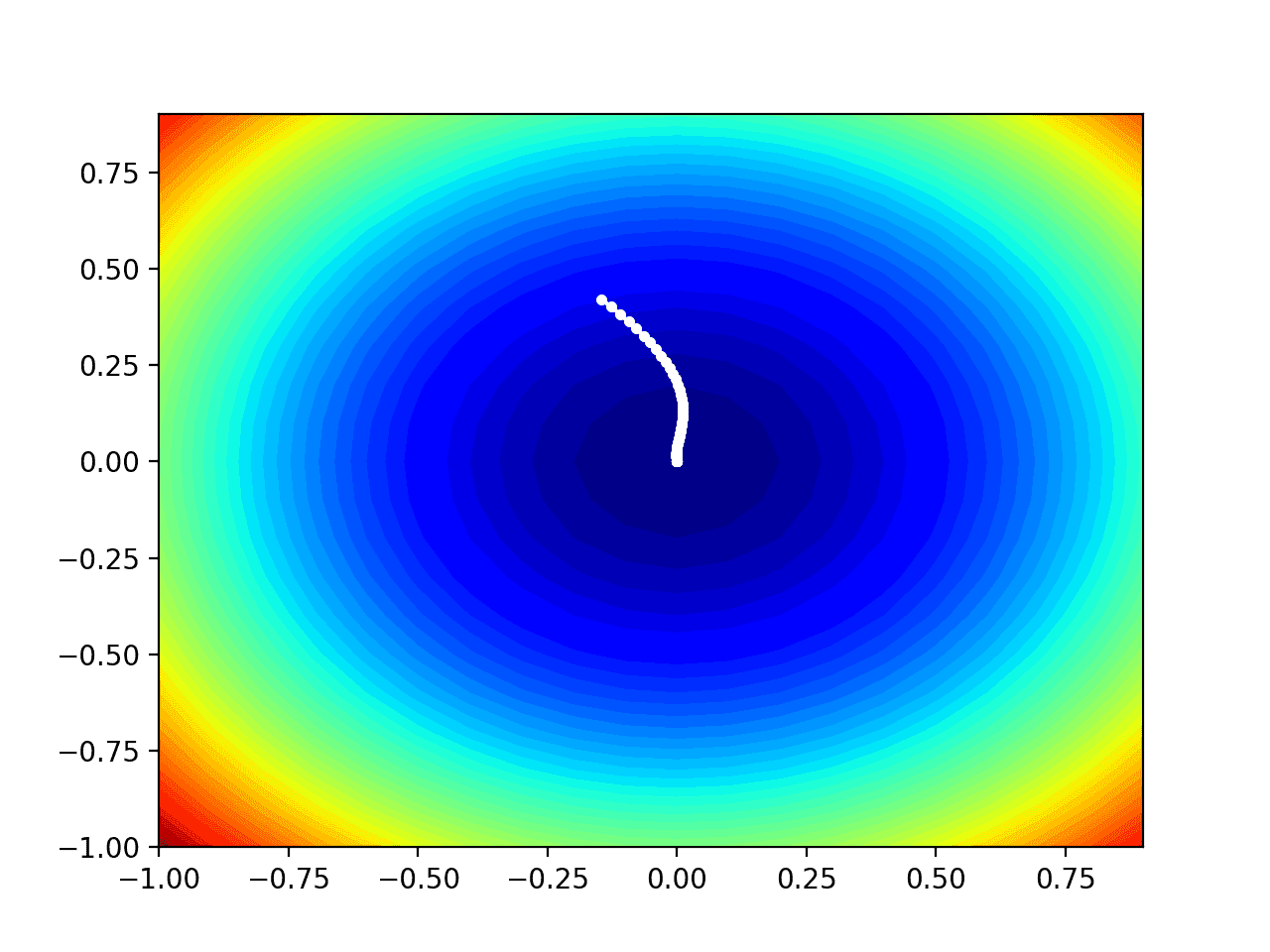
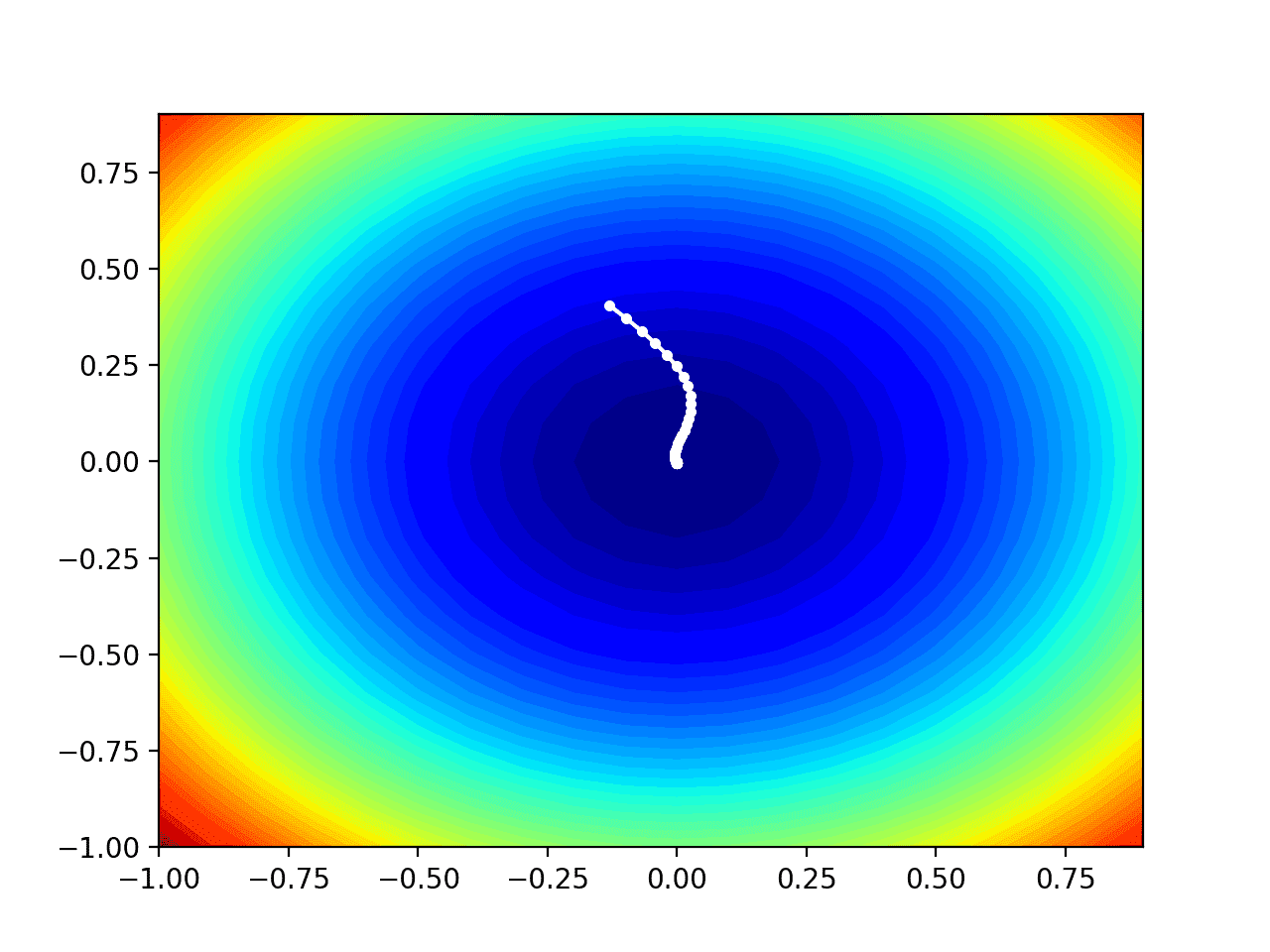
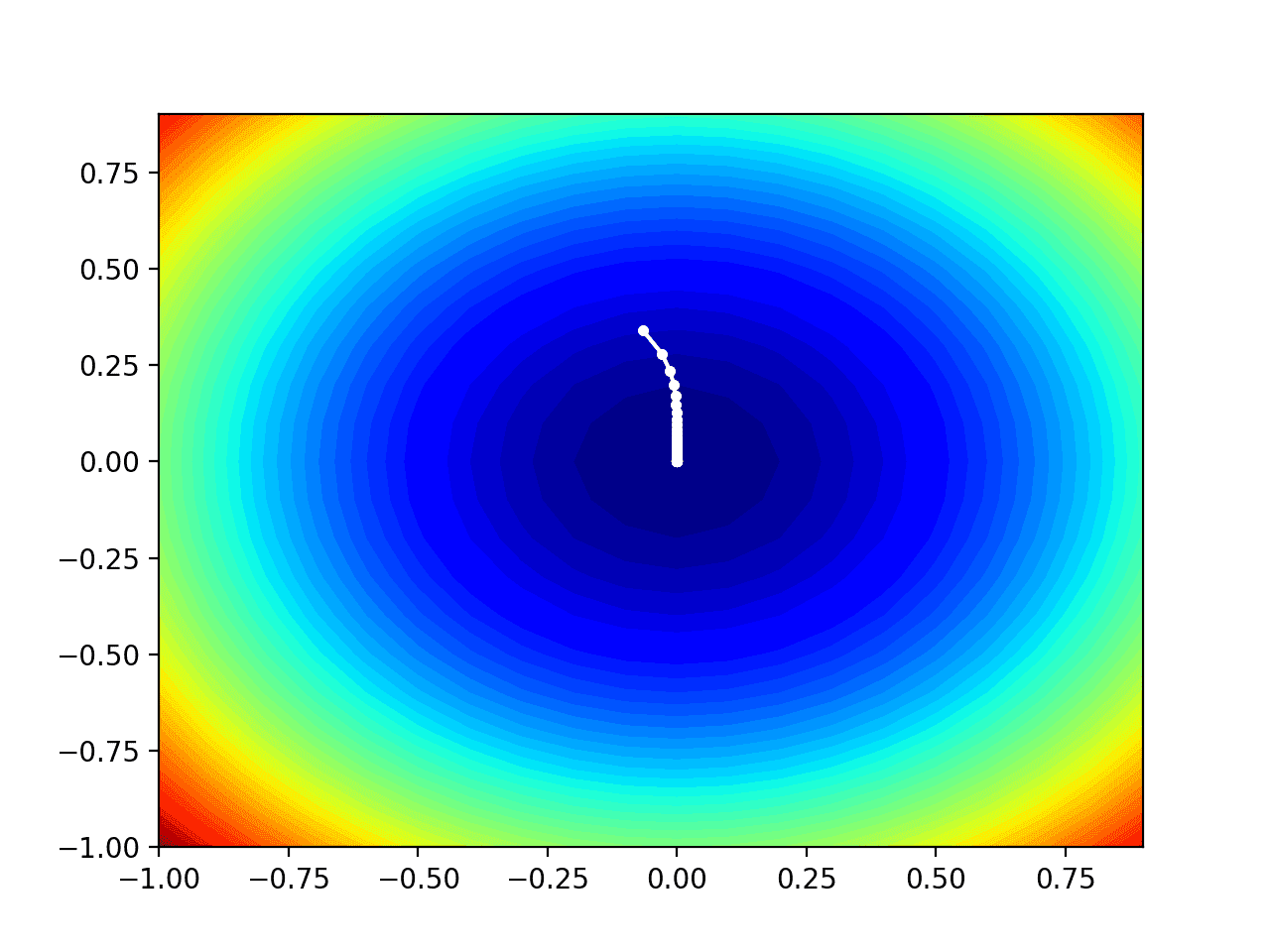
我们可以在域的等高线图上绘制AMSGrad搜索的进度。
这可以提供对算法迭代过程中搜索进展的直观感受。
我们必须更新*amsgrad()*函数以维护搜索期间找到的所有解决方案的列表,然后在搜索结束时返回此列表。
包含这些更改的更新版本函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# 带有AMSGrad的梯度下降算法 def amsgrad(objective, derivative, bounds, n_iter, alpha, beta1, beta2): solutions = list() # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 初始化矩向量 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] vhat = [0.0 for _ in range(bounds.shape[0])] # 运行梯度下降 for t in range(n_iter): # 计算梯度 g(t) g = derivative(x[0], x[1]) # 逐个变量更新 for i in range(x.shape[0]): # m(t) = beta1(t) * m(t-1) + (1 - beta1(t)) * g(t) m[i] = beta1**(t+1) * m[i] + (1.0 - beta1**(t+1)) * g[i] # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = (beta2 * v[i]) + (1.0 - beta2) * g[i]**2 # vhat(t) = max(vhat(t-1), v(t)) vhat[i] = max(vhat[i], v[i]) # x(t) = x(t-1) - alpha(t) * m(t) / sqrt(vhat(t))) x[i] = x[i] - alpha * m[i] / (sqrt(vhat[i]) + 1e-8) # 评估候选点 score = objective(x[0], x[1]) # 跟踪所有解决方案 solutions.append(x.copy()) # 报告进度 print('>%d f(%s) = %.5f' % (t, x, score)) return solutions |
然后我们可以像以前一样执行搜索,这次检索解决方案列表而不是最终的最佳解决方案。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
... # 初始化伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 定义总迭代次数 n_iter = 100 # 步长 alpha = 0.007 # 平均梯度因子 beta1 = 0.9 # 平均梯度平方因子 beta2 = 0.99 # 使用amsgrad执行梯度下降搜索 solutions = amsgrad(objective, derivative, bounds, n_iter, alpha, beta1, beta2) |
然后我们可以像以前一样创建目标函数的等高线图。
|
1 2 3 4 5 6 7 8 9 10 |
... # 以 0.1 为增量均匀采样输入范围 xaxis = arange(bounds[0,0], bounds[0,1], 0.1) yaxis = arange(bounds[1,0], bounds[1,1], 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用50个级别和jet颜色方案创建填充等高线图 pyplot.contourf(x, y, results, levels=50, cmap='jet') |
最后,我们可以将搜索过程中找到的每个解决方案绘制成一个由线连接的白点。
|
1 2 3 4 |
... # 将样本绘制为黑色圆圈 solutions = asarray(solutions) pyplot.plot(solutions[:, 0], solutions[:, 1], '.-', color='w') |
将所有内容整合在一起,下面列出了在测试问题上执行AMSGrad优化并绘制结果的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
# 在测试函数等高线图上绘制AMSGrad搜索的示例 from math import sqrt from numpy import asarray from numpy import arange from numpy.random import rand from numpy.random import seed from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return x**2.0 + y**2.0 # 目标函数的导数 def derivative(x, y): return asarray([x * 2.0, y * 2.0]) # 带有AMSGrad的梯度下降算法 def amsgrad(objective, derivative, bounds, n_iter, alpha, beta1, beta2): solutions = list() # 生成初始点 x = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 初始化矩向量 m = [0.0 for _ in range(bounds.shape[0])] v = [0.0 for _ in range(bounds.shape[0])] vhat = [0.0 for _ in range(bounds.shape[0])] # 运行梯度下降 for t in range(n_iter): # 计算梯度 g(t) g = derivative(x[0], x[1]) # 逐个变量更新 for i in range(x.shape[0]): # m(t) = beta1(t) * m(t-1) + (1 - beta1(t)) * g(t) m[i] = beta1**(t+1) * m[i] + (1.0 - beta1**(t+1)) * g[i] # v(t) = beta2 * v(t-1) + (1 - beta2) * g(t)^2 v[i] = (beta2 * v[i]) + (1.0 - beta2) * g[i]**2 # vhat(t) = max(vhat(t-1), v(t)) vhat[i] = max(vhat[i], v[i]) # x(t) = x(t-1) - alpha(t) * m(t) / sqrt(vhat(t))) x[i] = x[i] - alpha * m[i] / (sqrt(vhat[i]) + 1e-8) # 评估候选点 score = objective(x[0], x[1]) # 跟踪所有解决方案 solutions.append(x.copy()) # 报告进度 print('>%d f(%s) = %.5f' % (t, x, score)) return solutions # 初始化伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-1.0, 1.0], [-1.0, 1.0]]) # 定义总迭代次数 n_iter = 100 # 步长 alpha = 0.007 # 平均梯度因子 beta1 = 0.9 # 平均梯度平方因子 beta2 = 0.99 # 使用amsgrad执行梯度下降搜索 solutions = amsgrad(objective, derivative, bounds, n_iter, alpha, beta1, beta2) # 以 0.1 为增量均匀采样输入范围 xaxis = arange(bounds[0,0], bounds[0,1], 0.1) yaxis = arange(bounds[1,0], bounds[1,1], 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用50个级别和jet颜色方案创建填充等高线图 pyplot.contourf(x, y, results, levels=50, cmap='jet') # 将样本绘制为黑色圆圈 solutions = asarray(solutions) pyplot.plot(solutions[:, 0], solutions[:, 1], '.-', color='w') # 显示绘图 pyplot.show() |
运行示例像以前一样执行搜索,但在此情况下,创建了目标函数的等高线图。
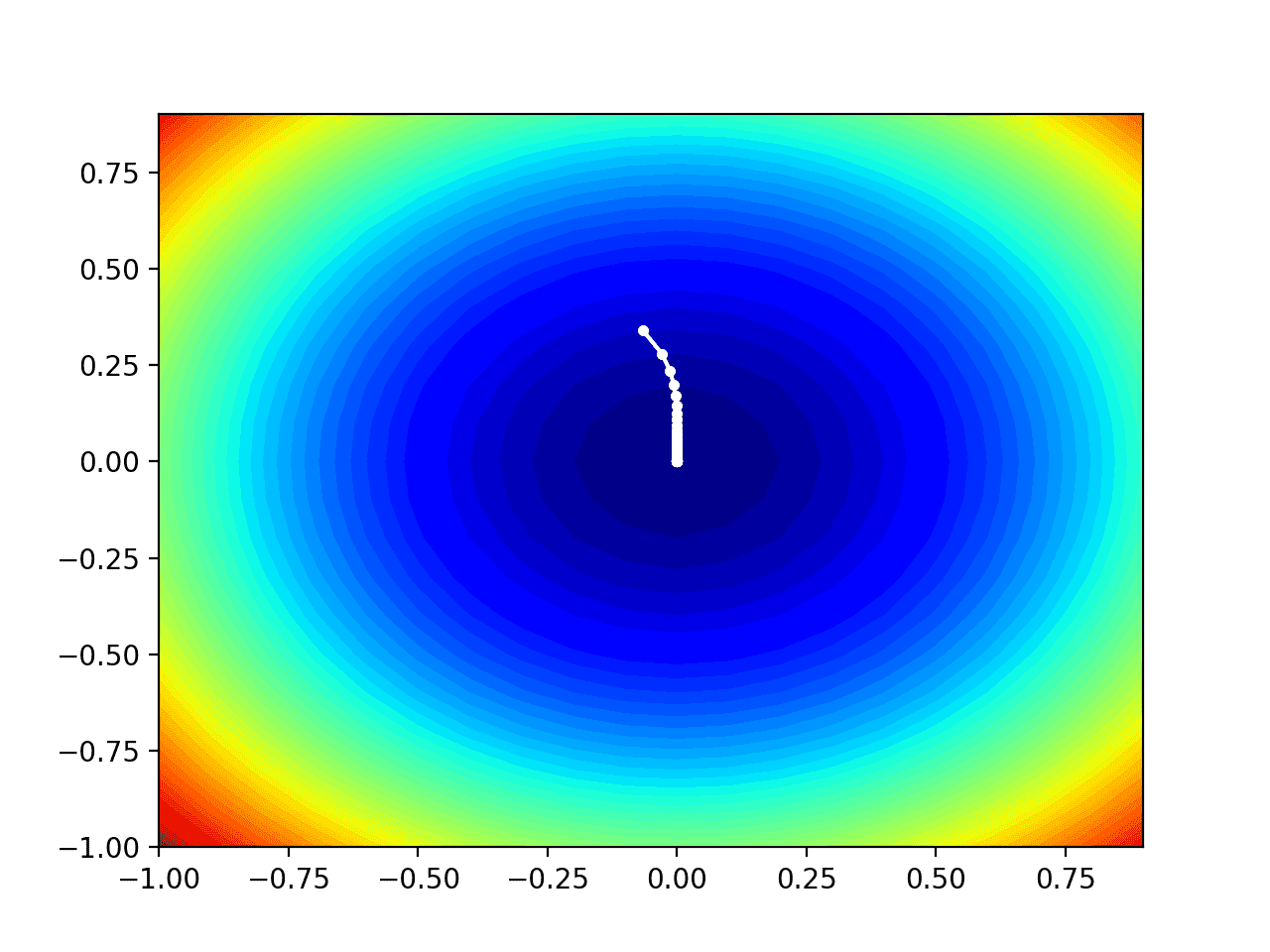
在这种情况下,我们可以看到搜索过程中找到的每个解决方案都显示为一个白点,从最优值上方开始,并逐渐靠近图中中心的最优值。
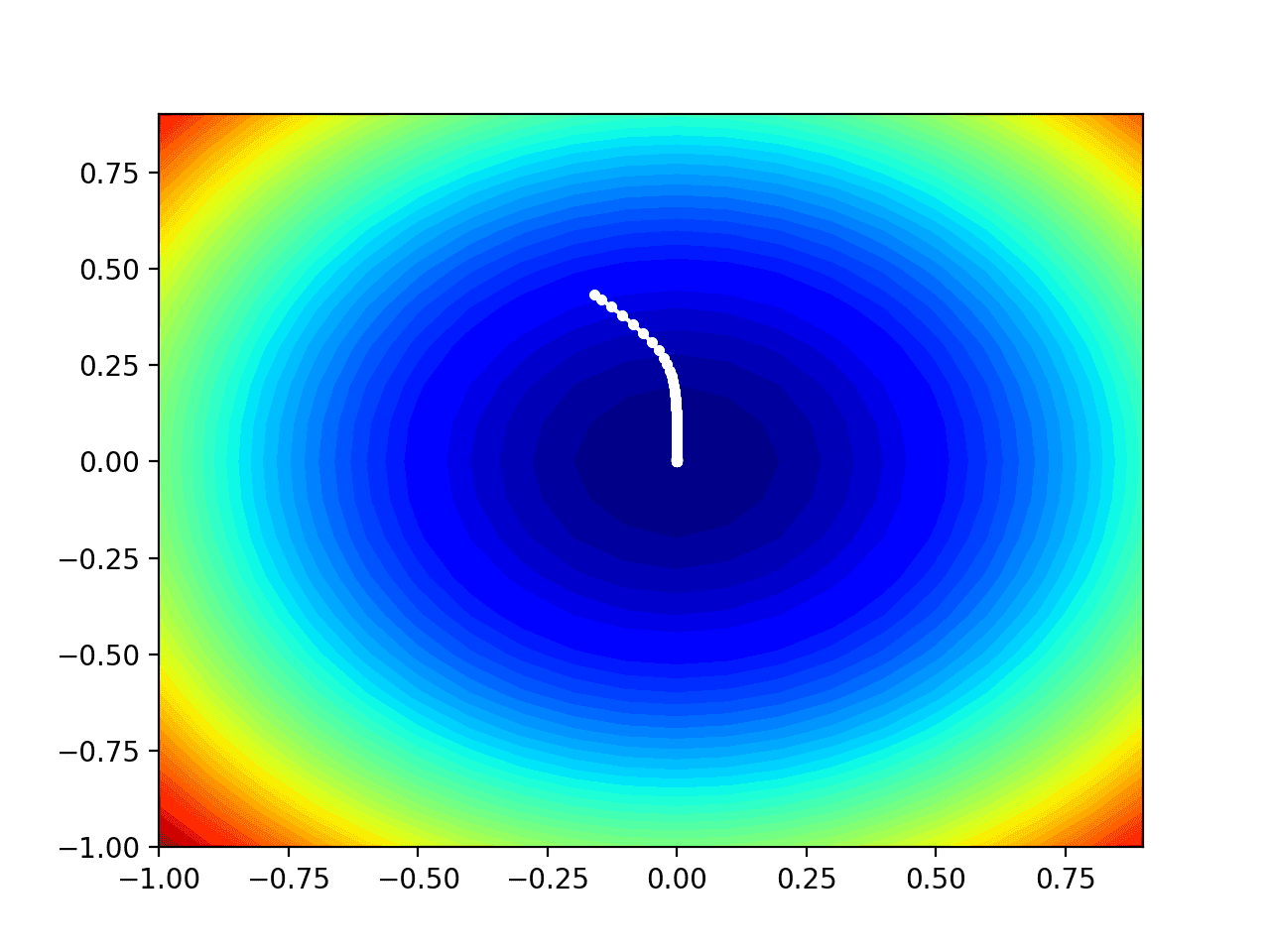
测试目标函数等高线图及AMSGrad搜索结果显示
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 关于Adam及其后续的收敛性, 2018.
- 梯度下降优化算法概述, 2016.
书籍
API
文章
- 梯度下降,维基百科.
- 随机梯度下降,维基百科.
- 梯度下降优化算法综述, 2016.
- AMSGrad实验, 2017.
总结
在本教程中,您将学习如何从头开始开发AMSGrad梯度下降优化。
具体来说,你学到了:
- 梯度下降是一种优化算法,它利用目标函数的梯度来导航搜索空间。
- AMSGrad是梯度下降的Adam版本的扩展,旨在加速优化过程。
- 如何从头开始实现AMSGrad优化算法,并将其应用于目标函数并评估结果。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。

嗨,Jason,
标题“AMSGrad优化算法”下的内容有一个小的笔误,在2处使用了AdaGrad而不是AMSGrad。
这不是笔误,因为AMSGrad是AdaGrad的扩展,因此我们先介绍AMSGrad。
感谢指教!
不客气!