梯度下降是一种优化算法,它沿着目标函数的负梯度方向进行,以找到函数的最小值。
梯度下降的一个问题是,在曲率大或梯度有噪声的优化问题中,它会在搜索空间中来回震荡,并且可能会卡在搜索空间中没有梯度的平坦区域。
动量是梯度下降优化算法的扩展,它允许搜索在搜索空间的某个方向上累积惯性,并克服有噪声梯度的振荡,以及跨越搜索空间的平坦区域。
在本教程中,您将了解带动量的梯度下降算法。
完成本教程后,您将了解:
- 梯度下降是一种优化算法,它利用目标函数的梯度来导航搜索空间。
- 通过利用过去更新搜索位置的动量,可以加速梯度下降。
- 如何实现带动量的梯度下降优化,并对其行为建立直观认识。
启动您的项目,阅读我的新书《机器学习优化》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
从零开始实现带动量的梯度下降
照片作者:Chris Barnes,保留部分权利。
教程概述
本教程分为三个部分;它们是:
- 梯度下降
- 动量
- 带动量的梯度下降
- 一维测试问题
- 梯度下降优化
- 梯度下降优化可视化
- 带动量的梯度下降优化
- 带动量的梯度下降优化可视化
梯度下降
梯度下降是一种优化算法。
它在技术上被称为一阶优化算法,因为它明确使用了目标函数的一阶导数。
一阶方法依赖梯度信息来帮助指导寻找最小值……
——第69页,《优化算法》,2019年。
一阶导数,或简称“导数”,是目标函数在特定点(例如,对于特定输入)的变化率或斜率。
如果目标函数有多个输入变量,则称其为多元函数,输入变量可以被视为一个向量。反过来,多元目标函数的导数也可以被视为一个向量,通常称为“梯度”。
- 梯度:多元目标函数的一阶导数。
导数或梯度指向特定输入处目标函数最陡峭上升的方向。
梯度下降指一种最小化优化算法,它沿着目标函数的负梯度方向“下坡”移动,以找到函数的最小值。
梯度下降算法需要一个要优化的目标函数以及目标函数的导数函数。目标函数 *f()* 为给定的输入集返回一个分数,导数函数 *f'*() 为给定的输入集提供目标函数的导数。
梯度下降算法需要问题中的一个起点(x),例如输入空间中随机选择的一个点。
然后计算导数,并在输入空间中迈出一步,预计会导致目标函数下坡移动(假设我们正在最小化目标函数)。
下行移动是通过计算在输入空间中移动的距离来实现的,该距离计算为步长(称为 *alpha* 或学习率)乘以梯度。然后从当前点减去该值,确保我们沿着与梯度相反的方向移动,即沿着目标函数下行。
- x = x – 步长 * f'(x)
目标函数在某一点处的斜率越大,梯度的绝对值越大,反过来,在搜索空间中采取的步长也越大。步长的大小使用步长超参数进行缩放。
- 步长(*alpha*):控制算法每次迭代中在搜索空间中沿着梯度移动多远的超参数,也称为学习率。
如果步长太小,在搜索空间中的移动会很小,搜索将花费很长时间。如果步长太大,搜索可能会在搜索空间中跳跃并跳过最优解。
现在我们已经熟悉了梯度下降优化算法,让我们来看看动量。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
动量
动量是梯度下降优化算法的扩展,通常称为带动量的梯度下降。
它旨在加速优化过程,例如减少达到最优值所需的函数评估次数,或提高优化算法的能力,例如获得更好的最终结果。
梯度下降算法的一个问题是,搜索的进程可能会根据梯度在搜索空间中来回震荡。例如,搜索可能朝着最小值方向下行,但在该过程中,它可能朝另一个方向移动,甚至上行,这取决于搜索过程中遇到的特定点(参数集)的梯度。
这会减慢搜索的进程,特别是对于那些目标函数的整体趋势或形状比沿途特定梯度更有用的优化问题。
解决此问题的一种方法是根据先前更新中遇到的梯度,向参数更新方程添加历史记录。
这种变化基于物理学中动量的比喻,其中一个方向上的加速度可以从过去的更新中累积。
动量这个名字来源于物理学的类比,其中负梯度是根据牛顿运动定律,在一个粒子通过参数空间移动的力。
— 第 296 页,《深度学习》,2016。
动量涉及添加一个额外的超参数,该超参数控制更新方程(即搜索空间中新点处的步长)中要包含的历史(动量)量。该超参数的值在 0.0 到 1.0 之间,通常接近 1.0,例如 0.8、0.9 或 0.99。动量为 0.0 时,与不带动量的梯度下降相同。
首先,我们将梯度下降更新方程分解为两部分:计算位置的变化以及将旧位置更新到新位置。
参数的变化计算为该点处的梯度乘以步长。
- change_x = step_size * f'(x)
新位置的计算方法是简单地从当前点减去变化量
- x = x – change_x
动量涉及保持位置的变化,并在后续的位移变化计算中使用它。
如果我们考虑随时间进行的更新,则当前迭代或时间 (t) 的更新将添加先前时间 (t-1) 使用的变化,并乘以动量超参数,如下所示:
- change_x(t) = step_size * f'(x(t-1)) + momentum * change_x(t-1)
然后按原样执行位置的更新。
- x(t) = x(t-1) – change_x(t)
位移的变化会累积搜索迭代过程中变化的幅度和方向,其大小与动量超参数成正比。
例如,较大的动量(例如 0.9)意味着更新会受到先前更新的强烈影响,而适度的动量(0.2)则影响很小。
动量算法会累积过去梯度的指数衰减的移动平均值,并继续沿着它们的变动方向移动。
— 第 296 页,《深度学习》,2016。
动量具有降低梯度变化的效果,从而降低了搜索空间中每个新点处的步长。
当成本表面高度非球形时,动量可以提高速度,因为它会抑制高曲率方向上的步长大小,从而在低曲率方向上产生更大的有效学习率。
— 第 21 页,《神经网络:技术琐事》,2012。
动量在目标函数具有大量曲率(例如,变化很大)的优化问题中最有用,这意味着梯度在搜索空间的相对较小区域内可能会发生很大变化。
动量方法旨在加速学习,尤其是在高曲率、小但一致的梯度或有噪声的梯度的情况下。
— 第 296 页,《深度学习》,2016。
当梯度是估计的(例如,来自模拟)并且可能是有噪声的(例如,当梯度方差很大时)也有帮助。
最后,当搜索空间平坦或接近平坦(例如,梯度为零)时,动量也很有帮助。动量允许搜索沿平坦区域之前的方向继续前进,并有助于跨越平坦区域。
现在我们已经熟悉了动量是什么,让我们来看一个实际的例子。
带动量的梯度下降
在本节中,我们将首先实现梯度下降优化算法,然后更新它以使用动量并比较结果。
一维测试问题
首先,让我们定义一个优化函数。
我们将使用一个简单的关于输入平方的一维函数,并将有效输入的范围定义为 -1.0 到 1.0。
下面的 objective() 函数实现了这个函数。
|
1 2 3 |
# 目标函数 def objective(x): return x**2.0 |
然后,我们可以采样该范围内的所有输入,并计算每个输入的客观函数值。
|
1 2 3 4 5 6 7 |
... # 定义输入范围 r_min, r_max = -1.0, 1.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max+0.1, 0.1) # 计算目标值 results = objective(inputs) |
最后,我们可以创建一个输入(x 轴)与目标函数值(y 轴)的折线图,以了解我们将要搜索的目标函数的形状。
|
1 2 3 4 5 |
... # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 显示绘图 pyplot.show() |
下面的示例将这些内容整合在一起,并提供了绘制一维测试函数的示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 简单函数的图 from numpy import arange from matplotlib import pyplot # 目标函数 def objective(x): return x**2.0 # 定义输入范围 r_min, r_max = -1.0, 1.0 # 以 0.1 为增量均匀采样输入范围 inputs = arange(r_min, r_max+0.1, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 显示绘图 pyplot.show() |
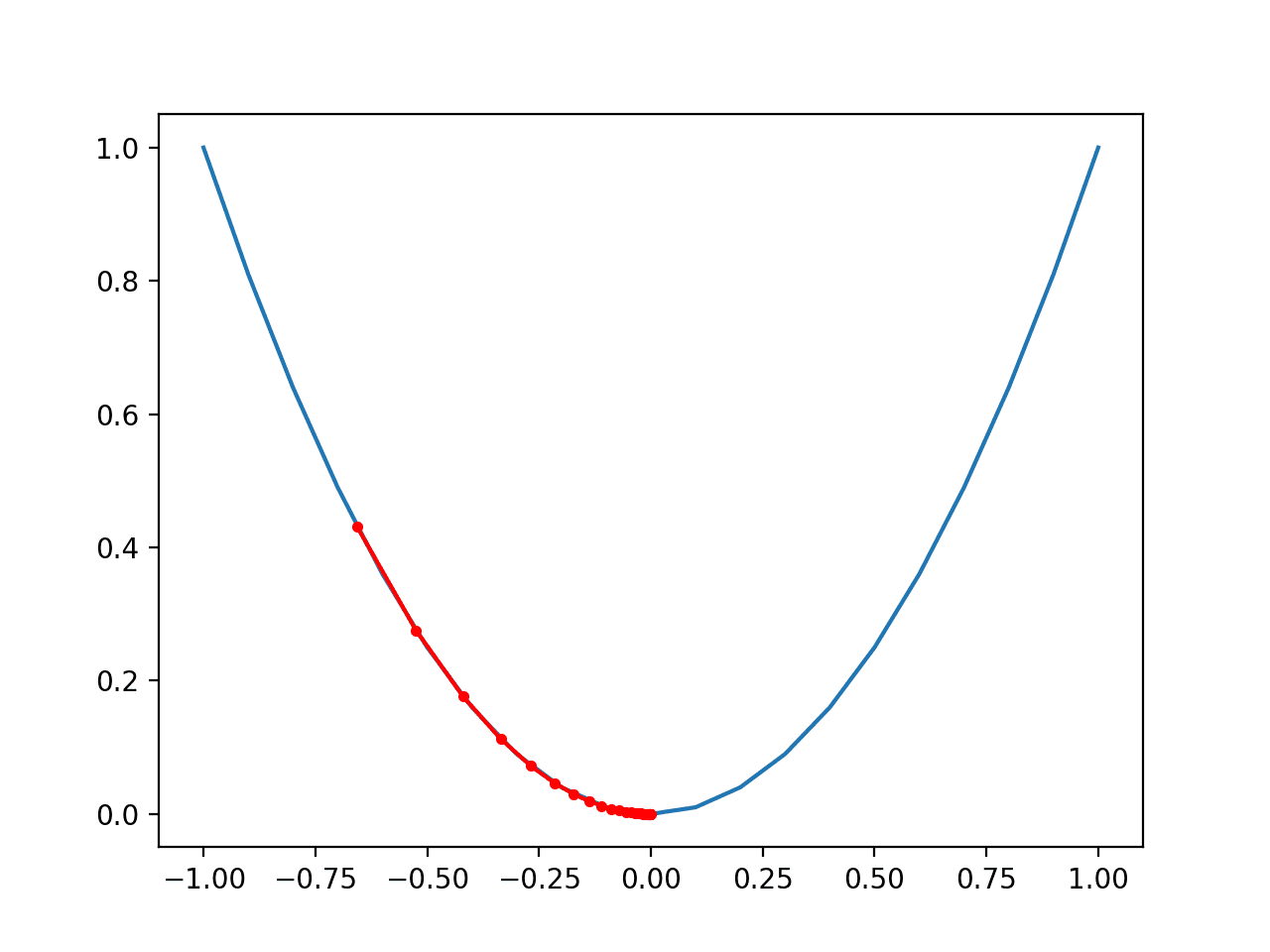
运行该示例会创建函数输入(x轴)和函数计算输出(y轴)的线图。
我们可以看到熟悉的 U 形,称为抛物线。
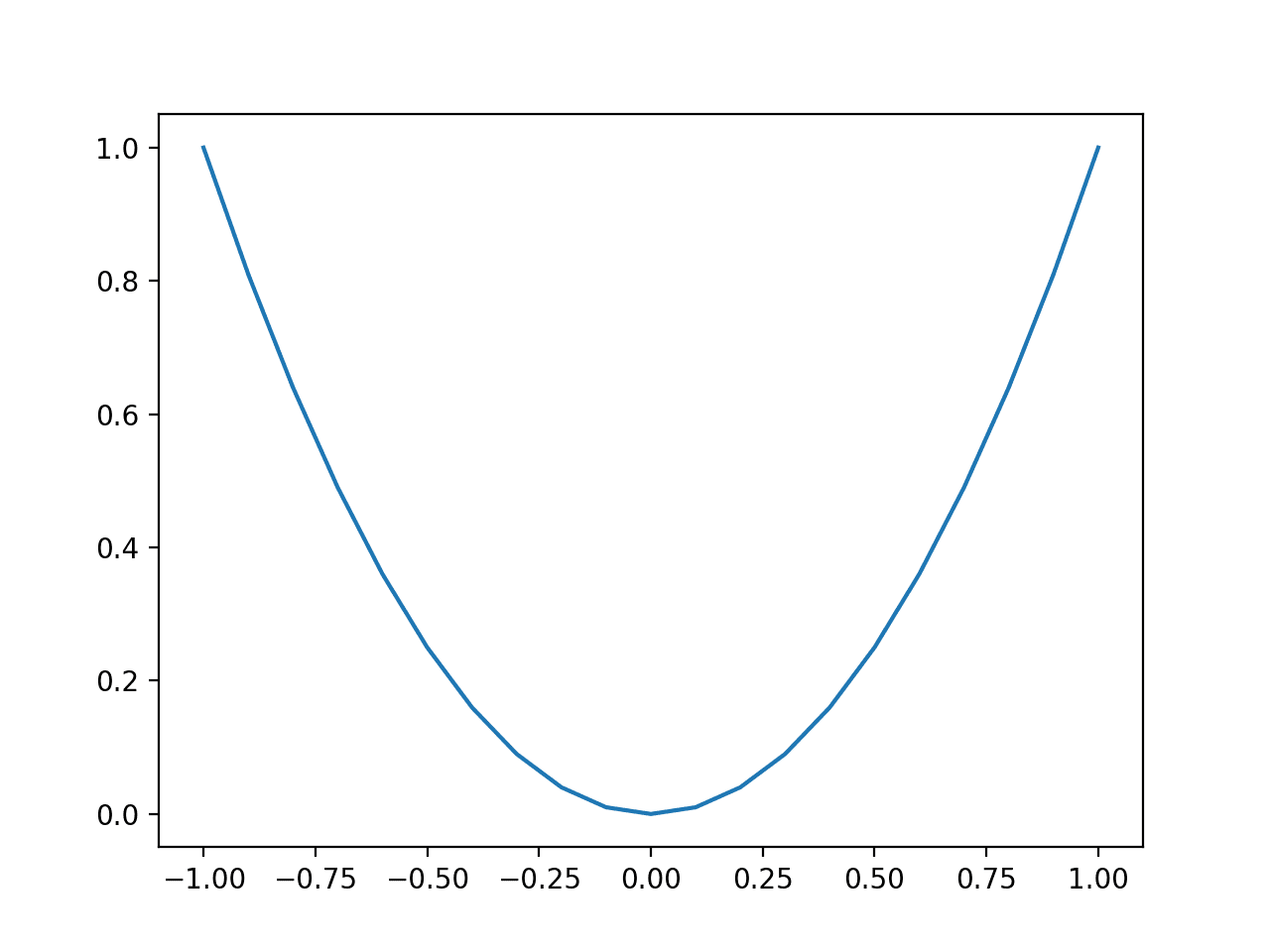
简单一维函数折线图
梯度下降优化
接下来,我们可以将梯度下降算法应用于该问题。
首先,我们需要一个计算目标函数导数的函数。
x^2 的导数是 2x,*derivative()* 函数如下实现。
|
1 2 3 |
# 目标函数的导数 def derivative(x): return x * 2.0 |
我们可以定义一个实现梯度下降优化算法的函数。
该过程包括从搜索空间中随机选择一个点开始,然后计算梯度,更新搜索空间中的位置,评估新位置,并报告进度。然后将此过程重复固定次数的迭代。最后从函数中返回最终点及其评估值。
下面的 *gradient_descent()* 函数实现了这一点,它接受目标函数和梯度函数的名称,以及目标函数的输入边界、迭代次数和步长,然后返回搜索结束时的解决方案及其评估值。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 梯度下降算法 def gradient_descent(objective, derivative, bounds, n_iter, step_size): # 生成初始点 solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 运行梯度下降 for i in range(n_iter): # 计算梯度 gradient = derivative(solution) # 迈出一步 solution = solution - step_size * gradient # 评估候选点 solution_eval = objective(solution) # 报告进度 print('>%d f(%s) = %.5f' % (i, solution, solution_eval)) return [solution, solution_eval] |
然后,我们可以定义目标函数的边界、步长和算法的迭代次数。
我们将使用 0.1 的步长和 30 次迭代,这两个值都是通过一些实验找到的。
伪随机数生成器的种子被固定,以便我们始终获得相同的随机数序列,在这种情况下,它确保了每次运行代码时搜索的起始点都相同(例如,一个远离最优值的有趣点)。
|
1 2 3 4 5 6 7 8 9 10 11 |
... # 初始化伪随机数生成器 seed(4) # 定义输入范围 bounds = asarray([[-1.0, 1.0]]) # 定义总迭代次数 n_iter = 30 # 定义最大步长 step_size = 0.1 # 执行梯度下降搜索 best, score = gradient_descent(objective, derivative, bounds, n_iter, step_size) |
将这一切结合起来,下面列出了将网格搜索应用于我们的一维测试函数的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# 用于一维函数的梯度下降示例 from numpy import asarray from numpy.random import rand from numpy.random import seed # 目标函数 def objective(x): return x**2.0 # 目标函数的导数 def derivative(x): return x * 2.0 # 梯度下降算法 def gradient_descent(objective, derivative, bounds, n_iter, step_size): # 生成初始点 solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 运行梯度下降 for i in range(n_iter): # 计算梯度 gradient = derivative(solution) # 迈出一步 solution = solution - step_size * gradient # 评估候选点 solution_eval = objective(solution) # 报告进度 print('>%d f(%s) = %.5f' % (i, solution, solution_eval)) return [solution, solution_eval] # 初始化伪随机数生成器 seed(4) # 定义输入范围 bounds = asarray([[-1.0, 1.0]]) # 定义总迭代次数 n_iter = 30 # 定义步长 step_size = 0.1 # 执行梯度下降搜索 best, score = gradient_descent(objective, derivative, bounds, n_iter, step_size) print('Done!') print('f(%s) = %f' % (best, score)) |
运行该示例从搜索空间中的一个随机点开始,然后应用梯度下降算法,并在过程中报告性能。
注意:由于算法的随机性或评估过程,或者数值精度的差异,您的结果可能有所不同。可以考虑运行该示例几次并比较平均结果。
在这种情况下,我们可以看到算法在大约 27 次迭代后找到了一个好的解决方案,函数评估值约为 0.0。
请注意,此函数的最佳值是 f(0.0) = 0.0。
我们期望带动量的梯度下降能够加速优化过程,并在更少的迭代次数中找到相似的评估结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
>0 f([0.74724774]) = 0.55838 >1 f([0.59779819]) = 0.35736 >2 f([0.47823856]) = 0.22871 >3 f([0.38259084]) = 0.14638 >4 f([0.30607268]) = 0.09368 >5 f([0.24485814]) = 0.05996 >6 f([0.19588651]) = 0.03837 >7 f([0.15670921]) = 0.02456 >8 f([0.12536737]) = 0.01572 >9 f([0.10029389]) = 0.01006 >10 f([0.08023512]) = 0.00644 >11 f([0.06418809]) = 0.00412 >12 f([0.05135047]) = 0.00264 >13 f([0.04108038]) = 0.00169 >14 f([0.0328643]) = 0.00108 >15 f([0.02629144]) = 0.00069 >16 f([0.02103315]) = 0.00044 >17 f([0.01682652]) = 0.00028 >18 f([0.01346122]) = 0.00018 >19 f([0.01076897]) = 0.00012 >20 f([0.00861518]) = 0.00007 >21 f([0.00689214]) = 0.00005 >22 f([0.00551372]) = 0.00003 >23 f([0.00441097]) = 0.00002 >24 f([0.00352878]) = 0.00001 >25 f([0.00282302]) = 0.00001 >26 f([0.00225842]) = 0.00001 >27 f([0.00180673]) = 0.00000 >28 f([0.00144539]) = 0.00000 >29 f([0.00115631]) = 0.00000 完成! f([0.00115631]) = 0.000001 |
梯度下降优化可视化
接下来,我们可以可视化搜索在目标函数图上的进展。
首先,我们可以修改 *gradient_descent()* 函数,使其将优化过程中找到的所有解决方案及其分数存储为列表,并在搜索结束时返回它们,而不是返回找到的最佳解决方案。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 梯度下降算法 def gradient_descent(objective, derivative, bounds, n_iter, step_size): # 跟踪所有解决方案 solutions, scores = list(), list() # 生成初始点 solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 运行梯度下降 for i in range(n_iter): # 计算梯度 gradient = derivative(solution) # 迈出一步 solution = solution - step_size * gradient # 评估候选点 solution_eval = objective(solution) # 存储解决方案 solutions.append(solution) scores.append(solution_eval) # 报告进度 print('>%d f(%s) = %.5f' % (i, solution, solution_eval)) return [solutions, scores] |
可以调用该函数,我们就可以获得搜索过程中找到的解决方案列表和分数。
|
1 2 3 |
... # 执行梯度下降搜索 solutions, scores = gradient_descent(objective, derivative, bounds, n_iter, step_size) |
我们可以创建一个目标函数的折线图,就像以前一样。
|
1 2 3 4 5 6 7 |
... # 以 0.1 为增量均匀采样输入范围 inputs = arange(bounds[0,0], bounds[0,1]+0.1, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) |
最后,我们可以将找到的每个解绘制为红点,并通过线条连接这些点,以便我们能看到搜索是如何向下移动的。
|
1 2 3 |
... # 绘制找到的解决方案 pyplot.plot(solutions, scores, '.-', color='red') |
将所有这些整合在一起,下面列出了将梯度下降搜索结果绘制到一维测试函数上的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
# 用于绘制梯度下降搜索在一维函数上的示例 from numpy import asarray from numpy import arange from numpy.random import rand from numpy.random import seed from matplotlib import pyplot # 目标函数 def objective(x): return x**2.0 # 目标函数的导数 def derivative(x): return x * 2.0 # 梯度下降算法 def gradient_descent(objective, derivative, bounds, n_iter, step_size): # 跟踪所有解决方案 solutions, scores = list(), list() # 生成初始点 solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 运行梯度下降 for i in range(n_iter): # 计算梯度 gradient = derivative(solution) # 迈出一步 solution = solution - step_size * gradient # 评估候选点 solution_eval = objective(solution) # 存储解决方案 solutions.append(solution) scores.append(solution_eval) # 报告进度 print('>%d f(%s) = %.5f' % (i, solution, solution_eval)) return [solutions, scores] # 初始化伪随机数生成器 seed(4) # 定义输入范围 bounds = asarray([[-1.0, 1.0]]) # 定义总迭代次数 n_iter = 30 # 定义步长 step_size = 0.1 # 执行梯度下降搜索 solutions, scores = gradient_descent(objective, derivative, bounds, n_iter, step_size) # 以 0.1 为增量均匀采样输入范围 inputs = arange(bounds[0,0], bounds[0,1]+0.1, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 绘制找到的解决方案 pyplot.plot(solutions, scores, '.-', color='red') # 显示绘图 pyplot.show() |
运行该示例将执行梯度下降搜索,就像以前一样,不同的是,在这种情况下,搜索过程中找到的每个点都会被绘制出来。
注意:由于算法的随机性或评估过程,或者数值精度的差异,您的结果可能有所不同。可以考虑运行该示例几次并比较平均结果。
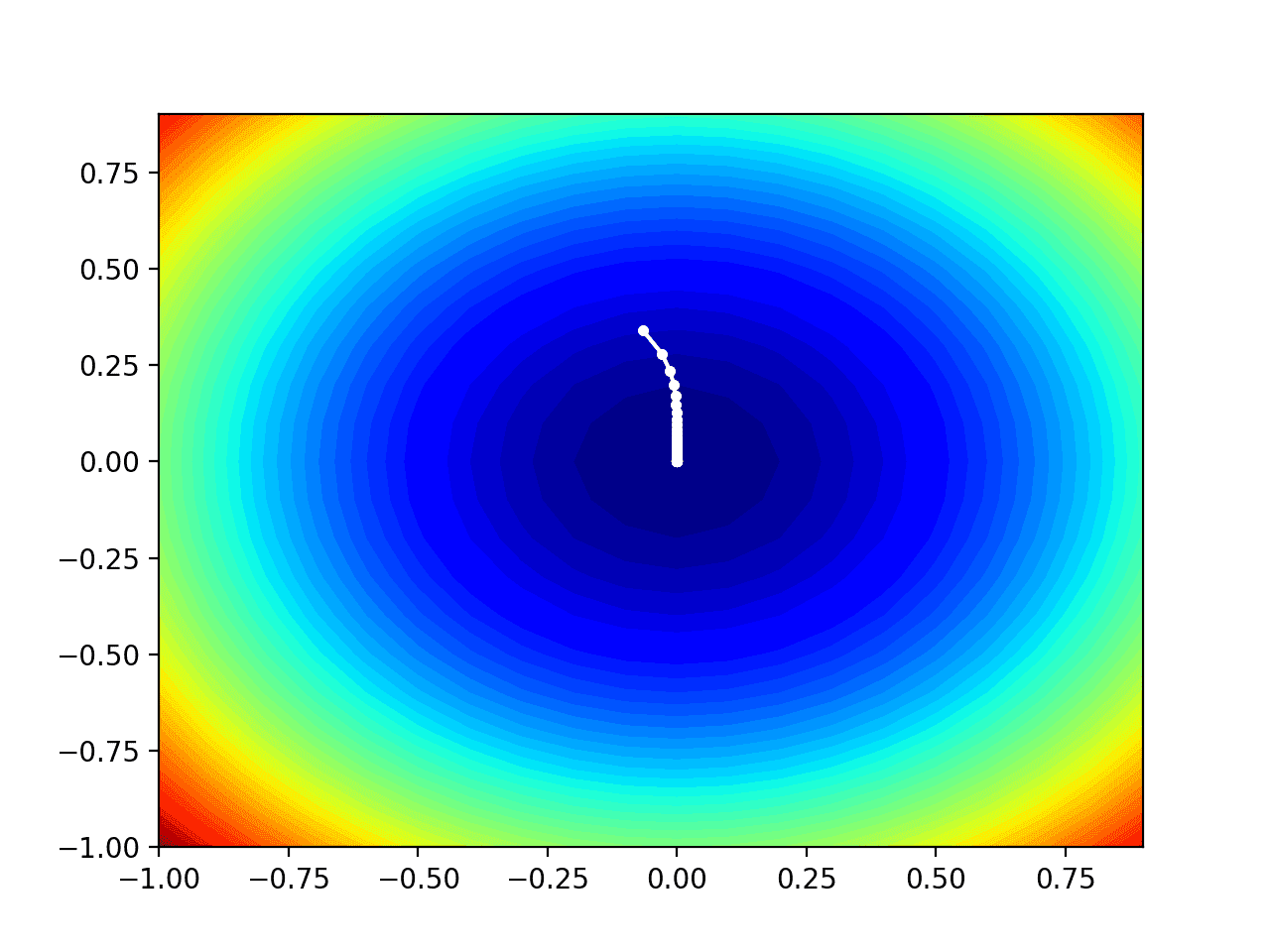
在这种情况下,我们可以看到搜索从函数右侧一半多一点的位置开始,然后逐步向下移动到盆地的底部。
我们可以看到,在目标函数曲率较大的部分,导数(梯度)也较大,因此步长也较大。同样,随着我们接近最优值,梯度变小,步长也随之变小。
这凸显了步长被用作目标函数梯度(曲率)幅度的比例因子。
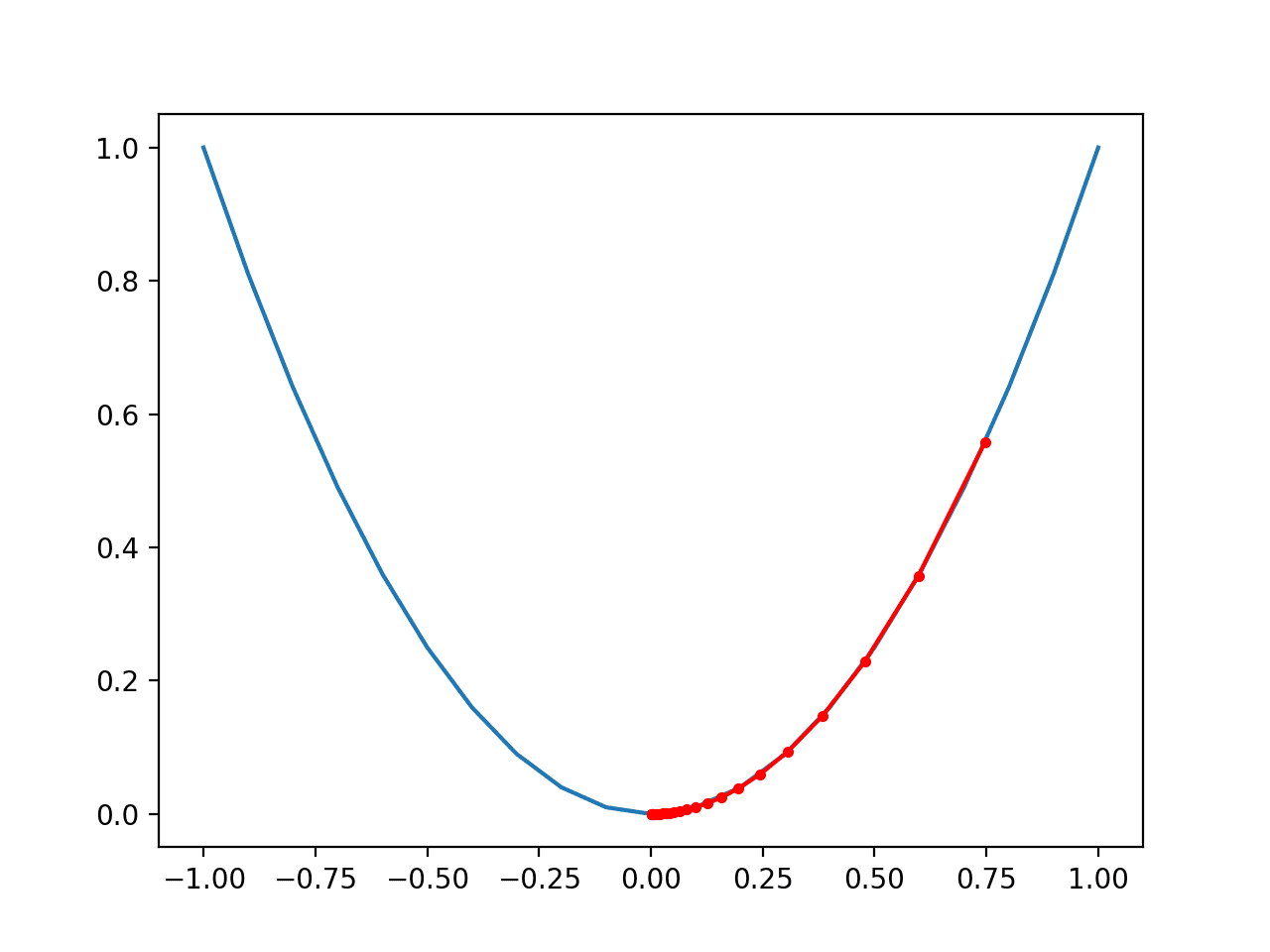
梯度下降在一维目标函数上进展图
带动量的梯度下降优化
接下来,我们可以更新梯度下降优化算法以使用动量。
这可以通过更新 *gradient_descent()* 函数以接受一个“momentum”参数来实现,该参数定义了搜索过程中使用的动量量。
解决方案的变化必须从前一个循环迭代中记住,初始值为 0.0。
|
1 2 3 |
... # 跟踪变化 change = 0.0 |
然后,我们可以将更新过程分解为首先计算梯度,然后计算解决方案的变化,计算新解决方案的位置,然后保存以备下一次迭代的变化。
|
1 2 3 4 5 6 7 8 9 |
... # 计算梯度 gradient = derivative(solution) # 计算更新 new_change = step_size * gradient + momentum * change # 迈出一步 solution = solution - new_change # 保存变化 change = new_change |
下面列出了带有这些更改的 *gradient_descent()* 函数的更新版本。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# 梯度下降算法 def gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum): # 生成初始点 solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 跟踪变化 change = 0.0 # 运行梯度下降 for i in range(n_iter): # 计算梯度 gradient = derivative(solution) # 计算更新 new_change = step_size * gradient + momentum * change # 迈出一步 solution = solution - new_change # 保存变化 change = new_change # 评估候选点 solution_eval = objective(solution) # 报告进度 print('>%d f(%s) = %.5f' % (i, solution, solution_eval)) return [solution, solution_eval] |
然后,我们可以选择一个动量值并将其传递给 *gradient_descent()* 函数。
经过一些试错,发现动量值为 0.3 在这个具有固定步长 0.1 的问题上是有效的。
|
1 2 3 4 5 |
... # 定义动量 momentum = 0.3 # 执行带动量的梯度下降搜索 best, score = gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum) |
将这些内容整合在一起,下面列出了带动量的梯度下降优化的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
# 用于一维函数的带动量梯度下降示例 from numpy import asarray from numpy.random import rand from numpy.random import seed # 目标函数 def objective(x): return x**2.0 # 目标函数的导数 def derivative(x): return x * 2.0 # 梯度下降算法 def gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum): # 生成初始点 solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 跟踪变化 change = 0.0 # 运行梯度下降 for i in range(n_iter): # 计算梯度 gradient = derivative(solution) # 计算更新 new_change = step_size * gradient + momentum * change # 迈出一步 solution = solution - new_change # 保存变化 change = new_change # 评估候选点 solution_eval = objective(solution) # 报告进度 print('>%d f(%s) = %.5f' % (i, solution, solution_eval)) return [solution, solution_eval] # 初始化伪随机数生成器 seed(4) # 定义输入范围 bounds = asarray([[-1.0, 1.0]]) # 定义总迭代次数 n_iter = 30 # 定义步长 step_size = 0.1 # 定义动量 momentum = 0.3 # 执行带动量的梯度下降搜索 best, score = gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum) print('Done!') print('f(%s) = %f' % (best, score)) |
运行该示例从搜索空间中的一个随机点开始,然后应用带动量的梯度下降算法,并在过程中报告性能。
注意:由于算法的随机性或评估过程,或者数值精度的差异,您的结果可能有所不同。可以考虑运行该示例几次并比较平均结果。
在这种情况下,我们可以看到算法在大约 13 次迭代后找到了一个好的解决方案,函数评估值约为 0.0。
正如预期的那样,这比不带动量的梯度下降更快(迭代次数更少),使用了相同的起始点和步长,而不带动量需要 27 次迭代。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
>0 f([0.74724774]) = 0.55838 >1 f([0.54175461]) = 0.29350 >2 f([0.37175575]) = 0.13820 >3 f([0.24640494]) = 0.06072 >4 f([0.15951871]) = 0.02545 >5 f([0.1015491]) = 0.01031 >6 f([0.0638484]) = 0.00408 >7 f([0.03976851]) = 0.00158 >8 f([0.02459084]) = 0.00060 >9 f([0.01511937]) = 0.00023 >10 f([0.00925406]) = 0.00009 >11 f([0.00564365]) = 0.00003 >12 f([0.0034318]) = 0.00001 >13 f([0.00208188]) = 0.00000 >14 f([0.00126053]) = 0.00000 >15 f([0.00076202]) = 0.00000 >16 f([0.00046006]) = 0.00000 >17 f([0.00027746]) = 0.00000 >18 f([0.00016719]) = 0.00000 >19 f([0.00010067]) = 0.00000 >20 f([6.05804744e-05]) = 0.00000 >21 f([3.64373635e-05]) = 0.00000 >22 f([2.19069576e-05]) = 0.00000 >23 f([1.31664443e-05]) = 0.00000 >24 f([7.91100141e-06]) = 0.00000 >25 f([4.75216828e-06]) = 0.00000 >26 f([2.85408468e-06]) = 0.00000 >27 f([1.71384267e-06]) = 0.00000 >28 f([1.02900153e-06]) = 0.00000 >29 f([6.17748881e-07]) = 0.00000 完成! f([6.17748881e-07]) = 0.000000 |
带动量的梯度下降优化可视化
最后,我们可以可视化带动量的梯度下降优化算法的进展。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
# 用于一维函数的带动量梯度下降示例的可视化 from numpy import asarray from numpy import arange from numpy.random import rand from numpy.random import seed from matplotlib import pyplot # 目标函数 def objective(x): return x**2.0 # 目标函数的导数 def derivative(x): return x * 2.0 # 梯度下降算法 def gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum): # 跟踪所有解决方案 solutions, scores = list(), list() # 生成初始点 solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 跟踪变化 change = 0.0 # 运行梯度下降 for i in range(n_iter): # 计算梯度 gradient = derivative(solution) # 计算更新 new_change = step_size * gradient + momentum * change # 迈出一步 solution = solution - new_change # 保存变化 change = new_change # 评估候选点 solution_eval = objective(solution) # 存储解决方案 solutions.append(solution) scores.append(solution_eval) # 报告进度 print('>%d f(%s) = %.5f' % (i, solution, solution_eval)) return [solutions, scores] # 初始化伪随机数生成器 seed(4) # 定义输入范围 bounds = asarray([[-1.0, 1.0]]) # 定义总迭代次数 n_iter = 30 # 定义步长 step_size = 0.1 # 定义动量 momentum = 0.3 # 执行带动量的梯度下降搜索 solutions, scores = gradient_descent(objective, derivative, bounds, n_iter, step_size, momentum) # 以 0.1 为增量均匀采样输入范围 inputs = arange(bounds[0,0], bounds[0,1]+0.1, 0.1) # 计算目标值 results = objective(inputs) # 绘制输入与结果的线图 pyplot.plot(inputs, results) # 绘制找到的解决方案 pyplot.plot(solutions, scores, '.-', color='red') # 显示绘图 pyplot.show() |
运行该示例将执行带动量的梯度下降搜索,与以前一样,不同的是,在这种情况下,搜索过程中找到的每个点都会被绘制出来。
注意:由于算法的随机性或评估过程,或者数值精度的差异,您的结果可能有所不同。可以考虑运行该示例几次并比较平均结果。
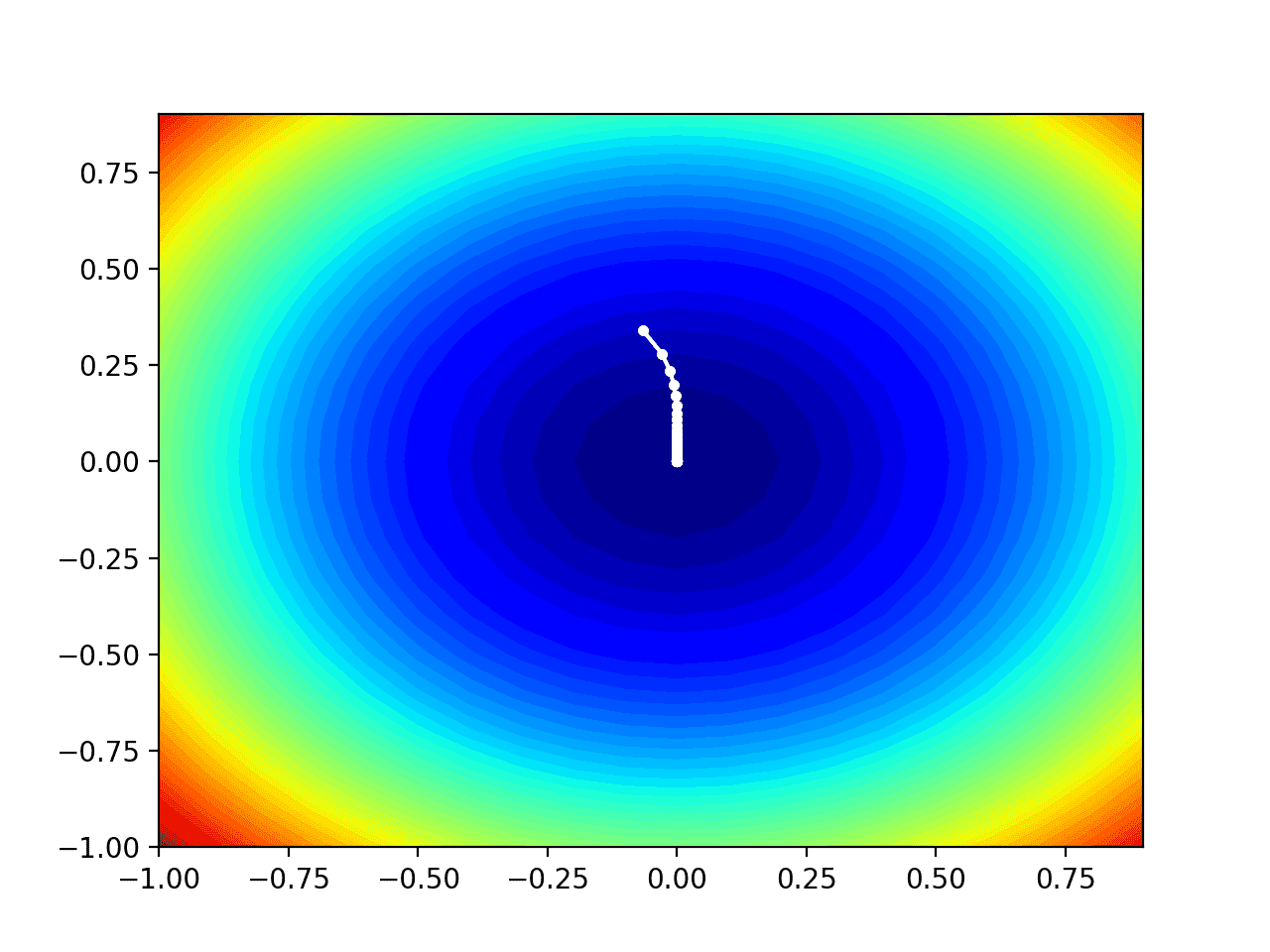
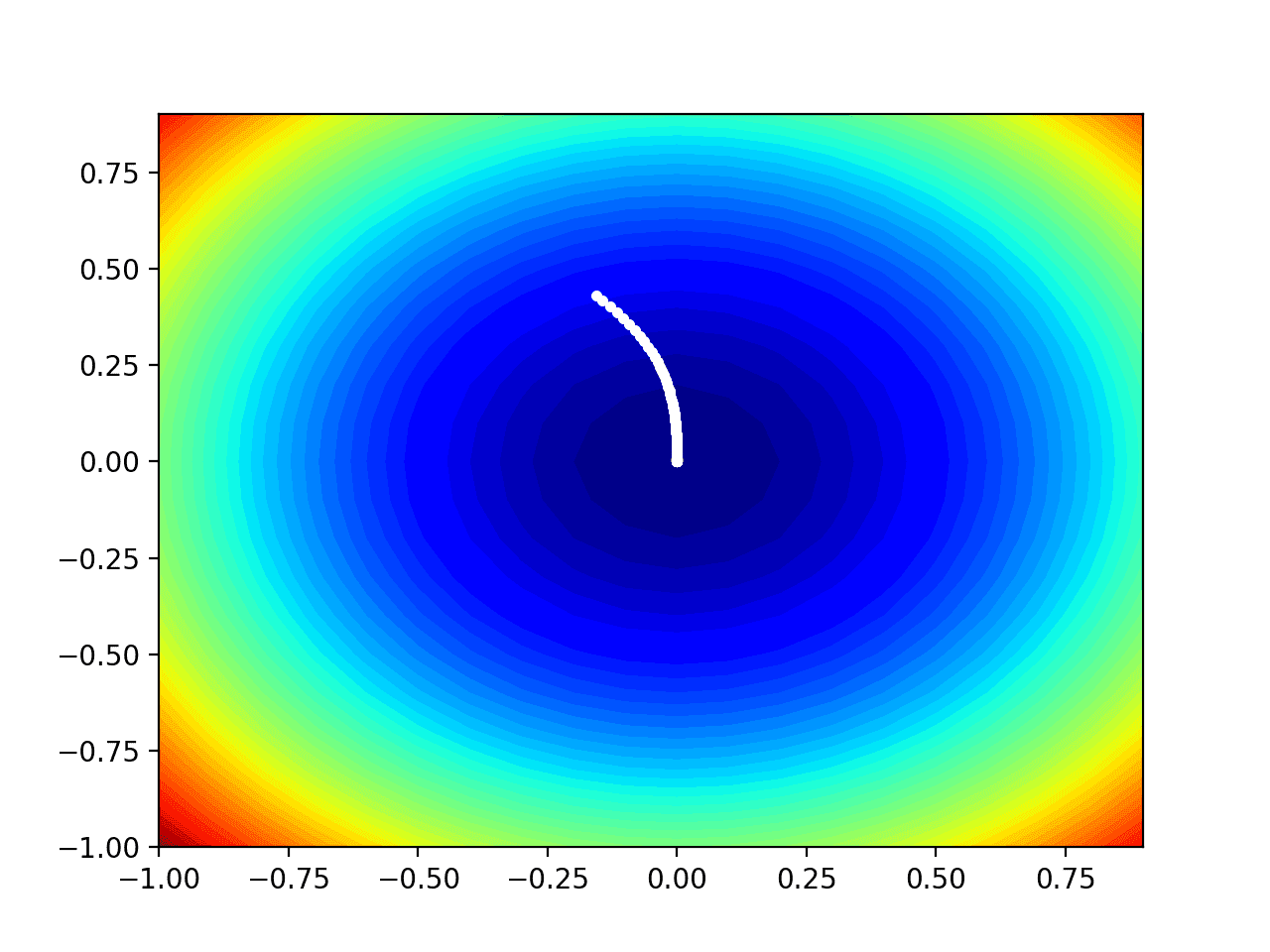
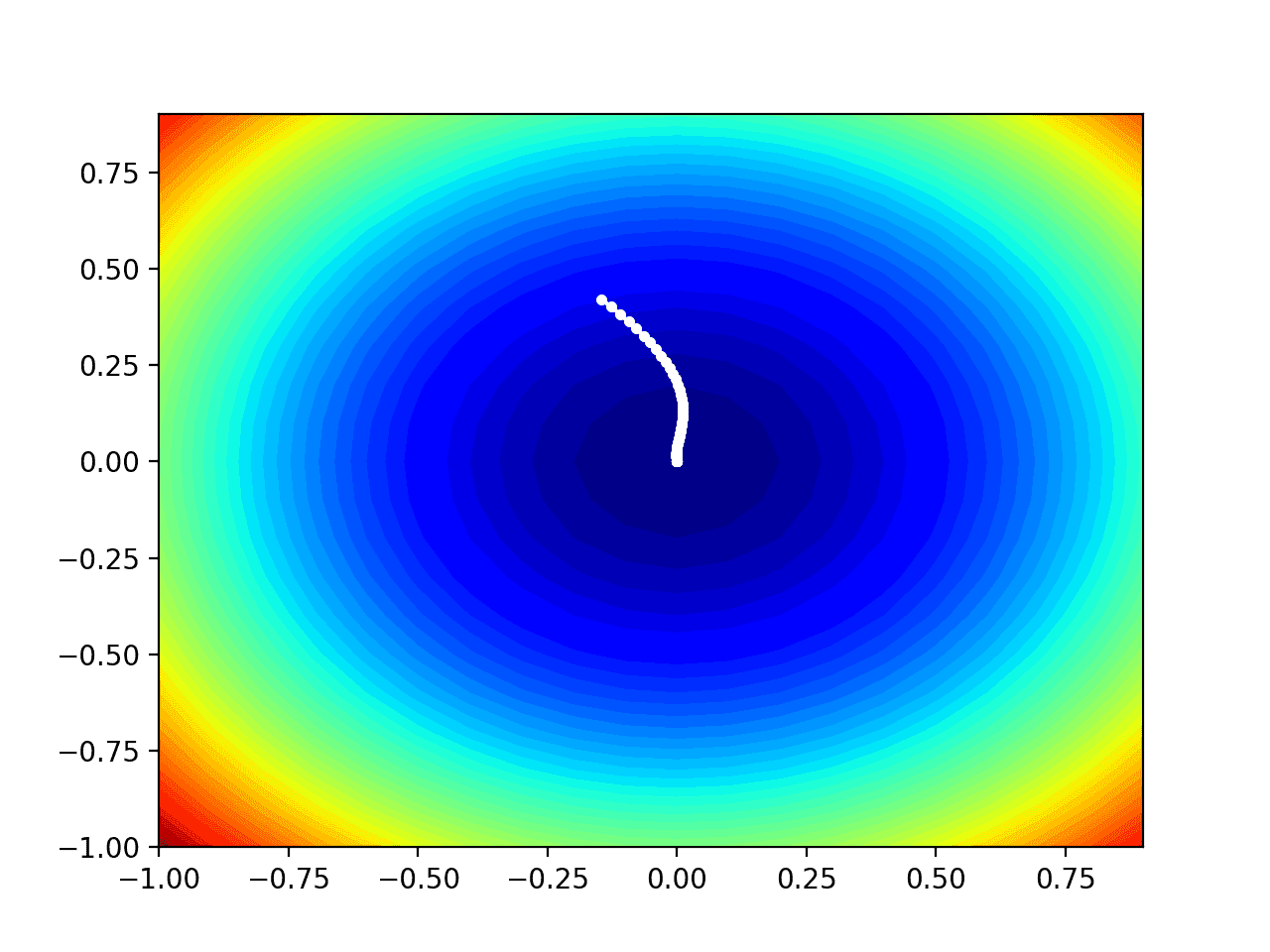
在这种情况下,如果我们将其与先前为梯度下降(不带动量)性能创建的图进行比较,我们可以看到搜索确实在更少的步骤中达到了最优值,在通往盆底的路径上标记为更少的不同红点。
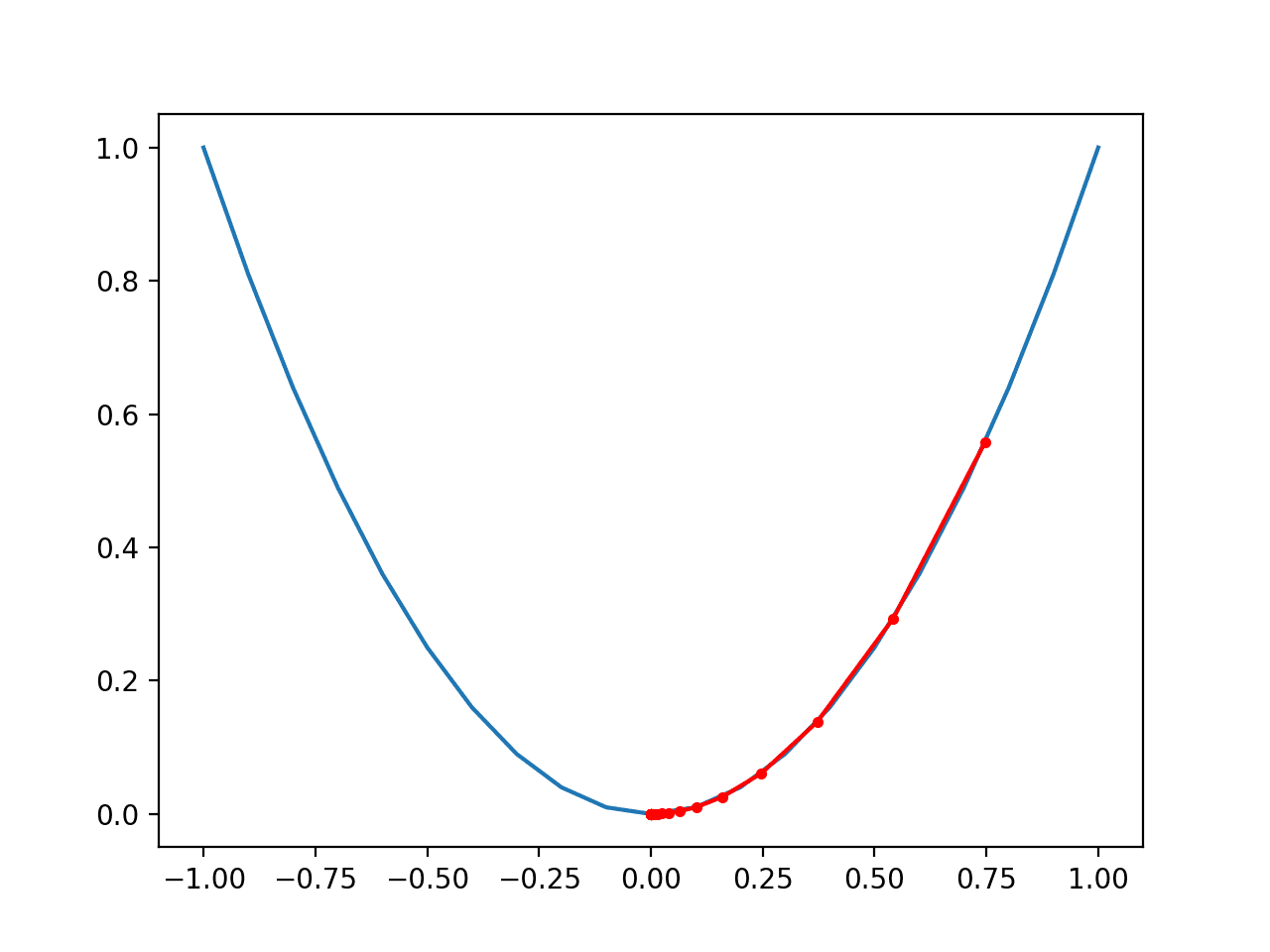
带动量的梯度下降在一维目标函数上进展图
作为扩展,尝试不同的动量值,例如 0.8,并查看生成的图。
请在下面的评论中告诉我您的发现。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 优化算法, 2019.
- 深度学习, 2016.
- 《神经网络精工:前馈人工神经网络中的监督学习》, 1999.
- 《用于模式识别的神经网络》, 1996.
- 神经网络:技术琐事, 2012.
API
文章
总结
在本教程中,您了解了带动量的梯度下降算法。
具体来说,你学到了:
- 梯度下降是一种优化算法,它利用目标函数的梯度来导航搜索空间。
- 通过利用过去更新搜索位置的动量,可以加速梯度下降。
- 如何实现带动量的梯度下降优化,并对其行为建立直观认识。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。

拥有此内容的网站
https://neoshare.net/machine-learning/gradient-descent-with-momentum-from-scratch/
直接从我的网站偷的!!!
别担心,谷歌会因为这些抄袭者(剽窃者)而受到惩罚,搜索排名会很差……
您接下来能否介绍一下最小化多个变量函数的案例?感谢您的帖子。
当然,请看这个例子
https://machinelearning.org.cn/adam-optimization-from-scratch/
嗨 Jason,一如既往的好文章。
如果你的函数没有导数怎么办?你会推荐什么?
选择一个好的动量值似乎也是一个优化问题。动量算法能否以递归方式使用?
您可以使用模式搜索,如 Nelder-Mead 方法。
https://machinelearning.org.cn/how-to-use-nelder-mead-optimization-in-python/
或者随机搜索,如随机爬山法。
https://machinelearning.org.cn/stochastic-hill-climbing-in-python-from-scratch/
是的,动量是另一个需要调整的超参数。
感谢这个很好的例子。我目前在模拟优化中使用有限差分来近似我的梯度。看看动量项是否能加速我的优化🙂
请尝试一下。我的印象是动量可能不会加速,但可以在遇到局部最优时帮助您摆脱过早收敛。
Jason,感谢您生动的解释。
在行业中常规应用的优化函数中,除了学习率和动量之外,还有其他超参数吗?
不客气。
没有,真的没有。
嗨 Jason,我长期以来一直在关注您的工作。我还买了您的几本书。Jason,您能否用仅包含输入特征 X 和输出特征 Y 的数据集来展示这些?这可以帮助我们更好地理解概念。
感谢您的建议!
嗨 Jason
精彩的文章,谢谢。
一个问题。文章开头有一个公式解释了动量是如何工作的。见下文
change_x(t) = step_size * f'(x(t-1)) + momentum * change_x(t-1)
它不应该是这样的吗?
change_x(t) = step_size * f'(x(t)) + momentum * change_x(t-1)
如果不是,我有点困惑)
嗨 Denis……你说得对。这个问题已经注意到。
这是否有效地将梯度相加,从而导致梯度爆炸?
嗨 Tom……以下资源从另一个角度解释了带动量梯度下降的好处。
https://distill.pub/2017/momentum/