深度学习技术能力的流行演示是图像数据中的目标识别。机器学习和深度学习目标识别的“hello world”是手写数字识别的 MNIST 数据集。在这篇文章中,您将学习如何在 PyTorch 中开发一个深度学习模型,以在 MNIST 手写数字识别任务上实现接近最先进的性能。完成本章后,您将了解:
- 如何使用 torchvision 加载 MNIST 数据集
- 如何开发和评估 MNIST 问题的基线神经网络模型
- 如何实现和评估 MNIST 的简单卷积神经网络
- 如何实现 MNIST 的最先进深度学习模型
通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。
让我们开始吧。

使用 PyTorch 中的 LeNet5 模型进行手写数字识别
图片来源:Johnny Wong。保留部分权利。
概述
本文分为五个部分,它们是:
- MNIST 手写数字识别问题
- 在 PyTorch 中加载 MNIST 数据集
- 基于多层感知器的基线模型
- 用于 MNIST 的简单卷积神经网络
- 用于 MNIST 的 LeNet5
MNIST 手写数字识别问题
MNIST 问题是一个经典的例子,可以展示卷积神经网络的强大能力。MNIST 数据集由 Yann LeCun、Corinna Cortes 和 Christopher Burges 开发,用于评估机器学习模型在手写数字分类问题上的性能。该数据集是从国家标准与技术研究院(NIST)提供的多个扫描文档数据集中构建的。这就是数据集名称的由来,即 Modified NIST 或 MNIST 数据集。
数字图像取自各种扫描文档,经过大小标准化和居中处理。这使其成为评估模型的优秀数据集,允许开发人员专注于机器学习,而无需进行最少的数据清理或准备。每张图像都是 28×28 像素的正方形(总共 784 像素)灰度图像。数据集的标准划分用于评估和比较模型,其中 60,000 张图像用于训练模型,另外 10,000 张图像用于测试。
这个问题的目标是识别图像上的数字。有十个数字(0到9)或十个类别需要预测。最先进的预测精度达到了 99.8% 的水平,这是通过大型卷积神经网络实现的。
想开始使用PyTorch进行深度学习吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
在 PyTorch 中加载 MNIST 数据集
torchvision 库是 PyTorch 的一个姊妹项目,它为计算机视觉任务提供专门的函数。torchvision 中有一个函数可以下载 MNIST 数据集供 PyTorch 使用。该数据集在第一次调用此函数时下载并本地存储,因此您将来无需再次下载。下面是一个小脚本,用于下载和可视化 MNIST 数据集训练子集中的前 16 张图像。
|
1 2 3 4 5 6 7 8 9 10 |
import matplotlib.pyplot as plt import torchvision train = torchvision.datasets.MNIST('./data', train=True, download=True) fig, ax = plt.subplots(4, 4, sharex=True, sharey=True) for i in range(4): for j in range(4): ax[i][j].imshow(train.data[4*i+j], cmap="gray") plt.show() |

基于多层感知器的基线模型
您是否真的需要像卷积神经网络这样复杂的模型才能在 MNIST 上获得最佳结果?使用一个简单的单隐藏层神经网络模型就可以获得不错的结果。在本节中,您将创建一个简单的多层感知器模型,其准确率达到 99.81%。您将以此作为基线,与更复杂的卷积神经网络模型进行比较。首先,让我们看看数据是什么样的。
|
1 2 3 4 5 6 7 8 9 10 |
import torch import torch.nn as nn import torch.optim as optim import torchvision # 加载 MNIST 数据 train = torchvision.datasets.MNIST('data', train=True, download=True) test = torchvision.datasets.MNIST('data', train=True, download=True) print(train.data.shape, train.targets.shape) print(test.data.shape, test.targets.shape) |
您应该看到
|
1 2 |
torch.Size([60000, 28, 28]) torch.Size([60000]) torch.Size([10000, 28, 28]) torch.Size([10000]) |
训练数据集的结构是一个三维数组,包含实例、图像高度和图像宽度。对于多层感知器模型,您必须将图像缩小为像素向量。在这种情况下,28×28 大小的图像将是 784 像素的输入向量。您可以使用 reshape() 函数轻松完成此转换。
像素值是介于 0 到 255 之间的灰度值。在使用神经网络模型时,对输入值进行缩放几乎总是一个好主意。由于比例是众所周知且表现良好的,因此您可以通过将每个值除以最大值 255,非常快速地将像素值归一化到 0 到 1 的范围。
在以下步骤中,您将转换数据集,将其转换为浮点数,并通过缩放浮点值对其进行归一化,并在下一步中轻松进行归一化。
|
1 2 3 4 5 |
# 每个样本变成 0-1 范围的值向量 X_train = train.data.reshape(-1, 784).float() / 255.0 y_train = train.targets X_test = test.data.reshape(-1, 784).float() / 255.0 y_test = test.targets |
输出目标 y_train 和 y_test 是 0 到 9 之间的整数形式的标签。这是一个多类别分类问题。您可以将这些标签转换为独热编码,或者像本例一样保留它们为整数标签。您将使用交叉熵函数评估模型性能,PyTorch 的交叉熵函数实现可以应用于独热编码目标或整数标签目标。
现在,您已准备好创建简单的神经网络模型。您将在 PyTorch Module 类中定义模型。
|
1 2 3 4 5 6 7 8 9 10 11 |
class Baseline(nn.Module): def __init__(self): super().__init__() self.layer1 = nn.Linear(784, 784) self.act1 = nn.ReLU() self.layer2 = nn.Linear(784, 10) def forward(self, x): x = self.act1(self.layer1(x)) x = self.layer2(x) return x |
该模型是一个简单的神经网络,包含一个隐藏层,其神经元数量与输入(784个)相同。隐藏层中的神经元使用 ReLU 激活函数。该模型的输出是 **logits**,这意味着它们是可以使用 softmax 函数转换为类似概率值的实数。您无需显式应用 softmax 函数,因为交叉熵函数将为您完成此操作。
您将使用随机梯度下降算法(学习率设置为 0.01)来优化此模型。训练循环如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
model = Baseline() optimizer = optim.SGD(model.parameters(), lr=0.01) loss_fn = nn.CrossEntropyLoss() loader = torch.utils.data.DataLoader(list(zip(X_train, y_train)), shuffle=True, batch_size=100) n_epochs = 10 for epoch in range(n_epochs): model.train() for X_batch, y_batch in loader: y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) optimizer.zero_grad() loss.backward() optimizer.step() # 验证 model.eval() y_pred = model(X_test) acc = (torch.argmax(y_pred, 1) == y_test).float().mean() print("Epoch %d: model accuracy %.2f%%" % (epoch, acc*100)) |
MNIST 数据集很小。这个例子应该在一分钟内完成,输出如下。这个简单的网络可以产生 92% 的准确率。
|
1 2 3 4 5 6 7 8 9 10 |
Epoch 0: 模型准确率 84.11% Epoch 1: 模型准确率 87.53% Epoch 2: 模型准确率 89.01% Epoch 3: 模型准确率 89.76% Epoch 4: 模型准确率 90.29% Epoch 5: 模型准确率 90.69% Epoch 6: 模型准确率 91.10% Epoch 7: 模型准确率 91.48% Epoch 8: 模型准确率 91.74% Epoch 9: 模型准确率 91.96% |
下面是上述 MNIST 数据集上的多层感知器分类的完整代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
import torch import torch.nn as nn import torch.optim as optim import torchvision # 加载 MNIST 数据 train = torchvision.datasets.MNIST('data', train=True, download=True) test = torchvision.datasets.MNIST('data', train=True, download=True) # 每个样本变成 0-1 范围的值向量 X_train = train.data.reshape(-1, 784).float() / 255.0 y_train = train.targets X_test = test.data.reshape(-1, 784).float() / 255.0 y_test = test.targets class Baseline(nn.Module): def __init__(self): super().__init__() self.layer1 = nn.Linear(784, 784) self.act1 = nn.ReLU() self.layer2 = nn.Linear(784, 10) def forward(self, x): x = self.act1(self.layer1(x)) x = self.layer2(x) return x model = Baseline() optimizer = optim.SGD(model.parameters(), lr=0.01) loss_fn = nn.CrossEntropyLoss() loader = torch.utils.data.DataLoader(list(zip(X_train, y_train)), shuffle=True, batch_size=100) n_epochs = 10 for epoch in range(n_epochs): model.train() for X_batch, y_batch in loader: y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) optimizer.zero_grad() loss.backward() optimizer.step() # 验证 model.eval() y_pred = model(X_test) acc = (torch.argmax(y_pred, 1) == y_test).float().mean() print("Epoch %d: model accuracy %.2f%%" % (epoch, acc*100)) |
用于 MNIST 的简单卷积神经网络
既然您已经了解了如何使用多层感知器模型对 MNIST 数据集进行分类。让我们继续尝试卷积神经网络模型。在本节中,您将为 MNIST 创建一个简单的 CNN,该 CNN 将演示如何使用现代 CNN 实现的所有方面,包括卷积层、池化层和 dropout 层。
在 PyTorch 中,卷积层应该作用于图像。图像的张量应该是像素值,其维度为 (样本数、通道数、高度、宽度),但是当您使用 PIL 等库加载图像时,像素通常以 (高度、宽度、通道数) 的维度数组形式呈现。转换成正确的张量格式可以通过 torchvision 库中的转换函数完成。
|
1 2 3 4 5 6 7 8 9 |
... transform = torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((0,), (128,)), ]) train = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform) test = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform) trainloader = torch.utils.data.DataLoader(train, shuffle=True, batch_size=100) testloader = torch.utils.data.DataLoader(test, shuffle=True, batch_size=100) |
您需要使用 DataLoader,因为转换是在从 DataLoader 读取数据时应用的。
接下来,定义您的神经网络模型。卷积神经网络比标准多层感知器更复杂,因此您将首先使用一个简单的结构,该结构使用了实现最先进结果的所有元素。下面总结了网络架构。
- 第一个隐藏层是卷积层,
nn.Conv2d()。该层将灰度图像转换为 10 个特征图,滤波器大小为 5×5,并使用 ReLU 激活函数。这是期望具有上述结构图像的输入层。 - 接下来是一个使用最大池化的池化层,
nn.MaxPool2d()。它配置为 2×2 的池化大小,步幅为 1。它的作用是在每个通道的 2×2 像素块中取最大值,并将该值分配给输出像素。结果是每个通道 27×27 像素的特征图。 - 下一层是使用 Dropout 的正则化层,
nn.Dropout()。它被配置为随机排除层中 20% 的神经元,以减少过拟合。 - 接下来是一个使用
nn.Flatten将 2D 矩阵数据转换为向量的层。它的输入有 10 个通道,每个通道的特征图大小为 27×27。该层允许输出由标准的、全连接层处理。 - 接下来是一个具有128个神经元的全连接层。使用了ReLU激活函数。
- 最后,输出层有十个神经元,对应十个类别。您可以通过在其上应用 softmax 函数将输出转换为类似概率的预测。
该模型使用交叉熵损失和 Adam 优化算法进行训练。其实现如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
class CNN(nn.Module): def __init__(self): super().__init__() self.conv = nn.Conv2d(1, 10, kernel_size=5, stride=1, padding=2) self.relu1 = nn.ReLU() self.pool = nn.MaxPool2d(kernel_size=2, stride=1) self.dropout = nn.Dropout(0.2) self.flat = nn.Flatten() self.fc = nn.Linear(27*27*10, 128) self.relu2 = nn.ReLU() self.output = nn.Linear(128, 10) def forward(self, x): x = self.relu1(self.conv(x)) x = self.pool(x) x = self.dropout(x) x = self.relu2(self.fc(self.flat(x))) x = self.output(x) return x model = CNN() optimizer = optim.Adam(model.parameters(), lr=0.01) loss_fn = nn.CrossEntropyLoss() n_epochs = 10 for epoch in range(n_epochs): model.train() for X_batch, y_batch in trainloader: y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) optimizer.zero_grad() loss.backward() optimizer.step() # 验证 model.eval() acc = 0 count = 0 for X_batch, y_batch in testloader: y_pred = model(X_batch) acc += (torch.argmax(y_pred, 1) == y_batch).float().sum() count += len(y_batch) acc = acc / count print("Epoch %d: 模型准确率 %.2f%%" % (epoch, acc*100)) |
运行上述代码需要几分钟,并产生以下结果:
|
1 2 3 4 5 6 7 8 9 10 |
Epoch 0: 模型准确率 81.74% Epoch 1: 模型准确率 85.38% Epoch 2: 模型准确率 86.37% Epoch 3: 模型准确率 87.75% Epoch 4: 模型准确率 88.00% Epoch 5: 模型准确率 88.17% Epoch 6: 模型准确率 88.81% Epoch 7: 模型准确率 88.34% Epoch 8: 模型准确率 88.86% Epoch 9: 模型准确率 88.75% |
结果不是最好的,但这展示了卷积层的工作原理。
下面是使用简单卷积网络的完整代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
import torch import torch.nn as nn import torch.optim as optim import torchvision # 加载 MNIST 数据 transform = torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((0,), (128,)), ]) train = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform) test = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform) trainloader = torch.utils.data.DataLoader(train, shuffle=True, batch_size=100) testloader = torch.utils.data.DataLoader(test, shuffle=True, batch_size=100) class CNN(nn.Module): def __init__(self): super().__init__() self.conv = nn.Conv2d(1, 10, kernel_size=5, stride=1, padding=2) self.relu1 = nn.ReLU() self.pool = nn.MaxPool2d(kernel_size=2, stride=1) self.dropout = nn.Dropout(0.2) self.flat = nn.Flatten() self.fc = nn.Linear(27*27*10, 128) self.relu2 = nn.ReLU() self.output = nn.Linear(128, 10) def forward(self, x): x = self.relu1(self.conv(x)) x = self.pool(x) x = self.dropout(x) x = self.relu2(self.fc(self.flat(x))) x = self.output(x) return x model = CNN() optimizer = optim.Adam(model.parameters()) loss_fn = nn.CrossEntropyLoss() n_epochs = 10 for epoch in range(n_epochs): model.train() for X_batch, y_batch in trainloader: y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) optimizer.zero_grad() loss.backward() optimizer.step() # 验证 model.eval() acc = 0 count = 0 for X_batch, y_batch in testloader: y_pred = model(X_batch) acc += (torch.argmax(y_pred, 1) == y_batch).float().sum() count += len(y_batch) acc = acc / count print("Epoch %d: 模型准确率 %.2f%%" % (epoch, acc*100)) |
用于 MNIST 的 LeNet5
前面的模型只有一个卷积层。当然,您可以添加更多层以构建更深的模型。神经网络中卷积层有效性的最早演示之一是“LeNet5”模型。该模型旨在解决 MNIST 分类问题。它有三个卷积层和两个全连接层,共同构成模型中的五个可训练层,正如其名称所示。
在它被开发的时候,使用双曲正切函数作为激活函数是很常见的。因此在这里也使用了它。该模型实现如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
class LeNet5(nn.Module): def __init__(self): super().__init__() self.conv1 = nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=2) self.act1 = nn.Tanh() self.pool1 = nn.AvgPool2d(kernel_size=2, stride=2) self.conv2 = nn.Conv2d(6, 16, kernel_size=5, stride=1, padding=0) self.act2 = nn.Tanh() self.pool2 = nn.AvgPool2d(kernel_size=2, stride=2) self.conv3 = nn.Conv2d(16, 120, kernel_size=5, stride=1, padding=0) self.act3 = nn.Tanh() self.flat = nn.Flatten() self.fc1 = nn.Linear(1*1*120, 84) self.act4 = nn.Tanh() self.fc2 = nn.Linear(84, 10) def forward(self, x): # 输入 1x28x28,输出 6x28x28 x = self.act1(self.conv1(x)) # 输入 6x28x28,输出 6x14x14 x = self.pool1(x) # 输入 6x14x14,输出 16x10x10 x = self.act2(self.conv2(x)) # 输入 16x10x10,输出 16x5x5 x = self.pool2(x) # 输入 16x5x5,输出 120x1x1 x = self.act3(self.conv3(x)) # 输入 120x1x1,输出 84 x = self.act4(self.fc1(self.flat(x))) # 输入 84,输出 10 x = self.fc2(x) return x |
与之前的模型相比,LeNet5 没有 Dropout 层(因为 Dropout 层是在 LeNet5 诞生几年后才发明的),并且使用平均池化而不是最大池化(即,对于一个 2×2 像素的补丁,它取像素值的平均值而不是最大值)。但 LeNet5 模型最显著的特点是它使用步幅和填充来将图像大小从 28×28 像素缩小到 1×1 像素,同时将通道数从一个(灰度)增加到 120。
填充意味着在图像边界添加值为 0 的像素,使其稍微变大。如果没有填充,卷积层的输出将小于其输入。步幅参数控制滤波器应移动多少才能在输出中生成下一个像素。通常为 1 以保持相同大小。如果大于 1,则输出是输入的**下采样**。因此,您在 LeNet5 模型中看到,池化层中使用步幅 2 将 28×28 像素的图像转换为 14×14。
训练这个模型与训练之前的卷积神经网络模型相同,如下所示:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
... model = LeNet5() optimizer = optim.Adam(model.parameters()) loss_fn = nn.CrossEntropyLoss() n_epochs = 10 for epoch in range(n_epochs): model.train() for X_batch, y_batch in trainloader: y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) optimizer.zero_grad() loss.backward() optimizer.step() # 验证 model.eval() acc = 0 count = 0 for X_batch, y_batch in testloader: y_pred = model(X_batch) acc += (torch.argmax(y_pred, 1) == y_batch).float().sum() count += len(y_batch) acc = acc / count print("Epoch %d: 模型准确率 %.2f%%" % (epoch, acc*100)) |
运行此代码,您可能会看到:
|
1 2 3 4 5 6 7 8 9 10 |
Epoch 0: 模型准确率 89.46% Epoch 1: 模型准确率 93.14% Epoch 2: 模型准确率 94.69% Epoch 3: 模型准确率 95.84% Epoch 4: 模型准确率 96.43% Epoch 5: 模型准确率 96.99% Epoch 6: 模型准确率 97.14% Epoch 7: 模型准确率 97.66% Epoch 8: 模型准确率 98.05% Epoch 9: 模型准确率 98.22% |
在这里,我们实现了超过 98% 的准确率。
以下是完整的代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
import torch import torch.nn as nn import torch.optim as optim import torchvision # 加载 MNIST 数据 transform = torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((0,), (128,)), ]) train = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform) test = torchvision.datasets.MNIST('data', train=True, download=True, transform=transform) trainloader = torch.utils.data.DataLoader(train, shuffle=True, batch_size=100) testloader = torch.utils.data.DataLoader(test, shuffle=True, batch_size=100) class LeNet5(nn.Module): def __init__(self): super().__init__() self.conv1 = nn.Conv2d(1, 6, kernel_size=5, stride=1, padding=2) self.act1 = nn.Tanh() self.pool1 = nn.AvgPool2d(kernel_size=2, stride=2) self.conv2 = nn.Conv2d(6, 16, kernel_size=5, stride=1, padding=0) self.act2 = nn.Tanh() self.pool2 = nn.AvgPool2d(kernel_size=2, stride=2) self.conv3 = nn.Conv2d(16, 120, kernel_size=5, stride=1, padding=0) self.act3 = nn.Tanh() self.flat = nn.Flatten() self.fc1 = nn.Linear(1*1*120, 84) self.act4 = nn.Tanh() self.fc2 = nn.Linear(84, 10) def forward(self, x): # 输入 1x28x28,输出 6x28x28 x = self.act1(self.conv1(x)) # 输入 6x28x28,输出 6x14x14 x = self.pool1(x) # 输入 6x14x14,输出 16x10x10 x = self.act2(self.conv2(x)) # 输入 16x10x10,输出 16x5x5 x = self.pool2(x) # 输入 16x5x5,输出 120x1x1 x = self.act3(self.conv3(x)) # 输入 120x1x1,输出 84 x = self.act4(self.fc1(self.flat(x))) # 输入 84,输出 10 x = self.fc2(x) return x model = LeNet5() optimizer = optim.Adam(model.parameters()) loss_fn = nn.CrossEntropyLoss() n_epochs = 10 for epoch in range(n_epochs): model.train() for X_batch, y_batch in trainloader: y_pred = model(X_batch) loss = loss_fn(y_pred, y_batch) optimizer.zero_grad() loss.backward() optimizer.step() # 验证 model.eval() acc = 0 count = 0 for X_batch, y_batch in testloader: y_pred = model(X_batch) acc += (torch.argmax(y_pred, 1) == y_batch).float().sum() count += len(y_batch) acc = acc / count print("Epoch %d: 模型准确率 %.2f%%" % (epoch, acc*100)) |
MNIST 资源
MNIST 数据集经过深入研究。以下是您可能希望查阅的一些额外资源。
- Yann LeCun, Corinna Cortes, 和 Christopher J. C. Burges. MNIST 手写数字数据库。
- Rodrigo Benenson。这张图像的类别是什么?分类数据集结果,2016。
- 数字识别器:使用著名的 MNIST 数据学习计算机视觉基础知识。Kaggle。
- Hubert Eichner. 用于 JavaScript 中手写数字识别的神经网络。
总结
在这篇文章中,您发现了 MNIST 手写数字识别问题以及使用 Keras 库在 Python 中开发的深度学习模型,这些模型能够取得出色的结果。通过本章的学习,您了解了:
- 如何使用 torchvision 在 PyTorch 中加载 MNIST 数据集
- 如何将 MNIST 数据集转换为 PyTorch 张量以供卷积神经网络使用
- 如何使用 PyTorch 为 MNIST 创建卷积神经网络模型
- 如何实现用于 MNIST 分类的 LeNet5 模型

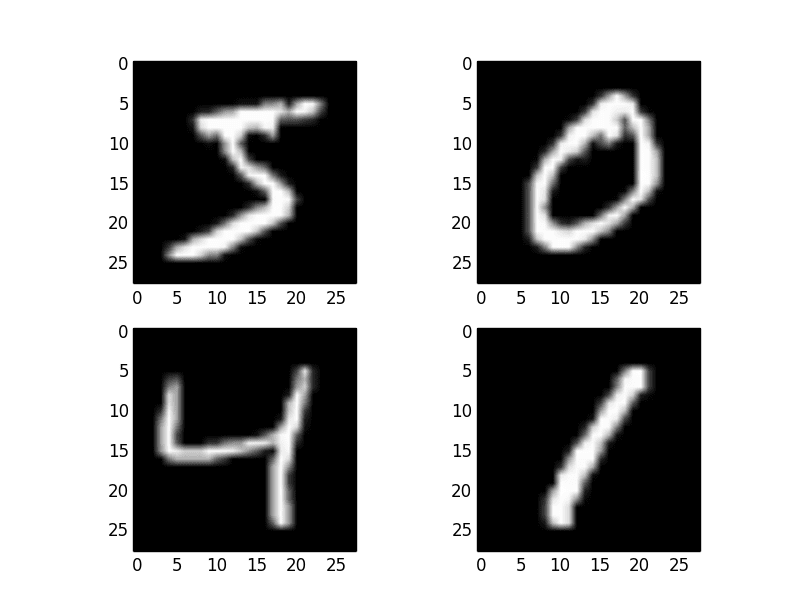




我认为测试数据集的 train 应该是 False。
哈哈,我来这里正是为了提出同样的看法
感谢这篇文章。
关于数据转换的一个问题
transform = torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize((0,), (128,)),
])
torchvision 文档中说 ToTensor 将图像数据从 [0,255] 范围转换为 [0.0,1.0]。这很好,但是应用 Normalize((0,), (128,)) 就没有意义了,因为这意味着除以 128。
我见过其他建议使用
transform = torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize((0.5,), (0.5,)),
])
这将把图像数据缩放到 [-1,1]。
你好 Michael…你的观察完全正确,所提供的转换管道中
Normalize((0,), (128,))的使用与数据归一化的通常意图不符。以下是详细说明:
###
ToTensor()的作用–
ToTensor()转换将图像数据从 PIL 图像或 NumPy 数组格式的范围[0, 255]转换为 PyTorch 张量,范围为[0.0, 1.0]。###
Normalize(mean, std)的作用–
Normalize((mean,), (std,))应用转换\[
\text{output} = \frac{\text{input} – \text{mean}}{\text{std}}
\]
其中
–
mean是要减去的平均值。–
std是要除以的标准差值。### 为什么
Normalize((0,), (128,))没有意义由于数据已经通过
ToTensor()缩放到[0.0, 1.0],因此应用Normalize((0,), (128,))意味着将缩放后的值除以128。这很可能是对归一化过程的错误或误解。相反,您通常会通过使用适当的mean和std值将数据归一化,使其均值为0.0,标准差为1.0。### 推荐的
Normalize((0.5,), (0.5,))– 使用
Normalize((0.5,), (0.5,))将数据从[0.0, 1.0]缩放到[-1.0, 1.0]。– 首先,减去
0.5将数据平移到[-0.5, 0.5]。– 然后,除以
0.5将其缩放到[-1.0, 1.0]。这对于输入数据在
[-1, 1]范围内表现良好的模型来说是一种常见做法。### LeNet-5 的正确转换
如果您遵循标准的 LeNet-5 实现,最好使用:
python
transform = torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize((0.5,), (0.5,)), # 将数据缩放到 [-1, 1]
])
或者,如果您希望基于数据集的统计数据(例如 MNIST)进行零均值和单位方差归一化,您可以使用:
python
transform = torchvision.transforms.Compose([
torchvision.transforms.ToTensor(),
torchvision.transforms.Normalize((0.1307,), (0.3081,)), # MNIST 的均值和标准差
])
这些统计数据(
mean=0.1307,std=0.3081)是根据 MNIST 数据集本身计算得出的,并在实践中被广泛使用。### 总结
– **
Normalize((0,), (128,))** 是不正确的,除非有特定的理由要除以 128(在这里不太可能)。– 使用 **
Normalize((0.5,), (0.5,))** 进行缩放到[-1, 1],或者如果需要零均值、单位方差归一化,则计算特定于数据集的mean和std。– 根据您使用的 LeNet-5 实现的输入期望选择归一化方法。