爬坡测试集是一种在不接触训练集甚至不开发预测模型的情况下,在机器学习竞赛中获得良好或完美预测的方法。
作为机器学习竞赛的一种方法,它理应受到鄙视,并且大多数竞赛平台都对其施加了限制以防止它,这一点很重要。
然而,在机器学习实践者参加竞赛时,会无意中进行测试集的爬坡。通过开发一个明确的测试集爬坡实现,可以更好地理解过度使用测试集来评估建模管道有多么容易导致过拟合测试数据集。
在本教程中,您将了解如何为机器学习爬坡测试集。
完成本教程后,您将了解:
- 通过爬坡测试集,即使不看训练数据集,也能做出完美的预测。
- 如何为分类和回归任务爬坡测试集。
- 当我们过度使用测试集来评估建模管道时,我们就是在隐式地爬坡测试集。
通过我的新书《机器学习数据准备》来启动您的项目,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
如何对机器学习的测试集进行爬山算法
照片作者:Stig Nygaard,部分权利保留。
教程概述
本教程分为五个部分;它们是:
- 爬坡测试集
- 爬坡算法
- 如何实现爬坡
- 爬坡糖尿病分类数据集
- 爬坡房价回归数据集
爬坡测试集
Kaggle等机器学习竞赛提供完整的训练数据集,以及测试集的输入。
给定竞赛的目标是预测测试集的此类标签或数值。解决方案将针对隐藏的测试集目标值进行评估,并相应地评分。在测试集上得分最高的提交者赢得比赛。
机器学习竞赛的挑战可以被构建为一个优化问题。传统上,竞赛参与者充当优化算法,探索不同的建模管道,这些管道产生不同的预测集,对预测进行评分,然后对管道进行更改,以期获得更高的分数。
此过程也可以直接用优化算法来建模,在从不查看训练集的情况下生成和评估候选预测。
通常,这被称为爬坡测试集,因为解决此问题最简单的优化算法之一就是爬坡算法。
尽管爬坡测试集在实际的机器学习竞赛中理应受到鄙视,但实现这种方法可以作为一种有趣的练习,以了解该方法的局限性以及测试集过拟合的危险。此外,即使不接触训练数据集就可以完美预测测试集的事实,常常让许多初级机器学习从业者感到震惊。
最重要的是,当我们反复评估不同的建模管道时,我们会隐式地爬坡测试集。风险在于,测试集的分数提高是以增加泛化误差为代价的,即在更广泛的问题上表现更差。
机器学习竞赛的组织者充分意识到这个问题,并施加预测评估限制来应对它,例如将评估限制为每天一次或几次,并报告隐藏测试集子集的分数,而不是整个测试集。有关更多信息,请参阅“进一步阅读”部分中列出的论文。
接下来,我们来看一下如何实现爬坡算法来优化测试集的预测。
想开始学习数据准备吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
爬坡算法
爬坡算法是一种非常简单的优化算法。
它涉及生成一个候选解决方案并对其进行评估。这是开始点,然后对其进行逐步改进,直到不再有进一步的改进,或者我们耗尽时间、资源或兴趣。
新的候选解决方案是从现有候选解决方案生成的。通常,这涉及对候选解决方案进行一次更改,对其进行评估,如果它与之前的当前解决方案一样好或更好,则接受该候选解决方案作为新的“当前”解决方案。否则,将其丢弃。
我们可能会认为只接受分数更好的候选者是个好主意。对于许多简单的问题,这是一个合理的方法,尽管在更复杂的问题上,为了帮助搜索过程在特征空间中扩展平坦区域(平台),期望接受具有相同分数的不同候选者。
当爬坡测试集时,候选解决方案是预测列表。对于二元分类任务,这是两个类别的0和1值列表。对于回归任务,这是目标变量范围内的数字列表。
对分类候选解决方案的修改是选择一个预测,并将其从0翻转为1或1翻转为0。对回归候选解决方案的修改是在列表中添加高斯噪声,或用新值替换列表中的某个值。
解决方案的评分涉及计算一个评分指标,例如分类任务的分类准确率或回归任务的平均绝对误差。
现在我们已经熟悉了算法,让我们来实现它。
如何实现爬坡
我们将基于合成分类任务来开发我们的爬坡算法。
首先,我们可以创建一个包含许多输入变量和 5,000 行示例的二元分类任务。然后,我们可以将数据集拆分为训练集和测试集。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 |
# 合成数据集示例。 from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split # 定义数据集 X, y = make_classification(n_samples=5000, n_features=20, n_informative=15, n_redundant=5, random_state=1) print(X.shape, y.shape) # 分割数据集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1) print(X_train.shape, X_test.shape, y_train.shape, y_test.shape) |
运行示例首先报告创建的数据集的形状,显示 5,000 行和 20 个输入变量。
然后,数据集被拆分为训练集和测试集,大约 3,300 用于训练,大约 1,600 用于测试。
|
1 2 |
(5000, 20) (5000,) (3350, 20) (1650, 20) (3350,) (1650,) |
现在我们可以开发一个爬坡器。
首先,我们可以创建一个函数来加载,或者在这种情况下,定义数据集。当我们要更改数据集时,可以稍后更新此函数。
|
1 2 3 |
# 加载或准备分类数据集 def load_dataset(): return make_classification(n_samples=5000, n_features=20, n_informative=15, n_redundant=5, random_state=1) |
接下来,我们需要一个函数来评估候选解决方案——即预测列表。
我们将使用分类准确率,其中分数范围从最差解决方案的 0 到完美预测集的 1。
|
1 2 3 |
# 评估一组预测 def evaluate_predictions(y_test, yhat): return accuracy_score(y_test, yhat) |
接下来,我们需要一个函数来创建候选解决方案的初始版本。
这是一个预测列表,包含 0 和 1 类标签,长度足以匹配测试集中的示例数量,在本例中为 1650。
我们可以使用 randint() 函数来生成 0 和 1 的随机值。
|
1 2 3 |
# 创建随机预测集 def random_predictions(n_examples): return [randint(0, 1) for _ in range(n_examples)] |
接下来,我们需要一个函数来创建候选解决方案的修改版本。
在这种情况下,这包括选择解决方案中的一个值并将其从 0 翻转为 1 或从 1 翻转为 0。
通常,在爬坡过程中,我们每次生成新的候选解决方案时只做一个更改,但我已经参数化了这个函数,以便您可以尝试进行多次更改。
|
1 2 3 4 5 6 7 8 9 10 |
# 修改当前预测集 def modify_predictions(current, n_changes=1): # 复制当前解决方案 updated = current.copy() for i in range(n_changes): # 选择一个要更改的点 ix = randint(0, len(updated)-1) # 翻转类标签 updated[ix] = 1 - updated[ix] return updated |
到目前为止,一切顺利。
接下来,我们可以开发执行搜索的函数。
首先,通过调用 random_predictions() 函数然后调用 evaluate_predictions() 函数来创建并评估初始解决方案。
然后,我们循环固定次数的迭代,通过调用 modify_predictions() 生成新的候选解决方案,对其进行评估,如果分数与当前解决方案相同或更好,则替换它。
循环将在我们完成预设的迭代次数(任意选择)或达到完美分数(在本例中我们知道是 1.0 的准确率(100%))时结束。
下面的 hill_climb_testset() 函数实现了这一点,它以测试集作为输入,并返回在爬坡过程中找到的最佳预测集。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 对一组预测运行爬坡 def hill_climb_testset(X_test, y_test, max_iterations): scores = list() # 生成初始解决方案 solution = random_predictions(X_test.shape[0]) # 评估初始解决方案 score = evaluate_predictions(y_test, solution) scores.append(score) # 爬坡至解决方案 for i in range(max_iterations): # 记录分数 scores.append(score) # 一旦达到最佳分数就停止 if score == 1.0: break # 生成新候选 candidate = modify_predictions(solution) # 评估候选 value = evaluate_predictions(y_test, candidate) # 检查是否相等或更好 if value >= score: solution, score = candidate, value print('>%d, score=%.3f' % (i, score)) return solution, scores |
就是这样。
完整的爬坡测试集示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
# 分类任务爬坡测试集示例 from random import randint from sklearn.datasets import make_classification from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score from matplotlib import pyplot # 加载或准备分类数据集 def load_dataset(): return make_classification(n_samples=5000, n_features=20, n_informative=15, n_redundant=5, random_state=1) # 评估一组预测 def evaluate_predictions(y_test, yhat): return accuracy_score(y_test, yhat) # 创建随机预测集 def random_predictions(n_examples): return [randint(0, 1) for _ in range(n_examples)] # 修改当前预测集 def modify_predictions(current, n_changes=1): # 复制当前解决方案 updated = current.copy() for i in range(n_changes): # 选择一个要更改的点 ix = randint(0, len(updated)-1) # 翻转类标签 updated[ix] = 1 - updated[ix] return updated # 对一组预测运行爬坡 def hill_climb_testset(X_test, y_test, max_iterations): scores = list() # 生成初始解决方案 solution = random_predictions(X_test.shape[0]) # 评估初始解决方案 score = evaluate_predictions(y_test, solution) scores.append(score) # 爬坡至解决方案 for i in range(max_iterations): # 记录分数 scores.append(score) # 一旦达到最佳分数就停止 if score == 1.0: break # 生成新候选 candidate = modify_predictions(solution) # 评估候选 value = evaluate_predictions(y_test, candidate) # 检查是否相等或更好 if value >= score: solution, score = candidate, value print('>%d, score=%.3f' % (i, score)) return solution, scores # 加载数据集 X, y = load_dataset() print(X.shape, y.shape) # 将数据集分割为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1) print(X_train.shape, X_test.shape, y_train.shape, y_test.shape) # 运行爬坡 yhat, scores = hill_climb_testset(X_test, y_test, 20000) # 绘制分数与迭代次数的关系图 pyplot.plot(scores) pyplot.show() |
运行示例将在 20,000 次迭代中运行搜索,或者在达到完美准确率时停止。
注意:您 每次运行的结果可能会有所不同,这可能是由于算法或评估程序的随机性,或数值精度的差异。考虑运行示例几次并比较平均结果。
在这种情况下,我们在大约 12,900 次迭代中找到了测试集的完美预测集。
请记住,这是在不接触训练数据集且不通过查看测试集目标值来作弊的情况下实现的。相反,我们只是优化了一组数字。
这里的教训是,反复评估建模管道与测试集,将做同样的事情,利用你作为爬坡优化算法。解决方案将过拟合到测试集。
|
1 2 3 4 5 6 7 8 |
... >8092, score=0.996 >8886, score=0.997 >9202, score=0.998 >9322, score=0.998 >9521, score=0.999 >11046, score=0.999 >12932, score=1.000 |
还会创建一个搜索进度的图。
这有助于了解优化算法的更改,例如更改的内容以及在爬坡过程中更改的方式,如何影响搜索的收敛性。
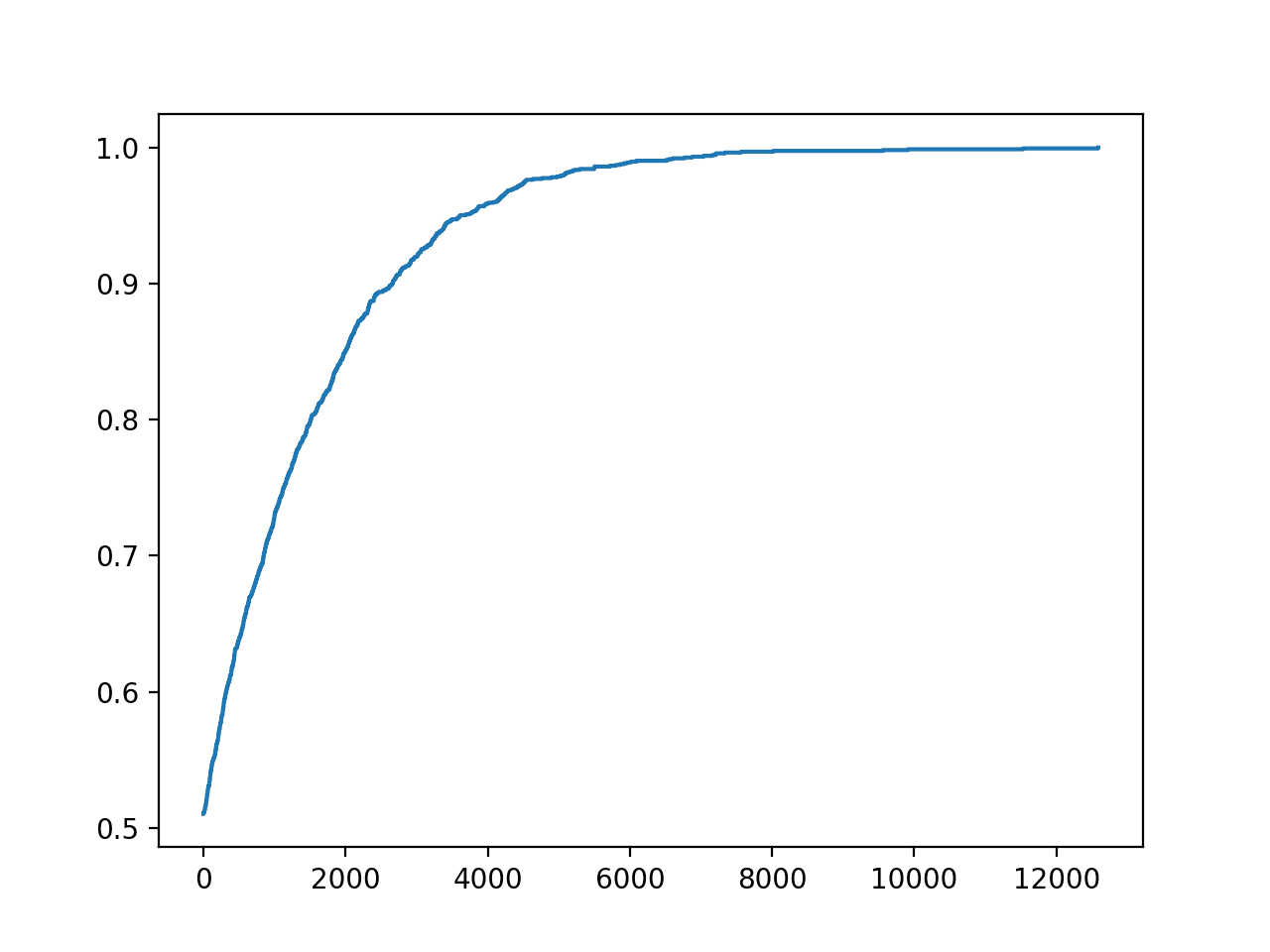
分类任务的准确率与爬坡优化迭代次数的折线图
现在我们熟悉了爬坡测试集,让我们在实际数据集上尝试这种方法。
爬坡糖尿病分类数据集
我们将使用糖尿病数据集作为探索爬坡测试集分类问题的基础。
每条记录都描述了一位女性的病史,预测是五年内是否会患糖尿病。
该数据集有八个输入变量和 768 行数据;输入变量都是数值型,目标值有两个类标签,即这是一个二元分类任务。
下面提供了该数据集前五行的样本。
|
1 2 3 4 5 6 |
6,148,72,35,0,33.6,0.627,50,1 1,85,66,29,0,26.6,0.351,31,0 8,183,64,0,0,23.3,0.672,32,1 1,89,66,23,94,28.1,0.167,21,0 0,137,40,35,168,43.1,2.288,33,1 ... |
我们可以使用 Pandas 直接加载数据集,如下所示。
|
1 2 3 4 5 6 |
# 加载或准备分类数据集 def load_dataset(): url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv' df = read_csv(url, header=None) data = df.values return data[:, :-1], data[:, -1] |
其余代码保持不变。
这是为了让您可以替换自己的二元分类任务并尝试一下。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
# 糖尿病数据集爬坡测试集示例 from random import randint from pandas import read_csv from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score from matplotlib import pyplot # 加载或准备分类数据集 def load_dataset(): url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv' df = read_csv(url, header=None) data = df.values return data[:, :-1], data[:, -1] # 评估一组预测 def evaluate_predictions(y_test, yhat): return accuracy_score(y_test, yhat) # 创建随机预测集 def random_predictions(n_examples): return [randint(0, 1) for _ in range(n_examples)] # 修改当前预测集 def modify_predictions(current, n_changes=1): # 复制当前解决方案 updated = current.copy() for i in range(n_changes): # 选择一个要更改的点 ix = randint(0, len(updated)-1) # 翻转类标签 updated[ix] = 1 - updated[ix] return updated # 对一组预测运行爬坡 def hill_climb_testset(X_test, y_test, max_iterations): scores = list() # 生成初始解决方案 solution = random_predictions(X_test.shape[0]) # 评估初始解决方案 score = evaluate_predictions(y_test, solution) scores.append(score) # 爬坡至解决方案 for i in range(max_iterations): # 记录分数 scores.append(score) # 一旦达到最佳分数就停止 if score == 1.0: break # 生成新候选 candidate = modify_predictions(solution) # 评估候选 value = evaluate_predictions(y_test, candidate) # 检查是否相等或更好 if value >= score: solution, score = candidate, value print('>%d, score=%.3f' % (i, score)) return solution, scores # 加载数据集 X, y = load_dataset() print(X.shape, y.shape) # 将数据集分割为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1) print(X_train.shape, X_test.shape, y_train.shape, y_test.shape) # 运行爬坡 yhat, scores = hill_climb_testset(X_test, y_test, 5000) # 绘制分数与迭代次数的关系图 pyplot.plot(scores) pyplot.show() |
运行示例会在搜索期间每次看到改进时报告迭代次数和准确率。
在这种情况下,我们使用较少的迭代次数,因为这是一个更简单的优化问题,因为我们需要进行的预测较少。
注意:您 每次运行的结果可能会有所不同,这可能是由于算法或评估程序的随机性,或数值精度的差异。考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到我们在大约 1,500 次迭代中获得了完美的准确率。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
... >617, score=0.961 >627, score=0.965 >650, score=0.969 >683, score=0.972 >743, score=0.976 >803, score=0.980 >817, score=0.984 >945, score=0.988 >1350, score=0.992 >1387, score=0.996 >1565, score=1.000 |
搜索过程的折线图也会被创建,显示收敛速度很快。
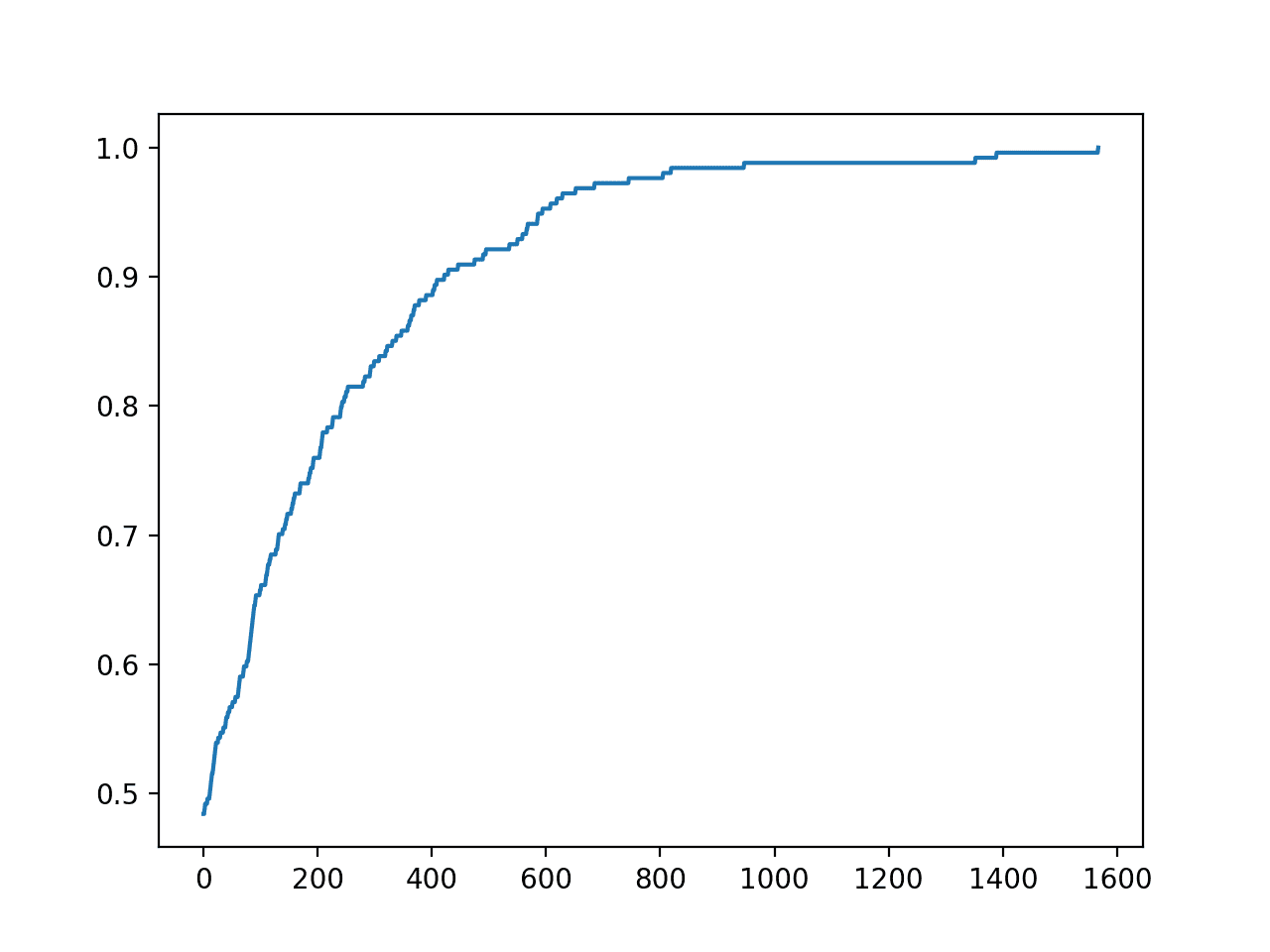
糖尿病数据集的准确率与爬坡优化迭代次数的折线图
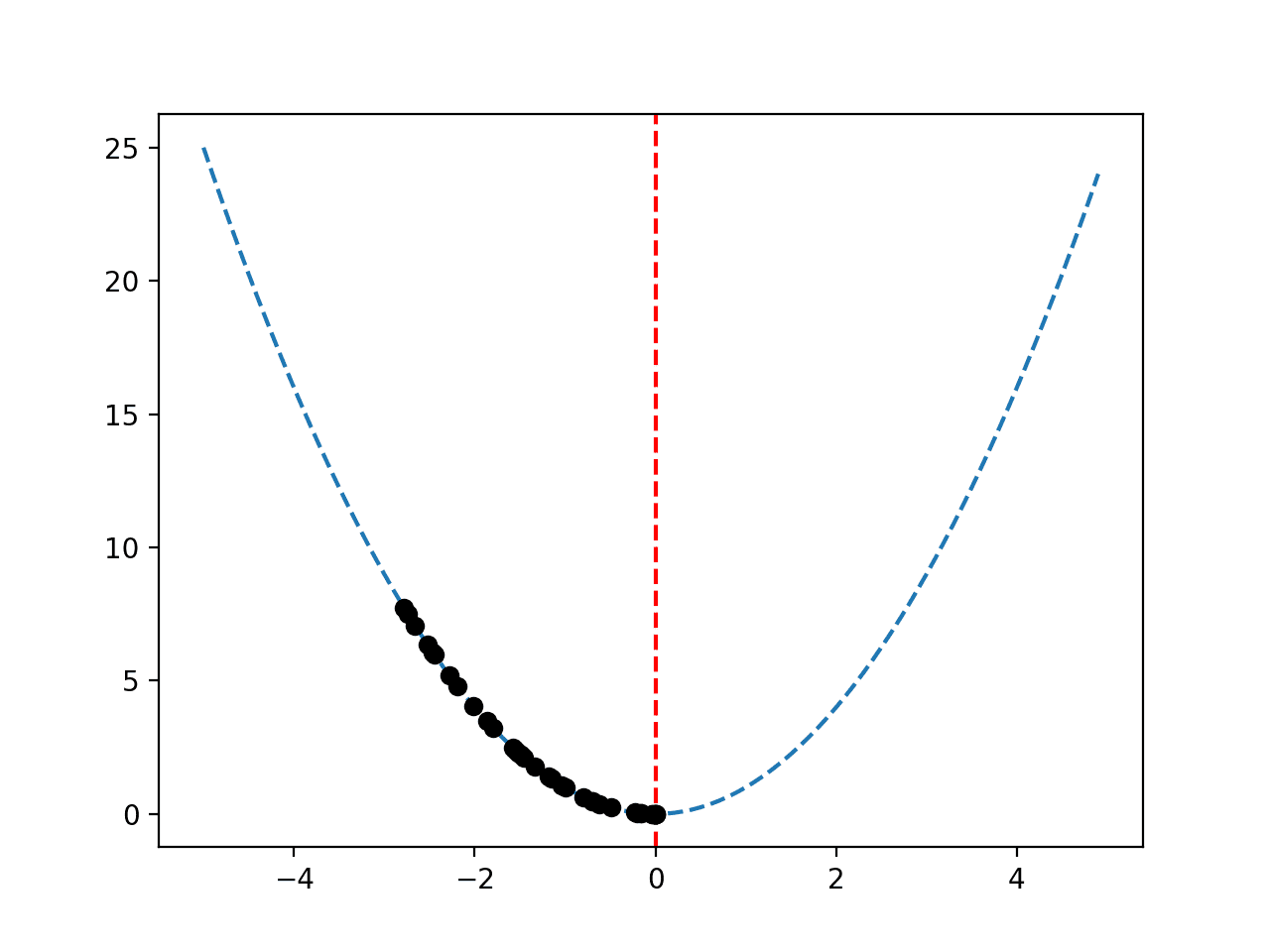
爬坡房价回归数据集
我们将使用房价数据集作为探索爬坡测试集回归问题的基础。
房价数据集涉及根据房屋及其邻里细节预测房屋价格(以千美元为单位)。
这是一个回归问题,意味着我们正在预测一个数值。有 506 个观测值,13 个输入变量和一个输出变量。
下面列出了前五行的样本。
|
1 2 3 4 5 6 |
0.00632,18.00,2.310,0,0.5380,6.5750,65.20,4.0900,1,296.0,15.30,396.90,4.98,24.00 0.02731,0.00,7.070,0,0.4690,6.4210,78.90,4.9671,2,242.0,17.80,396.90,9.14,21.60 0.02729,0.00,7.070,0,0.4690,7.1850,61.10,4.9671,2,242.0,17.80,392.83,4.03,34.70 0.03237,0.00,2.180,0,0.4580,6.9980,45.80,6.0622,3,222.0,18.70,394.63,2.94,33.40 0.06905,0.00,2.180,0,0.4580,7.1470,54.20,6.0622,3,222.0,18.70,396.90,5.33,36.20 ... |
首先,我们可以更新 load_dataset() 函数来加载房价数据集。
在加载数据集的过程中,我们将对目标值进行归一化。这将使爬坡预测更简单,因为我们可以将浮点值限制在 0 到 1 的范围内。
这通常不是必需的,只是此处用于简化搜索算法的方法。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 加载或准备分类数据集 def load_dataset(): url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv' df = read_csv(url, header=None) data = df.values X, y = data[:, :-1], data[:, -1] # 归一化目标值 scaler = MinMaxScaler() y = y.reshape((len(y), 1)) y = scaler.fit_transform(y) return X, y |
接下来,我们可以更新评分函数,使其使用预期值和预测值之间的平均绝对误差。
|
1 2 3 |
# 评估一组预测 def evaluate_predictions(y_test, yhat): return mean_absolute_error(y_test, yhat) |
我们还必须更新解决方案的表示形式,从 0 和 1 的标签更改为 0 到 1 之间的浮点值。
初始候选解决方案的生成必须更改为创建随机浮点数列表。
|
1 2 3 |
# 创建随机预测集 def random_predictions(n_examples): return [random() for _ in range(n_examples)] |
为了创建新的候选解决方案而对解决方案进行的单一更改,在这种情况下,涉及简单地用新的随机浮点数替换列表中随机选择的预测。
我选择这样做是因为它很简单。
|
1 2 3 4 5 6 7 8 9 10 |
# 修改当前预测集 def modify_predictions(current, n_changes=1): # 复制当前解决方案 updated = current.copy() for i in range(n_changes): # 选择一个要更改的点 ix = randint(0, len(updated)-1) # 翻转类标签 updated[ix] = random() return updated |
更好的方法是向现有值添加高斯噪声,我将此留给您作为扩展。如果您尝试了,请在下面的评论中告诉我。
例如
|
1 2 3 |
... # 添加高斯噪声 updated[ix] += gauss(0, 0.1) |
最后,必须更新搜索。
最佳值现在是 0.0 的误差,如果找到,则用于停止搜索。
|
1 2 3 4 |
... # 一旦达到最佳分数就停止 if score == 0.0: break |
我们还需要将搜索从最大化分数更改为最小化分数。
|
1 2 3 4 5 |
... # 检查是否相等或更好 if value <= score: solution, score = candidate, value print('>%d, score=%.3f' % (i, score)) |
包含这两项更改的更新搜索函数列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# 对一组预测运行爬坡 def hill_climb_testset(X_test, y_test, max_iterations): scores = list() # 生成初始解决方案 solution = random_predictions(X_test.shape[0]) # 评估初始解决方案 score = evaluate_predictions(y_test, solution) print('>%.3f' % score) # 爬坡至解决方案 for i in range(max_iterations): # 记录分数 scores.append(score) # 一旦达到最佳分数就停止 if score == 0.0: break # 生成新候选 candidate = modify_predictions(solution) # 评估候选 value = evaluate_predictions(y_test, candidate) # 检查是否相等或更好 if value <= score: solution, score = candidate, value print('>%d, score=%.3f' % (i, score)) return solution, scores |
将这些整合在一起,用于回归任务的爬坡测试集的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
# 房价数据集爬坡测试集示例 from random import random from random import randint from pandas import read_csv from sklearn.model_selection import train_test_split from sklearn.metrics import mean_absolute_error 从 sklearn.预处理 导入 MinMaxScaler from matplotlib import pyplot # 加载或准备分类数据集 def load_dataset(): url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv' df = read_csv(url, header=None) data = df.values X, y = data[:, :-1], data[:, -1] # 归一化目标值 scaler = MinMaxScaler() y = y.reshape((len(y), 1)) y = scaler.fit_transform(y) 返回 X, y # 评估一组预测 def evaluate_predictions(y_test, yhat): return mean_absolute_error(y_test, yhat) # 创建随机预测集 def random_predictions(n_examples): return [random() for _ in range(n_examples)] # 修改当前预测集 def modify_predictions(current, n_changes=1): # 复制当前解决方案 updated = current.copy() for i in range(n_changes): # 选择一个要更改的点 ix = randint(0, len(updated)-1) # 翻转类标签 updated[ix] = random() return updated # 对一组预测运行爬坡 def hill_climb_testset(X_test, y_test, max_iterations): scores = list() # 生成初始解决方案 solution = random_predictions(X_test.shape[0]) # 评估初始解决方案 score = evaluate_predictions(y_test, solution) print('>%.3f' % score) # 爬坡至解决方案 for i in range(max_iterations): # 记录分数 scores.append(score) # 一旦达到最佳分数就停止 if score == 0.0: break # 生成新候选 candidate = modify_predictions(solution) # 评估候选 value = evaluate_predictions(y_test, candidate) # 检查是否相等或更好 if value <= score: solution, score = candidate, value print('>%d, score=%.3f' % (i, score)) return solution, scores # 加载数据集 X, y = load_dataset() print(X.shape, y.shape) # 将数据集分割为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1) print(X_train.shape, X_test.shape, y_train.shape, y_test.shape) # 运行爬坡 yhat, scores = hill_climb_testset(X_test, y_test, 100000) # 绘制分数与迭代次数的关系图 pyplot.plot(scores) pyplot.show() |
运行示例会在搜索期间每次看到改进时报告迭代次数和 MAE。
在这种情况下,我们使用更多的迭代次数,因为这是一个更复杂的优化问题。用于创建候选解决方案的所选方法也使其更慢,并且我们实现完美误差的可能性更小。
事实上,我们不会实现完美的误差;相反,如果误差达到低于某个最小值的值(例如 1e-7 或目标域中有意义的值),则停止会更好。这也可以留给读者作为练习。
例如
|
1 2 3 4 |
... # 一旦达到足够好的程度就停止 if score <= 1e-7: break |
注意:您 每次运行的结果可能会有所不同,这可能是由于算法或评估程序的随机性,或数值精度的差异。考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到在运行结束时我们得到了一个很好的错误率。
|
1 2 3 4 5 6 7 8 9 10 11 |
... >95991, score=0.001 >96011, score=0.001 >96295, score=0.001 >96366, score=0.001 >96585, score=0.001 >97575, score=0.001 >98828, score=0.001 >98947, score=0.001 >99712, score=0.001 >99913, score=0.001 |
搜索进度的折线图也显示了收敛速度很快,并且在大部分迭代中都保持平稳。
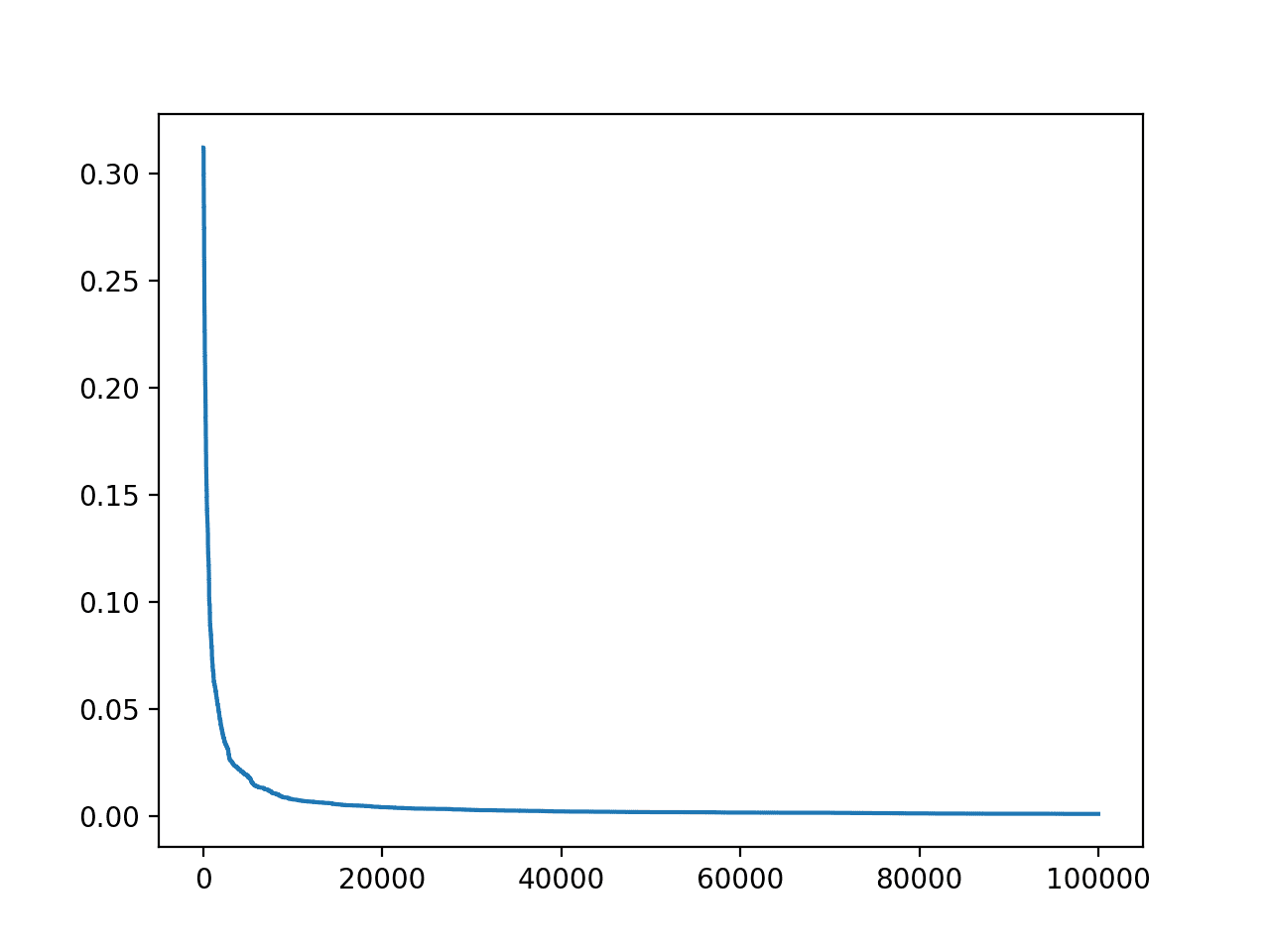
房屋数据集的准确率与爬山优化迭代次数的折线图
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 通过利用对数损失预言机来攀登 Kaggle 排行榜, 2018.
- 走向更好地理解排行榜, 2017.
- 梯子:机器学习竞赛的可靠排行榜, 2015.
文章
总结
在本教程中,您将了解如何为机器学习进行测试集爬山。
具体来说,你学到了:
- 通过爬坡测试集,即使不看训练数据集,也能做出完美的预测。
- 如何为分类和回归任务爬坡测试集。
- 当我们过度使用测试集来评估建模管道时,我们就是在隐式地爬坡测试集。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






非常好的文章,作为机器学习竞赛的新手,我希望您能发布更多此类比赛的技巧以及代码。谢谢。另外,如果您想在比赛中表现出色,您还建议阅读哪些博客?
谢谢。
这很大程度上取决于比赛。也许可以浏览最近的帖子或使用搜索框查找与您当前项目相关的帖子。
如果测试集没有标签,我不明白你如何在 ML 竞赛中使用它。也许我没有理解你的观点。你能解释一下吗?
您可以猜测提交标签,并使用排行榜的任何反馈作为爬山信号。
我不提倡这样做,这只是为了指出在没有真正学习映射函数的情况下获得更好性能的危险。
你好,我没有时间仔细阅读你的所有文章,你有很多资料,我也看了很多其他的东西。此外,我还有一份全职工作等等。我只是快速浏览了这篇文章,觉得很困惑,我引用说:
“……即使不接触训练数据集,测试集也可以被完美预测,这常常让许多初级机器学习从业者感到震惊。”
有一个使用测试集进行的评估。否则,你怎能期望系统学习?如果你不知道新的候选者是否有所改进呢?所以,在学习发生时不需要测试集这种说法根本不正确?
你关于从未“接触”数据集的说法并没有让我震惊,我根本不相信。更准确地说:这取决于你对“接触”的确切定义。例如,人工智能系统没有手可以实际触摸东西,而触摸抽象数据(非事物)是不可能的。所以从这个意义上说你是对的,但这将是一个无用的观察。因此,我认为你并不是指“触摸”,而是指“使用”或“需要”。然后我们就回到了“我不相信”的观点……
如果除了大量的文字和代码之外,还能对故事的要点进行简短的解释(对于那些没有时间深入阅读文章的人来说),那就太好了。现在我必须去维基百科查找爬山算法本质的更简洁的解释。
你说爬山很简单,那么只需要几行就可以解释其本质。
你也说它不被提倡,但没有说明原因。我猜这只是一个贪心算法,可能会收敛到局部最大值(我们在爬升),从而可能错过一个更好的全局最大值?
我现在听起来很负面,但别误会我的意思:你的文章很棒,你在 I 方面比我更有知识。无论如何,请继续创作这样的学习材料。
抱歉造成混淆。我认为“爬山测试集”这一节涵盖了你的大部分问题。
我的观点是,我们可以开发一个“模型”来正确预测测试集,而无需显式地拟合测试集,例如 model.fit(test_x, test_y)
是的,我们必须在整个过程中对模型进行评分,这至少需要通过模型评分对测试集进行*间接*访问——也许是通过第三方系统(例如排行榜)。
爬山是一种优化算法——文章中已说明并链接到维基百科文章。
它之所以不被提倡,是因为最坏的情况是作弊(无限次评估),或者是一种过拟合(有限次评估)。
你好 Jason,好文章。可能有一个拼写错误
“这个过程也可以直接用优化算法来建模,其中候选预测被生成和评估,而无需查看测试集。”
应该是
“并且在不查看训练集的情况下进行评估。”
谢谢,已修正。
强烈推荐。感谢分享您的工作。
谢谢!
尊敬的Jason博士,
您的网站上有许多练习/演示/教程,其中模型的准确率为 0.78。
假设我们将爬山算法应用于那些最初准确率为 0.78 的模型。假设结果产生的准确率为 0.99。爬山模型可以作为最终模型使用吗?
换句话说,如果爬山算法产生的准确率接近 1,为什么不“一直”使用这种算法,而不是在网站上使用的其他机器学习技术。
或者换一种说法。肯定有一个陷阱,使得准确率接近 1 是一个“梦想”。
谢谢你,
悉尼的Anthony
是的,爬山的问题在于它会过拟合测试集。
尊敬的Jason博士,
谢谢你,
悉尼的Anthony
尊敬的Jason博士,
我还有最后一个问题,拜托。
如果本教程的目的是演示过拟合测试集,为什么还要过拟合一个可能产生不可靠结果的模型?
谢谢你,
悉尼的Anthony
许多机器学习竞赛都侧重于找到一个在测试集上表现良好的模型,而不是一个在问题上表现良好的模型。
了解这种方法的陷阱、如何充分利用这种方法、如何在不拟合模型的情况下做出完美预测,这很有趣/很好。
尊敬的Jason博士,
再次感谢,
悉尼的Anthony