鉴于误差函数、学习率甚至目标变量的尺度选择,训练神经网络可能会变得不稳定。
训练期间权重的巨大更新可能导致数值溢出或下溢,通常被称为“梯度爆炸”。
梯度爆炸问题在循环神经网络(如LSTM)中更为常见,因为梯度在数百个输入时间步长上展开并累积。
解决梯度爆炸问题的一个常见且相对容易的方案是在误差反向传播到网络中并用于更新权重之前改变误差的导数。两种方法包括根据选定的向量范数重新缩放梯度,以及裁剪超出首选范围的梯度值。这些方法统称为“梯度裁剪”。
在本教程中,您将了解梯度爆炸问题以及如何使用梯度裁剪提高神经网络训练的稳定性。
完成本教程后,您将了解:
- 训练神经网络可能会变得不稳定,导致数值溢出或下溢,这被称为梯度爆炸。
- 通过缩放向量范数或将梯度值裁剪到一定范围来改变误差梯度,可以使训练过程保持稳定。
- 如何使用梯度裁剪方法更新回归预测建模问题中出现梯度爆炸的MLP模型,以实现稳定的训练过程。
用我的新书《更好的深度学习》来启动你的项目,书中包含分步教程和所有示例的 Python 源代码文件。
让我们开始吧。

如何使用梯度裁剪避免神经网络中的梯度爆炸
照片由Ian Livesey拍摄,保留部分权利。
教程概述
本教程分为六个部分;它们是:
- 梯度爆炸和裁剪
- Keras中的梯度裁剪
- 回归预测建模问题
- 具有梯度爆炸的多层感知机
- 采用梯度范数缩放的MLP
- 采用梯度值裁剪的MLP
梯度爆炸和裁剪
神经网络使用随机梯度下降优化算法进行训练。
这首先需要估计一个或多个训练示例的损失,然后计算损失的导数,该导数通过网络反向传播以更新权重。权重使用反向传播误差的一部分进行更新,由学习率控制。
权重更新可能非常大,以至于权重超出或低于其数值精度。实际上,当权重溢出或下溢时,它们可能取值为“NaN”或“Inf”,并且出于实际目的,网络从那时起将变得无用,因为信号流过无效权重时会永远预测NaN值。
出现的问题是,当参数梯度非常大时,梯度下降参数更新可能会将参数推得非常远,进入目标函数更大的区域,从而抵消了为达到当前解所做的许多工作。
— 第413页,深度学习,2016。
权重的下溢或溢出通常被称为网络训练过程的不稳定性,并以“梯度爆炸”命名,因为不稳定的训练过程导致网络无法以模型基本无用的方式进行训练。
在给定的神经网络中,例如卷积神经网络或多层感知机,这可能是由于配置选择不当造成的。一些例子包括:
- 学习率选择不当,导致权重更新过大。
- 数据准备不当,导致目标变量差异过大。
- 损失函数选择不当,导致计算出较大的误差值。
梯度爆炸也是循环神经网络(如长短期记忆网络)中的一个问题,因为误差梯度在展开的循环结构中累积。
通常可以通过仔细配置网络模型来避免梯度爆炸,例如选择较小的学习率、缩放目标变量和标准损失函数。然而,对于具有大量输入时间步的循环网络,梯度爆炸仍然可能是一个问题。
使用全梯度训练 LSTM 的一个困难是导数有时会变得过大,导致数值问题。为了防止这种情况,[我们]将损失相对于 LSTM 层网络输入的导数(在应用 sigmoid 和 tanh 函数之前)裁剪到预定义的范围内。
——《使用递归神经网络生成序列》,2013年。
解决梯度爆炸的一个常见方法是在误差导数反向传播到网络中并用于更新权重之前改变它。通过重新缩放误差导数,权重的更新也会被重新缩放,从而大大降低溢出或下溢的可能性。
更新误差导数主要有两种方法;它们是
- 梯度缩放。
- 梯度裁剪。
梯度缩放涉及标准化误差梯度向量,使向量范数(大小)等于定义的值,例如1.0。
……处理梯度范数突然增加的一个简单机制是,只要它们超过阈值,就重新缩放它们。
— 循环神经网络训练的难度,2013。
梯度裁剪涉及将梯度值(逐元素)强制设置为特定的最小值或最大值,如果梯度超出预期范围。
这些方法通常简称为“梯度裁剪”。
当传统的梯度下降算法建议进行非常大的步长时,梯度裁剪启发式方法会介入,将步长减小到足够小,使其不太可能超出梯度指示近似最陡下降方向的区域。
— 第289页,深度学习,2016。
它是一种只解决深度神经网络模型训练数值稳定性的方法,并不能提供任何一般的性能改进。
梯度向量范数或首选范围的值可以通过试错法、使用文献中常用的值或通过实验观察常见的向量范数或范围然后选择一个合理的值来配置。
在我们的实验中,我们注意到对于给定的任务和模型大小,训练对这个[梯度范数]超参数不是很敏感,即使对于相当小的阈值,算法也能很好地工作。
— 循环神经网络训练的难度,2013。
通常,网络中的所有层都使用相同的梯度裁剪配置。然而,也有一些示例允许输出层的误差梯度范围大于隐藏层。
输出导数 […] 被裁剪到 [−100, 100] 的范围,而 LSTM 导数被裁剪到 [−10, 10] 的范围。裁剪输出梯度对于数值稳定性至关重要;尽管如此,网络有时在训练后期,在它们开始对训练数据过拟合之后,仍然会出现数值问题。
——《使用递归神经网络生成序列》,2013年。
想要通过深度学习获得更好的结果吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
Keras中的梯度裁剪
Keras 支持对每个优化算法进行梯度裁剪,并且将相同的方案应用于模型中的所有层。
梯度裁剪可以与优化算法(例如随机梯度下降)一起使用,方法是在配置优化算法时包含一个额外的参数。
可以使用两种类型的梯度裁剪:梯度范数缩放和梯度值裁剪。
梯度范数缩放
梯度范数缩放涉及改变损失函数的导数,使其在梯度向量的 L2 向量范数(平方值之和)超过阈值时具有给定的向量范数。
例如,我们可以指定一个范数为 1.0,这意味着如果梯度向量的向量范数超过 1.0,则向量中的值将被重新缩放,使得向量的范数等于 1.0。
这可以通过在优化器上指定“clipnorm”参数在 Keras 中使用;例如
|
1 2 3 |
.... # 配置带有梯度范数裁剪的 SGD opt = SGD(lr=0.01, momentum=0.9, clipnorm=1.0) |
梯度值裁剪
梯度值裁剪涉及将损失函数的导数裁剪到给定值,如果梯度值小于负阈值或大于正阈值。
例如,我们可以指定一个范数为 0.5,这意味着如果梯度值小于 -0.5,则将其设置为 -0.5,如果大于 0.5,则将其设置为 0.5。
这可以通过在优化器上指定“clipvalue”参数在 Keras 中使用,例如:
|
1 2 3 |
... # 配置带有梯度值裁剪的 SGD opt = SGD(lr=0.01, momentum=0.9, clipvalue=0.5) |
回归预测建模问题
回归预测建模问题涉及预测一个实数值量。
我们可以使用 scikit-learn 库中make_regression() 函数提供的标准回归问题生成器。该函数将生成具有给定数量的输入变量、统计噪声和其他属性的简单回归问题示例。
我们将使用此函数定义一个具有 20 个输入特征的问题;其中 10 个特征有意义,10 个不相关。总共将随机生成 1,000 个示例。伪随机数生成器将被固定,以确保每次运行代码时我们都能获得相同的 1,000 个示例。
|
1 2 |
# 生成回归数据集 X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) |
每个输入变量都具有高斯分布,目标变量也是如此。
我们可以创建目标变量的图表,显示其分布和范围。完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 回归预测建模问题 from sklearn.datasets import make_regression from matplotlib import pyplot # 生成回归数据集 X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) # 目标变量的直方图 pyplot.subplot(121) pyplot.hist(y) # 目标变量的箱线图 pyplot.subplot(122) pyplot.boxplot(y) pyplot.show() |
运行示例将创建一个带有两个图的图形,显示目标变量的直方图和箱线图。
直方图显示目标变量的高斯分布。箱线图显示样本范围在 -400 到 400 之间,平均值约为 0.0。
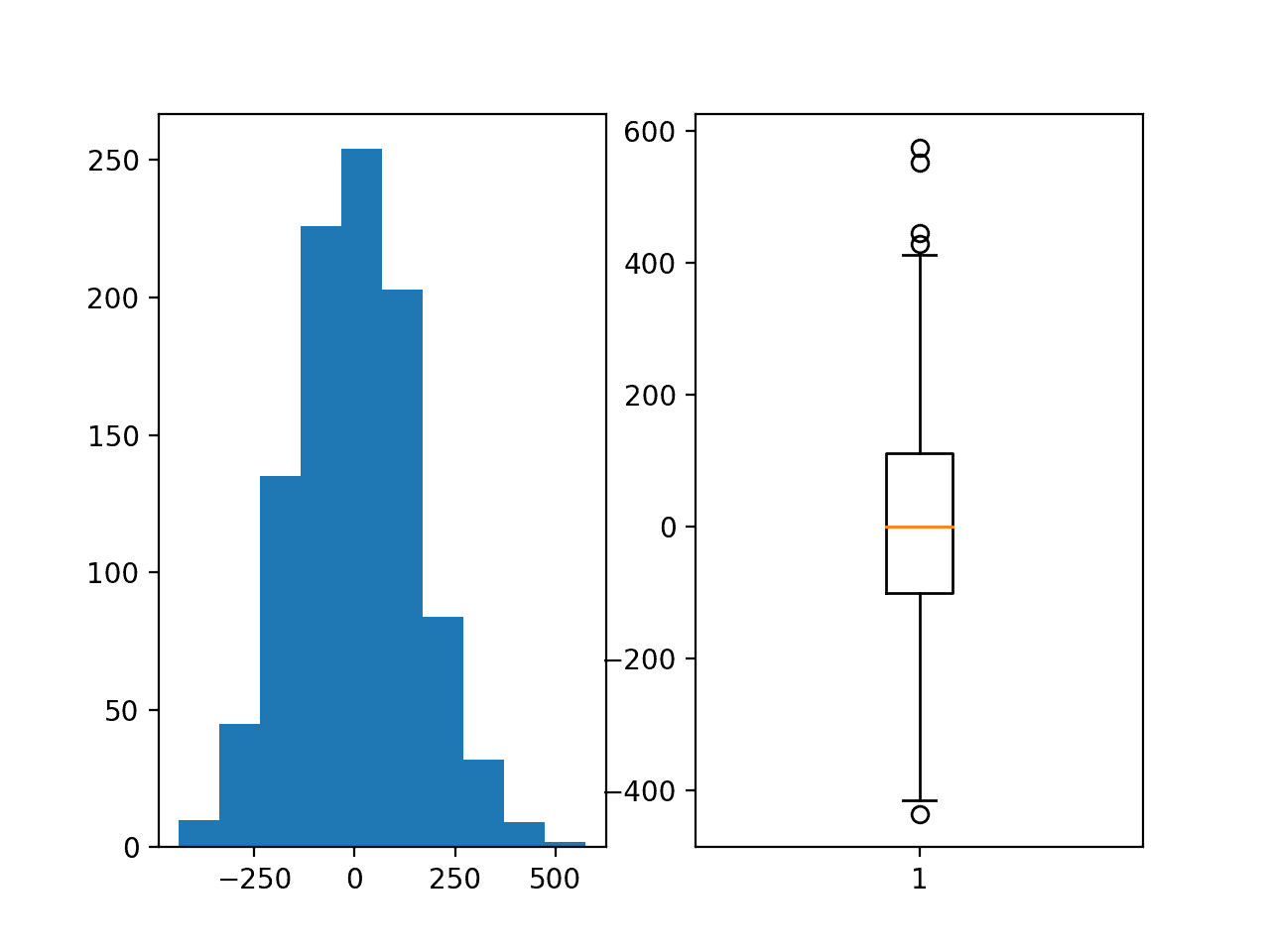
回归问题目标变量的直方图和箱线图
具有梯度爆炸的多层感知机
我们可以为回归问题开发一个多层感知机(MLP)模型。
该模型将在原始数据上进行演示,不进行任何输入或输出变量的缩放。这是一个演示梯度爆炸的好例子,因为一个训练用于预测未缩放目标变量的模型将导致误差梯度值在数百甚至数千,具体取决于训练期间使用的批次大小。如此大的梯度值很可能导致不稳定的学习或权重值的溢出。
第一步是将数据分成训练集和测试集,以便我们可以拟合和评估模型。我们将从域中生成 1,000 个示例,并将数据集分成两半,500 个示例用于训练集和测试集。
|
1 2 3 4 |
# 分割成训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] |
接下来,我们可以定义一个 MLP 模型。
该模型将期望问题中有20个输入变量的20个输入。将使用一个带有25个节点和整流线性激活函数的隐藏层。输出层有一个用于单个目标变量的节点和一个用于直接预测实值的线性激活函数。
|
1 2 3 4 |
# 定义模型 model = Sequential() model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='linear')) |
将使用均方误差损失函数优化模型,并使用随机梯度下降优化算法,其合理的默认配置为学习率为 0.01,动量为 0.9。
|
1 2 |
# 编译模型 model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01, momentum=0.9)) |
该模型将训练 100 个周期,并将测试集用作验证集,在每个训练周期结束时进行评估。
训练结束时,在训练集和测试集上计算均方误差,以了解模型学习问题的效果。
|
1 2 3 |
# 评估模型 train_mse = model.evaluate(trainX, trainy, verbose=0) test_mse = model.evaluate(testX, testy, verbose=0) |
最后,使用线图绘制每个训练周期结束时训练集和测试集上的均方误差学习曲线,提供学习曲线以了解模型在学习问题时的动态。
|
1 2 3 4 5 6 |
# 绘制训练过程中的损失 pyplot.title('Mean Squared Error') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
将这些元素联系起来,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# 回归问题中未缩放数据的MLP from sklearn.datasets import make_regression from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from matplotlib import pyplot # 生成回归数据集 X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) # 分割成训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 定义模型 model = Sequential() model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='linear')) # 编译模型 model.compile(loss='mean_squared_error', optimizer=SGD(lr=0.01, momentum=0.9)) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0) # 评估模型 train_mse = model.evaluate(trainX, trainy, verbose=0) test_mse = model.evaluate(testX, testy, verbose=0) print('训练集:%.3f,测试集:%.3f' % (train_mse, test_mse)) # 绘制训练过程中的损失 pyplot.title('Mean Squared Error') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
运行示例将拟合模型并计算训练集和测试集上的均方误差。
在这种情况下,模型无法学习问题,导致预测值为 NaN。模型权重在训练期间爆炸,因为计算出的权重更新误差非常大,进而导致误差梯度非常大。
|
1 |
训练集:NaN,测试集:NaN |
这表明需要对目标变量进行干预,模型才能学习这个问题。
创建了训练历史的线图,但由于模型几乎立即导致 NaN 均方误差,因此未显示任何内容。
传统的解决方案是使用标准化或归一化重新缩放目标变量,建议对 MLP 采用这种方法。然而,在这种情况下我们将研究的另一种方法是使用梯度裁剪。
采用梯度范数缩放的MLP
我们可以更新上一节中的模型训练,以添加梯度范数缩放。
这可以通过在优化器上设置“clipnorm”参数来实现。
例如,梯度可以重新缩放,使其向量范数(大小或长度)为 1.0,如下所示:
|
1 2 3 |
# 编译模型 opt = SGD(lr=0.01, momentum=0.9, clipnorm=1.0) model.compile(loss='mean_squared_error', optimizer=opt) |
进行了此更改的完整示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# 具有梯度范数缩放的回归问题非缩放数据的 MLP from sklearn.datasets import make_regression from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from matplotlib import pyplot # 生成回归数据集 X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) # 分割成训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 定义模型 model = Sequential() model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='linear')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9, clipnorm=1.0) model.compile(loss='mean_squared_error', optimizer=opt) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0) # 评估模型 train_mse = model.evaluate(trainX, trainy, verbose=0) test_mse = model.evaluate(testX, testy, verbose=0) print('训练集:%.3f,测试集:%.3f' % (train_mse, test_mse)) # 绘制训练过程中的损失 pyplot.title('Mean Squared Error') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
运行该示例将拟合模型并在训练集和测试集上进行评估,然后打印均方误差。
注意:由于算法或评估过程的随机性,或数值精度差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到将梯度缩放为向量范数1.0,使得模型稳定,能够学习问题并收敛到解决方案。
|
1 |
训练集:5.082,测试集:27.433 |
还创建了一个线图,显示了训练周期中训练集和测试集上的均方误差损失。
该图显示,损失从20,000以上的大值在20个时期内迅速下降到100以下的小值。
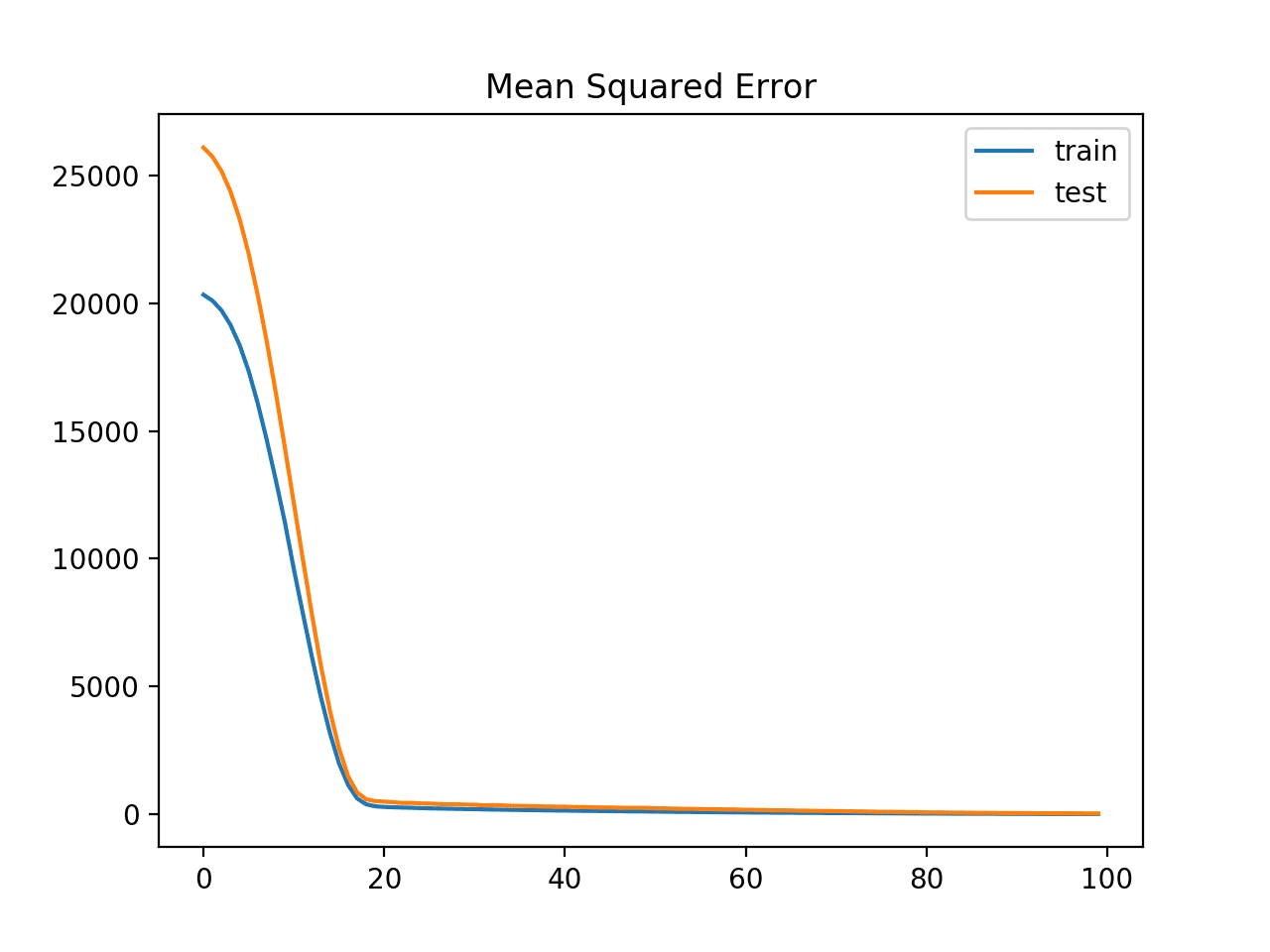
带梯度范数缩放的训练(蓝色)和测试(橙色)数据集在训练周期中的均方误差损失线图
向量范数 1.0 没有什么特别之处,可以评估其他值并比较所得模型的性能。
采用梯度值裁剪的MLP
解决梯度爆炸问题的另一个方法是,如果梯度变得过大或过小,就对其进行裁剪。
我们可以通过在优化算法配置中添加“clipvalue”参数来更新 MLP 的训练以使用梯度裁剪。例如,下面的代码将梯度裁剪到 [-5, 5] 的范围。
|
1 2 3 |
# 编译模型 opt = SGD(lr=0.01, momentum=0.9, clipvalue=5.0) model.compile(loss='mean_squared_error', optimizer=opt) |
带有梯度裁剪的 MLP 训练的完整示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# 回归问题中带有梯度裁剪的未缩放数据的 MLP from sklearn.datasets import make_regression from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from matplotlib import pyplot # 生成回归数据集 X, y = make_regression(n_samples=1000, n_features=20, noise=0.1, random_state=1) # 分割成训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 定义模型 model = Sequential() model.add(Dense(25, input_dim=20, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(1, activation='linear')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9, clipvalue=5.0) model.compile(loss='mean_squared_error', optimizer=opt) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=100, verbose=0) # 评估模型 train_mse = model.evaluate(trainX, trainy, verbose=0) test_mse = model.evaluate(testX, testy, verbose=0) print('训练集:%.3f,测试集:%.3f' % (train_mse, test_mse)) # 绘制训练过程中的损失 pyplot.title('Mean Squared Error') pyplot.plot(history.history['loss'], label='train') pyplot.plot(history.history['val_loss'], label='test') pyplot.legend() pyplot.show() |
运行此示例将拟合模型并在训练集和测试集上进行评估,然后打印均方误差。
注意:由于算法或评估过程的随机性,或数值精度差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
我们可以看到,在这种情况下,模型能够学习问题而不会出现梯度爆炸,在训练集和测试集上都取得了低于 10 的 MSE。
|
1 |
训练集:9.487,测试集:9.985 |
还创建了一个线图,显示了训练周期中训练集和测试集上的均方误差损失。
图表显示,模型学习问题很快,在短短几个训练周期内就实现了低于100的MSE损失。
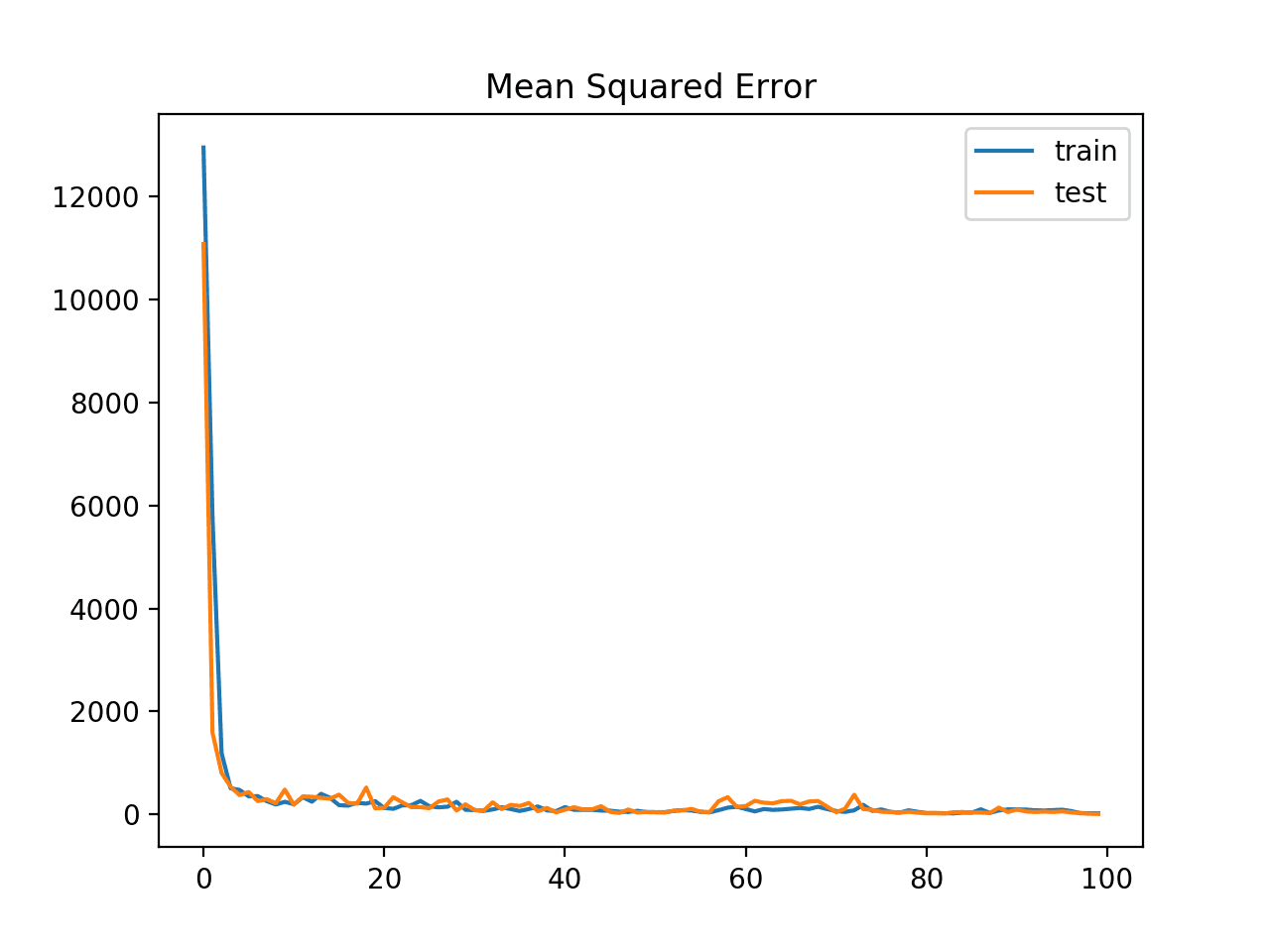
带有梯度值裁剪的训练(蓝色)和测试(橙色)数据集在训练周期中的均方误差损失线图
[-5, 5] 的裁剪范围是随意选择的;您可以尝试不同大小的范围,并比较学习速度和最终模型性能。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 向量范数值。更新示例以评估不同的梯度向量范数值并比较性能。
- 向量裁剪值。更新示例以评估不同的梯度值范围并比较性能。
- 向量范数和裁剪。更新示例以在同一训练运行中使用向量范数缩放和向量值裁剪的组合,并比较性能。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
书籍
论文
- 循环神经网络训练的难度, 2013.
- 使用循环神经网络生成序列, 2013.
API
总结
在本教程中,您了解了梯度爆炸问题以及如何使用梯度裁剪提高神经网络训练的稳定性。
具体来说,你学到了:
- 训练神经网络可能会变得不稳定,导致数值溢出或下溢,这被称为梯度爆炸。
- 通过改变误差梯度,无论是通过缩放向量范数还是将梯度值裁剪到一定范围,都可以使训练过程保持稳定。
- 如何使用梯度裁剪方法更新回归预测建模问题中出现梯度爆炸的MLP模型,以实现稳定的训练过程。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





这篇文章提供了非常丰富的信息。
谢谢。
这个人真是个天才。我敬佩他和他的工作、贡献。
谢谢李。我很高兴这些教程有所帮助。
我只是一个普通人。
感谢您有趣的教程!我有两个问题,希望能得到您的回复。
1. 缩放输入是否意味着不需要梯度缩放或裁剪?
2. 您通过一个示例展示了使用未缩放输入可能导致 nan 值,并应用了梯度裁剪来解决问题。是否有其他迹象表明设计的网络需要梯度裁剪/缩放?
不客气。
是否需要梯度缩放和裁剪取决于您的数据和模型。
是的,试试看,如果结果更好就保留它。或者在训练期间检查梯度是否非常大。
嗨 Jason
感谢您的教程!它们真的很有帮助。
我想知道MSE和梯度爆炸之间是否存在关系。我正在尝试创建一个神经网络,它适用于小输入/小层,但是一旦大小超过一个小阈值,损失就会直接变为 NaN。我想知道这是否正常,或者网络是否有问题(它使用 Dense、ReLU 和 sigmoid 层,带有 MSE,并实现了香草梯度下降)
谢谢
是也不是,但使用交叉熵也同样容易出现梯度爆炸。
Jason,这篇帖子太棒了。恭喜并万分感谢。我有一个问题。我建立了一个模型,并使用了以下这种循环正则化:
model.add(LSTM(64, return_sequences=True, recurrent_regularizer=l2(0.0015), input_shape=(timesteps, input_dim)))
model.add(Dropout(0.5))
model.add(LSTM(64, recurrent_regularizer=l2(0.0015), input_shape=(timesteps, input_dim))),
这和您上面提到的梯度缩放是一样的吗?
谢谢。
不是,“recurrent_regularizer”是权重衰减。
https://machinelearning.org.cn/how-to-reduce-overfitting-in-deep-learning-with-weight-regularization/
你好,
我正在训练一个用于二元任务的语义分割CNN模型,数据集极度不平衡。我尝试为我的模型使用Dice损失,但我的梯度发生了爆炸,解码器损失在~5000左右。我已经应用了梯度归一化,但损失值最低也只能达到~3000多。关于如何稳定训练有什么建议吗?对此的任何帮助将不胜感激。谢谢
或许确保您也对输入数据进行了缩放。
或许也添加一些权重正则化来保持权重较小。
你好 Jason,
当损失值很高时……损失值和梯度爆炸之间有关系吗?
2) 损失值为负数,这意味着什么?
是的,这可能会发生。
负损失很奇怪/不应该发生。
嗨,杰森,
LSTM可以在不使用特征提取的情况下读取EEG信号。
通常情况下,是的,您可以将时间序列序列传递给LSTM。
对输入数据进行缩放并使其平稳仍然是一个好主意。
谢谢你
不客气。
嗨 Jason,我很欣赏您的帖子。关于这篇帖子的一点评论:据我理解,梯度爆炸的主要问题是,在您的空间中可能会有很小的区域,其梯度远大于附近区域,这意味着一阶泰勒近似仅在很小的局部区域内有效。如果您的梯度下降算法进入这些高梯度区域之一,那么它最终会迈出很大一步,这会越过局部最小值,并且实际上不会改善损失函数(通常会适得其反),因为它会移动到局部梯度近似有效的区域之外。这不需要涉及任何溢出或下溢,即使在假设具有完美精度的计算机上也会发生。如果我错了,请纠正我!
也许吧。本教程更侧重于将梯度爆炸作为一种失败情况来解决,而不是猜测其原因。
这里对“下溢”的使用不正确。下溢发生在数字变得太小而无法表示时(而不是负无穷大)。请参阅维基百科。
感谢您的反馈,Mark!