深度学习神经网络模型的容量控制着其能够学习的映射函数的类型范围。
容量过小的模型无法学习训练数据集,这意味着它会欠拟合;而容量过大的模型可能会记忆训练数据集,这意味着它会过拟合,或者在优化过程中陷入停滞或迷失。
神经网络模型的容量通过配置节点数量和层数来定义。
在本教程中,您将学习如何控制神经网络模型的容量,以及容量如何影响模型学习的能力。
完成本教程后,您将了解:
- 神经网络模型的容量由模型中的节点数量和层数共同控制。
- 一个具有单个隐藏层和足够多节点的模型,理论上能够学习任何映射函数,但所选择的学习算法可能无法实现这种能力。
- 增加层数提供了一种以较少资源增加模型容量的捷径,并且现代技术允许学习算法成功训练深层模型。
用我的新书《更好的深度学习》来启动你的项目,书中包含分步教程和所有示例的 Python 源代码文件。
让我们开始吧。
- **2020年1月更新**:已针对 scikit-learn v0.22 API 的变更进行更新。

如何通过节点和层控制神经网络模型容量
照片由 Bernard Spragg. NZ 拍摄,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 控制神经网络模型容量
- 在 Keras 中配置节点和层
- 多类别分类问题
- 通过节点改变模型容量
- 通过层改变模型容量
控制神经网络模型容量
神经网络的目标是学习如何将输入示例映射到输出示例。
神经网络学习映射函数。网络的容量是指模型可以近似的函数类型的范围或广度。
非正式地说,模型的容量是其拟合各种函数的能力。
— 第111-112页,深度学习,2016年。
容量较小的模型可能无法充分学习训练数据集。容量较大的模型可以模拟更多不同类型的函数,并且可能能够学习一个函数,以充分将训练数据集中的输入映射到输出。而容量过大的模型可能会记忆训练数据集,导致泛化失败,或在寻找合适的映射函数时陷入困境或迷失。
通常,我们可以将模型容量视为控制模型是可能欠拟合还是过拟合训练数据集的因素。
我们可以通过改变模型的容量来控制模型是更容易过拟合还是欠拟合。
— 第111页,深度学习,2016年。
神经网络的容量可以通过模型的两个方面来控制:
- 节点数量。
- 层数。
拥有更多节点或更多层的模型具有更大的容量,因此可能能够学习更大范围的映射函数。
一个具有更多层和每层更多隐藏单元的模型具有更高的表示能力——它能够表示更复杂的函数。
— 第428页,深度学习,2016年。
一层中的节点数量被称为**宽度**。
开发具有一个层和许多节点的宽网络相对简单。理论上,具有足够多单个隐藏层节点的网络可以学习近似任何映射函数,尽管在实践中,我们不知道多少节点是足够的,也不知道如何训练这样的模型。
模型中的层数被称为**深度**。
增加深度可以增加模型容量。训练深层模型(即具有许多隐藏层的模型)比训练具有大量节点的单层网络在计算上更有效。
现代深度学习为监督学习提供了一个非常强大的框架。通过增加更多层和每层内的更多单元,深度网络可以表示日益复杂的函数。
— 第167页,深度学习,2016年。
传统上,由于梯度消失等问题,训练超过几层的神经网络模型一直具有挑战性。最近,现代方法允许训练深度网络模型,从而开发出具有惊人深度的模型,能够在各种领域的挑战性问题上实现令人印象深刻的性能。
想要通过深度学习获得更好的结果吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
在 Keras 中配置节点和层
Keras 允许您轻松地向模型添加节点和层。
配置模型节点
层的第一项参数指定了该层中使用的节点数量。
多层感知器(MLP)模型的全连接层通过 `Dense` 层添加。
例如,我们可以创建一个具有 32 个节点的单层全连接层,如下所示:
|
1 2 |
... layer = Dense(32) |
同样,循环神经网络层的节点数量也可以用相同的方式指定。
例如,我们可以创建一个具有 32 个节点(或单元)的 LSTM 层,如下所示:
|
1 2 |
... layer = LSTM(32) |
卷积神经网络 (CNN) 没有节点,而是指定过滤器图的数量和它们的形状。过滤器图的数量和大小定义了层的容量。
我们可以定义一个具有 32 个过滤器图,每个大小为 3x3 的二维 CNN,如下所示:
|
1 2 |
... layer = Conv2D(32, (3,3)) |
配置模型层
通过调用 `add()` 函数并传入层,可以将层添加到顺序模型中。
MLP 的全连接层可以通过重复调用 `add` 并传入配置好的 `Dense` 层来添加;例如:
|
1 2 3 4 |
... model = Sequential() model.add(Dense(32)) model.add(Dense(64)) |
同样,循环网络的层数也可以用相同的方式添加,以形成堆叠的循环模型。
一个重要的区别是循环层期望三维输入,因此前一个循环层必须返回完整的输出序列,而不是输入序列末尾每个节点的单个输出。
这可以通过将“return_sequences”参数设置为“True”来实现。例如:
|
1 2 3 4 |
... model = Sequential() model.add(LSTM(32, return_sequences=True)) model.add(LSTM(32)) |
卷积层可以 H 接堆叠,通常是将一到两个卷积层堆叠在一起,然后是一个池化层,再重复这种层模式;例如:
|
1 2 3 4 5 6 7 8 |
... model = Sequential() model.add(Conv2D(16, (3,3))) model.add(Conv2D(16, (3,3))) model.add(MaxPooling2D((2,2))) model.add(Conv2D(32, (3,3))) model.add(Conv2D(32, (3,3))) model.add(MaxPooling2D((2,2))) |
现在我们知道了如何在 Keras 中配置模型的节点和层数,接下来我们将探讨容量如何影响模型在多类分类问题上的性能。
多类别分类问题
我们将使用一个标准的多类分类问题作为基础,来演示模型容量对模型性能的影响。
scikit-learn 提供了 make_blobs() 函数,可用于创建具有指定样本数量、输入变量、类别以及类别内样本方差的多类别分类问题。
我们可以通过“n_features”参数配置问题具有特定数量的输入变量,通过“centers”参数配置特定数量的类别或中心。“random_state”可用于为伪随机数生成器设置种子,以确保每次调用函数时都得到相同的样本。
例如,下面的调用生成了 1,000 个用于三类问题和两个输入变量的示例。
|
1 2 3 |
... # 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) |
结果是我们可以建模的数据集的输入和输出元素。
为了了解问题的复杂性,我们可以在二维散点图上绘制每个点,并根据类别值对每个点进行着色。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# blob 数据集的散点图 from sklearn.datasets import make_blobs from matplotlib import pyplot from numpy import where # 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 每个类别值的散点图 for class_value in range(3): # 选择具有类标签的点的索引 row_ix = where(y == class_value) # 绘制不同颜色点的散点图 pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # 显示图 pyplot.show() |
运行示例会创建一个包含整个数据集的散点图。我们可以看到,选择的标准差为 2.0 意味着这些类别不是线性可分的(无法通过一条直线分隔),导致许多模糊点。
这是可取的,因为它意味着问题并非微不足道,并且将允许神经网络模型找到许多不同的“足够好”的候选解决方案。
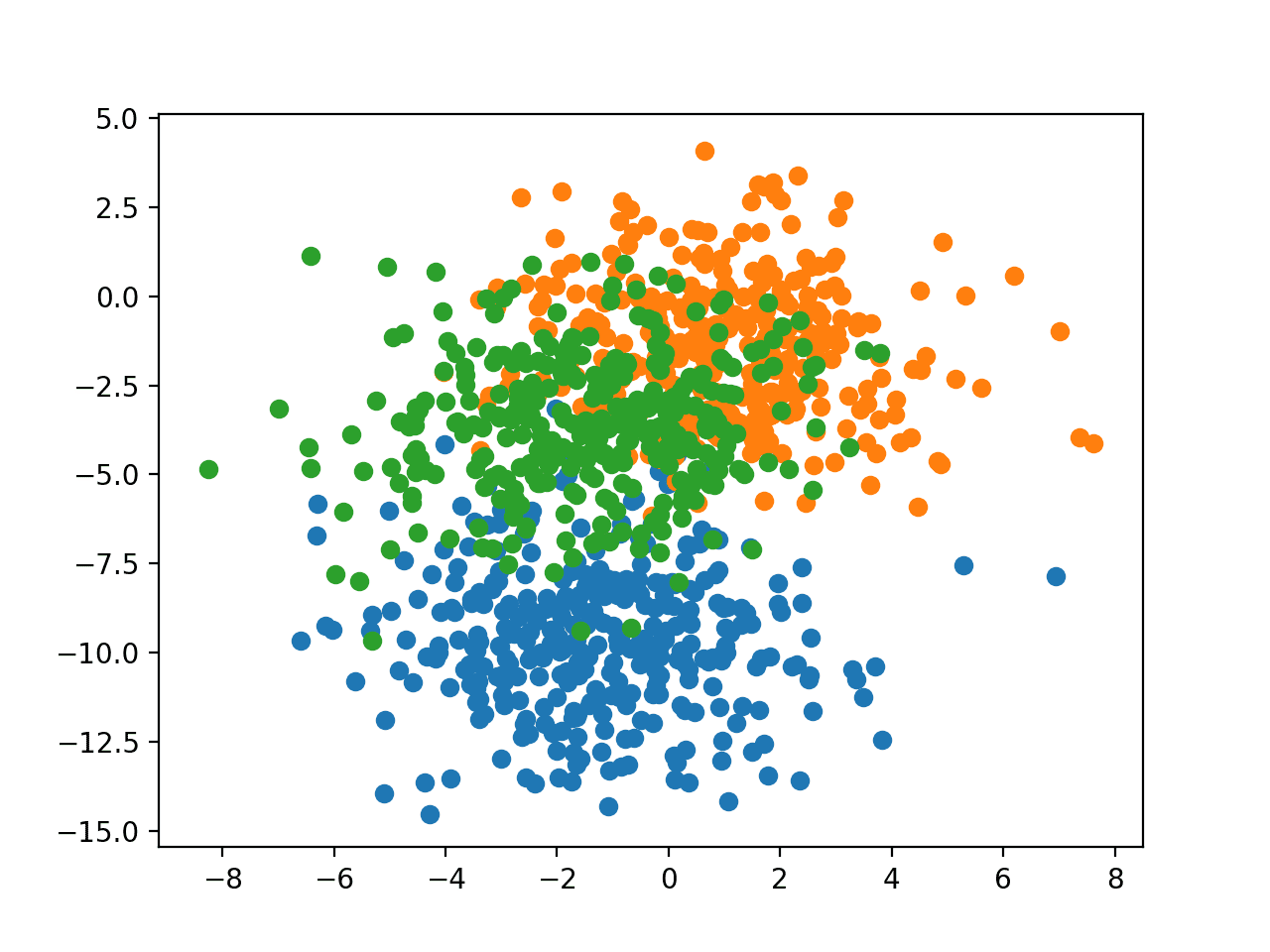
具有三个类别且点按类别值着色的 Blob 数据集散点图
为了探究模型容量,我们需要问题比三类和两个变量更复杂。
为了进行以下实验,我们将使用 100 个输入特征和 20 个类别;例如:
|
1 2 3 |
... # 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=20, n_features=100, cluster_std=2, random_state=2) |
通过节点改变模型容量
在本节中,我们将为 Blob 多类分类问题开发一个多层感知器模型(MLP),并演示节点数量对模型学习能力的影响。
我们可以从开发一个函数来准备数据集开始。
数据集的输入和输出元素可以使用上一节中描述的 `make_blobs()` 函数创建。
接下来,目标变量必须进行独热编码。这是为了让模型能够学习预测输入示例属于 20 个类别中每个类别的概率。
我们可以使用 to_categorical() Keras 实用函数 来完成此操作,例如:
|
1 2 |
# 独热编码输出变量 y = to_categorical(y) |
接下来,我们可以将 1,000 个示例分成两半,500 个示例用作训练数据集,500 个用于评估模型。
|
1 2 3 4 5 |
# 分割成训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy |
下面的 `create_dataset()` 函数将这些元素连接起来,并以输入和输出元素的形式返回训练集和测试集。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 准备多类分类数据集 def create_dataset(): # 生成 2d 分类数据集 X, y = make_blobs(n_samples=1000, centers=20, n_features=100, cluster_std=2, random_state=2) # 对输出变量进行独热编码 y = to_categorical(y) # 分割为训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy |
我们可以调用此函数来准备数据集。
|
1 2 |
# 准备数据集 trainX, trainy, testX, testy = create_dataset() |
接下来,我们可以定义一个函数,该函数将创建模型,在训练数据集上拟合它,然后在测试数据集上评估它。
模型需要知道输入变量的数量以配置输入层,以及目标类别的数量以配置输出层。这些属性可以直接从训练数据集中提取。
|
1 2 |
# 根据数据配置模型 n_input, n_classes = trainX.shape[1], testy.shape[1] |
我们将定义一个带有单个隐藏层的 MLP 模型,该模型使用修正线性激活函数和 He 随机权重初始化方法。
输出层将使用 softmax 激活函数来预测每个目标类别的概率。隐藏层中的节点数量将通过一个名为“n_nodes”的参数提供。
|
1 2 3 4 |
# 定义模型 model = Sequential() model.add(Dense(n_nodes, input_dim=n_input, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(n_classes, activation='softmax')) |
模型将使用随机梯度下降进行优化,学习率为 0.01,动量为 0.9,并使用适合多类别分类的分类交叉熵损失函数。
|
1 2 3 |
# 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) |
模型将训练 100 个 epoch,然后将在测试数据集上进行评估。
|
1 2 3 4 |
# 在训练集上拟合模型 history = model.fit(trainX, trainy, epochs=100, verbose=0) # 在测试集上评估模型 _, test_acc = model.evaluate(testX, testy, verbose=0) |
综合这些元素,下面的 `evaluate_model()` 函数接受节点数量和数据集作为参数,并返回每个 epoch 结束时的训练损失历史记录以及最终模型在测试数据集上的准确率。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 使用给定节点数量拟合模型,返回测试集准确率 def evaluate_model(n_nodes, trainX, trainy, testX, testy): # 根据数据配置模型 n_input, n_classes = trainX.shape[1], testy.shape[1] # 定义模型 model = Sequential() model.add(Dense(n_nodes, input_dim=n_input, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(n_classes, activation='softmax')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 在训练集上拟合模型 history = model.fit(trainX, trainy, epochs=100, verbose=0) # 在测试集上评估模型 _, test_acc = model.evaluate(testX, testy, verbose=0) return history, test_acc |
我们可以用不同数量的节点在隐藏层中调用这个函数。
问题相对简单;因此,我们将评估模型在 1 到 7 个节点下的性能。
我们期望随着节点数量的增加,模型容量也会增加,从而使模型能够更好地学习训练数据集,至少在学习算法的选定配置(例如学习率、批量大小和 epoch)限制的范围内是如此。
将打印每种配置的测试准确率,并绘制每种配置下训练准确率的学习曲线。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 评估模型并绘制给定节点数量的学习曲线 num_nodes = [1, 2, 3, 4, 5, 6, 7] for n_nodes in num_nodes: # 使用给定数量的节点评估模型 history, result = evaluate_model(n_nodes, trainX, trainy, testX, testy) # 总结最终测试集准确率 print('nodes=%d: %.3f' % (n_nodes, result)) # 绘制学习曲线 pyplot.plot(history.history['loss'], label=str(n_nodes)) # 显示绘图 pyplot.legend() pyplot.show() |
完整的代码清单如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
# 对不同节点数量的多类分类MLP学习曲线研究 from sklearn.datasets import make_blobs from keras.layers import Dense from keras.models import Sequential from keras.optimizers import SGD from keras.utils import to_categorical from matplotlib import pyplot # 准备多类分类数据集 def create_dataset(): # 生成 2d 分类数据集 X, y = make_blobs(n_samples=1000, centers=20, n_features=100, cluster_std=2, random_state=2) # 对输出变量进行独热编码 y = to_categorical(y) # 分割为训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy # 使用给定节点数量拟合模型,返回测试集准确率 def evaluate_model(n_nodes, trainX, trainy, testX, testy): # 根据数据配置模型 n_input, n_classes = trainX.shape[1], testy.shape[1] # 定义模型 model = Sequential() model.add(Dense(n_nodes, input_dim=n_input, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(n_classes, activation='softmax')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 在训练集上拟合模型 history = model.fit(trainX, trainy, epochs=100, verbose=0) # 在测试集上评估模型 _, test_acc = model.evaluate(testX, testy, verbose=0) return history, test_acc # 准备数据集 trainX, trainy, testX, testy = create_dataset() # 评估模型并绘制给定节点数量的学习曲线 num_nodes = [1, 2, 3, 4, 5, 6, 7] for n_nodes in num_nodes: # 使用给定数量的节点评估模型 history, result = evaluate_model(n_nodes, trainX, trainy, testX, testy) # 总结最终测试集准确率 print('nodes=%d: %.3f' % (n_nodes, result)) # 绘制学习曲线 pyplot.plot(history.history['loss'], label=str(n_nodes)) # 显示绘图 pyplot.legend() pyplot.show() |
运行示例首先打印每个模型配置的测试准确率。
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到,随着节点数量的增加,模型学习问题的能力也随之增强。这导致模型在测试数据集上的泛化误差逐渐降低,直到 6 和 7 个节点时,模型完美地学习了问题。
|
1 2 3 4 5 6 7 |
节点数=1: 0.138 节点数=2: 0.380 节点数=3: 0.582 节点数=4: 0.890 节点数=5: 0.844 节点数=6: 1.000 节点数=7: 1.000 |
还创建了一个折线图,显示了在 100 个训练 epoch 中,每种模型配置(隐藏层中 1 到 7 个节点)在训练数据集上的交叉熵损失。
我们可以看到,随着节点数量的增加,模型能够更好地减少损失,例如更好地学习训练数据集。此图显示了由隐藏层中的节点数量定义的模型容量与模型学习能力之间的直接关系。
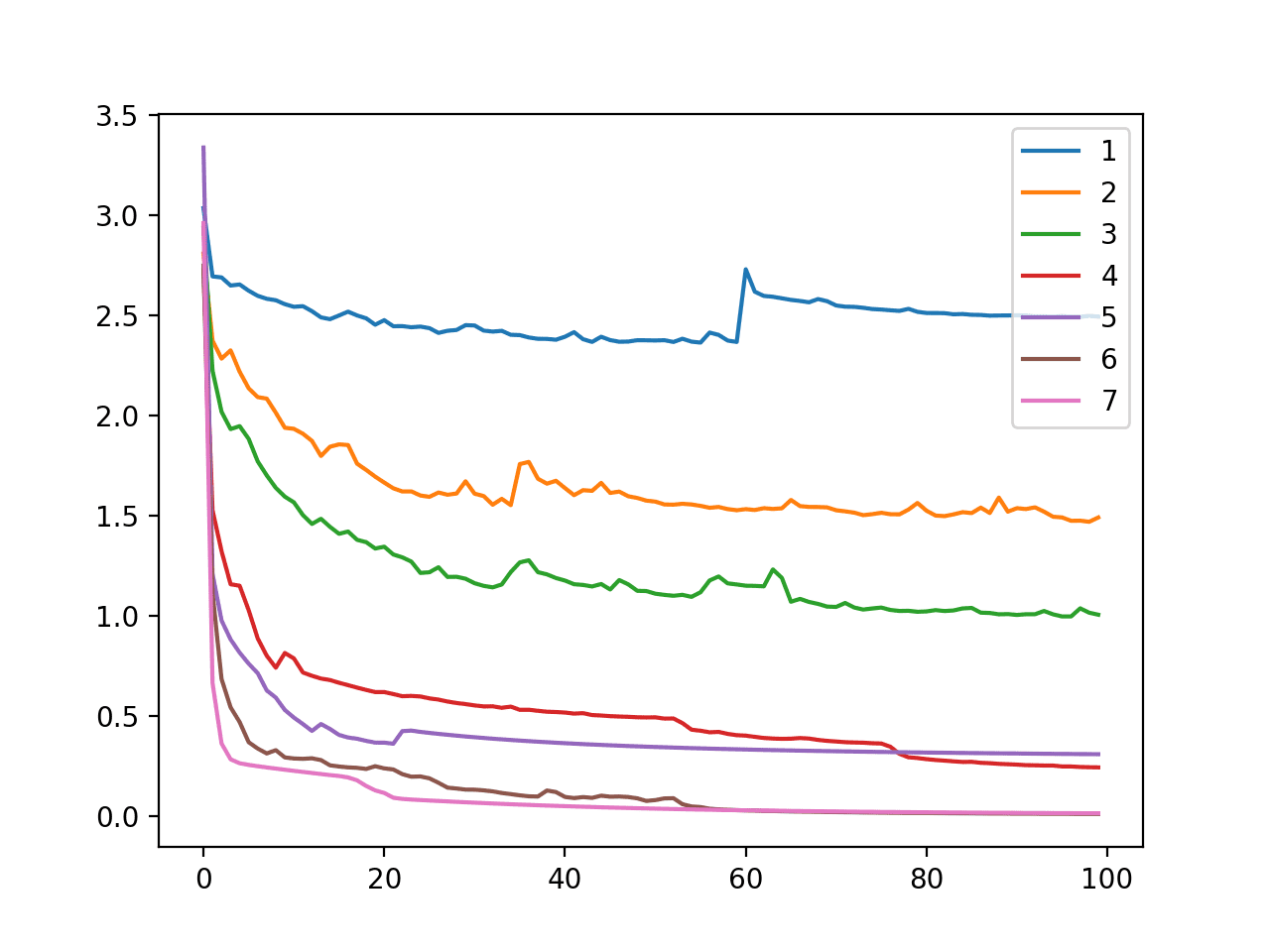
在多类分类问题(Blobs)上,改变模型节点数量时,MLP 在训练数据集上的交叉熵损失随训练周期的线图
节点数量可以增加到某个点(例如 1,000 个节点),此时学习算法将无法充分学习映射函数。
通过层改变模型容量
我们可以执行类似的分析,评估层数如何影响模型学习映射函数的能力。
增加层数通常可以极大地增加模型的容量,就像解决问题的计算和学习捷径一样。例如,一个具有 10 个节点的单隐藏层模型与一个具有两个隐藏层(每个隐藏层有 5 个节点)的模型并不等价。后者具有更大的容量。
危险在于,一个容量超出所需模型很可能会过拟合训练数据,就像节点过多的模型一样,层数过多的模型也可能无法学习训练数据集,在优化过程中迷失或陷入困境。
首先,我们可以更新 evaluate_model() 函数,以拟合具有给定层数的 MLP 模型。
我们从上一节中得知,一个具有约七个或更多节点并训练 100 个周期的 MLP 将完美地学习问题。因此,我们将在每个层中使用 10 个节点,以确保模型在单层中就具有足够的容量来学习问题。
更新后的函数如下所示,它将层数和数据集作为参数,并返回模型的训练历史和测试准确性。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 使用给定层数拟合模型,返回测试集准确率 def evaluate_model(n_layers, trainX, trainy, testX, testy): # 根据数据配置模型 n_input, n_classes = trainX.shape[1], testy.shape[1] # 定义模型 model = Sequential() model.add(Dense(10, input_dim=n_input, activation='relu', kernel_initializer='he_uniform')) for _ in range(1, n_layers): model.add(Dense(10, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(n_classes, activation='softmax')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, epochs=100, verbose=0) # 在测试集上评估模型 _, test_acc = model.evaluate(testX, testy, verbose=0) return history, test_acc |
鉴于单个隐藏层模型具有足够的容量来学习此问题,我们将探讨增加层数,直到学习算法变得不稳定并且无法再学习问题。
如果选择的建模问题更复杂,我们可以探索增加层数,并回顾模型性能的改进,直到出现收益递减的情况。
在这种情况下,我们将评估具有 1 到 5 个层的模型,并期望在某个时候,层数会导致所选学习算法无法适应训练数据的模型。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 评估模型并绘制给定层数模型的学习曲线 all_history = list() num_layers = [1, 2, 3, 4, 5] for n_layers in num_layers: # 评估具有给定层数的模型 history, result = evaluate_model(n_layers, trainX, trainy, testX, testy) print('layers=%d: %.3f' % (n_layers, result)) # 绘制学习曲线 pyplot.plot(history.history['loss'], label=str(n_layers)) pyplot.legend() pyplot.show() |
将这些元素联系起来,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
# 研究具有不同层数的多类分类 MLP 学习曲线 from sklearn.datasets import make_blobs from keras.models import Sequential from keras.layers import Dense from keras.optimizers import SGD from keras.utils import to_categorical from matplotlib import pyplot # 准备多类分类数据集 def create_dataset(): # 生成 2d 分类数据集 X, y = make_blobs(n_samples=1000, centers=20, n_features=100, cluster_std=2, random_state=2) # 对输出变量进行独热编码 y = to_categorical(y) # 分割为训练集和测试集 n_train = 500 trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] return trainX, trainy, testX, testy # 使用给定层数拟合模型,返回测试集准确率 def evaluate_model(n_layers, trainX, trainy, testX, testy): # 根据数据配置模型 n_input, n_classes = trainX.shape[1], testy.shape[1] # 定义模型 model = Sequential() model.add(Dense(10, input_dim=n_input, activation='relu', kernel_initializer='he_uniform')) for _ in range(1, n_layers): model.add(Dense(10, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(n_classes, activation='softmax')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(loss='categorical_crossentropy', optimizer=opt, metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, epochs=100, verbose=0) # 在测试集上评估模型 _, test_acc = model.evaluate(testX, testy, verbose=0) return history, test_acc # 获取数据集 trainX, trainy, testX, testy = create_dataset() # 评估模型并绘制给定层数模型的学习曲线 all_history = list() num_layers = [1, 2, 3, 4, 5] for n_layers in num_layers: # 评估具有给定层数的模型 history, result = evaluate_model(n_layers, trainX, trainy, testX, testy) print('layers=%d: %.3f' % (n_layers, result)) # 绘制学习曲线 pyplot.plot(history.history['loss'], label=str(n_layers)) pyplot.legend() pyplot.show() |
运行示例首先打印每个模型配置的测试准确率。
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到模型能够很好地学习问题,最多三层,然后开始出现问题。我们可以看到,性能在五层时确实下降,并且如果层数进一步增加,预计会继续下降。
|
1 2 3 4 5 |
层数=1:1.000 层数=2:1.000 层数=3:1.000 层数=4:0.948 层数=5:0.794 |
还创建了一个线图,显示了每个模型配置(1 到 5 层)在 100 个训练周期内,训练数据集上的交叉熵损失。
我们可以看到,具有 1、2 和 3 个模型(蓝色、橙色和绿色)的模型动态非常相似,能快速学习问题。
令人惊讶的是,具有四层和五层的训练损失显示出最初表现良好,然后突然上升的迹象,这表明模型可能陷入次优权重集,而不是过拟合训练数据集。
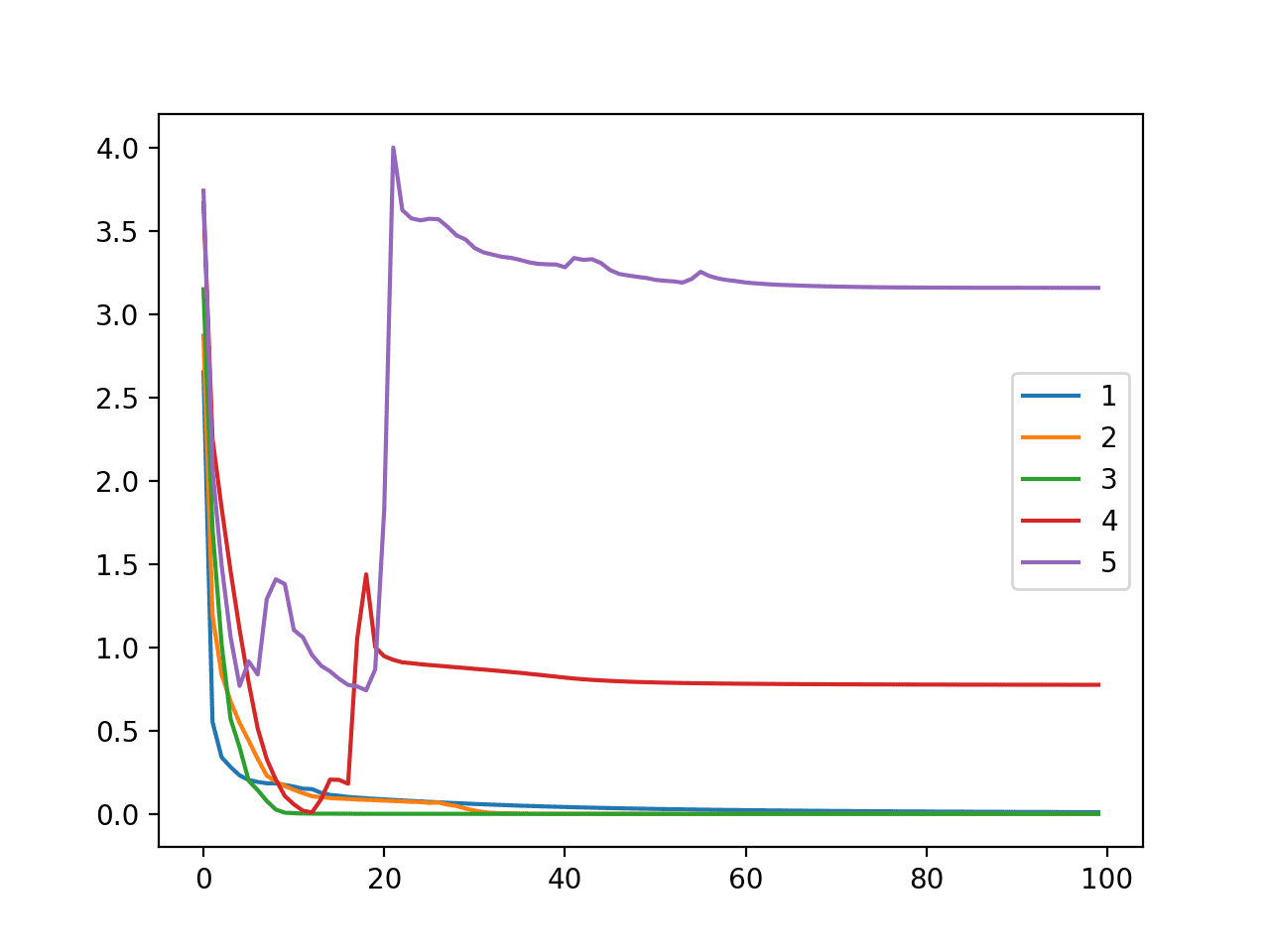
在多类分类问题(Blobs)上,改变模型层数时,MLP 在训练数据集上的交叉熵损失随训练周期的线图
分析表明,通过增加深度来增加模型容量是一种非常有效的工具,但必须谨慎使用,因为它可能很快导致一个容量很大的模型,而该模型可能无法轻易学习训练数据集。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 节点过多。更新增加节点数的实验,以找到学习算法不再能够学习问题的点。
- 重复评估。更新实验以使用重复评估每个配置,以应对学习算法的随机性。
- 更难的问题。在一个需要增加深度提供更大容量才能表现良好的问题上,重复增加层数的实验。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
书籍
- 《神经网络精工:前馈人工神经网络中的监督学习》, 1999.
- 深度学习, 2016.
API
文章
总结
在本教程中,您了解了如何控制神经网络模型的容量以及容量如何影响模型能够学习的内容。
具体来说,你学到了:
- 神经网络模型的容量由模型中的节点数量和层数共同控制。
- 具有单个隐藏层和足够数量节点的模型能够学习任何映射函数,但所选的学习算法可能能够或可能无法实现此能力。
- 增加层数提供了一种以较少资源增加模型容量的捷径,并且现代技术允许学习算法成功训练深层模型。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。






我有一个问题需要 20000 个输入节点。每个隐藏层中的层数和节点数作为实验的良好起点是多少?
2 万个输入特征?
如果是这样,尝试将它们减少到一个子集。
至于模型中的节点和层数,尝试不同的大小,看看什么效果好。更多详情请参阅此处
https://machinelearning.org.cn/faq/single-faq/how-many-layers-and-nodes-do-i-need-in-my-neural-network
你好 Jason,我可以知道为什么变量 X(trainX 和 testX 也是)不需要独热编码吗?
输入数据是数值数据,独热编码仅用于分类数据。
更多信息在这里
https://machinelearning.org.cn/why-one-hot-encode-data-in-machine-learning/
是否可以使用这些技术进行 k 折交叉验证而不是单独的测试集?
是的。
为什么分阶段优化?
你到底是什么意思?也许你可以详细说明一下?
除了连接隐藏层中的所有节点,我们如何才能仅选择偶数节点或奇数节点进行连接?
你可以用自定义代码来做,但我不相信默认的 Dense 层可以。
嘿,我注意到一件事,将节点数增加到极端(例如 512),然后再增加几层,可以使模型在测试样本上更准确。即使预测器数量很少,大约 50 个。样本量约为 100 万,但这是一个不平衡的数据集。我试图预测低频事件。
太棒了!
嗨,Jason,
我们如何提高机器学习模型的容量?
对于神经网络,增加更多层和节点。
其他模型——这取决于模型。
.
在上述问题中
数据拟合(训练)在 Xtrain,ytrain 上
数据评估在 Xtest,yest 上
大量节点提供高容量。
高容量导致过拟合。
1.
增加节点会增加模型学习能力;使用 7 个节点,模型完美地学习了问题。
使用 7 个节点难道不会导致数据过拟合吗?
但相反,它在测试集上表现非常好。
2.
无法理解哪个更好,
使用 7 个节点
或者
使用 5 个节点(似乎容量适中)。?
请帮忙。
我们并不是要解决测试问题,而是展示改变模型如何影响模型行为。
更大的容量可能过拟合,也可能不过拟合。
抱歉,如果这是一个愚蠢的问题,我正在努力学习机器学习,但我不知道去哪里寻找这个问题。假设我有一个学习模型,但我希望为模型本身构建一些可调整的参数。例如,一个模型已经过训练,可以模拟音频信号的变化,查看输入和输出样本。这很好。但是,假设我想为该模型添加一个增益调整。我想我可以通过在示例文件中设置不同级别的增益来重新训练数据,但我不知道该如何做。节点和层是否可以实现这一点,或者是否有其他方法可以添加模型中协同工作且可调整的组件?
您可以使用现有模型作为新模型的输入,或为问题创建新模型。
谢谢回复。我有点困惑,我的意思是我想让模型可调,这意味着我希望能够调整结果模型的增益。我的想法是构建一个接口来调整我训练的任何参数,如果这种事情是可能的话。如果我只是简单地将现有模型作为新模型的输入,我难道不会得到一个具有新增益设置的新模型吗?
不确定我是否理解,抱歉。也许可以尝试/原型设计,看看模型是否能达到您想要的结果/系统要求。
嗨 Jason!!我有一个月都在尝试解决 EMO-DB(7 个类别)的语音情感识别问题。
我的 MLP 结构如下:
1 个输入层
2 个隐藏层(Sigmoid 激活函数)
1 个输出层(Sigmoid 激活函数)
但我在验证集上没有得到好的结果,尽管问题有点困难,我的特征也不是很差……我想请教一下,我应该采取什么措施来提高准确性并降低训练中的 MSE……非常感谢
也许这里的一些提示会有所帮助
https://machinelearning.org.cn/start-here/#better
嗨,Jason,
我目前正在从事一个关于回归问题的项目。
数据集非常小(少于 500 个样本)。
在这种情况下,我构建了一个仅有一个隐藏层(大约 4 到 5 个节点)的神经网络。
我希望增加节点数量能够提高模型性能吗?
我尝试通过使用更多节点并评估误差来做这个实验。从我所看到的,没有趋势(更像是锯齿状)。
这正常吗?
我该如何解释?
尝试一下看看,您可能需要调整模型的其他方面,例如学习率。
我想增加 U-net 模型的深度。过滤器有 64、128、256、512……我想更深入。我该怎么做?
增加深度意味着增加更多层。最简单的方法是在顺序模型上,使用 Dense() 层多次调用 add()。
在密集神经网络中,我们能否对反向传播进行一些更改,使得只有其中一层的权重和偏差被更改,而其他层保持不变?
是的,您必须为每个层标记“layer.trainable = True”或“layer.trainable = False”。
嗨,Jason,
不错的教程。
我已有一个包含 7 层的 CNN 模型,其中 4 层为卷积层,3 层为全连接层。现在,如果输入特征的数量从 8 增加到 14,我应该尝试不同的滤波器大小、更多层还是每层更多的滤波器/神经元?
嗨 Sunila…你可能需要研究 AutoML
https://machinelearning.org.cn/autokeras-for-classification-and-regression/