集成学习是结合多个模型预测的方法。
在集成学习中,组成集成的模型必须表现良好并产生不同的预测误差,这一点很重要。以不同方式做出良好预测的模型可以产生更稳定且通常优于任何单个成员模型的预测结果。
实现模型之间差异的一种方法是在可用训练数据的不同子集上训练每个模型。模型通过使用重采样方法(例如交叉验证和自举法)在训练数据的不同子集上进行自然训练,这些方法旨在估计模型在未见数据上的平均性能。在此估计过程中使用的模型可以组合成所谓的基于重采样的集成,例如交叉验证集成或自举聚合(或 bagging)集成。
在本教程中,您将学习如何为深度学习神经网络模型开发一套不同的基于重采样的集成。
完成本教程后,您将了解:
- 如何使用随机分割估计模型性能并从模型中开发集成。
- 如何使用 10 折交叉验证估计性能并开发交叉验证集成。
- 如何使用自举法估计性能并使用 Bagging 集成组合模型。
用我的新书《更好的深度学习》来启动你的项目,书中包含分步教程和所有示例的 Python 源代码文件。
让我们开始吧。
- 2019 年 10 月更新:更新至 Keras 2.3 和 TensorFlow 2.0。
- 2020年1月更新:已针对 scikit-learn v0.22 API 的更改进行更新。

如何在 Keras 中为深度学习创建随机分割、交叉验证和 Bagging 集成
图片由 Gian Luca Ponti 拍摄,保留部分权利。
教程概述
本教程分为六个部分;它们是:
- 数据重采样集成
- 多类别分类问题
- 单个多层感知器模型
- 随机分割集成
- 交叉验证集成
- Bagging 集成
数据重采样集成
结合多个模型的预测可以产生更稳定的预测,并且在某些情况下,预测性能优于任何贡献模型。
有效的集成需要成员之间存在分歧。每个成员都必须具备技能(例如,表现优于随机机会),但理想情况下,以不同的方式表现良好。从技术上讲,我们可以说我们更喜欢集成成员的预测或预测误差之间的相关性较低。
鼓励集成之间差异的一种方法是对不同的训练数据集使用相同的学习算法。这可以通过重复重采样训练数据集来实现,该数据集反过来用于训练新模型。多个模型使用对训练数据略有不同的视角进行拟合,反过来会产生不同的错误,并且在组合时通常会产生更稳定和更好的预测。
我们可以将这些方法统称为数据重采样集成。
这种方法的一个好处是可以使用不使用训练数据集中所有样本的重采样方法。任何未用于拟合模型的样本都可以用作测试数据集,以估计所选模型配置的泛化误差。
有三种流行的重采样方法可用于创建重采样集成;它们是:
- 随机分割。数据集通过将数据随机分割为训练集和测试集进行重复采样。
- k 折交叉验证。数据集被分割成 k 个大小相等的折叠,训练 k 个模型,并且每个折叠都有机会用作保留集,其中模型在所有剩余折叠上进行训练。
- 自举聚合。随机样本带替换地收集,未包含在给定样本中的样本用作测试集。
也许最广泛使用的重采样集成方法是自举聚合,更常被称为 Bagging。带替换的重采样允许训练数据集中存在更多差异,从而使模型产生偏差,进而导致所得模型的预测之间存在更多差异。
重采样集成模型对您的项目做出了一些具体假设:
- 需要对未见数据的模型性能进行稳健估计;否则,可以使用单个训练/测试分割。
- 存在使用模型集成提高性能的潜力;否则,可以使用在所有可用数据上拟合的单个模型。
- 在训练数据集样本上拟合多个神经网络模型的计算成本不是过高;否则,所有资源都应该用于拟合单个模型。
神经网络模型具有极高的灵活性,因此鉴于在所有可用数据上训练的单个模型可以表现得如此出色,重采样集成所提供的性能提升并非总是可能的。
因此,使用重采样集成的最佳时机是需要对性能进行稳健估计,并且可以拟合多个模型来计算估计,但同时也要求在性能估计过程中创建的一个(或多个)模型用作最终模型(例如,不能在所有可用训练数据上拟合新的最终模型)。
现在我们熟悉了重采样集成方法,我们可以依次通过应用每种方法的示例。
想要通过深度学习获得更好的结果吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
多类别分类问题
我们将使用一个小的多类分类问题作为基础来演示模型重采样集成。
scikit-learn 类提供了make_blobs() 函数,可用于创建具有规定数量的样本、输入变量、类和类内样本方差的多类分类问题。
我们使用此问题,包含 1,000 个样本,具有输入变量(表示点的 x 和 y 坐标)以及每个组内点的标准差为 2.0。我们将使用相同的随机状态(伪随机数生成器的种子)来确保我们始终获得相同的 1,000 个点。
|
1 2 |
# 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) |
结果是我们可以建模的数据集的输入和输出元素。
为了了解问题的复杂性,我们可以在二维散点图上绘制每个点,并根据类别值对每个点进行着色。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# blob 数据集的散点图 from sklearn.datasets import make_blobs from matplotlib import pyplot from pandas import DataFrame # 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 散点图,点按类别值着色 df = DataFrame(dict(x=X[:,0], y=X[:,1], label=y)) colors = {0:'red', 1:'blue', 2:'green'} fig, ax = pyplot.subplots() grouped = df.groupby('label') for key, group in grouped: group.plot(ax=ax, kind='scatter', x='x', y='y', label=key, color=colors[key]) pyplot.show() |
运行此示例将生成整个数据集的散点图。我们可以看到,标准差为 2.0 意味着这些类不是线性可分的(不能用一条线分开),导致许多模糊的点。
这是可取的,因为它意味着问题并非微不足道,并且将允许神经网络模型找到许多不同的“足够好”的候选解决方案,从而导致高方差。
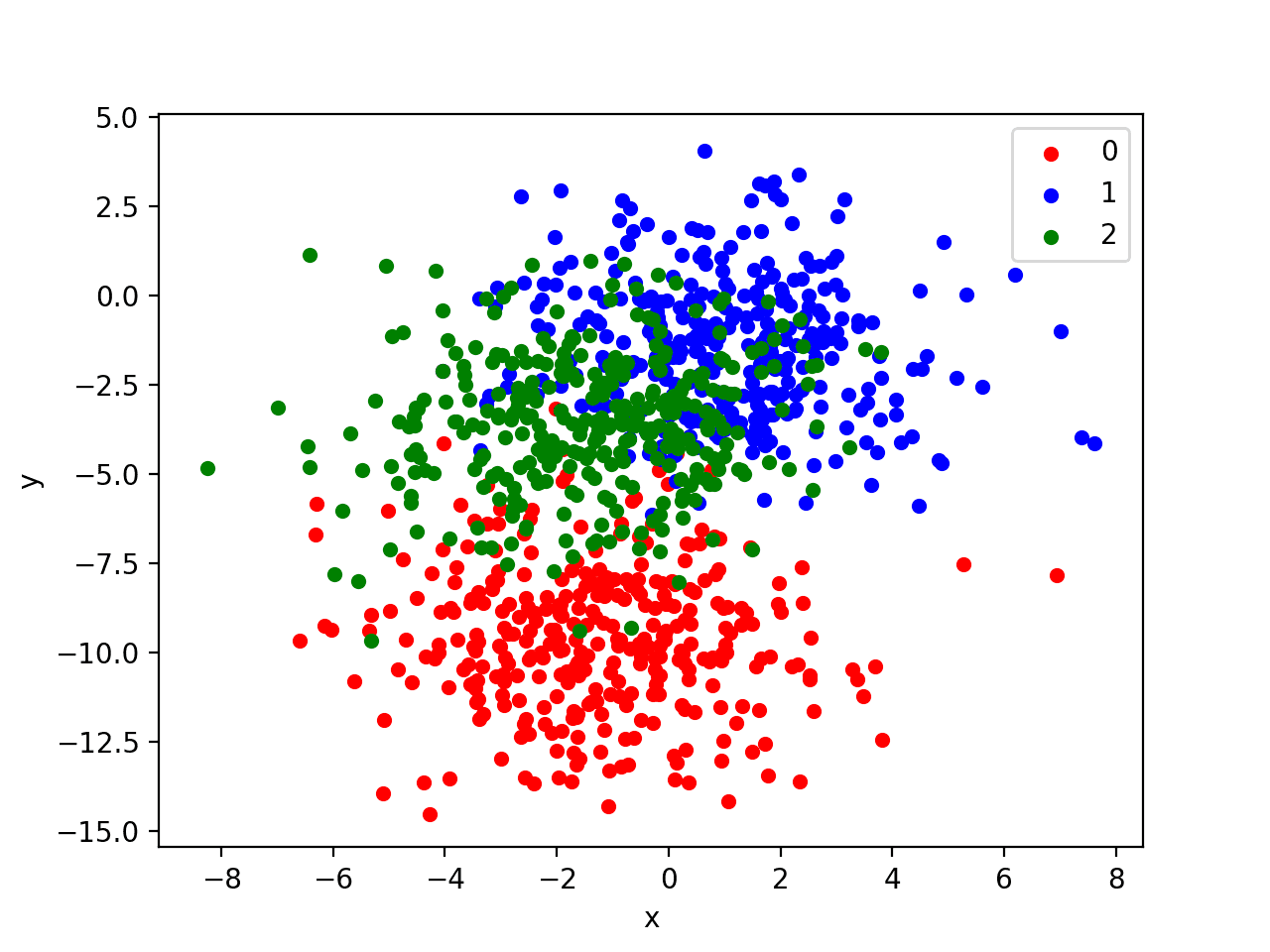
具有三个类别和按类别值着色的点的 Blob 数据集散点图
单个多层感知器模型
我们将定义一个多层感知器神经网络(MLP),它能很好地学习该问题。
该问题是一个多类分类问题,我们将使用输出层上的 softmax 激活函数对其进行建模。这意味着模型将预测一个包含 3 个元素的向量,其中包含样本属于 3 个类中每个类的概率。因此,第一步是对类值进行独热编码。
|
1 |
y = to_categorical(y) |
接下来,我们必须将数据集分成训练集和测试集。我们将使用测试集来评估模型的性能,并使用学习曲线绘制其在训练期间的性能。我们将使用 90% 的数据进行训练,10% 用于测试集。
我们选择了一个较大的分割,因为它是一个有噪声的问题,并且一个性能良好的模型需要尽可能多的数据来学习复杂的分类函数。
|
1 2 3 4 |
# 分割成训练集和测试集 n_train = int(0.9 * X.shape[0]) trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] |
接下来,我们可以定义和组合模型。
模型将期望包含两个输入变量的样本。然后,模型具有一个包含 50 个节点的隐藏层和修正线性激活函数,然后是一个包含 3 个节点的输出层,用于预测 3 个类中每个类的概率,以及一个 softmax 激活函数。
由于该问题是多类问题,我们将使用分类交叉熵损失函数来优化模型,并使用高效的Adam 版本的随机梯度下降。
|
1 2 3 4 5 |
# 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) |
模型经过 50 个训练周期拟合,我们将在每个周期在测试集上评估模型,将测试集用作验证集。
|
1 2 |
# 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=50, verbose=0) |
运行结束时,我们将评估模型在训练集和测试集上的性能。
|
1 2 3 4 |
# 评估模型 _, train_acc = model.evaluate(trainX, trainy, verbose=0) _, test_acc = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_acc, test_acc)) |
最后,我们将绘制模型在训练集和测试集上每个训练周期的准确率学习曲线。
|
1 2 3 4 5 |
# 绘制历史记录 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.legend() pyplot.show() |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# 为 blob 数据集开发一个 mlp from sklearn.datasets import make_blobs from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense from matplotlib import pyplot # 生成二维分类数据集 X, y = make_blobs(n_samples=1000, centers=3, n_features=2, cluster_std=2, random_state=2) # 独热编码输出变量 y = to_categorical(y) # 分割成训练集和测试集 n_train = int(0.9 * X.shape[0]) trainX, testX = X[:n_train, :], X[n_train:, :] trainy, testy = y[:n_train], y[n_train:] # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 history = model.fit(trainX, trainy, validation_data=(testX, testy), epochs=50, verbose=0) # 评估模型 _, train_acc = model.evaluate(trainX, trainy, verbose=0) _, test_acc = model.evaluate(testX, testy, verbose=0) print('Train: %.3f, Test: %.3f' % (train_acc, test_acc)) # 模型准确率的学习曲线 pyplot.plot(history.history['accuracy'], label='train') pyplot.plot(history.history['val_accuracy'], label='test') pyplot.legend() pyplot.show() |
运行示例首先打印最终模型在训练集和测试集上的性能。
注意:由于算法或评估过程的随机性,或者数值精度差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以看到模型在训练数据集上实现了约 83% 的准确率,在测试数据集上实现了约 86% 的准确率。
所选的将数据集分割成训练集和测试集意味着测试集很小,不具有代表性。反过来,测试集上的性能也不具有模型的代表性;在这种情况下,它是乐观偏差的。
|
1 |
训练:0.830,测试:0.860 |
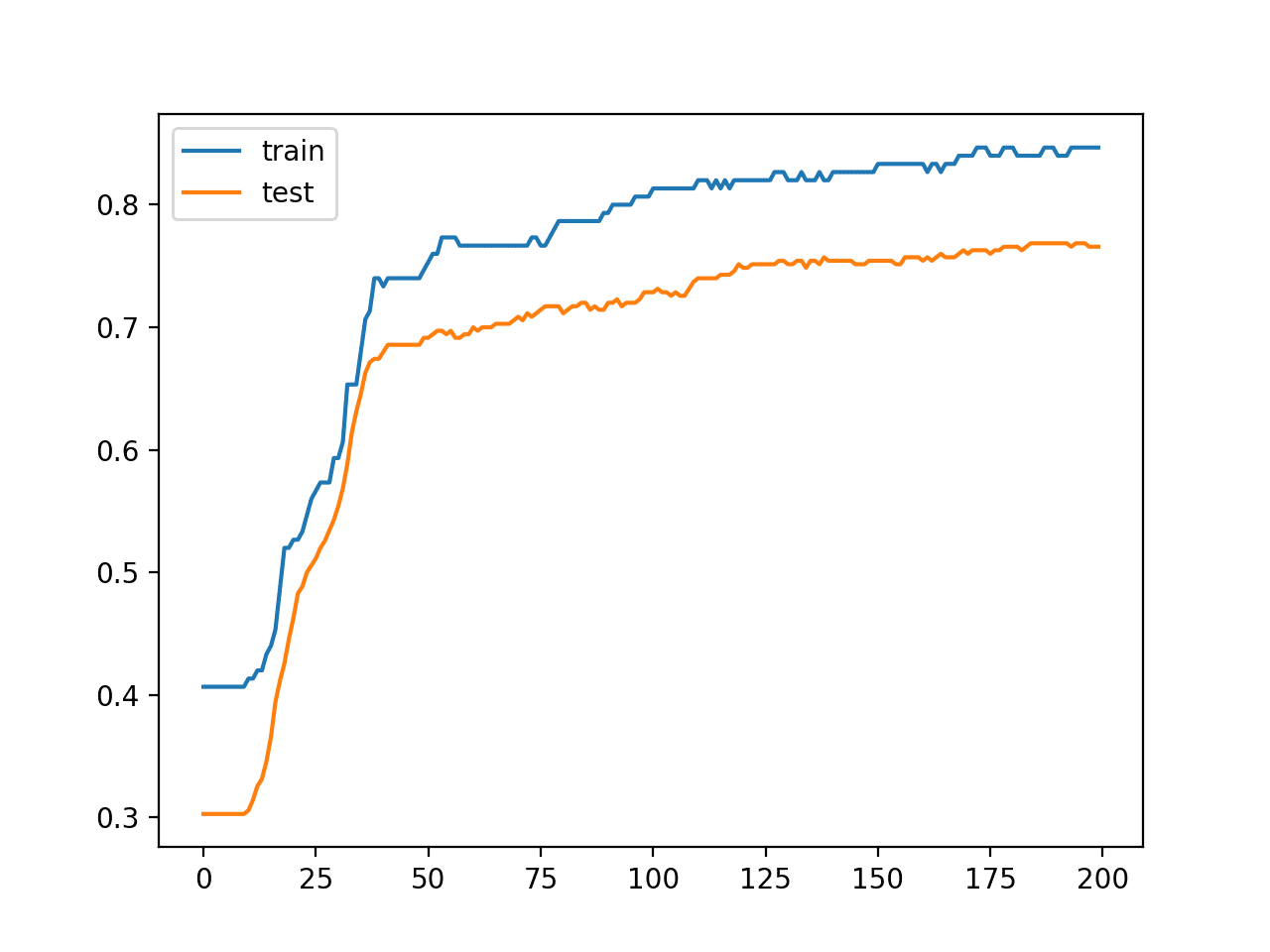
还创建了一条线图,显示了模型在训练集和测试集上每个训练周期的准确率学习曲线。
我们可以看到模型具有相当稳定的拟合。
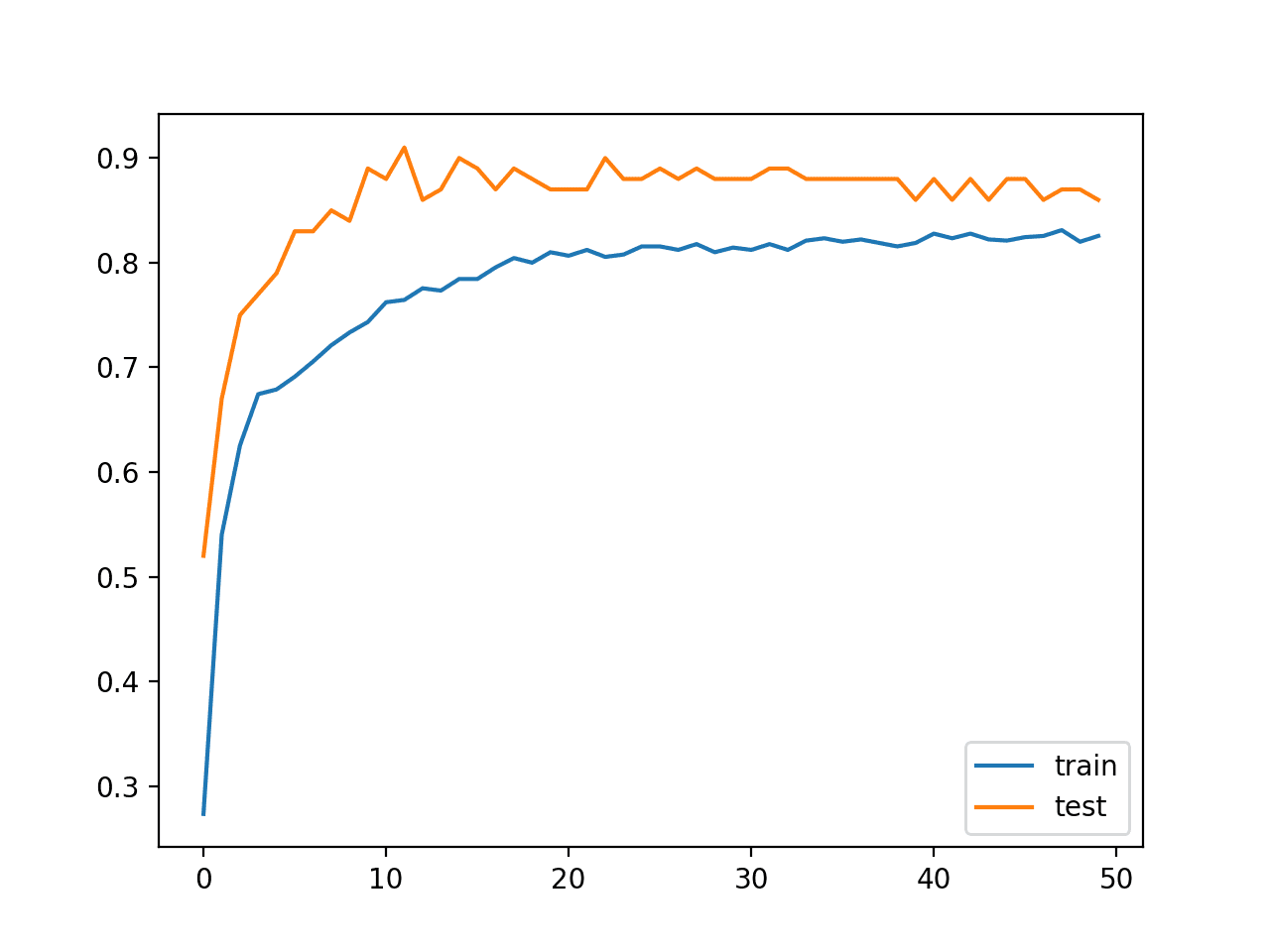
每个训练周期模型在训练和测试数据集上的准确率学习曲线图
随机分割集成
模型的不稳定性以及测试数据集的小规模意味着我们无法真正了解该模型在一般新数据上的表现如何。
我们可以尝试一种简单的重采样方法,即重复生成新的训练集和测试集随机分割,并拟合新模型。计算模型在每次分割中的平均性能将更好地估计模型的泛化误差。
然后我们可以将多个在随机分割上训练的模型结合起来,期望集成的性能可能比平均单个模型更稳定、更好。
我们将从问题域中生成 10 倍多的样本点,并将它们作为未见数据集保留。在此更大的数据集上评估模型将用作该问题模型泛化误差的代理或更准确的估计。
这个额外的数据集不是测试数据集。从技术上讲,它是为了本演示的目的,但我们假装在模型训练时无法获得这些数据。
|
1 2 3 4 |
# 生成二维分类数据集 dataX, datay = make_blobs(n_samples=55000, centers=3, n_features=2, cluster_std=2, random_state=2) X, newX = dataX[:5000, :], dataX[5000:, :] y, newy = datay[:5000], datay[5000:] |
所以现在我们有 5,000 个样本来训练我们的模型并估计其一般性能。我们还有 50,000 个样本可以用来更好地近似单个模型或集成的真实一般性能。
接下来,我们需要一个函数来拟合和评估训练数据集上的单个模型,并返回拟合模型在测试数据集上的性能。我们还需要已拟合的模型,以便我们可以将其用作集成的一部分。下面的 evaluate_model() 函数实现了这种行为。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 评估单个 mlp 模型 def evaluate_model(trainX, trainy, testX, testy): # 编码目标 trainy_enc = to_categorical(trainy) testy_enc = to_categorical(testy) # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 model.fit(trainX, trainy_enc, epochs=50, verbose=0) # 评估模型 _, test_acc = model.evaluate(testX, testy_enc, verbose=0) return model, test_acc |
接下来,我们可以创建训练数据集的随机分割,并在每个分割上拟合和评估模型。
我们可以使用 scikit-learn 库中的 train_test_split() 函数将数据集随机分割为训练集和测试集。它以 X 和 y 数组作为参数,“test_size”指定测试数据集的大小百分比。我们将使用 5,000 个样本的 10% 作为测试集。
然后我们可以调用 evaluate_model() 来拟合和评估模型。返回的准确率和模型可以添加到列表中以供以后使用。
在此示例中,我们将分割次数(以及拟合模型的数量)限制为 10 次。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 多次训练-测试分割 n_splits = 10 scores, members = list(), list() for _ in range(n_splits): # 分割数据 trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.10) # 评估模型 model, test_acc = evaluate_model(trainX, trainy, testX, testy) print('>%.3f' % test_acc) scores.append(test_acc) members.append(model) |
在拟合和评估模型之后,我们可以估计给定模型在所选领域配置下的预期性能。
|
1 2 |
# 汇总预期性能 print('Estimated Accuracy %.3f (%.3f)' % (mean(scores), std(scores))) |
我们不知道集合中有多少模型会有用。很可能存在一个收益递减点,在此之后,增加更多成员不再改变集合的性能。
尽管如此,我们可以评估从 1 到 10 种不同集合大小,并绘制它们在未见保留数据集上的性能。
我们还可以评估保留数据集上的每个模型,并计算这些分数的平均值,以更好地近似所选模型在预测问题上的真实性能。
|
1 2 3 4 5 6 7 8 9 |
# 在保留集上评估不同数量的集成 single_scores, ensemble_scores = list(), list() for i in range(1, n_splits+1): ensemble_score = evaluate_n_members(members, i, newX, newy) newy_enc = to_categorical(newy) _, single_score = members[i-1].evaluate(newX, newy_enc, verbose=0) print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score)) ensemble_scores.append(ensemble_score) single_scores.append(single_score) |
最后,我们可以比较并计算平均模型在预测问题上的一般性能的更稳健估计,然后将集成大小与保留数据集上的准确率绘制成图。
|
1 2 3 4 5 6 |
# 绘制分数与集成成员数量的关系 print('Accuracy %.3f (%.3f)' % (mean(single_scores), std(single_scores))) x_axis = [i for i in range(1, n_splits+1)] pyplot.plot(x_axis, single_scores, marker='o', linestyle='None') pyplot.plot(x_axis, ensemble_scores, marker='o') pyplot.show() |
将所有这些联系在一起,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |
# 在 blob 数据集上进行随机分割 mlp 集成 from sklearn.datasets import make_blobs from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense from matplotlib import pyplot from numpy import mean from numpy import std import numpy from numpy import array from numpy import argmax # 评估单个 mlp 模型 def evaluate_model(trainX, trainy, testX, testy): # 编码目标 trainy_enc = to_categorical(trainy) testy_enc = to_categorical(testy) # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 model.fit(trainX, trainy_enc, epochs=50, verbose=0) # 评估模型 _, test_acc = model.evaluate(testX, testy_enc, verbose=0) return model, test_acc # 为多类分类进行集成预测 def ensemble_predictions(members, testX): # 进行预测 yhats = [model.predict(testX) for model in members] yhats = array(yhats) # 跨集成成员求和 summed = numpy.sum(yhats, axis=0) # 跨类求 argmax result = argmax(summed, axis=1) return result # 评估集成中的特定数量成员 def evaluate_n_members(members, n_members, testX, testy): # 选择成员子集 subset = members[:n_members] # 进行预测 yhat = ensemble_predictions(subset, testX) # 计算准确率 return accuracy_score(testy, yhat) # 生成二维分类数据集 dataX, datay = make_blobs(n_samples=55000, centers=3, n_features=2, cluster_std=2, random_state=2) X, newX = dataX[:5000, :], dataX[5000:, :] y, newy = datay[:5000], datay[5000:] # 多次训练-测试分割 n_splits = 10 scores, members = list(), list() for _ in range(n_splits): # 分割数据 trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.10) # 评估模型 model, test_acc = evaluate_model(trainX, trainy, testX, testy) print('>%.3f' % test_acc) scores.append(test_acc) members.append(model) # 汇总预期性能 print('Estimated Accuracy %.3f (%.3f)' % (mean(scores), std(scores))) # 在保留集上评估不同数量的集成 single_scores, ensemble_scores = list(), list() for i in range(1, n_splits+1): ensemble_score = evaluate_n_members(members, i, newX, newy) newy_enc = to_categorical(newy) _, single_score = members[i-1].evaluate(newX, newy_enc, verbose=0) print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score)) ensemble_scores.append(ensemble_score) single_scores.append(single_score) # 绘制分数与集成成员数量的关系 print('Accuracy %.3f (%.3f)' % (mean(single_scores), std(single_scores))) x_axis = [i for i in range(1, n_splits+1)] pyplot.plot(x_axis, single_scores, marker='o', linestyle='None') pyplot.plot(x_axis, ensemble_scores, marker='o') pyplot.show() |
运行示例首先在数据集的 10 个不同随机分割(训练集和测试集)上拟合和评估 10 个模型。
根据这些分数,我们估计在数据集上拟合的平均模型将达到约 83% 的准确率,标准差约为 1.9%。
|
1 2 3 4 5 6 7 8 9 10 11 |
>0.816 >0.836 >0.818 >0.806 >0.814 >0.824 >0.830 >0.848 >0.868 >0.858 估计准确率 0.832 (0.019) |
然后,我们在未见数据集上评估每个模型的性能,以及从 1 到 10 个模型的集成性能。
注意:由于算法或评估过程的随机性,或者数值精度差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
从这些分数可以看出,对该问题平均模型性能的更准确估计约为 82%,并且估计性能是乐观的。
|
1 2 3 4 5 6 7 8 9 10 11 |
> 1: 单个=0.821,集成=0.821 > 2: 单个=0.821,集成=0.820 > 3: 单个=0.820,集成=0.820 > 4: 单个=0.820,集成=0.821 > 5: 单个=0.821,集成=0.821 > 6: 单个=0.820,集成=0.821 > 7: 单个=0.820,集成=0.821 > 8: 单个=0.820,集成=0.821 > 9: 单个=0.820,集成=0.820 > 10: 单个=0.820,集成=0.821 准确率 0.820 (0.000) |
准确率分数之间的许多差异都发生在百分之几的小数位上。
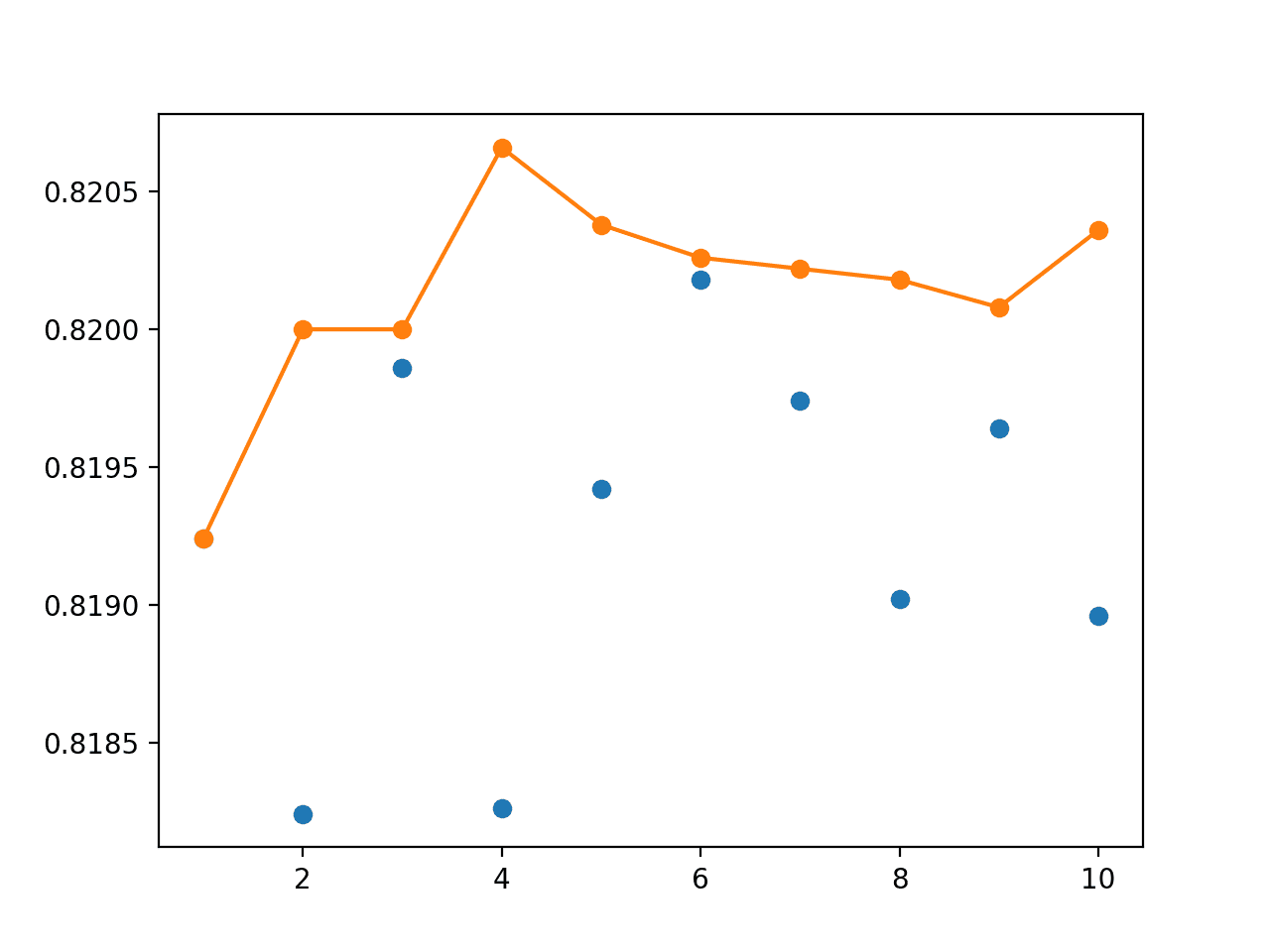
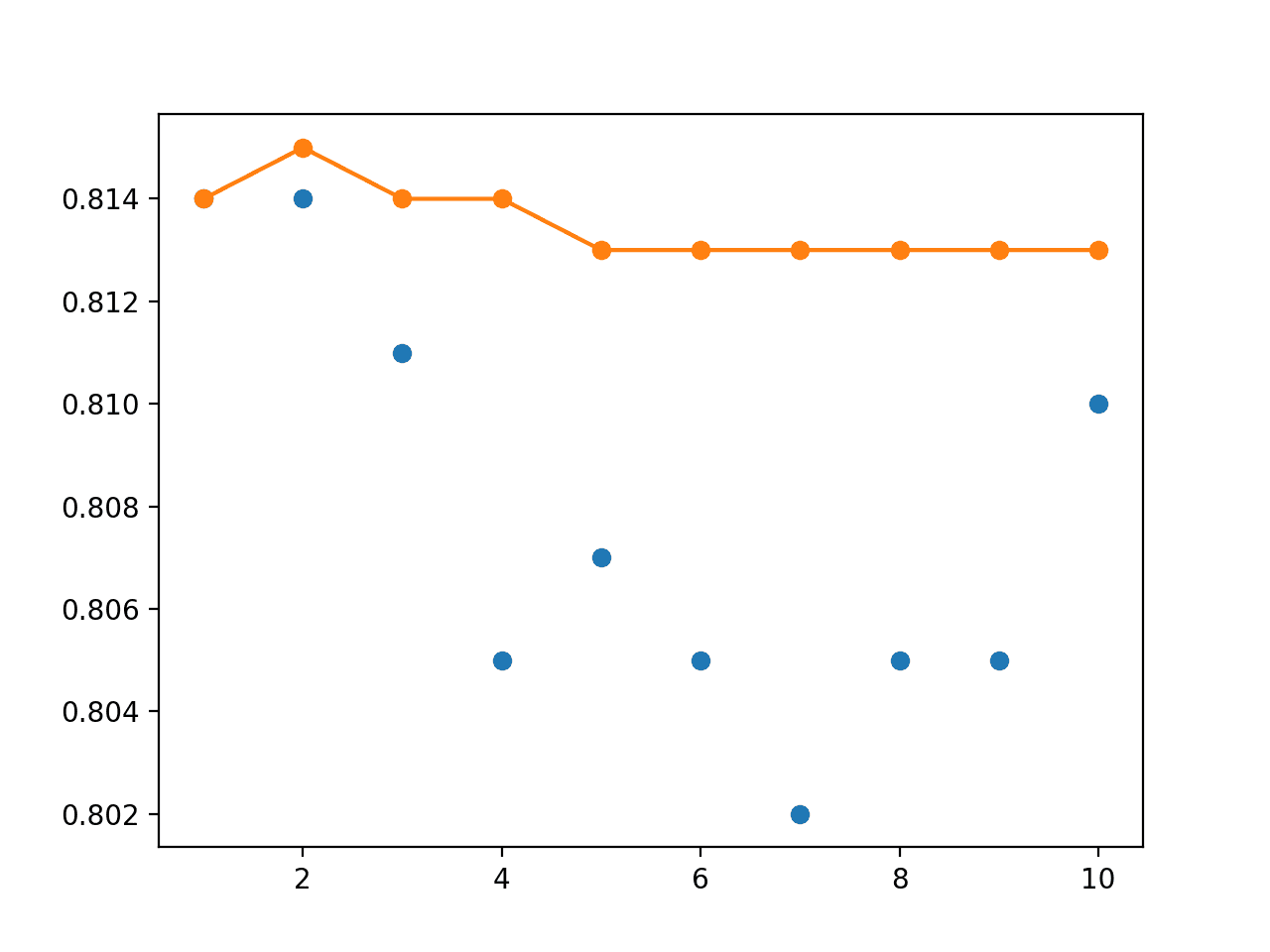
生成了一个图表,显示了每个单个模型在未见保留数据集上的准确率(蓝色点)以及具有给定数量成员(1-10 个)的集成的性能(橙色线和点)。
我们可以看到,至少在这种情况下,使用 4 到 8 个成员的集成可以获得比大多数单个运行更好的准确率(橙色线在许多蓝色点上方)。
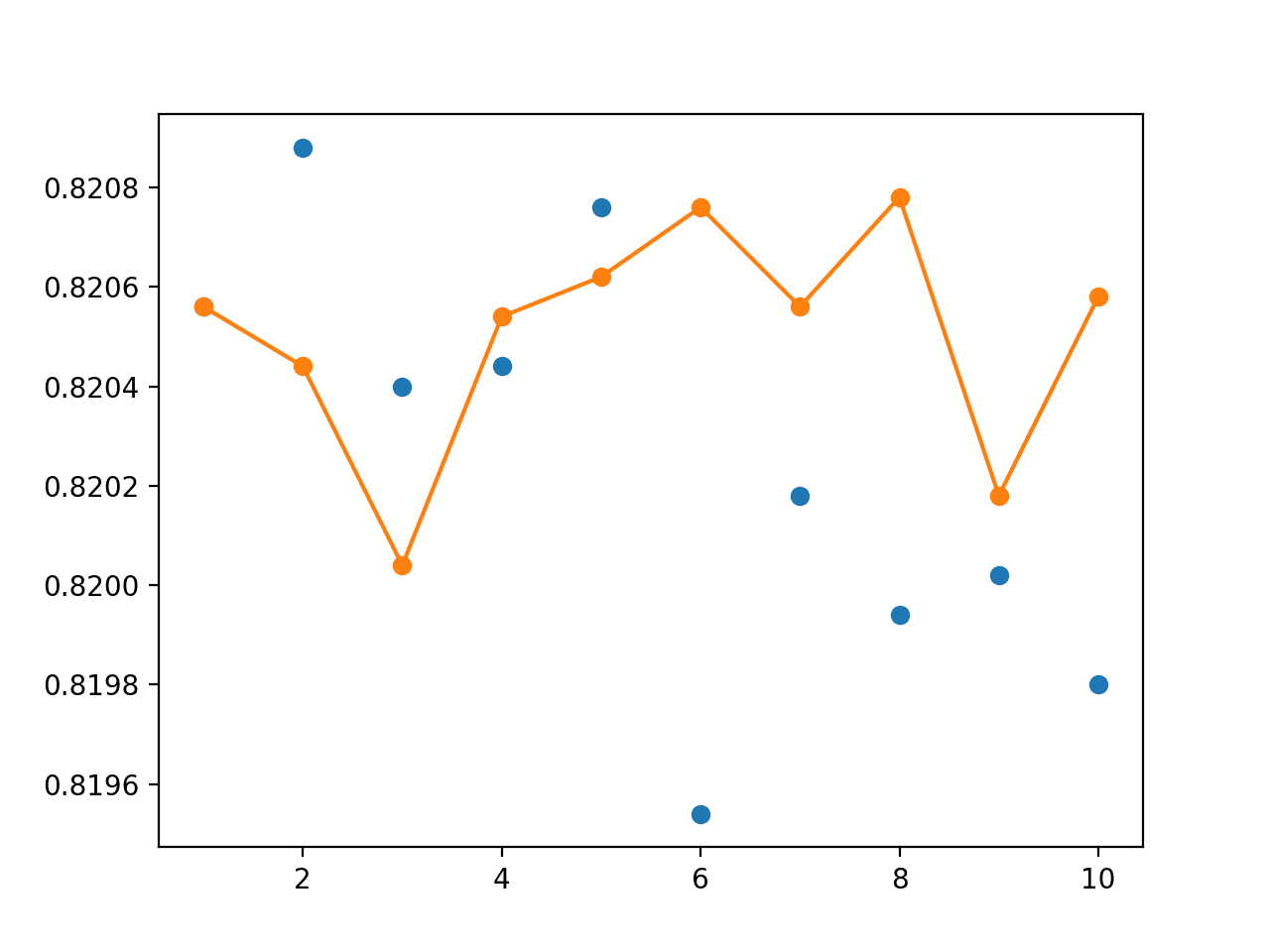
随机分割重采样中单个模型准确率(蓝点)与不同大小集成准确率的折线图
该图确实显示,一些单个模型可以比集成模型表现更好(蓝色点在橙色线上方),但我们无法选择这些模型。在这里,我们证明,在没有额外数据(例如样本外数据集)的情况下,由 4 到 8 个成员组成的集成将比随机选择的训练-测试模型平均表现更好。
更多的重复(例如 30 次或 100 次)可能会导致更稳定的集成性能。
交叉验证集成
重复随机分割作为估计模型平均性能的重采样方法存在一个问题,那就是它过于乐观。
一种旨在减少乐观偏差并因此被广泛使用的方法是k 折交叉验证法。
该方法偏差较小,因为数据集中每个样本仅在测试数据集中使用一次来估计模型性能,这与随机训练-测试分割不同,后者中给定样本可能会被多次用于评估模型。
该过程有一个名为 k 的单个参数,它指的是给定数据样本要分割成的组数。每个模型分数的平均值提供了对模型性能的偏差较小的估计。k 的典型值为 10。
由于神经网络模型的训练计算成本非常高,因此通常将交叉验证期间表现最好的模型用作最终模型。
或者,可以将交叉验证过程产生的模型结合起来,形成一个交叉验证集成,该集成在平均性能上可能优于任何单个模型。
我们可以使用 scikit-learn 中的 KFold 类将数据集分割成 k 折。它接受分割数量、是否打乱样本以及用于打乱前的伪随机数生成器种子作为参数。
|
1 2 3 |
# 准备 k 折交叉验证配置 n_folds = 10 kfold = KFold(n_folds, True, 1) |
一旦实例化该类,就可以对其进行枚举,以获取训练集和测试集的数据集的每个索引分割。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 交叉验证性能估计 scores, members = list(), list() for train_ix, test_ix in kfold.split(X): # 选择样本 trainX, trainy = X[train_ix], y[train_ix] testX, testy = X[test_ix], y[test_ix] # 评估模型 model, test_acc = evaluate_model(trainX, trainy, testX, testy) print('>%.3f' % test_acc) scores.append(test_acc) members.append(model) |
一旦在每个折叠上计算出分数,分数的平均值就可以用来报告该方法的预期性能。
|
1 2 |
# 汇总预期性能 print('Estimated Accuracy %.3f (%.3f)' % (mean(scores), std(scores))) |
现在我们已经收集了在 10 个折叠上评估的 10 个模型,我们可以使用它们来创建交叉验证集成。直观上似乎应该在集成中使用所有 10 个模型,但是,我们可以像上一节一样,评估从 1 到 10 个成员的每个集成子集的准确率。
下面列出了分析交叉验证集成的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
# blobs 数据集上的交叉验证 mlp 集成 from sklearn.datasets import make_blobs from sklearn.model_selection import KFold from sklearn.metrics import accuracy_score from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense from matplotlib import pyplot from numpy import mean from numpy import std import numpy from numpy import array from numpy import argmax # 评估单个 mlp 模型 def evaluate_model(trainX, trainy, testX, testy): # 编码目标 trainy_enc = to_categorical(trainy) testy_enc = to_categorical(testy) # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 model.fit(trainX, trainy_enc, epochs=50, verbose=0) # 评估模型 _, test_acc = model.evaluate(testX, testy_enc, verbose=0) return model, test_acc # 为多类分类进行集成预测 def ensemble_predictions(members, testX): # 进行预测 yhats = [model.predict(testX) for model in members] yhats = array(yhats) # 跨集成成员求和 summed = numpy.sum(yhats, axis=0) # 跨类求 argmax result = argmax(summed, axis=1) return result # 评估集成中的特定数量成员 def evaluate_n_members(members, n_members, testX, testy): # 选择成员子集 subset = members[:n_members] # 进行预测 yhat = ensemble_predictions(subset, testX) # 计算准确率 return accuracy_score(testy, yhat) # 生成二维分类数据集 dataX, datay = make_blobs(n_samples=55000, centers=3, n_features=2, cluster_std=2, random_state=2) X, newX = dataX[:5000, :], dataX[5000:, :] y, newy = datay[:5000], datay[5000:] # 准备 k 折交叉验证配置 n_folds = 10 kfold = KFold(n_folds, True, 1) # 交叉验证性能估计 scores, members = list(), list() for train_ix, test_ix in kfold.split(X): # 选择样本 trainX, trainy = X[train_ix], y[train_ix] testX, testy = X[test_ix], y[test_ix] # 评估模型 model, test_acc = evaluate_model(trainX, trainy, testX, testy) print('>%.3f' % test_acc) scores.append(test_acc) members.append(model) # 汇总预期性能 print('Estimated Accuracy %.3f (%.3f)' % (mean(scores), std(scores))) # 在保留集上评估不同数量的集成 single_scores, ensemble_scores = list(), list() for i in range(1, n_folds+1): ensemble_score = evaluate_n_members(members, i, newX, newy) newy_enc = to_categorical(newy) _, single_score = members[i-1].evaluate(newX, newy_enc, verbose=0) print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score)) ensemble_scores.append(ensemble_score) single_scores.append(single_score) # 绘制分数与集成成员数量的关系 print('Accuracy %.3f (%.3f)' % (mean(single_scores), std(single_scores))) x_axis = [i for i in range(1, n_folds+1)] pyplot.plot(x_axis, single_scores, marker='o', linestyle='None') pyplot.plot(x_axis, ensemble_scores, marker='o') pyplot.show() |
运行示例首先打印每个 10 个模型在交叉验证的每个折叠上的性能。
注意:由于算法或评估过程的随机性,或者数值精度差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
这些模型的平均性能约为 82%,这似乎比上一节中使用的随机分割方法不那么乐观。
|
1 2 3 4 5 6 7 8 9 10 11 |
>0.834 >0.870 >0.818 >0.806 >0.836 >0.804 >0.820 >0.830 >0.828 >0.822 估计准确率 0.827 (0.018) |
接下来,对未见保留集上的每个保存模型进行评估。
这些分数的平均值也约为 82%,这突出表明,至少在这种情况下,模型泛化性能的交叉验证估计是合理的。
|
1 2 3 4 5 6 7 8 9 10 11 |
> 1: 单个=0.819,集成=0.819 > 2: 单个=0.820,集成=0.820 > 3: 单个=0.820,集成=0.820 > 4: 单个=0.821,集成=0.821 > 5: 单个=0.820,集成=0.821 > 6: 单个=0.821,集成=0.821 > 7: 单个=0.820,集成=0.820 > 8: 单个=0.819,集成=0.821 > 9: 单个=0.820,集成=0.821 > 10: 单个=0.820,集成=0.821 准确率 0.820 (0.001) |
创建了单个模型准确率(蓝点)和集成大小与准确率(橙线)的折线图。
与前面的示例一样,模型性能之间的实际差异在于模型准确率的百分比分数。
橙色线显示,随着成员数量的增加,集成的准确率会增加到收益递减点。
我们可以看到,至少在这种情况下,在集成中使用四个或更多在交叉验证期间拟合的模型,其性能优于几乎所有单个模型。
我们还可以看到,在集成中使用所有模型的默认策略将是有效的。
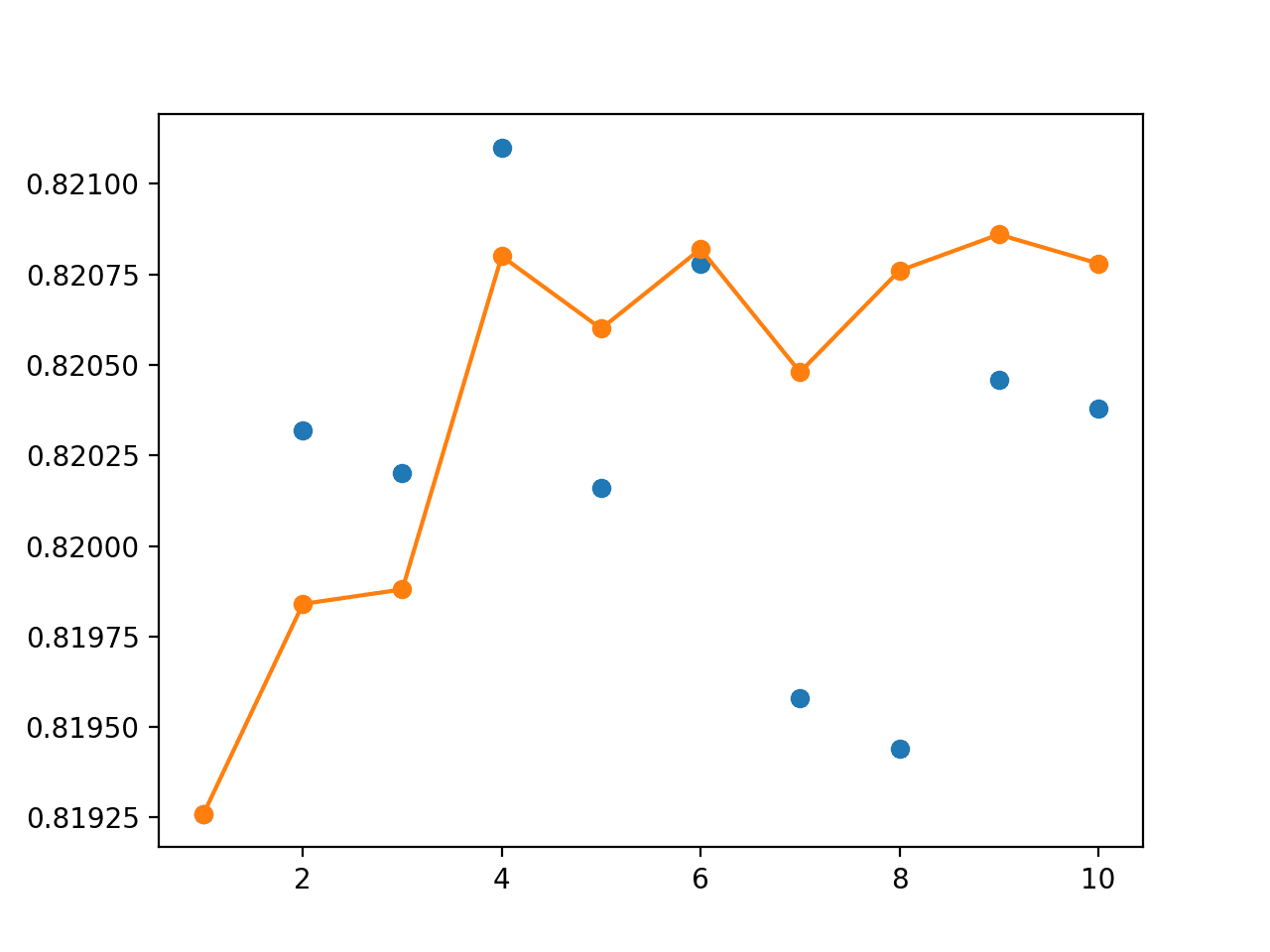
交叉验证重采样中单个模型准确率(蓝点)与不同大小集成准确率的折线图
Bagging 集成
从集成学习的角度来看,随机分割和 k 折交叉验证的局限性在于模型非常相似。
自举法是一种统计技术,通过对多个小数据样本的估计值进行平均来估计总体数量。
重要的是,样本是通过一次从大数据样本中抽取观察值并将其选择后返回到数据样本中来构建的。这允许给定观察值在一个给定的小样本中多次包含。这种抽样方法称为带替换抽样。
该方法可用于估计神经网络模型的性能。未在给定样本中选择的示例可用作测试集以估计模型的性能。
自举法是估计模型性能的稳健方法。它确实受到乐观偏差的一些影响,但在实践中通常与 k 折交叉验证几乎一样准确。
对于集成学习的好处是,每个模型都存在偏差,允许给定样本在样本中多次出现。这反过来意味着在这些样本上训练的模型将是偏差的,重要的是以不同的方式。结果可以是更准确的集成预测。
通常,在集成学习中使用自举法被称为自举聚合或 Bagging。
我们可以使用 scikit-learn 中的 resample() 函数进行带替换的子样本选择。该函数接受一个数组进行子样本选择和重采样大小作为参数。我们将在行索引中执行选择,然后我们可以使用这些行索引在 X 和 y 数组中选择行。
样本大小将为 4,500,即数据的 90%,尽管由于使用了重采样,测试集可能大于 10%,因为超过 500 个样本可能未被选中。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 多次训练-测试分割 n_splits = 10 scores, members = list(), list() for _ in range(n_splits): # 选择索引 ix = [i for i in range(len(X))] train_ix = resample(ix, replace=True, n_samples=4500) test_ix = [x for x in ix if x not in train_ix] # 选择数据 trainX, trainy = X[train_ix], y[train_ix] testX, testy = X[test_ix], y[test_ix] # 评估模型 model, test_acc = evaluate_model(trainX, trainy, testX, testy) print('>%.3f' % test_acc) scores.append(test_acc) members.append(model) |
在使用 Bagging 集成学习策略时,通常会使用简单的过拟合模型,如未剪枝的决策树。
过约束和过拟合的神经网络可能会带来更好的性能。尽管如此,在此示例中我们仍将使用与前几节相同的 MLP。
此外,通常在 Bagging 中会持续添加集成成员,直到集成的性能趋于稳定,因为 Bagging 不会使数据集过拟合。与之前的示例一样,我们再次将成员数量限制为 10。
下面列出了使用多层感知器估计模型性能和集成学习的自举聚合的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 |
# blobs 数据集上的 bagging mlp 集成 from sklearn.datasets import make_blobs from sklearn.utils import resample from sklearn.metrics import accuracy_score from keras.utils import to_categorical from keras.models import Sequential from keras.layers import Dense from matplotlib import pyplot from numpy import mean from numpy import std import numpy from numpy import array from numpy import argmax # 评估单个 mlp 模型 def evaluate_model(trainX, trainy, testX, testy): # 编码目标 trainy_enc = to_categorical(trainy) testy_enc = to_categorical(testy) # 定义模型 model = Sequential() model.add(Dense(50, input_dim=2, activation='relu')) model.add(Dense(3, activation='softmax')) model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']) # 拟合模型 model.fit(trainX, trainy_enc, epochs=50, verbose=0) # 评估模型 _, test_acc = model.evaluate(testX, testy_enc, verbose=0) return model, test_acc # 为多类分类进行集成预测 def ensemble_predictions(members, testX): # 进行预测 yhats = [model.predict(testX) for model in members] yhats = array(yhats) # 跨集成成员求和 summed = numpy.sum(yhats, axis=0) # 跨类求 argmax result = argmax(summed, axis=1) return result # 评估集成中的特定数量成员 def evaluate_n_members(members, n_members, testX, testy): # 选择成员子集 subset = members[:n_members] # 进行预测 yhat = ensemble_predictions(subset, testX) # 计算准确率 return accuracy_score(testy, yhat) # 生成二维分类数据集 dataX, datay = make_blobs(n_samples=55000, centers=3, n_features=2, cluster_std=2, random_state=2) X, newX = dataX[:5000, :], dataX[5000:, :] y, newy = datay[:5000], datay[5000:] # 多次训练-测试分割 n_splits = 10 scores, members = list(), list() for _ in range(n_splits): # 选择索引 ix = [i for i in range(len(X))] train_ix = resample(ix, replace=True, n_samples=4500) test_ix = [x for x in ix if x not in train_ix] # 选择数据 trainX, trainy = X[train_ix], y[train_ix] testX, testy = X[test_ix], y[test_ix] # 评估模型 model, test_acc = evaluate_model(trainX, trainy, testX, testy) print('>%.3f' % test_acc) scores.append(test_acc) members.append(model) # 汇总预期性能 print('Estimated Accuracy %.3f (%.3f)' % (mean(scores), std(scores))) # 在保留集上评估不同数量的集成 single_scores, ensemble_scores = list(), list() for i in range(1, n_splits+1): ensemble_score = evaluate_n_members(members, i, newX, newy) newy_enc = to_categorical(newy) _, single_score = members[i-1].evaluate(newX, newy_enc, verbose=0) print('> %d: single=%.3f, ensemble=%.3f' % (i, single_score, ensemble_score)) ensemble_scores.append(ensemble_score) single_scores.append(single_score) # 绘制分数与集成成员数量的关系 print('Accuracy %.3f (%.3f)' % (mean(single_scores), std(single_scores))) x_axis = [i for i in range(1, n_splits+1)] pyplot.plot(x_axis, single_scores, marker='o', linestyle='None') pyplot.plot(x_axis, ensemble_scores, marker='o') pyplot.show() |
运行示例将打印每个自举样本中未使用样本的模型性能。
注意:由于算法或评估过程的随机性,或者数值精度差异,您的结果可能会有所不同。考虑多次运行示例并比较平均结果。
我们可以看到,在这种情况下,模型的预期性能不如随机训练-测试分割乐观,并且可能与 k 折交叉验证的结果非常相似。
|
1 2 3 4 5 6 7 8 9 10 11 |
>0.829 >0.820 >0.830 >0.821 >0.831 >0.820 >0.834 >0.815 >0.829 >0.827 估计准确率 0.825 (0.006) |
也许是由于自举抽样过程,我们看到每个模型在更大的未见保留数据集上的实际性能略差。
考虑到自举法带替换抽样引入的偏差,这是意料之中的。
|
1 2 3 4 5 6 7 8 9 10 11 |
> 1: 单个=0.819,集成=0.819 > 2: 单个=0.818,集成=0.820 > 3: 单个=0.820,集成=0.820 > 4: 单个=0.818,集成=0.821 > 5: 单个=0.819,集成=0.820 > 6: 单个=0.820,集成=0.820 > 7: 单个=0.820,集成=0.820 > 8: 单个=0.819,集成=0.820 > 9: 单个=0.820,集成=0.820 > 10: 单个=0.819,集成=0.820 准确率 0.819 (0.001) |
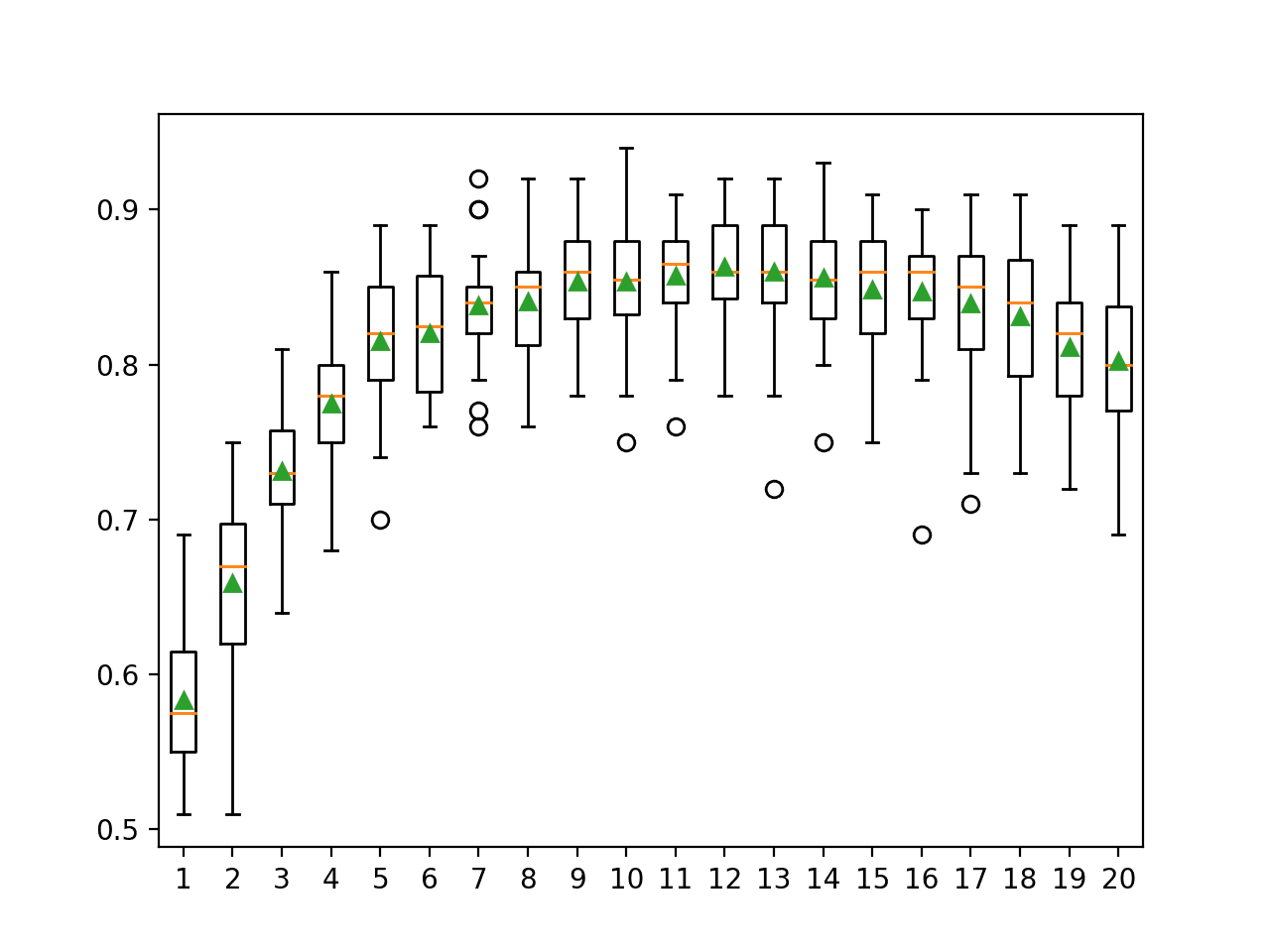
创建的折线图令人鼓舞。
我们看到,在约四个成员之后,bagging 集成在保留数据集上取得了比任何单个模型更好的性能。毫无疑问,这是因为单个模型的平均性能略低。
Bagging 中单个模型准确率(蓝点)与不同大小集成准确率的折线图
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 单个模型。将每个集成的性能与在所有可用数据上训练的一个模型进行比较。
- CV 集成大小。尝试交叉验证集成的更大和更小集成大小,并比较它们的性能。
- Bagging 集成限制。增加 Bagging 集成中的成员数量,以找到收益递减点。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
论文
- 神经网络集成、交叉验证和主动学习, 1995.
API
- Keras 顺序模型入门
- Keras核心层API
- scipy.stats.mode API
- numpy.argmax API
- sklearn.datasets.make_blobs API
- sklearn.model_selection.train_test_split API
- sklearn.model_selection.KFold API
- sklearn.utils.resample API
总结
在本教程中,您学习了如何为深度学习神经网络模型开发一套不同的基于重采样的集成。
具体来说,你学到了:
- 如何使用随机分割估计模型性能并从模型中开发集成。
- 如何使用 10 折交叉验证估计性能并开发交叉验证集成。
- 如何使用自举法估计性能并使用 Bagging 集成组合模型。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



尊敬的先生,非常感谢您的教程。它们对我有很大帮助,我尊重您的工作。关于上述教程的一个问题:是否可以使用上述集成方法与 CNN、RNN 而不是 MLP。谢谢
是的!
嗨
以下这句话中的“乐观”是什么意思?
“重复随机分割作为估计模型平均性能的重采样方法存在一个问题,那就是它过于乐观。”
谢谢
我建议模型性能的估计将是乐观的——例如,它将存在偏差,因为相同的样本将在重复分割中多次出现在测试集中。
请您更具体一些,我还是不明白您的意思。
同一个样本出现在测试集中,这可能好也可能坏,这取决于模型对测试集中给定特定样本的训练效果。所以,我的理解是,根据训练模型对给定具体测试样本的预测效果,人们可以既说乐观也可以说悲观。
谢谢
样本在不同分割中的重复使用(例如,相同数据出现在训练集或测试集中)将意味着模型以及准确率分数将存在偏差——一种不切实际的评估——与衡量性能所需的相似度过高或独立性不足。
这有帮助吗?
是的!
谢谢
你好 Jason。我是这个领域的新手(请原谅我的问题,如果它没有意义)。
考虑到我们有大量数据集,我们是否可以重复随机分割作为重采样方法,通过排除已经评估过的先前样本数据来估计平均性能?
你可以这样做,但普遍认为平均结果将存在偏差且过于乐观。
也许可以尝试 10 折交叉验证,它已被证明偏差较小。
谢谢 Jason。
我尝试了两种 Bagging 集成。我很好奇为什么所有成员的集成结果都是一致的。请看下面的打印输出。
>0.732
>0.803
>0.773
>0.763
>0.662
>0.755
>0.725
>0.758
>0.673
>0.774
估计准确率 0.742 (0.043)
> 1: 单个=0.824,集成=0.801
> 2: 单个=0.830,集成=0.801
> 3: 单个=0.784,集成=0.801
> 4: 单个=0.761,集成=0.801
> 5: 单个=0.784,集成=0.801
> 6: 单个=0.841,集成=0.801
> 7: 单个=0.801,集成=0.801
> 8: 单个=0.773,集成=0.801
> 9: 单个=0.807,集成=0.801
> 10: 单个=0.830,集成=0.801
干得好!
也许在您的运行中,结合模型并没有在小数点后三位提高性能。您可以尝试再次运行该示例。
嗨 Jason
我读过您的文档,写得非常好,但 ensemble_predictions 函数是如何工作的,以及为什么我们在此函数中求和并选择最大值?
该函数通过对集成中的每个模型进行概率预测,然后对预测概率求和,并选择总和值最大的结果来工作。
这有帮助吗?
Jason 您好
为什么我们不用均值代替和或最大值呢?
如果你愿意,可以使用平均值,试试看。
随机森林之所以强大,是因为它默认也为每棵树选择特征子集(通常子集中特征的数量等于总特征数量的平方根)。
此实现随机采样行,但未对每个“成员”的特征进行采样。这个缺陷可能值得解决;特征的随机子集化有助于避免特定特征的过拟合,并提供额外的性能提升。
无论如何,这是一个很棒的神经网络集成示例!
是的,这就是 Bagging 和随机森林的区别。
如果你想尝试随机森林的特征采样方法,你可以使用帖子中的示例作为起点。这应该是一个有趣的扩展。
感谢您的文章。我将 Bagging 代码用于我的数据集,它有点小。我得到了以下结果:
>0.265
>0.400
>0.457
>0.317
>0.424
>0.364
>0.270
>0.333
>0.471
>0.500
估计准确率 0.380 (0.079)
> 1: 单个=0.452,集成=0.452
> 2: 单个=0.417,集成=0.476
> 3: 单个=0.440,集成=0.452
> 4: 单个=0.393,集成=0.440
> 5: 单个=0.369,集成=0.440
> 6: 单个=0.452,集成=0.452
> 7: 单个=0.405,集成=0.464
> 8: 单个=0.393,集成=0.476
> 9: 单个=0.381,集成=0.452
> 10: 单个=0.476,集成=0.452
准确率 0.418 (0.034)
单个模型的准确率差异很大,我尝试了“n_splits”的不同值,但没有改变。这是我能得到的最好结果吗?这有什么意义吗?
有趣的结果,准确率非常低。
或许可以尝试多运行几次这个例子?
或许可以确认你的库是否是最新版本?
或许可以确认你是否完全复制了代码?
感谢您的发帖。请问为什么单一预测会优于集成预测?
LSTM集成预测
MAE:2.445500
MSE:5.984324
RMSE:2.446288
LSTM单一预测
MAE:0.087766
MSE:0.009079
RMSE:0.095284
另外
GRU集成预测
MAE:2.406450
MSE:5.791212
RMSE:2.406494
GRU单一预测
MAE:0.029207
MSE:0.001075
RMSE:0.032787
谢谢你
我们在这里展示的是装袋法,而不是试图以最优方式解决这个合成问题。
为你的特定数据集选择表现最好的方法。
感谢您的回复,不胜感激。
嗨,Jason,
在“随机分割集成”部分的末尾,您写道:“图表确实显示,一些单个模型可以比模型集成(橙色线上方的蓝色点)表现得更好,但我们无法选择这些模型。”
我想知道为什么我们不能选择这些模型,是因为这些模型在未见过的数据(除了这个特定的保留测试数据)上泛化效果不好吗?
谢谢!
我认为这个评论的意思是,我们选择模型是随机选择一个蓝点,而不是有意为之。我们无法选择一个“好”模型,因为我们不知道它好——当我们拟合一个单一模型时,我们没有参考点。
嗨 Jason
我有一个关于装袋法(可能是一个愚蠢的问题)的问题。假设我有一个分类问题,样本不平衡,是否可以使用装袋法作为重采样方法,使每个创建的模型都包含一个平衡的样本?是否可以通过装袋法解决不平衡分类问题?或者在这种情况下,使用分层k折交叉验证真的更好吗?
我没有明白在使用装袋法时,从初始集合创建的子集是随机的还是非随机的。
感谢您在这里的杰出工作,对我帮助很大!
是的,但你需要丢弃样本才能得到你的“平衡”样本。
其他方法可能更简单
https://machinelearning.org.cn/data-sampling-methods-for-imbalanced-classification/
所以,使用装袋法我必须丢弃初始集中的样本,是这样吗?
谢谢你,Jason。
为了达到所需的类别平衡——是的。
我们可以将装袋法和交叉验证结合起来使用吗?
谢谢你
当然,交叉验证评估的是装袋模型。
先生,在最优模型中,训练准确率应该更高还是测试准确率更高?
理想情况下,你希望训练和测试准确率相似。
如何获取此装袋集成深度学习模型的AUC图?
这会有帮助
https://machinelearning.org.cn/roc-curves-and-precision-recall-curves-for-classification-in-python/
布朗利博士您好,
我有一个关于使用二元分类器进行此操作的问题?如果所讨论的数据是二元分类任务,并且我们的神经网络使用一个带Sigmoid激活函数的单个密集神经元作为神经网络的输出,那么上面的“ensemble_predictions”预测方法会像现在一样工作吗?也就是说,它会以以下方式运行吗?
1). 我们将获得集成中每个模型的预测(每个模型一个浮点数)
2). 我们将每个数据点预测的所有模型的预测值相加
3). 由于我们正在进行二元分类,那么如果总和预测 > 0.5,我们分配类别标签0,如果总和预测 < 0.5,我们分配类别标签0?
这听起来正确吗?
非常感谢!
祝好,
Matt
所以方法会是这样的吗?
def evaluate_N_models(N, models, x_test, y_test)
sub_models = models[:N]
print(‘Len submodels: ‘, len(sub_models))
Y_vals = []
for model in sub_models
Y_vals.append(model.predict(x_test))
Y_vals = np.array(Y_vals)
print(‘yvals shape’, Y_vals.shape)
summed = np.sum(Y_vals, axis = 0)
print(‘summed shape’, np.array(summed).shape)
result = round_array(summed)
不,最简单的集成方法是计算子模型预测的众数(最常见的预测)。
谢谢。你在这篇文章里做的是软投票多数表决吗?如果你的子模型使用 sigmoid 输出激活函数,并且你有一个二元分类任务,为什么不能做同样的事情呢?
请看这个例子
https://machinelearning.org.cn/model-averaging-ensemble-for-deep-learning-neural-networks/
嗨 Jason
非常感谢这篇文章。
我有个问题
如果我理解正确,在集成学习中,我们取每个模型概率的平均值。
我不清楚为什么我们在以下函数中对值求和,
# 为多类分类进行集成预测
def ensemble_predictions(members, testX)
# 进行预测
yhats = [model.predict(testX) for model in members]
yhats = array(yhats)
# 对集成成员求和
summed = numpy.sum(yhats, axis=0)
# 对类别求argmax
result = argmax(summed, axis=1)
return result
请您帮忙解释一下。谢谢。
这叫做软投票,你可以在这里了解更多
https://machinelearning.org.cn/voting-ensembles-with-python/
非常感谢!
不客气。
嗨,Jason,这些例子对理解装袋法非常有帮助,但我在使用这些模型处理真实的未见过数据时遇到了一些困难。我的意思是,例如,在您的装袋解决方案中,我们看到在第4级时准确率最高。如果我没记错的话,如果我们使用前四个单一模型,我们就可以达到那个准确率,但是我们如何使用这四个模型来预测一些未见过的数据呢?
我们使用测试工具来估计未见过数据上的预期性能,例如交叉验证。
你好 Jason,关于神经网络使用 AdaBoost 方法如何?
如果你愿意,你可以。
我尝试将 LSTM 作为 AdaBoost 中的基学习器来实现,但在权重初始化方面感到困惑,您能指导我一下吗,或者您能推荐您的任何博客文章吗。谢谢。
这个教程是关于权重初始化的
https://machinelearning.org.cn/weight-initialization-for-deep-learning-neural-networks/
你好,先生
问候
非常感谢。我一直关注您的教程。我是这个领域的新手,我知道每当我遇到困难时,我都能在您的教程中找到解决方案。
先生,我正在研究斯坦福数据集,该数据集包含大约1.1万条评论用于情感分析。我尝试在此数据集上使用集成技术,看它是否能提高5个类别的准确率。在我尝试对我的数据集进行随机分割时,首先我尝试了不同的数据集划分。我得到了最佳的平均准确率(0.470),用于10次随机分割的4千条数据,但对于一般和其余的数据集,我得到了非常低的平均准确率(0.228)。
这是我尝试20次随机分割时的结果
>0.477
>0.455
>0.517
>0.468
>0.352
>0.482
>0.335
>0.430
>0.515
>0.368
>0.470
>0.430
>0.485
>0.500
>0.428
>0.472
>0.428
>0.450
>0.447
>0.428
估计准确率 0.447 (0.049)
> 1: 单一=0.193, 集成=0.193
> 2: 单一=0.217, 集成=0.203
> 3: 单一=0.196, 集成=0.202
> 4: 单一=0.219, 集成=0.204
> 5: 单一=0.132, 集成=0.196
> 6: 单一=0.182, 集成=0.192
> 7: 单一=0.104, 集成=0.184
> 8: 单一=0.221, 集成=0.190
> 9: 单一=0.167, 集成=0.187
> 10: 单一=0.219, 集成=0.187
> 11: 单一=0.169, 集成=0.186
> 12: 单一=0.270, 集成=0.194
> 13: 单一=0.223, 集成=0.197
> 14: 单一=0.193, 集成=0.197
> 15: 单一=0.209, 集成=0.197
> 16: 单一=0.181, 集成=0.195
> 17: 单一=0.204, 集成=0.195
> 18: 单一=0.214, 集成=0.194
> 19: 单一=0.225, 集成=0.196
> 20: 单一=0.245, 集成=0.199
请帮助我解释这些数据
谢谢
干得好。
或许可以尝试一系列数据准备方法、模型和模型配置,直到您发现最适合您的特定数据集的方法。
先生,我目前正在研究 adaboost-cnn 模型,我创建了一个模型,然后将该模型用作 adaboost 中的基本估计器,但我遇到了 KerasClassifier 不支持 sample_weight 的问题。先生,我该如何解决这个问题?您能指导我一下吗?
或许可以直接使用 Keras API。
先生,您能给我一个小的演示吗?
是的,博客上有很多使用keras API的例子,或许可以从这里开始
https://machinelearning.org.cn/start-here/#deeplearning
干得好!我非常喜欢这个!
谢谢Brad的反馈和支持!我们非常感谢!