Planet 数据集已成为标准的计算机视觉基准,涉及卫星图像的多标签分类或标记亚马逊热带雨林的内容。
该数据集是 Kaggle 网站上数据科学竞赛的基础,并且已经得到了有效的解决。尽管如此,它仍然可以作为学习和实践如何从零开始开发、评估和使用卷积深度学习神经网络进行图像分类的基础。
这包括如何开发一个强大的测试框架来估计模型的性能,如何探索模型的改进,以及如何保存模型并在以后加载它以对新数据进行预测。
在本教程中,您将了解如何开发一个卷积神经网络来分类亚马逊热带雨林的卫星照片。
完成本教程后,您将了解:
- 如何加载和准备亚马逊热带雨林的卫星照片以供建模。
- 如何从零开始开发卷积神经网络进行照片分类并提高模型性能。
- 如何开发最终模型并使用它对新数据进行临时预测。
使用我的新书《计算机视觉深度学习》来启动您的项目,其中包含分步教程和所有示例的Python 源代码文件。
让我们开始吧。
- 2019 年 9 月更新:更新了如何下载数据集的说明。
- 2019 年 10 月更新:更新了 Keras 2.3.0 和 TensorFlow 2.0.0。

如何开发卷积神经网络来分类亚马逊雨林的卫星照片
照片由 Anna & Michal 提供,部分权利保留。
教程概述
本教程分为七个部分,它们是:
- Planet 数据集简介
- 如何准备数据以供建模
- 模型评估指标
- 如何评估基线模型
- 如何提高模型性能
- 如何使用迁移学习
- 如何完成模型并进行预测
Planet 数据集简介
“Planet: Understanding the Amazon from Space”竞赛于 2017 年在 Kaggle 上举行。
比赛涉及对从巴西亚马逊雨林拍摄的卫星图像的小方块进行分类,根据 17 个类别进行分类,例如“农业”、“晴朗”和“水”。鉴于比赛的名称,该数据集通常被称为“Planet 数据集”。
彩色图像提供 TIFF 和 JPEG 格式,尺寸为 256×256 像素。训练数据集中提供了总共 40,779 张图像,测试集中提供了 40,669 张需要进行预测的图像。
该问题是多标签图像分类任务的一个示例,其中必须为每个标签预测一个或多个类标签。这与多类分类不同,在多类分类中,每张图像都从多个类别中分配一个类别。
训练数据集中为每张图像提供了多个类标签,并附带一个文件,将图像文件名映射到字符串类标签。
比赛大约进行了四个月(2017 年 4 月至 7 月),总共有 938 支队伍参加,围绕数据准备、数据增强和卷积神经网络的使用进行了大量讨论。
比赛由名为“bestfitting”的参赛者以 0.93398 的公共排行榜 F-beta 分数(在 66% 的测试数据集上)和 0.93317 的私有排行榜 F-beta 分数(在 34% 的测试数据集上)获胜。他的方法在其帖子“Planet: Understanding the Amazon from Space, 1st Place Winner’s Interview”中进行了描述,涉及一个管道和大量模型的集成,主要是带有迁移学习的卷积神经网络。
这是一场具有挑战性的比赛,尽管数据集仍然免费提供(如果您拥有 Kaggle 帐户),并且为练习航空和卫星数据集的卷积神经网络图像分类提供了一个很好的基准问题。
因此,通过手动设计的卷积神经网络通常可以获得大于 80 的 F-beta 分数,而使用迁移学习在此任务上则可以获得 89+ 的 F-beta 分数。
想通过深度学习实现计算机视觉成果吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
如何准备数据以供建模
第一步是下载数据集。
要下载数据文件,您必须拥有 Kaggle 帐户。如果您没有 Kaggle 帐户,可以在此处创建:Kaggle 主页。
可以从 Planet 数据页面下载数据集。此页面列出了为比赛提供的所有文件,尽管我们不需要下载所有文件。
在下载数据集之前,您必须单击“加入比赛”按钮。您可能需要同意比赛规则,然后数据集将可供下载。

加入比赛
要下载给定的文件,请单击文件旁边(右侧)出现的小下载按钮图标,就像下面的图片中所示一样。
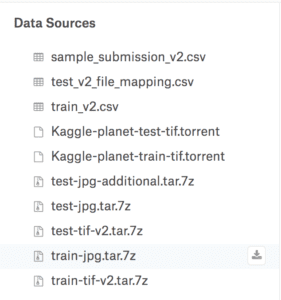
下载按钮示例,用于下载 Planet 数据集的文件
本教程所需的特定文件如下:
- train-jpg.tar.7z (600MB)
- train_v2.csv.zip (159KB)
注意: jpeg zip 文件可能没有 .7z 扩展名。如果有,请下载 .tar 版本。
下载完数据集文件后,您必须解压缩它们。CSV 文件的 .zip 文件可以使用您喜欢的解压缩程序进行解压缩。
包含 JPEG 图像的 .7z 文件也可以使用您喜欢的解压缩程序进行解压缩。如果这对您来说是一种新的 zip 格式,您可能需要额外的软件,例如 MacOS 上的“The Unarchiver”软件,或许多平台上的 p7zip。
例如,在大多数基于 POSIX 的工作站的命令行中,可以使用 p7zip 和 tar 文件按如下方式解压缩 .7z 文件:
|
1 2 3 4 |
7z x test-jpg.tar.7z tar -xvf test-jpg.tar 7z x train-jpg.tar.7z tar -xvf train-jpg.tar |
解压缩后,您将在当前工作目录中拥有一个 CSV 文件和一个目录,如下所示:
|
1 2 |
train-jpg/ train_v2.csv |
检查文件夹,您会看到许多 jpeg 文件。
检查 _train_v2.csv_ 文件,您将看到训练数据集(train-jpg/)中的 jpeg 文件与其类标签的映射,每个标签之间用空格分隔;例如:
|
1 2 3 4 5 6 7 |
image_name,tags train_0,haze primary train_1,agriculture clear primary water train_2,clear primary train_3,clear primary train_4,agriculture clear habitation primary road ... |
数据集必须在建模之前准备好。
我们可以探索至少两种方法:内存中方法和渐进式加载方法。
可以准备数据集,以便在拟合模型时将整个训练数据集加载到内存中。这将需要一台拥有足够 RAM 来容纳所有图像的机器(例如 32GB 或 64GB RAM),例如 Amazon EC2 实例,尽管训练模型的速度会大大加快。
或者,可以在训练期间按批次按需加载数据集。这将需要开发一个数据生成器。训练模型的速度会大大变慢,但可以在 RAM 较少的工作站(例如 8GB 或 16GB)上进行训练。
在本教程中,我们将采用前一种方法。因此,我强烈建议您在具有足够 RAM 和 GPU 访问权限的 Amazon EC2 实例上运行本教程,例如 p3.2xlarge 实例上的 Deep Learning AMI (Amazon Linux) AMI,其成本约为每小时 3 美元。有关如何设置 Amazon EC2 实例以进行深度学习的分步教程,请参阅帖子:
如果使用 EC2 实例对您来说不是一个选项,那么我将在下面提供一些提示,说明如何进一步减小训练数据集的大小,使其能够适应您工作站的内存,以便您可以完成本教程。
可视化数据集
第一步是检查训练数据集中的一些图像。
我们可以通过加载一些图像并使用 Matplotlib 将多张图像绘制在一张图中来做到这一点。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# plot the first 9 images in the planet dataset from matplotlib import pyplot from matplotlib.image import imread # define location of dataset folder = 'train-jpg/' # 绘制前几张图片 for i in range(9): # 定义子图 pyplot.subplot(330 + 1 + i) # define filename filename = folder + 'train_' + str(i) + '.jpg' # load image pixels image = imread(filename) # 绘制原始像素数据 pyplot.imshow(image) # 显示图 pyplot.show() |
运行示例会创建一个图,其中包含训练数据集的前九张图像。
我们可以看到这些确实是雨林的卫星照片。有些显示出明显的雾霾,有些显示出树木、道路或河流及其他结构。
这些图表明建模可能受益于数据增强以及使图像特征更可见的简单技术。

显示 Planet 数据集前九张图像的图
创建映射
下一步是了解可能分配给每张图像的标签。
我们可以直接使用 read_csv() Pandas 函数加载训练数据集(_train_v2.csv_)的 CSV 映射文件。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 |
# load and summarize the mapping file for the planet dataset from pandas import read_csv # load file as CSV filename = 'train_v2.csv' mapping_csv = read_csv(filename) # summarize properties print(mapping_csv.shape) print(mapping_csv[:10]) |
运行示例后,首先会总结训练数据集的形状。我们可以看到映射文件中确实有 40,479 个训练图像。
接下来,总结文件的前 10 行。我们可以看到文件中的第二列包含一个空格分隔的标签列表,用于分配给每张图像。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
(40479, 2) image_name tags 0 train_0 haze primary 1 train_1 agriculture clear primary water 2 train_2 clear primary 3 train_3 clear primary 4 train_4 agriculture clear habitation primary road 5 train_5 haze primary water 6 train_6 agriculture clear cultivation primary water 7 train_7 haze primary 8 train_8 agriculture clear cultivation primary 9 train_9 agriculture clear cultivation primary road |
我们需要一套所有已知的标签来分配给图像,还需要一个唯一且一致的整数来应用于每个标签。这样我们就可以使用 one-hot 编码为每张图像开发一个目标向量,例如一个全为零且在应用于图像的每个标签的索引处为一的向量。
这可以通过遍历“tags”列中的每一行,按空格分割标签,并将它们存储在一个集合中来实现。然后我们将拥有一个所有已知标签的集合。例如:
|
1 2 3 4 5 6 7 |
# create a set of labels labels = set() for i in range(len(mapping_csv)): # convert spaced separated tags into an array of tags tags = mapping_csv['tags'][i].split(' ') # add tags to the set of known labels labels.update(tags) |
然后可以按字母顺序列出它们,并为每个标签分配一个基于该字母顺序的整数。
这将意味着相同的标签将始终分配相同的整数以保持一致性。
|
1 2 3 4 |
# convert set of labels to a list to list labels = list(labels) # order set alphabetically labels.sort() |
我们可以创建一个字典,将标签映射到整数,以便我们可以对训练数据集进行编码以进行建模。
我们还可以创建一个从整数到字符串标签值的反向映射字典,这样稍后当模型进行预测时,我们可以将其转换为可读的内容。
|
1 2 3 |
# dict that maps labels to integers, and the reverse labels_map = {labels[i]:i for i in range(len(labels))} inv_labels_map = {i:labels[i] for i in range(len(labels))} |
我们可以将所有这些内容整合到一个名为 _create_tag_mapping()_ 的方便函数中,该函数将接收包含 _train_v2.csv_ 数据的已加载 DataFrame,并返回一个映射字典和一个反向映射字典。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# create a mapping of tags to integers given the loaded mapping file def create_tag_mapping(mapping_csv): # create a set of all known tags labels = set() for i in range(len(mapping_csv)): # convert spaced separated tags into an array of tags tags = mapping_csv['tags'][i].split(' ') # add tags to the set of known labels labels.update(tags) # convert set of labels to a list to list labels = list(labels) # order set alphabetically labels.sort() # dict that maps labels to integers, and the reverse labels_map = {labels[i]:i for i in range(len(labels))} inv_labels_map = {i:labels[i] for i in range(len(labels))} return labels_map, inv_labels_map |
我们可以试用此函数,看看我们有多少标签以及可以使用的标签;完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# create a mapping of tags to integers from pandas import read_csv # create a mapping of tags to integers given the loaded mapping file def create_tag_mapping(mapping_csv): # create a set of all known tags labels = set() for i in range(len(mapping_csv)): # convert spaced separated tags into an array of tags tags = mapping_csv['tags'][i].split(' ') # add tags to the set of known labels labels.update(tags) # convert set of labels to a list to list labels = list(labels) # order set alphabetically labels.sort() # dict that maps labels to integers, and the reverse labels_map = {labels[i]:i for i in range(len(labels))} inv_labels_map = {i:labels[i] for i in range(len(labels))} return labels_map, inv_labels_map # load file as CSV filename = 'train_v2.csv' mapping_csv = read_csv(filename) # create a mapping of tags to integers mapping, inv_mapping = create_tag_mapping(mapping_csv) print(len(mapping)) print(mapping) |
运行示例,我们可以看到数据集中总共有 17 个标签。
我们还可以看到映射字典,其中每个标签都被分配了一个一致且唯一的整数。这些标签似乎是对给定卫星图像中可能看到的特征类型的合理描述。
作为一个进一步的扩展,探索标签在图像中的分布,以查看它们在训练数据集中的分配或使用是平衡的还是不平衡的,可能会很有趣。这可以为预测问题的难度提供进一步的见解。
|
1 2 3 |
17 {'agriculture': 0, 'artisinal_mine': 1, 'bare_ground': 2, 'blooming': 3, 'blow_down': 4, 'clear': 5, 'cloudy': 6, 'conventional_mine': 7, 'cultivation': 8, 'habitation': 9, 'haze': 10, 'partly_cloudy': 11, 'primary': 12, 'road': 13, 'selective_logging': 14, 'slash_burn': 15, 'water': 16} |
我们还需要一个训练集文件名到图像标签的映射。
这是一个简单的字典,以图像的文件名作为键,以标签列表作为值。
下面的 _create_file_mapping()_ 函数实现了这一点,它还以加载的 _DataFrame_ 作为参数,并返回一个映射,其中每个文件名的标签值都存储为一个列表。
|
1 2 3 4 5 6 7 |
# create a mapping of filename to tags def create_file_mapping(mapping_csv): mapping = dict() for i in range(len(mapping_csv)): name, tags = mapping_csv['image_name'][i], mapping_csv['tags'][i] mapping[name] = tags.split(' ') return mapping |
我们现在可以准备数据集的图像部分。
创建内存数据集
我们需要能够将 JPEG 图像加载到内存中。
这可以通过枚举 _train-jpg/_ 文件夹中的所有文件来实现。Keras 通过 load_img() 函数提供了一个简单的 API 来从文件加载图像,并通过 _img_to_array()_ 函数将其转换为 NumPy 数组。
在加载图像的过程中,我们可以强制将图像尺寸减小以节省内存并加快训练速度。在这种情况下,我们将图像尺寸从 256×256 减半到 128×128。我们还将像素值存储为无符号 8 位整数(例如,值为 0 到 255)。
|
1 2 3 4 |
# 加载图片 photo = load_img(filename, target_size=(128,128)) # 转换为numpy数组 photo = img_to_array(photo, dtype='uint8') |
照片将代表模型的输入,但我们需要照片的输出。
然后,我们可以使用不带扩展名的文件名,通过上节开发的 _create_file_mapping()_ 函数准备的文件名到标签映射,来检索加载图像的标签。
|
1 2 |
# get tags tags = file_mapping(filename[:-4]) |
我们需要对图像的标签进行 one-hot 编码。这意味着我们需要一个 17 个元素的向量,其中每个存在的标签都为 1。我们可以从上节开发的 _create_tag_mapping()_ 函数创建的标签到整数的映射中获取放置 1 的索引。
下面的 _one_hot_encode()_ 函数实现了这一点,它以图像标签列表和标签到整数的映射作为参数,并将返回一个 17 个元素的 NumPy 数组,该数组描述了单个照片标签的 one-hot 编码。
|
1 2 3 4 5 6 7 8 |
# create a one hot encoding for one list of tags def one_hot_encode(tags, mapping): # create empty vector encoding = zeros(len(mapping), dtype='uint8') # mark 1 for each tag in the vector for tag in tags: encoding[mapping[tag]] = 1 return encoding |
我们现在可以加载整个训练数据集的输入(照片)和输出(one-hot 编码向量)。
下面的 _load_dataset()_ 函数实现了这一点,它以 JPEG 图像的路径、文件到标签的映射以及标签到整数的映射作为输入;它将为建模的 _X_ 和 _y_ 元素返回 NumPy 数组。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# load all images into memory def load_dataset(path, file_mapping, tag_mapping): photos, targets = list(), list() # enumerate files in the directory for filename in listdir(folder): # 加载图像 photo = load_img(path + filename, target_size=(128,128)) # 转换为numpy数组 photo = img_to_array(photo, dtype='uint8') # get tags tags = file_mapping[filename[:-4]] # one hot encode tags target = one_hot_encode(tags, tag_mapping) # 存储 photos.append(photo) targets.append(target) X = asarray(photos, dtype='uint8') y = asarray(targets, dtype='uint8') return X, y |
注意:这将把整个训练数据集加载到内存中,可能需要至少 128x128x3 x 40,479 张图像 x 8 位,或约 2 GB 的 RAM 才能容纳加载的照片。
如果您在这里或稍后建模时(像素为 16 或 32 位时)遇到内存不足的问题,请尝试将加载的照片尺寸减小到 32×32,或者在加载 20,000 张照片后停止循环。
加载后,我们可以将这些 NumPy 数组保存到文件中以供以后使用。
我们可以使用 save() 或 savez() NumPy 函数直接保存数组。相反,我们将使用 savez_compressed() NumPy 函数 以压缩格式一次性调用保存这两个数组,节省几兆字节的空间。在建模过程中,加载较小图像的数组将比每次都加载原始 JPEG 图像快得多。
|
1 2 |
# 将两个数组以压缩格式保存到单个文件中 savez_compressed('planet_data.npz', X, y) |
我们可以将所有这些整合起来,为内存建模准备 Planet 数据集,并将其保存到一个新的单个文件中,以便稍后快速加载。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 |
# 加载和准备 planet 数据集并保存到文件 from os import listdir from numpy import zeros from numpy import asarray from numpy import savez_compressed from pandas import read_csv from keras.preprocessing.image import load_img from keras.preprocessing.image import img_to_array # create a mapping of tags to integers given the loaded mapping file def create_tag_mapping(mapping_csv): # create a set of all known tags labels = set() for i in range(len(mapping_csv)): # convert spaced separated tags into an array of tags tags = mapping_csv['tags'][i].split(' ') # add tags to the set of known labels labels.update(tags) # convert set of labels to a list to list labels = list(labels) # order set alphabetically labels.sort() # dict that maps labels to integers, and the reverse labels_map = {labels[i]:i for i in range(len(labels))} inv_labels_map = {i:labels[i] for i in range(len(labels))} return labels_map, inv_labels_map # 创建文件名到标签列表的映射 def create_file_mapping(mapping_csv): mapping = dict() for i in range(len(mapping_csv)): name, tags = mapping_csv['image_name'][i], mapping_csv['tags'][i] mapping[name] = tags.split(' ') return mapping # create a one hot encoding for one list of tags def one_hot_encode(tags, mapping): # create empty vector encoding = zeros(len(mapping), dtype='uint8') # mark 1 for each tag in the vector for tag in tags: encoding[mapping[tag]] = 1 return encoding # load all images into memory def load_dataset(path, file_mapping, tag_mapping): photos, targets = list(), list() # enumerate files in the directory for filename in listdir(folder): # 加载图像 photo = load_img(path + filename, target_size=(128,128)) # 转换为numpy数组 photo = img_to_array(photo, dtype='uint8') # get tags tags = file_mapping[filename[:-4]] # one hot encode tags target = one_hot_encode(tags, tag_mapping) # 存储 photos.append(photo) targets.append(target) X = asarray(photos, dtype='uint8') y = asarray(targets, dtype='uint8') 返回 X, y # 加载映射文件 filename = 'train_v2.csv' mapping_csv = read_csv(filename) # create a mapping of tags to integers tag_mapping, _ = create_tag_mapping(mapping_csv) # 创建文件名到标签列表的映射 file_mapping = create_file_mapping(mapping_csv) # 加载 jpeg 图像 folder = 'train-jpg/' X, y = load_dataset(folder, file_mapping, tag_mapping) print(X.shape, y.shape) # 将两个数组以压缩格式保存到单个文件中 savez_compressed('planet_data.npz', X, y) |
运行示例首先加载整个数据集并总结其形状。我们可以确认输入样本 (X) 是 128×128 的彩色图像,输出样本是 17 维向量。
运行结束后,将保存一个名为 'planet_data.npz' 的文件,其中包含该数据集,大小约为 1.2 GB,由于压缩节省了约 700 MB。
|
1 |
(40479, 128, 128, 3) (40479, 17) |
之后可以使用 load() NumPy 函数轻松加载数据集,如下所示:
|
1 2 3 4 5 |
# 加载准备好的 planet 数据集 from numpy import load data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] print('Loaded: ', X.shape, y.shape) |
运行此小示例可确认数据集已正确加载。
|
1 |
Loaded: (40479, 128, 128, 3) (40479, 17) |
模型评估指标
在开始建模之前,我们必须选择一个性能指标。
对于具有均衡类别示例数量的二元分类任务,分类准确率通常是合适的。
在这种情况下,我们既不是处理二元分类任务,也不是处理多类分类任务;相反,这是一个多标签分类任务,标签数量不均衡,有些标签比其他标签使用得更频繁。
因此,Kaggle 竞赛组织者选择了 F-beta 指标,特别是 F2 分数。这是一个与 F1 分数(也称为 F 度量)相关的指标。
F1 分数计算 精确率和召回率 的平均值。您可能还记得,精确率和召回率的计算方法如下:
|
1 2 |
precision = true positives / (true positives + false positives) recall = true positives / (true positives + false negatives) |
精确率描述了模型在预测正类方面的优劣。召回率描述了在实际结果为正时,模型在预测正类方面的优劣。
F1 是这两个分数的平均值,特别是 调和平均数 而不是算术平均数,因为值是比例。在评估模型在不平衡数据集上的性能时,F1 比准确率更受青睐,其值在 0 和 1 之间,分别代表最差和最佳可能分数。
|
1 |
F1 = 2 x (precision x recall) / (precision + recall) |
F-beta 指标是 F1 的泛化,它允许引入一个称为 *beta* 的项,该项在计算平均值时决定了召回率相对于精确率的重要性。
|
1 |
F-Beta = (1 + Beta^2) x (precision x recall) / (Beta^2 x precision + recall) |
beta 的一个常见值是 2,竞赛中使用的值就是这个,其中召回率的权重是精确率的两倍。这通常被称为 F2 分数。
正类和负类的概念仅对二元分类问题有意义。由于我们正在预测多个类别,因此正类和负类以及相关术语是针对每个类别以“一对多”的方式计算的,然后对每个类别进行平均。
scikit-learn 库通过 fbeta_score() 函数提供了 F-beta 的实现。我们可以调用此函数来评估一组预测,并指定 beta 值为 2,同时将“average”参数设置为“samples”。
|
1 |
score = fbeta_score(y_true, y_pred, 2, average='samples') |
例如,我们可以在准备好的数据集上测试此功能。
我们可以将加载的数据集分割成单独的训练集和测试集,用于训练和评估此问题上的模型。这可以通过使用 train_test_split() 并指定 'random_state' 参数来实现,以便每次运行代码时都能获得相同的数据分割。
我们将使用 70% 作为训练集,30% 作为测试集。
|
1 |
trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1) |
下面的 load_dataset() 函数通过加载已保存的数据集,将其分割为训练集和测试集,并返回它们以供使用来实现这一点。
|
1 2 3 4 5 6 7 8 9 |
# 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] # 分割为训练集和测试集 trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1) print(trainX.shape, trainY.shape, testX.shape, testY.shape) return trainX, trainY, testX, testY |
然后,我们可以预测所有类别或 one-hot 编码向量中的所有 1 值。
|
1 2 3 |
# 进行全 1 预测 train_yhat = asarray([ones(trainY.shape[1]) for _ in range(trainY.shape[0])]) test_yhat = asarray([ones(testY.shape[1]) for _ in range(testY.shape[0])]) |
然后可以使用 scikit-learn 的 fbeta_score() 函数和训练集及测试集中的真实值来评估预测。
|
1 2 |
train_score = fbeta_score(trainY, train_yhat, 2, average='samples') test_score = fbeta_score(testY, test_yhat, 2, average='samples') |
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
# 测试 f-beta 分数 from numpy import load from numpy import ones from numpy import asarray from sklearn.model_selection import train_test_split from sklearn.metrics import fbeta_score # 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] # 分割为训练集和测试集 trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1) print(trainX.shape, trainY.shape, testX.shape, testY.shape) return trainX, trainY, testX, testY # 加载数据集 trainX, trainY, testX, testY = load_dataset() # 进行全 1 预测 train_yhat = asarray([ones(trainY.shape[1]) for _ in range(trainY.shape[0])]) test_yhat = asarray([ones(testY.shape[1]) for _ in range(testY.shape[0])]) # 评估预测 train_score = fbeta_score(trainY, train_yhat, 2, average='samples') test_score = fbeta_score(testY, test_yhat, 2, average='samples') print('All Ones: train=%.3f, test=%.3f' % (train_score, test_score)) |
运行此示例首先加载准备好的数据集,然后将其分割为训练集和测试集,并报告准备好的数据集的形状。我们可以看到训练数据集中有略多于 28,000 个样本,测试数据集中有略多于 12,000 个样本。
接下来,准备全 1 预测,然后进行评估并报告分数。我们可以看到,对两个数据集进行全 1 预测,得分约为 0.48。
|
1 2 |
(28335, 128, 128, 3) (28335, 17) (12144, 128, 128, 3) (12144, 17) All Ones: train=0.484, test=0.483 |
我们将需要 Keras 的 F-beta 分数计算版本作为指标。
在 Keras 库 2.0 版本之前,它曾支持此指标用于二元分类问题(2 个类别);我们可以在这里看到此旧版本的代码:metrics.py。此代码可用作定义新指标函数的基础,该函数可与 Keras 一起使用。在标题为“F-beta score for Keras”的 Kaggle 内核中也提出了此函数的一个版本。新函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
from keras import backend # 计算多类/多标签分类的 fbeta 分数 def fbeta(y_true, y_pred, beta=2): # 剪裁预测值 y_pred = backend.clip(y_pred, 0, 1) # 计算元素 tp = backend.sum(backend.round(backend.clip(y_true * y_pred, 0, 1)), axis=1) fp = backend.sum(backend.round(backend.clip(y_pred - y_true, 0, 1)), axis=1) fn = backend.sum(backend.round(backend.clip(y_true - y_pred, 0, 1)), axis=1) # 计算精确率 p = tp / (tp + fp + backend.epsilon()) # 计算召回率 r = tp / (tp + fn + backend.epsilon()) # 计算 fbeta,跨类别平均 bb = beta ** 2 fbeta_score = backend.mean((1 + bb) * (p * r) / (bb * p + r + backend.epsilon())) return fbeta_score |
它可以在 Keras 中编译模型时使用,通过 metrics 参数指定;例如:
|
1 2 |
... model.compile(... metrics=[fbeta]) |
我们可以测试这个新函数并将结果与 scikit-learn 函数进行比较,如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# 比较 sklearn 和 keras 之间的 f-beta 分数 from numpy import load from numpy import ones from numpy import asarray from sklearn.model_selection import train_test_split from sklearn.metrics import fbeta_score from keras import backend # 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] # 分割为训练集和测试集 trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1) print(trainX.shape, trainY.shape, testX.shape, testY.shape) return trainX, trainY, testX, testY # 计算多类/多标签分类的 fbeta 分数 def fbeta(y_true, y_pred, beta=2): # 剪裁预测值 y_pred = backend.clip(y_pred, 0, 1) # 计算元素 tp = backend.sum(backend.round(backend.clip(y_true * y_pred, 0, 1)), axis=1) fp = backend.sum(backend.round(backend.clip(y_pred - y_true, 0, 1)), axis=1) fn = backend.sum(backend.round(backend.clip(y_true - y_pred, 0, 1)), axis=1) # 计算精确率 p = tp / (tp + fp + backend.epsilon()) # 计算召回率 r = tp / (tp + fn + backend.epsilon()) # 计算 fbeta,跨类别平均 bb = beta ** 2 fbeta_score = backend.mean((1 + bb) * (p * r) / (bb * p + r + backend.epsilon())) return fbeta_score # 加载数据集 trainX, trainY, testX, testY = load_dataset() # 进行全 1 预测 train_yhat = asarray([ones(trainY.shape[1]) for _ in range(trainY.shape[0])]) test_yhat = asarray([ones(testY.shape[1]) for _ in range(testY.shape[0])]) # 使用 sklearn 评估预测 train_score = fbeta_score(trainY, train_yhat, 2, average='samples') test_score = fbeta_score(testY, test_yhat, 2, average='samples') print('All Ones (sklearn): train=%.3f, test=%.3f' % (train_score, test_score)) # 使用 keras 评估预测 train_score = fbeta(backend.variable(trainY), backend.variable(train_yhat)) test_score = fbeta(backend.variable(testY), backend.variable(test_yhat)) print('All Ones (keras): train=%.3f, test=%.3f' % (train_score, test_score)) |
运行示例后,将像以前一样加载数据集,在这种情况下,F-beta 将同时使用 scikit-learn 和 Keras 计算。我们可以看到两个函数都获得了相同的结果。
|
1 2 3 |
(28335, 128, 128, 3) (28335, 17) (12144, 128, 128, 3) (12144, 17) All Ones (sklearn): train=0.484, test=0.483 All Ones (keras): train=0.484, test=0.483 |
我们可以使用测试集上的 0.483 分数作为一个简单的预测,后续章节中的所有模型都可以与此进行比较,以确定它们是否具有技能。
如何评估基线模型
现在我们准备好为准备好的 planet 数据集开发和评估一个基线卷积神经网络模型。
我们将设计一个具有 VGG 类型结构的基线模型。即由小型 3×3 滤波器卷积层组成的块,然后是一个最大池化层,此模式重复进行,每次添加一个块时滤波器数量加倍。
具体来说,每个块将包含两个带有 3×3 滤波器的卷积层,使用 ReLU 激活和 He 权重初始化,并带有 same 填充,确保输出特征图具有相同的宽度和高度。之后将是一个具有 3×3 内核的最大池化层。将使用三个这样的块,分别带有 32、64 和 128 个滤波器。
|
1 2 3 4 5 6 7 8 9 10 |
model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=(128, 128, 3))) model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) |
最后一个池化层的输出将被展平并馈送到一个完全连接的层进行解释,最后到一个输出层进行预测。
模型必须为每个输出类生成一个 17 维向量,预测值在 0 和 1 之间。
|
1 2 3 |
model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(17, activation='sigmoid')) |
如果这是一个多类分类问题,我们将使用 softmax 激活函数和 分类交叉熵损失函数。这不适用于多标签分类,因为我们期望模型输出多个 1 值,而不是单个 1 值。在这种情况下,我们将使用输出层中的 sigmoid 激活函数,并优化二元交叉熵损失函数。
模型将使用具有保守 学习率 0.01 和动量 0.9 的 mini-batch 随机梯度下降进行优化,并且模型将在训练期间跟踪“fbeta”指标。
|
1 2 3 |
# 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) |
下面的 define_model() 函数将所有这些内容整合在一起,并对输入和输出的形状进行了参数化,以防您想通过更改这些值进行实验或在另一个数据集上重用代码。
该函数将返回一个准备好拟合 planet 数据集的模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=in_shape)) model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(out_shape, activation='sigmoid')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) return model |
将此模型选作基线模型有些随意。您可能希望尝试使用具有更少层或不同学习率的其他基线模型。
我们可以使用前一节开发的*load_dataset()*函数来加载数据集,并将其分割为训练集和测试集,用于拟合和评估已定义的模型。
在拟合模型之前,将对像素值进行归一化。我们将通过定义一个ImageDataGenerator实例并指定rescale参数为1.0/255.0来实现。这将按批次将像素值归一化为32位浮点值,这可能比一次性在内存中重新缩放所有像素值更节省内存。
|
1 2 |
# 创建数据生成器 datagen = ImageDataGenerator(rescale=1.0/255.0) |
我们可以从该数据生成器为训练集和测试集创建迭代器,在本例中,我们将使用相对较大的128张图像的批次大小来加速学习。
|
1 2 3 |
# 准备迭代器 train_it = datagen.flow(trainX, trainY, batch_size=128) test_it = datagen.flow(testX, testY, batch_size=128) |
然后可以使用训练迭代器来拟合已定义的模型,并在每个epoch结束时使用测试迭代器来评估测试数据集。模型将训练50个epoch。
|
1 2 3 |
# 拟合模型 history = model.fit_generator(train_it, steps_per_epoch=len(train_it), validation_data=test_it, validation_steps=len(test_it), epochs=50, verbose=0) |
拟合完成后,我们可以计算测试数据集上的最终损失和F-beta分数,以估计模型的技能。
|
1 2 3 |
# 评估模型 loss, fbeta = model.evaluate_generator(test_it, steps=len(test_it), verbose=0) print('> loss=%.3f, fbeta=%.3f' % (loss, fbeta)) |
调用fit_generator()函数来拟合模型,它返回一个包含每个epoch在训练集和测试集上记录的损失和F-beta分数的字典。我们可以绘制这些轨迹,以了解模型的学习动态。
summarize_diagnostics()函数将根据记录的历史数据创建一个图形,其中一个图显示损失,另一个图显示模型在每个训练epoch结束时在训练集(蓝线)和测试集(橙线)上的F-beta分数。
创建的图形将保存为与脚本同名但扩展名为“_plot.png”的PNG文件。这允许使用相同的测试套件处理多个不同的脚本文件以进行不同的模型配置,并将学习曲线保存在单独的文件中。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 绘制诊断学习曲线 def summarize_diagnostics(history): # 绘制损失 pyplot.subplot(211) pyplot.title('交叉熵损失') pyplot.plot(history.history['loss'], color='blue', label='train') pyplot.plot(history.history['val_loss'], color='orange', label='test') # 绘制准确率 pyplot.subplot(212) pyplot.title('Fbeta') pyplot.plot(history.history['fbeta'], color='blue', label='train') pyplot.plot(history.history['val_fbeta'], color='orange', label='test') # 保存图到文件 filename = sys.argv[0].split('/')[-1] pyplot.savefig(filename + '_plot.png') pyplot.close() |
我们可以将这一切整合起来,定义一个*run_test_harness()*函数来驱动测试套件,包括数据加载和准备,以及模型的定义、拟合和评估。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 运行测试工具以评估 cifar10 数据集上的模型 def run_test_harness(): # 加载数据集 trainX, trainY, testX, testY = load_dataset() # 创建数据生成器 datagen = ImageDataGenerator(rescale=1.0/255.0) # 准备迭代器 train_it = datagen.flow(trainX, trainY, batch_size=128) test_it = datagen.flow(testX, testY, batch_size=128) # 定义模型 model = define_model() # 拟合模型 history = model.fit_generator(train_it, steps_per_epoch=len(train_it), validation_data=test_it, validation_steps=len(test_it), epochs=50, verbose=0) # 评估模型 loss, fbeta = model.evaluate_generator(test_it, steps=len(test_it), verbose=0) print('> loss=%.3f, fbeta=%.3f' % (loss, fbeta)) # 学习曲线 summarize_diagnostics(history) |
下面列出了在planet数据集上评估基线模型的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
# planet数据集的基线模型 import sys from numpy import load from matplotlib import pyplot from sklearn.model_selection import train_test_split from keras import backend from keras.preprocessing.image import ImageDataGenerator from keras.models import Sequential 从 keras.layers 导入 Conv2D 从 keras.layers 导入 MaxPooling2D from keras.layers import Dense from keras.layers import Flatten from keras.optimizers import SGD # 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] # 分割为训练集和测试集 trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1) print(trainX.shape, trainY.shape, testX.shape, testY.shape) return trainX, trainY, testX, testY # 计算多类/多标签分类的 fbeta 分数 def fbeta(y_true, y_pred, beta=2): # 剪裁预测值 y_pred = backend.clip(y_pred, 0, 1) # 计算元素 tp = backend.sum(backend.round(backend.clip(y_true * y_pred, 0, 1)), axis=1) fp = backend.sum(backend.round(backend.clip(y_pred - y_true, 0, 1)), axis=1) fn = backend.sum(backend.round(backend.clip(y_true - y_pred, 0, 1)), axis=1) # 计算精确率 p = tp / (tp + fp + backend.epsilon()) # 计算召回率 r = tp / (tp + fn + backend.epsilon()) # 计算 fbeta,跨类别平均 bb = beta ** 2 fbeta_score = backend.mean((1 + bb) * (p * r) / (bb * p + r + backend.epsilon())) return fbeta_score # 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=in_shape)) model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(out_shape, activation='sigmoid')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) return model # 绘制诊断学习曲线 def summarize_diagnostics(history): # 绘制损失 pyplot.subplot(211) pyplot.title('交叉熵损失') pyplot.plot(history.history['loss'], color='blue', label='train') pyplot.plot(history.history['val_loss'], color='orange', label='test') # 绘制准确率 pyplot.subplot(212) pyplot.title('Fbeta') pyplot.plot(history.history['fbeta'], color='blue', label='train') pyplot.plot(history.history['val_fbeta'], color='orange', label='test') # 保存图到文件 filename = sys.argv[0].split('/')[-1] pyplot.savefig(filename + '_plot.png') pyplot.close() # 运行测试工具以评估 cifar10 数据集上的模型 def run_test_harness(): # 加载数据集 trainX, trainY, testX, testY = load_dataset() # 创建数据生成器 datagen = ImageDataGenerator(rescale=1.0/255.0) # 准备迭代器 train_it = datagen.flow(trainX, trainY, batch_size=128) test_it = datagen.flow(testX, testY, batch_size=128) # 定义模型 model = define_model() # 拟合模型 history = model.fit_generator(train_it, steps_per_epoch=len(train_it), validation_data=test_it, validation_steps=len(test_it), epochs=50, verbose=0) # 评估模型 loss, fbeta = model.evaluate_generator(test_it, steps=len(test_it), verbose=0) print('> loss=%.3f, fbeta=%.3f' % (loss, fbeta)) # 学习曲线 summarize_diagnostics(history) # 入口点,运行测试工具 run_test_harness() |
运行该示例首先加载数据集并将其分割为训练集和测试集。打印出训练集和测试集的每个输入和输出元素的形状,确认执行了与之前相同的数据分割。
模型被拟合和评估,并报告了模型在测试数据集上的最终F-beta分数。
注意:鉴于算法或评估程序的随机性,或数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
在本例中,基线模型达到了约0.831的F-beta分数,这比上一节中报告的0.483的朴素分数要好得多。这表明基线模型是有效的。
|
1 2 |
(28335, 128, 128, 3) (28335, 17) (12144, 128, 128, 3) (12144, 17) > loss=0.470, fbeta=0.831 |
此外,还会创建一个图形并将其保存到文件中,其中显示了模型在planet数据集上的训练集和测试集上的损失和F-beta学习曲线图。
在本例中,损失学习曲线的图表明模型过度拟合了训练数据集,可能在第50个epoch的第20个epoch左右,尽管过度拟合似乎并未对模型在F-beta分数方面的测试数据集性能产生负面影响。
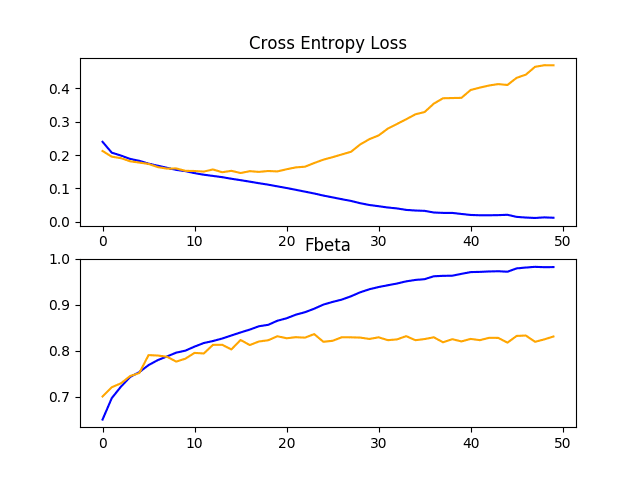
line plots showing loss and F-beta learning curves for the baseline model on the train and test datasets on the planet problem
现在我们有了数据集的基线模型,我们就有了一个坚实的实验和改进基础。
我们将在下一节中探讨一些改进模型性能的思路。
如何提高模型性能
在上一节中,我们定义了一个基线模型,可以作为在planet数据集上改进的基础。
该模型取得了不错的F-beta分数,尽管学习曲线表明模型过度拟合了训练数据集。解决过度拟合的两个常见方法是dropout正则化和数据增强。两者都有助于扰乱和减缓学习过程,特别是模型在训练epoch中改进的速度。
我们将在本节中探讨这两种方法。鉴于我们预计学习速度会减慢,我们将通过将训练epoch数从50增加到200来为模型提供更多学习时间。
Dropout 正则化
Dropout正则化是一种计算成本较低的深度神经网络正则化方法。
Dropout通过概率性地移除或“*丢弃*”层的输入来实现,这些输入可能是数据样本中的输入变量或来自前一层的激活。它模拟了大量具有非常不同网络结构的网络的行为,从而使网络中的节点对输入更具鲁棒性。
有关dropout的更多信息,请参阅本文
通常,可以在每个VGG块之后应用少量的dropout,并在模型输出层附近的完全连接层上应用更多的dropout。
下面是基线模型的更新版本中的*define_model()*函数,增加了Dropout。在本例中,每个VGG块后应用20%的dropout,在模型分类部分的全连接层后应用50%的较高dropout率。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=in_shape)) model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Dropout(0.2)) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Dropout(0.2)) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Dropout(0.2)) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dropout(0.5)) model.add(Dense(out_shape, activation='sigmoid')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) return model |
为完整起见,下面列出了带有dropout的基线模型在planet数据集上的完整代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 |
# planet数据集的带dropout的基线模型 import sys from numpy import load from matplotlib import pyplot from sklearn.model_selection import train_test_split from keras import backend from keras.preprocessing.image import ImageDataGenerator from keras.models import Sequential 从 keras.layers 导入 Conv2D 从 keras.layers 导入 MaxPooling2D from keras.layers import Dense from keras.layers import Flatten 从 keras.layers 导入 Dropout from keras.optimizers import SGD # 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] # 分割为训练集和测试集 trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1) print(trainX.shape, trainY.shape, testX.shape, testY.shape) return trainX, trainY, testX, testY # 计算多类/多标签分类的 fbeta 分数 def fbeta(y_true, y_pred, beta=2): # 剪裁预测值 y_pred = backend.clip(y_pred, 0, 1) # 计算元素 tp = backend.sum(backend.round(backend.clip(y_true * y_pred, 0, 1)), axis=1) fp = backend.sum(backend.round(backend.clip(y_pred - y_true, 0, 1)), axis=1) fn = backend.sum(backend.round(backend.clip(y_true - y_pred, 0, 1)), axis=1) # 计算精确率 p = tp / (tp + fp + backend.epsilon()) # 计算召回率 r = tp / (tp + fn + backend.epsilon()) # 计算 fbeta,跨类别平均 bb = beta ** 2 fbeta_score = backend.mean((1 + bb) * (p * r) / (bb * p + r + backend.epsilon())) return fbeta_score # 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=in_shape)) model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Dropout(0.2)) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Dropout(0.2)) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Dropout(0.2)) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dropout(0.5)) model.add(Dense(out_shape, activation='sigmoid')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) return model # 绘制诊断学习曲线 def summarize_diagnostics(history): # 绘制损失 pyplot.subplot(211) pyplot.title('交叉熵损失') pyplot.plot(history.history['loss'], color='blue', label='train') pyplot.plot(history.history['val_loss'], color='orange', label='test') # 绘制准确率 pyplot.subplot(212) pyplot.title('Fbeta') pyplot.plot(history.history['fbeta'], color='blue', label='train') pyplot.plot(history.history['val_fbeta'], color='orange', label='test') # 保存图到文件 filename = sys.argv[0].split('/')[-1] pyplot.savefig(filename + '_plot.png') pyplot.close() # 运行测试工具以评估 cifar10 数据集上的模型 def run_test_harness(): # 加载数据集 trainX, trainY, testX, testY = load_dataset() # 创建数据生成器 datagen = ImageDataGenerator(rescale=1.0/255.0) # 准备迭代器 train_it = datagen.flow(trainX, trainY, batch_size=128) test_it = datagen.flow(testX, testY, batch_size=128) # 定义模型 model = define_model() # 拟合模型 history = model.fit_generator(train_it, steps_per_epoch=len(train_it), validation_data=test_it, validation_steps=len(test_it), epochs=200, verbose=0) # 评估模型 loss, fbeta = model.evaluate_generator(test_it, steps=len(test_it), verbose=0) print('> loss=%.3f, fbeta=%.3f' % (loss, fbeta)) # 学习曲线 summarize_diagnostics(history) # 入口点,运行测试工具 run_test_harness() |
运行该示例首先拟合模型,然后报告模型在保留测试数据集上的性能。
注意:鉴于算法或评估程序的随机性,或数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
在本例中,我们可以看到模型性能的微小提升,从基线模型的约0.831的F-beta分数提高到增加dropout后的约0.859。
|
1 2 |
(28335, 128, 128, 3) (28335, 17) (12144, 128, 128, 3) (12144, 17) > loss=0.190, fbeta=0.859 |
回顾学习曲线,我们可以看到dropout对训练集和测试集上模型改进速度产生了一定的影响。
过度拟合已得到缓解或延迟,尽管性能可能在运行中期(约epoch 100)开始停滞。
结果表明可能需要进一步的正则化。这可以通过更大的dropout率和/或可能增加权重衰减来实现。此外,可以减小批次大小并减小学习率,这两者都可能进一步减缓模型的改进速度,可能对减少训练数据集的过度拟合产生积极影响。

line plots showing loss and F-beta learning curves for the baseline model with dropout on the train and test datasets on the planet problem
图像数据增强
图像数据增强是一种通过创建数据集中图像的修改版本来人工扩展训练数据集大小的技术。
在更多数据上训练深度学习神经网络模型可以产生更有效的模型,而增强技术可以创建图像的变体,从而提高拟合模型的泛化能力,将其所学知识应用于新图像。
数据增强也可以作为一种正则化技术,在训练数据中添加噪声,并鼓励模型学习对输入中的位置不变的相同特征。
对卫星照片的输入照片进行微小更改可能对这个问题很有用,例如水平翻转、垂直翻转、旋转、缩放以及更多。这些增强可以作为用于训练数据集的*ImageDataGenerator*实例的参数来指定。不应将增强用于测试数据集,因为我们希望评估模型在未修改的照片上的性能。
这要求我们为训练集和测试数据集使用单独的ImageDataGenerator实例,然后从各自的数据生成器创建训练集和测试集的迭代器。例如:
|
1 2 3 4 5 6 |
# 创建数据生成器 train_datagen = ImageDataGenerator(rescale=1.0/255.0, horizontal_flip=True, vertical_flip=True, rotation_range=90) test_datagen = ImageDataGenerator(rescale=1.0/255.0) # 准备迭代器 train_it = train_datagen.flow(trainX, trainY, batch_size=128) test_it = test_datagen.flow(testX, testY, batch_size=128) |
在本例中,训练数据集中的照片将通过随机水平和垂直翻转以及高达90度的随机旋转进行增强。与基线模型一样,训练和测试步骤中的照片的像素值将以相同方式缩放。
为完整起见,下面列出了带有训练数据增强的基线模型在planet数据集上的完整代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 |
# planet数据集的带数据增强的基线模型 import sys from numpy import load from matplotlib import pyplot from sklearn.model_selection import train_test_split from keras import backend from keras.preprocessing.image import ImageDataGenerator from keras.models import Sequential 从 keras.layers 导入 Conv2D 从 keras.layers 导入 MaxPooling2D from keras.layers import Dense from keras.layers import Flatten from keras.optimizers import SGD # 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] # 分割为训练集和测试集 trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1) print(trainX.shape, trainY.shape, testX.shape, testY.shape) return trainX, trainY, testX, testY # 计算多类/多标签分类的 fbeta 分数 def fbeta(y_true, y_pred, beta=2): # 剪裁预测值 y_pred = backend.clip(y_pred, 0, 1) # 计算元素 tp = backend.sum(backend.round(backend.clip(y_true * y_pred, 0, 1)), axis=1) fp = backend.sum(backend.round(backend.clip(y_pred - y_true, 0, 1)), axis=1) fn = backend.sum(backend.round(backend.clip(y_true - y_pred, 0, 1)), axis=1) # 计算精确率 p = tp / (tp + fp + backend.epsilon()) # 计算召回率 r = tp / (tp + fn + backend.epsilon()) # 计算 fbeta,跨类别平均 bb = beta ** 2 fbeta_score = backend.mean((1 + bb) * (p * r) / (bb * p + r + backend.epsilon())) return fbeta_score # 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): model = Sequential() model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same', input_shape=in_shape)) model.add(Conv2D(32, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(64, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(Conv2D(128, (3, 3), activation='relu', kernel_initializer='he_uniform', padding='same')) model.add(MaxPooling2D((2, 2))) model.add(Flatten()) model.add(Dense(128, activation='relu', kernel_initializer='he_uniform')) model.add(Dense(out_shape, activation='sigmoid')) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) return model # 绘制诊断学习曲线 def summarize_diagnostics(history): # 绘制损失 pyplot.subplot(211) pyplot.title('交叉熵损失') pyplot.plot(history.history['loss'], color='blue', label='train') pyplot.plot(history.history['val_loss'], color='orange', label='test') # 绘制准确率 pyplot.subplot(212) pyplot.title('Fbeta') pyplot.plot(history.history['fbeta'], color='blue', label='train') pyplot.plot(history.history['val_fbeta'], color='orange', label='test') # 保存图到文件 filename = sys.argv[0].split('/')[-1] pyplot.savefig(filename + '_plot.png') pyplot.close() # 运行测试工具以评估 cifar10 数据集上的模型 def run_test_harness(): # 加载数据集 trainX, trainY, testX, testY = load_dataset() # 创建数据生成器 train_datagen = ImageDataGenerator(rescale=1.0/255.0, horizontal_flip=True, vertical_flip=True, rotation_range=90) test_datagen = ImageDataGenerator(rescale=1.0/255.0) # 准备迭代器 train_it = train_datagen.flow(trainX, trainY, batch_size=128) test_it = test_datagen.flow(testX, testY, batch_size=128) # 定义模型 model = define_model() # 拟合模型 history = model.fit_generator(train_it, steps_per_epoch=len(train_it), validation_data=test_it, validation_steps=len(test_it), epochs=200, verbose=0) # 评估模型 loss, fbeta = model.evaluate_generator(test_it, steps=len(test_it), verbose=0) print('> loss=%.3f, fbeta=%.3f' % (loss, fbeta)) # 学习曲线 summarize_diagnostics(history) # 入口点,运行测试工具 run_test_harness() |
运行该示例首先拟合模型,然后报告模型在保留测试数据集上的性能。
注意:鉴于算法或评估程序的随机性,或数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
在本例中,我们可以看到性能有所提升,从基线模型的约0.831的F-beta分数提高到带有简单数据增强的基线模型的约0.882。
|
1 2 |
(28335, 128, 128, 3) (28335, 17) (12144, 128, 128, 3) (12144, 17) > loss=0.103, fbeta=0.882 |
回顾学习曲线,我们可以看到过度拟合受到了极大的影响。学习在100个epoch后仍然很好地进行,尽管可能在运行结束时显示出趋于平缓的迹象。结果表明可能需要进一步的增强或其他类型的正则化。
探索额外的图像增强技术可能会很有趣,这些技术可以进一步鼓励学习对输入中的位置不变的特征,例如缩放和平移。

line plots showing loss and F-beta learning curves for the baseline model with data augmentation on the train and test datasets on the planet problem
讨论
我们已经探讨了基线模型的两种不同改进。
结果总结如下,尽管考虑到算法的随机性,我们必须假设这些结果存在一些差异
- 基线+Dropout正则化: 0.859
- 基线 + 数据增强: 0.882
正如预期的那样,正则化技术的加入减慢了学习算法的进程并减少了过度拟合,从而提高了在保留数据集上的性能。很可能将这两种方法与训练epoch数的进一步增加相结合将带来进一步的改进。也就是说,dropout与数据增强的结合。
这仅仅是可以在此数据集上探索的改进类型的开始。除了调整描述的正则化方法外,还可以探索其他正则化方法,例如权重衰减和早停。
值得探索学习算法的变化,例如学习率的变化、学习率计划的使用或自适应学习率(如Adam)。
也可以探索备选的模型架构。预期的基线模型将提供比此问题可能需要的功能更多的容量,并且较小的模型可能训练得更快,进而可能带来更好的性能。
如何使用迁移学习
迁移学习涉及使用在相关任务上训练的模型的部分或全部。
Keras提供了一系列预先训练好的模型,可以通过Keras Applications API完全或部分加载和使用。
迁移学习的一个有用模型是VGG模型之一,例如VGG-16(16层),它在其开发时在ImageNet照片分类挑战中取得了顶尖的成绩。
该模型主要包含两部分:由VGG块组成的模型特征提取部分,以及由全连接层和输出层组成的分类器部分。
我们可以使用模型的特征提取部分,并添加一个针对planet数据集量身定制的新分类器部分。具体来说,我们可以在训练期间固定所有卷积层的权重,而只训练新的全连接层,这些层将学习解释模型提取的特征并进行一系列二元分类。
这可以通过加载VGG-16模型,移除模型输出端的全连接层,然后添加新的全连接层来解释模型输出并进行预测来实现。通过将“*include_top*”参数设置为“*False*”可以自动移除模型分类器部分,这还需要为模型指定输入形状,在本例中为(128, 128, 3)。这意味着加载的模型在最后一个最大池化层处结束,之后我们可以手动添加一个*Flatten*层和新的分类器全连接层。
下面的*define_model()*函数实现了这一点,并返回一个已准备好进行训练的新模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): # 加载模型 model = VGG16(include_top=False, input_shape=in_shape) # 将加载的层标记为不可训练 for layer in model.layers: layer.trainable = False # 添加新的分类器层 flat1 = Flatten()(model.layers[-1].output) class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1) output = Dense(out_shape, activation='sigmoid')(class1) # 定义新模型 model = Model(inputs=model.inputs, outputs=output) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) return model |
创建后,我们可以像以前一样在训练数据集上训练模型。
在这种情况下,不需要进行大量的训练,因为只有新的全连接层和输出层具有可训练的权重。因此,我们将训练epoch数固定为10。
VGG16模型在特定的ImageNet挑战数据集上进行了训练。因此,该模型期望输入图像是居中的。也就是说,将ImageNet训练数据集计算出的每个通道(红、绿、蓝)的平均像素值从输入中减去。
Keras提供了一个函数,可以通过*preprocess_input()*函数对单个照片执行此准备。尽管如此,我们可以通过将“*featurewise_center*”参数设置为“*True*”并通过手动指定用于居中的平均像素值(即ImageNet训练数据集的平均值:[123.68, 116.779, 103.939])来实现相同效果。
|
1 2 3 4 |
# 创建数据生成器 datagen = ImageDataGenerator(featurewise_center=True) # 指定用于居中的imagenet平均值 datagen.mean = [123.68, 116.779, 103.939] |
下面列出了VGG-16模型在planet数据集上进行迁移学习的完整代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 |
# vgg16 transfer learning on the planet dataset import sys from numpy import load from matplotlib import pyplot from sklearn.model_selection import train_test_split from keras import backend from keras.layers import Dense from keras.layers import Flatten from keras.optimizers import SGD from keras.applications.vgg16 import VGG16 from keras.models import Model from keras.preprocessing.image import ImageDataGenerator # 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] # 分割为训练集和测试集 trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1) print(trainX.shape, trainY.shape, testX.shape, testY.shape) return trainX, trainY, testX, testY # 计算多类/多标签分类的 fbeta 分数 def fbeta(y_true, y_pred, beta=2): # 剪裁预测值 y_pred = backend.clip(y_pred, 0, 1) # 计算元素 tp = backend.sum(backend.round(backend.clip(y_true * y_pred, 0, 1)), axis=1) fp = backend.sum(backend.round(backend.clip(y_pred - y_true, 0, 1)), axis=1) fn = backend.sum(backend.round(backend.clip(y_true - y_pred, 0, 1)), axis=1) # 计算精确率 p = tp / (tp + fp + backend.epsilon()) # 计算召回率 r = tp / (tp + fn + backend.epsilon()) # 计算 fbeta,跨类别平均 bb = beta ** 2 fbeta_score = backend.mean((1 + bb) * (p * r) / (bb * p + r + backend.epsilon())) return fbeta_score # 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): # 加载模型 model = VGG16(include_top=False, input_shape=in_shape) # 将加载的层标记为不可训练 for layer in model.layers: layer.trainable = False # 添加新的分类器层 flat1 = Flatten()(model.layers[-1].output) class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1) output = Dense(out_shape, activation='sigmoid')(class1) # 定义新模型 model = Model(inputs=model.inputs, outputs=output) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) return model # 绘制诊断学习曲线 def summarize_diagnostics(history): # 绘制损失 pyplot.subplot(211) pyplot.title('交叉熵损失') pyplot.plot(history.history['loss'], color='blue', label='train') pyplot.plot(history.history['val_loss'], color='orange', label='test') # 绘制准确率 pyplot.subplot(212) pyplot.title('Fbeta') pyplot.plot(history.history['fbeta'], color='blue', label='train') pyplot.plot(history.history['val_fbeta'], color='orange', label='test') # 保存图到文件 filename = sys.argv[0].split('/')[-1] pyplot.savefig(filename + '_plot.png') pyplot.close() # 运行测试工具以评估 cifar10 数据集上的模型 def run_test_harness(): # 加载数据集 trainX, trainY, testX, testY = load_dataset() # 创建数据生成器 datagen = ImageDataGenerator(featurewise_center=True) # specify imagenet mean values for centering datagen.mean = [123.68, 116.779, 103.939] # 准备迭代器 train_it = datagen.flow(trainX, trainY, batch_size=128) test_it = datagen.flow(testX, testY, batch_size=128) # 定义模型 model = define_model() # 拟合模型 history = model.fit_generator(train_it, steps_per_epoch=len(train_it), validation_data=test_it, validation_steps=len(test_it), epochs=20, verbose=0) # 评估模型 loss, fbeta = model.evaluate_generator(test_it, steps=len(test_it), verbose=0) print('> loss=%.3f, fbeta=%.3f' % (loss, fbeta)) # 学习曲线 summarize_diagnostics(history) # 入口点,运行测试工具 run_test_harness() |
运行该示例首先拟合模型,然后报告模型在保留测试数据集上的性能。
注意:鉴于算法或评估程序的随机性,或数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
在此情况下,我们可以看到模型获得了约0.860的F-beta分数,这比基线模型要好,但不如带图像数据增强的基线模型。
|
1 2 |
(28335, 128, 128, 3) (28335, 17) (12144, 128, 128, 3) (12144, 17) > loss=0.152, fbeta=0.860 |
回顾学习曲线,我们可以看到模型能快速拟合数据集,在仅几个训练周期内就表现出明显的过拟合。
结果表明,模型可以通过正则化来解决过拟合问题,并且可能需要对模型或学习过程进行其他更改,以减缓改进的速度。
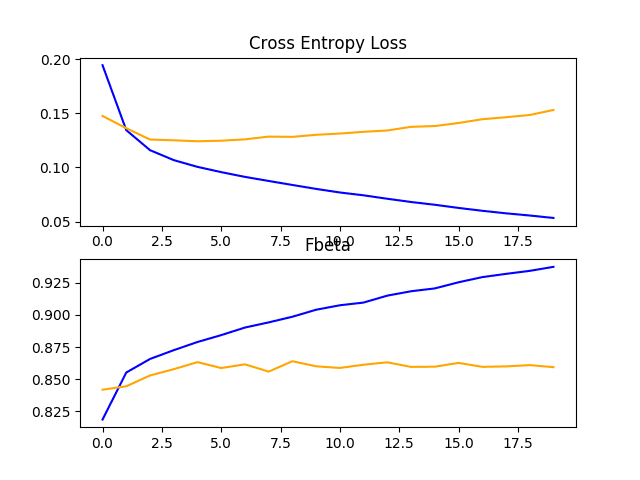
在Planet问题上,VGG-16模型在训练和测试数据集上的损失和F-Beta学习曲线的折线图
VGG-16模型被设计用于将物体照片分类到1000个类别中的一个。因此,它被设计用来捕捉物体的精细特征。我们可以推测,模型在更深层中学到的特征将代表ImageNet数据集中看到的更高阶特征,而这些特征可能与亚马逊雨林卫星照片的分类不直接相关。
为了解决这个问题,我们可以重新拟合VGG-16模型,并允许训练算法微调模型中某些层的权重。在这种情况下,我们将使三个卷积层(以及为保持一致性而添加的池化层)可训练。下面列出了`define_model()`函数的更新版本。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): # 加载模型 model = VGG16(include_top=False, input_shape=in_shape) # 将加载的层标记为不可训练 for layer in model.layers: layer.trainable = False # allow last vgg block to be trainable model.get_layer('block5_conv1').trainable = True model.get_layer('block5_conv2').trainable = True model.get_layer('block5_conv3').trainable = True model.get_layer('block5_pool').trainable = True # 添加新的分类器层 flat1 = Flatten()(model.layers[-1].output) class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1) output = Dense(out_shape, activation='sigmoid')(class1) # 定义新模型 model = Model(inputs=model.inputs, outputs=output) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) |
然后,可以使用此修改重新运行VGG-16在planet数据集上的迁移学习示例。
注意:鉴于算法或评估程序的随机性,或数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
在这种情况下,与直接使用的VGG-16模型特征提取模型相比,我们看到了模型性能的提升,F-beta分数从约0.860提高到约0.879。该分数接近在基线模型中添加图像数据增强后看到F-beta分数。
|
1 2 |
(28335, 128, 128, 3) (28335, 17) (12144, 128, 128, 3) (12144, 17) > loss=0.210, fbeta=0.879 |
回顾学习曲线,我们可以看到模型在运行早期仍然表现出相对较早地拟合训练数据集的过拟合迹象。结果表明,模型可能受益于使用dropout和/或其他正则化方法。
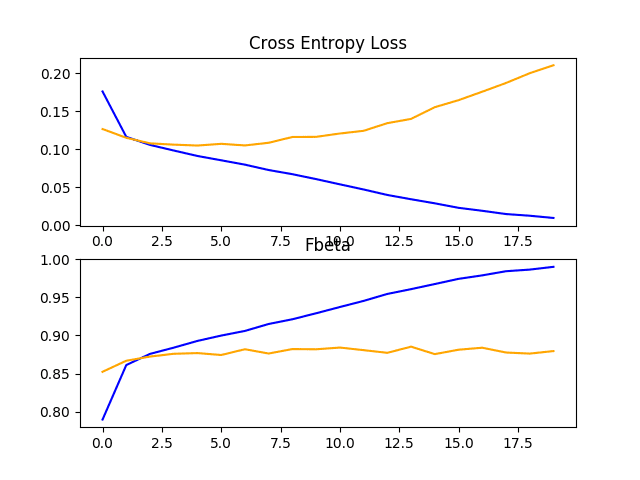
考虑到我们在基线模型中使用数据增强看到了显著的改进,看看是否可以使用数据增强来提高经过微调的VGG-16模型的性能可能很有趣。
在这种情况下,可以使用相同的`define_model()`函数,尽管在这种情况下,`run_test_harness()`可以更新为使用之前章节中进行的图像数据增强。我们预计数据增强的加入会减缓改进的速度。因此,我们将训练周期数从20增加到50,以便为模型提供更多时间来收敛。
下面列出了带有微调和数据增强的VGG-16的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 |
# vgg with fine-tuning and data augmentation for the planet dataset import sys from numpy import load from matplotlib import pyplot from sklearn.model_selection import train_test_split from keras import backend from keras.layers import Dense from keras.layers import Flatten from keras.optimizers import SGD from keras.applications.vgg16 import VGG16 from keras.models import Model from keras.preprocessing.image import ImageDataGenerator # 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] # 分割为训练集和测试集 trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1) print(trainX.shape, trainY.shape, testX.shape, testY.shape) return trainX, trainY, testX, testY # 计算多类/多标签分类的 fbeta 分数 def fbeta(y_true, y_pred, beta=2): # 剪裁预测值 y_pred = backend.clip(y_pred, 0, 1) # 计算元素 tp = backend.sum(backend.round(backend.clip(y_true * y_pred, 0, 1)), axis=1) fp = backend.sum(backend.round(backend.clip(y_pred - y_true, 0, 1)), axis=1) fn = backend.sum(backend.round(backend.clip(y_true - y_pred, 0, 1)), axis=1) # 计算精确率 p = tp / (tp + fp + backend.epsilon()) # 计算召回率 r = tp / (tp + fn + backend.epsilon()) # 计算 fbeta,跨类别平均 bb = beta ** 2 fbeta_score = backend.mean((1 + bb) * (p * r) / (bb * p + r + backend.epsilon())) return fbeta_score # 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): # 加载模型 model = VGG16(include_top=False, input_shape=in_shape) # 将加载的层标记为不可训练 for layer in model.layers: layer.trainable = False # allow last vgg block to be trainable model.get_layer('block5_conv1').trainable = True model.get_layer('block5_conv2').trainable = True model.get_layer('block5_conv3').trainable = True model.get_layer('block5_pool').trainable = True # 添加新的分类器层 flat1 = Flatten()(model.layers[-1].output) class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1) output = Dense(out_shape, activation='sigmoid')(class1) # 定义新模型 model = Model(inputs=model.inputs, outputs=output) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy', metrics=[fbeta]) return model # 绘制诊断学习曲线 def summarize_diagnostics(history): # 绘制损失 pyplot.subplot(211) pyplot.title('交叉熵损失') pyplot.plot(history.history['loss'], color='blue', label='train') pyplot.plot(history.history['val_loss'], color='orange', label='test') # 绘制准确率 pyplot.subplot(212) pyplot.title('Fbeta') pyplot.plot(history.history['fbeta'], color='blue', label='train') pyplot.plot(history.history['val_fbeta'], color='orange', label='test') # 保存图到文件 filename = sys.argv[0].split('/')[-1] pyplot.savefig(filename + '_plot.png') pyplot.close() # 运行测试工具以评估 cifar10 数据集上的模型 def run_test_harness(): # 加载数据集 trainX, trainY, testX, testY = load_dataset() # 创建数据生成器 train_datagen = ImageDataGenerator(featurewise_center=True, horizontal_flip=True, vertical_flip=True, rotation_range=90) test_datagen = ImageDataGenerator(featurewise_center=True) # specify imagenet mean values for centering train_datagen.mean = [123.68, 116.779, 103.939] test_datagen.mean = [123.68, 116.779, 103.939] # 准备迭代器 train_it = train_datagen.flow(trainX, trainY, batch_size=128) test_it = test_datagen.flow(testX, testY, batch_size=128) # 定义模型 model = define_model() # 拟合模型 history = model.fit_generator(train_it, steps_per_epoch=len(train_it), validation_data=test_it, validation_steps=len(test_it), epochs=50, verbose=0) # 评估模型 loss, fbeta = model.evaluate_generator(test_it, steps=len(test_it), verbose=0) print('> loss=%.3f, fbeta=%.3f' % (loss, fbeta)) # 学习曲线 summarize_diagnostics(history) # 入口点,运行测试工具 run_test_harness() |
运行该示例首先拟合模型,然后报告模型在保留测试数据集上的性能。
注意:鉴于算法或评估程序的随机性,或数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
在这种情况下,我们可以看到模型性能的进一步提升,F-beta分数从约0.879提高到约0.891。
|
1 2 |
(28335, 128, 128, 3) (28335, 17) (12144, 128, 128, 3) (12144, 17) > loss=0.100, fbeta=0.891 |
回顾学习曲线,我们可以看到数据增强再次对模型过拟合产生了巨大影响,在这种情况下,它稳定了学习,并将过拟合推迟到约第20个训练周期。

在Planet问题上,VGG-16模型在训练和测试数据集上的微调和数据增强的学习曲线折线图
讨论
在本节中,我们探索了三种不同的迁移学习案例
结果可以总结如下,尽管由于学习算法的随机性,我们必须假设这些结果存在一定的方差
- VGG-16模型: 0.860.
- VGG-16模型 + 微调: 0.879.
- VGG-16模型 + 微调 + 数据增强: 0.891.
选择VGG-16模型在某种程度上是任意的,因为它是一个较小且易于理解的模型。也可以使用其他模型作为迁移学习的基础,例如ResNet,它们可能能取得更好的性能。
此外,更多的微调也可能带来更好的性能。这可能包括调整更多特征提取层的权重,也许使用更小的学习率。这也可能包括修改模型以添加正则化,如dropout。
如何完成模型并进行预测
只要我们有想法、时间和资源来测试它们,模型改进过程就可以继续下去。
在某个时刻,必须选择并采用最终的模型配置。在这种情况下,我们将保持简单,并使用VGG-16迁移学习、微调和数据增强作为最终模型。
首先,我们将通过在整个训练数据集上拟合模型来完成我们的模型,并将模型保存到文件中以供将来使用。然后,我们将加载保存的模型,并使用它对单个图像进行预测。
保存最终模型
第一步是在整个训练数据集上拟合最终模型。
`load_dataset()`函数可以更新为不再将加载的数据集拆分为训练集和测试集。
|
1 2 3 4 5 6 |
# 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] return X, y |
`define_model()`函数可以按照上一节为带有微调和数据增强的VGG-16模型定义的相同方式使用。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): # 加载模型 model = VGG16(include_top=False, input_shape=in_shape) # 将加载的层标记为不可训练 for layer in model.layers: layer.trainable = False # allow last vgg block to be trainable model.get_layer('block5_conv1').trainable = True model.get_layer('block5_conv2').trainable = True model.get_layer('block5_conv3').trainable = True model.get_layer('block5_pool').trainable = True # 添加新的分类器层 flat1 = Flatten()(model.layers[-1].output) class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1) output = Dense(out_shape, activation='sigmoid')(class1) # 定义新模型 model = Model(inputs=model.inputs, outputs=output) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy') return model |
最后,我们只需要一个数据生成器和一个训练数据集的迭代器。
|
1 2 3 4 5 6 |
# 创建数据生成器 datagen = ImageDataGenerator(featurewise_center=True, horizontal_flip=True, vertical_flip=True, rotation_range=90) # 指定用于居中的imagenet平均值 datagen.mean = [123.68, 116.779, 103.939] # 准备迭代器 train_it = datagen.flow(X, y, batch_size=128) |
模型将训练50个周期,之后将通过调用模型的`save()`函数将其保存到H5文件中。
|
1 2 3 4 |
# 拟合模型 model.fit_generator(train_it, steps_per_epoch=len(train_it), epochs=50, verbose=0) # 保存模型 model.save('final_model.h5') |
注意:保存和加载Keras模型需要您的工作站上安装h5py库。
下面列出了在训练数据集上拟合最终模型并将其保存到文件的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
# 将最终模型保存到文件 from numpy import load from keras.preprocessing.image import ImageDataGenerator from keras.applications.vgg16 import VGG16 from keras.models import Model from keras.layers import Dense from keras.layers import Flatten from keras.optimizers import SGD # 加载训练和测试数据集 def load_dataset(): # 加载数据集 data = load('planet_data.npz') X, y = data['arr_0'], data['arr_1'] 返回 X, y # 定义cnn模型 def define_model(in_shape=(128, 128, 3), out_shape=17): # 加载模型 model = VGG16(include_top=False, input_shape=in_shape) # 将加载的层标记为不可训练 for layer in model.layers: layer.trainable = False # allow last vgg block to be trainable model.get_layer('block5_conv1').trainable = True model.get_layer('block5_conv2').trainable = True model.get_layer('block5_conv3').trainable = True model.get_layer('block5_pool').trainable = True # 添加新的分类器层 flat1 = Flatten()(model.layers[-1].output) class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1) output = Dense(out_shape, activation='sigmoid')(class1) # 定义新模型 model = Model(inputs=model.inputs, outputs=output) # 编译模型 opt = SGD(lr=0.01, momentum=0.9) model.compile(optimizer=opt, loss='binary_crossentropy') return model # 运行测试工具以评估 cifar10 数据集上的模型 def run_test_harness(): # 加载数据集 X, y = load_dataset() # 创建数据生成器 datagen = ImageDataGenerator(featurewise_center=True, horizontal_flip=True, vertical_flip=True, rotation_range=90) # specify imagenet mean values for centering datagen.mean = [123.68, 116.779, 103.939] # 准备迭代器 train_it = datagen.flow(X, y, batch_size=128) # 定义模型 model = define_model() # 拟合模型 model.fit_generator(train_it, steps_per_epoch=len(train_it), epochs=50, verbose=0) # 保存模型 model.save('final_model.h5') # 入口点,运行测试工具 run_test_harness() |
运行此示例后,您的当前工作目录中将有一个名为“final_model.h5”的大型91兆字节文件。
进行预测
我们可以使用保存的模型对新图像进行预测。
模型假定新图像是彩色的,并且已经被分割成256x256的方块。
下图是训练数据集中提取的一张图像,具体是文件`train_1.jpg`。

亚马逊雨林卫星图像样本用于预测
将其从训练数据目录复制到当前工作目录,并命名为“sample_image.jpg”,例如
|
1 |
cp train-jpg/train_1.jpg ./sample_image.jpg |
根据训练数据集的映射文件,该文件具有(不分顺序的)标签
- agriculture
- clear
- primary
- water
我们将假装这是一张全新的、未见过的图像,并按照要求准备好,看看如何使用我们保存的模型来预测该图像所代表的标签。
首先,我们可以加载图像并将其强制调整为128x128像素。然后可以将加载的图像调整大小,使其成为数据集中单个样本。像素值也必须进行中心化处理,以匹配模型训练过程中数据准备的方式。
`load_image()`函数实现了这一点,并将返回加载好的、可用于分类的图像。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 加载并准备图像 def load_image(filename): # 加载图像 img = load_img(filename, target_size=(128, 128)) # 转换为数组 img = img_to_array(img) # 重塑为具有 3 个通道的单个样本 img = img.reshape(1, 128, 128, 3) # center pixel data img = img.astype('float32') img = img - [123.68, 116.779, 103.939] return img |
接下来,我们可以像上一节一样加载模型,并调用`predict()`函数来预测图像的内容。
|
1 2 |
# 预测类别 result = model.predict(img) |
这将返回一个17个元素的向量,其中包含介于0和1之间的浮点值,这些值可以被解释为模型对照片可以标记为每个已知标签的置信度的概率。
我们可以将这些概率四舍五入为0或1,然后使用我们之前在`create_tag_mapping()`函数中准备好的反向映射,将值为“1”的向量索引转换为图像的标签。
`prediction_to_tags()`函数实现了这一点,它接受整数到标签的反向映射以及模型为照片预测的向量,并返回预测标签的列表。
|
1 2 3 4 5 6 7 |
# convert a prediction to tags def prediction_to_tags(inv_mapping, prediction): # round probabilities to {0, 1} values = prediction.round() # collect all predicted tags tags = [inv_mapping[i] for i in range(len(values)) if values[i] == 1.0] return tags |
我们可以将所有这些结合起来,为新照片进行预测。完整的示例将在下面列出。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
# make a prediction for a new image from pandas import read_csv from keras.preprocessing.image import load_img from keras.preprocessing.image import img_to_array from keras.models import load_model # create a mapping of tags to integers given the loaded mapping file def create_tag_mapping(mapping_csv): # create a set of all known tags labels = set() for i in range(len(mapping_csv)): # convert spaced separated tags into an array of tags tags = mapping_csv['tags'][i].split(' ') # add tags to the set of known labels labels.update(tags) # convert set of labels to a list to list labels = list(labels) # order set alphabetically labels.sort() # dict that maps labels to integers, and the reverse labels_map = {labels[i]:i for i in range(len(labels))} inv_labels_map = {i:labels[i] for i in range(len(labels))} return labels_map, inv_labels_map # convert a prediction to tags def prediction_to_tags(inv_mapping, prediction): # round probabilities to {0, 1} values = prediction.round() # collect all predicted tags tags = [inv_mapping[i] for i in range(len(values)) if values[i] == 1.0] return tags # 加载并准备图像 def load_image(filename): # 加载图像 img = load_img(filename, target_size=(128, 128)) # 转换为数组 img = img_to_array(img) # 重塑为具有 3 个通道的单个样本 img = img.reshape(1, 128, 128, 3) # center pixel data img = img.astype('float32') img = img - [123.68, 116.779, 103.939] return img # 加载图像并预测类别 def run_example(inv_mapping): # 加载图像 img = load_image('sample_image.jpg') # 加载模型 model = load_model('final_model.h5') # 预测类别 result = model.predict(img) print(result[0]) # map prediction to tags tags = prediction_to_tags(inv_mapping, result[0]) print(tags) # 加载映射文件 filename = 'train_v2.csv' mapping_csv = read_csv(filename) # create a mapping of tags to integers _, inv_mapping = create_tag_mapping(mapping_csv) # 入口点,运行示例 run_example(inv_mapping) |
运行示例首先加载并准备图像,加载模型,然后进行预测。
首先,打印原始的17个元素的预测向量。如果愿意,我们可以美化打印此向量并总结预测的置信度,即照片将被分配给每个标签。
接下来,对预测进行四舍五入,并将包含1值的向量索引反向映射到其标签字符串值。然后打印预测的标签。我们可以看到模型已正确预测了提供照片的已知标签。
可以尝试使用全新的照片重复此测试,例如测试集中的照片,在您手动建议了标签之后。
|
1 2 3 4 5 6 |
[9.0940112e-01 3.6541668e-03 1.5959743e-02 6.8241461e-05 8.5694155e-05 9.9828100e-01 7.4096164e-08 5.5998818e-05 3.6668104e-01 1.2538023e-01 4.6371704e-04 3.7660234e-04 9.9999273e-01 1.9014676e-01 5.6060363e-04 1.4613305e-03 9.5227945e-01] ['agriculture', 'clear', 'primary', 'water'] |
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 调整学习率。探索用于训练基线模型的学习算法的变化,例如替代学习率、学习率调度器或像Adam这样的自适应学习率算法。
- 正则化迁移学习模型。探索将更多正则化技术添加到迁移学习中,例如早期停止、dropout、权重衰减等,并比较结果。
- 测试时自动增强。更新模型以使用测试时预测,例如翻转、旋转和/或裁剪,以查看测试数据集上的预测性能是否可以进一步提高。
如果您探索了这些扩展中的任何一个,我很想知道。
请在下面的评论中发布您的发现。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
API
- Keras图像工具源代码.
- Keras 应用程序 API
- Keras 图像处理 API
- Keras 序列模型 API
- sklearn.metrics.fbeta_score.html API
- sklearn.model_selection.train_test_split API
- Keras度量源代码的旧版本(带有fbeta_score)。
- Keras的F-beta分数,Kaggle Kernel。
文章
- Planet:从太空理解亚马逊,Kaggle竞赛.
- 下载Planet数据集,Kaggle.
- Planet竞赛模型评估,Kaggle.
- Planet:从太空理解亚马逊,第一名获胜者访谈, 2017.
- F1 分数,维基百科
- 精确率和召回率,维基百科.
总结
在本教程中,您学习了如何开发一个卷积神经网络来分类亚马逊热带雨林的卫星照片。
具体来说,你学到了:
- 如何加载和准备亚马逊热带雨林的卫星照片以供建模。
- 如何从零开始开发卷积神经网络进行照片分类并提高模型性能。
- 如何开发最终模型并使用它对新数据进行临时预测。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。







如何进行分类分割,我的意思是为预测图像中的每个类着色,这将更有用,非常感谢您清晰的教程。
您可以使用 Mask RCNN 模型,该模型在本书中有所描述
https://machinelearning.org.cn/deep-learning-for-computer-vision/
太棒了,Jason!非常感谢
谢谢Greg!
亲爱的Jason;
非常感谢您的精彩教程。
可以使用.tif文件格式而不是.jpg文件格式来运行代码吗?
您能否指导一下如何使用坐标系来运行.tif格式?
对于迁移学习,您是否需要区分预训练、训练和验证集?
抱歉,我没有处理TIFF文件的示例。
总的来说,拥有独立的训练/测试/验证数据集是一个好主意。
当我尝试绘制我的卫星图像文件夹中的前9张图像(我已经准备好了)并输入我的文件夹路径“C:/Users/SHAHEEN/Desktop/data/train/train0.jpg”时,它显示FileNotFoundError: [Errno 2] No such file or directory。
请确保您已下载数据集并将其解压缩到当前工作目录中。
太棒了,Jason,真的太棒了。
谢谢!
嗨,Jason,
感谢您的帖子。是否有不使用Keras的`preprocess_input()`函数的原因?
好问题,您可以这样做,而且对于独立应用程序来说,也许应该这样做,但我们同时通过数据增强进行训练,实现了相同的效果。
嗨,Jason,
当我点击下载照片的链接时,我看到的是一个空白页面。有什么想法吗?
这是在Kaggle上吗?
https://www.kaggle.com/c/planet-understanding-the-amazon-from-space/data
下载开始了吗?
不可思议的文章!
我想,如果您尝试不同的模型,如果数据只使用生成器生成一次并保存为二进制矩阵,这是否会节省时间?我猜生成器会即时生成数据,并且每次都为每个模型执行相同的操作。或者,与CNN的计算时间相比,生成器使用的时间可以忽略不计?
谢谢。
我不明白,您在这篇文章中提到的生成器是什么意思?
嗨,Jason,
非常感谢您的精彩教程。我正在按照您的建议,在AWS p3.2x large实例上运行模型开发代码,使用“深度学习AMI (Amazon Linux)”。但我遇到了一个错误:
Error: Attempting to fetch value instead of handling error Internal: no supported devices found for platform CUDA
请建议可能是什么问题。
谢谢,
Aditya
这非常奇怪,我以前没见过。
也许可以确认您选择了正确的环境(source tensorflow…)?
也许可以尝试新实例?
也许可以联系AWS支持?
我无法下载数据集。当我将鼠标悬停在test-jpg.tar.7z上时,下载按钮根本不显示。
您必须先登录Kaggle。
我已经登录了,但仍然没有显示任何下载选项
尝试点击文件。
你必须接受这次比赛的规则
是的。
那些在文件上看到下载选项的人,请先加入提交,然后下载按钮就会出现在文件上
谢谢提示。
我在尝试进行预测时收到一个错误
ValueError: 未知度量函数:fbeta
该函数必须在其使用范围内。确保您已复制所有代码
https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
亲爱的 Jason,
我仔细检查了每一行,复制并运行了您的所有代码,但遇到了与 Dipanjan 相同的错误。然后我将 Keras 和 TensorFlow 降级到与您相同的版本,但预测部分仍然无法工作。
一些人在 TensorFlow 的 GitHub 仓库上发布了关于自定义度量的问题,但没有一个成功。我会继续研究并向您汇报,但您能否检查一下您是否将 fbeta 定义为一个新类?谢谢!
听到这个消息我很难过,我预计您还没有复制所有必需的代码。
尝试复制教程结尾的完整代码示例。
嗯,所以不是有必要重新定义 fbeta 或将自定义度量作为类,在 load_model() 中创建并将其作为对象传递?抱歉打扰您,我之所以这样问是因为 Keras 文档正在使用面向对象的演示,而 GitHub 上的一些人告诉我重写
“model = load_model(‘final_model.h5’)”
推广到
“model = load_model(‘final_model.h5’, custom_objects={‘fbeta’:fbeta})”,但我尝试了,但也没有起作用。
谢谢!
模型未保存 fbeta 度量,因此您在加载模型时不需要定义它,也不需要 custom_objects 参数。
请参阅标题为“保存最终模型”的部分。
没关系,我终于弄明白了。我买了您的 4 本 PDF,它们和这个教程一样精彩!我完成了大多数文本分析的深度学习项目,但从这个教程中学到了很多关于图像处理的知识。谢谢!
谢谢,很高兴听到您解决了问题!
我不清楚为什么数值标签 0-17 必须进行独热编码而不是直接使用。有人能帮我理解吗?谢谢
您是指类标签吗?
它有助于构建问题并通过交叉熵训练模型。
更多关于独热编码的信息,请参阅这篇帖子
https://machinelearning.org.cn/why-one-hot-encode-data-in-machine-learning/
是的,抱歉……类标签……因为它们已经进行了标签编码。谢谢您的回复和资源!
不客气。
在这一步:
photo = load_img(filename, target_size = (128,128))第一个参数不应该是文件或文件路径,而是 csv 吗?
而且,这不应该是:tags = create_file_mappings?我对这一行代码有点不明白。
tags = file_mapping(filename[:-4])
filename 是只调用了字典中的一个键吗?而 -4 只是为了举例说明?
是的,filename 指的是一张图片。请查看 load_dataset() 函数。
我也对 matan 的第二个问题感到好奇……它说 tags = file_mapping,但应该是 create_file_mapping 吗?没有定义 file_mapping?
它检索文件名而不带文件扩展名。
这在后面的几个地方也出现了,file_mapping 没有定义,它应该是 create_file_mapping 吗?
哦,好吧,那很傻,有道理……我唯一的问题是,当我运行那行代码时
tags = file_mapping[filename[:-4]]
我收到一个 KeyError:’FILENAME’……
您知道这是为什么吗?
嗨 Jason
非常有趣的文章。
您提到:“在这种情况下,我们既不处理二分类任务,也不处理多分类任务;相反,这是一个多标签分类任务,标签的数量不平衡,有些标签的使用频率比其他标签高。”
我的问题是,现在不需要平衡了吗?
(对于多分类问题,这通常需要进行。)
是的,如果可能的话,对观察到的标签进行一些平衡是个好主意。
这并非总是可能的。您可以查看模型产生的错误类型,如果它们主要是围绕特定标签,那么您可以考虑使用数据增强或过/欠采样方法来更好地表达该标签在训练数据集中的存在。
嗨 Jason
感谢您的回复。
我一直在查找一些论文和 Stack Overflow 等的讨论,发现对于多标签分类的类别平衡不像多分类问题那样直接。
例如,这里
https://stackoverflow.com/questions/48485870/multi-label-classification-with-class-weights-in-keras
或者这里
https://www.researchgate.net/publication/278699395_Managing_Imbalanced_Data_Sets_in_Multi-label_Problems_A_Case_Study_with_the_SMOTE_Algorithm
您用“这并非总是可能的”是指这个吗?
SMOTE 对表格数据非常有效。我不知道它在计算机视觉中的使用情况,但我预计会使用数据增强。
这是一个很好的问题。我认为可能需要研究/实验才能得到一个好的答案。
谢谢!考虑到时间有限,我将采用一些“启发式”的平衡方法。
这里验证前的额外缩进有什么影响?
history = model.fit_generator(train_it, steps_per_epoch=len(train_it),
validation_data=test_it, validation_steps=len(test_it), epochs=50, verbose=0)
那是一行很长的内容,我将其换成了两行。
谢谢您,先生!
如何让 loss 和 Fbeta 在每个 epoch 后都打印出来,以便查看进度,但更重要的是确认模型正在运行?我使用的是拥有 16 个 CPU 和 64 GB 内存的 Google Cloud Engine 实例,并且带有 dropout 的基线模型,200 个 epoch 已经运行了超过 12 个小时。
verbose=1
您好 Jason,文章写得很好。我正在尝试做类似的事情,有 200 个类。fbeta 从非常低的 0.03 开始(基本上相当于所有都是零或所有都是一)。标签集相对平衡,但无论我如何尝试数据增强、dropout、更多/更少的密集层、不同的优化器,似乎都无法取得进展。您有什么建议吗?
嗯,试试这个清单
https://machinelearning.org.cn/improve-deep-learning-performance/
试试这里的想法
https://machinelearning.org.cn/start-here/#better
您好,首先感谢您的精彩文章,我尝试改编此示例并使用 InceptionResnet-v2(相同数据集),重新训练最后六层并添加与此示例相同的分类层,我的训练损失总是在 0.7 到 0.1 之间,而验证损失总是高于 1(高达 10)(fbeta 分数对于训练和验证相似),我的模型是否过拟合,以及为什么我的 fbeta 分数在损失值(训练和验证)差异很大的情况下仍然相似?
听起来像是过拟合,请参阅此处以确认
https://machinelearning.org.cn/learning-curves-for-diagnosing-machine-learning-model-performance/
仅查看 loss 来判断您是否过拟合。fbeta 只是您用来评估模型的度量。loss 告诉您学习动态。
嗨
我有一个多标签图像分类问题,总共有 3 个标签(Label1、Label2、Label3),每个标签进一步有 3 个选项(L、M、H)
如何编码这种情况,以便我们可以用于训练?
独热编码。
如果我错了,请纠正我
正如我提到的,每个标签都有 3 个附加属性(L、M、H)
假设我们有 3 个输入(001、002 和 003)
并且对于每个输入,我们有一个向量 y,它看起来像
X Y 编码值
001 -> [L, M,L ] -> [ [1,0,0], [0,1,0], [1,0,0] ]
002 -> [H, M,L ] -> [ [0,0,1], [0,1,0], [1,0,0] ]
003 -> [H, H,H ] -> [ [0,0,1], [0,0,1], [0,0,1] ]
我说的对吗?
最后一层将总共有 9 个神经元
例如 model.add(Dense(9,activation=’sigmoid’))?
不太确定是否能一眼看懂。也许可以测试一下看看?
我以这种方式编码了所有标签
001 -> [L, M,L ] -> [ [1,0,0], [0,1,0], [1,0,0] ]
002 -> [H, M,L ] -> [ [0,0,1], [0,1,0], [1,0,0] ]
创建了一个神经网络
并在最后一层,我使用了这个
model.add(Dense(5))
model.add(Reshape( (5, 3) ))
model.add(Activation('softmax'))
“InvalidArgumentError: 输入到 reshape 的张量有 100 个值,但请求的形状有 300”
我认为您需要一个具有 3 个节点的 Dense 层,因为您正在预测 3 个类别标签的概率。
例如:
其实这只是一个想法,我在上面的评论中使用了 3 个标签,实际上我总共有 5 个标签,每个标签都有 3 个(L、M、H)属性。
是的,我尝试了
model.add(Dense(5,activation=’softmax’))
但仍然遇到问题,不知道哪里出错了
“InvalidArgumentError: logits and labels must be broadcastable: logits_size=[15,5] labels_size=[45,5]”
您能看一看这里吗
https://drive.google.com/open?id=156Ic6g-Ldcfy0q5B5tdQuZvTKm-xuFPh
我将非常感谢您,因为我被卡在这里好几天了
如果我使用
model.add(Dense(5,activation=’sigmoid’))
然后我遇到了
“InvalidArgumentError: Incompatible shapes: [15,5] vs. [15]”
如果您有 5 个类别,请确保您使用的是 categorical cross entropy loss,并且您已经对类标签进行了独热编码。
嗨
我需要确认我是否走在正确的方向
以下是详情
场景
我有一个多标签图像分类问题,总共有 5 个标签(Label1、Label2、Label3、Label4 和 Label5),每个标签进一步有 3 个选项(L、M、H)。
实际上,对于每个标签(Label1、Label2、Label3、Label4 和 Label5),我都有一个数字值,例如
Label1 —-> 5
Label2 —-> 90
Label3 —-> 30
Label4 —-> 20
Label5 —-> 67
我将上述数字转换为类别。例如,如果值
0 – 33 —– 我分配了‘L’
34 – 66 —– 我分配了‘M;
67 – 100 — 我分配了‘H’
我的 CSV 文件如下所示
Id Labels
001-01-01 L M L L M
001-01-02 M M H H H
001-01-03 L L L L M
.
.
.
.
300-01-15 M L M L H
在我的 CSV 中,在 Id 旁边,我在 images 文件夹中有图像。
所以首先我将上述标签转换为独热编码,如下所示
001-01-01 -> [L, M,L ] -> [ [1,0,0], [0,1,0], [1,0,0] ]
001-01-02 -> [H, M,L ] -> [ [0,0,1], [0,1,0], [1,0,0] ]
然后我创建了 CNN 并将图像输入网络。
我的最后一层如下所示
model.add(Dense(15))
model.add(Reshape((5,3)))
model.add(Activation('softmax'))
这是解决此类问题的正确方法吗?
我做了研发,但找不到类似的解决方案,所以需要确认,因为我是这个领域的初学者。
我不确定这个方法是否可靠。
这听起来像是一个有 5 个类别的多标签分类,每个标签有 3 个互斥的标签。
如果标签是二元的,那么上面的教程会很合适。相反,需要一种不同的方法,并且可能需要一些试错来确定编码标签的最佳方法。
乍一看,我没有太多好主意,也许是一个多输出模型,每个类别都有一个独热编码——这是我首先想到的一个合理的想法。
嗨
根据我的问题(如上所述),我这样进行了热编码
我将上述数字转换为类别。例如,如果值
0 – 33 —– 我分配了‘L’
34 – 66 —– 我分配了‘M;
67 – 100 — 我分配了‘H’
我的 CSV 文件如下所示
Id ————- > Labels
001-01-01 ————- > L M L L M
001-01-02 ————- > M M H H H
001-01-03 ————- > L L L L M
在我的 CSV 中,在 Id 旁边,我在 images 文件夹中有图像。
所以首先我将上述标签转换为独热编码,如下所示
001-01-01 -> [L, M,L ] -> [ [1,0,0], [0,1,0], [1,0,0] ]
001-01-02 -> [H, M,L ] -> [ [0,0,1], [0,1,0], [1,0,0] ]
然后我创建了 CNN 并将图像输入网络。
我的最后一层如下所示
model.add(Dense(15))
model.add(Reshape((5,3)))
model.add(Activation('softmax'))
我遵循了上述教程来实现这一点,我看到我达到了
loss: 5.9617 – acc: 0.6124 (训练和验证情况)
但在上述教程中,loss 也是(0.something),但在我的情况下是 5.something。
我对准确性测量感到困惑。
请告诉我如何以及什么是正确的方法。
也许尝试模型的其他配置?
也许尝试优化器的其他配置?
也许尝试其他模型?
也许尝试数据的其他准备?
更多建议在这里
https://machinelearning.org.cn/start-here/#better
嗨
我有一个关于模型性能的查询。
正如您在此教程中提到的,您的模型达到了 loss=0.100,fbeta=0.891。
这意味着您的模型达到了 89% 的准确率吗?
请告诉我这是什么意思。
在我的情况下
model.compile(loss=’binary_crossentropy’, optimizer=’adam’, metrics=[‘accuracy’])
loss: 0.5700 – acc: 0.7031 – val_loss: 0.5643 – val_acc: 0.6850
这是什么意思?
不,fbeta 不是准确率。更多关于 fbeta 的信息请参见此处。
https://en.wikipedia.org/wiki/F1_score
嗨,Jason,
我的数据集包含不同格式的图像:png 和 tif。所有数据集都需要相同的格式才能在训练期间获得更好的准确率,还是格式不会影响太多?
像 jpeg、png、tif 等图像格式在模型的准确性上有何不同?
感谢您发布的所有帖子,非常有帮助!
一旦将像素加载到内存中,它可能不会有任何区别。
嗨,Jason,
关于我之前询问的 fbeta 自定义度量问题,我能否知道是否需要自己定义一个“fbeta”变量,例如来自“fbeta(y_true, y_pred, beta=2)”函数
fbeta = fbeta(y_true, y_pred, beta=2)
还是在编译模型时调用函数?如果是,在编译模型时定义 fbeta 时,应该将什么内容准确地传递给 fbeta 函数?
我真的很想知道这个,因为我也注意到在这个教程中,您手动调用 fbeta 函数的唯一一次是在演示 Keras 和 Sklearn 如何为所有 1 的情况产生相同的训练和测试分数时。我认为我拥有正确的函数和代码,但缺少一行定义或正确调用 fbeta,然后再进行模型的预测。
谢谢!
fbeta 仅在评估模型时需要。
最终模型不应保存 fbeta 度量。因此,在加载它时,您不需要定义和使用 fbeta 度量。
如果您确实想保存/加载带有 fbeta 度量的模型,那么只需在 load_model() 函数中使用 custom_objects 参数,并确保在调用之前定义了该函数。
感谢您的教程 Jason。我在工作时看到了一些奇怪的现象。我的训练 loss 先下降,然后在第 8 个 epoch 后开始上升。训练数据肯定不应该发生这种情况。关于如何诊断问题的提示?谢谢!
不客气。
这可能有助于诊断工具
https://machinelearning.org.cn/start-here/#better
特别是这个
https://machinelearning.org.cn/learning-curves-for-diagnosing-machine-learning-model-performance/
你好 Jason,这篇读物太棒了。请问在这些图像分类中,指标是如何计算“正确”预测的数量的?一个预测需要 100% 匹配人类生成的标签才能被计为正确预测吗?例如,如果测试集中的一张图像有 5 个手动生成的标签,那么:(a) 模型预测了其中的 4 个,或者 (b) 模型预测了 7 个标签,其中 5 个是正确的,但有 2 个是多余的,或者 (c) 模型预测了 7 个标签,其中 4 个是正确的,但有 3 个是不正确的,情况如何?谢谢!
准确率计算方法是总正确预测数除以总预测数。
– 4/5 是 0.8 或 80% 的正确率。
– 5/7 约等于 0.71 或 71% 的正确率。
这有帮助吗?
Jason,抱歉我没有说清楚。我想我的问题是:“在图像分类中,如果模型在单个图像预测中正确地识别了部分标签,我们是否应该给模型‘部分学分’?” 我将使用这个虚构的包含 3 张图像的测试集作为示例
图像0 | 标签:A、B、C、D | 模型预测:A、B、C、D
图像1 | 标签:B、G、H、M | 模型预测:B、C、G、H
图像2 | 标签:A、D、F | 模型预测:A、D、F、K
您是否会认为这是 1/3 = 33% 的正确率,因为只有 3 张图像中的 1 张被预测得与手动标记的标签完全相同?
我们是否应该完全忽略图像 1 和图像 2 的尝试?在图像 2 中,模型实际上识别出了所有标签,但还多加了一个;而在图像 1 中,它没有正确预测所有标签。
谢谢!
这取决于训练期间选择的损失函数。
是的,您可以选择以这种方式评估测试集上的预测。
你好,先生,
感谢您提供如此精彩的教程。
我尝试为 MTFL 数据集实现了类似的代码,该数据集包含人脸图像,我们有三个标签:“性别”、“微笑”、“戴眼镜”。
当我尝试运行 `result = model.predict(image)` 然后打印 `result` 时,任何我运行的图像都输出 `[nan, nan, nan]`。
请帮忙。
这听起来像是一个很棒的项目!
听起来可能是权重出现了 NaN、溢出或欠拟合。
也许可以检查一下训练过程中的损失?
也许可以给权重添加正则化?
也许可以对输入进行缩放?
…
你好 Jason,谢谢你的帮助。
我终于发现,当我移除下面这四行代码时,预测就可以正确进行了。
如果我包含这四行,那么任何我预测的图像都会输出 `[0,0,0]`。
model.get_layer(‘block5_conv1’).trainable = True
model.get_layer(‘block5_conv2’).trainable = True
model.get_layer(‘block5_conv3’).trainable = True
model.get_layer(‘block5_pool’).trainable = True
如果您知道原因,请帮忙解答。
我无法解释您的说法。
修改
class1 = Dense(128, activation=’relu’, kernel_initializer=’he_uniform’)(flat1)
推广到
class1 = Dense(128, activation=’softmax’, kernel_initializer=’he_uniform’)(flat1)
对我来说是有效的
感谢您的及时回复。
我注意到一件奇怪的事情是,当我运行 `model.predict` 时,在使用 fbeta 矩阵的模型(“讨论”部分之前的代码)上,它会产生所需的结果。
但是,当我像教程末尾您写的那样保存模型(“保存最终模型”部分),然后加载模型进行预测时,它会给出 NaN 值。
这可能是什么原因?
也许可以确认一下保存和加载是否正确?
也许可以确认一下您是否复制了所有代码?
也许可以确认一下您的环境是最新的?
也许可以尝试重新运行所有内容?
我想检测疾病,我正在尝试阿尔茨海默病数据集,请发送用于单张图像预测的图像分类代码,我有 4 个类别,请将代码发送到我的电子邮件地址。
您可以在此处开始图像分类教程
https://machinelearning.org.cn/start-here/#dlfcv
您能为我推荐如何使用 tiff 图像数据集吗?因为我正在处理另一个只有 tiff 格式图像的数据集,所以我被卡住了。请推荐。
谢谢你。
抱歉,我认为我没有处理 tiff 图像的教程,也许这个可以给您一些想法。
https://machinelearning.org.cn/how-to-load-and-manipulate-images-for-deep-learning-in-python-with-pil-pillow/
Jason,非常喜欢这篇文章。我正在学习神经网络的知识,有一个非常基本的问题:一个神经网络可以识别多个分类吗?因为层的权重和偏差必须与样本数据匹配才能进行调整,所以每次这样调整都会破坏之前的调整。所以在我看来,一个神经网络只能识别一个分类。如果不是,一个神经网络可以识别数百种不同的东西吗?我希望您能指出我理解神经网络局限性的方向。
谢谢!
是的。模型通过示例进行学习,因此它可以对领域中的任何新示例进行预测。是的,一个已经训练好的模型可以无限期地使用——至少直到问题发生变化为止。
也许这有助于理解如何使用训练好的模型进行临时预测。
https://machinelearning.org.cn/how-to-make-classification-and-regression-predictions-for-deep-learning-models-in-keras/
非常感谢!
不客气。
嗨,Jason,
您的计算机视觉书籍和代码中是否涵盖了多标签分类?
是的,本书中出现了此示例的一个版本。
嗨,Jason,
我购买了您的 `machine_learning_mastery_with_python`、`data_preparation_for_machine_learning`、
`imbalanced-classification-with-python` 和 `machine-learning-algorithms-from-scratch`
这些书籍。
您能否告诉我多标签分类问题示例写在哪里?这将非常有帮助。
提前感谢!🙂
抱歉,我没有涵盖多标签分类的书籍,我希望将来能详细介绍这个主题。
嗨,Jason,
一如既往的精彩教程,非常鼓舞人心。谢谢。
我对您的迁移学习 VGG16 模型进行了以下实验,与大家分享。
I) 小评论
– 我无法在 `train_test_split()` 函数上使用“stratify”参数(更合适),因为每个标签类型不再只有一个样本。
– 为了能够加载用我们自己的‘fbeta’指标定义的已训练的 .h5 模型(我在模型拟合结束时编译模型,通过删除 fbeta 指标参数),以便之后我们可以毫无问题地加载模型。
– 我将 `preprocess_input` 函数应用于所有图像,以避免使用您提供的特定值进行特征中心化。
– 为了应用渐进式训练,即使不应用数据增强,我也可以使用 Keras 函数 `ImageDataGenerator()`,但没有任何参数(空的)……因此,之后我们可以将 `fit_generator` 应用于输入-输出模型。
– 因为我们加载了 Keras App VGG16,所以我还使用这个完整的模型来预测亚马逊卫星图像,仅供娱乐……我为示例图像获得了“poncho”类别!
II) 实验
– 我用“Inceptionv3” Keras App 替换了 VGG16,用于特征提取,通常比 VGG16 具有更好的 ImageNet 结果,但令我惊讶的是,我的 fbeta 分数仅为 64.5%。我不知道为什么。
– 我研究了结果对输入像素图像分辨率(64、128 和 224)的敏感性,对于 (64,64) 像素图像,我比 (128,128) 的结果低 2%……但令人惊讶的是,使用更多方形像素 (224,224) 的 fbeta 分数比 (128,128) 低。我不知道为什么。此外,使用 (224,224) 像素分辨率进行训练需要 45 分钟才能完成一个 epoch,而使用 128x128 分辨率只需 15 分钟,时间太多了。
– 我研究了结果对 VGG16 层训练数量(解冻以根据亚马逊图像重新训练)的敏感性,并且当我解冻 VGG16 App 的更多层(例如 block4 加上 block5)时,我获得了 4% 的改进。但当我尝试解冻更多层时,我也得到了“nan”结果。我不知道为什么。
我想尝试比较这种多标签分类技术与图像字幕技术(NLP+图像特征提取),遵循您的图像字幕教程(但将 5 个描述替换为单个描述,并带有相应的多标签词)。我猜这个简单的多标签分类应该表现更好。
再次感谢您精彩的教程。
此致,
JG
做得很好,感谢分享 JG!
你好 Jason,很棒的教程,非常直观。
但是我无法将预测值映射到标签以进行多项预测,我一直收到这个错误。
ValueError:包含多个元素的数组的真值不明确。请使用 a.any() 或 a.all()
您能给我一些建议吗?
很抱歉听到您遇到这个问题,您能确认您的 Keras 和 TensorFlow 库是最新的吗?
此外,这些建议可能有所帮助。
https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
Jason 教授您好
您能否帮助我如何对多个类别进行分类,然后根据分类的类别,如何对该类别内的类别进行分类?
听起来像是层次分类。
我没有示例,但也许您可以开始尝试,我可以回答您在此过程中遇到的更具体的问题。
Jason 教授您好,我终于意识到我的数据集结构与 CIFAR-100 相似。但是,我不知道如何加载我的数据?如何将它们分割成训练集和测试集,就像 CIFAR 数据集那样?
如果您没有在您的网站上涵盖此主题,您能提供一些指导吗?
提前感谢。
这将向您展示如何加载每张图像。
https://machinelearning.org.cn/how-to-load-convert-and-save-images-with-the-keras-api/
这将向您展示如何加载更大的数据集。
https://machinelearning.org.cn/how-to-load-large-datasets-from-directories-for-deep-learning-with-keras/
感谢教程!
在遥感任务中,我们通常最终会得到一个显示不同类别的不同颜色分类图,但在本例中,您只是预测了标签,而不是对输入图像进行分类或分割成相应的标签,例如,我如何知道输入图像中像素(i,j)的类别或标签?
另外,在遥感中,您通常处理尺寸为 5000*5000 的大场景。将这个大场景变成 128x128 的图像块后,我们应该如何将其还原回我们主要的分类场景 (5000*5000)?如果您能解释一下,那就太好了。
是的,这是一个多标签分类任务。
听起来您描述的是目标检测。
我没有遥感图像中目标检测的示例,但也许这可以作为起点。
https://machinelearning.org.cn/how-to-perform-object-detection-in-photographs-with-mask-r-cnn-in-keras/
嗨,Jason,
非常感谢您提供的精彩教程。我真的很喜欢这篇文章。实际上,我正试图将这个多标签分类示例用于我自己的项目,该项目是预测图像的 11 个类别。这是一个多类别分类问题,而不是多标签分类问题。我的数据集包含 2428 张 jpg 图像。但是,在您想要创建数据集的那个部分,对于这行代码 “tags = file_mapping[filename[:-4]]”,我收到了一个错误。我认为这与向量的维度有关。我不知道如何修复它,我真的很感谢您的帮助。另外,我正在使用 Google Colab 运行代码,但是当我尝试在 Google Colab 上运行 Planet 数据集的代码时,它无法创建 npz 文件,这很奇怪。
我找到了这篇文章,您推荐给一些人关于多类别分类问题
https://machinelearning.org.cn/how-to-develop-a-cnn-from-scratch-for-cifar-10-photo-classification/
我最好从那里开始我的工作,而不是处理多标签分类问题?
我真的很感谢您的指导。
不客气。
上面教程中用于加载数据集的代码特定于该特定数据集。您必须编写自定义代码来加载您自己的特定数据集。
每当我使用 `datagen.mean = [123.68, 116.779, 103.939]` 时,并且我打印出来查看值,它们都变成了负数。
也许检查一下您的代码,您可能引入了错误。
Jason 教授您好,
当我尝试运行代码时,在模型评估部分,我总是遇到“fbeta_score() 接受 2 个位置参数,但提供了 3 个位置参数(和 1 个仅关键字参数)”。
您能提供解决该错误的建议吗?谢谢。
你好 Toto…你复制粘贴了代码吗?这可能是导致问题的原因。
你好 James,
我想将我的图像分为三个类别(干燥、潮湿和黑暗)。
以下是代码。
# planet数据集的基线模型
import sys
from numpy import load
from matplotlib import pyplot
from sklearn.model_selection import train_test_split
from keras import backend
from keras.preprocessing.image import ImageDataGenerator
来自 keras.models import Sequential
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
from keras.layers import Dense
from keras.layers import Flatten
from tensorflow.keras.optimizers import SGD
import tensorflow as tf
# 加载训练和测试数据集
def load_dataset()
# 加载数据集
data = load(‘/Data_set.npz’)
X, y = data[‘arr_0’], data[‘arr_1′]
# 分割成训练集和测试集
trainX, testX, trainY, testY = train_test_split(X, y, test_size=0.3, random_state=1)
print(trainX.shape, trainY.shape, testX.shape, testY.shape)
return trainX, trainY, testX, testY
# 计算多类/多标签分类的 fbeta 分数
# def fbeta(y_true, y_pred, beta=2)
# # 裁剪预测
# y_pred = backend.clip(y_pred, 0, 1)
# # 计算要素
# tp = backend.sum(backend.round(backend.clip(y_true * y_pred, 0, 1)), axis=1)
# fp = backend.sum(backend.round(backend.clip(y_pred – y_true, 0, 1)), axis=1)
# fn = backend.sum(backend.round(backend.clip(y_true – y_pred, 0, 1)), axis=1)
# # 计算精确率
# p = tp / (tp + fp + backend.epsilon())
# # 计算召回率
# r = tp / (tp + fn + backend.epsilon())
# # 计算 fbeta,跨类别平均
# bb = beta ** 2
# fbeta_score = backend.mean((1 + bb) * (p * r) / (bb * p + r + backend.epsilon()))
# return fbeta_score
# 定义cnn模型
def define_model(in_shape=(224, 224, 3), out_shape=1)
model = Sequential()
model.add(Conv2D(32, (3, 3), activation=’relu’, kernel_initializer=’he_uniform’, padding=’same’, input_shape=in_shape))
model.add(Conv2D(32, (3, 3), activation=’relu’, kernel_initializer=’he_uniform’, padding=’same’))
model.add(MaxPooling2D((2, 2)))
model.add(Conv2D(64, (3, 3), activation=’relu’, kernel_initializer=’he_uniform’, padding=’same’))
model.add(Conv2D(64, (3, 3), activation=’relu’, kernel_initializer=’he_uniform’, padding=’same’))
model.add(MaxPooling2D((2, 2)))
model.add(Conv2D(128, (3, 3), activation=’relu’, kernel_initializer=’he_uniform’, padding=’same’))
model.add(Conv2D(128, (3, 3), activation=’relu’, kernel_initializer=’he_uniform’, padding=’same’))
model.add(MaxPooling2D((2, 2)))
model.add(Flatten())
model.add(Dense(128, activation=’relu’, kernel_initializer=’he_uniform’))
model.add(Dense(out_shape, activation=’softmax’))
# 编译模型
opt = SGD(lr=0.01, momentum=0.9)
model.compile(optimizer=opt, loss=’categorical_crossentropy’, metrics=[‘accuracy’])
return model
# 绘制诊断学习曲线
def summarize_diagnostics(history)
# 绘制损失
pyplot.subplot(211)
pyplot.title(‘交叉熵损失’)
pyplot.plot(history.history[‘loss’], color=’blue’, label=’train’)
pyplot.plot(history.history[‘val_loss’], color=’orange’, label=’test’)
# 绘制准确率
pyplot.subplot(212)
pyplot.title(‘accuracy’)
pyplot.plot(history.history[‘fbeta’], color=’blue’, label=’train’)
pyplot.plot(history.history[‘val_fbeta’], color=’orange’, label=’test’)
# 保存绘图到文件
filename = ‘/gdrive/MyDrive/’
pyplot.savefig(filename + ‘BaseLine_1.png’)
pyplot.close()
# 运行测试工具以评估 cifar10 数据集上的模型
def run_test_harness()
# 加载数据集
trainX, trainY, testX, testY = load_dataset()
# 创建数据生成器
datagen = ImageDataGenerator(rescale=1.0/255.0)
# 准备迭代器
train_it = datagen.flow(trainX, trainY, batch_size=32)
test_it = datagen.flow(testX, testY, batch_size=32)
# 定义模型
model = define_model()
# 拟合模型
history = model.fit_generator(train_it, steps_per_epoch=len(train_it),
validation_data=test_it, validation_steps=len(test_it), epochs=15, verbose=0)
# 评估模型
loss, fbeta = model.evaluate_generator(test_it, steps=len(test_it), verbose=0)
print(‘> loss=%.3f, fbeta=%.3f’ % (loss, fbeta))
# 学习曲线
summarize_diagnostics(history)
# 入口点,运行测试工具
run_test_harness()
我运行了代码,没有出现错误,但显示“loss=0.00 and accuracy=0.000”。
这是什么意思?有什么问题?
请帮助
抱歉,您的代码太长,我无法阅读和调试。但零损失和零准确率似乎有些矛盾。我建议您检查传递给 `compile()` 函数的参数是否与您打算做的相符。