用于预测空气污染日的概率预测模型

空气污染的特征是地表臭氧浓度。

根据风速和温度等气象测量数据，可以预测明天地表臭氧是否会达到足够高的水平，从而发布公共空气污染警告。

这是一个用于时间序列分类数据集的标准机器学习数据集的基础，简称为“臭氧预测问题”。该数据集描述了休斯顿地区七年来的气象观测数据，以及臭氧水平是否超过了临界空气污染水平。

在本教程中，您将学习如何探索这些数据并开发一个概率预测模型，以预测德克萨斯州休斯顿的空气污染。

完成本教程后，您将了解：

• 如何加载和准备臭氧日标准机器学习预测建模问题。
• 如何开发一个朴素预测模型，并使用Brier技能分数评估预测。
• 如何使用决策树集成开发熟练模型，并通过对成功模型的超参数调优进一步提高技能。

我的新书《时间序列深度学习》将助您启动项目，其中包含所有示例的分步教程和Python源代码文件。

让我们开始吧。

如何开发预测空气污染日的概率预测模型
图片由paramita拍摄，保留部分权利。

教程概述

本教程分为五个部分；它们是：

1. 臭氧预测问题
2. 加载和检查数据
3. 朴素预测模型
4. 集成树预测模型
5. 调整梯度提升

臭氧预测问题

空气污染可定义为地表臭氧含量高，常被称为“坏臭氧”，以区别于高层大气的臭氧。

臭氧预测问题是一个时间序列分类预测问题，它涉及预测第二天是否为高空气污染日（臭氧日）。气象组织可以利用臭氧日的预测来警告公众，以便他们采取预防措施。

该数据集最初由Kun Zhang等人在2006年的论文《预测偏斜偏置随机臭氧日：分析与解决方案》中研究，随后又在其后续论文《预测偏斜偏置随机臭氧日：分析、解决方案及展望》中再次研究。

这是一个具有挑战性的问题，因为高臭氧水平的物理机制（或当时不）完全理解，这意味着预测不能像其他气象预测（如温度和降雨）那样基于物理模拟。

该数据集被用作开发预测模型的基础，这些模型除了少数已知与实际化学过程相关的变量外，还使用了大量可能或可能不与预测臭氧水平相关的变量。

然而，环境科学家普遍认为，目前尚未探索的大量其他特征很可能有助于构建高度准确的臭氧预测模型。然而，对这些特征究竟是什么以及它们在臭氧形成中如何相互作用知之甚少。[...]今天的环境科学尚不知道如何使用它们。这为数据挖掘提供了绝佳的机会。

— 预测偏斜偏置随机臭氧日：分析与解决方案，2006。

预测次日高地表臭氧水平是一个具有挑战性的问题，已知其本质是随机的。这意味着预计将存在预测误差。因此，最好以概率方式对预测问题进行建模，并根据前一天或几天观测到的数据，预测臭氧日或非臭氧日的概率。

该数据集包含德克萨斯州休斯顿、加尔维斯顿和布拉佐里亚地区七年（1998-2004年，共2536天）的每日气象变量观测数据，以及是否出现臭氧日。

每天共观测到72个变量，其中许多变量被认为与预测问题相关，其中10个变量已根据物理学证实相关。

[...]在这72个特征中，只有约10个特征已被环境科学家证实有用且相关，而其他60个特征的关联性目前尚无经验或理论信息。然而，空气质量控制科学家长期以来一直在猜测其中一些特征可能有用，但尚未能发展理论或使用模拟来证明其关联性。

— 预测偏斜偏置随机臭氧日：分析与解决方案，2006。

有24个变量跟踪每小时的风速，另有24个变量跟踪一天中每小时的温度。数据集提供了两个版本，测量值的平均周期不同，分别为1小时和8小时。

似乎缺少但可能有用的是每天观测到的臭氧值，而不是二分法的臭氧日/非臭氧日。参数模型中使用的其他测量值也未提供。

有趣的是，一个基于1999年EPA指南《臭氧预报程序开发指南》中描述的参数臭氧预报模型被用作基线。该文档还描述了验证臭氧预报系统的标准方法论。

总之，这是一个具有挑战性的预测问题，因为

• 变量数量庞大，其重要性通常未知。
• 输入变量及其相互关系可能随时间变化。
• 许多变量存在缺失观测值，需要进行处理。
• 非臭氧日（非事件）远多于臭氧日（事件），导致类别高度不平衡。

加载和检查数据

该数据集可从UCI机器学习存储库获取。

• 臭氧水平检测数据集

本教程中，我们将只查看8小时数据。下载“eighthr.data”并将其放置在当前工作目录中。

检查数据文件，我们可以看到不同尺度的观测值。

浏览文件，例如到2003年初，我们可以看到缺失的观测值用“?”标记。

首先，我们可以使用read_csv() 函数将数据加载为 Pandas DataFrame。数据没有标题，我们可以解析第一列中的日期并将其用作索引；完整的示例如下所示。

运行示例确认有2534天的数据和73个变量。

我们还可以看到类别不平衡的性质，其中略多于93%的日子是非臭氧日，而大约6%的日子是臭氧日。

我们还可以绘制七年间输出变量的折线图，以了解臭氧日是否发生在一年中的特定时间。

运行示例会创建七年间输出变量的折线图。

我们可以看到，每年的年中都有臭氧日群集：北半球的夏季或温暖月份。

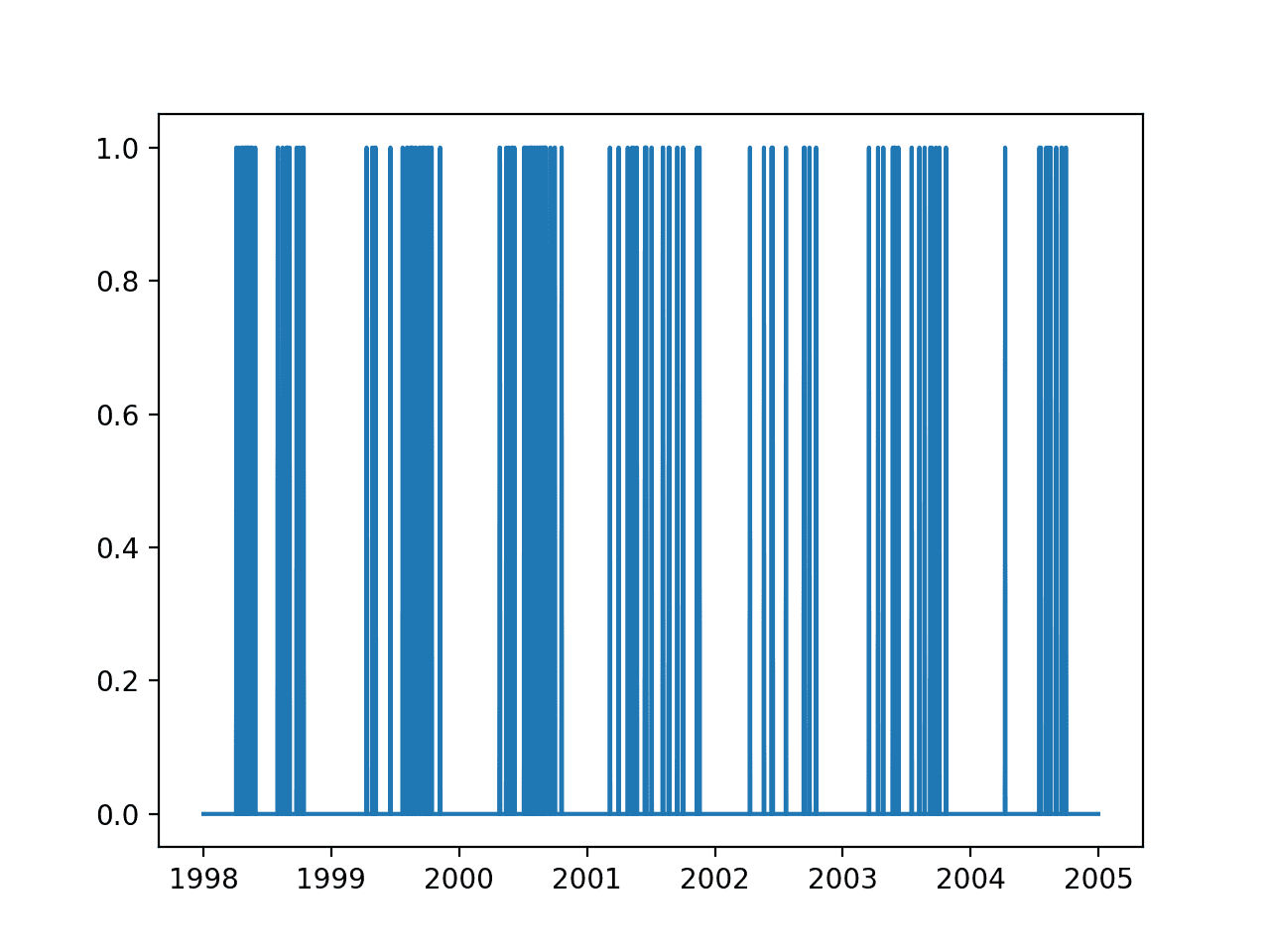
输出变量七年来的折线图

通过简要回顾观测结果，我们可以对如何准备数据有了一些想法。

• 缺失数据需要处理。
• 最简单的框架是根据今天的观测值预测明天的臭氧日。
• 温度可能与季节或一年中的时间相关，并且可能是一个有用的预测因子。
• 数据变量可能需要缩放（归一化），甚至可能需要标准化，具体取决于所选的算法。
• 预测概率将提供比预测类别值更细致的见解。
• 也许我们可以用五年（约72%）来训练模型，用剩下的两年（约28%）来测试模型。

我们可以进行一些最少的数据准备工作。

以下示例加载数据集，将缺失观测值替换为0.0，将数据构造成一个监督学习问题（根据今天的观测值预测明天的臭氧），并根据两年大致天数将数据拆分为训练集和测试集。

您可以探索其他替换缺失值的方法，例如填充平均值。此外，2004年是闰年，因此数据拆分为训练集和测试集并非严格的5-2年拆分，但对于本教程来说已经足够接近。

运行示例将训练集和测试集保存到 CSV 文件，并总结了这两个数据集的形状。

朴素预测模型

一个朴素的模型会预测每天臭氧日的概率。

这是一种朴素的方法，因为它除了事件的基本发生率之外不使用任何信息。在气象预报的验证中，这被称为气候学预报。

我们可以从训练数据集中估计臭氧日的概率，如下所示。

然后，我们可以预测测试数据集中每天臭氧日的朴素概率。

一旦我们有了预测，我们就可以对其进行评估。

评估概率预测的有用指标是布里尔分数。该分数可以被认为是预测概率（例如5%）与预期概率（0%或1%）之间的均方误差。它是测试数据集中每天所犯错误的平均值。

我们感兴趣的是最小化布里尔分数，值越小越好，例如误差越小。

我们可以使用scikit-learn库中的brier_score_loss()函数来评估预测的布里尔分数。

一个模型要想具有技巧性，其得分必须优于朴素预测模型的得分。

我们可以通过计算布里尔技巧分数 (BSS) 来使其显而易见，该分数根据朴素预测对布里尔分数 (BS) 进行归一化。

我们期望朴素预测计算出的BSS为0.0。展望未来，我们感兴趣的是最大化这个分数，即更大的BSS分数更好。

朴素预测的完整示例如下。

注意：由于算法或评估过程的随机性，或者数值精度的差异，您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。

运行示例，我们可以看到臭氧日事件的朴素概率约为7.2%。

使用基本发生率作为预测，布里尔技巧为0.039，预期布里尔技巧分数为0.0（忽略符号）。

我们现在准备探索一些机器学习方法，看看我们是否能为这个预测增加技巧。

请注意，原始论文直接使用精确度和召回率评估方法的技能，这是一种令人惊讶的方法，用于在方法之间进行直接比较。

也许你可以探索的另一个衡量标准是ROC曲线下面积（ROC AUC）。绘制最终模型的ROC曲线将允许模型操作员选择一个阈值，以在真阳性（命中）和假阳性（误报）率之间提供所需的平衡水平。

集成树预测模型

原始论文报道了袋装决策树取得了一些成功。

尽管我们选择的归纳学习器并非详尽无遗，但本文表明归纳学习可以是臭氧水平预测的首选方法，并且基于集成的概率树比现有方法提供更好的预测（更高的召回率和精确率）。

— 预测偏斜偏置随机臭氧日：分析与解决方案，2006。

这并不奇怪，原因有以下几点

• 袋装决策树不需要任何数据缩放。
• 袋装决策树会自动执行一种特征选择，忽略不相关的特征。
• 袋装决策树预测的概率校准合理（例如与SVM不同）。

这表明在测试机器学习算法解决问题时，这是一个很好的起点。

我们可以通过快速抽查scikit-learn库中一组标准集成树方法的性能来快速开始，这些方法采用默认配置，并将树的数量设置为100。

具体来说，这些方法是

• 袋装决策树（BaggingClassifier）
• 极端随机树（ExtraTreesClassifier）
• 随机梯度提升（GradientBoostingClassifier）
• 随机森林（RandomForestClassifier）

首先，我们必须将训练和测试数据集拆分为输入（X）和输出（y）组件，以便我们可以拟合sklearn模型。

我们还需要朴素预测的布里尔分数，以便正确计算新模型的布里尔技能分数。

我们可以泛化地评估单个 scikit-learn 模型的技能。

下面定义了名为 evaluate_once() 的函数，该函数拟合并评估给定的已定义和配置的 scikit-learn 模型，并返回布里尔技能分数 (BSS)。

集成树是一种随机机器学习方法。

这意味着当在相同数据上训练相同模型的相同配置时，它们会做出不同的预测。为了纠正这一点，我们可以多次评估给定模型，例如10次，并计算每次运行的平均技能。

以下函数将评估给定模型10次，打印平均BSS分数，并返回用于分析的分数总体。

我们现在准备评估一套集成决策树算法。

完整的示例如下所示。

运行示例总结了每个模型在10次运行中平均的BSS。

注意：由于算法或评估过程的随机性，或者数值精度的差异，您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。

从平均BSS分数来看，表明极端随机树、随机梯度提升和随机森林模型最具技巧。

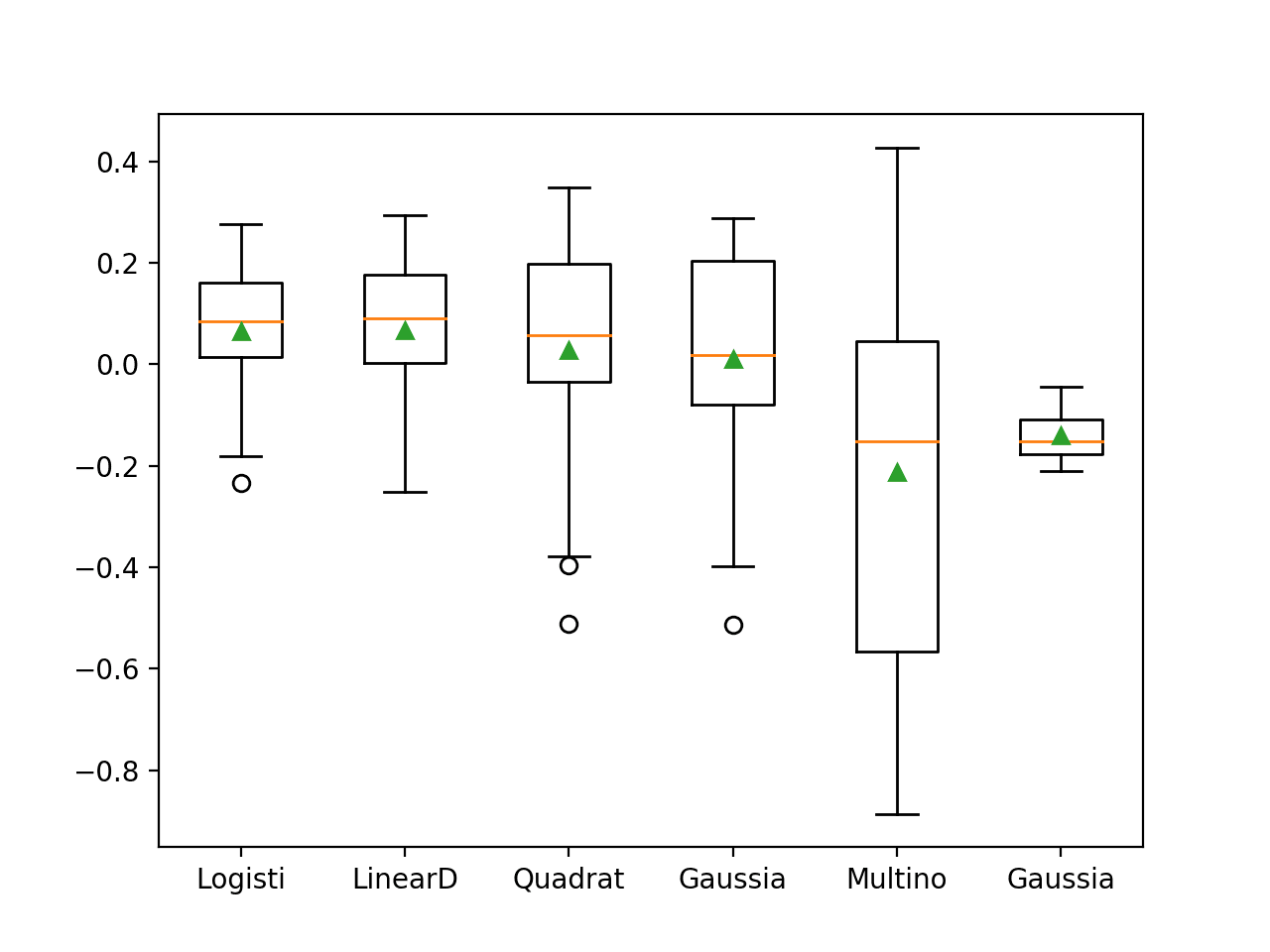
绘制了每个模型分数的箱线图。

所有模型的所有运行都显示出优于朴素预测的技能（正分数），这非常令人鼓舞。

极端随机树、随机梯度提升和随机森林的BSS分数分布都看起来令人鼓舞。

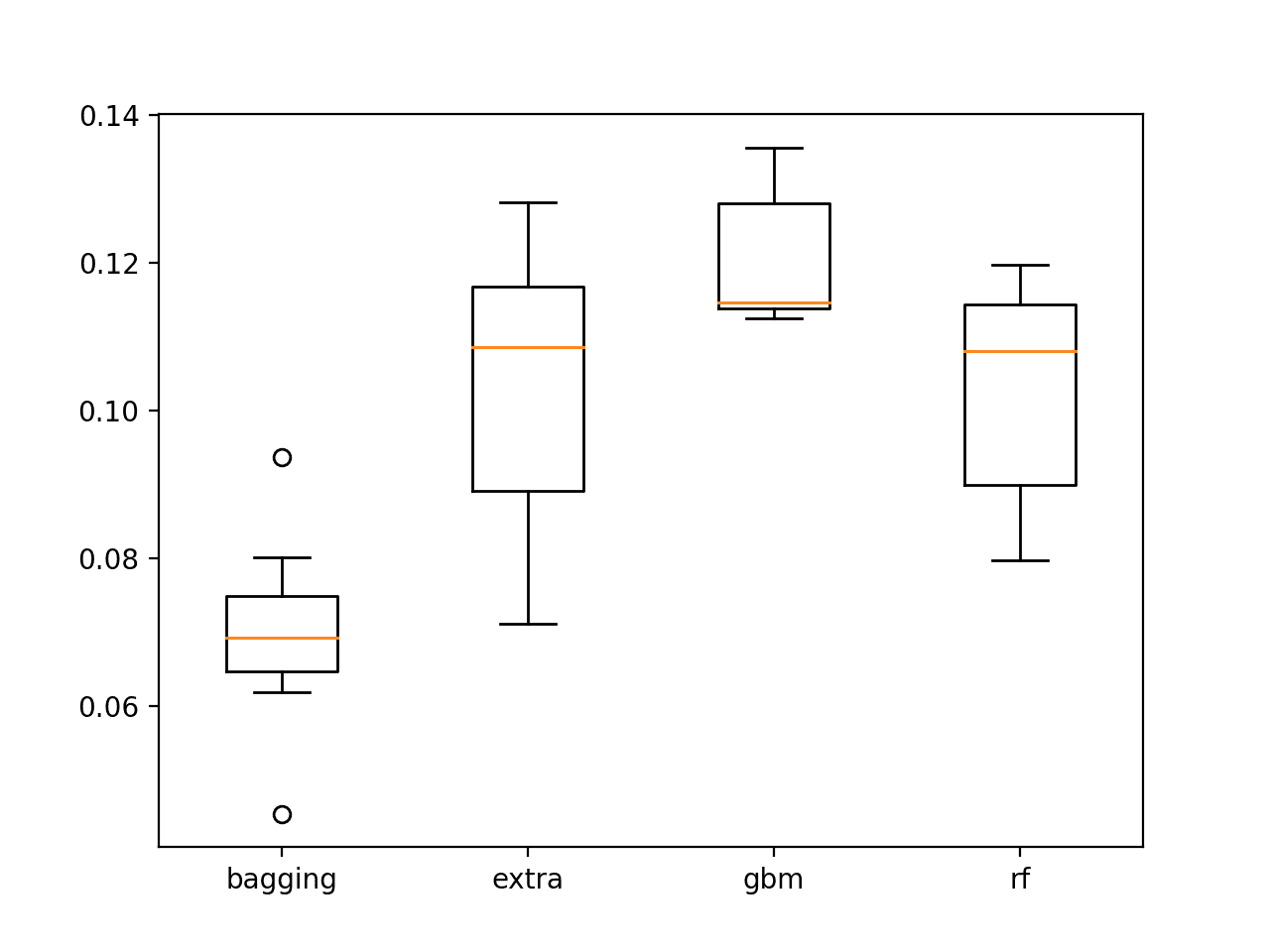
集成决策树在测试集上的BSS分数箱线图

调整梯度提升

鉴于随机梯度提升看起来很有前景，值得探讨模型性能是否可以通过一些参数调优进一步提升。

模型有许多参数可以调整，但调整模型的一些良好启发式方法包括：

• 降低学习率（learning_rate）同时增加决策树的数量（n_estimators）。
• 增加决策树的最大深度（max_depth），同时减少可用于拟合树的样本数量（samples）。

与其网格搜索值，我们可以根据这些原则抽查一些参数。如果您有时间和计算资源，可以自己探索这些参数的网格搜索。

我们将比较四种 GBM 模型配置

• 基线：如上一节中测试的（learning_rate=0.1，n_estimators=100，subsample=1.0，max_depth=3）
• lr，学习率较低，树更多（learning_rate=0.01，n_estimators=500，subsample=1.0，max_depth=3）
• depth，增加最大树深度并减少数据集采样（learning_rate=0.1，n_estimators=100，subsample=0.7，max_depth=）
• all，包含所有修改。

完整的示例如下所示。

运行示例将打印每个模型在10次运行中平均的BSS，用于每种配置。

注意：由于算法或评估过程的随机性，或者数值精度的差异，您的结果可能会有所不同。请考虑多次运行示例并比较平均结果。

结果表明，单独改变学习率和树的数量就比默认配置有所提升。

结果还表明，包含所有更改的“all”配置产生了最佳的平均BSS。

创建了每种配置的BSS分数箱线图。我们可以看到，包含所有更改的配置明显优于基线模型和其他配置组合。

也许通过对模型参数进行微调，甚至可能获得进一步的改进。

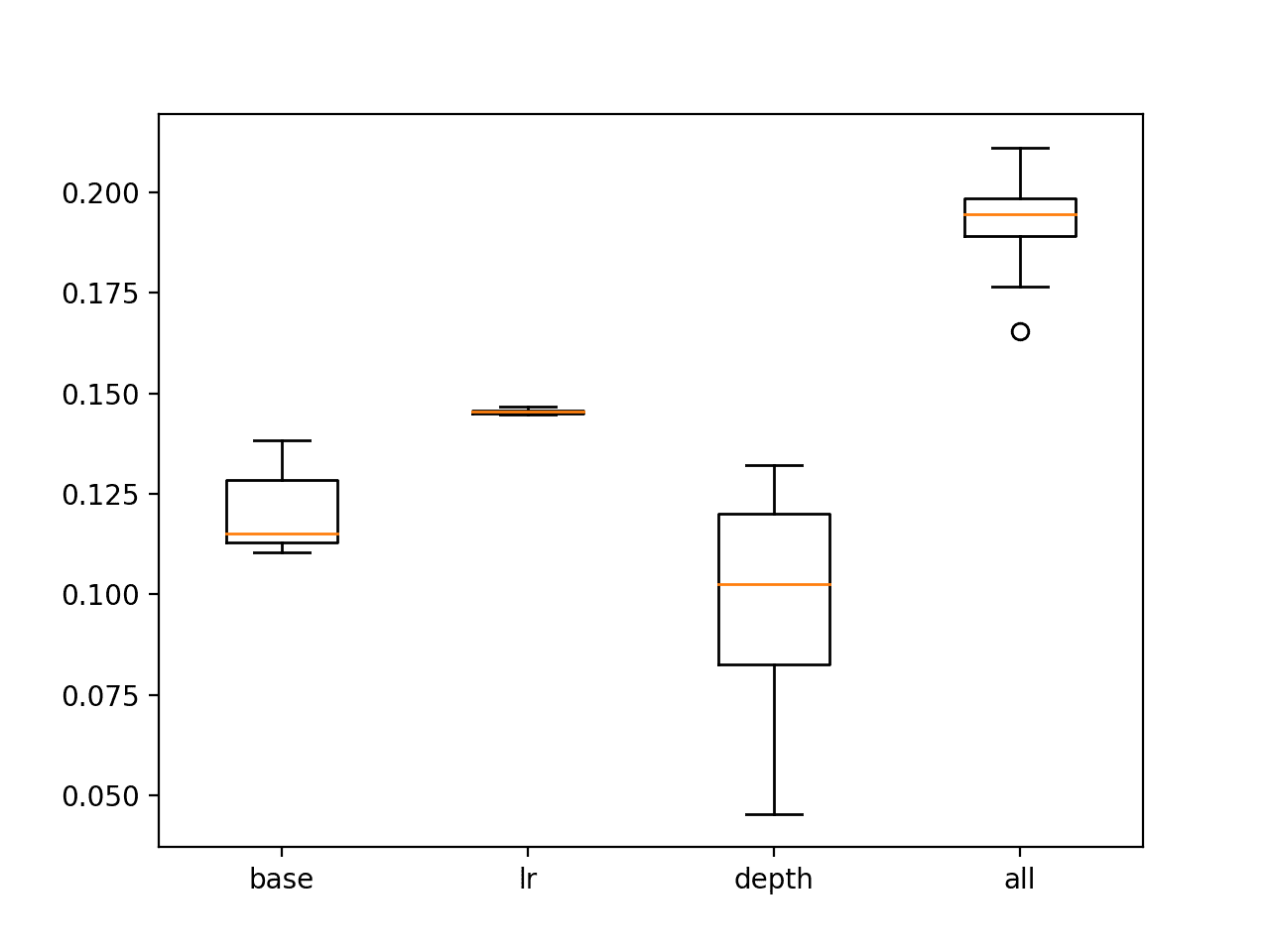
经过调优的GBM模型在测试集上的BSS分数箱线图

有趣的是，获取论文中描述的参数模型以及使用它所需的数据，以便将其技能与此最终模型的技能进行比较。

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

• 探索使用来自多个先前日期的观测值来构建模型。
• 探索使用ROC曲线图和ROC AUC指标进行模型评估。
• 网格搜索梯度提升模型参数，并可能探索其他实现，例如XGBoost。

如果您探索了这些扩展中的任何一个，我很想知道。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

• 臭氧水平检测数据集，UCI机器学习存储库.
• 预测偏斜偏置随机臭氧日：分析与解决方案, 2006.
• 预测偏斜偏置随机臭氧日：分析、解决方案及展望, 2008.
• CAWCR 验证页面
• 维基百科上的受试者工作特征

总结

在本教程中，您学习了如何开发一个概率预测模型，以预测德克萨斯州休斯顿的空气污染。

具体来说，你学到了：

• 如何加载和准备臭氧日标准机器学习预测建模问题。
• 如何开发一个朴素预测模型，并使用Brier技能分数评估预测。
• 如何使用决策树集成开发熟练模型，并通过对成功模型的超参数调优进一步提高技能。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

...只需几行python代码

在我的新电子书中探索如何实现
用于时间序列预测的深度学习

它提供关于以下主题的自学教程：
CNN、LSTM、多元预测、多步预测等等...

最终将深度学习应用于您的时间序列预测项目

跳过学术理论。只看结果。

查看内容