通常情况下,开发概率模型本身就具有挑战性,当病例分布存在偏差,即不平衡数据集时,这种挑战性会更大。
Haberman 数据集描述了 20 世纪 50 年代和 60 年代乳腺癌患者五年或更长的生存情况,其中大部分是幸存的患者。这个标准的机器学习数据集可以作为开发概率模型的基础,该模型可以根据患者的一些详细信息来预测其生存概率。
鉴于数据集中病例分布的偏差,必须仔细考虑预测模型的选择,以确保预测的概率是校准过的;同时也要仔细考虑模型评估的选择,以确保模型是根据其预测概率的准确性来选择,而不是根据生还或未生还的生硬类别标签。
在本教程中,您将学习如何开发一个模型来预测不平衡数据集上患者的生存概率。
完成本教程后,您将了解:
- 如何加载和探索数据集,并为数据准备和模型选择提供思路。
- 如何评估一系列概率模型,并通过适当的数据准备来提高它们的性能。
- 如何拟合最终模型,并使用它来预测特定病例的概率。
开始您的项目,请参阅我的新书《Python 中的不平衡分类》,其中包含分步教程以及所有示例的Python 源代码文件。
让我们开始吧。

如何开发乳腺癌患者生存的概率模型
照片由 Tanja-Milfoil 拍摄,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- Haberman 乳腺癌生存数据集
- 探索数据集
- 模型测试和基线结果
- 评估概率模型
- 概率算法评估
- 带缩放输入的模型评估
- 带幂变换的模型评估
- 对新数据进行预测
Haberman 乳腺癌生存数据集
在这个项目中,我们将使用一个小的乳腺癌生存数据集,通常称为“Haberman 数据集”。
该数据集描述了乳腺癌患者的数据,结果是患者的生存情况。具体来说,患者是否存活了五年或更长时间,或者患者是否未存活。
这是在不平衡分类研究中使用的标准数据集。根据数据集描述,这些手术是在 1958 年至 1970 年间在芝加哥大学 Billings Hospital 进行的。
数据集中有 306 个样本,有 3 个输入变量;它们是:
- 患者手术时的年龄。
- 手术年份的两位数字。
- 检测到的“阳性腋下淋巴结”数量,这是衡量癌症扩散程度的指标。
因此,除了数据集中可用的信息外,我们无法控制构成数据集的样本选择或在这些样本中使用哪些特征。
尽管该数据集描述了乳腺癌患者的生存情况,但考虑到数据集规模较小,并且数据是基于几十年前的乳腺癌诊断和手术,因此基于此数据集构建的任何模型都不太可能具有泛化能力。
明确地说,我们不是在“解决乳腺癌”。我们正在研究一个标准的不平衡分类数据集。
你可以在此处了解更多关于此数据集的信息:
我们将选择将此数据集框架化为患者生存概率的预测。
也就是说:
给定患者的乳腺癌手术细节,患者生存五年或更长时间的概率是多少?
这将为探索可以预测概率而非类别标签的概率算法,以及用于评估预测概率而非类别标签的模型的指标奠定基础。
接下来,我们仔细看看数据。
想要开始学习不平衡分类吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
探索数据集
首先,下载数据集并将其保存在当前工作目录中,名称为“haberman.csv”。
查看文件内容。
文件的前几行应如下所示
|
1 2 3 4 5 6 7 8 9 10 11 |
30,64,1,1 30,62,3,1 30,65,0,1 31,59,2,1 31,65,4,1 33,58,10,1 33,60,0,1 34,59,0,2 34,66,9,2 34,58,30,1 ... |
我们可以看到,患者的年龄如 30 或 31(第 1 列),手术年份如 64 和 62,分别代表 1964 年和 1962 年(第 2 列),以及“腋下淋巴结”的值为 1 和 0。
所有值都是数字;具体来说,它们是整数。没有用“?”字符标记的缺失值。
我们还可以看到,类别标签(第 3 列)的值是 1 表示患者生存,2 表示患者未生存。
首先,我们可以加载 CSV 数据集,并使用五数概括法总结每一列。可以使用 read_csv() Pandas 函数将数据集加载为DataFrame,指定位置和列名,因为没有标题行。
|
1 2 3 4 5 6 7 |
... # 定义数据集位置 filename = 'haberman.csv' # 定义数据集列名 columns = ['age', 'year', 'nodes', 'class'] # 将csv文件加载为数据框 dataframe = read_csv(filename, header=None, names=columns) |
然后,我们可以调用 describe() 函数来生成每列的五数概括报告,并打印报告内容。
列的五数概括包含有用的细节,如最小值和最大值,以及平均值和标准差(如果变量是高斯分布则很有用),以及 25%、50% 和 75% 的四分位数(如果变量不是高斯分布则很有用)。
|
1 2 3 4 |
... # 总结每一列 report = dataframe.describe() print(report) |
将所有内容汇总起来,加载和总结数据集列的完整示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 加载并汇总数据集 from pandas import read_csv # 定义数据集位置 filename = 'haberman.csv' # 定义数据集列名 columns = ['age', 'year', 'nodes', 'class'] # 将csv文件加载为数据框 dataframe = read_csv(filename, header=None, names=columns) # 总结每一列 report = dataframe.describe() print(report) |
运行该示例将加载数据集,并报告三个输入变量和一个输出变量的五数概括。
从年龄来看,我们可以看到最年轻的患者是 30 岁,最年长的患者是 83 岁;这是一个相当大的范围。患者的平均年龄约为 52 岁。如果癌症的发生是某种程度上随机的,我们可以预期这种分布是高斯的。
我们可以看到,所有手术都发生在 1958 年至 1969 年之间。如果乳腺癌患者的数量随时间大致固定,我们可以预期该变量遵循均匀分布。
我们可以看到淋巴结的值在 0 到 52 之间。这可能与淋巴结相关的癌症诊断有关。
|
1 2 3 4 5 6 7 8 9 |
年龄 年份 淋巴结 类别 计数 306.000000 306.000000 306.000000 306.000000 平均值 52.457516 62.852941 4.026144 1.264706 标准差 10.803452 3.249405 7.189654 0.441899 最小值 30.000000 58.000000 0.000000 1.000000 25% 44.000000 60.000000 0.000000 1.000000 50% 52.000000 63.000000 1.000000 1.000000 75% 60.750000 65.750000 4.000000 2.000000 最大值 83.000000 69.000000 52.000000 2.000000 |
所有变量都是整数。因此,查看每个变量的直方图以了解变量的分布可能很有帮助。
这可能有助于我们在之后选择对数据分布或数据尺度敏感的模型,在这种情况下,我们可能需要转换或重新缩放数据。
我们可以通过调用 hist() 函数来创建 DataFrame 中每个变量的直方图。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 创建每个变量的直方图 from pandas import read_csv from matplotlib import pyplot # 定义数据集位置 filename = 'haberman.csv' # 定义数据集列名 columns = ['age', 'year', 'nodes', 'class'] # 将csv文件加载为数据框 dataframe = read_csv(filename, header=None, names=columns) # 创建每个变量的直方图 dataframe.hist() pyplot.show() |
运行该示例将为每个变量创建直方图。
我们可以看到,年龄似乎呈现高斯分布,正如我们所料。我们还可以看到,年份大多呈现均匀分布,但在第一年有一个异常值,显示的操作数量几乎翻倍。
我们可以看到淋巴结呈现指数型分布,大部分样本显示 0 个淋巴结,之后有一个长尾。为了使该分布不那么集中,可能需要进行转换。
最后,我们可以看到两个类别的分布不均,显示生存病例大约是未生存病例的 2 到 3 倍。
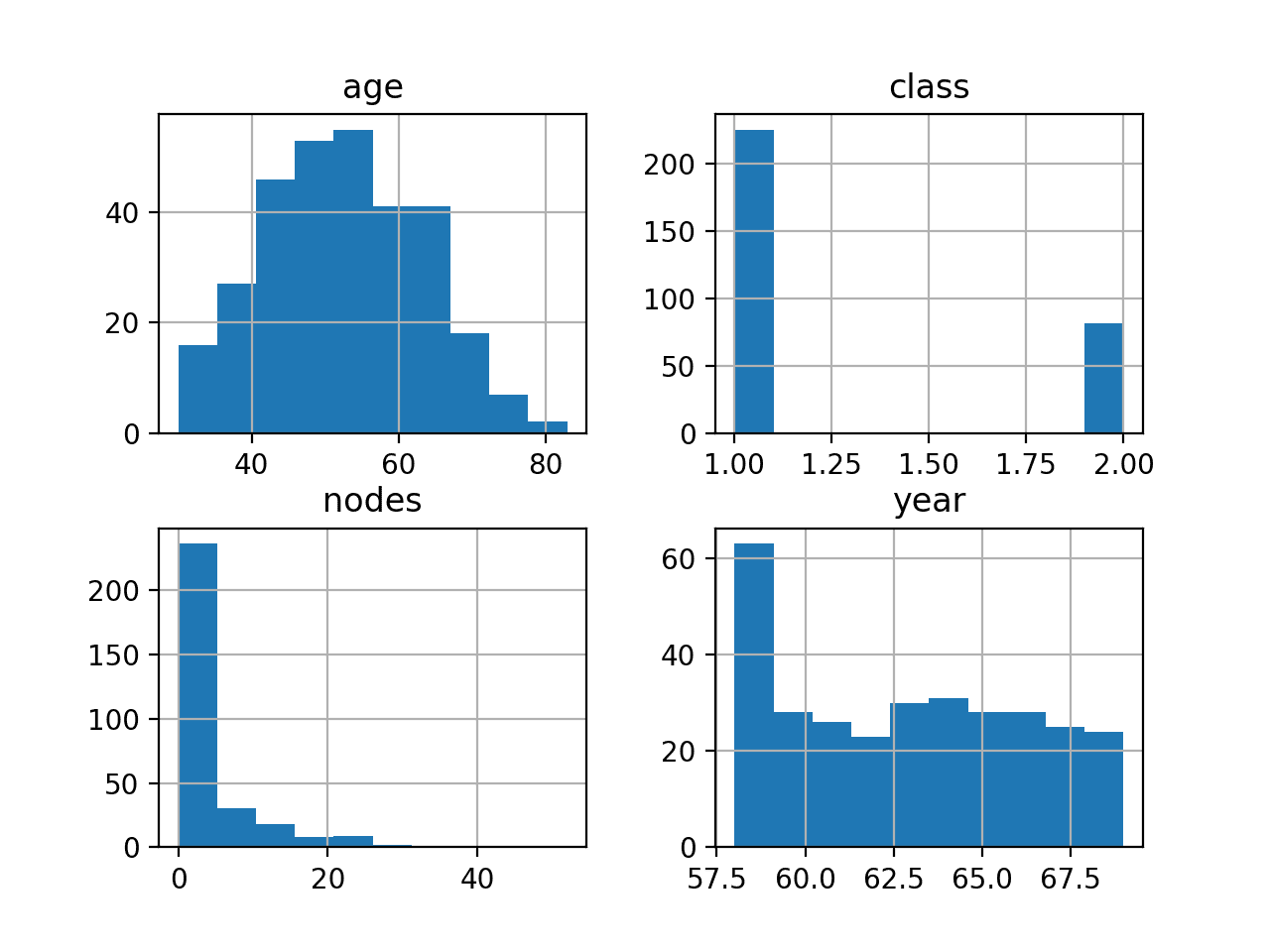
Haberman 乳腺癌生存数据集各变量的直方图
了解数据集的实际不平衡程度可能会有所帮助。
我们可以使用 Counter 对象来计算每个类别中的样本数量,然后使用这些计数来汇总分布。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 汇总类别比例 from pandas import read_csv from collections import Counter # 定义数据集位置 filename = 'haberman.csv' # 定义数据集列名 columns = ['age', 'year', 'nodes', 'class'] # 将csv文件加载为数据框 dataframe = read_csv(filename, header=None, names=columns) # 总结类别分布 target = dataframe['class'].values counter = Counter(target) for k,v in counter.items(): per = v / len(target) * 100 print('Class=%d, Count=%d, Percentage=%.3f%%' % (k, v, per)) |
运行该示例将汇总数据集的类别分布。
我们可以看到,类别 1(生存)有最多的样本,为 225 个,约占数据集的 74%。类别 2(未生存)样本较少,为 81 个,约占数据集的 26%。
类别分布存在偏差,但并非严重不平衡。
|
1 2 |
类别=1, 计数=225, 百分比=73.529% 类别=2, 计数=81, 百分比=26.471% |
现在我们已经审阅了数据集,接下来我们将开发一个测试工具来评估候选模型。
模型测试和基线结果
我们将使用重复分层 k 折交叉验证来评估候选模型。
k 折交叉验证程序提供了一个很好的模型性能总体估计,该估计不会过于乐观地有偏差,至少与单个训练-测试分割相比是这样。我们将使用 k=10,这意味着每折将包含 306/10 或约 30 个样本。
分层意味着每折将包含相同的类别样本混合,即约 74% 的生存和 26% 的非生存。
重复意味着将进行多次评估过程,以帮助避免偶然结果并更好地捕捉所选模型的方差。我们将进行三次重复。
这意味着一个模型将进行 10 * 3 = 30 次拟合和评估,并将报告这些运行的平均值和标准差。
这可以通过使用RepeatedStratifiedKFold scikit-learn 类来实现。
鉴于我们有兴趣预测生存概率,我们需要一个性能指标来根据预测概率评估模型的准确性。在这种情况下,我们将使用 Brier 分数,它计算预测概率和期望概率之间的均方误差。
这可以使用 brier_score_loss() scikit-learn 函数进行计算。此分数是最小化的,完美分数为 0.0。通过将预测分数与参考分数进行比较,我们可以将分数反转为最大化,显示模型与参考模型相比提高了多少,范围从 0.0(相同)到 1.0(完美准确性)。任何分数低于 0.0 的模型都表示准确性不如参考模型。这称为 Brier 技能分数,简称 BSS。
- Brier 技能分数 = 1.0 – (模型 Brier 分数 / 参考 Brier 分数)
对于不平衡数据集,通常将少数类建模为正类。在此数据集中,正类代表未生存。这意味着我们将预测未生存的概率,并且需要计算预测概率的补数才能获得生存概率。
因此,我们可以将 1 类值(生存)映射为负类,类别标签为 0;将 2 类值(未生存)映射为正类,类别标签为 1。这可以通过 LabelEncoder 类来实现。
例如,下面的 load_dataset() 函数将加载数据集,将变量列分为输入和输出,然后将目标变量编码为 0 和 1。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) return X, y |
接下来,我们可以计算模型的 Brier 技能分数。
首先,我们需要一个参考预测的 Brier 分数。对于预测概率的问题,参考预测是数据集中正类别标签的概率。
在这种情况下,正类别标签代表未生存,在数据集中约占 26%。因此,预测约 0.26471 代表了该数据集上预测模型的性能最差或基线性能。任何 Brier 分数优于此的模型都具有一定的技能,而 Brier 分数低于此的模型则没有技能。Brier 技能分数捕获了这种重要的关系。我们可以自动计算 k 折交叉验证过程中每个训练集的此默认预测策略的 Brier 分数,然后将其用作给定模型的比较点。
|
1 2 3 4 |
... # 计算参考 Brier 分数 ref_probs = [0.26471 for _ in range(len(y_true))] bs_ref = brier_score_loss(y_true, ref_probs) |
然后,可以为模型的预测计算 Brier 分数,并用于计算 Brier 技能分数。
下面的 brier_skill_score() 函数实现了这一点,并计算了在同一测试集上给定的一组真实标签和预测值的 Brier 技能分数。任何 BSS 高于 0.0 的模型都表示在该数据集上具有技能。
|
1 2 3 4 5 6 7 8 9 10 |
# 计算 Brier 技能分数 (BSS) def brier_skill_score(y_true, y_prob): # 计算参考 Brier 分数 pos_prob = count_nonzero(y_true) / len(y_true) ref_probs = [pos_prob for _ in range(len(y_true))] bs_ref = brier_score_loss(y_true, ref_probs) # 计算模型 Brier 分数 bs_model = brier_score_loss(y_true, y_prob) # 计算技能分数 return 1.0 - (bs_model / bs_ref) |
接下来,我们可以利用 brier_skill_score() 函数来评估模型,使用重复分层 k 折交叉验证。
为了使用我们的自定义性能指标,我们可以使用 make_scorer() scikit-learn 函数,它接受我们的自定义函数名称并创建一个可以用于评估 scikit-learn API 模型的指标。我们将 needs_proba 参数设置为 True,以确保被评估的模型使用 predict_proba() 函数进行预测,以确保它们给出概率而不是类别标签。
|
1 2 3 |
... # 定义模型评估指标 metric = make_scorer(brier_skill_score, needs_proba=True) |
下面的 evaluate_model() 函数使用我们的自定义评估指标定义了评估过程,它接收整个训练数据集和模型作为输入,然后返回每个折叠和每个重复的分数样本。
|
1 2 3 4 5 6 7 8 9 |
# 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(brier_skill_score, needs_proba=True) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) return scores |
最后,我们可以使用我们的三个函数来评估一个模型。
首先,我们可以加载数据集并总结输入和输出数组,以确认它们已正确加载。
|
1 2 3 4 5 6 7 |
... # 定义数据集位置 full_path = 'haberman.csv' # 加载数据集 X, y = load_dataset(full_path) # 总结已加载的数据集 print(X.shape, y.shape, Counter(y)) |
在这种情况下,我们将评估基线策略,即预测训练集中的正例分布作为测试集中每个病例的概率。
这可以通过 DummyClassifier 类自动实现,并将“策略”设置为“prior”,它将预测训练数据集中每个类别的先验概率,对于正类别,我们知道这个概率大约是 0.26471。
|
1 2 3 |
... # 定义参考模型 model = DummyClassifier(strategy='prior') |
然后,我们可以通过调用我们的 evaluate_model() 函数来评估模型,并报告结果的平均值和标准差。
|
1 2 3 4 5 |
... # 评估模型 scores = evaluate_model(X, y, model) # 总结性能 print('平均 BSS: %.3f (%.3f)' % (mean(scores), std(scores))) |
将所有内容整合起来,使用 Brier 技能分数在 Haberman 乳腺癌生存数据集上评估基线模型的完整示例如下。
我们期望基线模型获得 BSS 为 0.0,即与参考模型相同,因为它是参考模型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
# Haberman 数据集的基线模型和测试框架 from collections import Counter from numpy import mean from numpy import std from pandas import read_csv from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import brier_score_loss from sklearn.metrics import make_scorer from sklearn.dummy import DummyClassifier # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 计算 Brier 技能分数 (BSS) def brier_skill_score(y_true, y_prob): # 计算参考 Brier 分数 ref_probs = [0.26471 for _ in range(len(y_true))] bs_ref = brier_score_loss(y_true, ref_probs) # 计算模型 Brier 分数 bs_model = brier_score_loss(y_true, y_prob) # 计算技能分数 return 1.0 - (bs_model / bs_ref) # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(brier_skill_score, needs_proba=True) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义数据集位置 full_path = 'haberman.csv' # 加载数据集 X, y = load_dataset(full_path) # 总结已加载的数据集 print(X.shape, y.shape, Counter(y)) # 定义参考模型 model = DummyClassifier(strategy='prior') # 评估模型 scores = evaluate_model(X, y, model) # 总结性能 print('平均 BSS: %.3f (%.3f)' % (mean(scores), std(scores))) |
运行该示例首先加载数据集,并如预期报告案例数量为 306,以及负类和正类别的类别分布。
然后,使用重复分层 k 折交叉验证来评估具有默认策略的DummyClassifier,并报告 Brier 技能分数的平均值和标准差为 0.0。这符合我们的预期,因为我们正在使用测试框架来评估参考策略。
|
1 2 |
(306, 3) (306,) Counter({0: 225, 1: 81}) 平均 BSS: -0.000 (0.000) |
现在我们有了测试工具和性能基线,我们可以开始评估该数据集上的一些模型。
评估概率模型
在本节中,我们将使用上一节开发的测试框架来评估一系列算法,然后是这些算法的改进,例如数据准备方案。
概率算法评估
我们将评估一系列已知有效的预测概率的模型。
具体来说,这些模型是在概率框架下拟合的,并明确为每个样本预测校准过的概率。因此,即使存在类别不平衡,它们也适合此数据集。
我们将评估以下六种使用 scikit-learn 库实现的概率模型:
- 逻辑回归 (LogisticRegression)
- 线性判别分析 (LinearDiscriminantAnalysis)
- 二次判别分析 (QuadraticDiscriminantAnalysis)
- 高斯朴素贝叶斯 (GaussianNB)
- 多项式朴素贝叶斯 (MultinomialNB)
- 高斯过程分类器 (GaussianProcessClassifier)
我们有兴趣直接比较这些算法的结果。我们将根据平均分数以及分数的分布来比较每种算法。
我们可以定义一个我们想要评估的模型列表,每个模型都带有其默认配置或配置为不产生警告。
|
1 2 3 4 5 |
... # 定义模型 models = [LogisticRegression(solver='lbfgs'), LinearDiscriminantAnalysis(), QuadraticDiscriminantAnalysis(), GaussianNB(), MultinomialNB(), GaussianProcessClassifier()] |
然后,我们可以枚举每个模型,记录模型的唯一名称,对其进行评估,并报告平均 BSS,然后将结果存储到运行结束。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
... names, values = list(), list() # 评估每个模型 for model in models: # 获取模型的名称 name = type(model).__name__[:7] # 评估模型并存储结果 scores = evaluate_model(X, y, model) # 总结并存储 print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) names.append(name) values.append(scores) |
在运行结束时,我们可以创建一个箱线图,显示每种算法的结果分布,其中箱显示分数的 25%、50% 和 75% 百分位数,三角形显示平均结果。每个图的须线可以帮助了解每个分布的极值。
|
1 2 3 4 |
... # 绘制结果图 pyplot.boxplot(values, labels=names, showmeans=True) pyplot.show() |
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
# 比较Haberman数据集上的概率模型 from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import brier_score_loss from sklearn.metrics import make_scorer from sklearn.linear_model import LogisticRegression from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis from sklearn.naive_bayes import GaussianNB from sklearn.naive_bayes import MultinomialNB from sklearn.gaussian_process import GaussianProcessClassifier # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 计算 Brier 技能分数 (BSS) def brier_skill_score(y_true, y_prob): # 计算参考 Brier 分数 ref_probs = [0.26471 for _ in range(len(y_true))] bs_ref = brier_score_loss(y_true, ref_probs) # 计算模型 Brier 分数 bs_model = brier_score_loss(y_true, y_prob) # 计算技能分数 return 1.0 - (bs_model / bs_ref) # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(brier_skill_score, needs_proba=True) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义数据集位置 full_path = 'haberman.csv' # 加载数据集 X, y = load_dataset(full_path) # 定义模型 models = [LogisticRegression(solver='lbfgs'), LinearDiscriminantAnalysis(), QuadraticDiscriminantAnalysis(), GaussianNB(), MultinomialNB(), GaussianProcessClassifier()] names, values = list(), list() # 评估每个模型 for model in models: # 获取模型的名称 name = type(model).__name__[:7] # 评估模型并存储结果 scores = evaluate_model(X, y, model) # 总结并存储 print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) names.append(name) values.append(scores) # 绘制结果图 pyplot.boxplot(values, labels=names, showmeans=True) pyplot.show() |
运行示例首先总结每个算法的BSS的均值和标准差(分数越高越好)。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑运行几次示例并比较平均结果。
在这种情况下,结果表明只有两种算法不具备技能,显示负分数,并且LogisticRegression (LR) 和 LinearDiscriminantAnalysis (LDA) 算法可能是表现最佳的。
|
1 2 3 4 5 6 |
>Logisti 0.064 (0.123) >LinearD 0.067 (0.136) >Quadrat 0.027 (0.212) >Gaussia 0.011 (0.209) >Multino -0.213 (0.380) >Gaussia -0.141 (0.047) |
创建箱线图来总结结果的分布。
有趣的是,大多数(如果不是全部)算法都显示出一种分布,表明它们在某些运行中可能不具备技能。两个表现最佳的模型之间的分布看起来大致相当,因此基于平均性能选择模型可能是一个好的开始。
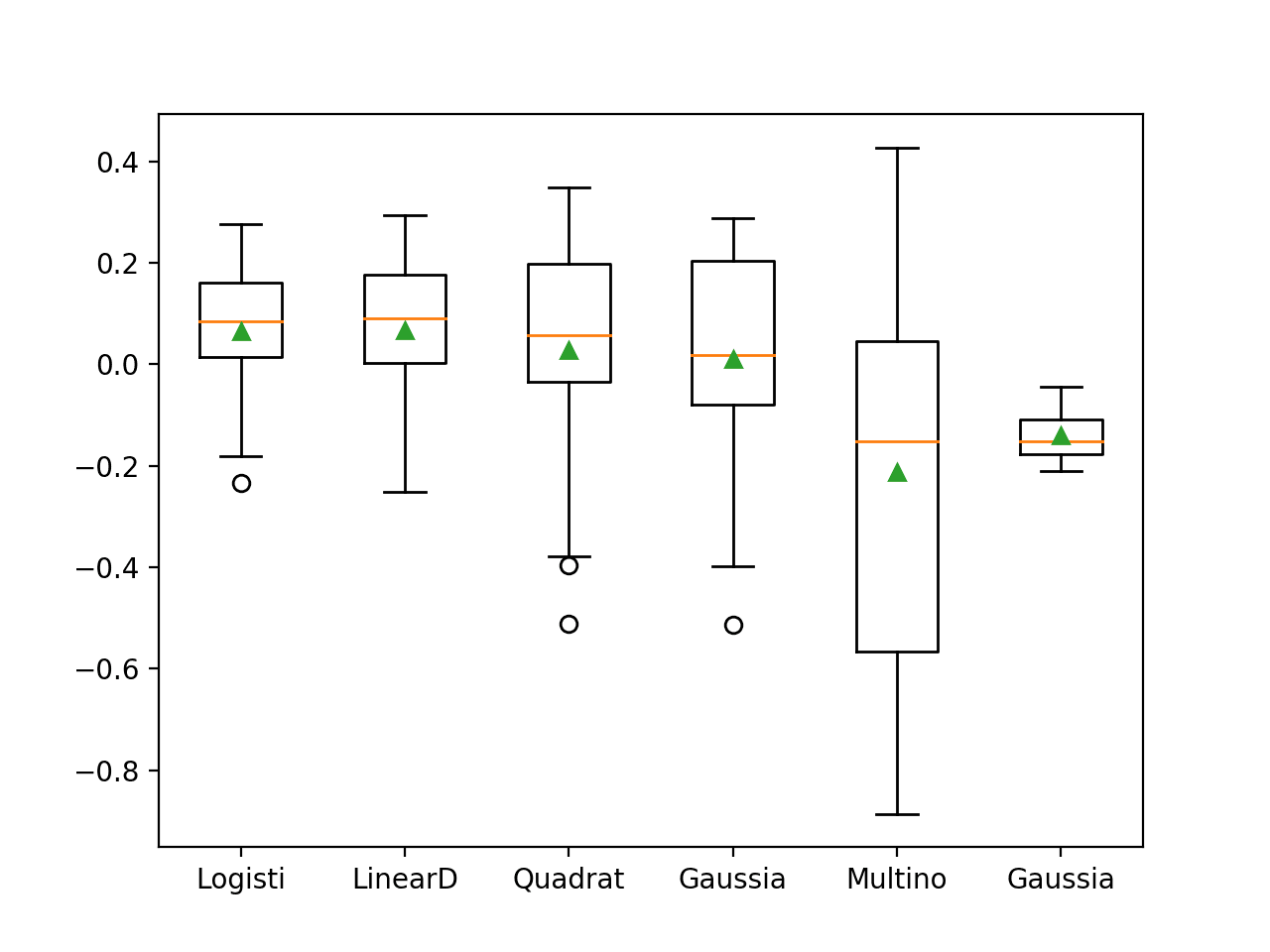
Haberman乳腺癌生存数据集上概率模型的箱线图
这是一个好的开始;让我们看看是否可以通过基本的数据准备来改进结果。
带缩放输入的模型评估
对于某些算法,如果变量具有不同的测量单位(在本例中如此),则对数据进行缩放可能是一种好习惯。
诸如LR和LDA之类的算法对数据敏感,并假设输入变量服从高斯分布,而我们并非在所有情况下都有此分布。
尽管如此,我们可以通过包装每个模型到一个Pipeline中来测试算法,其中第一步是StandardScaler,它将在训练数据集上正确拟合,并在每个k折交叉验证评估中应用于测试数据集,从而防止任何数据泄露。我们将删除MultinomialNB算法,因为它不支持负输入值。
我们可以通过将每个模型包装到Pipeline中来实现这一点,其中第一步是StandardScaler,它将在训练数据集上正确拟合,并应用于测试数据集,以防止数据泄露。
|
1 2 3 4 5 |
... # 创建一个pipeline pip = Pipeline(steps=[('t', StandardScaler()),('m',model)]) # 评估模型并存储结果 scores = evaluate_model(X, y, pip) |
下面列出了使用标准化输入数据评估剩余五个算法的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
# 在haberman数据集上比较具有标准化输入的概率模型 from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import brier_score_loss from sklearn.metrics import make_scorer from sklearn.linear_model import LogisticRegression from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis from sklearn.naive_bayes import GaussianNB from sklearn.gaussian_process import GaussianProcessClassifier from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 计算 Brier 技能分数 (BSS) def brier_skill_score(y_true, y_prob): # 计算参考 Brier 分数 ref_probs = [0.26471 for _ in range(len(y_true))] bs_ref = brier_score_loss(y_true, ref_probs) # 计算模型 Brier 分数 bs_model = brier_score_loss(y_true, y_prob) # 计算技能分数 return 1.0 - (bs_model / bs_ref) # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(brier_skill_score, needs_proba=True) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义数据集位置 full_path = 'haberman.csv' # 加载数据集 X, y = load_dataset(full_path) # 定义模型 models = [LogisticRegression(solver='lbfgs'), LinearDiscriminantAnalysis(), QuadraticDiscriminantAnalysis(), GaussianNB(), GaussianProcessClassifier()] names, values = list(), list() # 评估每个模型 for model in models: # 获取模型的名称 name = type(model).__name__[:7] # 创建一个pipeline pip = Pipeline(steps=[('t', StandardScaler()),('m',model)]) # 评估模型并存储结果 scores = evaluate_model(X, y, pip) # 总结并存储 print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) names.append(name) values.append(scores) # 绘制结果图 pyplot.boxplot(values, labels=names, showmeans=True) pyplot.show() |
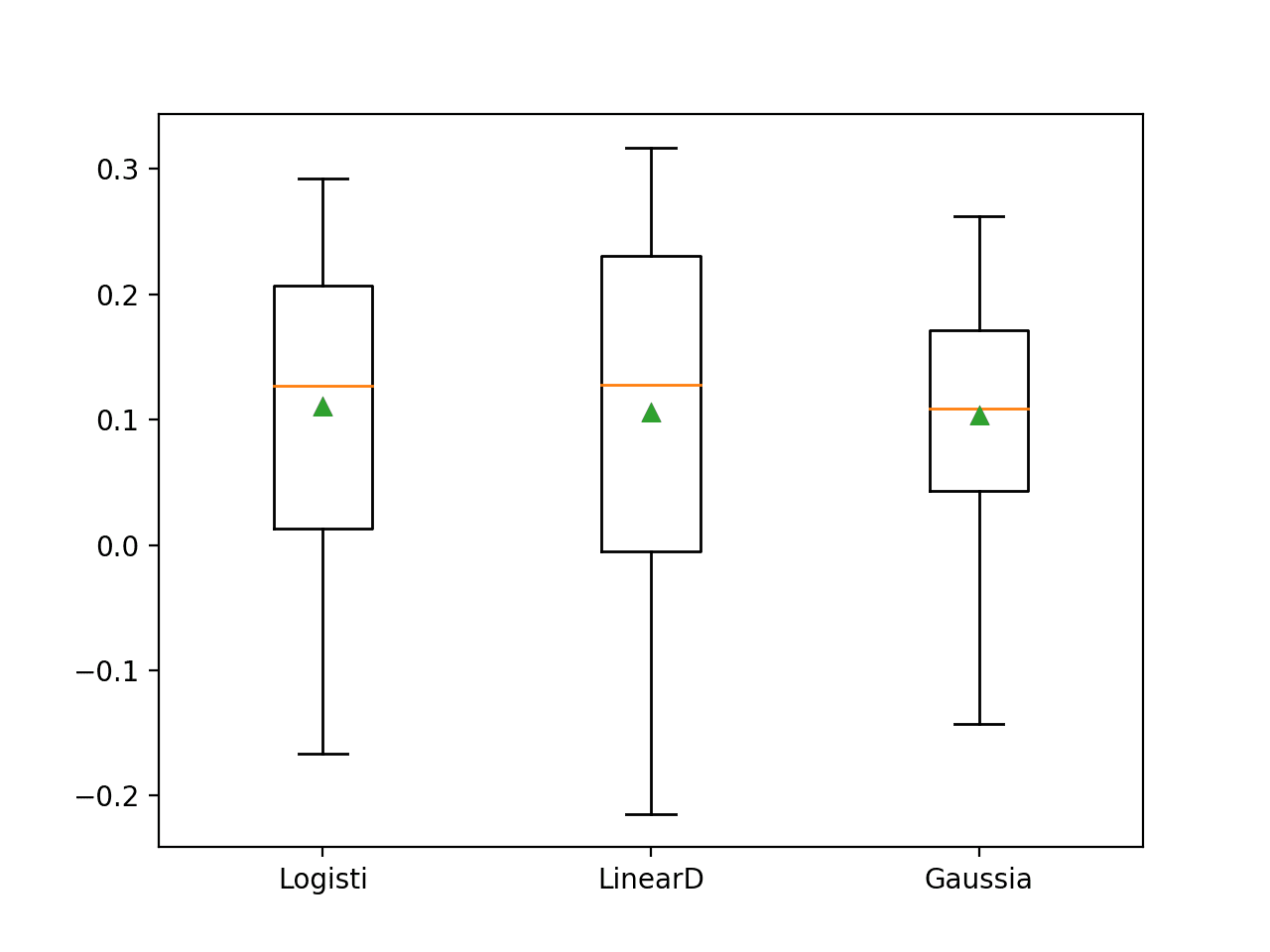
再次运行示例,总结了每个算法的BSS的均值和标准差。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑运行几次示例并比较平均结果。
在这种情况下,我们可以看到标准化对算法的影响不大,高斯过程分类器(GPC)除外。标准化后的GPC性能飙升,成为表现最佳的技术。这突显了准备数据以满足每个模型期望的重要性。
|
1 2 3 4 5 |
>Logisti 0.065 (0.121) >LinearD 0.067 (0.136) >Quadrat 0.027 (0.212) >Gaussia 0.011 (0.209) >Gaussia 0.092 (0.106) |
为每个算法的结果创建箱线图,显示了均值性能(绿色三角形)的差异以及三种表现最佳方法之间得分的相似分布。
这表明所有三种概率方法都在发现输入到数据集中概率的相同一般映射。

Haberman乳腺癌生存数据集上带有数据标准化的概率模型的箱线图
还有更多的数据准备工作可以使输入变量更像高斯分布,例如幂变换。
使用幂变换进行模型评估
幂变换,如Box-Cox和Yeo-Johnson变换,旨在将分布更改为更像高斯分布。
这将有助于我们数据集中的“年龄”输入变量,并可能有助于“节点”变量,并稍微解开分布。
我们可以使用scikit-learn的PowerTransformer类来执行Yeo-Johnson变换,并根据数据集自动确定最佳参数,例如如何最好地使每个变量更像高斯分布。重要的是,此转换器还将在转换过程中标准化数据集,确保我们保留上一节中看到的收益。
幂变换可能会使用log()函数,该函数对零值不起作用。我们的数据集中有零值,因此在进行幂变换之前,我们将使用MinMaxScaler来缩放数据集。
同样,我们可以在Pipeline中使用此转换器,以确保它在训练数据集上拟合,并正确应用于训练和测试数据集,而不会发生数据泄露。
|
1 2 3 4 5 |
... # 创建一个pipeline pip = Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()),('m',model)]) # 评估模型并存储结果 scores = evaluate_model(X, y, pip) |
我们将重点关注三个表现最佳的方法,即LR、LDA和GPC。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
# 在haberman数据集上使用幂变换比较概率模型 from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import brier_score_loss from sklearn.metrics import make_scorer from sklearn.linear_model import LogisticRegression from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.discriminant_analysis import QuadraticDiscriminantAnalysis from sklearn.naive_bayes import GaussianNB from sklearn.gaussian_process import GaussianProcessClassifier from sklearn.pipeline import Pipeline from sklearn.preprocessing import PowerTransformer from sklearn.preprocessing import MinMaxScaler # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 计算 Brier 技能分数 (BSS) def brier_skill_score(y_true, y_prob): # 计算参考 Brier 分数 ref_probs = [0.26471 for _ in range(len(y_true))] bs_ref = brier_score_loss(y_true, ref_probs) # 计算模型 Brier 分数 bs_model = brier_score_loss(y_true, y_prob) # 计算技能分数 return 1.0 - (bs_model / bs_ref) # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(brier_skill_score, needs_proba=True) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义数据集位置 full_path = 'haberman.csv' # 加载数据集 X, y = load_dataset(full_path) # 定义模型 models = [LogisticRegression(solver='lbfgs'), LinearDiscriminantAnalysis(), GaussianProcessClassifier()] names, values = list(), list() # 评估每个模型 for model in models: # 获取模型的名称 name = type(model).__name__[:7] # 创建一个pipeline pip = Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()),('m',model)]) # 评估模型并存储结果 scores = evaluate_model(X, y, pip) # 总结并存储 print('>%s %.3f (%.3f)' % (name, mean(scores), std(scores))) names.append(name) values.append(scores) # 绘制结果图 pyplot.boxplot(values, labels=names, showmeans=True) pyplot.show() |
再次运行示例,总结了每个算法的BSS的均值和标准差。
注意:由于算法或评估程序的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑运行几次示例并比较平均结果。
在这种情况下,我们可以看到评估的三个模型的模型技能进一步提升。我们可以看到LR的表现优于其他两种方法。
|
1 2 3 |
>Logisti 0.111 (0.123) >LinearD 0.106 (0.147) >Gaussia 0.103 (0.096) |
为每个算法的结果创建箱线图,表明LR相对于排名第二的LDA,可能具有更小、更集中的分布。
所有方法平均而言仍然显示出技能,然而得分的分布表明在某些情况下得分会降至0.0(无技能)以下。
Haberman乳腺癌生存数据集上带有幂变换的概率模型的箱线图
对新数据进行预测
我们将选择具有对输入数据进行幂变换的Logistic Regression模型作为我们的最终模型。
我们可以定义该模型并将其拟合到整个训练数据集上。
|
1 2 3 4 |
... # 拟合模型 model = Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()),('m',LogisticRegression(solver='lbfgs'))]) model.fit(X, y) |
拟合后,我们可以通过调用predict_proba()函数来使用它为新数据进行预测。这将为每次预测返回两个概率,第一个是生存概率,第二个是非生存概率,即其补数。
例如
|
1 2 3 4 5 |
... row = [31,59,2] yhat = model.predict_proba([row]) # 获取生存百分比 p_survive = yhat[0, 0] * 100 |
为了演示这一点,我们可以使用拟合的模型对一些已知生存和一些已知未生存的案例进行概率预测。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
# 拟合模型并对haberman数据集进行预测 from pandas import read_csv from sklearn.preprocessing import LabelEncoder from sklearn.linear_model import LogisticRegression from sklearn.pipeline import Pipeline from sklearn.preprocessing import PowerTransformer from sklearn.preprocessing import MinMaxScaler # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 定义数据集位置 full_path = 'haberman.csv' # 加载数据集 X, y = load_dataset(full_path) # 拟合模型 model = Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()),('m',LogisticRegression(solver='lbfgs'))]) model.fit(X, y) # 一些生存案例 print('生存案例:') data = [[31,59,2], [31,65,4], [34,60,1]] for row in data: # 进行预测 yhat = model.predict_proba([row]) # 获取生存百分比 p_survive = yhat[0, 0] * 100 # 总结 print('>data=%s, Survival=%.3f%%' % (row, p_survive)) # 一些非生存案例 print('非生存案例:') data = [[44,64,6], [34,66,9], [38,69,21]] for row in data: # 进行预测 yhat = model.predict_proba([row]) # 获取生存百分比 p_survive = yhat[0, 0] * 100 # 总结 print('data=%s, Survival=%.3f%%' % (row, p_survive)) |
首先运行示例,在整个训练数据集上拟合模型。
然后,使用拟合的模型来预测我们知道患者生存的案例的生存概率,这些案例是从数据集中选择的。我们可以看到,对于选定的生存案例,生存概率很高,在77%到86%之间。
然后,将一些非生存案例作为输入到模型中,并预测生存概率。正如我们所希望的那样,生存概率适中,在53%到63%之间。
|
1 2 3 4 5 6 7 8 |
生存案例 >data=[31, 59, 2], Survival=83.597% >data=[31, 65, 4], Survival=77.264% >data=[34, 60, 1], Survival=86.776% 非生存案例 data=[44, 64, 6], Survival=63.092% data=[34, 66, 9], Survival=63.452% data=[38, 69, 21], Survival=53.389% |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
API
- pandas.read_csv API
- pandas.DataFrame.describe API
- pandas.DataFrame.hist API
- sklearn.model_selection.RepeatedStratifiedKFold API.
- sklearn.preprocessing.LabelEncoder API.
- sklearn.preprocessing.PowerTransformer API
数据集 (Dataset)
总结
在本教程中,您学习了如何开发一个模型来预测不平衡数据集上患者的生存概率。
具体来说,你学到了:
- 如何加载和探索数据集,并为数据准备和模型选择提供思路。
- 如何评估一系列概率模型,并通过适当的数据准备来提高它们的性能。
- 如何拟合最终模型,并使用它来预测特定病例的概率。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





如果有人在运行代码时遇到“序列化错误”,请将n_jobs设置为1而不是-1。
这很奇怪,Mark。也许是你的Python安装出了问题?
“我们还可以看到类标签(第3列)的值是1表示患者生存,2表示患者未生存。”……这是一个笔误。应该是第4列。
这是正确的,我们这里指的是NumPy中的列数组索引。
另外一点是,对于较大的数据集,即使单独运行时,GaussianProcessClassifier()也会让我的电脑进入睡眠状态,我不得不重启。其他模型则没有这个问题。
顺便说一句,这是一篇很棒的文章
谢谢。
是的,GPC可能会这样。
1. Briar分数是如何估算的?它是否需要任何用户经验或自动?
2. 我理解它对患者进行分类。我还想知道疾病严重程度的幅度值与每行数据之间的关系。
谢谢。
什么是“Briar分数”?
您是指“Brier skill”吗?如果是这样,您可以在此处了解更多信息。
https://machinelearning.org.cn/probability-metrics-for-imbalanced-classification/
该模型预测生存的可能性,它仅限于此。也许您可以拟合一个具有不同目标的模型?
您能告诉我brier_skill_score方法中参数的含义吗?我只能理解y_test和y_prob。
是的,请看这个
https://machinelearning.org.cn/probability-metrics-for-imbalanced-classification/
亲爱的 Jason,
我有一个普遍的问题。在生存分析中,患者对齐至关重要,通常可以通过两种方式进行。第一种方法是根据患者进入研究的日期对患者进行对齐,第二种方法是根据患者的结局(failure)进行对齐。您能否帮助我理解这些对齐是如何进行的?特别是第二种方法(基于结局的对齐)以及从编程的角度来看。您有这方面的博客文章吗?很遗憾,我找不到相关的博客。
提前非常感谢。
抱歉,我没有关于生存分析的教程,我无法就这个主题提供好的建议。