随着智能电表和太阳能电池板等发电技术的广泛应用,大量的用电数据可供使用。
这些数据代表了一个与电力相关的多元时间序列,进而可以用于建模甚至预测未来的用电量。
自相关模型非常简单,可以提供一种快速有效的方法,对电力消耗进行精确的一步和多步预测。
在本教程中,您将学习如何开发和评估自回归模型,用于家庭电力消耗的多步预测。
完成本教程后,您将了解:
- 如何为单变量时间序列数据创建和分析自相关和偏自相关图。
- 如何利用自相关图中的发现来配置自回归模型。
- 如何开发和评估用于进行一周预测的自相关模型。
通过我的新书《深度学习时间序列预测》启动您的项目,书中包含所有示例的分步教程和Python源代码文件。
让我们开始吧。
- 2020 年 12 月更新:将 ARIMA API 更新为最新版本的 statsmodels。

如何开发家庭用电量自回归预测模型
图片来源:wongaboo,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 问题描述
- 加载并准备数据集
- 模型评估
- 自相关分析
- 开发自回归模型
问题描述
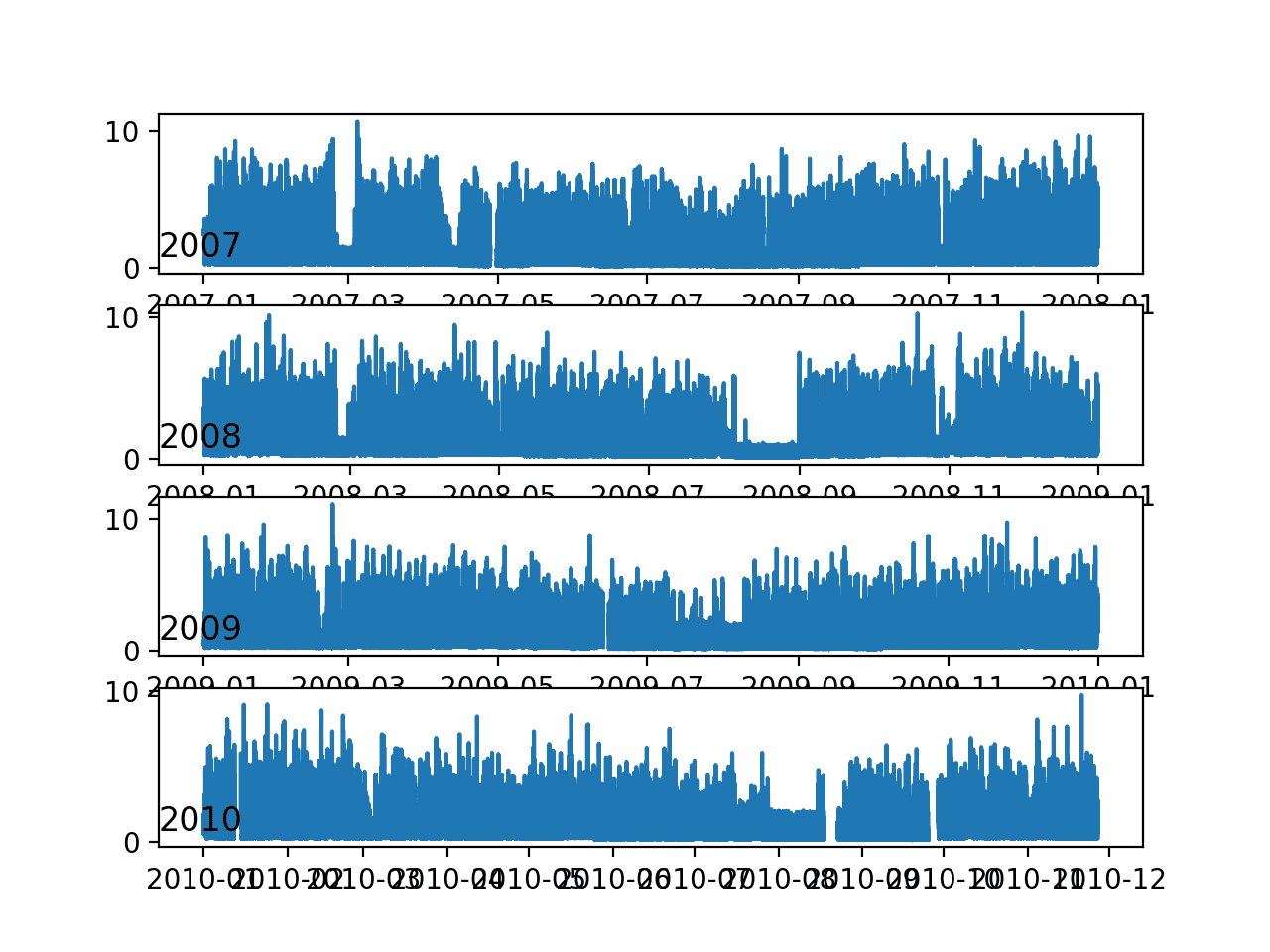
“家庭电力消耗”数据集是一个多元时间序列数据集,描述了一个家庭四年间的电力消耗。
数据收集于 2006 年 12 月至 2010 年 11 月期间,每分钟收集一次家庭用电量的观测值。
它是一个多元序列,包含七个变量(除了日期和时间);它们是
- global_active_power:家庭消耗的总有功功率(千瓦)。
- global_reactive_power:家庭消耗的总无功功率(千瓦)。
- voltage:平均电压(伏特)。
- global_intensity:平均电流强度(安培)。
- sub_metering_1:厨房的有功电能(瓦时有功电能)。
- sub_metering_2:洗衣房的有功电能(瓦时有功电能)。
- sub_metering_3:气候控制系统的有功电能(瓦时有功电能)。
有功电能和无功电能指的是交流电的技术细节。
第四个子计量变量可以通过将三个定义的子计量变量的总和从总有功电能中减去来创建,如下所示
|
1 |
sub_metering_remainder = (global_active_power * 1000 / 60) - (sub_metering_1 + sub_metering_2 + sub_metering_3) |
加载并准备数据集
该数据集可以从 UCI 机器学习仓库下载,为一个 20 兆字节的 .zip 文件
下载数据集并将其解压缩到当前工作目录。现在您将拥有文件“household_power_consumption.txt”,其大小约为 127 兆字节,并包含所有观测值。
我们可以使用 read_csv() 函数加载数据,并将前两列合并为一个日期时间列,我们可以将其用作索引。
|
1 2 |
# 加载所有数据 dataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime']) |
接下来,我们可以将用“?”字符表示的所有缺失值标记为 NaN 值,这是一个浮点数。
这将允许我们以一个浮点值数组而不是混合类型(效率较低)来处理数据。
|
1 2 3 4 |
# 标记所有缺失值 dataset.replace('?', nan, inplace=True) # 使数据集数值化 dataset = dataset.astype('float32') |
现在我们需要填补已标记的缺失值。
一个非常简单的方法是复制前一天同一时间的观测值。我们可以在一个名为 fill_missing() 的函数中实现这一点,该函数将接收数据的 NumPy 数组并复制 24 小时前的值。
|
1 2 3 4 5 6 7 |
# 用一天前同一时间的值填充缺失值 def fill_missing(values): one_day = 60 * 24 for row in range(values.shape[0]): for col in range(values.shape[1]): if isnan(values[row, col]): values[row, col] = values[row - one_day, col] |
我们可以直接将此函数应用于 DataFrame 中的数据。
|
1 2 |
# 填充缺失值 fill_missing(dataset.values) |
现在我们可以创建一个新列,其中包含子计量的剩余部分,使用上一节中的计算。
|
1 2 3 |
# 添加一个用于子计量剩余部分的新列 values = dataset.values dataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6]) |
现在我们可以将清理后的数据集保存到一个新文件中;在这种情况下,我们只需将文件扩展名更改为 .csv 并将数据集保存为“household_power_consumption.csv”。
|
1 2 |
# 保存更新后的数据集 dataset.to_csv('household_power_consumption.csv') |
将所有这些串联起来,加载、清理和保存数据集的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# 加载和清理数据 from numpy import nan from numpy import isnan from pandas import read_csv from pandas import to_numeric # 用一天前同一时间的值填充缺失值 def fill_missing(values): one_day = 60 * 24 for row in range(values.shape[0]): for col in range(values.shape[1]): if isnan(values[row, col]): values[row, col] = values[row - one_day, col] # 加载所有数据 dataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime']) # 标记所有缺失值 dataset.replace('?', nan, inplace=True) # 使数据集数值化 dataset = dataset.astype('float32') # 填充缺失值 fill_missing(dataset.values) # 添加一个用于子计量剩余部分的新列 values = dataset.values dataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6]) # 保存更新后的数据集 dataset.to_csv('household_power_consumption.csv') |
运行示例会创建一个新的文件“household_power_consumption.csv”,我们可以将其作为建模项目的起点。
时间序列深度学习需要帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
模型评估
在本节中,我们将考虑如何为家庭用电数据集开发和评估预测模型。
本节分为四个部分;它们是
- 问题构建
- 评估指标
- 训练集和测试集
- 逐时验证
问题构建
有许多方法可以利用和探索家庭用电量数据集。
在本教程中,我们将使用数据来探索一个非常具体的问题;那就是
鉴于最近的用电量,未来一周的预期用电量是多少?
这要求预测模型预测未来七天每天的总有功功率。
从技术上讲,由于存在多个预测步骤,这种问题框架被称为多步时间序列预测问题。使用多个输入变量的模型可能被称为多元多步时间序列预测模型。
这种类型的模型可能有助于家庭规划开支。它也可能有助于供应方规划特定家庭的电力需求。
这种数据集的框架还表明,将每分钟的用电量观测值下采样到每日总计可能很有用。这不是必需的,但考虑到我们关注的是每天的总功率,这样做是合理的。
我们可以使用 Pandas DataFrame 上的 resample() 函数轻松实现这一点。使用参数“D”调用此函数允许按日期时间索引的已加载数据按天分组(查看所有偏移别名)。然后,我们可以计算每天所有观测值的总和,并为八个变量中的每个变量创建每日电力消耗数据的新数据集。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 将分钟数据重新采样为每天的总量 from pandas import read_csv # 加载新文件 dataset = read_csv('household_power_consumption.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime']) # 将数据重新采样为每日数据 daily_groups = dataset.resample('D') daily_data = daily_groups.sum() # 总结 print(daily_data.shape) print(daily_data.head()) # 保存 daily_data.to_csv('household_power_consumption_days.csv') |
运行示例将创建一个新的每日总用电量数据集,并将结果保存到一个名为“household_power_consumption_days.csv”的单独文件中。
我们可以将其用作拟合和评估所选问题框架的预测模型的数据集。
评估指标
预测将由七个值组成,未来一周的每一天一个值。
在多步预测问题中,通常会单独评估每个预测时间步长。这有几个原因
- 评论特定提前期(例如,+1 天与 +3 天)的技能。
- 根据模型在不同提前期(例如,+1 天擅长的模型与 +5 天擅长的模型)的技能来对比模型。
总功率的单位是千瓦,如果误差度量也使用相同的单位会很有用。均方根误差 (RMSE) 和平均绝对误差 (MAE) 都符合这一要求,尽管 RMSE 更常用,并将在本教程中采用。与 MAE 不同,RMSE 对预测误差的惩罚更重。
此问题的性能指标将是第 1 天到第 7 天每个提前期的 RMSE。
作为一种捷径,为了帮助模型选择,使用单个分数来总结模型的性能可能很有用。
可以使用的一个可能分数是所有预测天的 RMSE。
下面的 evaluate_forecasts() 函数将实现此行为,并根据多个七天预测返回模型的性能。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 针对期望值评估一个或多个每周预测 def evaluate_forecasts(actual, predicted): scores = list() # 计算每一天的 RMSE 分数 for i in range(actual.shape[1]): # 计算 mse mse = mean_squared_error(actual[:, i], predicted[:, i]) # 计算 rmse rmse = sqrt(mse) # 存储 scores.append(rmse) # 计算整体 RMSE s = 0 for row in range(actual.shape[0]): for col in range(actual.shape[1]): s += (actual[row, col] - predicted[row, col])**2 score = sqrt(s / (actual.shape[0] * actual.shape[1])) return score, scores |
运行函数将首先返回与日期无关的整体 RMSE,然后返回每天的 RMSE 分数数组。
训练集和测试集
我们将使用前三年的数据进行预测模型训练,并使用最后一年进行模型评估。
给定数据集中的数据将划分为标准周。这些周以周日开始,以周六结束。
这是一种现实且有用的模型框架使用方式,可以预测未来一周的电力消耗。它也有助于建模,模型可以用于预测特定的一天(例如星期三)或整个序列。
我们将把数据划分为标准周,从测试数据集倒序进行。
数据的最后一年是 2010 年,2010 年的第一个星期日是 1 月 3 日。数据于 2010 年 11 月中旬结束,数据中最近的最后一个星期六是 11 月 20 日。这提供了 46 周的测试数据。
下面提供了测试数据集的每日数据的起始行和结束行以供确认。
|
1 2 3 |
2010-01-03,2083.4539999999984,191.61000000000055,350992.12000000034,8703.600000000033,3842.0,4920.0,10074.0,15888.233355799992 ... 2010-11-20,2197.006000000004,153.76800000000028,346475.9999999998,9320.20000000002,4367.0,2947.0,11433.0,17869.76663959999 |
每日数据始于 2006 年末。
数据集中的第一个星期日是 12 月 17 日,这是数据的第二行。
将数据组织成标准周后,用于训练预测模型的完整标准周有 159 个。
|
1 2 3 |
2006-12-17,3390.46,226.0059999999994,345725.32000000024,14398.59999999998,2033.0,4187.0,13341.0,36946.66673200004 ... 2010-01-02,1309.2679999999998,199.54600000000016,352332.8399999997,5489.7999999999865,801.0,298.0,6425.0,14297.133406600002 |
下面的 split_dataset() 函数将每日数据拆分为训练集和测试集,并将每个数据集组织成标准周。
使用数据集的已知信息,使用特定的行偏移量来分割数据。然后使用 NumPy split() 函数将分割后的数据集组织成周数据。
|
1 2 3 4 5 6 7 8 |
# 将单变量数据集拆分为训练/测试集 def split_dataset(data): # 拆分为标准周 train, test = data[1:-328], data[-328:-6] # 重构为每周数据的窗口 train = array(split(train, len(train)/7)) test = array(split(test, len(test)/7)) return train, test |
我们可以通过加载每日数据集并打印训练集和测试集的第一行和最后一行数据来测试此函数,以确认它们符合上述预期。
完整的代码示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 拆分为标准周 from numpy import split from numpy import array from pandas import read_csv # 将单变量数据集拆分为训练/测试集 def split_dataset(data): # 拆分为标准周 train, test = data[1:-328], data[-328:-6] # 重构为每周数据的窗口 train = array(split(train, len(train)/7)) test = array(split(test, len(test)/7)) return train, test # 加载新文件 dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime']) train, test = split_dataset(dataset.values) # 验证训练数据 print(train.shape) print(train[0, 0, 0], train[-1, -1, 0]) # 验证测试数据 print(test.shape) print(test[0, 0, 0], test[-1, -1, 0]) |
运行示例表明,训练集确实有 159 周的数据,而测试集有 46 周的数据。
我们可以看到,训练集和测试集的第一行和最后一行的总有功功率与我们定义为每个集合标准周边界的特定日期的数据相匹配。
|
1 2 3 4 |
(159, 7, 8) 3390.46 1309.2679999999998 (46, 7, 8) 2083.4539999999984 2197.006000000004 |
逐时验证
模型将使用一种名为滚动预测的方案进行评估。
在这种情况下,模型需要进行一周的预测,然后将该周的实际数据提供给模型,以便将其作为后续一周预测的基础。这既符合模型在实际中可能的使用方式,也有利于模型利用可用的最佳数据。
我们可以在下面通过分离输入数据和输出/预测数据来演示这一点。
|
1 2 3 4 5 |
输入,预测 [第1周] 第2周 [第1周 + 第2周] 第3周 [第1周 + 第2周 + 第3周] 第4周 ... |
在此数据集上评估预测模型的逐周验证方法在下面实现,命名为 evaluate_model()。
函数的名称作为参数“model_func”提供给模型。此函数负责定义模型、在训练数据上拟合模型并进行一周预测。
然后,使用先前定义的 evaluate_forecasts() 函数,根据测试数据集评估模型所做的预测。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 评估单个模型 def evaluate_model(model_func, train, test): # 历史数据是每周数据的列表 history = [x for x in train] # 对每一周进行前向验证 predictions = list() for i in range(len(test)): # 预测这一周 yhat_sequence = model_func(history) # 存储预测结果 predictions.append(yhat_sequence) # 获取实际观测值并添加到历史记录中,用于预测下一周 history.append(test[i, :]) predictions = array(predictions) # 评估每周的预测天数 score, scores = evaluate_forecasts(test[:, :, 0], predictions) return score, scores |
一旦我们对模型进行了评估,我们就可以总结其性能。
下面的 *summarize_scores()* 函数将模型的性能显示为一行,以便与其他模型进行轻松比较。
|
1 2 3 4 |
# 总结得分 def summarize_scores(name, score, scores): s_scores = ', '.join(['%.1f' % s for s in scores]) print('%s: [%.3f] %s' % (name, score, s_scores)) |
我们现在拥有所有要素,可以开始评估数据集上的预测模型。
自相关分析
统计相关性概括了两个变量之间关系的强度。
我们可以假设每个变量的分布都符合 高斯 (钟形曲线) 分布。如果情况确实如此,我们可以使用皮尔逊相关系数来概括变量之间的相关性。
皮尔逊相关系数是一个介于 -1 和 1 之间的数字,分别描述负相关或正相关。值为零表示没有相关性。
我们可以计算时间序列观测值与先前时间步长的观测值(称为滞后)之间的相关性。由于时间序列观测值的相关性是与相同序列在先前时间的值计算的,这被称为序列相关性,或自相关性。
时间序列按滞后绘制的自相关图称为自相关函数,或简称 ACF。此图有时也称为相关图,或自相关图。
偏自相关函数或 PACF 是时间序列中一个观测值与先前时间步长的观测值之间关系的摘要,其中去除了中间观测值的关系。
一个观测值与先前时间步长的观测值之间的自相关性包含直接相关性和间接相关性。这些间接相关性是观测值与中间时间步长观测值相关性的线性函数。
偏自相关函数试图消除的正是这些间接相关性。不深入数学细节,这就是偏自相关的直观概念。
我们可以分别使用 plot_acf() 和 plot_pacf() statsmodels 函数来计算和绘制自相关和偏自相关图。
为了计算和绘制自相关,我们必须将数据转换为单变量时间序列。具体来说,是观察到的每日总功耗。
下面的 to_series() 函数将接受分为每周窗口的多元数据,并返回一个单一的单变量时间序列。
|
1 2 3 4 5 6 7 |
# 将每周多元数据窗口转换为总功率序列 def to_series(data): # 提取每周的总功率 series = [week[:, 0] for week in data] # 扁平化为一个单一序列 series = array(series).flatten() return series |
我们可以为准备好的训练数据集调用此函数。
首先,必须加载每日用电量数据集。
|
1 2 |
# 加载新文件 dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime']) |
然后必须将数据集拆分为训练集和测试集,并采用标准的周窗口结构。
|
1 2 |
# 分割成训练集和测试集 train, test = split_dataset(dataset.values) |
随后可以从训练数据集中提取每日用电量的单变量时间序列。
|
1 2 |
# 将训练数据转换为序列 series = to_series(train) |
然后我们可以创建一个包含 ACF 和 PACF 图的单一图。可以指定滞后时间步长的数量。我们将其固定为一年的每日观测值,即 365 天。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 图形 pyplot.figure() lags = 365 # acf axis = pyplot.subplot(2, 1, 1) plot_acf(series, ax=axis, lags=lags) # pacf axis = pyplot.subplot(2, 1, 2) plot_pacf(series, ax=axis, lags=lags) # 显示图 pyplot.show() |
完整的示例如下所示。
我们预计明天和未来一周的电力消耗将取决于前几天的电力消耗。因此,我们预计在 ACF 和 PACF 图中会看到强烈的自相关信号。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# 总功率的 ACF 和 PACF 图 from numpy import split from numpy import array from pandas import read_csv from matplotlib import pyplot from statsmodels.graphics.tsaplots import plot_acf from statsmodels.graphics.tsaplots import plot_pacf # 将单变量数据集拆分为训练/测试集 def split_dataset(data): # 拆分为标准周 train, test = data[1:-328], data[-328:-6] # 重构为每周数据的窗口 train = array(split(train, len(train)/7)) test = array(split(test, len(test)/7)) return train, test # 将每周多元数据窗口转换为总功率序列 def to_series(data): # 提取每周的总功率 series = [week[:, 0] for week in data] # 扁平化为一个单一序列 series = array(series).flatten() return series # 加载新文件 dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime']) # 分割成训练集和测试集 train, test = split_dataset(dataset.values) # 将训练数据转换为序列 series = to_series(train) # 图形 pyplot.figure() lags = 365 # acf axis = pyplot.subplot(2, 1, 1) plot_acf(series, ax=axis, lags=lags) # pacf axis = pyplot.subplot(2, 1, 2) plot_pacf(series, ax=axis, lags=lags) # 显示图 pyplot.show() |
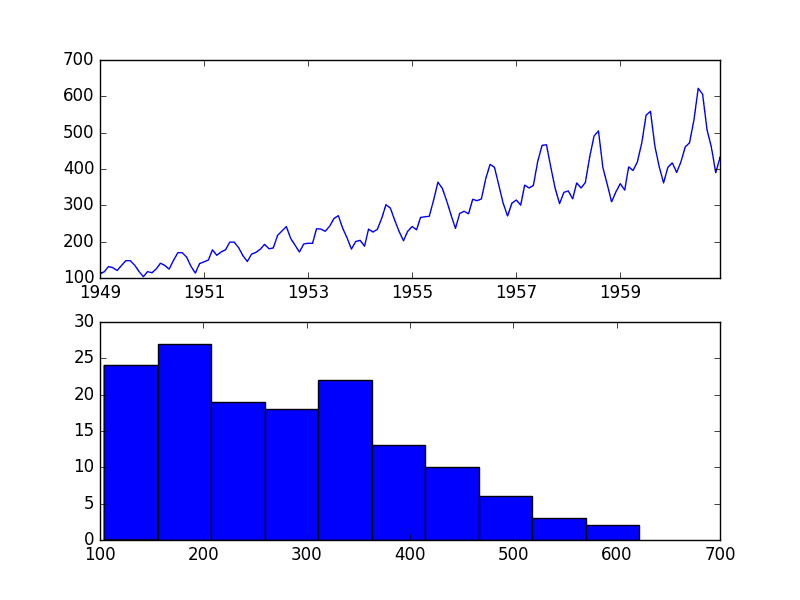
运行该示例会生成一个包含 ACF 和 PACF 图的单个图形。
这些图非常密集,难以阅读。尽管如此,我们也许能看到熟悉的自回归模式。
我们还可能看到一年后的一些显著滞后观测值。进一步的调查可能会表明存在季节性自相关分量,这并不是一个令人惊讶的发现。
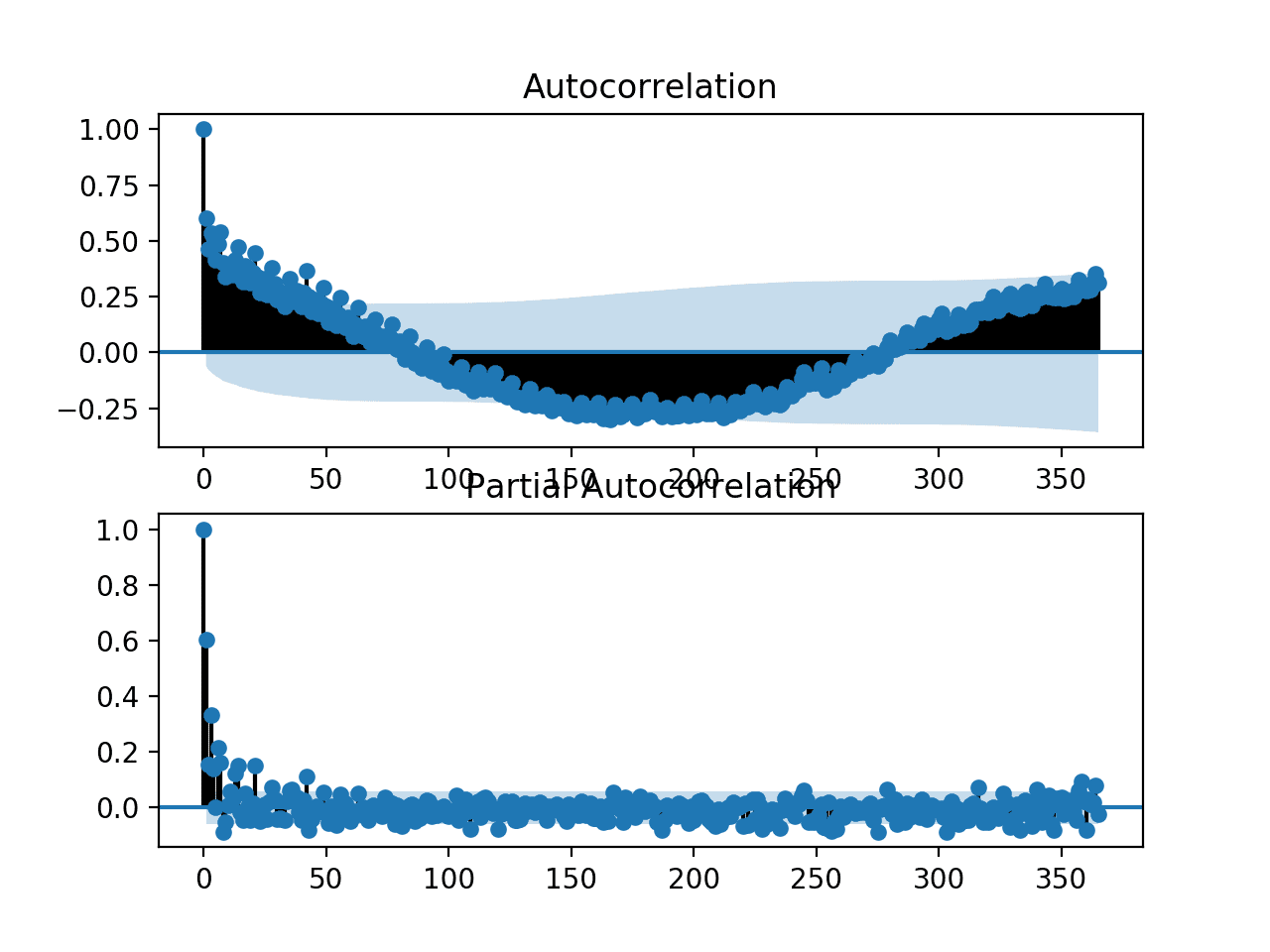
电力消耗单变量序列的 ACF 和 PACF 图
我们可以放大图形并将滞后观测值的数量从 365 更改为 50。
|
1 |
lags = 50 |
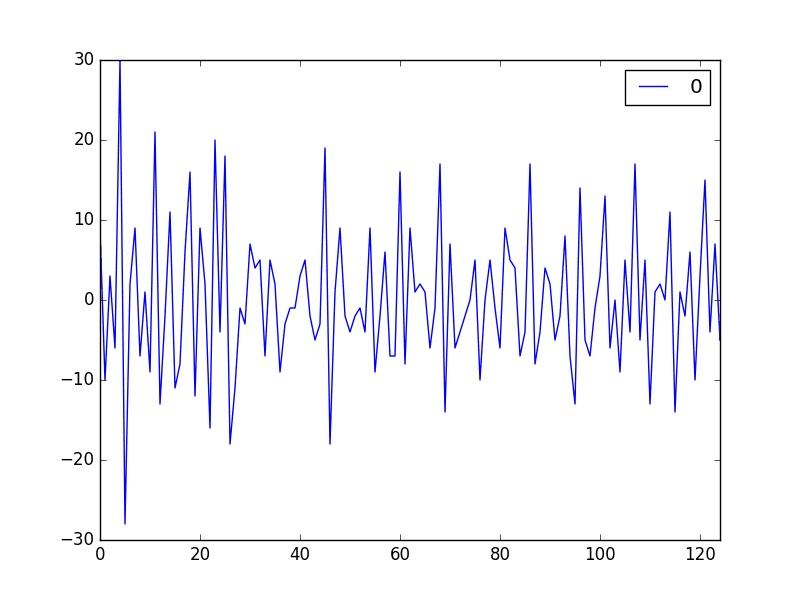
重新运行更改后的代码示例会生成放大版的图形,且杂乱程度大大降低。
我们可以清楚地看到这两个图表中的自回归模式。这种模式由两个元素组成:
- ACF:大量显著的滞后观测值,随着滞后时间的增加而缓慢衰减。
- PACF:少量显著的滞后观测值,随着滞后时间的增加而急剧下降。
ACF 图表显示存在强大的自相关分量,而 PACF 图表则表明该分量在大约前七个滞后观测值中是独特的。
这表明一个好的初始模型将是 AR(7);即一个使用七个滞后观测值作为输入的自回归模型。
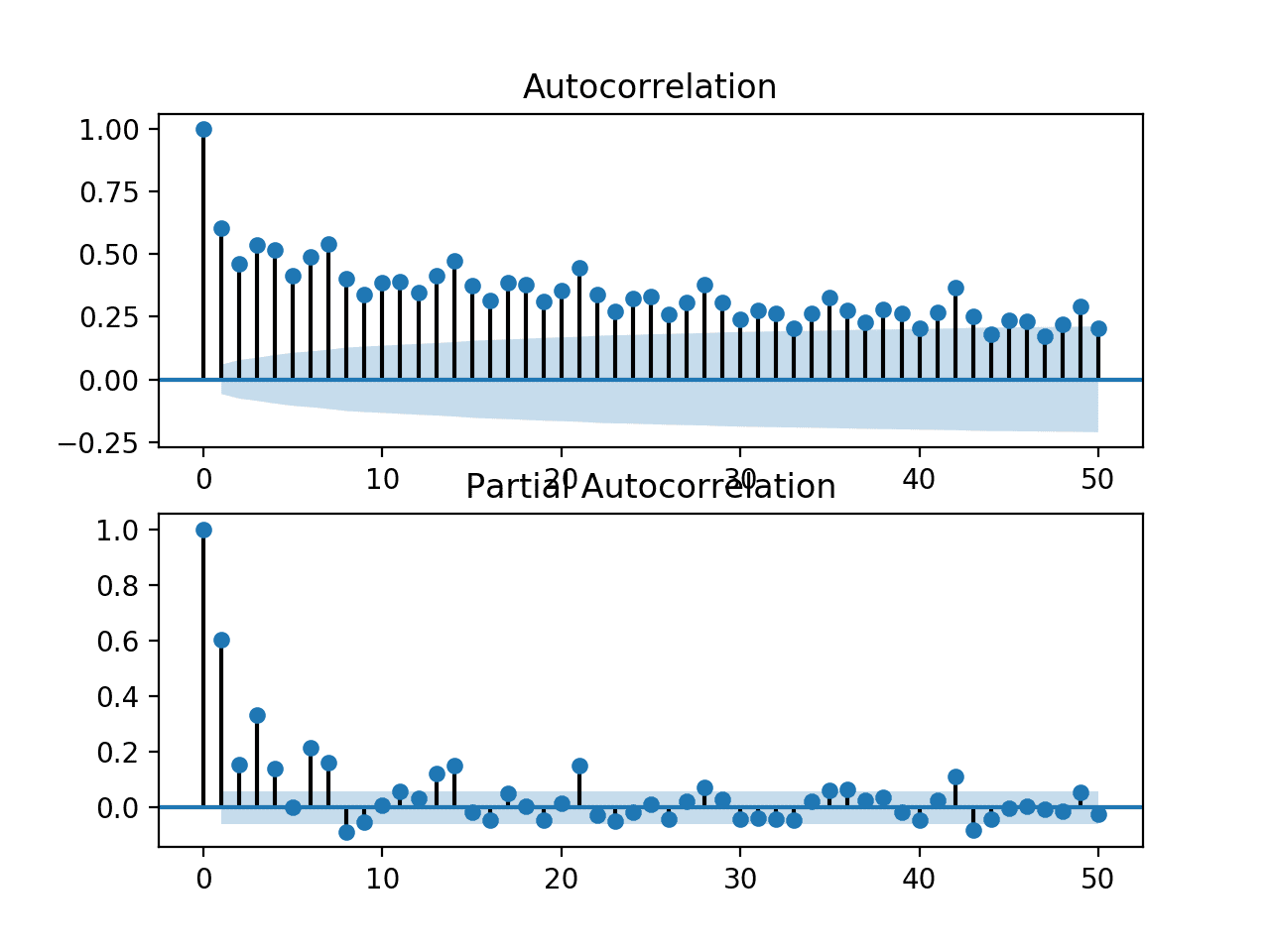
功耗单变量序列的局部放大 ACF 和 PACF 图
开发自回归模型
我们可以为每日功耗的单变量序列开发一个自回归模型。
Statsmodels 库提供了多种开发 AR 模型的方法,例如使用 AR、ARMA、ARIMA 和 SARIMAX 类。
我们将使用 ARIMA 实现,因为它易于扩展到差分和移动平均。
首先,由数周先前的观测值组成的“历史数据”必须转换为每日功耗的单变量时间序列。我们可以使用上一节中开发的 to_series() 函数。
|
1 2 |
# 将历史数据转换为单变量序列 series = to_series(history) |
接下来,可以通过向 ARIMA 类的构造函数传递参数来定义 ARIMA 模型。
我们将指定一个 AR(7) 模型,在 ARIMA 表示法中是 ARIMA(7,0,0)。
|
1 2 |
# 定义模型 model = ARIMA(series, order=(7,0,0)) |
接下来,可以在训练数据上拟合模型。
|
1 2 |
# 拟合模型 model_fit = model.fit() |
现在模型已经拟合完成,我们可以进行预测。
可以通过调用 predict() 函数并向其传递日期区间或相对于训练数据的索引来进行预测。我们将使用从训练数据之后的第一个时间步开始的索引,并将其再延长六天,总共得到一个超出训练数据集的七天预测期。
|
1 2 |
# 进行预测 yhat = model_fit.predict(len(series), len(series)+6) |
我们可以将所有这些封装到一个名为 arima_forecast() 的函数中,该函数接受历史数据并返回一周的预测。
|
1 2 3 4 5 6 7 8 9 10 11 |
# arima 预测 def arima_forecast(history): # 将历史数据转换为单变量序列 series = to_series(history) # 定义模型 model = ARIMA(series, order=(7,0,0)) # 拟合模型 model_fit = model.fit() # 进行预测 yhat = model_fit.predict(len(series), len(series)+6) return yhat |
此函数可以直接用于前面描述的测试工具。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 |
# arima 预测 from math import sqrt from numpy import split from numpy import array from pandas import read_csv from sklearn.metrics import mean_squared_error from matplotlib import pyplot from statsmodels.tsa.arima.model import ARIMA # 将单变量数据集拆分为训练/测试集 def split_dataset(data): # 拆分为标准周 train, test = data[1:-328], data[-328:-6] # 重构为每周数据的窗口 train = array(split(train, len(train)/7)) test = array(split(test, len(test)/7)) return train, test # 针对期望值评估一个或多个每周预测 def evaluate_forecasts(actual, predicted): scores = list() # 计算每一天的 RMSE 分数 for i in range(actual.shape[1]): # 计算 mse mse = mean_squared_error(actual[:, i], predicted[:, i]) # 计算 rmse rmse = sqrt(mse) # 存储 scores.append(rmse) # 计算整体 RMSE s = 0 for row in range(actual.shape[0]): for col in range(actual.shape[1]): s += (actual[row, col] - predicted[row, col])**2 score = sqrt(s / (actual.shape[0] * actual.shape[1])) return score, scores # 总结得分 def summarize_scores(name, score, scores): s_scores = ', '.join(['%.1f' % s for s in scores]) print('%s: [%.3f] %s' % (name, score, s_scores)) # 评估单个模型 def evaluate_model(model_func, train, test): # 历史数据是每周数据的列表 history = [x for x in train] # 对每一周进行前向验证 predictions = list() for i in range(len(test)): # 预测这一周 yhat_sequence = model_func(history) # 存储预测结果 predictions.append(yhat_sequence) # 获取实际观测值并添加到历史记录中,用于预测下一周 history.append(test[i, :]) predictions = array(predictions) # 评估每周的预测天数 score, scores = evaluate_forecasts(test[:, :, 0], predictions) return score, scores # 将每周多元数据窗口转换为总功率序列 def to_series(data): # 提取每周的总功率 series = [week[:, 0] for week in data] # 扁平化为一个单一序列 series = array(series).flatten() return series # arima 预测 def arima_forecast(history): # 将历史数据转换为单变量序列 series = to_series(history) # 定义模型 model = ARIMA(series, order=(7,0,0)) # 拟合模型 model_fit = model.fit() # 进行预测 yhat = model_fit.predict(len(series), len(series)+6) return yhat # 加载新文件 dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime']) # 分割成训练集和测试集 train, test = split_dataset(dataset.values) # 定义我们要评估的模型的名称和函数 models = dict() models['arima'] = arima_forecast # 评估每个模型 days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat'] for name, func in models.items(): # 评估并获取分数 score, scores = evaluate_model(func, train, test) # 汇总分数 summarize_scores(name, score, scores) # 绘制分数 pyplot.plot(days, scores, marker='o', label=name) # 显示图 pyplot.legend() pyplot.show() |
运行示例首先打印 AR(7) 模型在测试数据集上的性能。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的 结果可能有所不同。考虑多次运行示例并比较平均结果。
我们可以看到该模型的总体 RMSE 约为 381 千瓦。
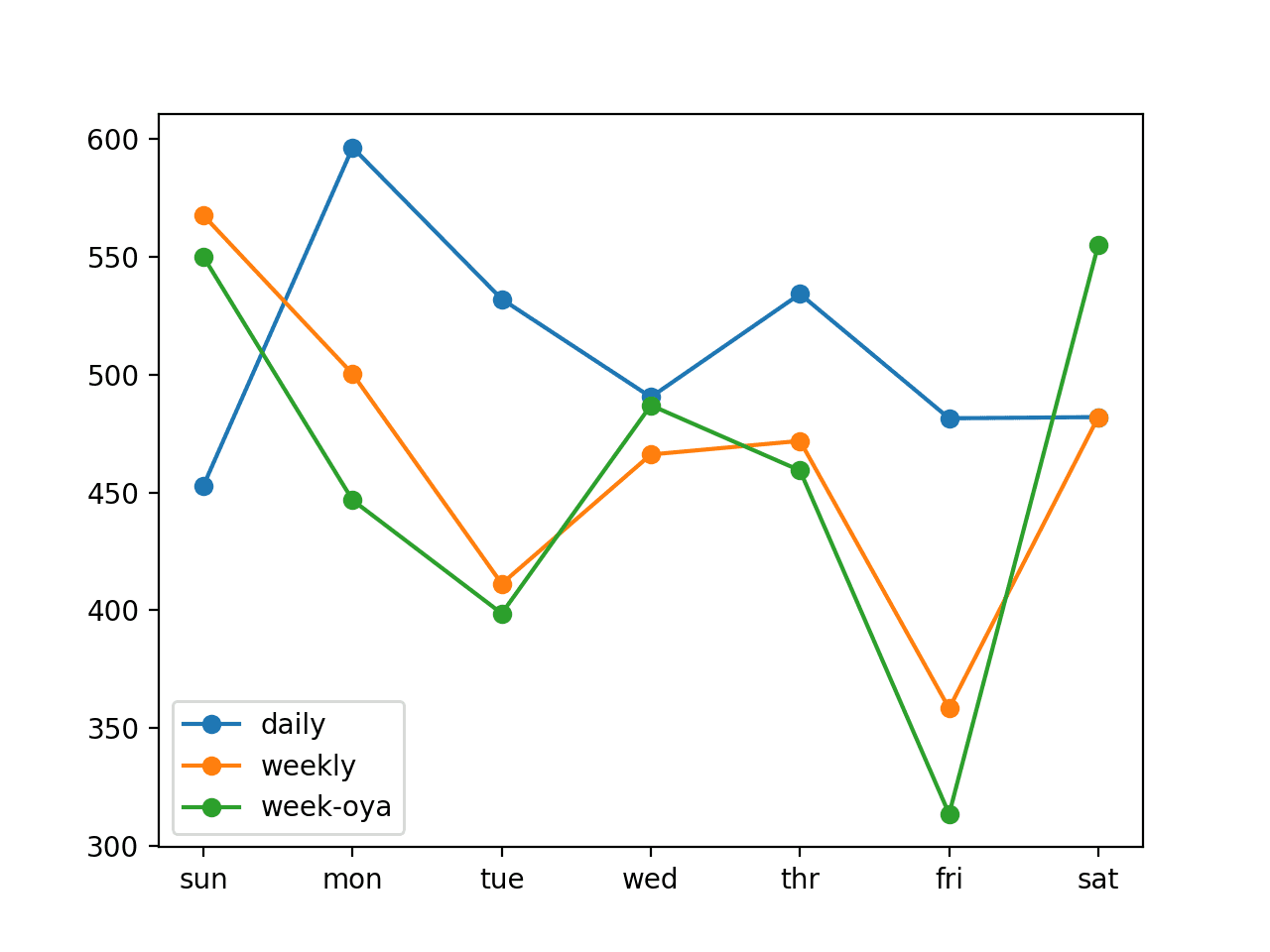
与朴素预测模型(例如使用一年前同一时间的观测值预测未来一周的模型,其总体 RMSE 约为 465 千瓦)相比,该模型具有技能。
|
1 |
arima: [381.636] 393.8, 398.9, 357.0, 377.2, 393.9, 306.1, 432.2 |
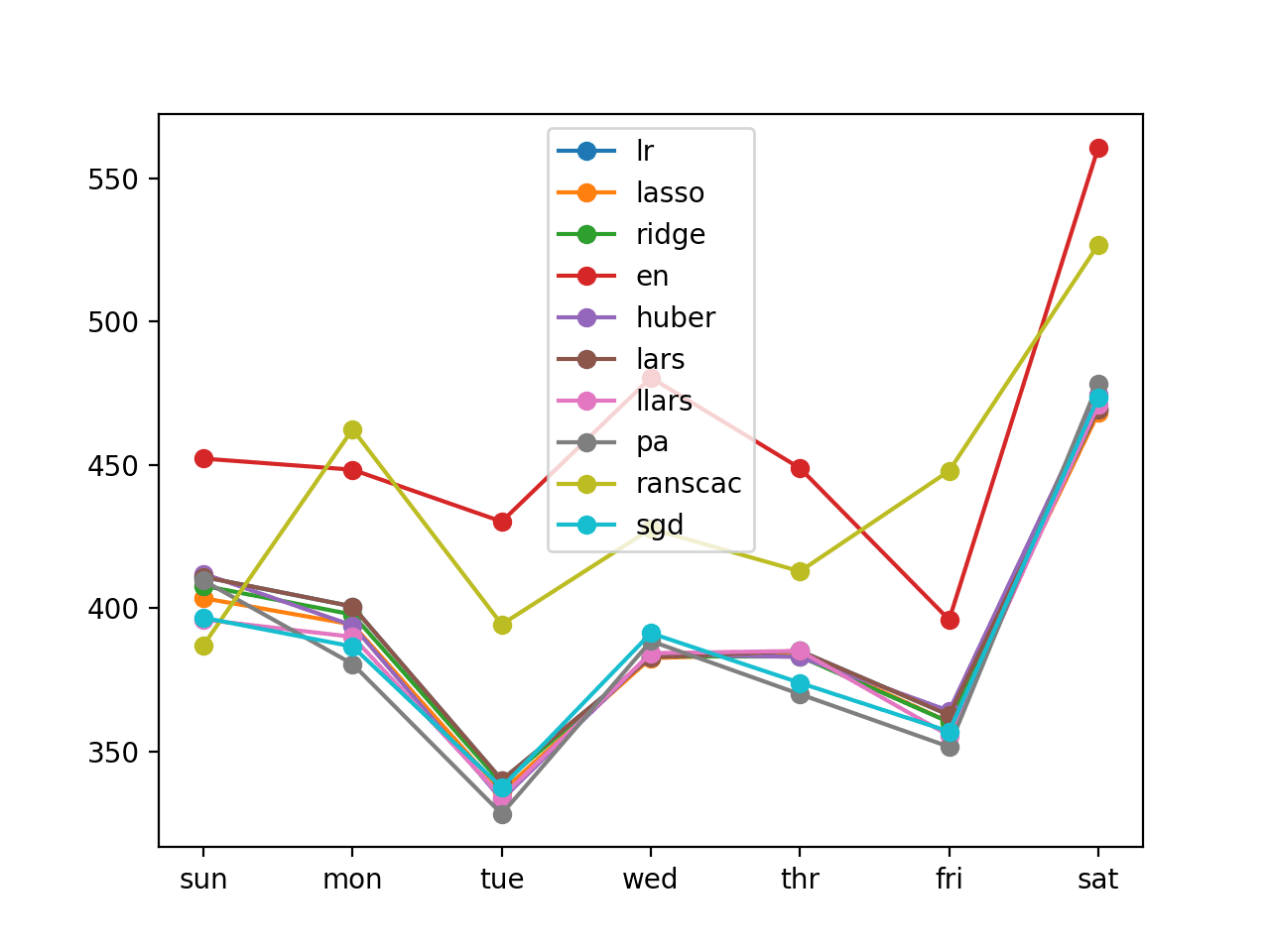
还创建了预测的折线图,显示了预测七个提前期中每个提前期的 RMSE(千瓦)。
我们可以看到一个有趣的模式。
我们可能会期望较早的提前期比较晚的提前期更容易预测,因为每个连续的提前期误差会累积。
相反,我们看到周五(提前期 +6)最容易预测,而周六(提前期 +7)最难预测。我们还可以看到,其余提前期的误差都相似,在中高 300 千瓦范围内。
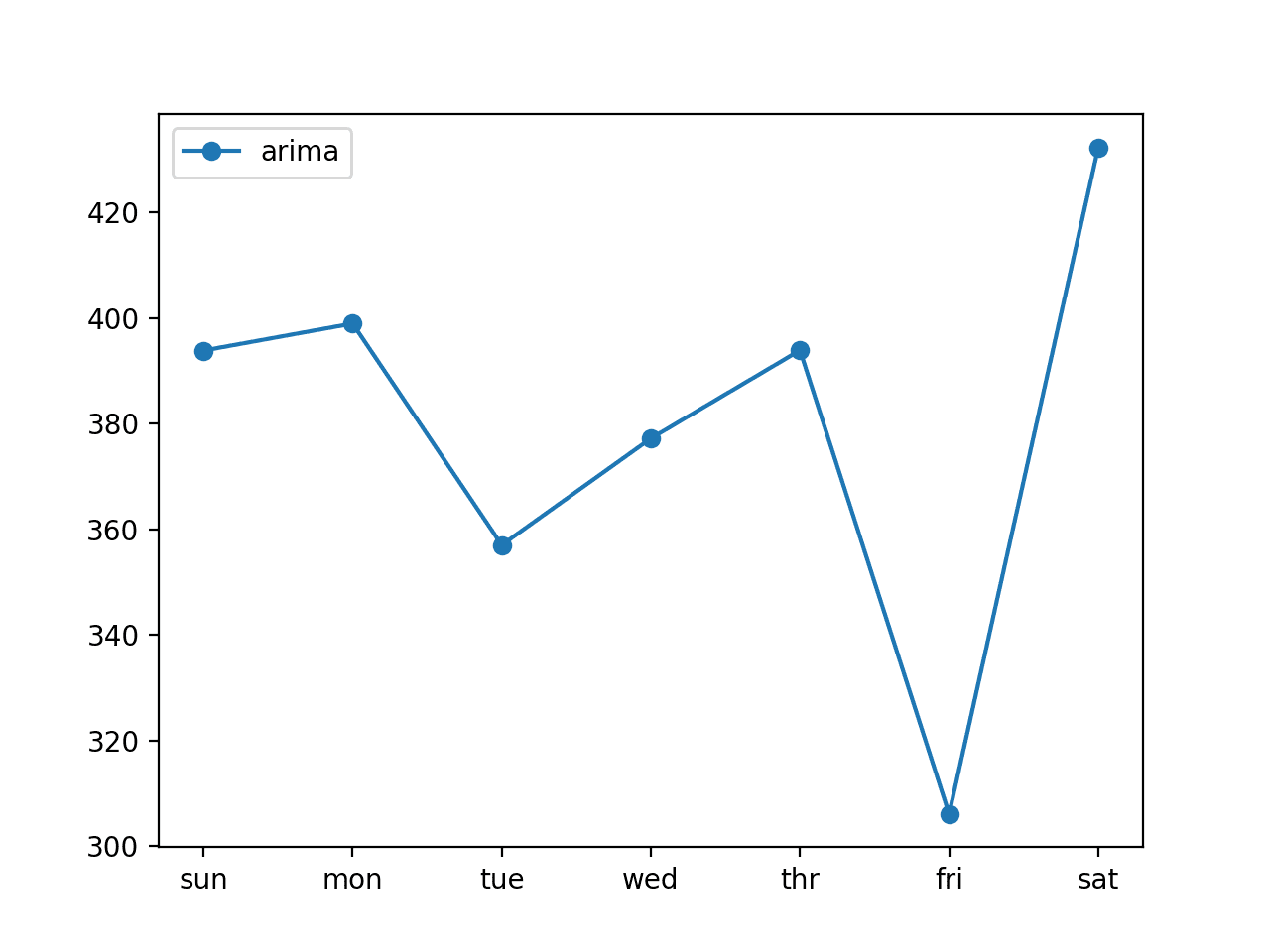
ARIMA 预测误差的折线图,显示每个预测提前期的误差
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 调整 ARIMA。ARIMA 模型的参数未调整。探索或搜索一系列 ARIMA 参数(q、d、p),看看性能是否可以进一步提高。
- 探索季节性 AR。探索是否可以通过包含季节性自回归元素来提高 AR 模型的性能。这可能需要使用 SARIMA 模型。
- 探索数据准备。模型直接在原始数据上拟合。探索标准化、归一化甚至幂变换是否可以进一步提高 AR 模型的技能。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
API
- pandas.read_csv API
- pandas.DataFrame.resample API
- 重采样偏移别名
- sklearn.metrics.mean_squared_error API
- numpy.split API
- statsmodels.graphics.tsaplots.plot_acf API
- statsmodels.graphics.tsaplots.plot_pacf API
文章
总结
在本教程中,您学习了如何开发和评估用于家庭用电量多步预测的自回归模型。
具体来说,你学到了:
- 如何为单变量时间序列数据创建和分析自相关和偏自相关图。
- 如何利用自相关图中的发现来配置自回归模型。
- 如何开发和评估用于进行一周预测的自相关模型。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。


很棒的文章。想知道这与使用 Prophet 的时间序列预测相比如何?
谢谢你
谢谢。
也许可以进行比较?
很棒的阅读,谢谢。
不客气。
很棒的工作,你真正地对这个预测进行了深入的概述。谢谢
谢谢 Alex。
LSTM 似乎不适合自回归类型的问题。所以这种方法是最好的解决方案。但是你的帖子有一些 LSTM 和 CNN 模型来解决这种自回归类型的问题
有时混合模型可以表现得非常好。
model = ARIMA(series, order=(7,0,0))
“7”表示滞后吗?我测试了 8,有些日子比设置为 7 时表现更好。
每次运行结果都相同,而深度学习的结果每次运行都不同。
是的。
你说的“深度学习”是什么意思?
如何在 ARIMA() 中设置机器精度?
我注意到模型训练中的机器精度是 2.220D-16,但有时它无法收敛
不确定你是否可以,也不想。这是 statsmodels 下库的限制。
我们每次评估模型时,模型都会同时拟合吗?
在 for 循环中,历史数据的值会实时更新。
是的,这称为步进式验证。
谢谢,我发现深度学习模型并不是每次都更新的
你具体指的是什么?
感谢您提供如此有用的信息
很高兴它有帮助。
我只有一个问题,为什么你不添加一张图表来显示预测值与实际真实值的比较?
感谢您的建议。
如果您需要制作预测图的帮助,可以从这里开始
https://machinelearning.org.cn/start-here/#timeseries
您好,我可以使用和修改代码并引用本文用于我的科学项目吗?
是的,听起来很棒。
我们可以使用这个数据集和代码来预测即将到来的账单吗?
或许可以试试看?
嗨,Jason,
我刚接触数据学习。我无法理解你如何在这里分割训练集和测试集
train, test = data[1:-328], data[-328:-6]
你为什么取值 328。你能给我解释一下上面的代码行吗?
是的,我们正在使用数组切片。您可以在此处了解更多关于 Python 中数组切片的信息
https://machinelearning.org.cn/index-slice-reshape-numpy-arrays-machine-learning-python/
我遇到了以下错误:
浮点型对象没有 len(),并且数组分割不会导致行上的相等划分
train,test = split_dataset(dataset,values)
听到您遇到这个问题,我很遗憾,这或许能帮到您。
https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
说真的,Jason,你真的很棒。我刚刚意识到有时甚至读取文件都不容易。但你的代码像魔法一样有效
谢谢!
以下是最近发表在《应用能源杂志》上的一篇关于基于一种新颖的萤火虫算法增强的混合神经模糊推理系统预测大学建筑能耗的文章
该论文题目为:一种基于混合神经模糊推理系统的时间序列预测算法在能耗预测中的应用
论文链接
https://www.researchgate.net/publication/340824789_A_hybrid_neuro-fuzzy_inference_system-based_algorithm_for_time_series_forecasting_applied_to_energy_consumption_prediction
https://www.sciencedirect.com/science/article/abs/pii/S030626192030489X
感谢分享。你分享这个确切是为了什么?
你好 Jason,
我一直在读你的深度学习时间序列书,它真是太棒了。一切都解释得非常清楚。
关于上面和书中关于能源消耗的例子,我注意到这个例子是针对单个家庭的。那么当你有一千甚至数百万个家庭时,你将如何解决这个问题呢?
按位置进行分割并获得 n 个预测会是一个好主意吗?还是预测每个家庭的能源消耗会更好?(我不确定任何机器学习算法或计算机是否能支持如此大量的输出。)
非常感谢,Cristina
谢谢!
很棒的问题,你可以开发一个模型来学习不同房屋的行为,这会给你一些想法
https://machinelearning.org.cn/faq/single-faq/how-to-develop-forecast-models-for-multiple-sites
非常感谢 Jason!我非常感谢您的回答,我会查看那个链接。
Jason,非常感谢。我查看了您回复中提供的链接。但我还有两个问题:
1. 当您说“为所有站点开发一个模型”时,您是指生成类似这样的内容吗?
# 每个家庭的序列(例如,1000 个家庭)。
# h1 -> 1,2,3,…,n_step
# h2 -> 1,2,3,…,n_step
# h1000 -> 1,2,3,…,n_step
# 创建数据集
对于每个 serie_house
data_set = to_supervised(serie_house) # 您书中实现的函数
big_data_set = concatenate(big_data_set,data_set) # 用于行
因此 big_data_set 包含所有家庭的所有有监督数据集。如果这是正确的,那么打乱 big_data_set 会是个好主意吗?
2. 当您说“为每组站点开发一个模型”时,您是指类似这样的内容吗?
第 1 组:低收入家庭
第 2 组:高收入家庭
然后,要对这种情况进行建模,我们应该应用与第 1 点相同的循环吗?
再次非常感谢,并为冗长的消息致歉。🙂
也许可以。
您可以根据您的项目进行解释。也许可以尝试几种方法,看看哪种方法效果好/最好。
我正在处理能源消耗数据。如果您不介意,请分享给我
rashfat2018@gmail.com
不客气。
非常感谢亲爱的杰森……总是最好的
不客气。
Jason……我的项目可以使用相同的代码吗?我有时用电数据,天气数据,20 栋建筑的数据和能源消耗数据……
当然可以。
您好 Jason,为什么您只使用单变量时间序列来训练模型?
子计量和其他变量,以及无功功率,对您的时间序列预测不重要吗?
只是一个例子。
这是使用所有变量的不同示例
https://machinelearning.org.cn/how-to-develop-lstm-models-for-multi-step-time-series-forecasting-of-household-power-consumption/
我认为步进式验证是对测试数据的作弊。不是吗?
不行。
如何检查我们的预测是否正确,如果正确,正确到什么程度?我们可以在一张图上绘制实际消耗量和我们的预测来检查吗?
嗨 Hitesh…以下资源可能会提供帮助:
https://deepchecks.com/how-to-check-the-accuracy-of-your-machine-learning-model/
https://vitalflux.com/steps-for-evaluating-validating-time-series-models/
谢谢,我对性能矩阵和准确性有了概念,但我还有一些问题,我已在下方发布。
我们预测了什么?一周的能源消耗?
我们可以在一张图上打印实际消耗数据与预测消耗数据吗?
我们可以预测一整月的数据吗?
我们可以在整个程序中使用数据帧而不是数组吗?我们能得到按日期预测的结果吗?如何将其与实际数据进行比较?
嗨,为什么你们没有处理异常值?
嗨 Zaid…这只是为了让示例简洁。一般来说,你是对的,这种分析和处理应该成为每个数据管道的一部分。
如果你对如何处理这个主题有任何疑问,请告诉我们。