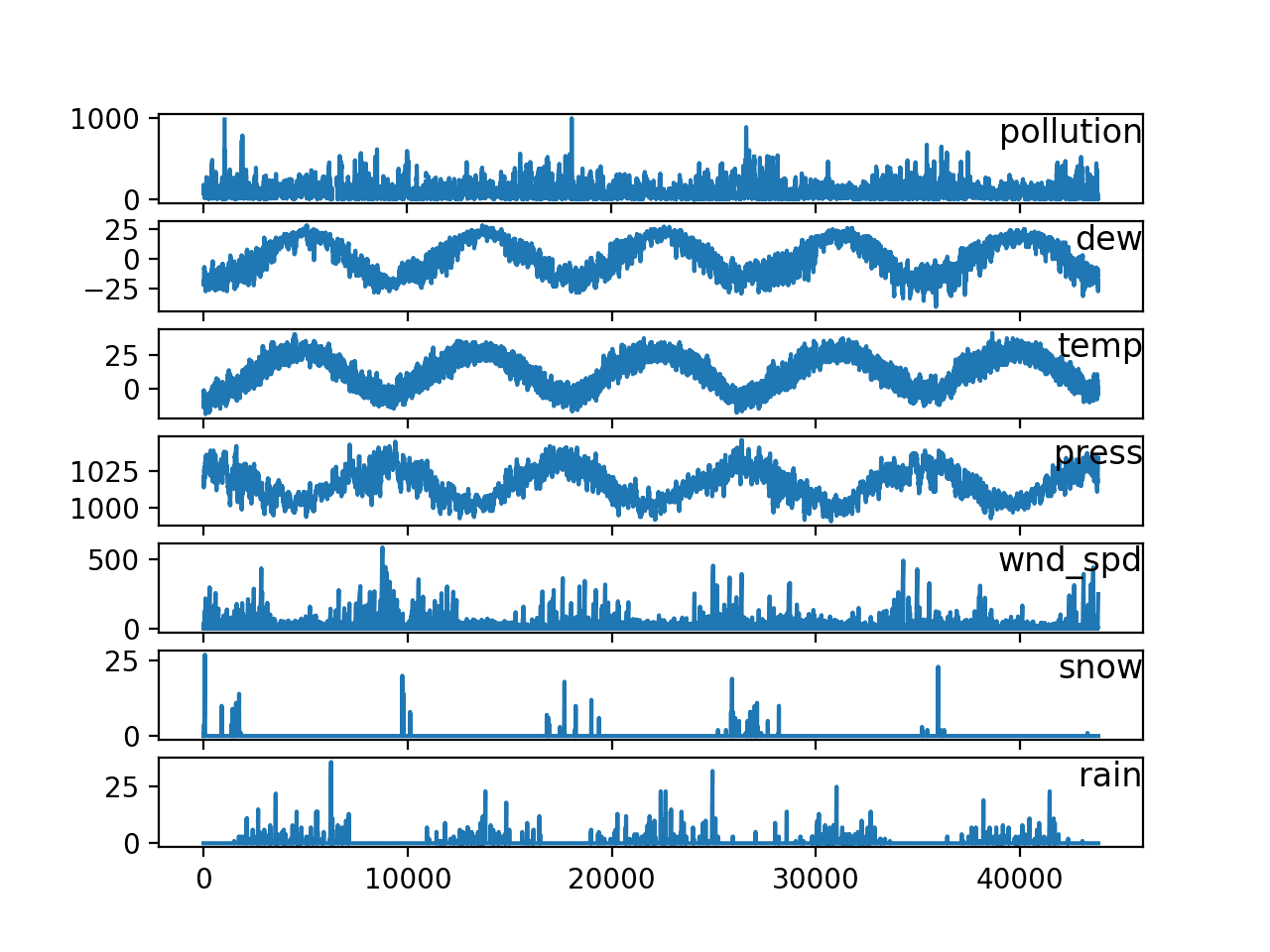
真实的的时间序列预测由于许多原因而具有挑战性,这些原因不仅限于问题的特性,例如拥有多个输入变量、需要预测多个时间步,以及需要为多个物理站点执行相同类型的预测。
EMC 数据科学全球黑客松数据集,或简称“*空气质量预测*”数据集,描述了多个站点上的天气状况,并需要预测未来三天的空气质量测量值。
处理新的时间序列预测数据集时,一个重要的第一步是建立一个模型性能基线,用于比较所有其他更复杂的策略的技能。基线预测策略简单快捷。它们被称为“朴素”策略,因为它们对具体的预测问题几乎或根本不作假设。
在本教程中,您将了解如何为多步多变量空气污染时间序列预测问题开发朴素预测方法。
完成本教程后,您将了解:
- 如何为空气质量数据集开发一个用于评估预测策略的测试框架。
- 如何开发使用整个训练数据集数据的全局朴素预测策略。
- 如何开发使用被预测特定时间间隔数据的局部朴素预测策略。
用我的新书 时间序列深度学习预测 启动您的项目,包括*分步教程*和所有示例的*Python源代码*文件。
让我们开始吧。

如何为多站点多变量空气污染时间序列预测开发基线预测
图片来自 DAVID HOLT,部分权利保留。
教程概述
本教程分为六个部分;它们是:
- 问题描述
- 朴素方法
- 模型评估
- 全局朴素方法
- 分块朴素方法
- 结果总结
问题描述
空气质量预测数据集描述了多个站点的天气状况,需要预测未来三天内的空气质量测量值。
具体来说,天气观测值(如温度、气压、风速和风向)每小时为多个站点提供八天的数据。目标是在多个站点预测未来3天的空气质量测量值。预测提前期不是连续的;相反,必须在72小时的预测期内预测特定的提前期。它们是:
|
1 |
+1, +2, +3, +4, +5, +10, +17, +24, +48, +72 |
此外,数据集被划分为不相交但连续的数据块,其中包含八天的数据,然后是需要预测的三天。
并非所有站点或数据块都提供所有观测数据,也并非所有站点或数据块都提供所有输出变量。存在大量缺失数据,必须加以解决。
该数据集在 2012 年 Kaggle 网站上作为短期机器学习竞赛(或黑客马拉松)的基础。
比赛的提交结果通过对参与者隐藏的真实观测值进行评估,并使用平均绝对误差(MAE)进行评分。在由于数据缺失无法进行预测的情况下,提交时需要指定-1,000,000的值。实际上,提供了一个插入缺失值的模板,并且要求所有提交都采用该模板(真是麻烦)。
一位获胜者在保留的测试集(私有排行榜)上使用滞后观测值的随机森林实现了 0.21058 的 MAE。该解决方案的详细说明可在以下帖子中找到
在本教程中,我们将探讨如何为该问题开发朴素预测,这些预测可用作基线,以确定模型是否在该问题上具有技能。
时间序列深度学习需要帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
朴素预测方法
预测性能的基线提供了比较点。
它是您问题上所有其他建模技术的参考点。如果一个模型获得的性能等于或低于基线,则应修复或放弃该技术。
用于生成预测以计算基线性能的技术必须易于实现,并且对问题细节朴素。原则是,如果一种复杂的预测方法无法超越一种几乎不使用或不使用问题特定信息的模型,那么它就没有技能。
存在一些问题无关的预测方法,可以并且应该首先使用,然后是使用少量问题特定信息的朴素方法。
可以使用的两个问题无关的朴素预测方法示例包括:
- 将每个序列的最后一个观测值持续保留。
- 预测每个序列的观测值平均值。
数据被分成时间块或时间间隔。每个时间块都有多个变量,分布在多个站点,需要进行预测。在此类数据组织的分块级别上,持续预测方法是有意义的。
可以探索其他持续方法,例如:
- 将前一天对未来三天的观测值作为下三天预测值,针对每个序列。
- 将前三天对未来三天的观测值作为下三天预测值,针对每个序列。
这些是值得探索的基线方法,但大量缺失的数据以及大多数数据块的不连续结构使得在没有非平凡数据准备的情况下难以实现它们。
预测平均观测值可以进一步细化,例如:
- 预测每个序列的全局(跨块)平均值。
- 预测每个序列的局部(块内)平均值。
需要对每个序列进行三天的预测,但起始时间不同,例如一天中的不同时间。因此,每个块的预测提前期将落在一天中的不同小时。
对预测平均值的进一步细化是结合正在预测的小时数,例如:
- 预测每个预测提前期的小时数全局(跨块)平均值。
- 预测每个预测提前期的小时数局部(块内)平均值。
许多变量在多个站点上进行测量;因此,可以使用跨序列的信息,例如在计算平均值或每个小时的平均值以进行预测提前期时。这些很有趣,但可能超出了朴素的范畴。
这是一个不错的起点,尽管您可能还想进一步细化朴素方法并作为练习进行探索。请记住,目标是使用非常少的问题特定信息来开发预测基线。
总而言之,我们将针对此问题研究五种不同的朴素预测方法,其中最好的方法将提供性能下限,其他模型可以与之进行比较。它们是:
- 每个序列的全局平均值
- 每个序列的预测提前期全局平均值
- 每个序列的局部持续值
- 每个序列的局部平均值
- 每个序列的预测提前期局部平均值
模型评估
在评估朴素预测方法之前,我们必须开发一个测试工具。
这至少包括如何准备数据以及如何评估预测。
加载数据集
第一步是下载数据集并将其加载到内存中。
可以从 Kaggle 网站免费下载数据集。您可能需要创建帐户并登录才能下载数据集。
将整个数据集(例如“下载所有”)下载到您的工作站,并在当前工作目录中解压缩存档到名为“AirQualityPrediction”的文件夹中。
我们的重点将放在“TrainingData.csv”文件,该文件包含训练数据集,特别是以数据块形式存在的数据,其中每个数据块是八个连续的观测日和目标变量。
我们可以使用 Pandas 的 read_csv() 函数将数据文件加载到内存中,并指定第 0 行作为标题行。
|
1 2 |
# 加载数据集 dataset = read_csv('AirQualityPrediction/TrainingData.csv', header=0) |
我们可以按“chunkID”变量(列索引 1)对数据进行分组。
首先,让我们获取唯一块标识符的列表。
|
1 |
chunk_ids = unique(values[:, 1]) |
然后,我们可以收集每个块标识符的所有行,并将它们存储在字典中以便于访问。
|
1 2 3 4 5 |
chunks = dict() # 按块 ID 排序行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks[chunk_id] = values[selection, :] |
下面定义了一个名为 to_chunks() 的函数,该函数接受加载数据的 NumPy 数组,并返回一个从 chunk_id 到块行的字典。
|
1 2 3 4 5 6 7 8 9 10 |
# 按“chunkID”拆分数据集,返回一个 ID 到行的字典 def to_chunks(values, chunk_ix=1): chunks = dict() # 获取唯一的块 ID chunk_ids = unique(values[:, chunk_ix]) # 按块 ID 分组行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks[chunk_id] = values[selection, :] return chunks |
加载数据集并将其拆分为块的完整示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# 加载数据并拆分为块 from numpy import unique from pandas import read_csv # 按“chunkID”拆分数据集,返回一个 ID 到行的字典 def to_chunks(values, chunk_ix=1): chunks = dict() # 获取唯一的块 ID chunk_ids = unique(values[:, chunk_ix]) # 按块 ID 分组行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks[chunk_id] = values[selection, :] return chunks # 加载数据集 dataset = read_csv('AirQualityPrediction/TrainingData.csv', header=0) # 按块分组数据 values = dataset.values chunks = to_chunks(values) print('Total Chunks: %d' % len(chunks)) |
运行示例会打印数据集中块的数量。
|
1 |
总块数:208 |
数据准备
现在我们知道如何加载数据并将其拆分为块,我们可以将其分成训练和测试数据集。
每个块包含八天每小时的观测数据,尽管每个块中实际观测的数量可能差异很大。
我们可以将每个块的前五天的观测数据用于训练,后三天用于测试。
每条观测记录都有一个名为“*position_within_chunk*”的行,其值从 1 到 192(8 天 * 24 小时)不等。因此,我们可以将此列值小于或等于 120(5 * 24)的所有行作为训练数据,将大于 120 的值作为测试数据。
此外,任何在训练或测试拆分中没有观测值的块都可以被视为不可用而丢弃。
在使用朴素模型时,我们只对目标变量感兴趣,而对输入气象变量不感兴趣。因此,我们可以删除输入数据,让训练和测试数据仅包含每个块的 39 个目标变量,以及块内位置和观测小时。
下面的 split_train_test() 函数实现了此行为;给定一个块字典,它将每个块拆分为训练和测试块数据的列表。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 将每个块拆分为训练/测试集 def split_train_test(chunks, row_in_chunk_ix=2): train, test = list(), list() # 前 5 天的每小时观测数据用于训练 cut_point = 5 * 24 # 枚举块 for k,rows in chunks.items(): # 按“position_within_chunk”拆分块行 train_rows = rows[rows[:,row_in_chunk_ix] <= cut_point, :] test_rows = rows[rows[:,row_in_chunk_ix] > cut_point, :] if len(train_rows) == 0 or len(test_rows) == 0: print('>dropping chunk=%d: train=%s, test=%s' % (k, train_rows.shape, test_rows.shape)) continue # 存储块 ID、块内位置、小时和所有目标 indices = [1,2,5] + [x for x in range(56,train_rows.shape[1])] train.append(train_rows[:, indices]) test.append(test_rows[:, indices]) return train, test |
我们不需要整个测试数据集;相反,我们只需要三天内特定提前期处的观测数据,特别是以下提前期
|
1 |
+1, +2, +3, +4, +5, +10, +17, +24, +48, +72 |
其中,每个提前期都相对于训练期结束。
首先,我们可以将这些提前期放入一个函数中,以便于引用
|
1 2 3 |
# 返回相对预测提前期的列表 def get_lead_times(): return [1, 2 ,3, 4, 5, 10, 17, 24, 48, 72] |
接下来,我们可以将测试数据集缩减为仅包含首选提前期的数据。
我们可以通过查看“position_within_chunk”列,并使用提前期作为训练数据集结束的偏移量来实现,例如 120 + 1、120 + 2 等。
如果在测试集中找到匹配的行,则保存该行,否则生成一行 NaN 观测值。
下面的 to_forecasts() 函数实现了此功能,并返回一个 NumPy 数组,其中每个块的每个预测提前期都有一行。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# 将测试块中的行转换为预测 def to_forecasts(test_chunks, row_in_chunk_ix=1): # 获取提前期 lead_times = get_lead_times() # 前 5 天的每小时观测数据用于训练 cut_point = 5 * 24 forecasts = list() # 枚举每个块 for rows in test_chunks: chunk_id = rows[0, 0] # 枚举每个提前期 for tau in lead_times: # 确定我们想要的提前期在块中的行 offset = cut_point + tau # 使用块中的行号检索提前期的数据 row_for_tau = rows[rows[:,row_in_chunk_ix]==offset, :] # 检查我们是否有数据 if len(row_for_tau) == 0: # 创建一个模拟行 [chunk, position, hour] + [nan...] row = [chunk_id, offset, nan] + [nan for _ in range(39)] forecasts.append(row) else: # 存储预测行 forecasts.append(row_for_tau[0]) return array(forecasts) |
我们可以将所有这些结合起来,将数据集拆分为训练集和测试集,并将结果保存到新文件中。
完整的代码示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
# 将数据拆分为训练集和测试集 from numpy import unique from numpy import nan from numpy import array from numpy import savetxt from pandas import read_csv # 按“chunkID”拆分数据集,返回一个 ID 到行的字典 def to_chunks(values, chunk_ix=1): chunks = dict() # 获取唯一的块 ID chunk_ids = unique(values[:, chunk_ix]) # 按块 ID 分组行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks[chunk_id] = values[selection, :] return chunks # 将每个块拆分为训练/测试集 def split_train_test(chunks, row_in_chunk_ix=2): train, test = list(), list() # 前 5 天的每小时观测数据用于训练 cut_point = 5 * 24 # 枚举块 for k,rows in chunks.items(): # 按“position_within_chunk”拆分块行 train_rows = rows[rows[:,row_in_chunk_ix] <= cut_point, :] test_rows = rows[rows[:,row_in_chunk_ix] > cut_point, :] if len(train_rows) == 0 or len(test_rows) == 0: print('>dropping chunk=%d: train=%s, test=%s' % (k, train_rows.shape, test_rows.shape)) continue # 存储块 ID、块内位置、小时和所有目标 indices = [1,2,5] + [x for x in range(56,train_rows.shape[1])] train.append(train_rows[:, indices]) test.append(test_rows[:, indices]) return train, test # 返回相对预测提前期的列表 def get_lead_times(): return [1, 2 ,3, 4, 5, 10, 17, 24, 48, 72] # 将测试块中的行转换为预测 def to_forecasts(test_chunks, row_in_chunk_ix=1): # 获取提前期 lead_times = get_lead_times() # 前 5 天的每小时观测数据用于训练 cut_point = 5 * 24 forecasts = list() # 枚举每个块 for rows in test_chunks: chunk_id = rows[0, 0] # 枚举每个提前期 for tau in lead_times: # 确定我们想要的提前期在块中的行 offset = cut_point + tau # 使用块中的行号检索提前期的数据 row_for_tau = rows[rows[:,row_in_chunk_ix]==offset, :] # 检查我们是否有数据 if len(row_for_tau) == 0: # 创建一个模拟行 [chunk, position, hour] + [nan...] row = [chunk_id, offset, nan] + [nan for _ in range(39)] forecasts.append(row) else: # 存储预测行 forecasts.append(row_for_tau[0]) return array(forecasts) # 加载数据集 dataset = read_csv('AirQualityPrediction/TrainingData.csv', header=0) # 按块分组数据 values = dataset.values chunks = to_chunks(values) # 分割成训练/测试集 train, test = split_train_test(chunks) # 将训练块平铺成行 train_rows = array([row for rows in train for row in rows]) # print(train_rows.shape) print('Train Rows: %s' % str(train_rows.shape)) # 仅将训练数据缩减到预测提前期 test_rows = to_forecasts(test) print('Test Rows: %s' % str(test_rows.shape)) # 保存数据集 savetxt('AirQualityPrediction/naive_train.csv', train_rows, delimiter=',') savetxt('AirQualityPrediction/naive_test.csv', test_rows, delimiter=',') |
运行示例首先会提示块 69 因数据不足而被从数据集中删除。
然后我们可以看到,训练集和测试集中各有 42 列,其中一列用于块 ID,一列用于块内位置,一列用于一天中的小时,以及 39 个训练变量。
我们还可以看到,测试数据集的版本明显较小,只包含预测提前期处的行。
新的训练和测试数据集分别保存在“naive_train.csv”和“naive_test.csv”文件中。
|
1 2 3 |
>正在删除块=69:训练=(0, 95),测试=(28, 95) 训练行数: (23514, 42) 测试行数: (2070, 42) |
预测评估
一旦做出预测,就需要对其进行评估。
为了评估预测,拥有更简单的格式会很有帮助。例如,我们将使用 [块][变量][时间] 的三维结构,其中变量是从 0 到 38 的目标变量编号,时间是从 0 到 9 的提前期索引。
模型预计将以这种格式进行预测。
我们还可以重新构造测试数据集,使其具有此数据集以进行比较。下面的 prepare_test_forecasts() 函数实现了此功能。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 将块中的测试数据集转换为 [块][变量][时间] 格式 def prepare_test_forecasts(test_chunks): predictions = list() # 枚举要预测的块 for rows in test_chunks: # 枚举块的目标 chunk_predictions = list() for j in range(3, rows.shape[1]): yhat = rows[:, j] chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) |
我们将使用平均绝对误差 (MAE) 来评估模型。这是竞赛中使用的指标,考虑到目标变量的非高斯分布,这是一个明智的选择。
如果提前期在测试集中不包含任何数据(例如 NaN),则不会为此预测计算错误。如果提前期在测试集中有数据但在预测中没有数据,则观测值的全部幅度将被视为错误。最后,如果测试集有一个观测值并且进行了预测,那么将绝对差值记录为错误。
calculate_error() 函数实现了这些规则并返回给定预测的误差。
|
1 2 3 4 5 6 7 |
# 计算实际值和预测值之间的误差 def calculate_error(actual, predicted): # 如果预测值为 nan,则给出完整的实际值 if isnan(predicted): return abs(actual) # 计算绝对差值 return abs(actual - predicted) |
误差在所有块和所有提前期上求和,然后求平均值。
将计算总体 MAE,但我们还将计算每个预测提前期的 MAE。这通常有助于模型选择,因为某些模型在不同的提前期可能表现不同。
下面的 evaluate_forecasts() 函数实现了此功能,它计算给定预测和预期值(以 [块][变量][时间] 格式)的 MAE 和每个提前期 MAE。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# 评估 [块][变量][时间] 格式的预测 def evaluate_forecasts(predictions, testset): lead_times = get_lead_times() total_mae, times_mae = 0.0, [0.0 for _ in range(len(lead_times))] total_c, times_c = 0, [0 for _ in range(len(lead_times))] # 枚举测试块 for i in range(len(test_chunks)): # 转换为预测 actual = testset[i] predicted = predictions[i] # 枚举目标变量 for j in range(predicted.shape[0]): # 枚举提前期 for k in range(len(lead_times)): # 如果实际值为 nan 则跳过 if isnan(actual[j, k]): continue # 计算误差 error = calculate_error(actual[j, k], predicted[j, k]) # 更新统计数据 total_mae += error times_mae[k] += error total_c += 1 times_c[k] += 1 # 归一化求和的绝对误差 total_mae /= total_c times_mae = [times_mae[i]/times_c[i] for i in range(len(times_mae))] return total_mae, times_mae |
一旦我们评估了模型,我们就可以展示它。
下面的 summarize_error() 函数首先打印模型性能的一行摘要,然后创建每个预测提前期的 MAE 图。
|
1 2 3 4 5 6 7 8 9 10 |
# 总结得分 def summarize_error(name, total_mae, times_mae): # 打印摘要 lead_times = get_lead_times() formatted = ['+%d %.3f' % (lead_times[i], times_mae[i]) for i in range(len(lead_times))] s_scores = ', '.join(formatted) print('%s: [%.3f MAE] %s' % (name, total_mae, s_scores)) # 绘制摘要 pyplot.plot([str(x) for x in lead_times], times_mae, marker='.') pyplot.show() |
现在我们准备开始探索朴素预测方法的性能。
全局朴素方法
在本节中,我们将探讨使用训练数据集中的所有数据,而不是仅限于我们正在预测的块的朴素预测方法。
我们将研究两种方法:
- 预测每条系列的平均值
- 预测每条系列每小时的平均值
预测每条系列的平均值
第一步是实现一个通用函数,用于为每个数据块进行预测。
该函数接收训练数据集和测试集的输入列(数据块 ID、数据块中的位置和小时),并以期望的 3D 格式 _[数据块][变量][时间]_ 返回所有数据块的预测。
该函数枚举预测中的数据块,然后枚举 39 个目标列,调用另一个名为 _forecast_variable()_ 的新函数,以便为给定目标变量的每个超前时间进行预测。
完整的函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 为每个数据块进行预测,返回 [数据块][变量][时间] def forecast_chunks(train_chunks, test_input): lead_times = get_lead_times() predictions = list() # 枚举要预测的块 for i in range(len(train_chunks)): # 枚举块的目标 chunk_predictions = list() for j in range(39): yhat = forecast_variable(train_chunks, train_chunks[i], test_input[i], lead_times, j) chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) |
现在我们可以实现一个 _forecast_variable()_ 的版本,它计算给定系列的平均值,并为每个超前时间预测该平均值。
首先,我们必须收集所有数据块中目标列的所有观测值,然后计算观测值的平均值,同时忽略 NaN 值。 _nanmean()_ NumPy 函数将计算数组的平均值并忽略 _NaN_ 值。
下面的 _forecast_variable()_ 函数实现了此行为。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): # 将目标数字转换为列号 col_ix = 3 + target_ix # 从所有数据块收集观测值 all_obs = list() for chunk in train_chunks: all_obs += [x for x in chunk[:, col_ix]] # 返回平均值,忽略 nan value = nanmean(all_obs) return [value for _ in lead_times] |
现在我们拥有了所需的一切。
下面列出了预测所有超前时间中每条系列的全局平均值的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 |
# 预测全局平均值 从 numpy 导入 loadtxt from numpy import nan from numpy import isnan from numpy import count_nonzero from numpy import unique from numpy import array from numpy import nanmean from matplotlib import pyplot # 按“chunkID”分割数据集,返回块列表 def to_chunks(values, chunk_ix=0): chunks = list() # 获取唯一的块 ID chunk_ids = unique(values[:, chunk_ix]) # 按块 ID 分组行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks.append(values[selection, :]) return chunks # 返回相对预测提前期的列表 def get_lead_times(): return [1, 2 ,3, 4, 5, 10, 17, 24, 48, 72] # 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): # 将目标数字转换为列号 col_ix = 3 + target_ix # 从所有数据块收集观测值 all_obs = list() for chunk in train_chunks: all_obs += [x for x in chunk[:, col_ix]] # 返回平均值,忽略 nan value = nanmean(all_obs) return [value for _ in lead_times] # 为每个数据块进行预测,返回 [数据块][变量][时间] def forecast_chunks(train_chunks, test_input): lead_times = get_lead_times() predictions = list() # 枚举要预测的块 for i in range(len(train_chunks)): # 枚举块的目标 chunk_predictions = list() for j in range(39): yhat = forecast_variable(train_chunks, train_chunks[i], test_input[i], lead_times, j) chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 将块中的测试数据集转换为 [块][变量][时间] 格式 def prepare_test_forecasts(test_chunks): predictions = list() # 枚举要预测的块 for rows in test_chunks: # 枚举块的目标 chunk_predictions = list() for j in range(3, rows.shape[1]): yhat = rows[:, j] chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 计算实际值和预测值之间的误差 def calculate_error(actual, predicted): # 如果预测值为 nan,则给出完整的实际值 if isnan(predicted): return abs(actual) # 计算绝对差值 return abs(actual - predicted) # 评估 [块][变量][时间] 格式的预测 def evaluate_forecasts(predictions, testset): lead_times = get_lead_times() total_mae, times_mae = 0.0, [0.0 for _ in range(len(lead_times))] total_c, times_c = 0, [0 for _ in range(len(lead_times))] # 枚举测试块 for i in range(len(test_chunks)): # 转换为预测 actual = testset[i] predicted = predictions[i] # 枚举目标变量 for j in range(predicted.shape[0]): # 枚举提前期 for k in range(len(lead_times)): # 如果实际值为 nan 则跳过 if isnan(actual[j, k]): continue # 计算误差 error = calculate_error(actual[j, k], predicted[j, k]) # 更新统计数据 total_mae += error times_mae[k] += error total_c += 1 times_c[k] += 1 # 归一化求和的绝对误差 total_mae /= total_c times_mae = [times_mae[i]/times_c[i] for i in range(len(times_mae))] return total_mae, times_mae # 总结得分 def summarize_error(name, total_mae, times_mae): # 打印摘要 lead_times = get_lead_times() formatted = ['+%d %.3f' % (lead_times[i], times_mae[i]) for i in range(len(lead_times))] s_scores = ', '.join(formatted) print('%s: [%.3f MAE] %s' % (name, total_mae, s_scores)) # 绘制摘要 pyplot.plot([str(x) for x in lead_times], times_mae, marker='.') pyplot.show() # 加载数据集 train = loadtxt('AirQualityPrediction/naive_train.csv', delimiter=',') test = loadtxt('AirQualityPrediction/naive_test.csv', delimiter=',') # 按块分组数据 train_chunks = to_chunks(train) test_chunks = to_chunks(test) # 预测 test_input = [rows[:, :3] for rows in test_chunks] forecast = forecast_chunks(train_chunks, test_input) # 评估预测 actual = prepare_test_forecasts(test_chunks) total_mae, times_mae = evaluate_forecasts(forecast, actual) # 总结预测 summarize_error('Global Mean', total_mae, times_mae) |
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
运行该示例时,首先会打印出总体 MAE 0.634,然后是每个预测超前时间的 MAE 分数。
|
1 |
# 全局平均值:[0.634 MAE] +1 0.635, +2 0.629, +3 0.638, +4 0.650, +5 0.649, +10 0.635, +17 0.634, +24 0.641, +48 0.613, +72 0.618 |
创建了一个折线图,显示了从+1小时到+72小时的每个预测超前时间的 MAE 分数。
我们看不到预测超前时间与预测误差之间有明显的关联,这可能与更具技能的模型一致。
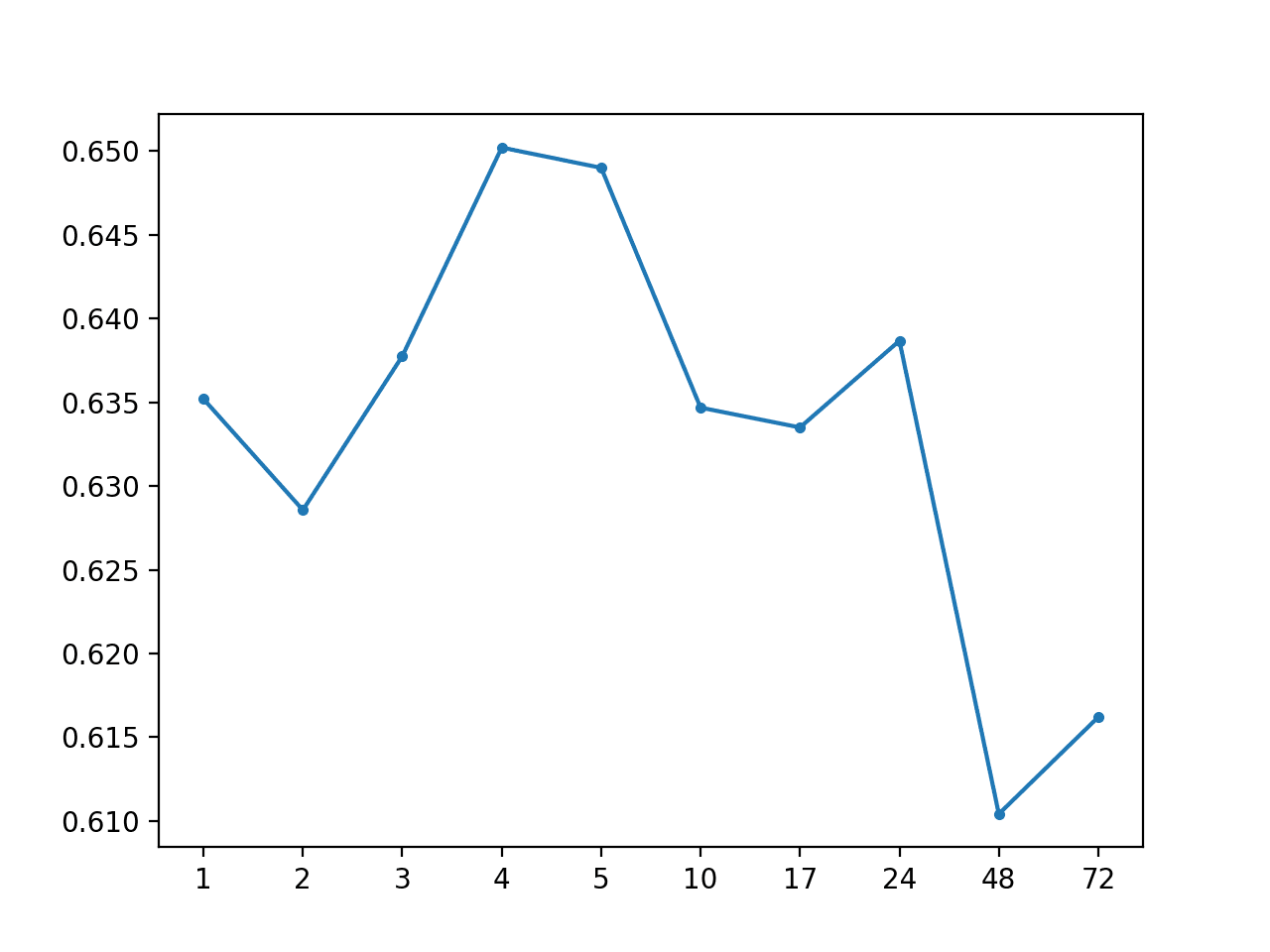
全局平均值预测超前时间 MAE
我们可以更新该示例,以预测全局中位数而不是平均值。
考虑到数据似乎显示出非高斯分布的特征,中位数可能比平均值更能代表该数据的中心趋势。
NumPy 提供了 _nanmedian()_ 函数,我们可以在 _forecast_variable()_ 函数中将其替换 _nanmean()_。
下面列出了完整的更新示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 |
# 预测全局中位数 从 numpy 导入 loadtxt from numpy import nan from numpy import isnan from numpy import count_nonzero from numpy import unique from numpy import array from numpy import nanmedian from matplotlib import pyplot # 按“chunkID”分割数据集,返回块列表 def to_chunks(values, chunk_ix=0): chunks = list() # 获取唯一的块 ID chunk_ids = unique(values[:, chunk_ix]) # 按块 ID 分组行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks.append(values[selection, :]) return chunks # 返回相对预测提前期的列表 def get_lead_times(): return [1, 2 ,3, 4, 5, 10, 17, 24, 48, 72] # 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): # 将目标数字转换为列号 col_ix = 3 + target_ix # 从所有数据块收集观测值 all_obs = list() for chunk in train_chunks: all_obs += [x for x in chunk[:, col_ix]] # 返回平均值,忽略 nan value = nanmedian(all_obs) return [value for _ in lead_times] # 为每个数据块进行预测,返回 [数据块][变量][时间] def forecast_chunks(train_chunks, test_input): lead_times = get_lead_times() predictions = list() # 枚举要预测的块 for i in range(len(train_chunks)): # 枚举块的目标 chunk_predictions = list() for j in range(39): yhat = forecast_variable(train_chunks, train_chunks[i], test_input[i], lead_times, j) chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 将块中的测试数据集转换为 [块][变量][时间] 格式 def prepare_test_forecasts(test_chunks): predictions = list() # 枚举要预测的块 for rows in test_chunks: # 枚举块的目标 chunk_predictions = list() for j in range(3, rows.shape[1]): yhat = rows[:, j] chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 计算实际值和预测值之间的误差 def calculate_error(actual, predicted): # 如果预测值为 nan,则给出完整的实际值 if isnan(predicted): return abs(actual) # 计算绝对差值 return abs(actual - predicted) # 评估 [块][变量][时间] 格式的预测 def evaluate_forecasts(predictions, testset): lead_times = get_lead_times() total_mae, times_mae = 0.0, [0.0 for _ in range(len(lead_times))] total_c, times_c = 0, [0 for _ in range(len(lead_times))] # 枚举测试块 for i in range(len(test_chunks)): # 转换为预测 actual = testset[i] predicted = predictions[i] # 枚举目标变量 for j in range(predicted.shape[0]): # 枚举提前期 for k in range(len(lead_times)): # 如果实际值为 nan 则跳过 if isnan(actual[j, k]): continue # 计算误差 error = calculate_error(actual[j, k], predicted[j, k]) # 更新统计数据 total_mae += error times_mae[k] += error total_c += 1 times_c[k] += 1 # 归一化求和的绝对误差 total_mae /= total_c times_mae = [times_mae[i]/times_c[i] for i in range(len(times_mae))] return total_mae, times_mae # 总结得分 def summarize_error(name, total_mae, times_mae): # 打印摘要 lead_times = get_lead_times() formatted = ['+%d %.3f' % (lead_times[i], times_mae[i]) for i in range(len(lead_times))] s_scores = ', '.join(formatted) print('%s: [%.3f MAE] %s' % (name, total_mae, s_scores)) # 绘制摘要 pyplot.plot([str(x) for x in lead_times], times_mae, marker='.') pyplot.show() # 加载数据集 train = loadtxt('AirQualityPrediction/naive_train.csv', delimiter=',') test = loadtxt('AirQualityPrediction/naive_test.csv', delimiter=',') # 按块分组数据 train_chunks = to_chunks(train) test_chunks = to_chunks(test) # 预测 test_input = [rows[:, :3] for rows in test_chunks] forecast = forecast_chunks(train_chunks, test_input) # 评估预测 actual = prepare_test_forecasts(test_chunks) total_mae, times_mae = evaluate_forecasts(forecast, actual) # 总结预测 summarize_error('Global Median', total_mae, times_mae) |
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
运行该示例显示 MAE 下降到约 0.59,这表明使用中位数作为中心趋势确实可能是一个更好的基线策略。
|
1 |
全局中位数:[0.598 MAE] +1 0.601, +2 0.594, +3 0.600, +4 0.611, +5 0.615, +10 0.594, +17 0.592, +24 0.602, +48 0.585, +72 0.580 |
还创建了 MAE 按超前时间绘制的折线图。
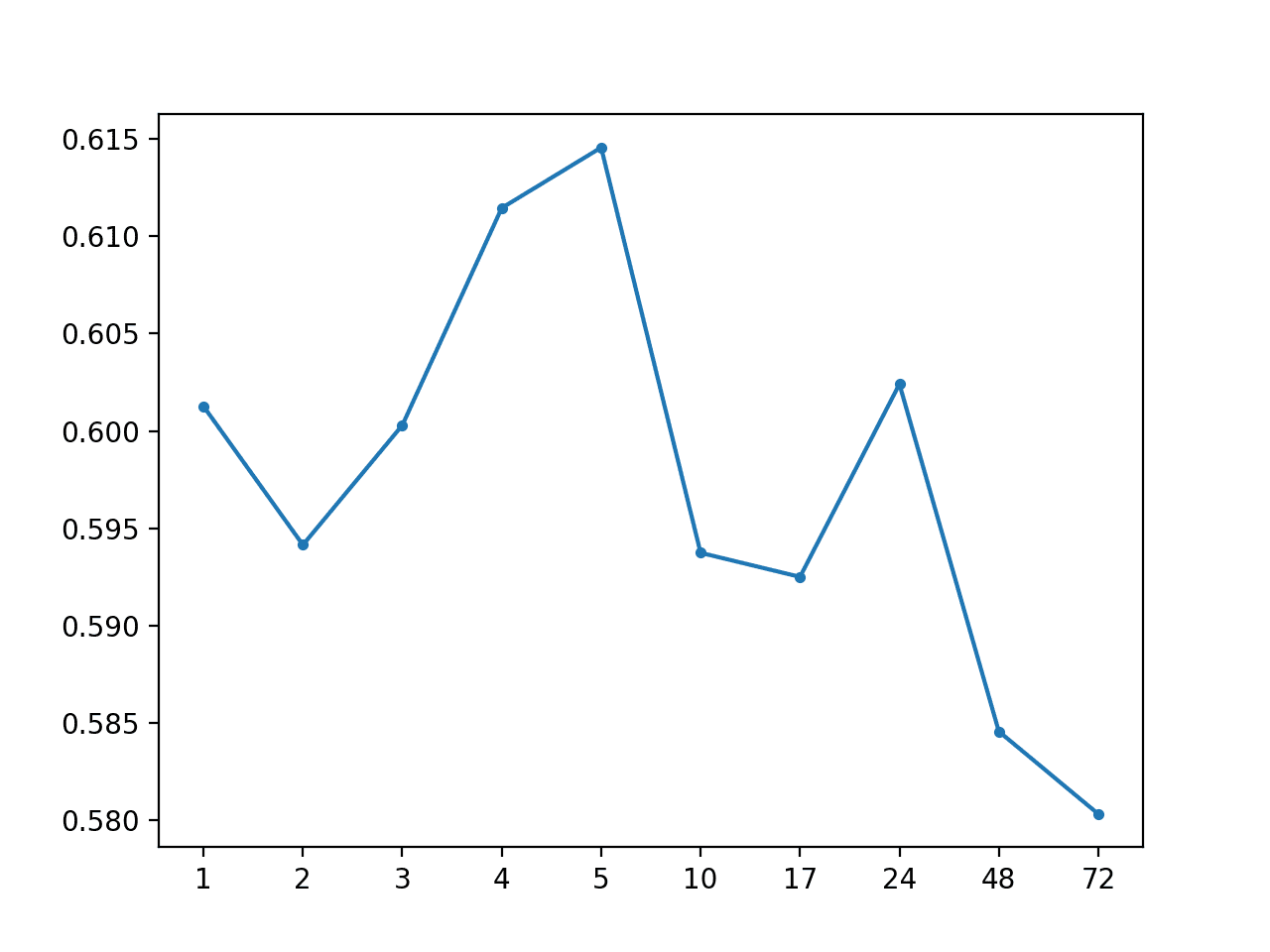
全局中位数预测超前时间 MAE
预测每条系列每小时的平均值
我们可以更新该策略,通过仅包含与预测超前时间具有相同一天中的小时的行来计算每条系列的中心趋势。
例如,如果 +1 超前时间的小时是 6(例如 06:00 或早上 6 点),那么我们可以找到训练数据集中所有数据块中该小时的所有其他行,并计算给定目标变量的该类行的中位数。
我们在测试数据集中记录一天中的小时,并使其在进行预测时可供模型使用。一个棘手的问题是,在某些情况下,测试数据集中没有给定超前时间的记录,并且需要用 _NaN_ 值(包括小时的 _NaN_ 值)来生成一个。在这些情况下,不需要进行预测,因此我们将跳过它们并预测一个 _NaN_ 值。
下面的 _forecast_variable()_ 函数实现了此行为,为给定变量的每个超前时间返回预测。
它的效率不高,并且首先为每个变量的每个小时预先计算中位数可能更有效率,然后使用查找表进行预测。目前效率不是问题,因为我们正在寻找模型性能的基线。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): forecast = list() # 将目标数字转换为列号 col_ix = 3 + target_ix # 枚举提前期 for i in range(len(lead_times)): # 获取此预测超前时间的小时 hour = chunk_test[i, 2] # 检查是否没有测试数据 if isnan(hour): forecast.append(nan) continue # 获取此小时的所有行 all_rows = list() for rows in train_chunks: [all_rows.append(row) for row in rows[rows[:,2]==hour]] # 计算目标的集中趋势 all_rows = array(all_rows) value = nanmedian(all_rows[:, col_ix]) forecast.append(value) return forecast |
下面列出了预测每小时全局中位数的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 |
# 预测每小时的全局中位数 从 numpy 导入 loadtxt from numpy import nan from numpy import isnan from numpy import count_nonzero from numpy import unique from numpy import array from numpy import nanmedian from matplotlib import pyplot # 按“chunkID”分割数据集,返回块列表 def to_chunks(values, chunk_ix=0): chunks = list() # 获取唯一的块 ID chunk_ids = unique(values[:, chunk_ix]) # 按块 ID 分组行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks.append(values[selection, :]) return chunks # 返回相对预测提前期的列表 def get_lead_times(): return [1, 2, 3, 4, 5, 10, 17, 24, 48, 72] # 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): forecast = list() # 将目标数字转换为列号 col_ix = 3 + target_ix # 枚举提前期 for i in range(len(lead_times)): # 获取此预测超前时间的小时 hour = chunk_test[i, 2] # 检查是否没有测试数据 if isnan(hour): forecast.append(nan) continue # 获取此小时的所有行 all_rows = list() for rows in train_chunks: [all_rows.append(row) for row in rows[rows[:,2]==hour]] # 计算目标的集中趋势 all_rows = array(all_rows) value = nanmedian(all_rows[:, col_ix]) forecast.append(value) return forecast # 为每个数据块进行预测,返回 [数据块][变量][时间] def forecast_chunks(train_chunks, test_input): lead_times = get_lead_times() predictions = list() # 枚举要预测的块 for i in range(len(train_chunks)): # 枚举块的目标 chunk_predictions = list() for j in range(39): yhat = forecast_variable(train_chunks, train_chunks[i], test_input[i], lead_times, j) chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 将块中的测试数据集转换为 [块][变量][时间] 格式 def prepare_test_forecasts(test_chunks): predictions = list() # 枚举要预测的块 for rows in test_chunks: # 枚举块的目标 chunk_predictions = list() for j in range(3, rows.shape[1]): yhat = rows[:, j] chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 计算实际值和预测值之间的误差 def calculate_error(actual, predicted): # 如果预测值为 nan,则给出完整的实际值 if isnan(predicted): return abs(actual) # 计算绝对差值 return abs(actual - predicted) # 评估 [块][变量][时间] 格式的预测 def evaluate_forecasts(predictions, testset): lead_times = get_lead_times() total_mae, times_mae = 0.0, [0.0 for _ in range(len(lead_times))] total_c, times_c = 0, [0 for _ in range(len(lead_times))] # 枚举测试块 for i in range(len(test_chunks)): # 转换为预测 actual = testset[i] predicted = predictions[i] # 枚举目标变量 for j in range(predicted.shape[0]): # 枚举提前期 for k in range(len(lead_times)): # 如果实际值为 nan 则跳过 if isnan(actual[j, k]): continue # 计算误差 error = calculate_error(actual[j, k], predicted[j, k]) # 更新统计数据 total_mae += error times_mae[k] += error total_c += 1 times_c[k] += 1 # 归一化求和的绝对误差 total_mae /= total_c times_mae = [times_mae[i]/times_c[i] for i in range(len(times_mae))] return total_mae, times_mae # 总结得分 def summarize_error(name, total_mae, times_mae): # 打印摘要 lead_times = get_lead_times() formatted = ['+%d %.3f' % (lead_times[i], times_mae[i]) for i in range(len(lead_times))] s_scores = ', '.join(formatted) print('%s: [%.3f MAE] %s' % (name, total_mae, s_scores)) # 绘制摘要 pyplot.plot([str(x) for x in lead_times], times_mae, marker='.') pyplot.show() # 加载数据集 train = loadtxt('AirQualityPrediction/naive_train.csv', delimiter=',') test = loadtxt('AirQualityPrediction/naive_test.csv', delimiter=',') # 按块分组数据 train_chunks = to_chunks(train) test_chunks = to_chunks(test) # 预测 test_input = [rows[:, :3] for rows in test_chunks] forecast = forecast_chunks(train_chunks, test_input) # 评估预测 actual = prepare_test_forecasts(test_chunks) total_mae, times_mae = evaluate_forecasts(forecast, actual) # 总结预测 summarize_error('Global Median by Hour', total_mae, times_mae) |
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
运行该示例总结了该模型的性能,MAE 约为 0.567,这比上面的全局中位数策略有所改进。
|
1 |
每小时全局中位数:[0.567 MAE] +1 0.573, +2 0.565, +3 0.567, +4 0.579, +5 0.589, +10 0.559, +17 0.565, +24 0.567, +48 0.558, +72 0.551 |
还创建了 MAE 按超前时间绘制的折线图,显示 +72 的总体预测误差最低。这很有趣,可能表明基于小时的信息在更复杂的模型中有用。
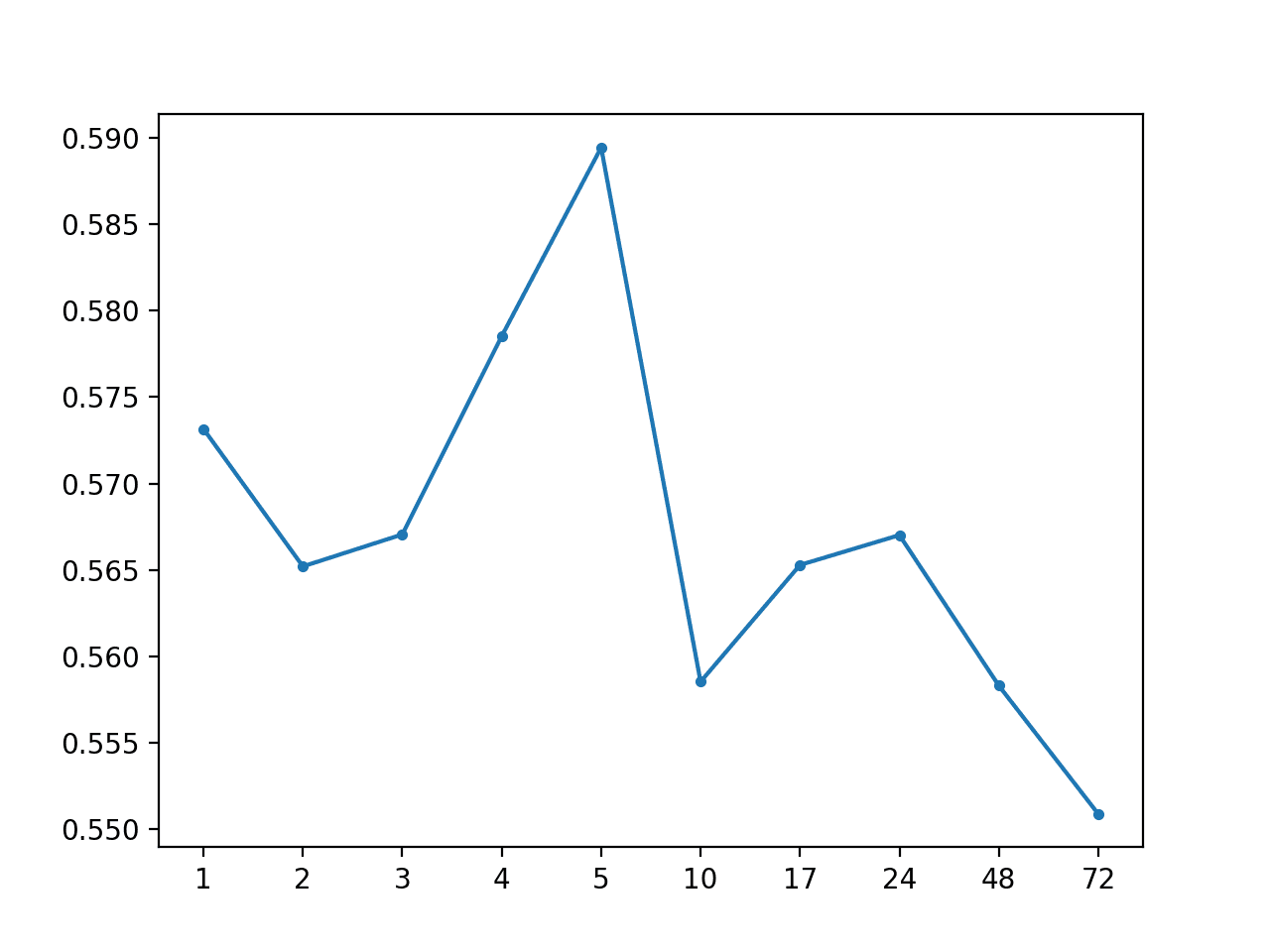
每小时全局中位数预测超前时间 MAE
分块朴素方法
使用来自数据块本身的信息可能比使用来自整个训练数据集的全局信息具有更强的预测能力。
我们可以通过三种本地或特定数据块的朴素预测方法来探索这一点;它们是:
- 预测每条系列的最后一次观测值
- 预测每条系列的平均值
- 预测每条系列每小时的平均值
最后两种是上一节中评估的全局策略的数据块特定版本。
预测每条系列的最后一次观测值
预测数据块中最后一个非 NaN 观测值可能是最简单的模型,通常称为持久性模型或朴素模型。
下面的 _forecast_variable()_ 函数实现了此预测策略。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): # 将目标数字转换为列号 col_ix = 3 + target_ix # 提取该系列的历史记录 history = chunk_train[:, col_ix] # 如果我们找不到任何有效数据,则持久化一个 nan persisted = nan # 反向枚举历史记录,寻找第一个非 NaN 值 for value in reversed(history): if not isnan(value): persisted = value break # 对所有超前时间持久化相同的值 forecast = [persisted for _ in range(len(lead_times))] return forecast |
下面列出了在测试集上评估持久性预测策略的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 |
# 持久化最后一次观测值 从 numpy 导入 loadtxt from numpy import nan from numpy import isnan from numpy import count_nonzero from numpy import unique from numpy import array from numpy import nanmedian from matplotlib import pyplot # 按“chunkID”分割数据集,返回块列表 def to_chunks(values, chunk_ix=0): chunks = list() # 获取唯一的块 ID chunk_ids = unique(values[:, chunk_ix]) # 按块 ID 分组行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks.append(values[selection, :]) return chunks # 返回相对预测提前期的列表 def get_lead_times(): return [1, 2, 3, 4, 5, 10, 17, 24, 48, 72] # 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): # 将目标数字转换为列号 col_ix = 3 + target_ix # 提取该系列的历史记录 history = chunk_train[:, col_ix] # 如果我们找不到任何有效数据,则持久化一个 nan persisted = nan # 反向枚举历史记录,寻找第一个非 NaN 值 for value in reversed(history): if not isnan(value): persisted = value break # 对所有超前时间持久化相同的值 forecast = [persisted for _ in range(len(lead_times))] return forecast # 为每个数据块进行预测,返回 [数据块][变量][时间] def forecast_chunks(train_chunks, test_input): lead_times = get_lead_times() predictions = list() # 枚举要预测的块 for i in range(len(train_chunks)): # 枚举块的目标 chunk_predictions = list() for j in range(39): yhat = forecast_variable(train_chunks, train_chunks[i], test_input[i], lead_times, j) chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 将块中的测试数据集转换为 [块][变量][时间] 格式 def prepare_test_forecasts(test_chunks): predictions = list() # 枚举要预测的块 for rows in test_chunks: # 枚举块的目标 chunk_predictions = list() for j in range(3, rows.shape[1]): yhat = rows[:, j] chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 计算实际值和预测值之间的误差 def calculate_error(actual, predicted): # 如果预测值为 nan,则给出完整的实际值 if isnan(predicted): return abs(actual) # 计算绝对差值 return abs(actual - predicted) # 评估 [块][变量][时间] 格式的预测 def evaluate_forecasts(predictions, testset): lead_times = get_lead_times() total_mae, times_mae = 0.0, [0.0 for _ in range(len(lead_times))] total_c, times_c = 0, [0 for _ in range(len(lead_times))] # 枚举测试块 for i in range(len(test_chunks)): # 转换为预测 actual = testset[i] predicted = predictions[i] # 枚举目标变量 for j in range(predicted.shape[0]): # 枚举提前期 for k in range(len(lead_times)): # 如果实际值为 nan 则跳过 if isnan(actual[j, k]): continue # 计算误差 error = calculate_error(actual[j, k], predicted[j, k]) # 更新统计数据 total_mae += error times_mae[k] += error total_c += 1 times_c[k] += 1 # 归一化求和的绝对误差 total_mae /= total_c times_mae = [times_mae[i]/times_c[i] for i in range(len(times_mae))] return total_mae, times_mae # 总结得分 def summarize_error(name, total_mae, times_mae): # 打印摘要 lead_times = get_lead_times() formatted = ['+%d %.3f' % (lead_times[i], times_mae[i]) for i in range(len(lead_times))] s_scores = ', '.join(formatted) print('%s: [%.3f MAE] %s' % (name, total_mae, s_scores)) # 绘制摘要 pyplot.plot([str(x) for x in lead_times], times_mae, marker='.') pyplot.show() # 加载数据集 train = loadtxt('AirQualityPrediction/naive_train.csv', delimiter=',') test = loadtxt('AirQualityPrediction/naive_test.csv', delimiter=',') # 按块分组数据 train_chunks = to_chunks(train) test_chunks = to_chunks(test) # 预测 test_input = [rows[:, :3] for rows in test_chunks] forecast = forecast_chunks(train_chunks, test_input) # 评估预测 actual = prepare_test_forecasts(test_chunks) total_mae, times_mae = evaluate_forecasts(forecast, actual) # 总结预测 summarize_error('Persistence', total_mae, times_mae) |
运行该示例会打印出总体 MAE 和每个预测超前时间的 MAE。
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
我们可以看到,持久性预测似乎优于之前章节中评估的所有全局策略。
这为在建模此问题中特定于数据块的信息很重要这一合理假设提供了一些支持。
|
1 |
持久性:[0.520 MAE] +1 0.217, +2 0.330, +3 0.400, +4 0.471, +5 0.515, +10 0.648, +17 0.656, +24 0.589, +48 0.671, +72 0.708 |
创建了 MAE 按预测超前时间绘制的折线图。
重要的是,该图显示了随着预测超前时间的增加而增加误差的预期行为。也就是说,预测未来越远,挑战越大,反过来,预期会产生越多的误差。
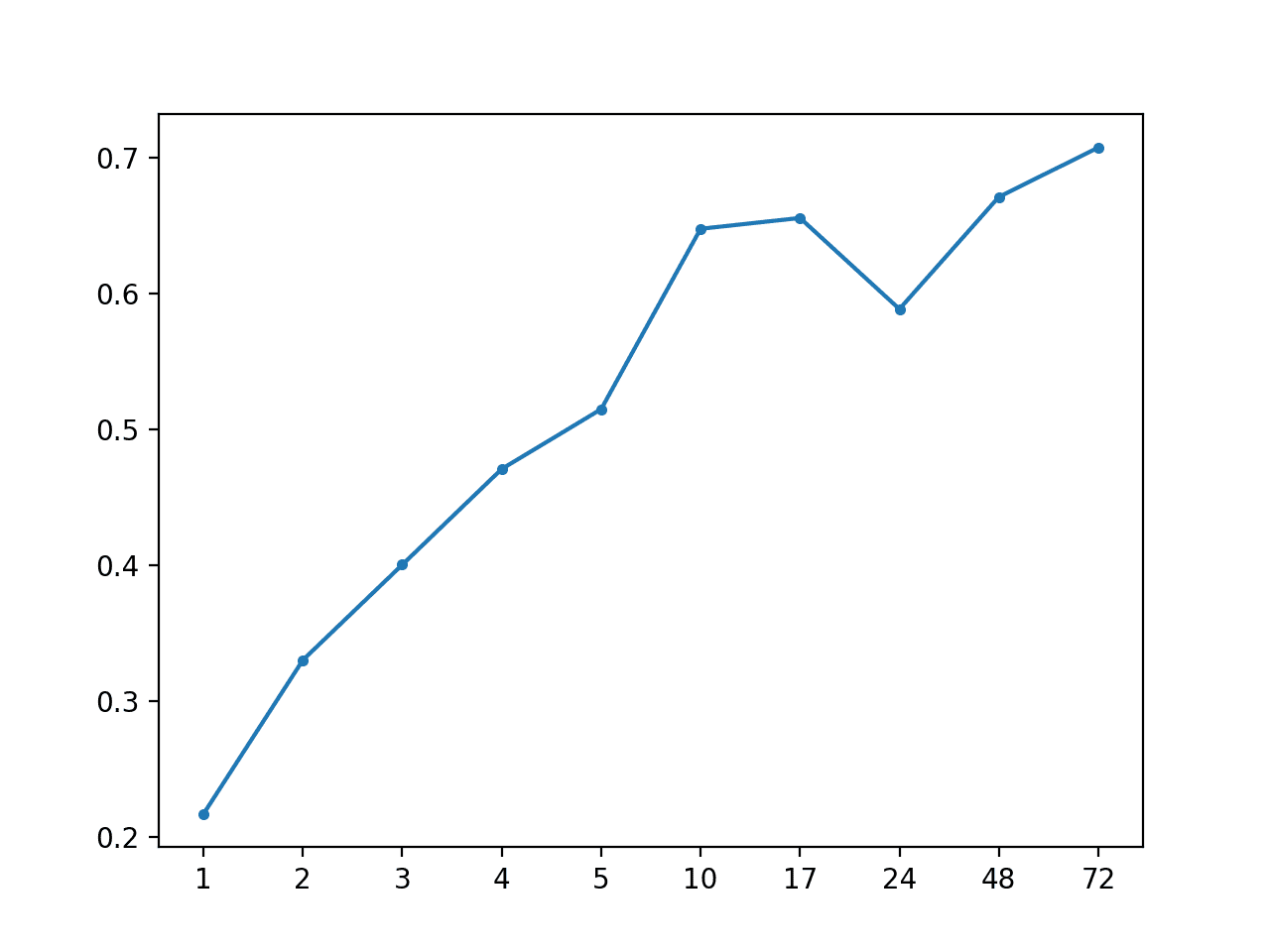
持久性预测超前时间 MAE
预测每条系列的平均值
与其持久化系列的最后一次观测值,不如持久化数据块中使用的系列的平均值。
具体来说,我们可以计算系列的中间值,正如我们在上一节中所发现的,这似乎能带来更好的性能。
_forecast_variable()_ 实现此本地策略。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): # 将目标数字转换为列号 col_ix = 3 + target_ix # 提取该系列的历史记录 history = chunk_train[:, col_ix] # 计算中心趋势 value = nanmedian(history) # 对所有超前时间持久化相同的值 forecast = [value for _ in range(len(lead_times))] return forecast |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 |
# 预测本地中位数 从 numpy 导入 loadtxt from numpy import nan from numpy import isnan from numpy import count_nonzero from numpy import unique from numpy import array from numpy import nanmedian from matplotlib import pyplot # 按“chunkID”分割数据集,返回块列表 def to_chunks(values, chunk_ix=0): chunks = list() # 获取唯一的块 ID chunk_ids = unique(values[:, chunk_ix]) # 按块 ID 分组行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks.append(values[selection, :]) return chunks # 返回相对预测提前期的列表 def get_lead_times(): return [1, 2, 3, 4, 5, 10, 17, 24, 48, 72] # 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): # 将目标数字转换为列号 col_ix = 3 + target_ix # 提取该系列的历史记录 history = chunk_train[:, col_ix] # 计算中心趋势 value = nanmedian(history) # 对所有超前时间持久化相同的值 forecast = [value for _ in range(len(lead_times))] return forecast # 为每个数据块进行预测,返回 [数据块][变量][时间] def forecast_chunks(train_chunks, test_input): lead_times = get_lead_times() predictions = list() # 枚举要预测的块 for i in range(len(train_chunks)): # 枚举块的目标 chunk_predictions = list() for j in range(39): yhat = forecast_variable(train_chunks, train_chunks[i], test_input[i], lead_times, j) chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 将块中的测试数据集转换为 [块][变量][时间] 格式 def prepare_test_forecasts(test_chunks): predictions = list() # 枚举要预测的块 for rows in test_chunks: # 枚举块的目标 chunk_predictions = list() for j in range(3, rows.shape[1]): yhat = rows[:, j] chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 计算实际值和预测值之间的误差 def calculate_error(actual, predicted): # 如果预测值为 nan,则给出完整的实际值 if isnan(predicted): return abs(actual) # 计算绝对差值 return abs(actual - predicted) # 评估 [块][变量][时间] 格式的预测 def evaluate_forecasts(predictions, testset): lead_times = get_lead_times() total_mae, times_mae = 0.0, [0.0 for _ in range(len(lead_times))] total_c, times_c = 0, [0 for _ in range(len(lead_times))] # 枚举测试块 for i in range(len(test_chunks)): # 转换为预测 actual = testset[i] predicted = predictions[i] # 枚举目标变量 for j in range(predicted.shape[0]): # 枚举提前期 for k in range(len(lead_times)): # 如果实际值为 nan 则跳过 if isnan(actual[j, k]): continue # 计算误差 error = calculate_error(actual[j, k], predicted[j, k]) # 更新统计数据 total_mae += error times_mae[k] += error total_c += 1 times_c[k] += 1 # 归一化求和的绝对误差 total_mae /= total_c times_mae = [times_mae[i]/times_c[i] for i in range(len(times_mae))] return total_mae, times_mae # 总结得分 def summarize_error(name, total_mae, times_mae): # 打印摘要 lead_times = get_lead_times() formatted = ['+%d %.3f' % (lead_times[i], times_mae[i]) for i in range(len(lead_times))] s_scores = ', '.join(formatted) print('%s: [%.3f MAE] %s' % (name, total_mae, s_scores)) # 绘制摘要 pyplot.plot([str(x) for x in lead_times], times_mae, marker='.') pyplot.show() # 加载数据集 train = loadtxt('AirQualityPrediction/naive_train.csv', delimiter=',') test = loadtxt('AirQualityPrediction/naive_test.csv', delimiter=',') # 按块分组数据 train_chunks = to_chunks(train) test_chunks = to_chunks(test) # 预测 test_input = [rows[:, :3] for rows in test_chunks] forecast = forecast_chunks(train_chunks, test_input) # 评估预测 actual = prepare_test_forecasts(test_chunks) total_mae, times_mae = evaluate_forecasts(forecast, actual) # 总结预测 summarize_error('Local Median', total_mae, times_mae) |
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
运行该示例总结了此朴素策略的性能,显示 MAE 约为 0.568,这比上面的持久性策略差。
|
1 |
本地中位数:[0.568 MAE] +1 0.535, +2 0.542, +3 0.550, +4 0.568, +5 0.568, +10 0.562, +17 0.567, +24 0.605, +48 0.590, +72 0.593 |
还创建了 MAE 按预测超前时间绘制的折线图,显示了熟悉的误差随超前时间增加的曲线。
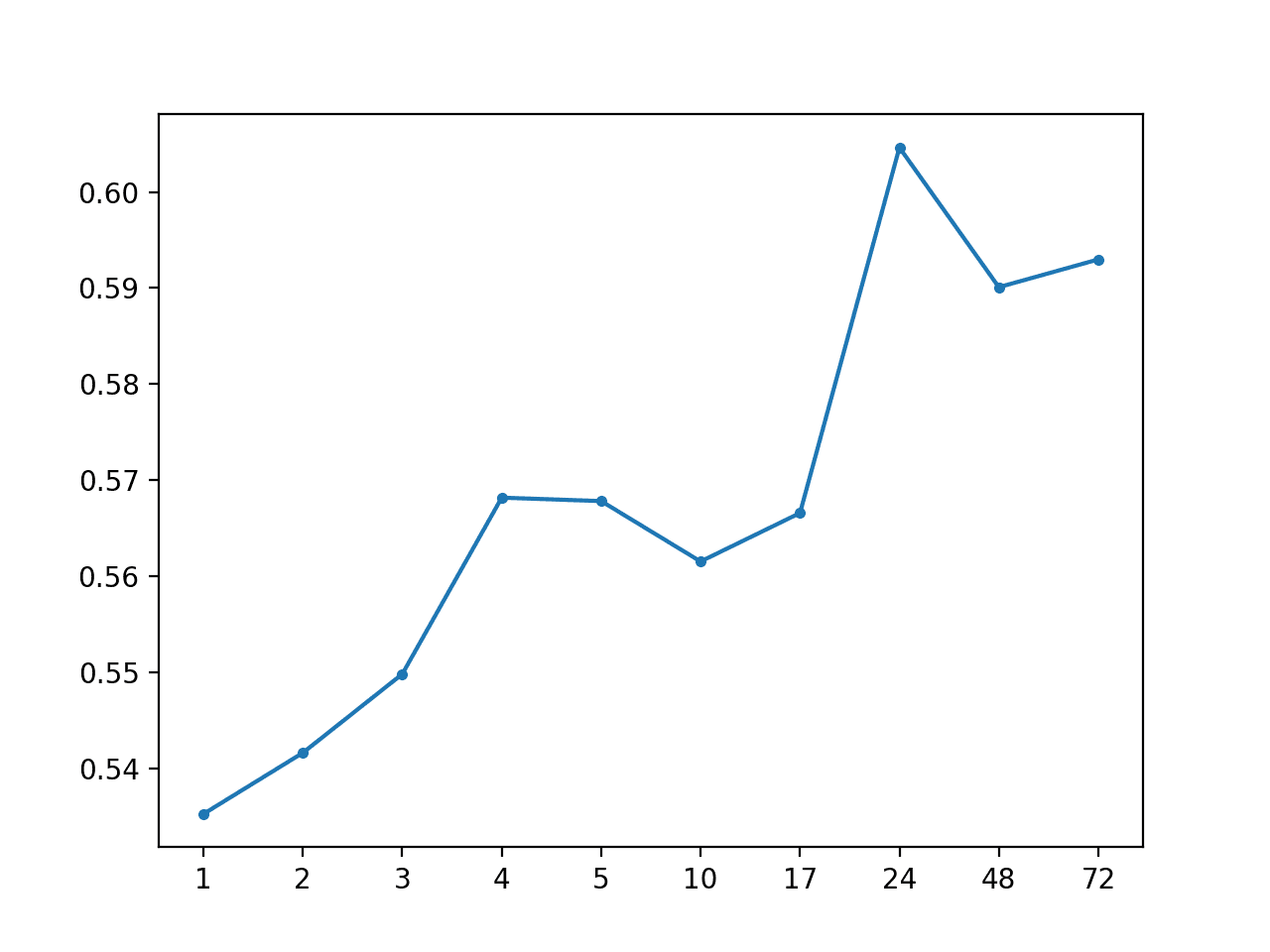
本地中位数预测超前时间 MAE
预测每条系列每小时的平均值
最后,我们可以通过在每个预测超前时间使用该系列每小时的平均值来调整持久性策略。
这种方法在全局策略中被发现是有效的。它可能在仅使用数据块中的数据时也有效,尽管有使用更小数据样本的风险。
下面的 _forecast_variable()_ 函数实现了此策略,首先找到具有预测超前时间小时的所有行,然后计算这些行中给定目标变量的中位数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): forecast = list() # 将目标数字转换为列号 col_ix = 3 + target_ix # 枚举提前期 for i in range(len(lead_times)): # 获取此预测超前时间的小时 hour = chunk_test[i, 2] # 检查是否没有测试数据 if isnan(hour): forecast.append(nan) continue # 选择数据块中具有此小时的行 selected = chunk_train[chunk_train[:,2]==hour] # 计算目标的集中趋势 value = nanmedian(selected[:, col_ix]) forecast.append(value) return forecast |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
# 预测每小时的本地中位数 从 numpy 导入 loadtxt from numpy import nan from numpy import isnan from numpy import unique from numpy import array from numpy import nanmedian from matplotlib import pyplot # 按“chunkID”分割数据集,返回块列表 def to_chunks(values, chunk_ix=0): chunks = list() # 获取唯一的块 ID chunk_ids = unique(values[:, chunk_ix]) # 按块 ID 分组行 for chunk_id in chunk_ids: selection = values[:, chunk_ix] == chunk_id chunks.append(values[selection, :]) return chunks # 返回相对预测提前期的列表 def get_lead_times(): return [1, 2, 3, 4, 5, 10, 17, 24, 48, 72] # 为一个变量预测所有超前时间 def forecast_variable(train_chunks, chunk_train, chunk_test, lead_times, target_ix): forecast = list() # 将目标数字转换为列号 col_ix = 3 + target_ix # 枚举提前期 for i in range(len(lead_times)): # 获取此预测超前时间的小时 hour = chunk_test[i, 2] # 检查是否没有测试数据 if isnan(hour): forecast.append(nan) continue # 选择数据块中具有此小时的行 selected = chunk_train[chunk_train[:,2]==hour] # 计算目标的集中趋势 value = nanmedian(selected[:, col_ix]) forecast.append(value) return forecast # 为每个数据块进行预测,返回 [数据块][变量][时间] def forecast_chunks(train_chunks, test_input): lead_times = get_lead_times() predictions = list() # 枚举要预测的块 for i in range(len(train_chunks)): # 枚举块的目标 chunk_predictions = list() for j in range(39): yhat = forecast_variable(train_chunks, train_chunks[i], test_input[i], lead_times, j) chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 将块中的测试数据集转换为 [块][变量][时间] 格式 def prepare_test_forecasts(test_chunks): predictions = list() # 枚举要预测的块 for rows in test_chunks: # 枚举块的目标 chunk_predictions = list() for j in range(3, rows.shape[1]): yhat = rows[:, j] chunk_predictions.append(yhat) chunk_predictions = array(chunk_predictions) predictions.append(chunk_predictions) return array(predictions) # 计算实际值和预测值之间的误差 def calculate_error(actual, predicted): # 如果预测值为 nan,则给出完整的实际值 if isnan(predicted): return abs(actual) # 计算绝对差值 return abs(actual - predicted) # 评估 [块][变量][时间] 格式的预测 def evaluate_forecasts(predictions, testset): lead_times = get_lead_times() total_mae, times_mae = 0.0, [0.0 for _ in range(len(lead_times))] total_c, times_c = 0, [0 for _ in range(len(lead_times))] # 枚举测试块 for i in range(len(test_chunks)): # 转换为预测 actual = testset[i] predicted = predictions[i] # 枚举目标变量 for j in range(predicted.shape[0]): # 枚举提前期 for k in range(len(lead_times)): # 如果实际值为 nan 则跳过 if isnan(actual[j, k]): continue # 计算误差 error = calculate_error(actual[j, k], predicted[j, k]) # 更新统计数据 total_mae += error times_mae[k] += error total_c += 1 times_c[k] += 1 # 归一化求和的绝对误差 total_mae /= total_c times_mae = [times_mae[i]/times_c[i] for i in range(len(times_mae))] return total_mae, times_mae # 总结得分 def summarize_error(name, total_mae, times_mae): # 打印摘要 lead_times = get_lead_times() formatted = ['+%d %.3f' % (lead_times[i], times_mae[i]) for i in range(len(lead_times))] s_scores = ', '.join(formatted) print('%s: [%.3f MAE] %s' % (name, total_mae, s_scores)) # 绘制摘要 pyplot.plot([str(x) for x in lead_times], times_mae, marker='.') pyplot.show() # 加载数据集 train = loadtxt('AirQualityPrediction/naive_train.csv', delimiter=',') test = loadtxt('AirQualityPrediction/naive_test.csv', delimiter=',') # 按块分组数据 train_chunks = to_chunks(train) test_chunks = to_chunks(test) # 预测 test_input = [rows[:, :3] for rows in test_chunks] forecast = forecast_chunks(train_chunks, test_input) # 评估预测 actual = prepare_test_forecasts(test_chunks) total_mae, times_mae = evaluate_forecasts(forecast, actual) # 总结预测 summarize_error('Local Median by Hour', total_mae, times_mae) |
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能有所不同。考虑运行该示例几次并比较平均结果。
运行该示例打印出约 0.574 的总体 MAE,这比相同的全局变体策略要差。
正如预期的那样,这很可能是由于样本量小,即每个预测最多贡献五行训练数据。
|
1 |
每小时本地中位数:[0.574 MAE] +1 0.561, +2 0.559, +3 0.568, +4 0.577, +5 0.577, +10 0.556, +17 0.551, +24 0.588, +48 0.601, +72 0.608 |
还创建了 MAE 按预测超前时间绘制的折线图,显示了熟悉的误差随超前时间增加的曲线。
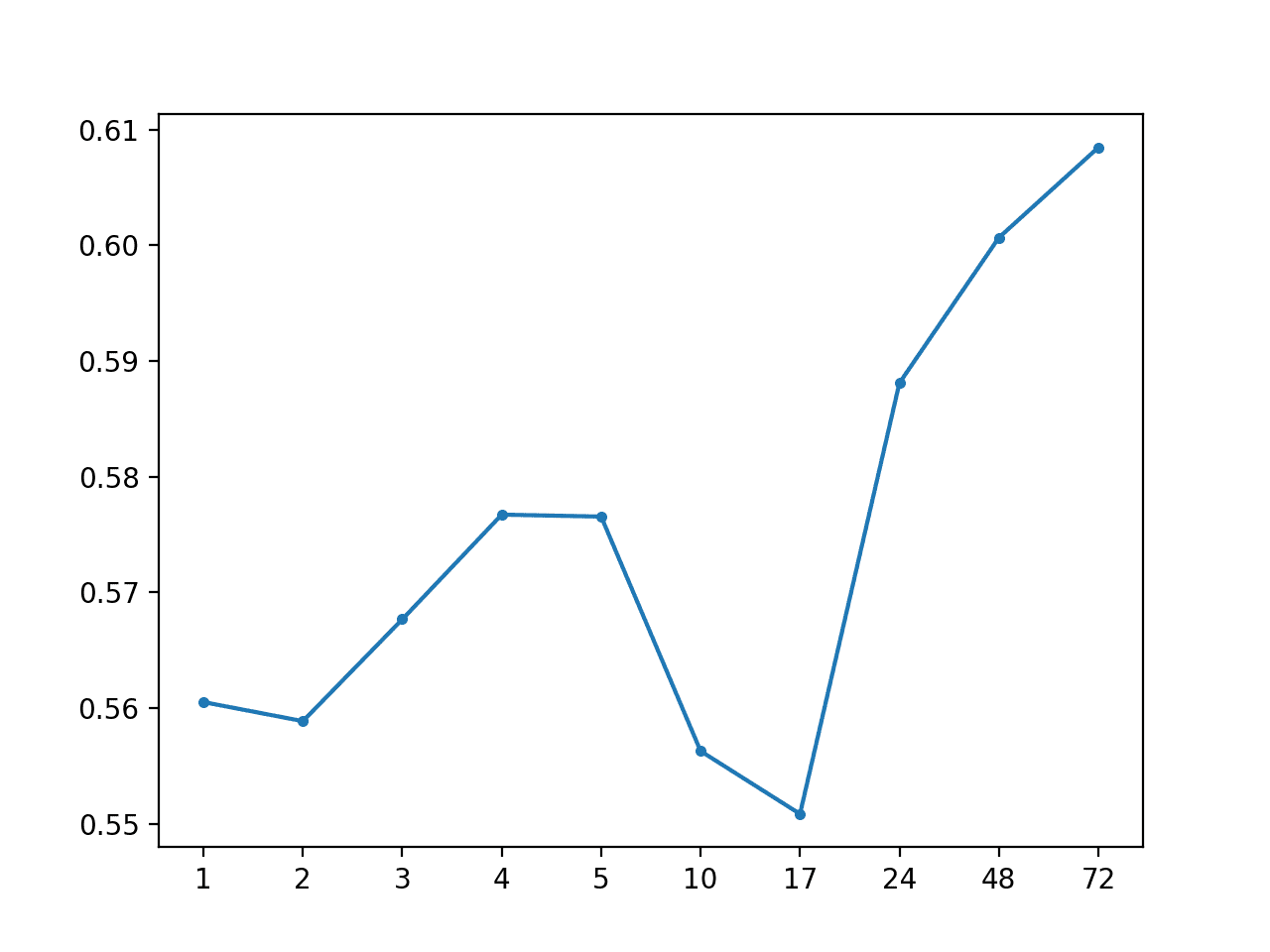
每小时本地中位数预测超前时间 MAE
结果总结
我们可以总结本教程中回顾的所有朴素预测方法的性能。
下面的示例使用“g”代表全局,“l”代表本地,“h”代表每小时变体的简写列出了每种方法。示例创建一个条形图,以便我们可以根据其相对性能比较朴素策略。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 结果总结 from matplotlib import pyplot # 结果 results = { 'g-mean':0.634, 'g-med':0.598, 'g-med-h':0.567, 'l-per':0.520, 'l-med':0.568, 'l-med-h':0.574} # 绘图 pyplot.bar(results.keys(), results.values()) locs, labels = pyplot.xticks() pyplot.setp(labels, rotation=30) pyplot.show() |
运行该示例创建了一个条形图,比较了六种策略的 MAE。
我们可以看到,持久性策略优于所有其他方法,而第二好的策略是每小时的全局中位数。
在此训练/测试分离数据集上评估的模型必须获得低于 0.520 的总体 MAE 才能被视为有技能。
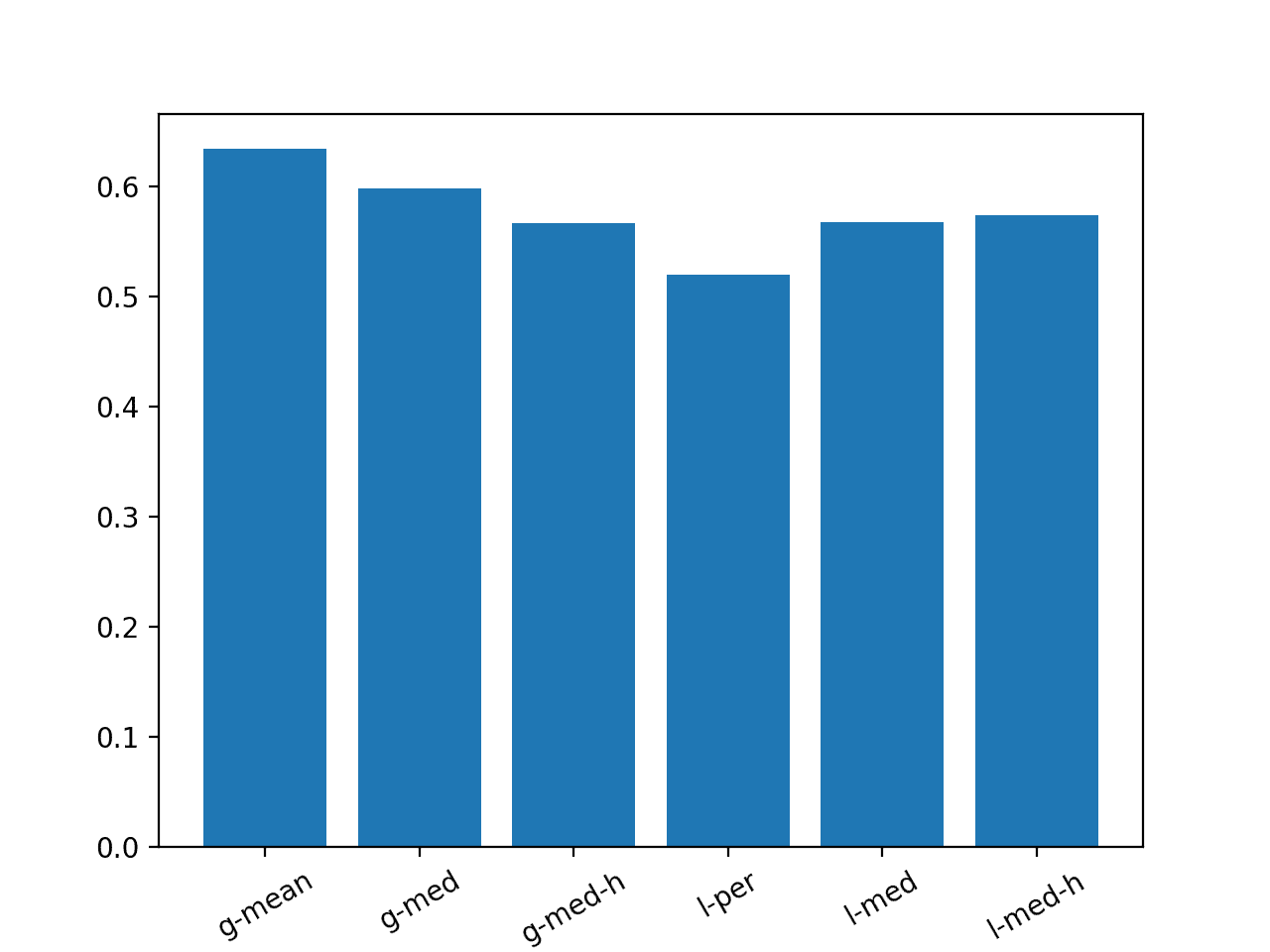
朴素预测方法摘要条形图
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 跨站点朴素预测。开发一种朴素预测策略,该策略使用跨站点的每种变量信息,例如不同站点的同一变量的不同目标变量。
- 混合方法。开发一种混合预测策略,该策略结合了本教程中描述的在不同超前时间使用的两种或多种朴素预测策略的要素。
- 朴素方法集成。开发一种集成预测策略,该策略创建本教程中描述的两种或多种预测策略的线性组合。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
文章
总结
在本教程中,您学习了如何为多步多元空气污染时间序列预测问题开发朴素预测方法。
具体来说,你学到了:
- 如何为空气质量数据集开发一个用于评估预测策略的测试框架。
- 如何开发使用整个训练数据集数据的全局朴素预测策略。
- 如何开发使用被预测特定时间间隔数据的局部朴素预测策略。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





这是如何
chunk_ids = unique(values[:, 1])
生成唯一标识符列表?
当我看到“unique”时,我想到了 set()。我不理解上面的代码行。
是的,一个集合,在这种情况下是第一列中的唯一值列表。
你好,
感谢精彩的教程。只是一个小小的说明——对我来说,如果使用 Pandas 数据框,理解这些步骤会更容易/更快。
一切顺利!
谢谢。
什么是提前期?
相对于当前时间预测未来某个时间点。
这是一个抽象,一个符号时间。
例如,提前期为+10意味着预测未来10个时间单位,而不管我们想使用什么数据来做预测,或者何时做预测。
提前期为+25小时意味着我们对一个模型感兴趣,该模型可以预测一天或24小时外的结果,而不管我们何时想做出预测。
嗨,Jason,
我不明白为什么提前期必须是“+1, +2, +3, +4, +5, +10, +17, +24, +48, +72”?
谢谢你。
它们是相对于当前时间的正时间。
您可以选择其他时间,在这个问题中选择了这些提前期。
这有帮助吗?
这很有帮助。谢谢!
嗨,Jason,
感谢您的精彩博文。
您是否有任何 LSTM 示例可以解决多站点多变量多步预测问题?或者使用 LSTM 解决这类问题是否是一个好主意?
我有一个来自多个站点的多变量数据集。我目前使用 LSTM 对来自 1 个站点的多步进行预测,但我想将所有站点的数据纳入一个模型中,以便我可以泛化我的模型以在所有站点上工作。
我不知道从哪里开始。
谢谢
我在这方面有一些建议
https://machinelearning.org.cn/faq/single-faq/how-to-develop-forecast-models-for-multiple-sites