如何开发用于时间序列预测的多层感知器模型

多层感知器，简称 MLP，可以应用于时间序列预测。

使用 MLP 进行时间序列预测的挑战在于数据准备。具体来说，滞后观测值必须扁平化为特征向量。

在本教程中，您将学习如何针对一系列标准时间序列预测问题开发一套 MLP 模型。

本教程的目标是为每种类型的时间序列问题提供每个模型的独立示例，作为您可以复制和改编以解决您的特定时间序列预测问题的模板。

在本教程中，您将学习如何针对一系列标准时间序列预测问题开发一套多层感知器模型。

完成本教程后，您将了解：

• 如何开发用于单变量时间序列预测的 MLP 模型。
• 如何开发用于多变量时间序列预测的 MLP 模型。
• 如何开发用于多步时间序列预测的 MLP 模型。

使用我的新书深度学习时间序列预测启动您的项目，包括分步教程和所有示例的Python 源代码文件。

让我们开始吧。

如何开发用于时间序列预测的多层感知器模型
图片由土地管理局提供，保留部分权利。

教程概述

本教程分为四个部分；它们是

1. 单变量 MLP 模型
2. 多变量 MLP 模型
3. 多步 MLP 模型
4. 多变量多步 MLP 模型

单变量 MLP 模型

多层感知器，简称 MLP，可用于建模单变量时间序列预测问题。

单变量时间序列是包含具有时间顺序的单个观测序列的数据集，需要一个模型从过去的观测序列中学习以预测序列中的下一个值。

本节分为两部分；它们是

1. 数据准备
2. MLP 模型

数据准备

在对单变量序列建模之前，必须对其进行准备。

MLP 模型将学习一个函数，该函数将过去的观测序列作为输入映射到输出观测。因此，观测序列必须转换为模型可以学习的多个示例。

考虑一个给定的单变量序列

我们可以将序列分成多个输入/输出模式，称为样本，其中三个时间步用作输入，一个时间步用作输出，用于学习一步预测。

下面的 `split_sequence()` 函数实现了这种行为，它将给定的单变量序列分成多个样本，其中每个样本具有指定的时间步数，并且输出是一个时间步。

我们可以在上面小巧的人造数据集上演示这个函数。

完整的示例如下所示。

运行该示例将单变量序列分成六个样本，其中每个样本有三个输入时间步和一个输出时间步。

现在我们知道了如何准备用于建模的单变量序列，接下来我们看看如何开发一个 MLP 模型来学习输入到输出的映射。

MLP 模型

一个简单的 MLP 模型有一个单层隐藏节点，以及一个用于进行预测的输出层。

我们可以如下定义一个用于单变量时间序列预测的 MLP。

定义中重要的是输入的形状；即模型期望的每个样本的输入（以时间步长数表示）。

输入的时间步数是我们选择的在准备数据集时作为 `split_sequence()` 函数的参数。

每个样本的输入维度在第一个隐藏层的定义中的input_dim参数中指定。从技术上讲，模型将每个时间步长视为一个单独的特征，而不是单独的时间步长。

我们几乎总是有多个样本，因此，模型将期望训练数据的输入组件具有维度或形状

我们上一节中的split_sequence()函数以[样本，特征]的形状输出X，可用于建模。

模型使用Adam 版本的随机梯度下降进行拟合，并使用均方误差或“mse”损失函数进行优化。

定义模型后，我们可以在训练数据集上对其进行拟合。

模型拟合后，我们可以使用它进行预测。

我们可以通过提供输入来预测序列中的下一个值

并期望模型能预测出类似这样的结果

模型期望输入形状是二维的，具有[样本，特征]，因此，我们必须在进行预测之前重塑单个输入样本，例如形状为[1, 3]，表示 1 个样本和 3 个时间步长作为输入特征。

我们可以将所有这些结合起来，演示如何为单变量时间序列预测开发 MLP 并进行单次预测。

运行该示例会准备数据、拟合模型并进行预测。

注意：考虑到算法或评估过程的随机性，或数值精度上的差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

我们可以看到模型预测了序列中的下一个值。

多变量 MLP 模型

多变量时间序列数据是指每个时间步有多个观测值的数据。

对于多变量时间序列数据，我们可能需要两种主要模型；它们是

1. 多输入序列。
2. 多并行序列。

让我们依次看看每一个。

多输入序列

一个问题可能有两个或多个并行输入时间序列和一个依赖于输入时间序列的输出时间序列。

输入时间序列是并行的，因为每个序列在相同的时间步长都有一个观测值。

我们可以用一个简单的例子来演示，其中有两个并行的输入时间序列，输出序列是输入序列的简单相加。

我们可以将这三个数据数组重塑为单个数据集，其中每行是一个时间步长，每列是一个单独的时间序列。这是在 CSV 文件中存储并行时间序列的标准方式。

完整的示例如下所示。

运行该示例会打印数据集，其中每行是一个时间步，每个两输入一输出并行时间序列的列。

与单变量时间序列一样，我们必须将这些数据结构化为包含输入和输出样本的样本。

我们需要将数据分成样本，同时保持两个输入序列中观测值的顺序。

如果我们选择三个输入时间步，那么第一个样本将如下所示

输入

输出

也就是说，每个并行序列的前三个时间步长作为输入提供给模型，模型将此与第三个时间步长处的输出序列中的值相关联，在这种情况下为 65。

我们可以看到，在将时间序列转换为用于训练模型的输入/输出样本时，我们将不得不丢弃输出时间序列中的一些值，因为在之前的时间步长中输入时间序列中没有这些值。反过来，输入时间步长数量的选择将对使用的训练数据量产生重要影响。

我们可以定义一个名为 `split_sequences()` 的函数，它将接收我们定义的以时间步为行、并行序列为列的数据集，并返回输入/输出样本。

我们可以使用每个输入时间序列的三个时间步作为输入，在我们的数据集上测试这个函数。

完整的示例如下所示。

运行示例首先打印 X 和 y 组件的形状。

我们可以看到 X 组件具有三维结构。

第一个维度是样本数，本例中为 7。第二个维度是每个样本的时间步长数，本例中为 3，即传递给函数的值。最后，最后一个维度指定了并行时间序列的数量或变量的数量，本例中为 2，表示两个并行序列。

然后，我们可以看到打印了每个样本的输入和输出，显示了每个两个输入序列的三个时间步以及每个样本的相关输出。

在 MLP 拟合此数据之前，我们必须扁平化输入样本的形状。

MLP 要求每个样本的输入部分的形状是一个向量。对于多变量输入，我们将有多个向量，每个时间步长一个。

我们可以扁平化每个输入样本的时间结构，以便

变为

首先，我们可以计算每个输入向量的长度，即时间步长数乘以特征数或时间序列数。然后我们可以使用这个向量大小来重塑输入。

我们现在可以为多变量输入定义一个 MLP 模型，其中向量长度用于输入维度参数。

进行预测时，模型需要两个输入时间序列的三个时间步。

我们可以预测输出序列中的下一个值，提供以下输入值

1 个样本、3 个时间步长和 2 个变量的形状将是 [1, 3, 2]。我们必须再次将其重塑为 1 个样本，包含 6 个元素的向量或 [1, 6]

我们期望序列中的下一个值是 100 + 105 或 205。

完整的示例如下所示。

注意：考虑到算法或评估过程的随机性，或数值精度上的差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

运行该示例会准备数据、拟合模型并进行预测。

还有另一种更精细的建模问题的方法。

每个输入序列可以由一个单独的 MLP 处理，并且每个子模型的输出可以在进行输出序列预测之前进行组合。

我们可以将此称为多头输入 MLP 模型。根据建模问题的具体情况，它可能提供更大的灵活性或更好的性能。

这种类型的模型可以使用 Keras 函数式 API 在 Keras 中定义。

首先，我们可以将第一个输入模型定义为一个 MLP，其输入层期望具有 n_steps 特征的向量。

我们可以用同样的方式定义第二个输入子模型。

现在两个输入子模型都已定义，我们可以将每个模型的输出合并成一个长向量，该向量可以在进行输出序列预测之前进行解释。

然后我们可以将输入和输出连接起来。

下图提供了该模型的示意图，包括每个层的输入和输出形状。

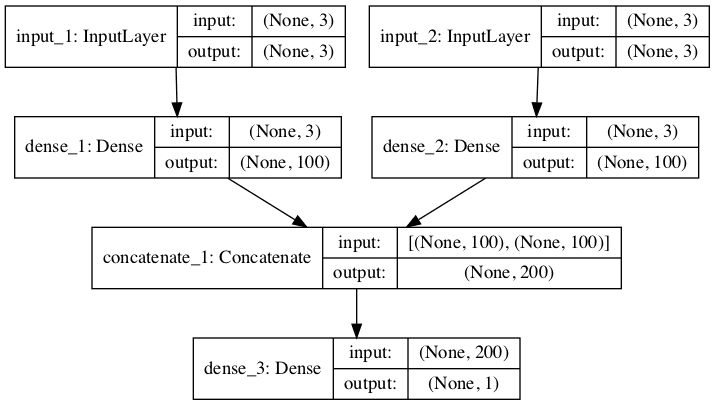
多头 MLP 用于多变量时间序列预测的图示

此模型要求输入提供为包含两个元素的列表，其中列表中的每个元素包含一个子模型的数据。

为了实现这一点，我们可以将 3D 输入数据分成两个单独的输入数据数组：即从形状为 [7, 3, 2] 的一个数组到形状为 [7, 3] 的两个 2D 数组。

然后可以提供这些数据来拟合模型。

同样，在进行单个一步预测时，我们必须将单个样本的数据准备为两个单独的二维数组。

我们可以将所有这些结合起来；完整的示例如下所示。

注意：考虑到算法或评估过程的随机性，或数值精度上的差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

运行该示例会准备数据、拟合模型并进行预测。

多并行序列

另一种时间序列问题是存在多个并行时间序列，并且必须为每个序列预测一个值。

例如，给定上一节中的数据

我们可能希望预测下一个时间步的三个时间序列中的每一个的值。

这可以被称为多变量预测。

同样，必须将数据拆分为输入/输出样本才能训练模型。

该数据集的第一个样本将如下所示

输入

输出

下面的 `split_sequences()` 函数将把以时间步为行、每列一个序列的多个并行时间序列分割成所需的输入/输出形状。

我们可以在人造问题上演示这一点；完整的示例如下所示。

运行示例首先打印已准备好的 X 和 y 组件的形状。

X 的形状是三维的，包括样本数（6）、每个样本选择的时间步长数（3）以及并行时间序列或特征数（3）。

y 的形状是二维的，正如我们对样本数（6）和每个样本要预测的时间变量数（3）所预期的那样。

然后，打印每个样本，显示每个样本的输入和输出组件。

我们现在准备好用这些数据拟合一个 MLP 模型。

与前面多变量输入的情况一样，我们必须将输入数据样本的三维结构扁平化为二维结构 [样本, 特征]，其中滞后观测值被模型视为特征。

模型输出将是一个向量，其中每个元素对应三个不同时间序列中的一个。

我们现在可以定义我们的模型，使用扁平化向量长度作为输入层，并使用时间序列数量作为进行预测时的向量长度。

我们可以通过提供每个序列的三个时间步作为输入，预测三个并行序列中的每个序列的下一个值。

进行单次预测的输入形状必须是 1 个样本，3 个时间步长和 3 个特征，即 [1, 3, 3]。同样，我们可以将其扁平化为 [1, 6] 以满足模型的预期。

我们预期向量输出为

我们可以将所有这些结合起来，演示下面用于多变量输出时间序列预测的 MLP。

注意：考虑到算法或评估过程的随机性，或数值精度上的差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

运行该示例会准备数据、拟合模型并进行预测。

与多输入序列一样，还有另一种更精细的建模问题的方法。

每个输出序列可以由一个单独的输出 MLP 模型处理。

我们可以将其称为多输出 MLP 模型。根据建模问题的具体情况，它可能提供更大的灵活性或更好的性能。

这种类型的模型可以使用 Keras 函数式 API 在 Keras 中定义。

首先，我们可以将输入模型定义为一个 MLP，其输入层期望扁平化的特征向量。

然后我们可以为我们希望预测的三个序列中的每一个定义一个输出层，其中每个输出子模型将预测一个时间步长。

然后我们可以将输入层和输出层连接成一个单一的模型。

为了使模型架构清晰，下面的示意图清楚地显示了模型的三个独立输出层以及每个层的输入和输出形状。

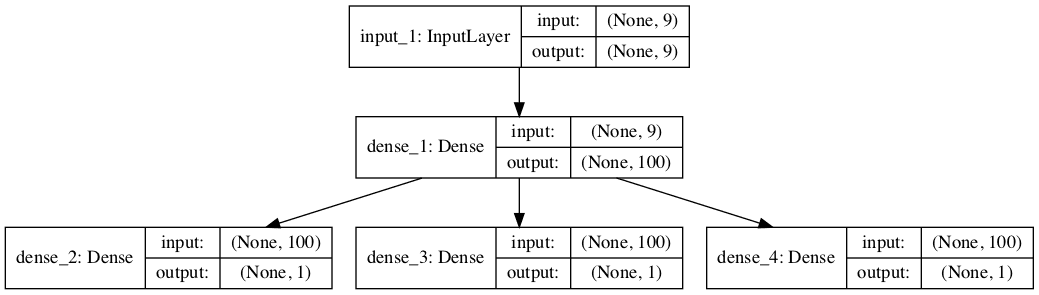
多输出 MLP 用于多变量时间序列预测的图示

训练模型时，每个样本将需要三个独立的输出数组。

我们可以通过将形状为 [7, 3] 的输出训练数据转换为形状为 [7, 1] 的三个数组来实现此目的。

这些数组可以在训练期间提供给模型。

将所有这些联系在一起，完整的示例如下。