如何使用 ReLU 解决梯度消失问题

梯度消失问题是您在训练深度神经网络时可能遇到的不稳定行为的一个示例。

它描述了深度多层前馈网络或循环神经网络无法将有用的梯度信息从模型的输出端传播回模型输入端附近的层的情况。

结果是，具有许多层的模型通常无法在给定数据集上学习，或者具有许多层的模型过早地收敛到次优解。

人们提出并研究了许多修复和变通方法，例如替代权重初始化方案、无监督预训练、分层训练以及梯度下降的变体。也许最常见的改变是使用修正线性激活函数，它已成为新的默认值，而不是在 1990 年代末和 2000 年代默认的双曲正切激活函数。

在本教程中，您将学习如何诊断训练神经网络模型时出现的梯度消失问题，以及如何使用替代激活函数和权重初始化方案来解决它。

完成本教程后，您将了解：

• 梯度消失问题限制了使用双曲正切等经典流行激活函数的深度神经网络的发展。
• 如何使用 ReLU 和 He 权重初始化修复用于分类的深度神经网络多层感知器。
• 如何使用 TensorBoard 诊断梯度消失问题并确认 ReLU 对改善模型梯度流的影响。

用我的新书《更好的深度学习》来启动你的项目，书中包含分步教程和所有示例的 Python 源代码文件。

让我们开始吧。

• 2019 年 10 月更新：更新至 Keras 2.3 和 TensorFlow 2.0。

如何使用修正线性激活函数解决梯度消失问题
图片由Liam Moloney拍摄，保留部分权利。

教程概述

本教程分为五个部分；它们是：

1. 梯度消失问题
2. 两圆二分类问题
3. 用于两圆问题的多层感知器模型
4. 带有 ReLU 的更深层 MLP 模型用于两圆问题
5. 审查训练期间的平均梯度大小

梯度消失问题

神经网络使用随机梯度下降进行训练。

这首先涉及计算模型产生的预测误差，并使用该误差估计用于更新网络中每个权重的梯度，以便下次产生的误差更小。这个误差梯度通过网络从输出层向输入层反向传播。

使用多层训练神经网络是可取的，因为增加更多层会增加网络的容量，使其能够学习大型训练数据集并有效表示从输入到输出的更复杂映射函数。

训练多层网络（例如深度神经网络）的一个问题是，梯度在反向传播通过网络时会急剧减小。当它到达靠近模型输入端的层时，误差可能非常小，以至于可能几乎没有影响。因此，这个问题被称为“梯度消失”问题。

梯度消失使得难以知道参数应该朝哪个方向移动以改善成本函数……

— 第 290 页，《深度学习》，2016 年。

事实上，误差梯度在深度神经网络中可能不稳定，不仅会消失，还会爆炸，其中梯度在反向传播通过网络时呈指数增长。这被称为“梯度爆炸”问题。

梯度消失一词指的是，在前馈网络 (FFN) 中，反向传播的误差信号通常会随着距最后一层的距离呈指数级下降（或上升）。

— 《用于训练非常深的前馈网络的随机游走初始化》，2014 年。

梯度消失是循环神经网络的一个特殊问题，因为网络的更新涉及针对每个输入时间步展开网络，实际上创建了一个需要权重更新的非常深的网络。一个适度的循环神经网络可能有 200 到 400 个输入时间步，概念上导致一个非常深的网络。

梯度消失问题可能在多层感知器中表现为模型在训练期间改进速度缓慢，可能还有过早收敛，例如，持续训练不会导致任何进一步的改进。检查训练期间权重的变化，我们会发现靠近输出层的层发生的变化更多（即学习更多），而靠近输入层的层发生的变化更少。

有许多技术可以用于减少前馈神经网络梯度消失问题的影响，最显著的是替代权重初始化方案和替代激活函数的使用。

为了解决梯度消失问题，人们研究并应用了各种训练深度网络（前馈和循环）的方法，例如预训练、更好的随机初始缩放、更好的优化方法、特定架构、正交初始化等。

— 《用于训练非常深的前馈网络的随机游走初始化》，2014 年。

在本教程中，我们将仔细研究替代权重初始化方案和激活函数的使用，以允许训练更深的神经网络模型。

两圆二分类问题

作为我们探索的基础，我们将使用一个非常简单的二分类问题。

scikit-learn 类提供了make_circles() 函数，可用于创建具有指定样本数量和统计噪声的二分类问题。

每个示例都有两个输入变量，它们定义了二维平面上点的 *x* 和 *y* 坐标。这些点按两个同心圆（它们具有相同的中心）排列，分别代表两个类别。

数据集中的点数由参数指定，其中一半将从每个圆中抽取。可以通过“*noise*”参数在采样点时添加高斯噪声，该参数定义了噪声的标准差，其中 0.0 表示没有噪声或点完全从圆中抽取。可以通过“*random_state*”参数指定伪随机数生成器的种子，该参数允许每次调用函数时采样完全相同的点。

下面的示例从两个圆中生成 1,000 个带噪声的示例，并使用值 1 作为伪随机数生成器的种子。

我们可以创建数据集的图表，绘制输入变量 (*X*) 的 *x* 和 *y* 坐标，并根据类别值（0 或 1）为每个点着色。

完整的示例如下所示。

运行示例会创建一个图，显示 1,000 个生成的数据点，每个点的类别值用于为每个点着色。

我们可以看到类别 0 的点是蓝色的，代表外圆，类别 1 的点是橙色的，代表内圆。

生成样本的统计噪声意味着两个圆之间的点存在一些重叠，这增加了一些问题的歧义，使其变得不那么简单。这是可取的，因为神经网络可能会选择在两个圆之间对点进行分类的许多可能解决方案之一，并且总是会犯一些错误。

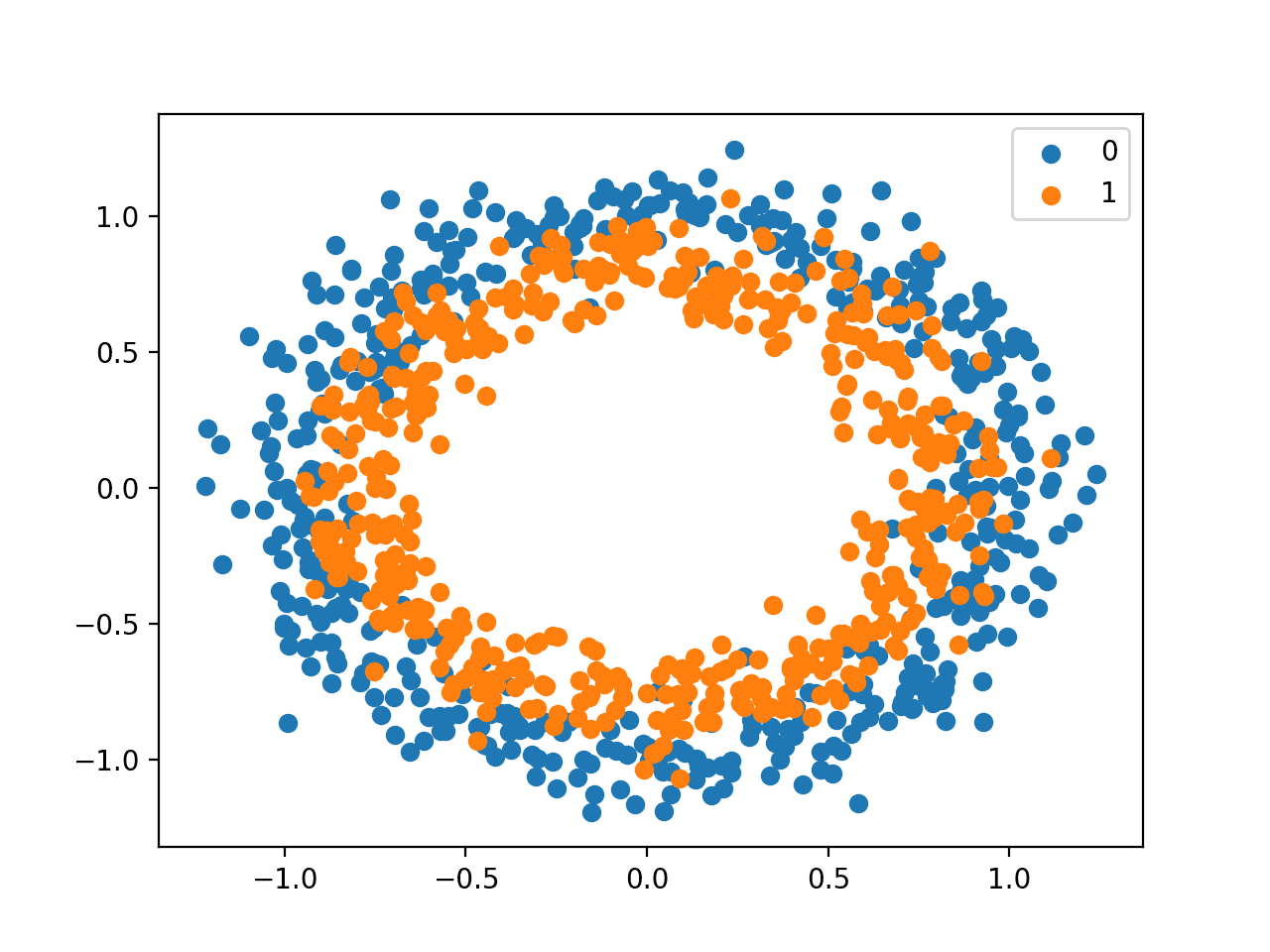
带有类别值着色点的圆形数据集散点图

现在我们已经定义了一个问题作为我们探索的基础，我们可以着手开发一个模型来解决它。

用于两圆问题的多层感知器模型

我们可以开发一个多层感知器模型来解决两圆问题。

这将是一个简单的前馈神经网络模型，按照我们在 1990 年代末和 2000 年代初所学的方式设计。

首先，我们将从两圆问题中生成 1,000 个数据点，并将输入重新缩放到 [-1, 1] 范围。数据几乎已经在这个范围内，但我们会确保。

通常，我们会使用训练数据集准备数据缩放，并将其应用于测试数据集。为了在本教程中保持简单，我们将在将所有数据拆分为训练集和测试集之前对其进行缩放。

接下来，我们将把数据分成训练集和测试集。

一半数据将用于训练，其余 500 个示例将用作测试集。在本教程中，测试集也将用作验证数据集，以便我们可以在训练期间了解模型在保留集上的表现。

接下来，我们将定义模型。

该模型将有一个具有两个输入的输入层，用于数据集中的两个变量，一个具有五个节点的隐藏层，以及一个用于预测类别概率的具有一个节点的输出层。隐藏层将使用双曲正切激活函数（tanh），输出层将使用逻辑激活函数（sigmoid）来预测类别 0 或类别 1 或介于两者之间的值。

在隐藏层中使用双曲正切激活函数是 1990 年代和 2000 年代最佳实践，通常在隐藏层中使用时比逻辑函数表现更好。将网络权重初始化为来自均匀分布的小随机值也是一种好做法。在这里，我们将权重从 [0.0, 1.0] 范围随机初始化。

该模型使用二元交叉熵损失函数，并使用学习率为 0.01、动量为 0.9 的随机梯度下降进行优化。

模型训练 500 个训练 epoch，并在每个 epoch 结束时与训练数据集一起评估测试数据集。

模型拟合后，将在训练集和测试集上进行评估，并显示准确率分数。

最后，将模型在训练每个步骤中的准确率绘制成折线图，显示模型学习问题的动态。

将所有这些联系在一起，完整的示例如下。

运行示例会在几秒钟内拟合模型。

注意：由于算法或评估过程的随机性，或数值精度差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

我们可以看到，在这种情况下，模型很好地学习了问题，在训练集和测试集上都达到了大约 81.6% 的准确率。

创建了模型在训练集和测试集上的准确率折线图，显示了模型在 500 个训练 epoch 中学习问题时的性能变化。

该图表表明，对于这次运行，性能在第 300 个 epoch 左右开始放缓，训练集和测试集的准确率均约为 80%。

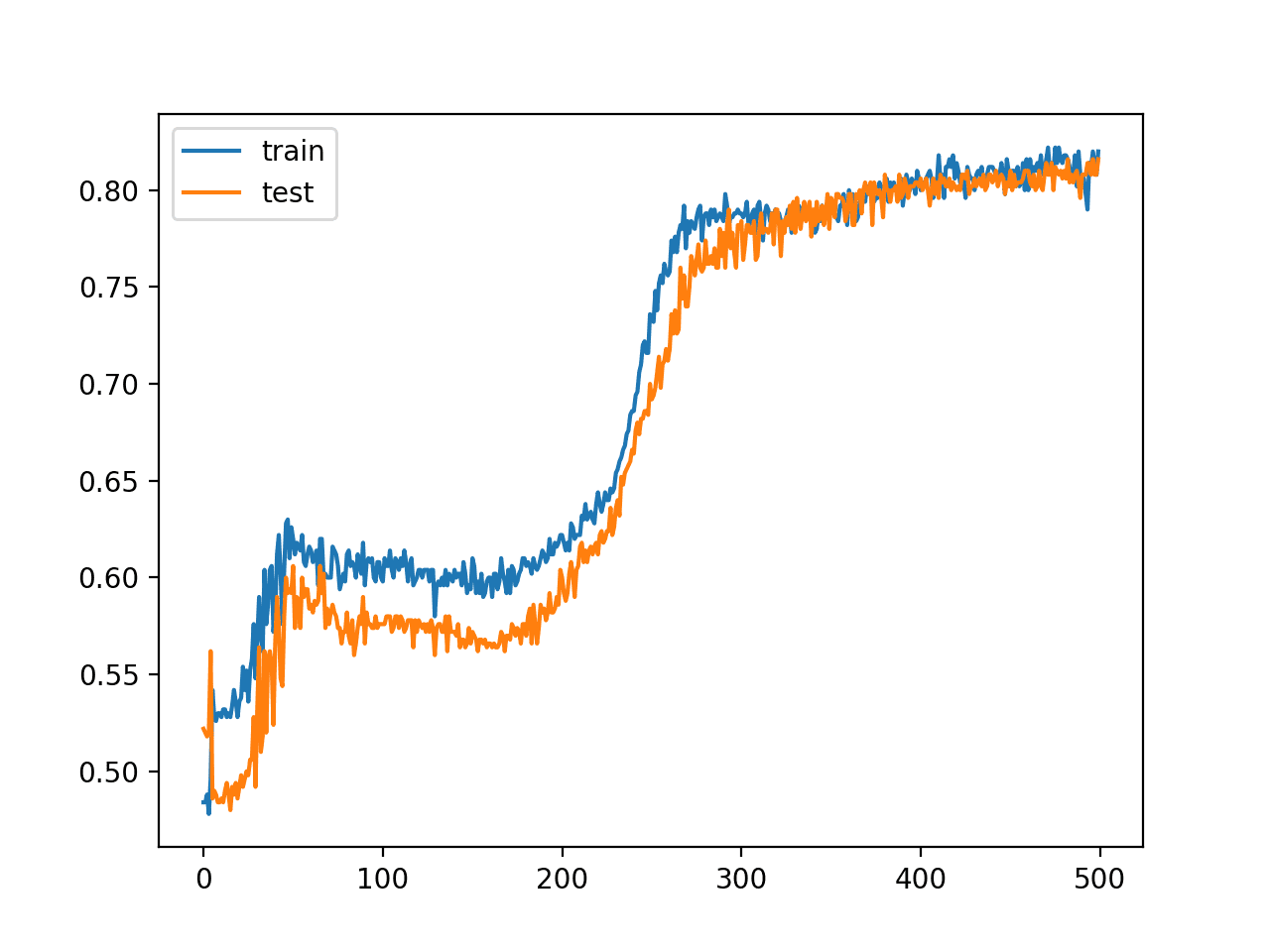
两圆问题中 MLP 训练 epoch 上的训练集和测试集准确率折线图

现在我们已经了解了如何使用 tanh 激活函数为两圆问题开发经典 MLP，我们可以着手修改模型以拥有更多隐藏层。

两圆问题的更深层 MLP 模型

传统上，开发深度多层感知器模型具有挑战性。

使用双曲正切激活函数的深度模型不容易训练，这种性能不佳的大部分原因归咎于梯度消失问题。

我们可以尝试使用上一节中开发的 MLP 模型来调查这一点。

隐藏层数可以从 1 增加到 5；例如

然后我们可以重新运行示例并审查结果。

下面列出了更深层 MLP 的完整示例。

运行示例首先打印拟合模型在训练集和测试集上的性能。

注意：由于算法或评估过程的随机性，或数值精度差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

在这种情况下，我们可以看到在训练集和测试集上的性能都相当差，准确率约为 50%。这表明按此配置的模型既无法学习问题也无法推广解决方案。

模型在训练期间在训练集和测试集上的准确率折线图也说明了类似的情况。我们可以看到性能很差，并且随着训练的进行实际上变得更差。

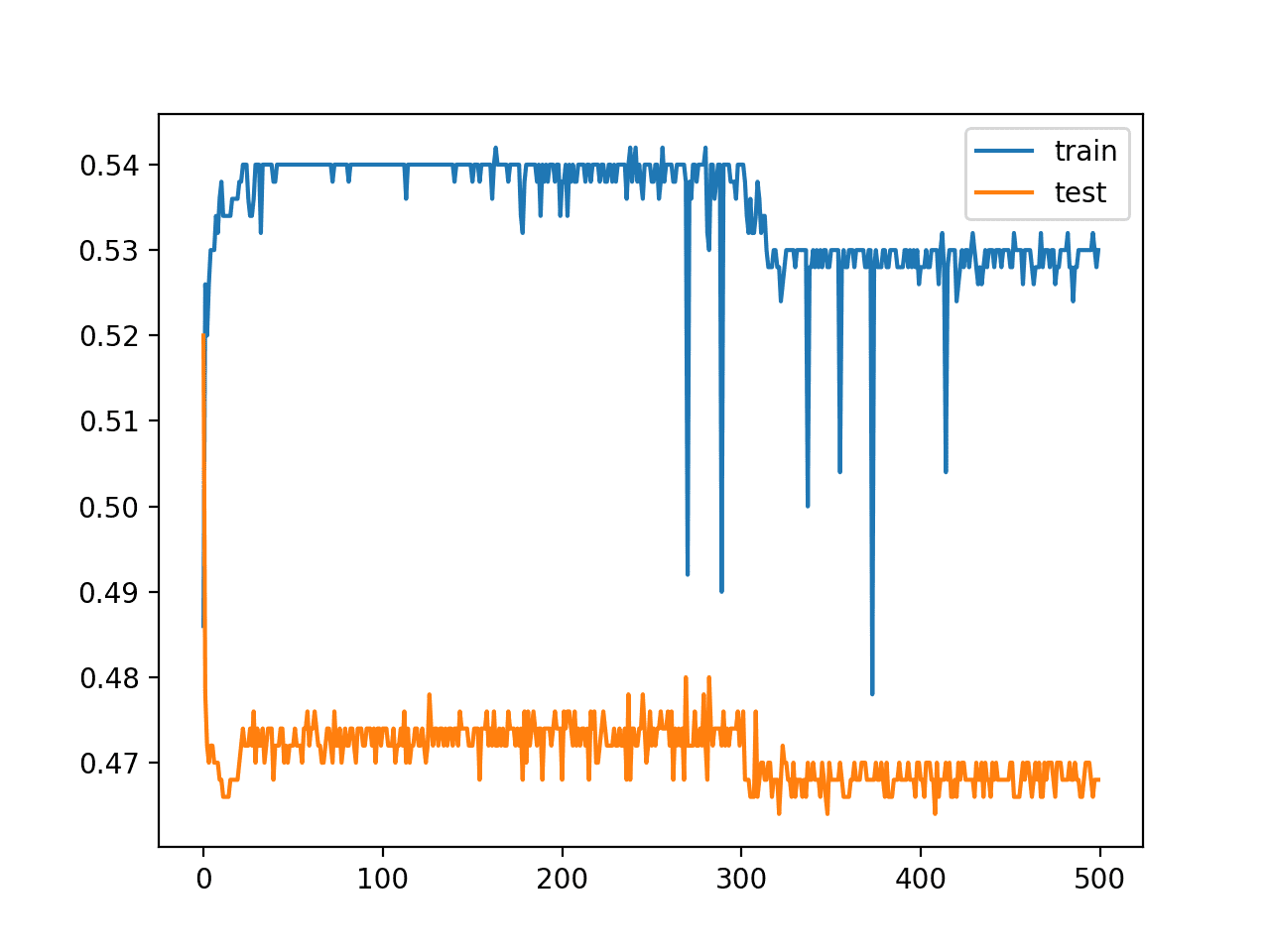
两圆问题中深度 MLP 训练 epoch 上的训练集和测试集准确率折线图

带有 ReLU 的更深层 MLP 模型用于两圆问题

修正线性激活函数已取代双曲正切激活函数，成为开发多层感知器网络以及 CNN 等其他网络类型时新的首选默认值。

这是因为激活函数看起来和行为都像一个线性函数，使其更容易训练且不易饱和，但实际上是一个非线性函数，将负输入强制为 0 值。它被认为是解决训练深度模型时梯度消失问题的一种可能方法。

当使用修正线性激活函数（简称 ReLU）时，最好使用 He 权重初始化方案。我们可以使用 ReLU 和 He 初始化定义具有五个隐藏层的 MLP，如下所示。

综合起来，完整的代码示例如下。

运行示例会打印模型在训练集和测试集上的性能。

注意：由于算法或评估过程的随机性，或数值精度差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

在这种情况下，我们可以看到这个微小的变化使模型能够学习问题，在两个数据集上都达到了大约 84% 的准确率，优于使用 tanh 激活函数的单层模型。

还创建了模型在训练 epoch 中在训练集和测试集上的准确率折线图。该图显示了与我们目前所见截然不同的动态。

模型似乎快速学习了问题，在大约 100 个 epoch 中收敛到解决方案。

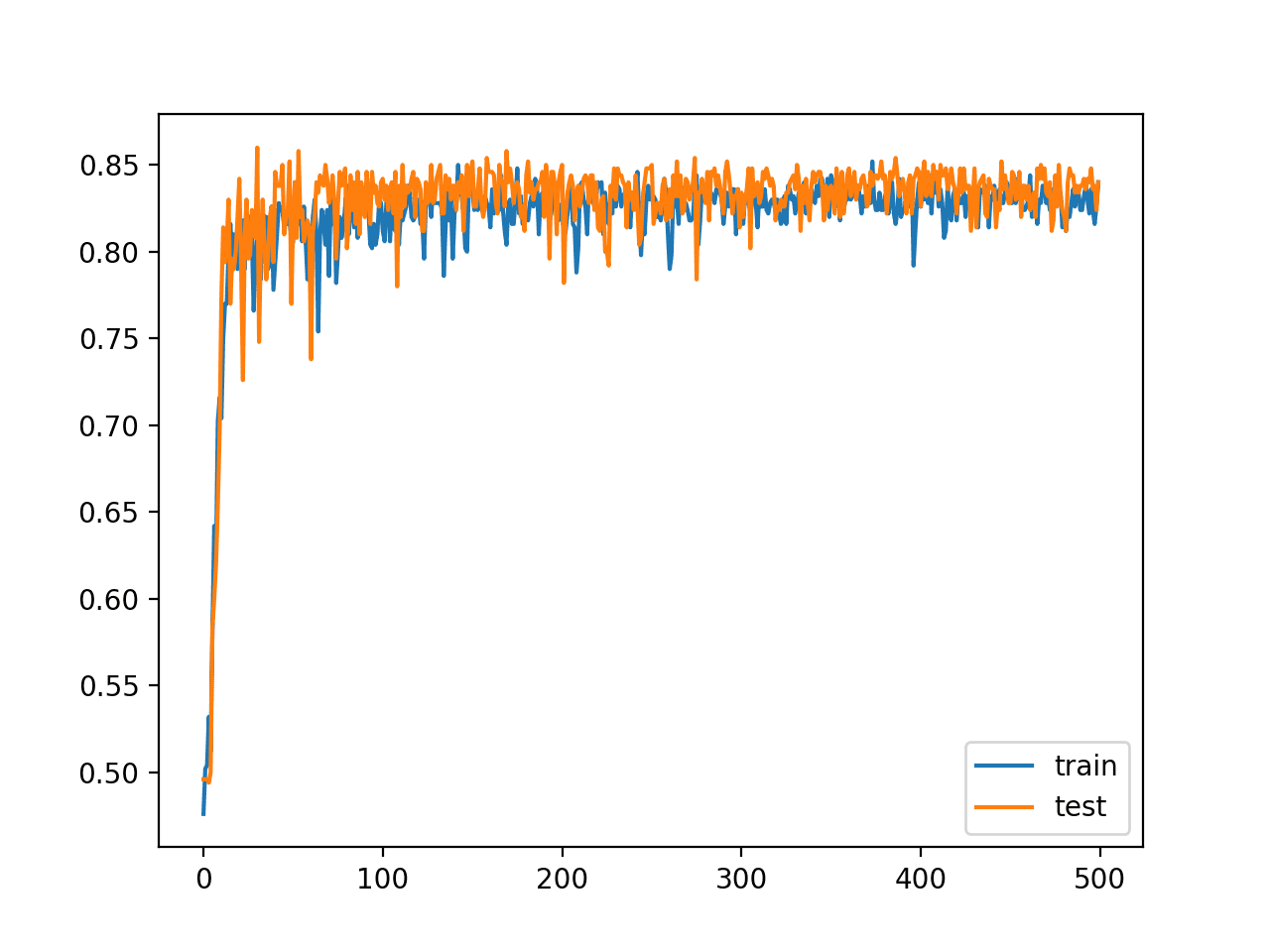
两圆问题中带 ReLU 的深度 MLP 训练 epoch 上的训练集和测试集准确率折线图

使用 ReLU 激活函数使我们能够针对这个简单的问题拟合一个更深的模型，但这种能力并非无限延伸。例如，增加层数会导致学习速度变慢，直到大约 20 层时模型无法再学习该问题，至少在所选配置下是这样。

例如，下面是具有 15 个隐藏层的相同模型的训练和测试准确率折线图，显示它仍然能够学习问题。

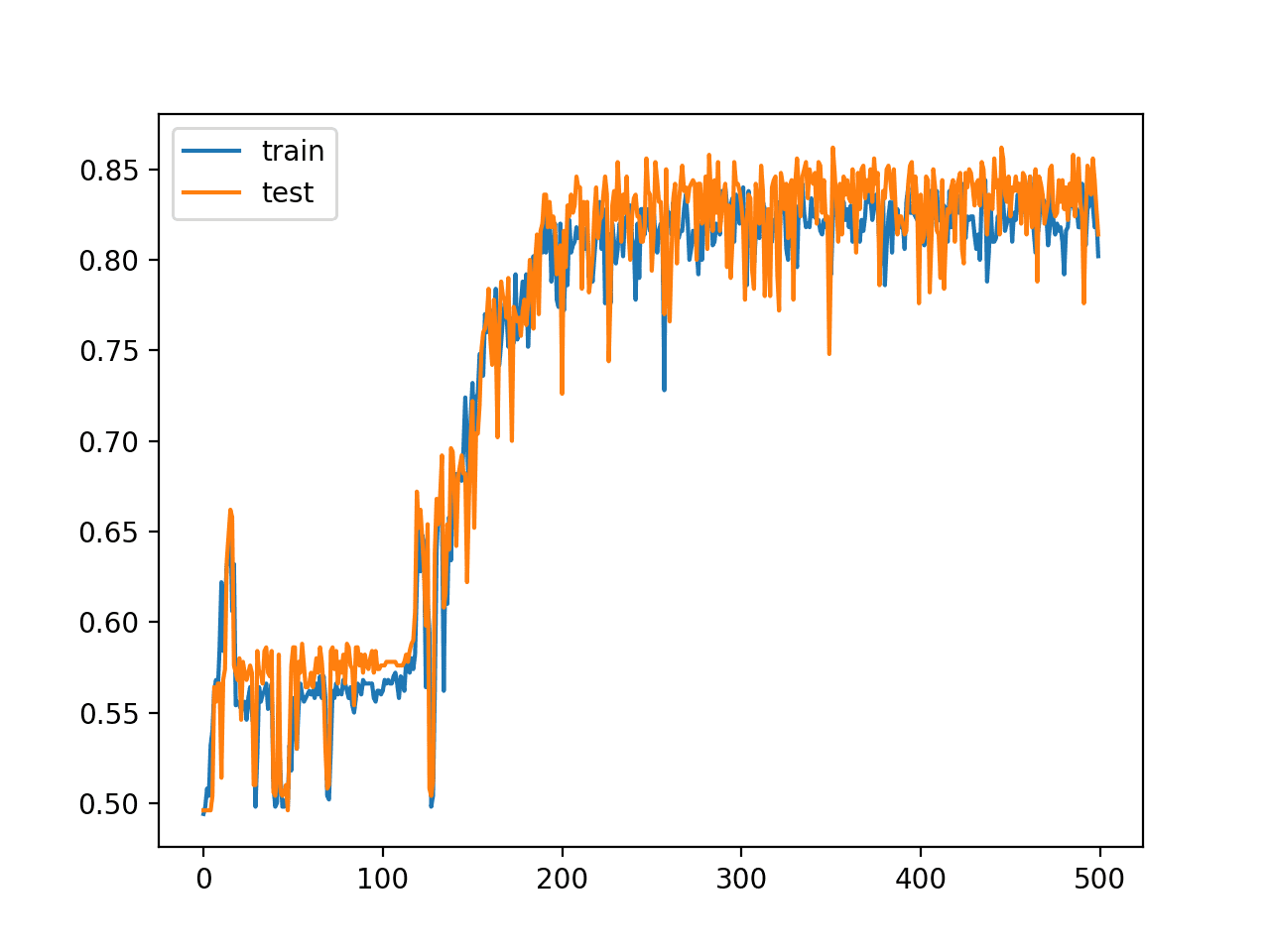
带 ReLU 的深度 MLP 具有 15 个隐藏层的训练 epoch 上的训练集和测试集准确率折线图

下面是具有 20 层的相同模型的训练和测试准确率随 epoch 变化的折线图，显示该配置不再能够学习问题。

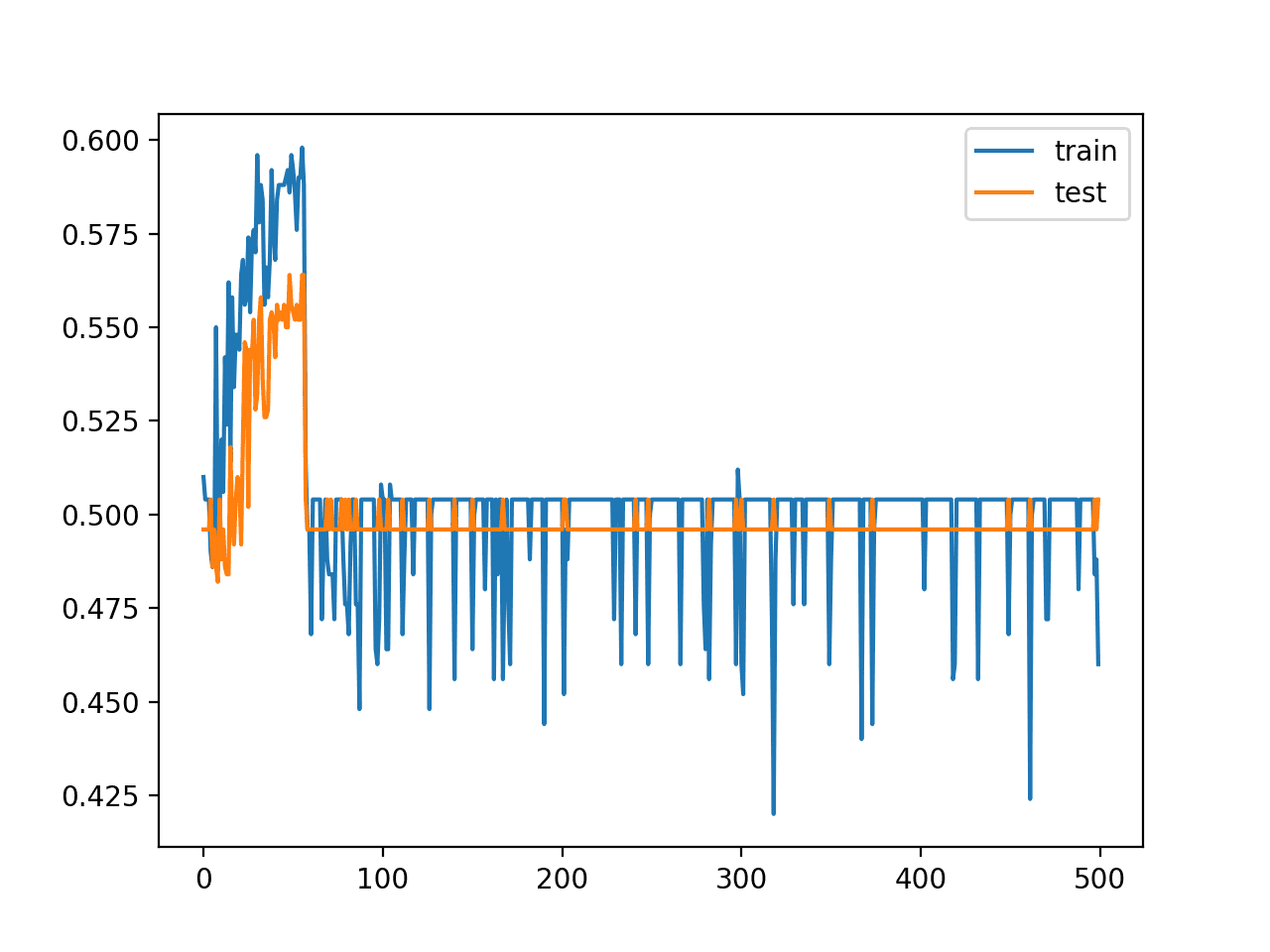
带 ReLU 的深度 MLP 具有 20 个隐藏层的训练 epoch 上的训练集和测试集准确率折线图

尽管使用了 ReLU 有效，但我们无法确信 tanh 函数的失败是由于梯度消失，而 ReLU 的成功是由于它克服了这个问题。

审查训练期间的平均梯度大小

本节假设您正在使用带有 Keras 的 TensorFlow 后端。如果不是这种情况，您可以跳过本节。

在使用 tanh 激活函数的情况下，我们知道网络有足够的容量来学习问题，但层数的增加阻碍了它这样做。

诊断梯度消失是性能不佳的原因很难。一个可能的信号是查看每个训练 epoch 每层的平均梯度大小。

我们预计靠近输出层的层具有比靠近输入层的层更大的平均梯度。

Keras 提供了TensorBoard 回调，可用于在训练期间记录模型的属性，例如每层的平均梯度。然后可以使用 TensorFlow 提供的 TensorBoard 界面查看这些统计信息。

我们可以配置此回调，以记录每个训练 epoch 每层的平均梯度，然后确保在训练模型时使用该回调。

我们可以使用此回调首先调查使用双曲正切激活函数拟合的深度模型中梯度的动态，然后将动态与使用修正线性激活函数拟合的相同模型进行比较。

首先，下面列出了使用 tanh 和 TensorBoard 回调的深度 MLP 模型的完整示例。

运行示例会创建一个新的“logs/”子目录，其中包含一个文件，其中包含回调在训练期间记录的统计信息。

我们可以在 TensorBoard Web 界面中查看统计信息。界面可以从命令行启动，需要您指定 logs 目录的完整路径。

例如，如果您在“/code”目录中运行代码，则 logs 目录的完整路径将是“/code/logs/”。

以下是用于启动 TensorBoard 界面在命令行（命令提示符）上执行的命令。请务必更改 logs 目录的路径。

接下来，打开您的网络浏览器并输入以下 URL

• https://:6006

如果一切顺利，您将看到 TensorBoard Web 界面。

可以在界面的“Distributions”（分布）和“Histograms”（直方图）选项卡下查看每个训练 epoch 每层平均梯度的图。可以使用搜索过滤器“kernel_0_grad”过滤图，仅显示稠密层的梯度，排除偏置。

注意：由于算法或评估过程的随机性，或数值精度差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

首先，为 6 个层（5 个隐藏层，1 个输出层）中的每个层创建折线图。图的名称指示层，其中“dense_1”表示输入层之后的隐藏层，“dense_6”表示输出层。

我们可以看到输出层在整个运行过程中有大量的活动，每个 epoch 的平均梯度大约在 0.05 到 0.1 之间。我们还可以在第一个隐藏层中看到一些活动，其范围相似。因此，梯度正在通过第一个隐藏层，但最后一层和最后一个隐藏层正在看到大部分活动。

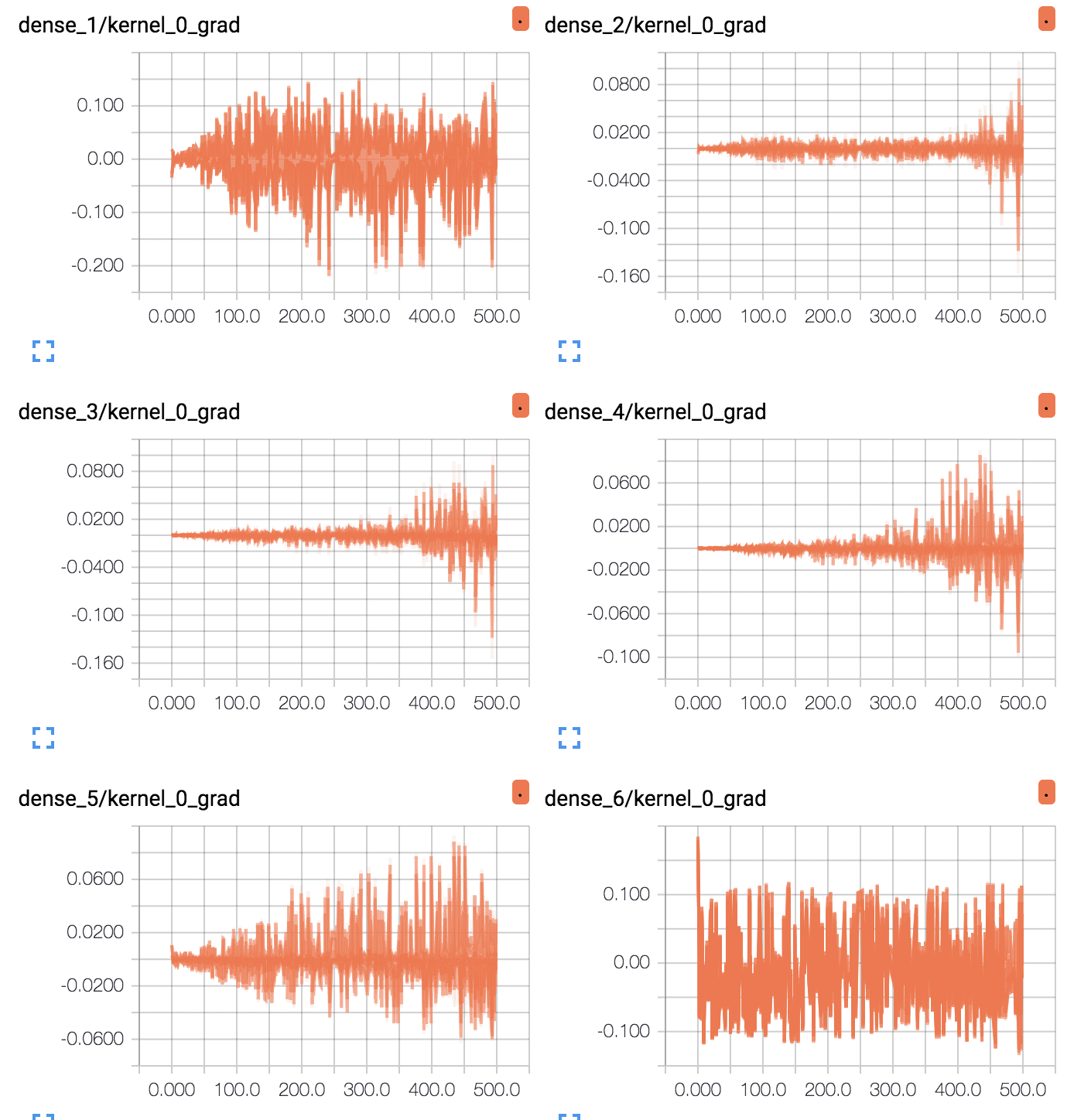
带 Tanh 的深度 MLP 每层平均梯度的 TensorBoard 折线图

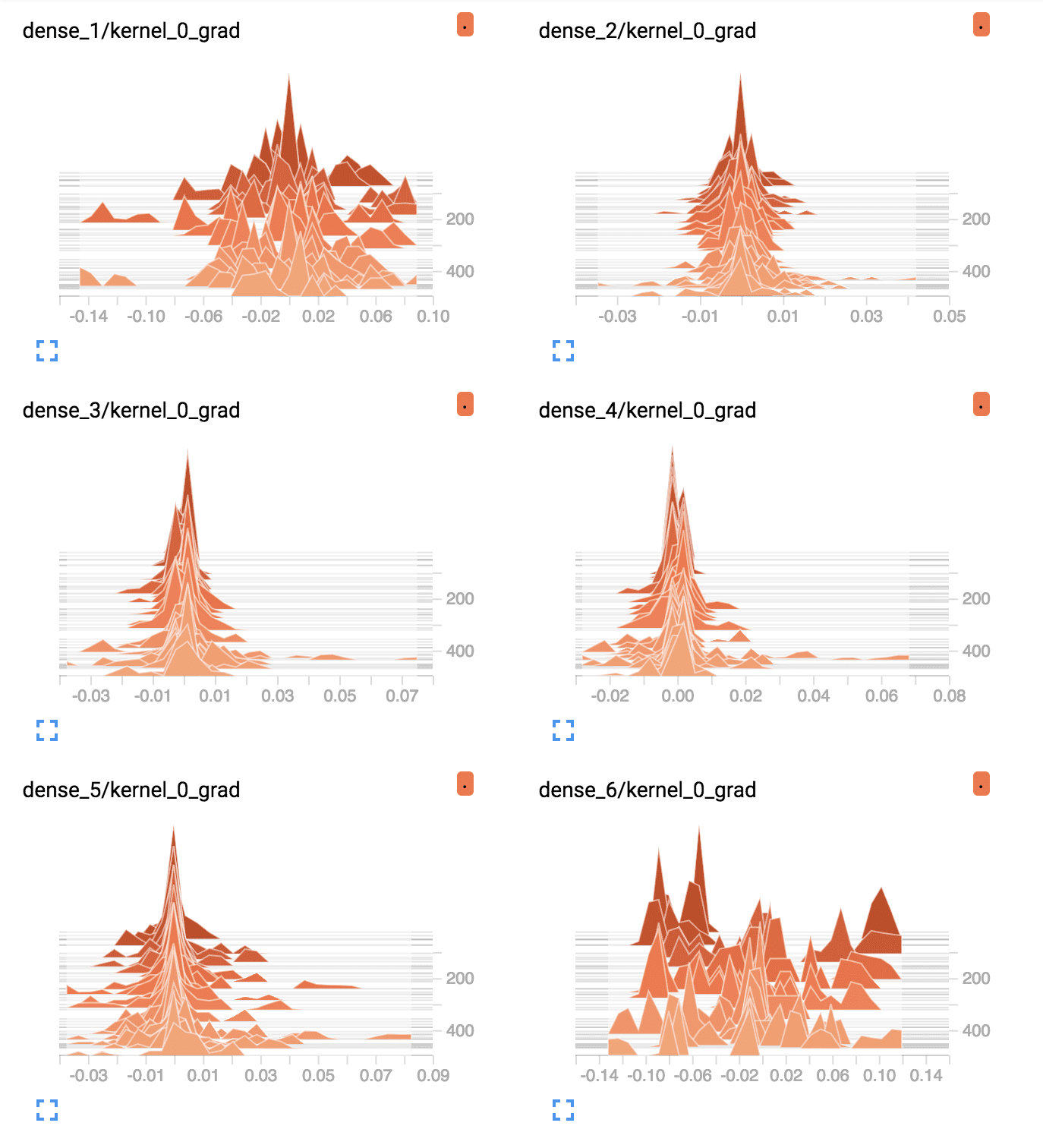
带 Tanh 的深度 MLP 每层平均梯度的 TensorBoard 密度图

我们可以从带有 ReLU 激活函数的深度 MLP 中收集相同的信息。

完整的示例如下所示。

如果您是 TensorBoard 界面的新手，它可能会令人困惑。

为了保持简单，在运行第二个示例之前删除“logs”子目录。

运行后，您可以以相同的方式启动 TensorBoard 界面，并通过网络浏览器访问它。

与带有 tanh 的深度模型梯度相比，每个训练 epoch 每层平均梯度的图显示了不同的情况。

我们可以看到，第一个隐藏层看到更多的梯度，更一致地具有更大的传播范围，大约为 0.2 到 0.4，而 tanh 则为 0.05 和 0.1。我们还可以看到中间隐藏层看到大的梯度。

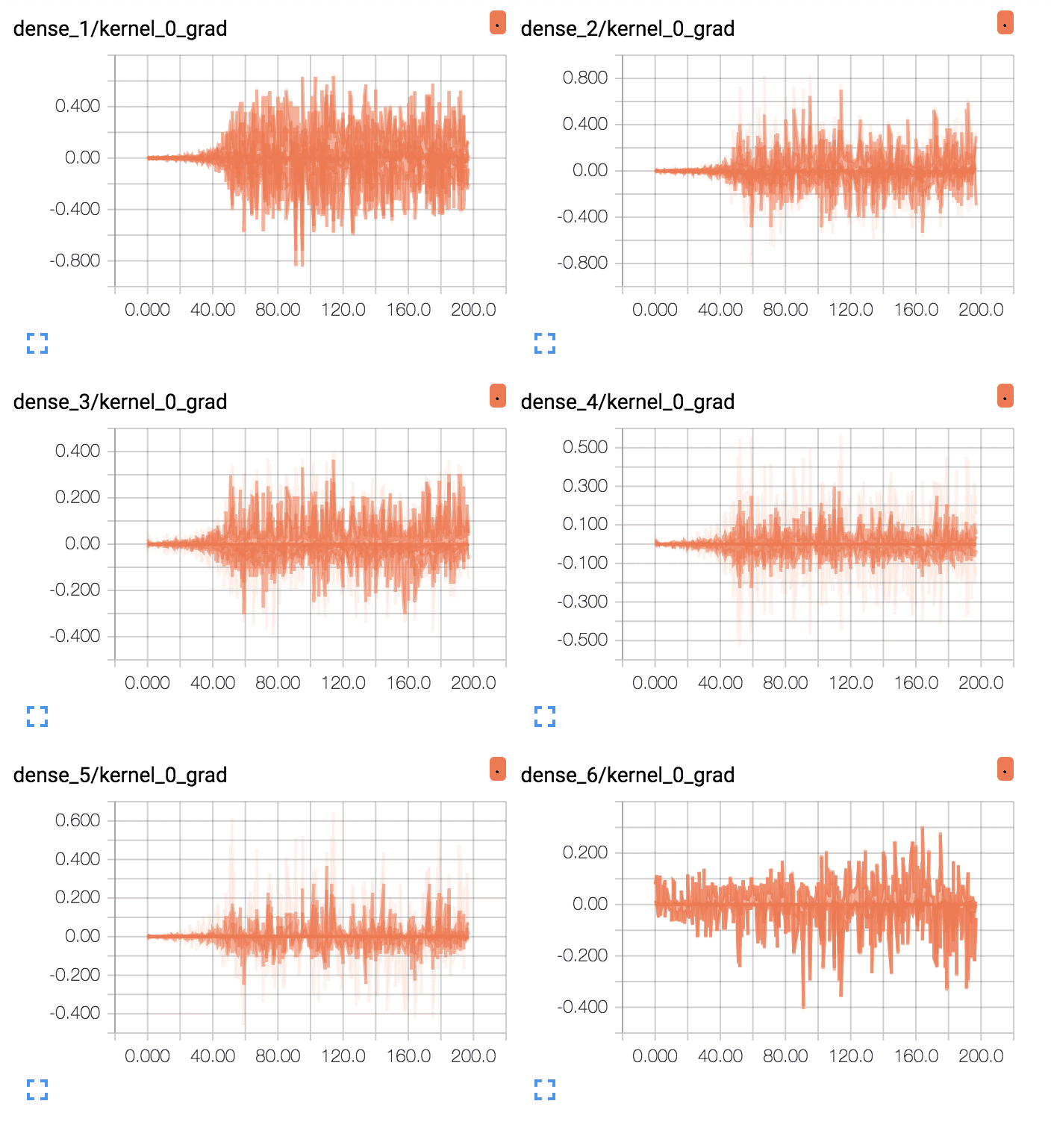
带 ReLU 的深度 MLP 每层平均梯度的 TensorBoard 折线图

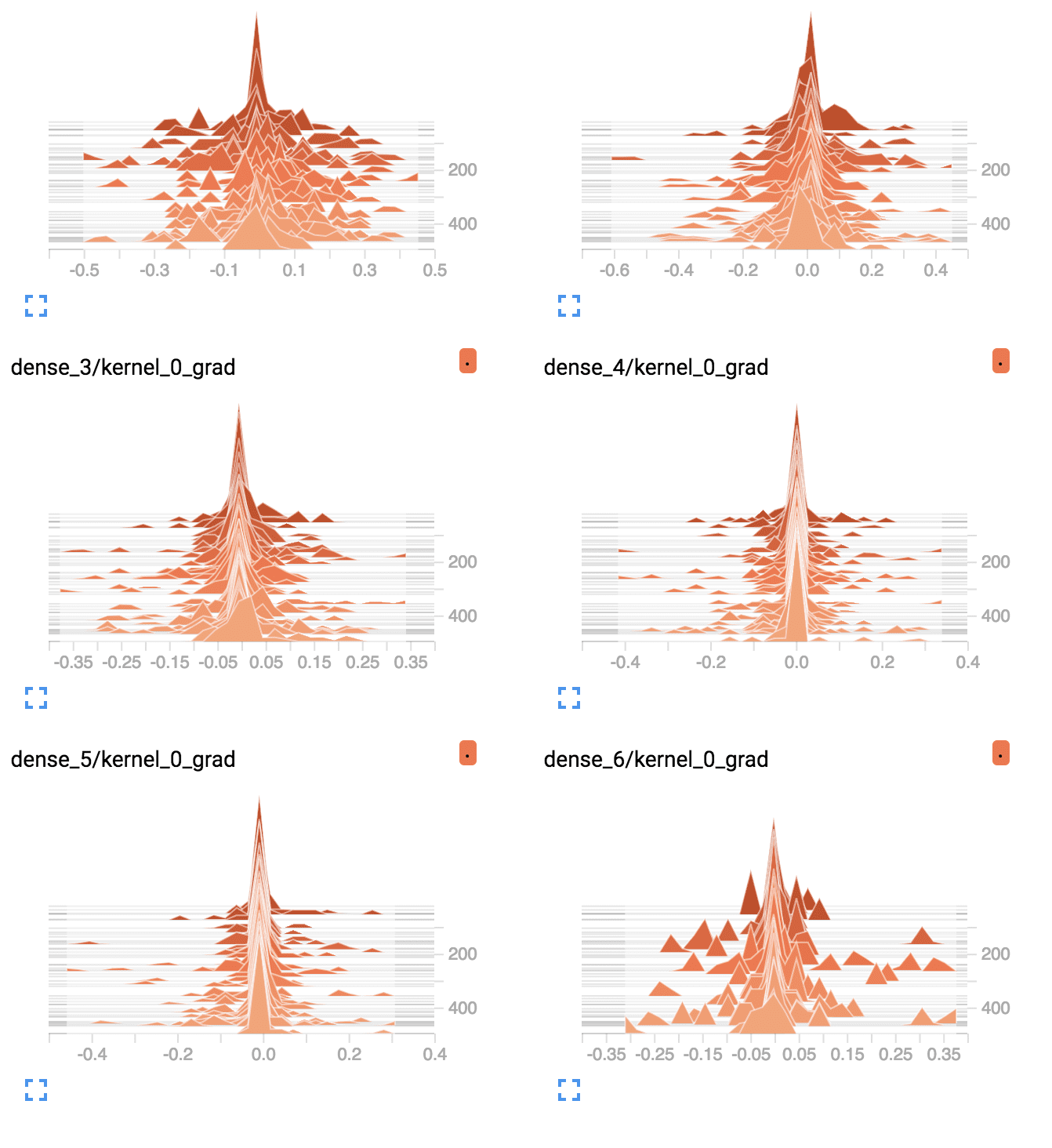
带 ReLU 的深度 MLP 每层平均梯度的 TensorBoard 密度图

ReLU 激活函数允许在训练期间更多的梯度向后流过模型，这可能是性能提高的原因。

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

• 权重初始化。更新使用 tanh 激活的深度 MLP 以使用 Xavier 均匀权重初始化并报告结果。
• 学习算法。更新使用 tanh 激活的深度 MLP 以使用自适应学习算法（例如 Adam）并报告结果。
• 权重变化。更新 tanh 和 relu 示例以记录和绘制每个 epoch 模型权重的L1 向量范数，作为训练期间每个层变化量的代理，并比较结果。
• 研究模型深度。使用 MLP 和 tanh 激活创建一个实验，并报告模型性能，因为隐藏层数从 1 增加到 10。
• 增加广度。将带有 tanh 激活的 MLP 的隐藏层中的节点数从 5 增加到 25，并报告层数从 1 增加到 10 时的性能。

如果您探索了这些扩展中的任何一个，我很想知道。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

文章

• 深度学习神经网络中修正线性激活单元 (ReLU) 的简介

论文

• 用于训练非常深的前馈网络的随机游走初始化, 2014.
• 循环网络中的梯度流：学习长期依赖的困难, 2001.

书籍

• 8.2.5 节 长期依赖，《深度学习》, 2016.
• 第 5 章 为什么深度神经网络难以训练？，《神经网络与深度学习》.

API

• RandomUniform Keras 权重初始化 API
• SGD Keras 优化器 API
• TensorBoard Keras 回调 API
• TensorFlow TensorBoard 指南

文章

• 梯度消失问题，维基百科.

总结

在本教程中，您了解了如何诊断训练神经网络模型时出现的梯度消失问题，以及如何使用替代激活函数和权重初始化方案来解决它。

具体来说，你学到了：

• 梯度消失问题限制了使用双曲正切等经典流行激活函数的深度神经网络的发展。
• 如何使用 ReLU 和 He 权重初始化修复用于分类的深度神经网络多层感知器。
• 如何使用 TensorBoard 诊断梯度消失问题并确认 ReLU 对改善模型梯度流的影响。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

今天就开发更好的深度学习模型！

更快地训练，减少过拟合，以及集成方法

...只需几行python代码

在我的新电子书中探索如何实现
更好的深度学习

它提供关于以下主题的自学教程：
权重衰减、批量归一化、dropout、模型堆叠等等...

为你的项目带来更好的深度学习！

跳过学术理论。只看结果。

查看内容