如何对时间序列预测的 SARIMA 超参数进行网格搜索

作者： Jason Brownlee 发布于 2020 年 8 月 28 日在深度学习时间序列 83 条评论

季节性自回归积分移动平均（SARIMA）模型是一种用于对可能包含趋势和季节性成分的单变量时间序列数据进行建模的方法。

它是一种有效的时间序列预测方法，但需要仔细分析和领域专业知识才能配置七个或更多的模型超参数。

另一种配置模型的方法是利用快速并行的现代硬件，对一系列超参数配置进行网格搜索，以发现最佳配置。通常，这个过程可以揭示出非直观的模型配置，从而导致比通过仔细分析指定的配置更低的预测误差。

在本教程中，您将学习如何开发一个框架，用于对单变量时间序列预测的 SARIMA 模型所有超参数进行网格搜索。

完成本教程后，您将了解：

如何从头开始使用滚动预测验证开发一个网格搜索 SARIMA 模型的框架。
如何对每日出生时间序列数据的 SARIMA 模型超参数进行网格搜索。
如何对洗发水销售、汽车销售和气温的月度时间序列数据的 SARIMA 模型超参数进行网格搜索。

通过我的新书《深度学习时间序列预测》**启动您的项目**，其中包括**分步教程**和所有示例的 **Python 源代码**文件。

让我们开始吧。

2019 年 4 月更新：更新了数据集链接。

How to Grid Search SARIMA Model Hyperparameters for Time Series Forecasting in Python

如何在 Python 中对 SARIMA 模型超参数进行时间序列预测的网格搜索
图片由 Thomas 提供，保留部分权利。

教程概述

本教程分为六个部分；它们是：

SARIMA 用于时间序列预测
开发网格搜索框架
案例研究 1：无趋势或季节性
案例研究 2：趋势
案例研究 3：季节性
案例研究 4：趋势和季节性

SARIMA 用于时间序列预测

季节性自回归积分移动平均（SARIMA 或季节性 ARIMA）是 ARIMA 的扩展，明确支持具有季节性成分的单变量时间序列数据。

它增加了三个新的超参数，用于指定序列季节性成分的自回归 (AR)、差分 (I) 和移动平均 (MA)，以及一个额外的季节性周期参数。

季节性 ARIMA 模型通过在 ARIMA 中包含额外的季节性项来形成 […] 模型中的季节性部分包含的项与模型的非季节性成分非常相似，但它们涉及季节性周期的滞后。

— 第 242 页，《预测：原理与实践》，2013 年。

配置 SARIMA 需要为序列的趋势和季节性元素选择超参数。

有三个趋势元素需要配置。

它们与 ARIMA 模型相同；具体来说是

p：趋势自回归阶数。
d：趋势差分阶数。
q：趋势移动平均阶数。

有四个不属于 ARIMA 的季节性元素必须配置；它们是

**P**：季节性自回归阶数。
**D**：季节性差分阶数。
**Q**：季节性移动平均阶数。
**m**：一个季节性周期的时间步数。

总的来说，SARIMA 模型的表示方式为

SARIMA(p,d,q)(P,D,Q)m

1	SARIMA(p,d,q)(P,D,Q)m

SARIMA 模型可以通过模型配置参数包含 ARIMA、ARMA、AR 和 MA 模型。

模型的趋势和季节性超参数可以通过分析自相关和偏自相关图来配置，这需要一定的专业知识。

另一种方法是网格搜索一系列模型配置，并找出哪些配置最适合特定的单变量时间序列。

季节性 ARIMA 模型可能会有大量的参数和项组合。因此，在拟合数据时尝试各种模型，并使用适当的标准选择最佳拟合模型是合适的...

— 第 143-144 页，《R 语言时间序列入门》，2009 年。

这种方法在现代计算机上比分析过程更快，并且可以揭示可能不明显但导致较低预测误差的惊人发现。

时间序列深度学习需要帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

开发网格搜索框架

在本节中，我们将开发一个框架，用于对给定单变量时间序列预测问题的 SARIMA 模型超参数进行网格搜索。

我们将使用 statsmodels 库提供的 SARIMA 实现。

该模型具有控制序列、趋势和季节性模型性质的超参数，具体如下：

**order**：一个包含 p、d 和 q 参数的元组，用于趋势建模。
**seasonal_order**：一个包含 P、D、Q 和 m 参数的元组，用于季节性建模。
**trend**：一个参数，用于控制确定性趋势模型，可以是 'n'、'c'、't'、'ct'，分别代表无趋势、常数、线性以及常数加线性趋势。

如果您对您的问题足够了解，可以指定一个或多个这些参数，那么您应该指定它们。如果不行，您可以尝试网格搜索这些参数。

我们可以先定义一个函数，该函数将用给定的配置拟合模型并进行一步预测。

下面的 *sarima_forecast()* 实现了此行为。

该函数接受一个连续的先前观测值数组或列表，以及一个用于配置模型的配置参数列表，具体包括两个元组和一个用于趋势阶数、季节性阶数趋势和参数的字符串。

我们还试图通过放宽约束来使模型更稳健，例如数据必须是平稳的，并且 MA 变换是可逆的。

# one-step sarima forecast
def sarima_forecast(history, config):
	order, sorder, trend = config
	# define model
	model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)
	# fit model
	model_fit = model.fit(disp=False)
	# make one step forecast
	yhat = model_fit.predict(len(history), len(history))
	return yhat[0]

# 一步 SARIMA 预测

def sarima_forecast(history, config):

order, sorder, trend = config

# 定义模型

model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)

# 拟合模型

model_fit = model.fit(disp=False)

# 进行一步预测

yhat = model_fit.predict(len(history), len(history))

return yhat[0]

接下来，我们需要构建一些函数，用于通过滚动预测验证重复拟合和评估模型，包括将数据集拆分为训练集和测试集，以及评估一步预测。

我们可以根据指定的拆分大小（例如，在测试集中使用的数据的时间步数）使用切片拆分列表或 NumPy 数组数据。

下面的 *train_test_split()* 函数针对提供的数据集和测试集中指定的时间步数实现此功能。

# split a univariate dataset into train/test sets
def train_test_split(data, n_test):
	return data[:-n_test], data[-n_test:]

# 将单变量数据集拆分为训练/测试集

def train_test_split(data, n_test):

return data[:-n_test], data[-n_test:]

在对测试数据集中的每个步骤进行预测后，需要将它们与测试集进行比较以计算误差分数。

时间序列预测有许多流行的误差分数。在这种情况下，我们将使用均方根误差 (RMSE)，但您可以将其更改为您偏好的度量，例如 MAPE、MAE 等。

下面的 *measure_rmse()* 函数将根据实际值（测试集）和预测值列表计算 RMSE。

# root mean squared error or rmse
def measure_rmse(actual, predicted):
	return sqrt(mean_squared_error(actual, predicted))

# 均方根误差或 RMSE

def measure_rmse(actual, predicted):

return sqrt(mean_squared_error(actual, predicted))

我们现在可以实现滚动预测验证方案。这是评估时间序列预测模型的标准方法，它尊重观测值的时间顺序。

首先，使用 *train_test_split()* 函数将提供的单变量时间序列数据集拆分为训练集和测试集。然后枚举测试集中的观测值数量。对于每个观测值，我们基于所有历史数据拟合一个模型并进行一步预测。然后将该时间步的真实观测值添加到历史数据中，并重复此过程。调用 *sarima_forecast()* 函数以拟合模型并进行预测。最后，通过调用 *measure_rmse()* 函数，将所有一步预测与实际测试集进行比较，从而计算误差分数。

下面的 *walk_forward_validation()* 函数实现了这一点，它接受一个单变量时间序列、测试集中使用的时间步数和一个模型配置数组。

# walk-forward validation for univariate data
def walk_forward_validation(data, n_test, cfg):
	predictions = list()
	# split dataset
	train, test = train_test_split(data, n_test)
	# seed history with training dataset
	history = [x for x in train]
	# step over each time-step in the test set
	for i in range(len(test)):
		# fit model and make forecast for history
		yhat = sarima_forecast(history, cfg)
		# store forecast in list of predictions
		predictions.append(yhat)
		# add actual observation to history for the next loop
		history.append(test[i])
	# estimate prediction error
	error = measure_rmse(test, predictions)
	return error

# 单变量数据的滚动预测验证

def walk_forward_validation(data, n_test, cfg):

predictions = list()

# 拆分数据集

train, test = train_test_split(data, n_test)

# 用训练数据集初始化历史数据

history = [x for x in train]

# 遍历测试集中的每个时间步

for i in range(len(test)):

# 拟合模型并对历史数据进行预测

yhat = sarima_forecast(history, cfg)

# 将预测结果存储在预测列表中

predictions.append(yhat)

# 将实际观测值添加到历史数据中以进行下一次循环

history.append(test[i])

# 估计预测误差

error = measure_rmse(test, predictions)

return error

如果您对进行多步预测感兴趣，可以更改 *sarima_forecast()* 函数中对 *predict()* 的调用，并更改 *measure_rmse()* 函数中的误差计算。

我们可以使用不同的模型配置列表重复调用 *walk_forward_validation()*。

一个可能的问题是，某些模型配置组合可能无法调用模型并会引发异常，例如指定了季节性结构的某些方面但没有全部指定。

此外，某些模型在某些数据上也可能引发警告，例如由 statsmodels 库调用的线性代数库。

我们可以在网格搜索期间捕获异常并忽略警告，方法是将所有对 *walk_forward_validation()* 的调用包装在一个 try-except 块和一个忽略警告的块中。我们还可以添加调试支持来禁用这些保护，以防我们想了解实际发生的情况。最后，如果发生错误，我们可以返回 None 结果，否则我们可以打印一些关于每个评估模型技能的信息。当评估大量模型时，这很有帮助。

下面的 *score_model()* 函数实现了这一点，并返回一个 (key 和 result) 元组，其中 key 是测试模型配置的字符串版本。

# score a model, return None on failure
def score_model(data, n_test, cfg, debug=False):
	result = None
	# convert config to a key
	key = str(cfg)
	# show all warnings and fail on exception if debugging
	if debug:
		result = walk_forward_validation(data, n_test, cfg)
	else:
		# one failure during model validation suggests an unstable config
		try:
			# never show warnings when grid searching, too noisy
			with catch_warnings():
				filterwarnings("ignore")
				result = walk_forward_validation(data, n_test, cfg)
		except:
			error = None
	# check for an interesting result
	if result is not None:
		print(' > Model[%s] %.3f' % (key, result))
	return (key, result)

# 评估模型，失败时返回 None

def score_model(data, n_test, cfg, debug=False):

result = None

# 将配置转换为键

key = str(cfg)

# 如果在调试，则显示所有警告并在异常时失败

if debug:

result = walk_forward_validation(data, n_test, cfg)

else:

# 模型验证过程中的一次失败表明配置不稳定

try:

# 网格搜索时从不显示警告，太嘈杂

with catch_warnings():

filterwarnings("ignore")

result = walk_forward_validation(data, n_test, cfg)

except:

error = None

# 检查是否有有趣的结果

if result is not None:

print(' > Model[%s] %.3f' % (key, result))

return (key, result)

接下来，我们需要一个循环来测试不同的模型配置列表。

这是驱动网格搜索过程的主要函数，它将为每个模型配置调用 *score_model()* 函数。

我们可以通过并行评估模型配置来显著加快网格搜索过程。一种方法是使用 Joblib 库。

我们可以定义一个 Parallel 对象，指定要使用的核心数量，并将其设置为您的硬件中检测到的核心数量。

executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')

1	executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')

然后，我们可以创建一个任务列表以并行执行，这将是对我们拥有的每个模型配置调用 *score_model()* 函数。

tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)

1	tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)

最后，我们可以使用 Parallel 对象并行执行任务列表。

scores = executor(tasks)

1	scores = executor(tasks)

就是这样。

我们还可以提供一个非并行版本的模型配置评估，以防我们想要调试某些东西。

scores = [score_model(data, n_test, cfg) for cfg in cfg_list]

1	scores = [score_model(data, n_test, cfg) for cfg in cfg_list]

评估配置列表的结果将是一个元组列表，每个元组包含一个总结特定模型配置的名称，以及以 RMSE 或 None（如果存在错误）表示的模型误差。

我们可以过滤掉所有分数为 None 的结果。

scores = [r for r in scores if r[1] != None]

1	scores = [r for r in scores if r[1] != None]

然后我们可以按升序（最佳在前）对列表中所有元组进行排序，然后返回此分数列表以供审查。

下面的 *grid_search()* 函数实现了此行为，它接受一个单变量时间序列数据集、一个模型配置列表（列表的列表）和测试集中使用的时间步数。可选的 *parallel* 参数允许打开或关闭跨所有核心的模型评估，默认情况下为打开。

# grid search configs
def grid_search(data, cfg_list, n_test, parallel=True):
	scores = None
	if parallel:
		# execute configs in parallel
		executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')
		tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)
		scores = executor(tasks)
	else:
		scores = [score_model(data, n_test, cfg) for cfg in cfg_list]
	# remove empty results
	scores = [r for r in scores if r[1] != None]
	# sort configs by error, asc
	scores.sort(key=lambda tup: tup[1])
	return scores

# 网格搜索配置

def grid_search(data, cfg_list, n_test, parallel=True):

scores = None

if parallel:

# 并行执行配置

executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')

tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)

scores = executor(tasks)

else:

scores = [score_model(data, n_test, cfg) for cfg in cfg_list]

# 移除空结果

scores = [r for r in scores if r[1] != None]

# 按误差升序排序配置

scores.sort(key=lambda tup: tup[1])

return scores

我们快完成了。

剩下的唯一一件事是定义要用于数据集的模型配置列表。

我们可以通用地定义它。我们可能想要指定的唯一参数是序列中季节性成分的周期性（如果存在）。默认情况下，我们将假设没有季节性成分。

下面的 *sarima_configs()* 函数将创建要评估的模型配置列表。

配置假设趋势和季节性的 AR、MA 和 I 分量均为低阶，例如关闭 (0) 或在 [1,2] 中。如果您认为阶数可能更高，您可能需要扩展这些范围。可以指定可选的季节性周期列表，您甚至可以更改函数以指定您可能了解的其他时间序列元素。

理论上，有 1,296 种可能的模型配置需要评估，但实际上，许多配置将无效并导致错误，我们将捕获并忽略这些错误。

# create a set of sarima configs to try
def sarima_configs(seasonal=[0]):
	models = list()
	# define config lists
	p_params = [0, 1, 2]
	d_params = [0, 1]
	q_params = [0, 1, 2]
	t_params = ['n','c','t','ct']
	P_params = [0, 1, 2]
	D_params = [0, 1]
	Q_params = [0, 1, 2]
	m_params = seasonal
	# create config instances
	for p in p_params:
		for d in d_params:
			for q in q_params:
				for t in t_params:
					for P in P_params:
						for D in D_params:
							for Q in Q_params:
								for m in m_params:
									cfg = [(p,d,q), (P,D,Q,m), t]
									models.append(cfg)
	return models

# 创建一组要尝试的 sarima 配置

def sarima_configs(seasonal=[0]):

models = list()

# 定义配置列表

p_params = [0, 1, 2]

d_params = [0, 1]

q_params = [0, 1, 2]

t_params = ['n','c','t','ct']

P_params = [0, 1, 2]

D_params = [0, 1]

Q_params = [0, 1, 2]

m_params = seasonal

# 创建配置实例

for p in p_params:

for d in d_params:

for q in q_params:

for t in t_params:

for P in P_params:

for D in D_params:

for Q in Q_params:

for m in m_params:

cfg = [(p,d,q), (P,D,Q,m), t]

models.append(cfg)

返回 models

我们现在有了一个框架，用于通过一步滚动预测验证对 SARIMA 模型超参数进行网格搜索。

它是通用的，适用于作为列表或 NumPy 数组提供的任何内存中单变量时间序列。

我们可以通过在一个构造的 10 步数据集上测试它来确保所有部分协同工作。

完整的示例如下所示。

# grid search sarima hyperparameters
from math import sqrt
from multiprocessing import cpu_count
from joblib import Parallel
from joblib import delayed
from warnings import catch_warnings
from warnings import filterwarnings
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.metrics import mean_squared_error

# one-step sarima forecast
def sarima_forecast(history, config):
	order, sorder, trend = config
	# define model
	model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)
	# fit model
	model_fit = model.fit(disp=False)
	# make one step forecast
	yhat = model_fit.predict(len(history), len(history))
	return yhat[0]

# root mean squared error or rmse
def measure_rmse(actual, predicted):
	return sqrt(mean_squared_error(actual, predicted))

# split a univariate dataset into train/test sets
def train_test_split(data, n_test):
	return data[:-n_test], data[-n_test:]

# walk-forward validation for univariate data
def walk_forward_validation(data, n_test, cfg):
	predictions = list()
	# split dataset
	train, test = train_test_split(data, n_test)
	# seed history with training dataset
	history = [x for x in train]
	# step over each time-step in the test set
	for i in range(len(test)):
		# fit model and make forecast for history
		yhat = sarima_forecast(history, cfg)
		# store forecast in list of predictions
		predictions.append(yhat)
		# add actual observation to history for the next loop
		history.append(test[i])
	# estimate prediction error
	error = measure_rmse(test, predictions)
	return error

# score a model, return None on failure
def score_model(data, n_test, cfg, debug=False):
	result = None
	# convert config to a key
	key = str(cfg)
	# show all warnings and fail on exception if debugging
	if debug:
		result = walk_forward_validation(data, n_test, cfg)
	else:
		# one failure during model validation suggests an unstable config
		try:
			# never show warnings when grid searching, too noisy
			with catch_warnings():
				filterwarnings("ignore")
				result = walk_forward_validation(data, n_test, cfg)
		except:
			error = None
	# check for an interesting result
	if result is not None:
		print(' > Model[%s] %.3f' % (key, result))
	return (key, result)

# grid search configs
def grid_search(data, cfg_list, n_test, parallel=True):
	scores = None
	if parallel:
		# execute configs in parallel
		executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')
		tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)
		scores = executor(tasks)
	else:
		scores = [score_model(data, n_test, cfg) for cfg in cfg_list]
	# remove empty results
	scores = [r for r in scores if r[1] != None]
	# sort configs by error, asc
	scores.sort(key=lambda tup: tup[1])
	return scores

# create a set of sarima configs to try
def sarima_configs(seasonal=[0]):
	models = list()
	# define config lists
	p_params = [0, 1, 2]
	d_params = [0, 1]
	q_params = [0, 1, 2]
	t_params = ['n','c','t','ct']
	P_params = [0, 1, 2]
	D_params = [0, 1]
	Q_params = [0, 1, 2]
	m_params = seasonal
	# create config instances
	for p in p_params:
		for d in d_params:
			for q in q_params:
				for t in t_params:
					for P in P_params:
						for D in D_params:
							for Q in Q_params:
								for m in m_params:
									cfg = [(p,d,q), (P,D,Q,m), t]
									models.append(cfg)
	return models

if __name__ == '__main__':
	# define dataset
	data = [10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0]
	print(data)
	# data split
	n_test = 4
	# model configs
	cfg_list = sarima_configs()
	# grid search
	scores = grid_search(data, cfg_list, n_test)
	print('done')
	# list top 3 configs
	for cfg, error in scores[:3]:
		print(cfg, error)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

# 网格搜索 SARIMA 超参数

from math import sqrt

from multiprocessing import cpu_count

from joblib import Parallel

from joblib import delayed

from warnings import catch_warnings

from warnings import filterwarnings

from statsmodels.tsa.statespace.sarimax import SARIMAX

from sklearn.metrics import mean_squared_error

# 一步 SARIMA 预测

def sarima_forecast(history, config):

order, sorder, trend = config

# 定义模型

model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)

# 拟合模型

model_fit = model.fit(disp=False)

# 进行一步预测

yhat = model_fit.predict(len(history), len(history))

return yhat[0]

# 均方根误差或 RMSE

def measure_rmse(actual, predicted):

return sqrt(mean_squared_error(actual, predicted))

# 将单变量数据集拆分为训练/测试集

def train_test_split(data, n_test):

return data[:-n_test], data[-n_test:]

# 单变量数据的滚动预测验证

def walk_forward_validation(data, n_test, cfg):

predictions = list()

# 拆分数据集

train, test = train_test_split(data, n_test)

# 用训练数据集初始化历史数据

history = [x for x in train]

# 遍历测试集中的每个时间步

for i in range(len(test)):

# 拟合模型并对历史数据进行预测

yhat = sarima_forecast(history, cfg)

# 将预测结果存储在预测列表中

predictions.append(yhat)

# 将实际观测值添加到历史数据中以进行下一次循环

history.append(test[i])

# 估计预测误差

error = measure_rmse(test, predictions)

return error

# 评估模型，失败时返回 None

def score_model(data, n_test, cfg, debug=False):

result = None

# 将配置转换为键

key = str(cfg)

# 如果在调试，则显示所有警告并在异常时失败

if debug:

result = walk_forward_validation(data, n_test, cfg)

else:

# 模型验证过程中的一次失败表明配置不稳定

try:

# 网格搜索时从不显示警告，太嘈杂

with catch_warnings():

filterwarnings("ignore")

result = walk_forward_validation(data, n_test, cfg)

except:

error = None

# 检查是否有有趣的结果

if result is not None:

print(' > Model[%s] %.3f' % (key, result))

return (key, result)

# 网格搜索配置

def grid_search(data, cfg_list, n_test, parallel=True):

scores = None

if parallel:

# 并行执行配置

executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')

tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)

scores = executor(tasks)

else:

scores = [score_model(data, n_test, cfg) for cfg in cfg_list]

# 移除空结果

scores = [r for r in scores if r[1] != None]

# 按误差升序排序配置

scores.sort(key=lambda tup: tup[1])

返回分数

# 创建一组要尝试的 sarima 配置

def sarima_configs(seasonal=[0]):

models = list()

# 定义配置列表

p_params = [0, 1, 2]

d_params = [0, 1]

q_params = [0, 1, 2]

t_params = ['n','c','t','ct']

P_params = [0, 1, 2]

D_params = [0, 1]

Q_params = [0, 1, 2]

m_params = seasonal

# 创建配置实例

for p in p_params:

for d in d_params:

for q in q_params:

for t in t_params:

for P in P_params:

for D in D_params:

for Q in Q_params:

for m in m_params:

cfg = [(p,d,q), (P,D,Q,m), t]

models.append(cfg)

return models

if __name__ == '__main__':

# 定义数据集

data = [10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0]

print(data)

# 数据分割

n_test = 4

# 模型配置

cfg_list = sarima_configs()

# 网格搜索

scores = grid_search(data, cfg_list, n_test)

print('完成')

# 列出前 3 个配置

for cfg, error in scores[:3]:

print(cfg, error)

运行示例首先打印人工生成的时间序列数据集。

接下来，模型配置及其误差在评估时会报告，为简洁起见，下文已截断。

最后，报告了前三个配置的配置和误差。我们可以看到，许多模型在这个简单的线性递增人工时间序列问题上实现了完美的性能。

[10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0]

...
 > Model[[(2, 0, 0), (2, 0, 0, 0), 'ct']] 0.001
 > Model[[(2, 0, 0), (2, 0, 1, 0), 'ct']] 0.000
 > Model[[(2, 0, 1), (0, 0, 0, 0), 'n']] 0.000
 > Model[[(2, 0, 1), (0, 0, 1, 0), 'n']] 0.000
done

[(2, 1, 0), (1, 0, 0, 0), 'n'] 0.0
[(2, 1, 0), (2, 0, 0, 0), 'n'] 0.0
[(2, 1, 1), (1, 0, 1, 0), 'n'] 0.0

[10.0, 20.0, 30.0, 40.0, 50.0, 60.0, 70.0, 80.0, 90.0, 100.0]

...

> 模型[[(2, 0, 0), (2, 0, 0, 0), 'ct']] 0.001

> 模型[[(2, 0, 0), (2, 0, 1, 0), 'ct']] 0.000

> 模型[[(2, 0, 1), (0, 0, 0, 0), 'n']] 0.000

> 模型[[(2, 0, 1), (0, 0, 1, 0), 'n']] 0.000

完成

[(2, 1, 0), (1, 0, 0, 0), 'n'] 0.0

[(2, 1, 0), (2, 0, 0, 0), 'n'] 0.0

[(2, 1, 1), (1, 0, 1, 0), 'n'] 0.0

现在我们有了一个对 SARIMA 模型超参数进行网格搜索的稳健框架，让我们在标准单变量时间序列数据集套件上测试它。

这些数据集是用于演示目的而选择的；我并不是说 SARIMA 模型是每个数据集的最佳方法；在某些情况下，ETS 或其他方法可能更合适。

案例研究 1：无趋势或季节性

“每日女性出生人数”数据集汇总了 1959 年美国加利福尼亚州每日女性出生总数。

该数据集没有明显的趋势或季节性成分。

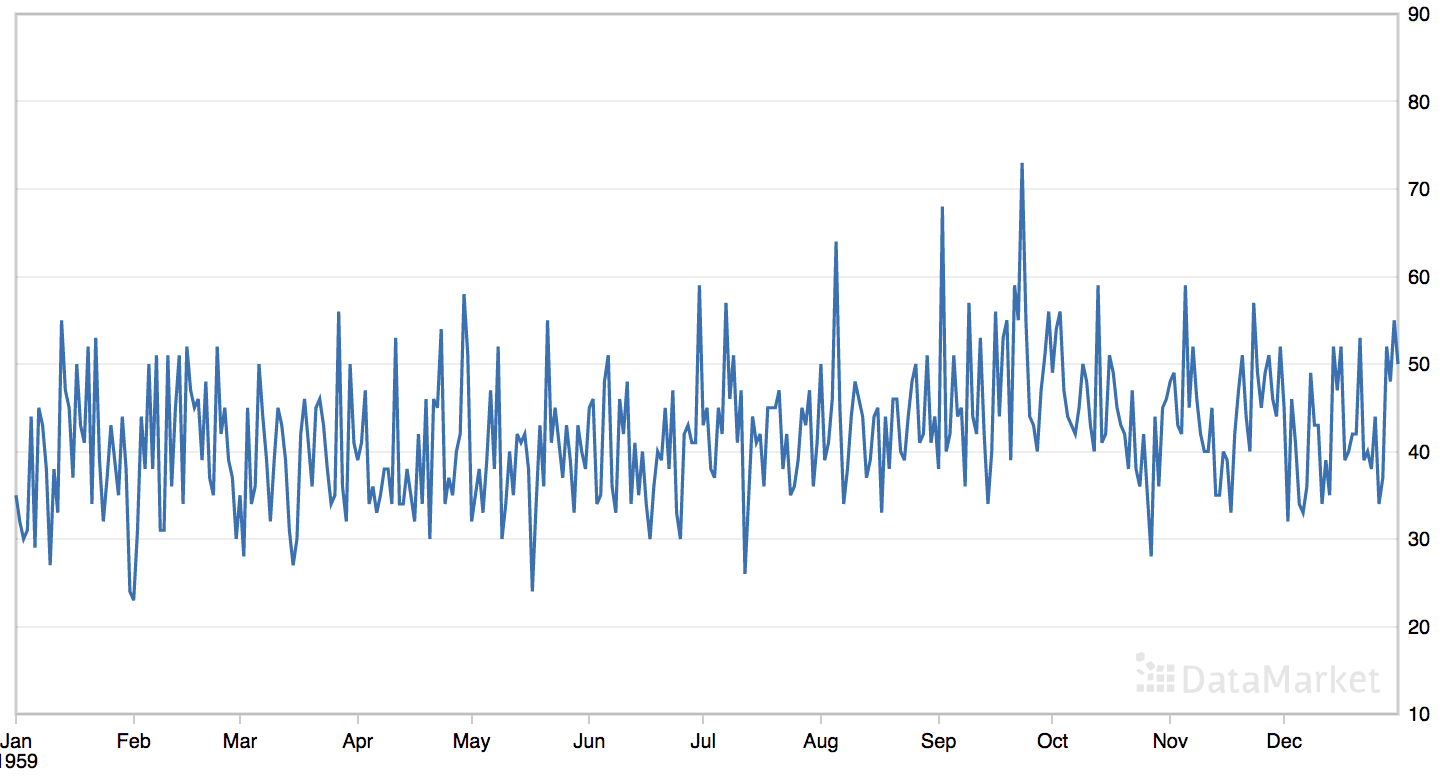
Line Plot of the Daily Female Births Dataset

每日女性出生人数数据集的线图

直接从这里下载数据集

daily-total-female-births.csv

将文件保存为“_daily-total-female-births.csv_”在当前工作目录中。

我们可以使用 *read_csv()* 函数将此数据集加载为 Pandas 序列。

series = read_csv('daily-total-female-births.csv', header=0, index_col=0)

1	series = read_csv('daily-total-female-births.csv', header=0, index_col=0)

数据集有一年，即 365 个观测值。我们将使用前 200 个进行训练，其余 165 个作为测试集。

下面列出了对每日女性单变量时间序列预测问题进行网格搜索的完整示例。

# grid search sarima hyperparameters for daily female dataset
from math import sqrt
from multiprocessing import cpu_count
from joblib import Parallel
from joblib import delayed
from warnings import catch_warnings
from warnings import filterwarnings
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.metrics import mean_squared_error
from pandas import read_csv

# one-step sarima forecast
def sarima_forecast(history, config):
	order, sorder, trend = config
	# define model
	model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)
	# fit model
	model_fit = model.fit(disp=False)
	# make one step forecast
	yhat = model_fit.predict(len(history), len(history))
	return yhat[0]

# root mean squared error or rmse
def measure_rmse(actual, predicted):
	return sqrt(mean_squared_error(actual, predicted))

# split a univariate dataset into train/test sets
def train_test_split(data, n_test):
	return data[:-n_test], data[-n_test:]

# walk-forward validation for univariate data
def walk_forward_validation(data, n_test, cfg):
	predictions = list()
	# split dataset
	train, test = train_test_split(data, n_test)
	# seed history with training dataset
	history = [x for x in train]
	# step over each time-step in the test set
	for i in range(len(test)):
		# fit model and make forecast for history
		yhat = sarima_forecast(history, cfg)
		# store forecast in list of predictions
		predictions.append(yhat)
		# add actual observation to history for the next loop
		history.append(test[i])
	# estimate prediction error
	error = measure_rmse(test, predictions)
	return error

# score a model, return None on failure
def score_model(data, n_test, cfg, debug=False):
	result = None
	# convert config to a key
	key = str(cfg)
	# show all warnings and fail on exception if debugging
	if debug:
		result = walk_forward_validation(data, n_test, cfg)
	else:
		# one failure during model validation suggests an unstable config
		try:
			# never show warnings when grid searching, too noisy
			with catch_warnings():
				filterwarnings("ignore")
				result = walk_forward_validation(data, n_test, cfg)
		except:
			error = None
	# check for an interesting result
	if result is not None:
		print(' > Model[%s] %.3f' % (key, result))
	return (key, result)

# grid search configs
def grid_search(data, cfg_list, n_test, parallel=True):
	scores = None
	if parallel:
		# execute configs in parallel
		executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')
		tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)
		scores = executor(tasks)
	else:
		scores = [score_model(data, n_test, cfg) for cfg in cfg_list]
	# remove empty results
	scores = [r for r in scores if r[1] != None]
	# sort configs by error, asc
	scores.sort(key=lambda tup: tup[1])
	return scores

# create a set of sarima configs to try
def sarima_configs(seasonal=[0]):
	models = list()
	# define config lists
	p_params = [0, 1, 2]
	d_params = [0, 1]
	q_params = [0, 1, 2]
	t_params = ['n','c','t','ct']
	P_params = [0, 1, 2]
	D_params = [0, 1]
	Q_params = [0, 1, 2]
	m_params = seasonal
	# create config instances
	for p in p_params:
		for d in d_params:
			for q in q_params:
				for t in t_params:
					for P in P_params:
						for D in D_params:
							for Q in Q_params:
								for m in m_params:
									cfg = [(p,d,q), (P,D,Q,m), t]
									models.append(cfg)
	return models

if __name__ == '__main__':
	# load dataset
	series = read_csv('daily-total-female-births.csv', header=0, index_col=0)
	data = series.values
	print(data.shape)
	# data split
	n_test = 165
	# model configs
	cfg_list = sarima_configs()
	# grid search
	scores = grid_search(data, cfg_list, n_test)
	print('done')
	# list top 3 configs
	for cfg, error in scores[:3]:
		print(cfg, error)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

# 对每日女性数据集的 sarima 超参数进行网格搜索

from math import sqrt

from multiprocessing import cpu_count

from joblib import Parallel

from joblib import delayed

from warnings import catch_warnings

from warnings import filterwarnings

from statsmodels.tsa.statespace.sarimax import SARIMAX

from sklearn.metrics import mean_squared_error

from pandas import read_csv

# 一步 SARIMA 预测

def sarima_forecast(history, config):

order, sorder, trend = config

# 定义模型

model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)

# 拟合模型

model_fit = model.fit(disp=False)

# 进行一步预测

yhat = model_fit.predict(len(history), len(history))

return yhat[0]

# 均方根误差或 RMSE

def measure_rmse(actual, predicted):

return sqrt(mean_squared_error(actual, predicted))

# 将单变量数据集拆分为训练/测试集

def train_test_split(data, n_test):

return data[:-n_test], data[-n_test:]

# 单变量数据的滚动预测验证

def walk_forward_validation(data, n_test, cfg):

predictions = list()

# 拆分数据集

train, test = train_test_split(data, n_test)

# 用训练数据集初始化历史数据

history = [x for x in train]

# 遍历测试集中的每个时间步

for i in range(len(test)):

# 拟合模型并对历史数据进行预测

yhat = sarima_forecast(history, cfg)

# 将预测结果存储在预测列表中

predictions.append(yhat)

# 将实际观测值添加到历史数据中以进行下一次循环

history.append(test[i])

# 估计预测误差

error = measure_rmse(test, predictions)

return error

# 评估模型，失败时返回 None

def score_model(data, n_test, cfg, debug=False):

result = None

# 将配置转换为键

key = str(cfg)

# 如果在调试，则显示所有警告并在异常时失败

if debug:

result = walk_forward_validation(data, n_test, cfg)

else:

# 模型验证过程中的一次失败表明配置不稳定

try:

# 网格搜索时从不显示警告，太嘈杂

with catch_warnings():

filterwarnings("ignore")

result = walk_forward_validation(data, n_test, cfg)

except:

error = None

# 检查是否有有趣的结果

if result is not None:

print(' > Model[%s] %.3f' % (key, result))

return (key, result)

# 网格搜索配置

def grid_search(data, cfg_list, n_test, parallel=True):

scores = None

if parallel:

# 并行执行配置

executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')

tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)

scores = executor(tasks)

else:

scores = [score_model(data, n_test, cfg) for cfg in cfg_list]

# 移除空结果

scores = [r for r in scores if r[1] != None]

# 按误差升序排序配置

scores.sort(key=lambda tup: tup[1])

返回分数

# 创建一组要尝试的 sarima 配置

def sarima_configs(seasonal=[0]):

models = list()

# 定义配置列表

p_params = [0, 1, 2]

d_params = [0, 1]

q_params = [0, 1, 2]

t_params = ['n','c','t','ct']

P_params = [0, 1, 2]

D_params = [0, 1]

Q_params = [0, 1, 2]

m_params = seasonal

# 创建配置实例

for p in p_params:

for d in d_params:

for q in q_params:

for t in t_params:

for P in P_params:

for D in D_params:

for Q in Q_params:

for m in m_params:

cfg = [(p,d,q), (P,D,Q,m), t]

models.append(cfg)

return models

if __name__ == '__main__':

# 加载数据集

series = read_csv('daily-total-female-births.csv', header=0, index_col=0)

data = series.values

print(data.shape)

# 数据分割

n_test = 165

# 模型配置

cfg_list = sarima_configs()

# 网格搜索

scores = grid_search(data, cfg_list, n_test)

print('完成')

# 列出前 3 个配置

for cfg, error in scores[:3]:

print(cfg, error)

在现代硬件上运行该示例可能需要几分钟。

模型配置和 RMSE 在模型评估时打印。运行结束时报告前三个模型配置及其误差。

**注意**：由于算法或评估过程的随机性，或数值精度的差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

我们可以看到，最佳结果是 RMSE 约为 6.77 次出生，配置如下

顺序: (1, 0, 2)
季节性顺序: (1, 0, 1, 0)
**趋势参数**：“t”表示线性趋势

令人惊讶的是，包含一些季节性元素的配置导致了最低的误差。我不会猜到这种配置，很可能只会使用 ARIMA 模型。

...
> Model[[(2, 1, 2), (1, 0, 1, 0), 'ct']] 6.905
> Model[[(2, 1, 2), (2, 0, 0, 0), 'ct']] 7.031
> Model[[(2, 1, 2), (2, 0, 1, 0), 'ct']] 6.985
> Model[[(2, 1, 2), (1, 0, 2, 0), 'ct']] 6.941
> Model[[(2, 1, 2), (2, 0, 2, 0), 'ct']] 7.056
done

[(1, 0, 2), (1, 0, 1, 0), 't'] 6.770349800255089
[(0, 1, 2), (1, 0, 2, 0), 'ct'] 6.773217122759515
[(2, 1, 1), (2, 0, 2, 0), 'ct'] 6.886633191752254

...

> 模型[[(2, 1, 2), (1, 0, 1, 0), 'ct']] 6.905

> 模型[[(2, 1, 2), (2, 0, 0, 0), 'ct']] 7.031

> 模型[[(2, 1, 2), (2, 0, 1, 0), 'ct']] 6.985

> 模型[[(2, 1, 2), (1, 0, 2, 0), 'ct']] 6.941

> 模型[[(2, 1, 2), (2, 0, 2, 0), 'ct']] 7.056

完成

[(1, 0, 2), (1, 0, 1, 0), 't'] 6.770349800255089

[(0, 1, 2), (1, 0, 2, 0), 'ct'] 6.773217122759515

[(2, 1, 1), (2, 0, 2, 0), 'ct'] 6.886633191752254

案例研究 2：趋势

“洗发水”数据集汇总了三年期间洗发水的月销售额。

该数据集包含一个明显的趋势，但没有明显的季节性成分。

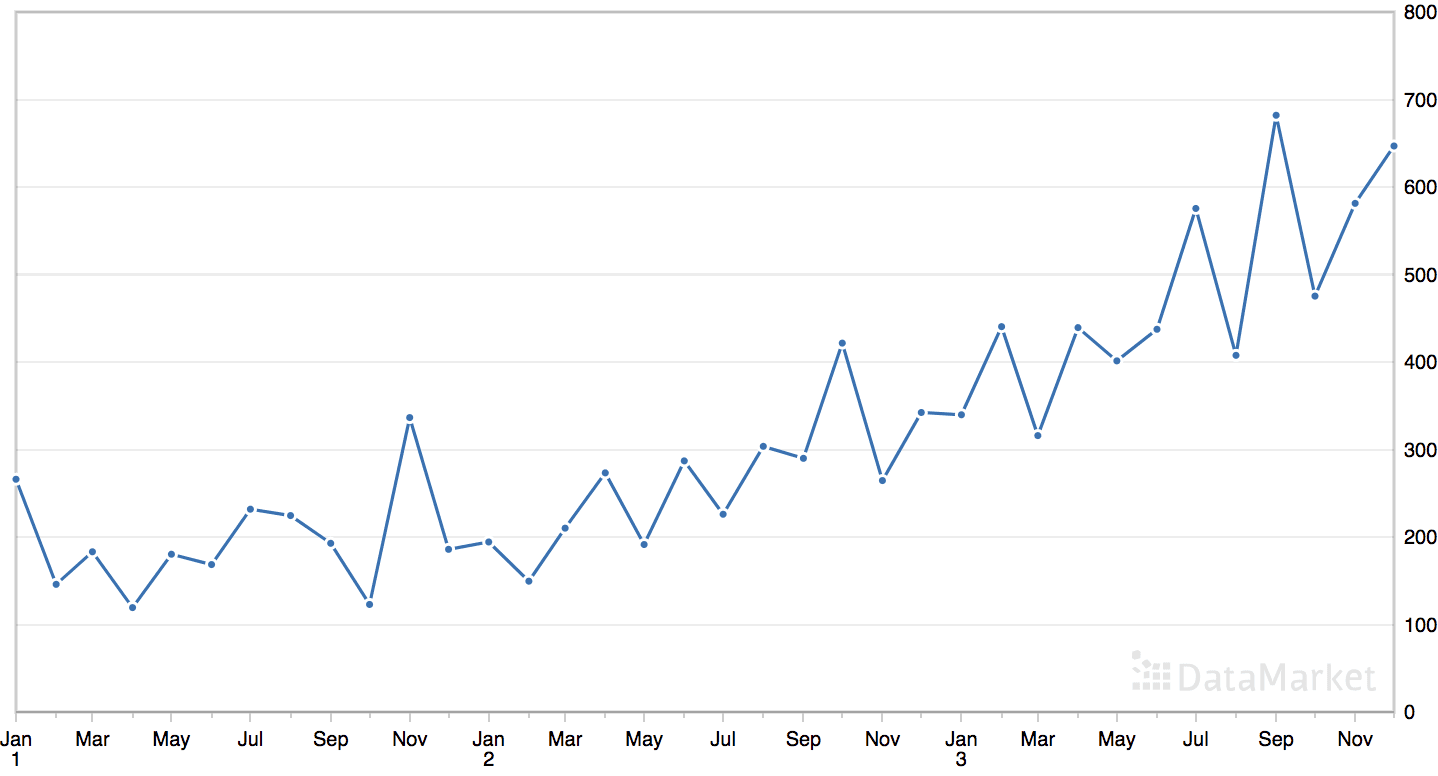
Line Plot of the Monthly Shampoo Sales Dataset

月度洗发水销售数据集的线图

直接从这里下载数据集

shampoo.csv

将文件保存为“shampoo.csv”在当前工作目录中。

我们可以使用 *read_csv()* 函数将此数据集加载为 Pandas 序列。

# parse dates
def custom_parser(x):
	return datetime.strptime('195'+x, '%Y-%m')

# load dataset
series = read_csv('shampoo.csv', header=0, index_col=0, date_parser=custom_parser)

# 解析日期

def custom_parser(x):

return datetime.strptime('195'+x, '%Y-%m')

# 加载数据集

series = read_csv('shampoo.csv', header=0, index_col=0, date_parser=custom_parser)

数据集有三年，即 36 个观测值。我们将使用前 24 个进行训练，其余 12 个作为测试集。

下面列出了对洗发水销售单变量时间序列预测问题进行网格搜索的完整示例。

# grid search sarima hyperparameters for monthly shampoo sales dataset
from math import sqrt
from multiprocessing import cpu_count
from joblib import Parallel
from joblib import delayed
from warnings import catch_warnings
from warnings import filterwarnings
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.metrics import mean_squared_error
from pandas import read_csv
from pandas import datetime

# one-step sarima forecast
def sarima_forecast(history, config):
	order, sorder, trend = config
	# define model
	model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)
	# fit model
	model_fit = model.fit(disp=False)
	# make one step forecast
	yhat = model_fit.predict(len(history), len(history))
	return yhat[0]

# root mean squared error or rmse
def measure_rmse(actual, predicted):
	return sqrt(mean_squared_error(actual, predicted))

# split a univariate dataset into train/test sets
def train_test_split(data, n_test):
	return data[:-n_test], data[-n_test:]

# walk-forward validation for univariate data
def walk_forward_validation(data, n_test, cfg):
	predictions = list()
	# split dataset
	train, test = train_test_split(data, n_test)
	# seed history with training dataset
	history = [x for x in train]
	# step over each time-step in the test set
	for i in range(len(test)):
		# fit model and make forecast for history
		yhat = sarima_forecast(history, cfg)
		# store forecast in list of predictions
		predictions.append(yhat)
		# add actual observation to history for the next loop
		history.append(test[i])
	# estimate prediction error
	error = measure_rmse(test, predictions)
	return error

# score a model, return None on failure
def score_model(data, n_test, cfg, debug=False):
	result = None
	# convert config to a key
	key = str(cfg)
	# show all warnings and fail on exception if debugging
	if debug:
		result = walk_forward_validation(data, n_test, cfg)
	else:
		# one failure during model validation suggests an unstable config
		try:
			# never show warnings when grid searching, too noisy
			with catch_warnings():
				filterwarnings("ignore")
				result = walk_forward_validation(data, n_test, cfg)
		except:
			error = None
	# check for an interesting result
	if result is not None:
		print(' > Model[%s] %.3f' % (key, result))
	return (key, result)

# grid search configs
def grid_search(data, cfg_list, n_test, parallel=True):
	scores = None
	if parallel:
		# execute configs in parallel
		executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')
		tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)
		scores = executor(tasks)
	else:
		scores = [score_model(data, n_test, cfg) for cfg in cfg_list]
	# remove empty results
	scores = [r for r in scores if r[1] != None]
	# sort configs by error, asc
	scores.sort(key=lambda tup: tup[1])
	return scores

# create a set of sarima configs to try
def sarima_configs(seasonal=[0]):
	models = list()
	# define config lists
	p_params = [0, 1, 2]
	d_params = [0, 1]
	q_params = [0, 1, 2]
	t_params = ['n','c','t','ct']
	P_params = [0, 1, 2]
	D_params = [0, 1]
	Q_params = [0, 1, 2]
	m_params = seasonal
	# create config instances
	for p in p_params:
		for d in d_params:
			for q in q_params:
				for t in t_params:
					for P in P_params:
						for D in D_params:
							for Q in Q_params:
								for m in m_params:
									cfg = [(p,d,q), (P,D,Q,m), t]
									models.append(cfg)
	return models


# parse dates
def custom_parser(x):
	return datetime.strptime('195'+x, '%Y-%m')

if __name__ == '__main__':
	# load dataset
	series = read_csv('shampoo.csv', header=0, index_col=0, date_parser=custom_parser)
	data = series.values
	print(data.shape)
	# data split
	n_test = 12
	# model configs
	cfg_list = sarima_configs()
	# grid search
	scores = grid_search(data, cfg_list, n_test)
	print('done')
	# list top 3 configs
	for cfg, error in scores[:3]:
		print(cfg, error)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

# 对月度洗发水销售数据集的 sarima 超参数进行网格搜索

from math import sqrt

from multiprocessing import cpu_count

from joblib import Parallel

from joblib import delayed

from warnings import catch_warnings

from warnings import filterwarnings

from statsmodels.tsa.statespace.sarimax import SARIMAX

from sklearn.metrics import mean_squared_error

from pandas import read_csv

from pandas import datetime

# 一步 SARIMA 预测

def sarima_forecast(history, config):

order, sorder, trend = config

# 定义模型

model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)

# 拟合模型

model_fit = model.fit(disp=False)

# 进行一步预测

yhat = model_fit.predict(len(history), len(history))

return yhat[0]

# 均方根误差或 RMSE

def measure_rmse(actual, predicted):

return sqrt(mean_squared_error(actual, predicted))

# 将单变量数据集拆分为训练/测试集

def train_test_split(data, n_test):

return data[:-n_test], data[-n_test:]

# 单变量数据的滚动预测验证

def walk_forward_validation(data, n_test, cfg):

predictions = list()

# 拆分数据集

train, test = train_test_split(data, n_test)

# 用训练数据集初始化历史数据

history = [x for x in train]

# 遍历测试集中的每个时间步

for i in range(len(test)):

# 拟合模型并对历史数据进行预测

yhat = sarima_forecast(history, cfg)

# 将预测结果存储在预测列表中

predictions.append(yhat)

# 将实际观测值添加到历史数据中以进行下一次循环

history.append(test[i])

# 估计预测误差

error = measure_rmse(test, predictions)

return error

# 评估模型，失败时返回 None

def score_model(data, n_test, cfg, debug=False):

result = None

# 将配置转换为键

key = str(cfg)

# 如果在调试，则显示所有警告并在异常时失败

if debug:

result = walk_forward_validation(data, n_test, cfg)

else:

# 模型验证过程中的一次失败表明配置不稳定

try:

# 网格搜索时从不显示警告，太嘈杂

with catch_warnings():

filterwarnings("ignore")

result = walk_forward_validation(data, n_test, cfg)

except:

error = None

# 检查是否有有趣的结果

if result is not None:

print(' > Model[%s] %.3f' % (key, result))

return (key, result)

# 网格搜索配置

def grid_search(data, cfg_list, n_test, parallel=True):

scores = None

if parallel:

# 并行执行配置

executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')

tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)

scores = executor(tasks)

else:

scores = [score_model(data, n_test, cfg) for cfg in cfg_list]

# 移除空结果

scores = [r for r in scores if r[1] != None]

# 按误差升序排序配置

scores.sort(key=lambda tup: tup[1])

返回分数

# 创建一组要尝试的 sarima 配置

def sarima_configs(seasonal=[0]):

models = list()

# 定义配置列表

p_params = [0, 1, 2]

d_params = [0, 1]

q_params = [0, 1, 2]

t_params = ['n','c','t','ct']

P_params = [0, 1, 2]

D_params = [0, 1]

Q_params = [0, 1, 2]

m_params = seasonal

# 创建配置实例

for p in p_params:

for d in d_params:

for q in q_params:

for t in t_params:

for P in P_params:

for D in D_params:

for Q in Q_params:

for m in m_params:

cfg = [(p,d,q), (P,D,Q,m), t]

models.append(cfg)

返回模型

# 解析日期

def custom_parser(x):

return datetime.strptime('195'+x, '%Y-%m')

if __name__ == '__main__':

# 加载数据集

series = read_csv('shampoo.csv', header=0, index_col=0, date_parser=custom_parser)

data = series.values

print(data.shape)

# 数据分割

n_test = 12

# 模型配置

cfg_list = sarima_configs()

# 网格搜索

scores = grid_search(data, cfg_list, n_test)

print('完成')

# 列出前 3 个配置

for cfg, error in scores[:3]:

print(cfg, error)

在现代硬件上运行该示例可能需要几分钟。

模型配置和 RMSE 在模型评估时打印。运行结束时报告前三个模型配置及其误差。

**注意**：由于算法或评估过程的随机性，或数值精度的差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

我们可以看到，最佳结果是 RMSE 约为 54.76 销售额，配置如下

趋势订单: (0, 1, 2)
季节性顺序: (2, 0, 2, 0)
**趋势参数**：“t”（线性趋势）

...
> Model[[(2, 1, 2), (1, 0, 1, 0), 'ct']] 68.891
> Model[[(2, 1, 2), (2, 0, 0, 0), 'ct']] 75.406
> Model[[(2, 1, 2), (1, 0, 2, 0), 'ct']] 80.908
> Model[[(2, 1, 2), (2, 0, 1, 0), 'ct']] 78.734
> Model[[(2, 1, 2), (2, 0, 2, 0), 'ct']] 82.958
done
[(0, 1, 2), (2, 0, 2, 0), 't'] 54.767582003072874
[(0, 1, 1), (2, 0, 2, 0), 'ct'] 58.69987083057107
[(1, 1, 2), (0, 0, 1, 0), 't'] 58.709089340600094

...

> 模型[[(2, 1, 2), (1, 0, 1, 0), 'ct']] 68.891

> 模型[[(2, 1, 2), (2, 0, 0, 0), 'ct']] 75.406

> 模型[[(2, 1, 2), (1, 0, 2, 0), 'ct']] 80.908

> 模型[[(2, 1, 2), (2, 0, 1, 0), 'ct']] 78.734

> 模型[[(2, 1, 2), (2, 0, 2, 0), 'ct']] 82.958

完成

[(0, 1, 2), (2, 0, 2, 0), 't'] 54.767582003072874

[(0, 1, 1), (2, 0, 2, 0), 'ct'] 58.69987083057107

[(1, 1, 2), (0, 0, 1, 0), 't'] 58.709089340600094

案例研究 3：季节性

“月平均气温”数据集总结了 1920 年至 1939 年间英国诺丁汉城堡的月平均气温（华氏度）。

该数据集具有明显的季节性成分，但没有明显的趋势。

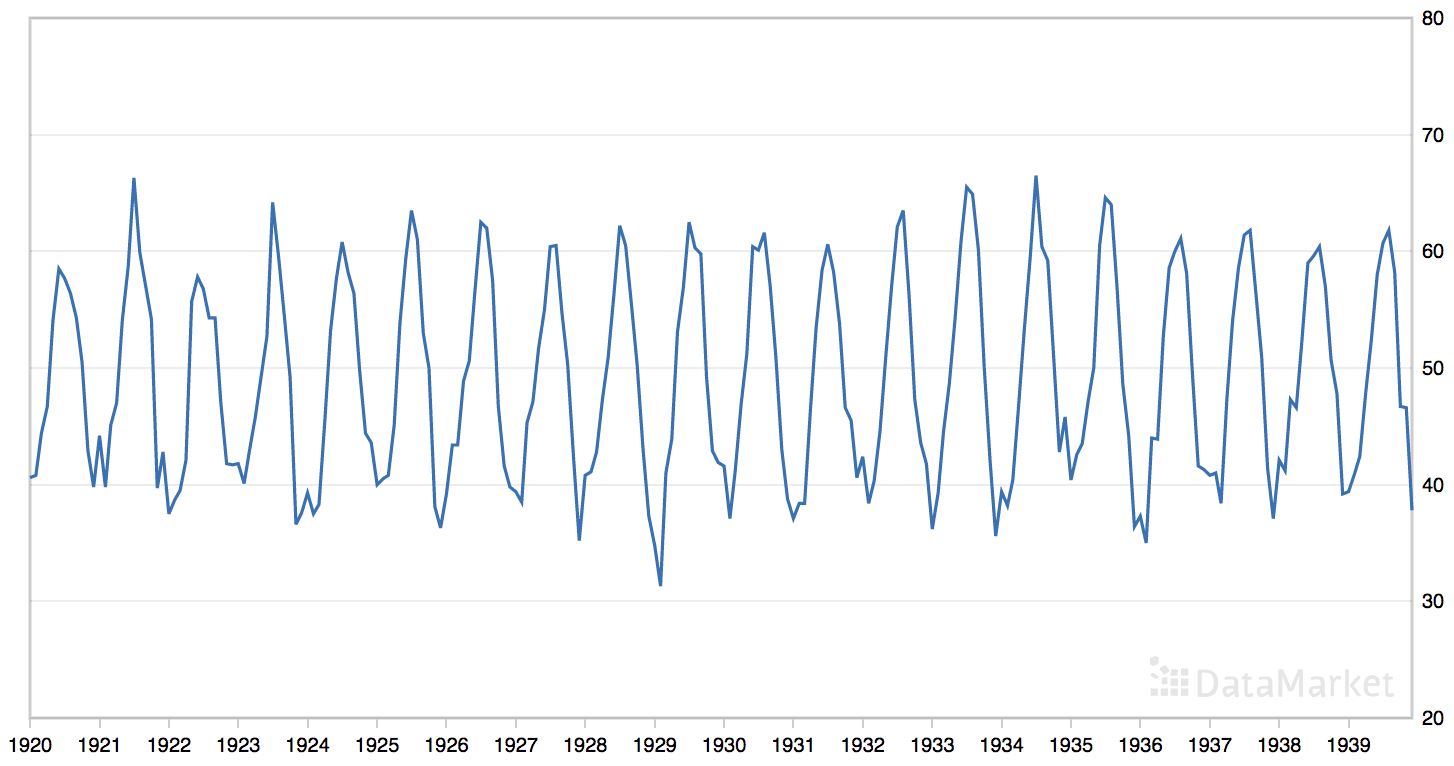
Line Plot of the Monthly Mean Temperatures Dataset

月平均气温数据集的线图

直接从这里下载数据集

monthly-mean-temp.csv

将文件保存为“_monthly-mean-temp.csv_”在当前工作目录中。

我们可以使用 *read_csv()* 函数将此数据集加载为 Pandas 序列。

series = read_csv('monthly-mean-temp.csv', header=0, index_col=0)

1	series = read_csv('monthly-mean-temp.csv', header=0, index_col=0)

数据集包含 20 年，即 240 个观测值。我们将数据集裁剪到最近五年的数据（60 个观测值），以加快模型评估过程，并使用最近一年（即 12 个观测值）作为测试集。

# trim dataset to 5 years
data = data[-(5*12):]

1 2	# 将数据集裁剪为 5 年 data = data[-(5*12):]

季节性成分的周期约为一年，即 12 个观测值。在准备模型配置时，我们将此作为 *sarima_configs()* 函数调用中的季节性周期。

# model configs
cfg_list = sarima_configs(seasonal=[0, 12])

1 2	# 模型配置 cfg_list = sarima_configs(seasonal=[0, 12])

下面列出了对月平均气温时间序列预测问题进行网格搜索的完整示例。

# grid search sarima hyperparameters for monthly mean temp dataset
from math import sqrt
from multiprocessing import cpu_count
from joblib import Parallel
from joblib import delayed
from warnings import catch_warnings
from warnings import filterwarnings
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.metrics import mean_squared_error
from pandas import read_csv

# one-step sarima forecast
def sarima_forecast(history, config):
	order, sorder, trend = config
	# define model
	model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)
	# fit model
	model_fit = model.fit(disp=False)
	# make one step forecast
	yhat = model_fit.predict(len(history), len(history))
	return yhat[0]

# root mean squared error or rmse
def measure_rmse(actual, predicted):
	return sqrt(mean_squared_error(actual, predicted))

# split a univariate dataset into train/test sets
def train_test_split(data, n_test):
	return data[:-n_test], data[-n_test:]

# walk-forward validation for univariate data
def walk_forward_validation(data, n_test, cfg):
	predictions = list()
	# split dataset
	train, test = train_test_split(data, n_test)
	# seed history with training dataset
	history = [x for x in train]
	# step over each time-step in the test set
	for i in range(len(test)):
		# fit model and make forecast for history
		yhat = sarima_forecast(history, cfg)
		# store forecast in list of predictions
		predictions.append(yhat)
		# add actual observation to history for the next loop
		history.append(test[i])
	# estimate prediction error
	error = measure_rmse(test, predictions)
	return error

# score a model, return None on failure
def score_model(data, n_test, cfg, debug=False):
	result = None
	# convert config to a key
	key = str(cfg)
	# show all warnings and fail on exception if debugging
	if debug:
		result = walk_forward_validation(data, n_test, cfg)
	else:
		# one failure during model validation suggests an unstable config
		try:
			# never show warnings when grid searching, too noisy
			with catch_warnings():
				filterwarnings("ignore")
				result = walk_forward_validation(data, n_test, cfg)
		except:
			error = None
	# check for an interesting result
	if result is not None:
		print(' > Model[%s] %.3f' % (key, result))
	return (key, result)

# grid search configs
def grid_search(data, cfg_list, n_test, parallel=True):
	scores = None
	if parallel:
		# execute configs in parallel
		executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')
		tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)
		scores = executor(tasks)
	else:
		scores = [score_model(data, n_test, cfg) for cfg in cfg_list]
	# remove empty results
	scores = [r for r in scores if r[1] != None]
	# sort configs by error, asc
	scores.sort(key=lambda tup: tup[1])
	return scores

# create a set of sarima configs to try
def sarima_configs(seasonal=[0]):
	models = list()
	# define config lists
	p_params = [0, 1, 2]
	d_params = [0, 1]
	q_params = [0, 1, 2]
	t_params = ['n','c','t','ct']
	P_params = [0, 1, 2]
	D_params = [0, 1]
	Q_params = [0, 1, 2]
	m_params = seasonal
	# create config instances
	for p in p_params:
		for d in d_params:
			for q in q_params:
				for t in t_params:
					for P in P_params:
						for D in D_params:
							for Q in Q_params:
								for m in m_params:
									cfg = [(p,d,q), (P,D,Q,m), t]
									models.append(cfg)
	return models

if __name__ == '__main__':
	# load dataset
	series = read_csv('monthly-mean-temp.csv', header=0, index_col=0)
	data = series.values
	# trim dataset to 5 years
	data = data[-(5*12):]
	# data split
	n_test = 12
	# model configs
	cfg_list = sarima_configs(seasonal=[0, 12])
	# grid search
	scores = grid_search(data, cfg_list, n_test)
	print('done')
	# list top 3 configs
	for cfg, error in scores[:3]:
		print(cfg, error)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

# 对月平均气温数据集的 sarima 超参数进行网格搜索

from math import sqrt

from multiprocessing import cpu_count

from joblib import Parallel

from joblib import delayed

from warnings import catch_warnings

from warnings import filterwarnings

from statsmodels.tsa.statespace.sarimax import SARIMAX

from sklearn.metrics import mean_squared_error

from pandas import read_csv

# 一步 SARIMA 预测

def sarima_forecast(history, config):

order, sorder, trend = config

# 定义模型

model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)

# 拟合模型

model_fit = model.fit(disp=False)

# 进行一步预测

yhat = model_fit.predict(len(history), len(history))

return yhat[0]

# 均方根误差或 RMSE

def measure_rmse(actual, predicted):

return sqrt(mean_squared_error(actual, predicted))

# 将单变量数据集拆分为训练/测试集

def train_test_split(data, n_test):

return data[:-n_test], data[-n_test:]

# 单变量数据的滚动预测验证

def walk_forward_validation(data, n_test, cfg):

predictions = list()

# 拆分数据集

train, test = train_test_split(data, n_test)

# 用训练数据集初始化历史数据

history = [x for x in train]

# 遍历测试集中的每个时间步

for i in range(len(test)):

# 拟合模型并对历史数据进行预测

yhat = sarima_forecast(history, cfg)

# 将预测结果存储在预测列表中

predictions.append(yhat)

# 将实际观测值添加到历史数据中以进行下一次循环

history.append(test[i])

# 估计预测误差

error = measure_rmse(test, predictions)

return error

# 评估模型，失败时返回 None

def score_model(data, n_test, cfg, debug=False):

result = None

# 将配置转换为键

key = str(cfg)

# 如果在调试，则显示所有警告并在异常时失败

if debug:

result = walk_forward_validation(data, n_test, cfg)

else:

# 模型验证过程中的一次失败表明配置不稳定

try:

# 网格搜索时从不显示警告，太嘈杂

with catch_warnings():

filterwarnings("ignore")

result = walk_forward_validation(data, n_test, cfg)

except:

error = None

# 检查是否有有趣的结果

if result is not None:

print(' > Model[%s] %.3f' % (key, result))

return (key, result)

# 网格搜索配置

def grid_search(data, cfg_list, n_test, parallel=True):

scores = None

if parallel:

# 并行执行配置

executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')

tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)

scores = executor(tasks)

else:

scores = [score_model(data, n_test, cfg) for cfg in cfg_list]

# 移除空结果

scores = [r for r in scores if r[1] != None]

# 按误差升序排序配置

scores.sort(key=lambda tup: tup[1])

返回分数

# 创建一组要尝试的 sarima 配置

def sarima_configs(seasonal=[0]):

models = list()

# 定义配置列表

p_params = [0, 1, 2]

d_params = [0, 1]

q_params = [0, 1, 2]

t_params = ['n','c','t','ct']

P_params = [0, 1, 2]

D_params = [0, 1]

Q_params = [0, 1, 2]

m_params = seasonal

# 创建配置实例

for p in p_params:

for d in d_params:

for q in q_params:

for t in t_params:

for P in P_params:

for D in D_params:

for Q in Q_params:

for m in m_params:

cfg = [(p,d,q), (P,D,Q,m), t]

models.append(cfg)

return models

if __name__ == '__main__':

# 加载数据集

series = read_csv('monthly-mean-temp.csv', header=0, index_col=0)

data = series.values

# 将数据集裁剪为 5 年

data = data[-(5*12):]

# 数据分割

n_test = 12

# 模型配置

cfg_list = sarima_configs(seasonal=[0, 12])

# 网格搜索

scores = grid_search(data, cfg_list, n_test)

print('完成')

# 列出前 3 个配置

for cfg, error in scores[:3]:

print(cfg, error)

在现代硬件上运行该示例可能需要几分钟。

模型配置和 RMSE 在模型评估时打印。运行结束时报告前三个模型配置及其误差。

**注意**：由于算法或评估过程的随机性，或数值精度的差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

我们可以看到，最佳结果是 RMSE 约为 1.5 度，配置如下

趋势订单: (0, 0, 0)
季节性顺序: (1, 0, 1, 12)
**趋势参数**：“n”（无趋势）

正如我们所预期的，该模型没有趋势成分，并具有一个 12 个月季节性 ARMA 成分。

...
> Model[[(2, 1, 2), (2, 1, 0, 12), 't']] 4.599
> Model[[(2, 1, 2), (1, 1, 0, 12), 'ct']] 2.477
> Model[[(2, 1, 2), (2, 0, 0, 12), 'ct']] 2.548
> Model[[(2, 1, 2), (2, 0, 1, 12), 'ct']] 2.893
> Model[[(2, 1, 2), (2, 1, 0, 12), 'ct']] 5.404
done

[(0, 0, 0), (1, 0, 1, 12), 'n'] 1.5577613610905712
[(0, 0, 0), (1, 1, 0, 12), 'n'] 1.6469530713847962
[(0, 0, 0), (2, 0, 0, 12), 'n'] 1.7314448163607488

...

> 模型[[(2, 1, 2), (2, 1, 0, 12), 't']] 4.599

> 模型[[(2, 1, 2), (1, 1, 0, 12), 'ct']] 2.477

> 模型[[(2, 1, 2), (2, 0, 0, 12), 'ct']] 2.548

> 模型[[(2, 1, 2), (2, 0, 1, 12), 'ct']] 2.893

> 模型[[(2, 1, 2), (2, 1, 0, 12), 'ct']] 5.404

完成

[(0, 0, 0), (1, 0, 1, 12), 'n'] 1.5577613610905712

[(0, 0, 0), (1, 1, 0, 12), 'n'] 1.6469530713847962

[(0, 0, 0), (2, 0, 0, 12), 'n'] 1.7314448163607488

案例研究 4：趋势和季节性

“月度汽车销量”数据集总结了 1960 年至 1968 年间加拿大魁北克的月度汽车销量。

该数据集具有明显的趋势和季节性成分。

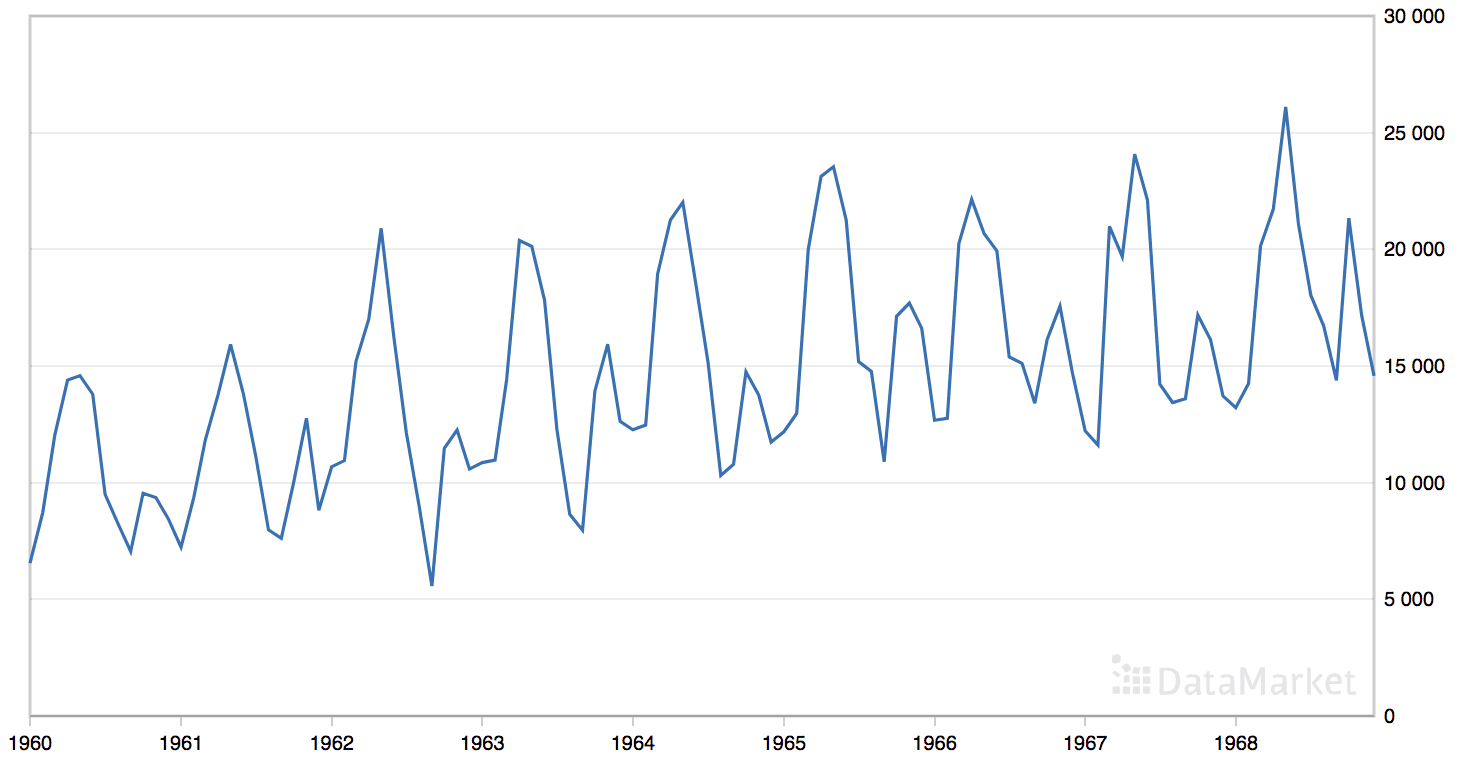
Line Plot of the Monthly Car Sales Dataset

月度汽车销量数据集的线图

直接从这里下载数据集

monthly-car-sales.csv

将文件保存为“_monthly-car-sales.csv_”在当前工作目录中。

我们可以使用 *read_csv()* 函数将此数据集加载为 Pandas 序列。

series = read_csv('monthly-car-sales.csv', header=0, index_col=0)

1	series = read_csv('monthly-car-sales.csv', header=0, index_col=0)

数据集包含 9 年，即 108 个观测值。我们将使用最后一年（即 12 个观测值）作为测试集。

季节性成分的周期可以是 6 个月或 12 个月。在准备模型配置时，我们将在调用 *sarima_configs()* 函数时同时尝试这两种季节性周期。

# model configs
cfg_list = sarima_configs(seasonal=[0,6,12])

1 2	# 模型配置 cfg_list = sarima_configs(seasonal=[0,6,12])

下面列出了对月度汽车销量时间序列预测问题进行网格搜索的完整示例。

# grid search sarima hyperparameters for monthly car sales dataset
from math import sqrt
from multiprocessing import cpu_count
from joblib import Parallel
from joblib import delayed
from warnings import catch_warnings
from warnings import filterwarnings
from statsmodels.tsa.statespace.sarimax import SARIMAX
from sklearn.metrics import mean_squared_error
from pandas import read_csv

# one-step sarima forecast
def sarima_forecast(history, config):
	order, sorder, trend = config
	# define model
	model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)
	# fit model
	model_fit = model.fit(disp=False)
	# make one step forecast
	yhat = model_fit.predict(len(history), len(history))
	return yhat[0]

# root mean squared error or rmse
def measure_rmse(actual, predicted):
	return sqrt(mean_squared_error(actual, predicted))

# split a univariate dataset into train/test sets
def train_test_split(data, n_test):
	return data[:-n_test], data[-n_test:]

# walk-forward validation for univariate data
def walk_forward_validation(data, n_test, cfg):
	predictions = list()
	# split dataset
	train, test = train_test_split(data, n_test)
	# seed history with training dataset
	history = [x for x in train]
	# step over each time-step in the test set
	for i in range(len(test)):
		# fit model and make forecast for history
		yhat = sarima_forecast(history, cfg)
		# store forecast in list of predictions
		predictions.append(yhat)
		# add actual observation to history for the next loop
		history.append(test[i])
	# estimate prediction error
	error = measure_rmse(test, predictions)
	return error

# score a model, return None on failure
def score_model(data, n_test, cfg, debug=False):
	result = None
	# convert config to a key
	key = str(cfg)
	# show all warnings and fail on exception if debugging
	if debug:
		result = walk_forward_validation(data, n_test, cfg)
	else:
		# one failure during model validation suggests an unstable config
		try:
			# never show warnings when grid searching, too noisy
			with catch_warnings():
				filterwarnings("ignore")
				result = walk_forward_validation(data, n_test, cfg)
		except:
			error = None
	# check for an interesting result
	if result is not None:
		print(' > Model[%s] %.3f' % (key, result))
	return (key, result)

# grid search configs
def grid_search(data, cfg_list, n_test, parallel=True):
	scores = None
	if parallel:
		# execute configs in parallel
		executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')
		tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)
		scores = executor(tasks)
	else:
		scores = [score_model(data, n_test, cfg) for cfg in cfg_list]
	# remove empty results
	scores = [r for r in scores if r[1] != None]
	# sort configs by error, asc
	scores.sort(key=lambda tup: tup[1])
	return scores

# create a set of sarima configs to try
def sarima_configs(seasonal=[0]):
	models = list()
	# define config lists
	p_params = [0, 1, 2]
	d_params = [0, 1]
	q_params = [0, 1, 2]
	t_params = ['n','c','t','ct']
	P_params = [0, 1, 2]
	D_params = [0, 1]
	Q_params = [0, 1, 2]
	m_params = seasonal
	# create config instances
	for p in p_params:
		for d in d_params:
			for q in q_params:
				for t in t_params:
					for P in P_params:
						for D in D_params:
							for Q in Q_params:
								for m in m_params:
									cfg = [(p,d,q), (P,D,Q,m), t]
									models.append(cfg)
	return models

if __name__ == '__main__':
	# load dataset
	series = read_csv('monthly-car-sales.csv', header=0, index_col=0)
	data = series.values
	print(data.shape)
	# data split
	n_test = 12
	# model configs
	cfg_list = sarima_configs(seasonal=[0,6,12])
	# grid search
	scores = grid_search(data, cfg_list, n_test)
	print('done')
	# list top 3 configs
	for cfg, error in scores[:3]:
		print(cfg, error)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

# 对月度汽车销量数据集的 sarima 超参数进行网格搜索

from math import sqrt

from multiprocessing import cpu_count

from joblib import Parallel

from joblib import delayed

from warnings import catch_warnings

from warnings import filterwarnings

from statsmodels.tsa.statespace.sarimax import SARIMAX

from sklearn.metrics import mean_squared_error

from pandas import read_csv

# 一步 SARIMA 预测

def sarima_forecast(history, config):

order, sorder, trend = config

# 定义模型

model = SARIMAX(history, order=order, seasonal_order=sorder, trend=trend, enforce_stationarity=False, enforce_invertibility=False)

# 拟合模型

model_fit = model.fit(disp=False)

# 进行一步预测

yhat = model_fit.predict(len(history), len(history))

return yhat[0]

# 均方根误差或 RMSE

def measure_rmse(actual, predicted):

return sqrt(mean_squared_error(actual, predicted))

# 将单变量数据集拆分为训练/测试集

def train_test_split(data, n_test):

return data[:-n_test], data[-n_test:]

# 单变量数据的滚动预测验证

def walk_forward_validation(data, n_test, cfg):

predictions = list()

# 拆分数据集

train, test = train_test_split(data, n_test)

# 用训练数据集初始化历史数据

history = [x for x in train]

# 遍历测试集中的每个时间步

for i in range(len(test)):

# 拟合模型并对历史数据进行预测

yhat = sarima_forecast(history, cfg)

# 将预测结果存储在预测列表中

predictions.append(yhat)

# 将实际观测值添加到历史数据中以进行下一次循环

history.append(test[i])

# 估计预测误差

error = measure_rmse(test, predictions)

return error

# 评估模型，失败时返回 None

def score_model(data, n_test, cfg, debug=False):

result = None

# 将配置转换为键

key = str(cfg)

# 如果在调试，则显示所有警告并在异常时失败

if debug:

result = walk_forward_validation(data, n_test, cfg)

else:

# 模型验证过程中的一次失败表明配置不稳定

try:

# 网格搜索时从不显示警告，太嘈杂

with catch_warnings():

filterwarnings("ignore")

result = walk_forward_validation(data, n_test, cfg)

except:

error = None

# 检查是否有有趣的结果

if result is not None:

print(' > Model[%s] %.3f' % (key, result))

return (key, result)

# 网格搜索配置

def grid_search(data, cfg_list, n_test, parallel=True):

scores = None

if parallel:

# 并行执行配置

executor = Parallel(n_jobs=cpu_count(), backend='multiprocessing')

tasks = (delayed(score_model)(data, n_test, cfg) for cfg in cfg_list)

scores = executor(tasks)

else:

scores = [score_model(data, n_test, cfg) for cfg in cfg_list]

# 移除空结果

scores = [r for r in scores if r[1] != None]

# 按误差升序排序配置

scores.sort(key=lambda tup: tup[1])

返回分数

# 创建一组要尝试的 sarima 配置

def sarima_configs(seasonal=[0]):

models = list()

# 定义配置列表

p_params = [0, 1, 2]

d_params = [0, 1]

q_params = [0, 1, 2]

t_params = ['n','c','t','ct']

P_params = [0, 1, 2]

D_params = [0, 1]

Q_params = [0, 1, 2]

m_params = seasonal

# 创建配置实例

for p in p_params:

for d in d_params:

for q in q_params:

for t in t_params:

for P in P_params:

for D in D_params:

for Q in Q_params:

for m in m_params:

cfg = [(p,d,q), (P,D,Q,m), t]

models.append(cfg)

return models

if __name__ == '__main__':

# 加载数据集

series = read_csv('monthly-car-sales.csv', header=0, index_col=0)

data = series.values

print(data.shape)

# 数据分割

n_test = 12

# 模型配置

cfg_list = sarima_configs(seasonal=[0,6,12])

# 网格搜索

scores = grid_search(data, cfg_list, n_test)

print('完成')

# 列出前 3 个配置

for cfg, error in scores[:3]:

print(cfg, error)

在现代硬件上运行该示例可能需要几分钟。

模型配置和 RMSE 在模型评估时打印。运行结束时报告前三个模型配置及其误差。

**注意**：由于算法或评估过程的随机性，或数值精度的差异，您的结果可能会有所不同。考虑多次运行示例并比较平均结果。

我们可以看到，最佳结果是 RMSE 约为 1,551 辆汽车销售额，配置如下

趋势订单: (0, 0, 0)
季节性顺序: (1, 1, 0, 12)
**趋势参数**：“t”（线性趋势）

> Model[[(2, 1, 2), (2, 1, 1, 6), 'ct']] 2246.248
> Model[[(2, 1, 2), (2, 0, 2, 12), 'ct']] 10710.462
> Model[[(2, 1, 2), (2, 1, 2, 6), 'ct']] 2183.568
> Model[[(2, 1, 2), (2, 1, 0, 12), 'ct']] 2105.800
> Model[[(2, 1, 2), (2, 1, 1, 12), 'ct']] 2330.361
> Model[[(2, 1, 2), (2, 1, 2, 12), 'ct']] 31580326686.803
done
[(0, 0, 0), (1, 1, 0, 12), 't'] 1551.8423920342414
[(0, 0, 0), (2, 1, 1, 12), 'c'] 1557.334614575545
[(0, 0, 0), (1, 1, 0, 12), 'c'] 1559.3276311282675

> 模型[[(2, 1, 2), (2, 1, 1, 6), 'ct']] 2246.248

> 模型[[(2, 1, 2), (2, 0, 2, 12), 'ct']] 10710.462

> 模型[[(2, 1, 2), (2, 1, 2, 6), 'ct']] 2183.568

> 模型[[(2, 1, 2), (2, 1, 0, 12), 'ct']] 2105.800

> 模型[[(2, 1, 2), (2, 1, 1, 12), 'ct']] 2330.361

> 模型[[(2, 1, 2), (2, 1, 2, 12), 'ct']] 31580326686.803

完成

[(0, 0, 0), (1, 1, 0, 12), 't'] 1551.8423920342414

[(0, 0, 0), (2, 1, 1, 12), 'c'] 1557.334614575545

[(0, 0, 0), (1, 1, 0, 12), 'c'] 1559.3276311282675

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

**数据转换**。更新框架以支持可配置的数据转换，例如归一化和标准化。
**绘制预测图**。更新框架以使用最佳配置重新拟合模型并预测整个测试数据集，然后将预测与测试集中的实际观测值进行比较绘制图。
**调整历史数据量**。更新框架以调整用于拟合模型的历史数据量（例如，在 10 年最高温度数据的情况下）。

如果您探索了这些扩展中的任何一个，我很想知道。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

文章

书籍

第 8 章 ARIMA 模型，《预测：原理与实践》，2013 年。
第 7 章，非平稳模型，《R 语言时间序列入门》，2009 年。

API

文章

维基百科上的自回归积分移动平均

总结

在本教程中，您学习了如何开发一个框架，用于对单变量时间序列预测的 SARIMA 模型所有超参数进行网格搜索。

具体来说，你学到了：

如何从头开始使用滚动预测验证开发一个网格搜索 SARIMA 模型的框架。
如何对每日出生时间序列数据的 SARIMA 模型超参数进行网格搜索。
如何对洗发水销售、汽车销售和气温的月度时间序列数据的 SARIMA 模型超参数进行网格搜索。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

如何在 Python 中对三重指数平滑进行时间序列预测的网格搜索

如何对单变量时间序列预测的朴素方法进行网格搜索

83 条对《如何对 SARIMA 超参数进行时间序列预测的网格搜索》的回应

张博 2018 年 10 月 24 日上午 11:53 #

感谢分享。您能支持支付宝或微信支付吗？因为我在中国，Visa 或 PayPal 支付有点复杂。

回复
- Jason Brownlee 2018 年 10 月 24 日下午 2:44 #
  
  感谢您的建议，我在这里回答这个问题
  https://machinelearning.org.cn/faq/single-faq/can-i-pay-via-wechat-pay-or-alipay
  
  回复
Fedor 2018 年 10 月 25 日下午 6:25 #

非常感谢这篇文章。它确实令人印象深刻，但八个嵌套的 for 循环不符合 Pythonic 风格。也许有更智能的方法可以做到这一点。例如，使用 'itertools.product'

回复
- Jason Brownlee 2018 年 10 月 26 日上午 5:33 #
  
  我完全同意！
  
  是的，笛卡尔积或类似的东西。
  
  回复
Jonathan Mackenzie 2018 年 10 月 26 日下午 12:04 #

感谢分享，我一直在学习 ARIMA 以应用于我的应用程序。我从《预测原理与实践》中学到了很多，它有一个在线开放文本版本：https://otexts.org/fpp2/arima.html

我对 SARIMA（或者也许只是 statsmodels）的主要问题之一是它不能很好地处理非常大的数据集。我有大约 6 年的时间序列数据，每 5 分钟记录一次，季节长度为 1 天或 1 周，即周一上午 9 点很可能与下周一上午 9 点相关，这在差分和 ACF 图中有所体现。有没有更好的方法或更好的库来做这件事？

回复
- Jason Brownlee 2018 年 10 月 26 日下午 2:42 #
  
  您可以尝试暴露/工程化特征，然后直接用线性回归模型拟合数据。
  
  回复
Stefan 2018 年 11 月 14 日上午 3:01 #

嗨，Jason，

你可能已经知道了，但是下面的包旨在将 R 的 auto.arima 转换为 python。它对我很有效。

https://pypi.ac.cn/project/pyramid-arima/

回复
- Jason Brownlee 2018 年 11 月 14 日上午 7:36 #
  
  不错的发现！
  
  回复
mamina sahu 2018 年 11 月 15 日下午 8:01 #

感谢分享..

回复
- Jason Brownlee 2018年11月16日上午6:14 #
  
  很高兴它有帮助。
  
  回复
Leandro Rabelo 2019年1月24日上午7:56 #

当你不使用季节性顺序时，比如

Model[[(2, 1, 2), (1, 0, 2, 0), ‘ct’]]

这难道不是意味着我们正在将AR、I和M参数求和吗？在这种情况下，我们最终不会得到这样的模型吗？

(3,1,4) 'ct'

谢谢！

回复
- Jason Brownlee 2019年1月24日下午1:22 #
  
  嗯，我不这么认为。我觉得这些操作是独立的，不是累积的。
  
  也许可以比较两种配置的结果以确定？
  
  回复
- H Zhang 2019年12月20日上午3:09 #
  
  我的想法是：在Model[[(2, 1, 2), (1, 0, 2, 0), 'ct']]中，s=0（季节性周期性）意味着没有季节性。在季节性配置(P,D,Q,s)中，当s=0时，P,D,Q不可解释，应强制设为0。Model[[(2, 1, 2), (1, 0, 2, 0), 'ct']]不是有意义的配置，应排除。案例1的最终配置，特别是'ct'，不直观。
  
  回复
  - Jason Brownlee 2019年12月20日上午6:51 #
    
    太棒了！
    
    回复
Jyotirmoy Banik 2019年3月6日上午8:46 #

感谢您逐步写出所有步骤。但是，我尝试运行了一些示例代码（第一个和最后一个）。我正在Windows 10上使用Jupyter notebook和Python 3。不幸的是，在这两种情况下，notebook在执行过程中都冻结并永远停在那里。我是不是遗漏了什么？

回复
- Jason Brownlee 2019年3月6日上午8:48 #
  
  我建议从命令行运行示例。
  
  回复
matt 2019年3月10日上午12:27 #

你好 Jason，

关于机器学习的精彩网站，您的书籍非常棒。我是一个初学者，我正在阅读您所有的书籍并尝试运行程序。我尝试在python 3上运行程序“案例研究1：无趋势或季节性”，但程序未完成。您的程序仍在运行！
你想终止它吗？) 能帮我一下吗？谢谢

回复
- Jason Brownlee 2019年3月10日上午8:18 #
  
  我建议从命令行运行，并确保您的库是最新的。
  
  我这里有一些更多的建议
  https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
  
  回复
Lola 2019年3月30日上午9:40 #

非常感谢这篇有用的文章！我对案例研究4有一个问题——RMSE最小的最佳拟合模型具有趋势阶数（p=0,d=0,q=0），其中d=0表示模型不需要进行一阶差分来消除趋势。但是，我们确实观察到数据中存在明显的趋势。这会是一个冲突吗？谢谢！

回复
- Jason Brownlee 2019年3月31日上午9:24 #
  
  也许可以尝试用线性回归模型对趋势建模，然后手动减去它，看看是否会降低误差？
  
  回复
Mau 2019年5月24日上午11:51 #

非常感谢您的代码，我想知道是否有办法将“print(cfg, error)”这部分转换为数据框或输出表。

回复
- Jason Brownlee 2019年5月24日下午2:30 #
  
  当然。配置是一个元组，您可以将其转换为任何您想要的东西。
  
  回复
  - Mau 2019年5月30日上午11:27 #
    
    亲爱的Jason，我一直在尝试将元组导出到数据框，但我无法做到。在案例研究2的第132和133行，我将代码更改为
    
    for cfg, error in scores[:3]
    df=pd.DataFrame(cfg, error)
    output_table = df
    
    我没有成功，所以我尝试了
    
    for cfg, error in scores[:3]
    df.append({'cfg': cfg, 'error': error},ignore_index=True)
    output_table = df
    
    我知道这不是一个Sarima问题，但我会感谢你的帮助
    
    回复
    - Jason Brownlee 2019年5月30日下午2:53 #
      
      我很乐意帮助，但我没有能力为您编写/调试代码片段，抱歉。
      
      也许可以尝试在 stackoverflow 上发布？
      
      回复
Ashwath Salimath 2019年6月14日上午12:41 #

Jason，我的问题是关于SARIMA所需的时间。有没有办法减少搜索空间或我们正在尝试的参数组合？请告诉我。谢谢。

回复
- Jason Brownlee 2019年6月14日上午6:49 #
  
  是的，您可以使用ACF/PACF图来估计参数
  https://machinelearning.org.cn/gentle-introduction-autocorrelation-partial-autocorrelation/
  
  回复
sravya 2019年6月25日上午4:16 #

你好Jason，在我的数据集上使用网格搜索代码只显示了人为的时间序列数据。模型配置没有打印到Jupyter notebook的控制台。但也没有错误。请帮我找出我可能犯的错误。

回复
- Jason Brownlee 2019年6月25日上午6:29 #
  
  我建议不要使用笔记本，而是从命令行运行代码。
  
  回复
Alex R. 2019年6月27日上午3:51 #

你好，Jason。这里的案例很棒。用Google Colab TPU，第一个案例完成了，但花了很长时间:) 谢谢。

回复
- Jason Brownlee 2019年6月27日上午8:01 #
  
  干得好！
  
  回复
shweta 2019年8月28日下午5:07 #

当我执行上述案例研究代码时
出现以下错误
AttributeError: 无法获取属性“score_model”

回复
- Jason Brownlee 2019年8月29日上午6:01 #
  
  很抱歉听到这个消息，我在这里有一些建议。
  https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
  
  回复
H Pires 2019年9月5日上午12:21 #

你好

有没有办法使用多进程来加快处理速度？

谢谢你

回复
- Jason Brownlee 2019年9月5日上午6:56 #
  
  它已经这样做了！
  
  回复
Tolga 2019年10月28日上午6:40 #

一个关于超参数调优的精彩教程！但是，我在sarima_configs函数的输出中遇到了一个问题。输出的形状不允许在sarima_forecast函数中进行“order, sorder, trend = config”。这个问题发生在我用python3运行其中一个示例代码时。

回复
- Tolga 2019年10月28日上午6:45 #
  
  很抱歉打扰您，我之前的消息是我的错误。
  
  回复
  - Jason Brownlee 2019年10月28日上午6:56 #
    
    不客气。
    
    回复
mahnaz 2019年11月11日下午1:57 #

感谢Jason您的出色工作。
我在哪里可以找到数据集？

回复
- Jason Brownlee 2019年11月12日上午6:32 #
  
  谢谢！
  
  每个数据集都在帖子中链接。
  
  回复
Olivier 2019年12月10日下午8:48 #

你好 Jason，
非常感谢您的网站，我从阅读您的博客中学到了很多。

复杂的课题对我的大脑来说变得易懂了……

我正在测试这篇文章的最后一段代码：关于每月汽车销量的SARIMA网格搜索。
在不使用并行模式的情况下，它运行完美。
我更新了joblib，但当我切换到并行模式时仍然出现以下错误

ValueError: 设计矩阵的无效值。需要2维或3维数组，得到1维

我正在搜索，但如果您有任何想法……

非常感谢，

回复
- Olivier 2019年12月10日下午9:07 #
  
  更准确地说
  如果parallel=True且debug=False，那么它永远不会结束或需要很长时间。
  如果parallel=True且debug=True，则会引发错误。
  此致，
  
  回复
  - Jason Brownlee 2019年12月11日上午6:57 #
    
    是的，将 debug 设置为 False。
    
    回复
- Jason Brownlee 2019年12月11日上午6:52 #
  
  谢谢！
  
  我没有见过那个错误，抱歉。也许可以确认您所有的python库都已更新？
  
  回复
Jonathan 2020年1月21日上午2:51 #

你好，

我很好奇是否可以只使用AIC（由model.fit()在整个数据上给出）来比较哪个模型最好（并移除“walk_forward_validation”）？这样做有意义吗？

谢谢，

回复
- Jason Brownlee 2020年1月21日上午7:17 #
  
  也许吧。我没有这样做过，你可能需要稍微尝试一下。
  
  回复
  - Snehansu Sekhar Sahu 2021年1月11日下午9:37 #
    
    有道理。
    
    model_fit = model.fit(disp=False)
    
    此外，model_fit.mse将返回mean_squared_error。
    人们应该能够使用model_fit.aic来比较哪个模型最好（并移除“walk_forward_validation”）。
    
    回复
Portia 2020年3月9日上午12:23 #

非常棒的阅读，我如何将其扩展以考虑外生变量。

回复
- Jason Brownlee 2020年3月9日上午7:17 #
  
  使用“exog”参数
  https://statsmodels.cn/dev/generated/statsmodels.tsa.statespace.sarimax.SARIMAX.html
  
  回复
Portia 2020年3月30日下午10:30 #

嗨，Jason，感谢您的阅读，我已经修改了脚本以添加我自己的数据，使用相同的参数配置，但是出于某种原因，我只会显示4个模型。有什么可能导致这种情况吗？

回复
- Jason Brownlee 2020年3月31日上午8:10 #
  
  也许您引入了一个错误？
  
  回复
Imran 2020年5月7日下午1:54 #

Jason，这篇文章非常有帮助！您知道如何同时考虑每周和每年的季节性吗？例如，在每日数据集中，既有每周季节性，也有每年（每365天发生一次）季节性。如何识别该数据集的“m”阶？

回复
- Jason Brownlee 2020年5月8日上午6:17 #
  
  谢谢！
  
  我记得SARIMA支持两个周期，但我可能错了。
  
  一种方法是在建模之前，手动对每个周期的数据进行季节性调整/差分。
  
  回复
Sigried 2020年5月15日下午10:46 #

你好 Jason，

首先，非常感谢您的网站上提供的有用文章。我是机器学习新手，正在通过您的书籍自学基础知识。

我想进行多步预测，并通过您的网格搜索方法评估一些参数。
由于该方法是为一步预测编写的，我想知道，当我计划进行多步预测时，具体需要更改什么？
在您的文章中，您说：“如果您对进行多步预测感兴趣，可以更改sarima_forecast()函数中对predict()的调用，并更改measure_rmse()函数中误差的计算。”
这到底是什么意思？抱歉，这基本上是我第一次接触这个话题。

再次非常感谢您的工作，我真的很感激！:)

也祝您有美好的一天

回复
- Jason Brownlee 2020年5月16日上午6:13 #
  
  不客气。
  
  – 也许可以尝试独立拟合模型并进行多步预测，以熟悉API。
  – 然后评估该预测，以了解如何评估多步预测。
  – 然后尝试使用您学到的知识修改这个高级示例。
  
  回复
Jonathan 2020年5月19日上午9:02 #

Jason，也感谢您提供这篇文章。那么，在确定了sarima模型的参数后，我应该按照您在arima文章中概述的相同步骤进行操作吗？

https://machinelearning.org.cn/time-series-forecast-study-python-monthly-sales-french-champagne/

回复
- Jason Brownlee 2020年5月19日下午1:24 #
  
  是的，如果这对您有帮助的话。
  
  回复
fjj80 2020年6月5日上午11:10 #

嗨，Jason，
很奇怪，statsmodels中有些东西变了。

这是我从案例2（洗发水）得到的输出
....
> Model[[(2, 1, 2), (0, 0, 0, 0), ‘n’]] 89.615
> Model[[(2, 1, 1), (0, 0, 0, 0), ‘ct’]] 61.799
> Model[[(2, 1, 2), (0, 0, 0, 0), ‘t’]] 65.569
> Model[[(2, 1, 2), (0, 0, 0, 0), ‘c’]] 86.904
> Model[[(2, 1, 2), (0, 0, 0, 0), ‘ct’]] 60.817
完成
[(2, 1, 2), (0, 0, 0, 0), 'ct'] 60.817175487660776
[(1, 0, 2), (0, 0, 0, 0), 't'] 60.91750969204128
[(1, 1, 1), (0, 0, 0, 0), 'ct'] 61.64542070109567

这和你的答案不一样。

我认为只有ARIMA，而不是SARIMA在工作。我设置了debug=True
我捕获到了这条消息

ValueError: 如果包含季节性AR、MA或差分，则必须包含非零季节性周期性。

我认为带有数据=[10.0 ... 的朴素示例也不起作用，尽管答案是正确的。我没有检查案例1（出生），因为它需要很长时间。但它可能也会失败。

我的版本.py是

python 版本 : 3.8.2 (默认, 2020年3月26日, 15:53:00)
[GCC 7.3.0]
scipy: 1.4.1
numpy: 1.18.1
matplotlib: 3.2.1
pandas: 1.0.3
statsmodels: 0.11.1
sklearn: 0.22.1
tensorflow: 2.2.0

有人抱怨上面有些配置无效，看来SARIMAX开发人员设置了某种“严格”模式。

谢谢你！！

回复
- Jason Brownlee 2020年6月5日下午1:42 #
  
  有意思。谢谢！
  
  回复
- ashraf khan 2022年4月15日上午6:26 #
  
  # 使用以下异常处理来跳过无效配置
  
  def walk_forward_validation(data, n_test, cfg)
  predictions = list()
  
  train, test = train_test_split(data, n_test)
  # 使用训练数据集初始化历史数据
  history = [x for x in train]
  
  # 遍历测试集中的每个时间步
  for i in range(len(test))
  # 拟合模型并对历史数据进行预测
  尝试
  yhat = sarima_forecast(history, cfg)
  # 将预测结果存储到预测列表中
  predictions.append(yhat)
  # 将实际观测值添加到历史数据中以供下一次循环使用
  history.append(test[i])
  except
  return None
  
  error = measure_rmse(test, predictions)
  return error
  
  回复
Antonello 2020年6月17日上午4:14 #

嗨，Jason，

非常感谢您的教程。它非常清晰和有帮助，即使对于像我这样的初学者也是如此。

不幸的是，我遇到了和上一个用户同样的问题。它像ARIMA模型的网格搜索一样工作，但在季节性参数上不起作用。

为了进行SARIMA的网格搜索，您能帮我更新代码吗？

…
> Model[[(2, 1, 1), (0, 0, 0, 0), ‘ct’]] 9.430
> Model[[(2, 1, 2), (0, 0, 0, 0), ‘c’]] 9.210
> Model[[(2, 1, 2), (0, 0, 0, 0), ‘t’]] 9.294
> Model[[(2, 1, 2), (0, 0, 0, 0), ‘ct’]] 9.576
完成
[(2, 0, 2), (0, 0, 0, 0), 'c'] 9.200387448030902
[(1, 0, 2), (0, 0, 0, 0), 'c'] 9.201872299489434
[(1, 0, 1), (0, 0, 0, 0), 'c'] 9.204556169539375

回复
- Jason Brownlee 2020年6月17日上午6:28 #
  
  谢谢，我会调查。
  
  回复
  - AM 2021年10月4日上午3:21 #
    
    嗨，Jason，
    我想知道这个问题是否已得到解决。我使用示例时遇到了同样的问题，没有生成季节性分量。
    
    回复
    - Adrian Tam 2021年10月6日上午8:14 #
      
      在我看来，最新版本的库没有问题。您看到了不同的情况吗？请告诉我您正在运行哪个示例，以便我进行调查。
      
      回复
Pawe 2020年8月3日下午7:48 #

你好，Jason。
如果我想估计预测的置信区间怎么办？
例如，我想找到一个95%的真实值不会超过的区间。
是不是这样？
X – 1.96*(np.std(X)/np.sqrt(n)) < X < X + 1.96*(np.std(X)/np.sqrt(n))

谢谢？！

回复
- Jason Brownlee 2020年8月4日上午6:36 #
  
  我相信 API 通过 forecast() 函数提供了这个（预测区间）
  https://machinelearning.org.cn/time-series-forecast-uncertainty-using-confidence-intervals-python/
  
  回复
ahmad 2020年8月10日下午8:24 #

感谢您的详细文章。如果每天有2880个观测值（观测值之间有30秒的间隔），SARIMA的季节周期和其他参数将是多少？

回复
- Jason Brownlee 2020年8月11日上午6:31 #
  
  您可以尝试从 ACF/PACF 图中估计参数，或者像上面一样对超参数进行网格搜索。
  
  回复
Sam 2020年8月26日下午3:40 #

嗨Jason，我有一个小时数据集，季节性参数会是什么？24表示每小时的季节性吗？

回复
- Jason Brownlee 2020年8月27日上午6:11 #
  
  如果您有小时数据且周期为24小时，那么可以尝试将季节性值设为24。
  
  回复
Dave C 2021年8月8日上午2:45 #

嗨，Jason，

这很棒，但我很难理解如何将外生变量包含到您的函数中。我尝试的每一种方法都会出现“IndexError: list index out of range”错误。您能提供一个包含外生变量的额外示例/案例吗？

回复
- Jason Brownlee 2021年8月8日上午5:10 #
  
  这可能有帮助
  https://machinelearning.org.cn/time-series-forecasting-methods-in-python-cheat-sheet/
  
  回复
fons 2021年10月8日下午3:19 #

我可以用两年的数据进行训练，只测试五天吗？因为它需要很长时间。

回复
- Adrian Tam 2021年10月13日上午5:18 #
  
  是的，但您的测试分数会比较粗糙。
  
  回复
Fons 2021年10月8日下午3:54 #

另一个问题
我可以在训练数据之前使用移动平均线（7天平均）或Savitzky-Golay滤波器来降噪吗？

回复
- Adrian Tam 2021年10月13日上午5:19 #
  
  模型的MA部分应该能处理好，因此它应该不是不必要的。但是，您可以尝试看看您的结果如何。
  
  回复
Sahil 2022年3月3日上午5:19 #

嗨Jason！感谢您提供这篇非常详细的指南。我想知道pmdarima中的auto_arima是否与您提到的功能相同。

回复
- James Carmichael 2022年3月3日下午1:41 #
  
  嗨，Sahil……如果您不确定数据集的季节性分量，我建议您尝试ARIMA的各种版本。我还建议您尝试LSTM模型并将其性能与ARIMA模型进行比较。
  
  https://machinelearning.org.cn/how-to-develop-lstm-models-for-time-series-forecasting/
  
  回复
jinYang 2022年4月28日下午6:06 #

你好博士。我有一份数据，这份数据集是植物的收成数据，所以每年只有大约两个月的数据，大约48或50天的数据，其他天没有收成可以视为0，并且原始数据看起来很稳定，当我使用SAIMAX进行预测时，我应该如何选择我的周期，我应该选择48吗？还是应该将所有其他日期填充为0，然后循环选择12？
期待您的回复♥
jinyang

回复
- James Carmichael 2022年4月29日上午10:28 #
  
  嗨，JinYang……以下内容可能会有所帮助。
  
  https://machinelearning.org.cn/handle-missing-timesteps-sequence-prediction-problems-python/
  
  回复
  - jinYang 2022年4月29日下午12:45 #
    
    这篇文章对我有很大的帮助，但对不起，也许我没有表达清楚，当我尝试使用网格搜索方法寻找参数时，我必须定义一个边界，例如seasonal=[0, X]这个X值我应该尝试取多大？
    
    回复
jinYang 2022年4月29日下午12:45 #

这篇文章对我有很大的帮助，但对不起，也许我没有表达清楚，当我尝试使用网格搜索方法寻找参数时，我必须定义一个边界，例如seasonal=[0, X]这个X值我应该尝试取多大？

回复
Vi 2023年2月25日上午1:50 #

有没有什么原因导致唯一的三个输出都显示None错误？

[(0, 0, 0), (0, 0, 0, 0), 'n'] None
[(0, 0, 0), (0, 0, 0, 12), 'n'] None
[(0, 0, 0), (0, 0, 1, 0), 'n'] None

回复
- James Carmichael 2023年2月25日上午10:15 #
  
  嗨，Vi……没有别的原因，这只是所考虑数据的结果。
  
  回复

导航

如何对时间序列预测的 SARIMA 超参数进行网格搜索

教程概述

SARIMA 用于时间序列预测

时间序列深度学习需要帮助吗？

开发网格搜索框架

案例研究 1：无趋势或季节性

案例研究 2：趋势

案例研究 3：季节性

案例研究 4：趋势和季节性

扩展

进一步阅读

文章

书籍

API

文章

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

83 条对《如何对 SARIMA 超参数进行时间序列预测的网格搜索》的回应

发表评论点击此处取消回复。

导航

教程概述

SARIMA 用于时间序列预测

时间序列深度学习需要帮助吗？

开发网格搜索框架

案例研究 1：无趋势或季节性

案例研究 2：趋势

案例研究 3：季节性

案例研究 4：趋势和季节性

扩展

进一步阅读

文章

书籍

API

文章

总结

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

最终将深度学习应用于您的时间序列预测项目

关于此主题的更多信息

83 条对《如何对 SARIMA 超参数进行时间序列预测的网格搜索》的回应

发表评论 点击此处取消回复。

发表评论点击此处取消回复。