如何加载、可视化和探索多元多步时间序列数据集

真实世界的时间序列预测之所以具有挑战性，原因有很多，不仅限于诸如多个输入变量、需要预测多个时间步长以及需要为多个物理站点执行相同类型的预测等问题特征。

EMC 数据科学全球黑客马拉松数据集，简称“空气质量预测”数据集，描述了多个站点的天气状况，并要求预测未来三天的空气质量测量值。

在本教程中，您将发现并探索空气质量预测数据集，该数据集代表了一个具有挑战性的多元、多站点和多步时间序列预测问题。

完成本教程后，您将了解：

• 如何加载和探索数据集的块结构。
• 如何探索和可视化数据集的输入和目标变量。
• 如何利用新获得的理解来概述一系列用于构建问题、准备数据和建模数据集的方法。

通过我的新书《时间序列预测深度学习》启动您的项目，其中包括分步教程和所有示例的 Python 源代码文件。

让我们开始吧。

• 2019 年 4 月更新：修复了总缺失值计算中的错误（感谢 zhangzhe）。

如何加载、可视化和探索复杂多元多步时间序列预测数据集
摄影：H Matthew Howarth，保留部分权利。

教程概述

本教程分为七个部分，它们是：

1. 问题描述
2. 加载数据集
3. 分块数据结构
4. 输入变量
5. 目标变量
6. 目标变量的一个难题
7. 建模思考

问题描述

EMC 数据科学全球黑客马拉松数据集，简称“空气质量预测”数据集，描述了多个站点的天气状况，并要求预测未来三天的空气质量测量值。

具体来说，多个站点的温度、压力、风速和风向等气象观测数据以小时为单位提供了八天的数据。目标是预测未来三天多个站点的空气质量测量值。预测提前期不是连续的；相反，必须在 72 小时预测期内预测特定的提前期；它们是

此外，数据集被划分为不相交但连续的数据块，其中包含八天的数据，然后是需要预测的三天。

并非所有站点或数据块都提供所有观测数据，也并非所有站点或数据块都提供所有输出变量。存在大量缺失数据，必须加以解决。

该数据集在 2012 年 Kaggle 网站上作为短期机器学习竞赛（或黑客马拉松）的基础。

竞赛的提交结果根据保密的真实观测值进行评估，并使用平均绝对误差 (MAE) 进行评分。提交要求在因数据缺失而无法进行预测的情况下指定值 -1,000,000。事实上，提供了一个插入缺失值的模板，并要求所有提交都必须采用该模板（真麻烦）。

一位获胜者在保留的测试集（私有排行榜）上使用滞后观测值的随机森林实现了 0.21058 的 MAE。该解决方案的详细说明可在以下帖子中找到

• 将所有内容扔进随机森林：本·哈姆纳谈赢得空气质量预测黑客马拉松, 2012.

在本教程中，我们将探索此数据集，以便更好地理解预测问题的性质并提出建模方法。

加载数据集

第一步是下载数据集并将其加载到内存中。

可以从 Kaggle 网站免费下载数据集。您可能需要创建帐户并登录才能下载数据集。

将整个数据集，例如“Download All”，下载到您的工作站，并将存档文件解压到当前工作目录中，文件夹名为“AirQualityPrediction”

• EMC 数据科学全球黑客马拉松（空气质量预测）数据

您应该在 AirQualityPrediction/ 文件夹中有五个文件；它们是

• SiteLocations.csv
• SiteLocations_with_more_sites.csv
• SubmissionZerosExceptNAs.csv
• TrainingData.csv
• sample_code.r

我们的重点将是“TrainingData.csv”，其中包含训练数据集，特别是分块的数据，每个分块是连续八天的观测值和目标变量。

在撰写本文时，该数据集的测试数据集（每个分块的剩余三天）不可用。

打开“TrainingData.csv”文件并查看内容。解压后的数据文件相对较小（21 兆字节），可以轻松加载到内存中。

查看文件内容，我们可以看到数据文件包含一个标题行。

我们还可以看到缺失数据用“NA”值标记，Pandas 会自动将其转换为 NumPy.NaN。

我们可以看到“weekday”列包含作为字符串的日期，而所有其他数据都是数字。

以下是数据文件的前几行为参考。

我们可以使用 Pandas 的 read_csv() 函数将数据文件加载到内存中，并指定第 0 行作为标题行。

我们还可以快速了解数据集中有多少缺失数据。我们可以通过首先修剪前几列以删除字符串工作日数据并将剩余列转换为浮点值来实现。

然后，我们可以计算缺失观测值的总数以及缺失值的百分比。

完整的示例如下所示。

运行示例首先打印加载数据集的形状。

我们可以看到大约有 37,000 行和 95 列。我们知道这些数字具有误导性，因为数据实际上被分成块，并且列被分成不同站点上的相同观测值。

我们还可以看到超过 40% 的数据缺失。这很多。数据非常零散，在建模问题之前，我们需要很好地理解这一点。

分块数据结构

一个好的起点是根据块来查看数据。

块持续时间

我们可以按“chunkID”变量（列索引 1）对数据进行分组。

如果每个块是八天，并且观测值是每小时一次，那么我们预计每个块有 (8 * 24) 或 192 行数据。

如果数据有 37,821 行，那么一定有大于或小于 192 小时的块，因为 37,821/192 大约是 196.9 个块。

首先，我们将数据分割成块。我们可以先获取唯一的块标识符列表。

然后，我们可以收集每个块标识符的所有行，并将它们存储在字典中以便于访问。

下面定义了一个名为 to_chunks() 的函数，该函数接受加载数据的 NumPy 数组，并返回一个从 chunk_id 到块行的字典。

数据文件中的“position_within_chunk”表示行在块内的顺序。在此阶段，我们假设行已排序，无需再次排序。对原始数据文件的粗略浏览似乎证实了这一假设。

一旦数据被排序到块中，我们就可以计算每个块中的行数并查看分布，例如使用箱线图。

将所有这些联系起来的完整示例列在下面

运行示例首先打印数据集中块的数量。

我们可以看到有 208 个，这表明每小时观测值的数量确实必须因块而异。

创建了一个箱线图和块持续时间直方图。我们可以看到中位数确实是 192，这意味着大多数块有八天的观测值或接近八天的观测值。

我们还可以看到持续时间的尾部很长，低至约 25 行。尽管这些情况不多，但我们预计由于数据不足，这将很难预测。

分布也提出了关于每个块内观测值的连续性问题。

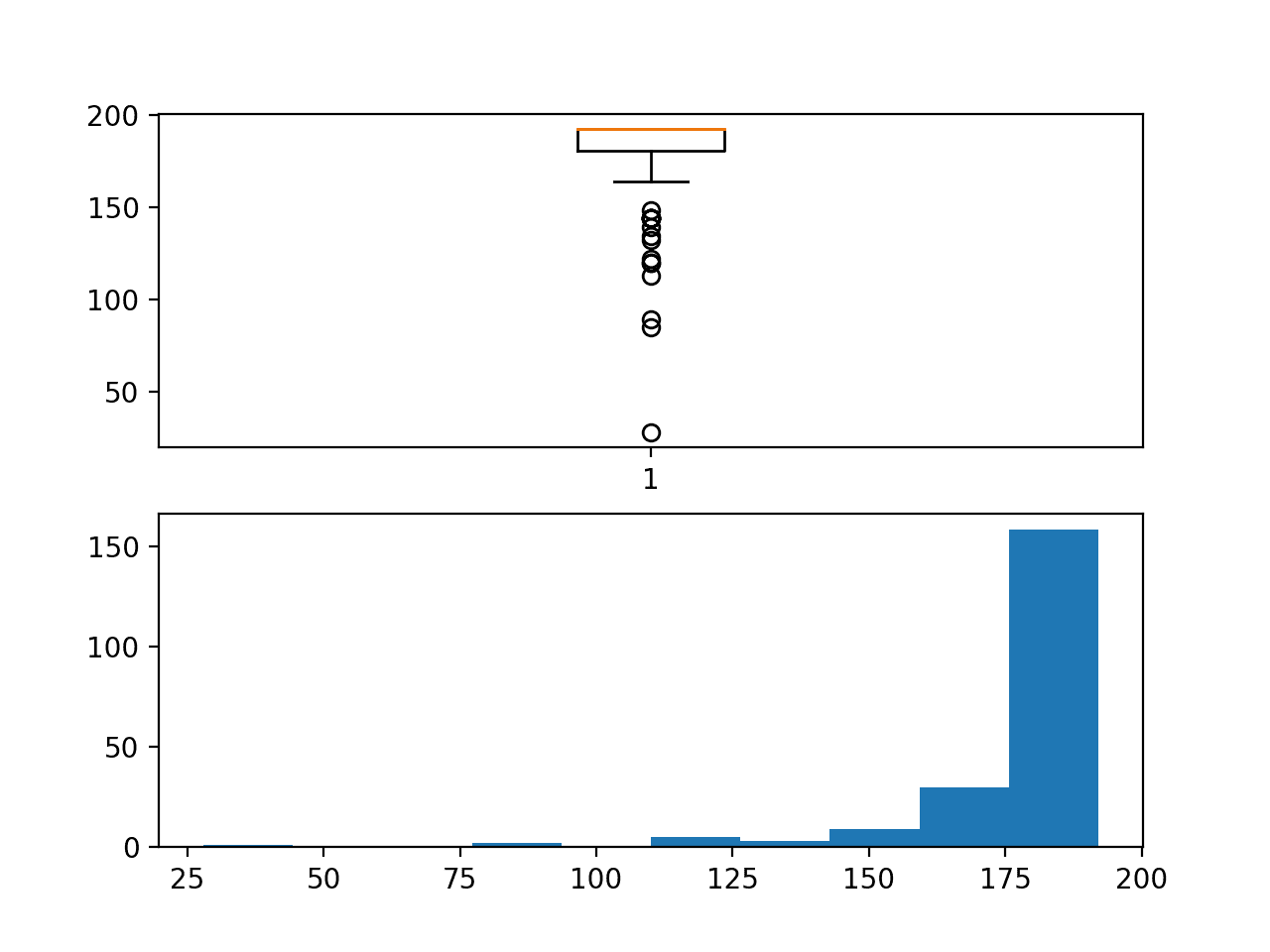
箱线图和按小时计算的块持续时间直方图

块的连续性

了解那些没有完整八天数据的块内观测值的连续性（或不连续性）可能会有所帮助。

一种考虑方法是为每个不连续的块创建一条线图，并显示观测值中的空白。

我们可以在单个图上完成此操作。每个块都有一个唯一的标识符，从 1 到 208，我们可以将其用作序列的值，并通过图上不会出现的 NaN 值标记八天间隔内的缺失观测值。

反之，我们可以假设所有时间步长在块内都有 NaN 值，然后使用“position_within_chunk”列（索引 2）来确定确实有值的时间步长并用块 ID 标记它们。

下面的 plot_discontinuous_chunks() 函数实现了这种行为，为每个缺少行的块在同一图上创建了一个序列或线。期望是线条中的中断将帮助我们了解这些不完整的块是连续的还是不连续的。

完整的示例如下所示。

运行示例将创建一个单独的图，其中包含每个包含缺失数据的块的一条线。

每个块线条中断的数量和长度反映了每个块内观测值的不连续程度。

许多块确实有很长一段连续数据，这对建模来说是个好兆头。

在某些情况下，块的观测值很少，并且存在的观测值是小片连续的。这些可能难以建模。

此外，并非所有这些块在块末尾都有观测值：即需要预测之前的时期。对于那些试图保持最近观测值的模型来说，这些尤其是一个挑战。

块中序列数据的不连续性也将使模型评估变得具有挑战性。例如，当观测值零散时，不能简单地将块数据一分为二，对前半部分进行训练，对后半部分进行测试。至少，在考虑不完整的块数据时是这样。

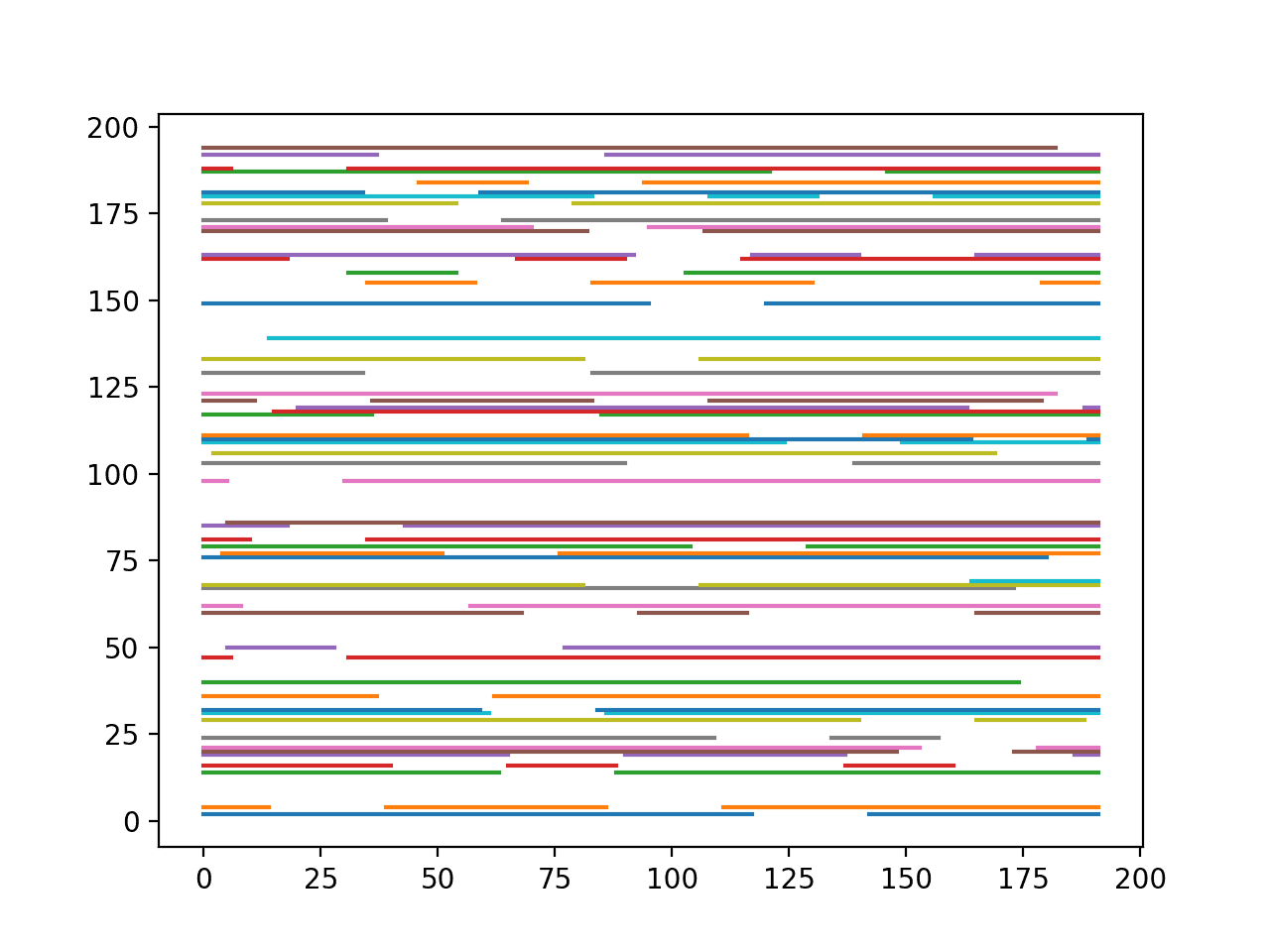
不连续观测块的线图

块内每日覆盖范围

块的不连续性也表明，查看每个块所覆盖的小时数可能很重要。

在一组环境数据中，一天中的时间非常重要，如果每个块的开始和结束时间在一天中有所不同，那么那些假定每个块都涵盖相同的每日或每周周期的模型可能会出现问题。

我们可以通过绘制每个块的第一个小时（在 24 小时制中）的分布来快速检查这一点。

直方图中的 bin 数量设置为 24，以便我们可以清楚地看到 24 小时制中一天中每个小时的分布。

此外，在收集块的第一个小时时，我们注意只从那些拥有八天完整数据的块中收集它，以防有缺失数据的块在块开始时没有观测值，我们知道这种情况确实会发生。

完整的示例如下所示。

运行示例将创建每个块中第一个小时的箱线图和直方图。

我们可以看到开始时间在一天中的 24 小时内分布相当均匀。

此外，这意味着每个块的预测间隔在 24 小时内也会有所不同。这给那些可能期望标准三天预测期（午夜到午夜）的模型带来了一个难题。

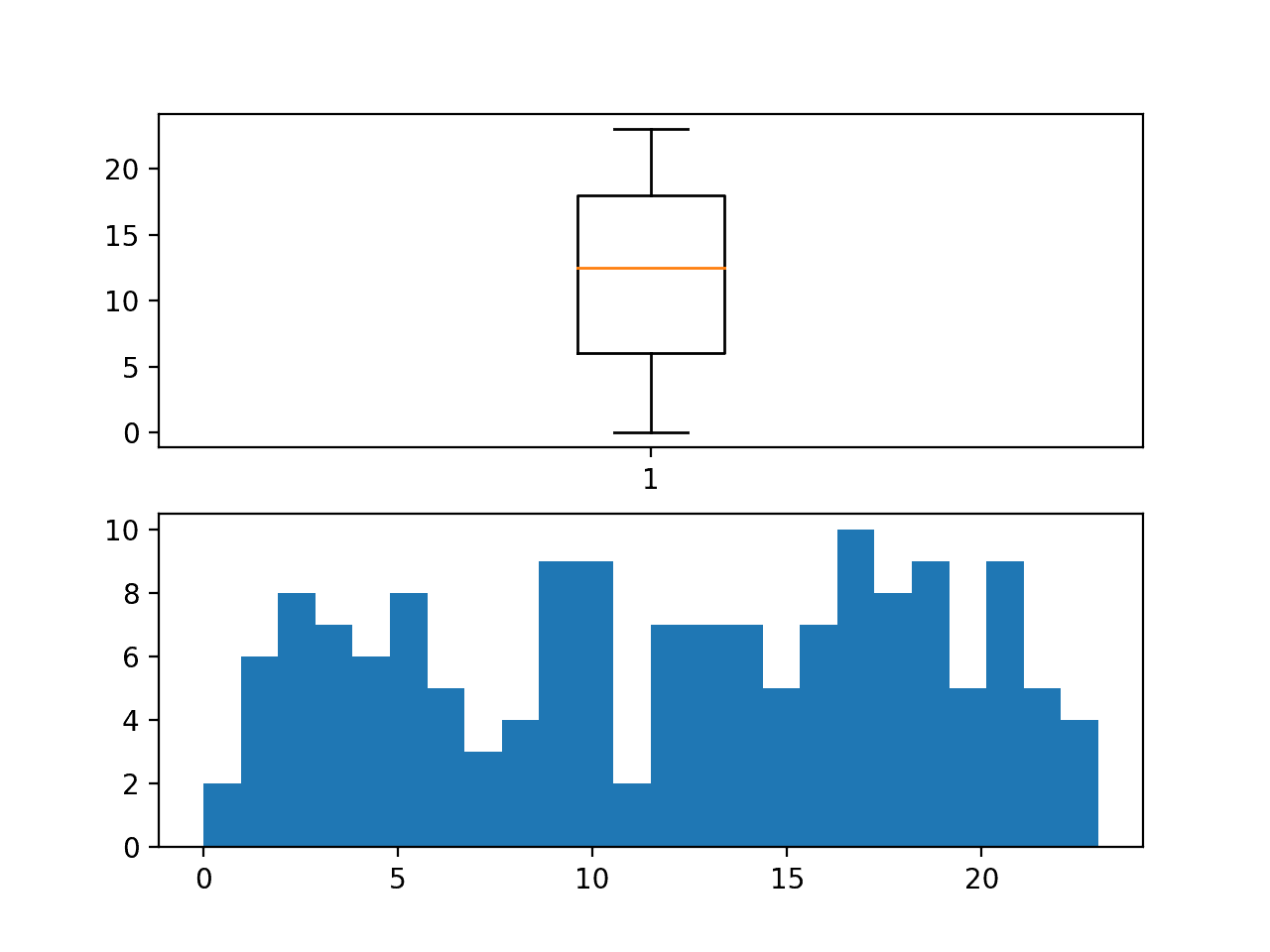
每个块内观测值的第一个小时的分布

现在我们对数据的块结构有了一些了解，让我们仔细看看描述气象观测值的输入变量。

输入变量

有 56 个输入变量。

前六个（索引 0 到 5）是块和观测时间相关的元数据信息。它们是

其余 50 个描述了特定地点的气象信息；它们是

实际上，只有八个气象输入变量

这些变量记录在 23 个独特站点；它们是

数据非常复杂。

并非所有变量都在所有站点记录。

目标变量中使用的站点标识符存在一些重叠，例如 1、50、64 等。

目标变量中使用的某些站点标识符在输入变量中未使用，例如 4002。还有一些站点标识符在输入变量中使用了，但在目标标识符中未使用，例如 15。

这至少表明并非所有变量都在所有位置记录。记录站点的站点之间存在异构性。此外，仅收集给定类型测量值或收集所有测量值的站点可能存在特殊之处。

让我们仔细看看输入变量的数据。

块的输入时态结构

我们可以从查看每个块输入的结构和分布开始。

前几个包含八天观测值的块的 chunkId 分别是 1、3 和 5。

我们可以枚举所有输入列，并为每个列创建一个线图。这将为每个输入变量创建一个时间序列线图，以粗略了解每个变量随时间的变化。

我们可以对几个块重复此操作，以了解时间结构在块之间可能如何不同。

下面的 plot_chunk_inputs() 函数以块格式获取数据和要绘制的块 ID 列表。它将创建一个包含 50 个线图的图形，每个输入变量一个，每个图 n 条线，每个块一条。

完整的示例如下所示。

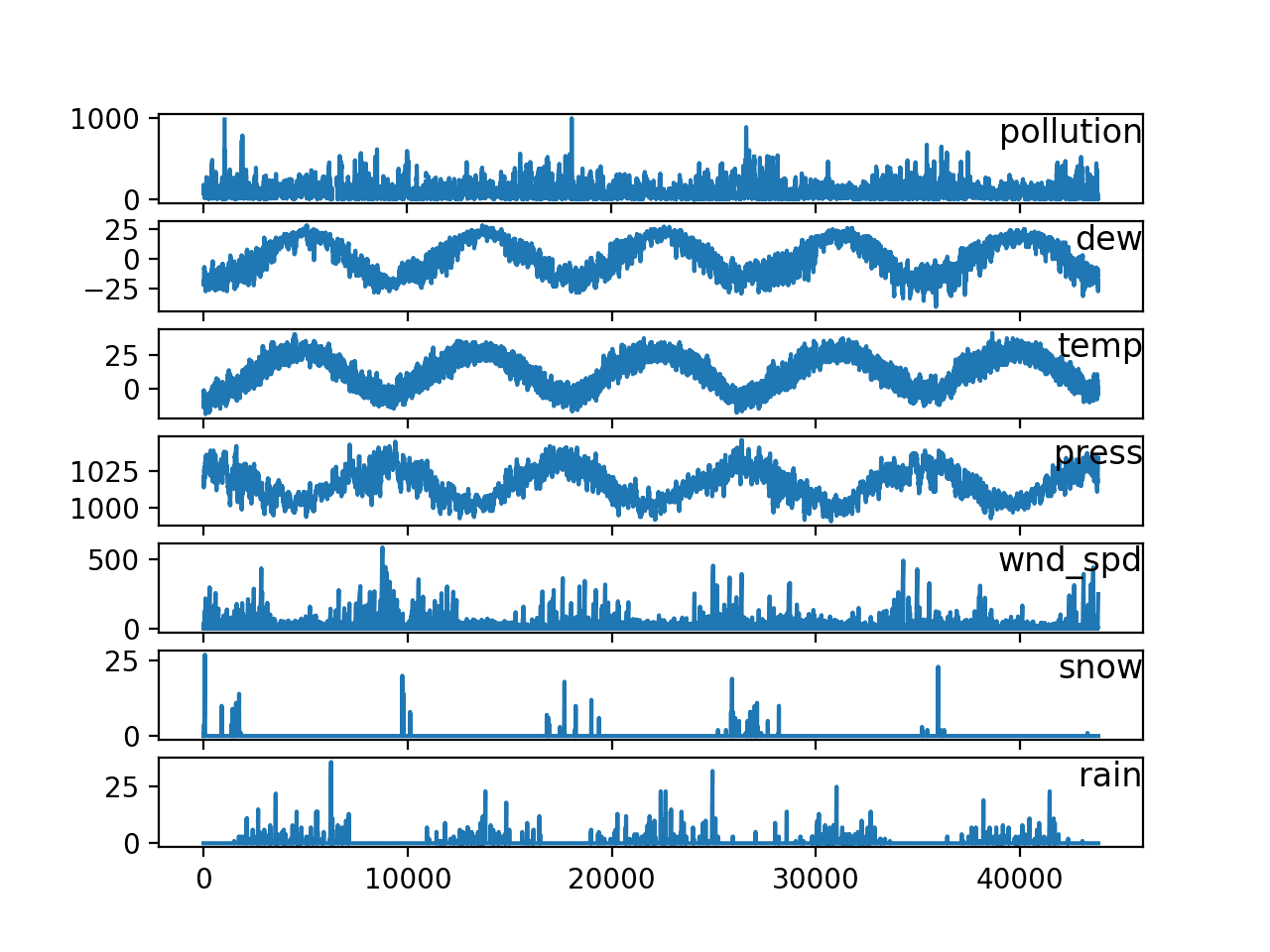
运行示例将创建一个包含 50 条线图的单个图形，每个气象输入变量一个。

这些图很难看清，因此您可能需要增加创建图形的大小。

我们可以看到前五个变量的观测值看起来相当完整；它们是太阳辐射、风速和风向。其余变量看起来相当零散，至少对于这个块是这样。

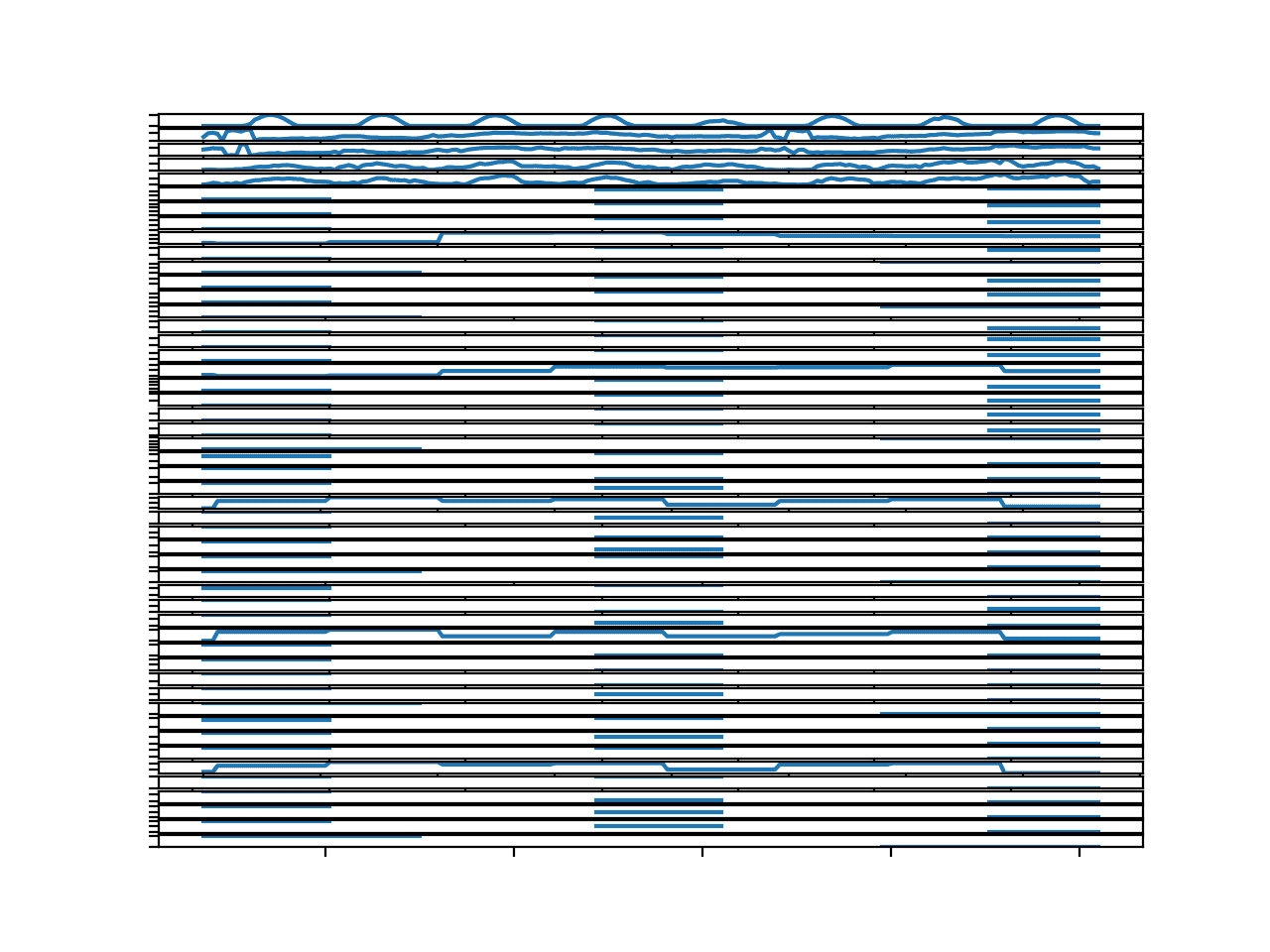
一个块所有输入变量的并行时间序列线图

我们可以更新示例并绘制前三个具有完整八天观测值的块的输入变量。

运行示例将创建相同的 50 条线图，每个图包含三条序列或线，每个块一条。

同样，该图使得单个图难以看清，因此您可能需要增大图的大小才能更好地查看模式。

我们可以看到这三个图在每个线图中确实显示了相似的结构。这是一个有用的发现，因为它表明在多个块中建模相同的变量可能很有用。

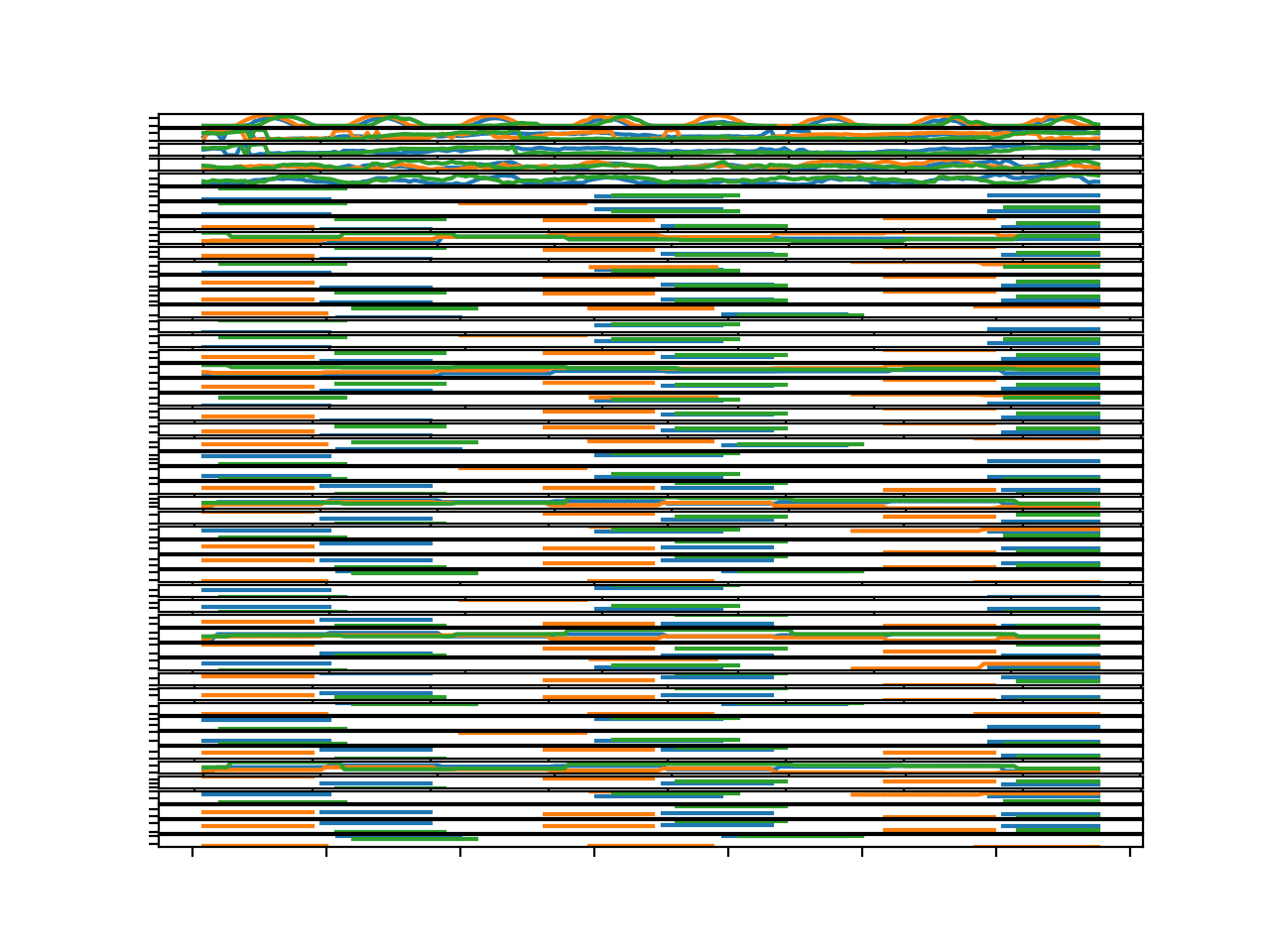
三个块所有输入变量的并行时间序列线图

这确实提出了一个问题，即变量的分布在站点之间是否存在很大差异。

输入数据分布

我们可以使用箱线图粗略地查看输入变量的分布。

下面的 plot_chunk_input_boxplots() 将为单个块的数据创建每个输入特征的箱线图。

完整的示例如下所示。

运行示例将创建 50 个箱线图，每个箱线图对应训练数据集中第一个块中的一个输入变量观测值。

我们可以看到相同类型的变量可能具有相同的观测值分布，并且每组变量似乎具有不同的单位。例如，风向可能是度，压力是百帕，温度是摄氏度，等等。

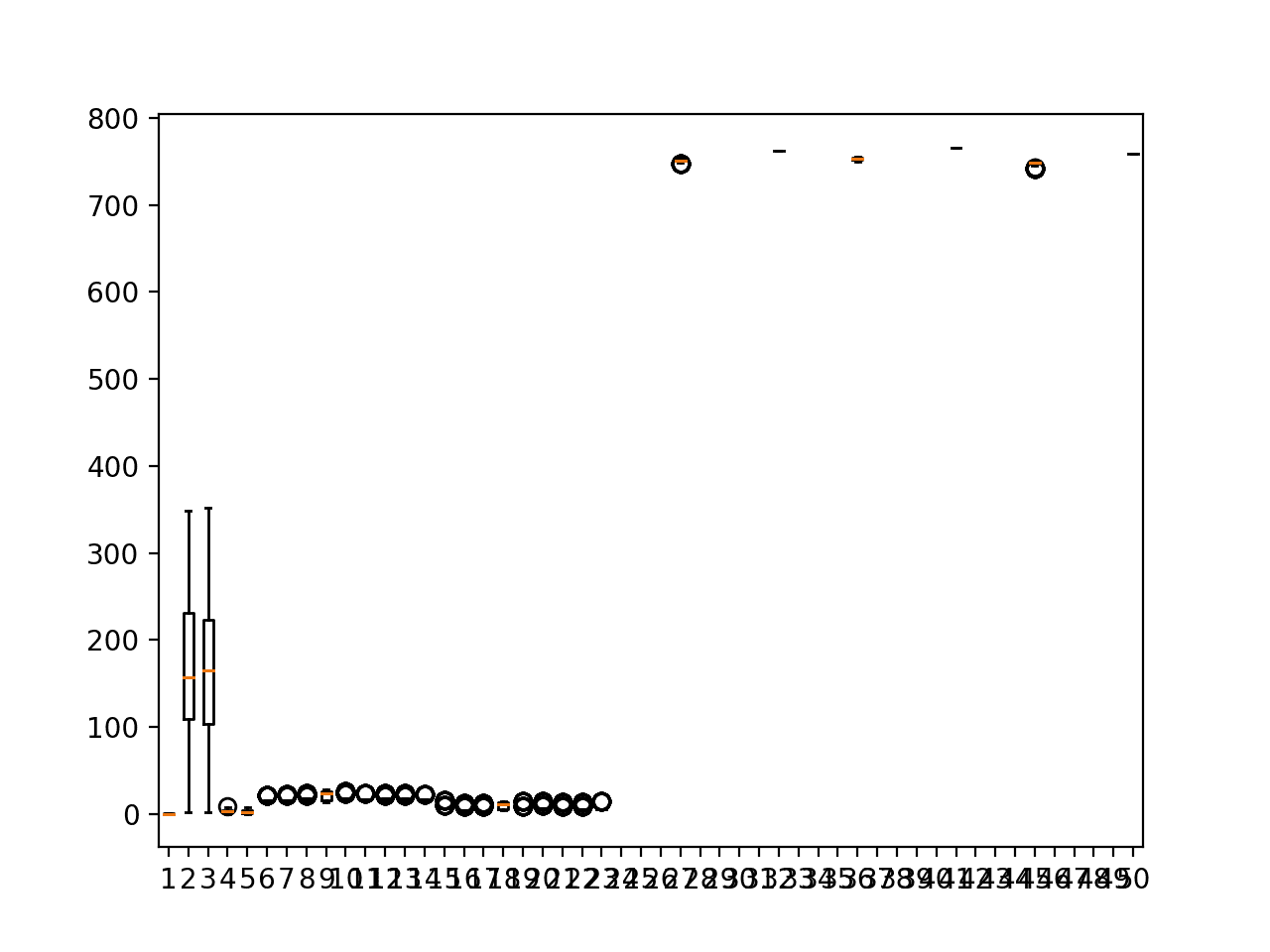
一个块的输入变量箱线图

进一步调查八种变量类型中每种变量的分布和扩散可能很有趣。这留作进一步的练习。

我们对输入变量有一些粗略的了解，或许它们可能有助于预测目标变量。我们不能确定。

现在我们可以将注意力转向目标变量。

目标变量

预测问题的目标是预测三天内多个站点上的多个变量。

有 39 个时间序列变量需要预测。

从列标题来看，它们是

这些列标题的命名约定是

我们可以通过一点正则表达式将这些列标题转换为一个包含变量 ID 和站点 ID 的小型数据集。

结果如下

很有用的是，目标按变量 ID 分组。

我们可以看到一个变量可能需要在多个站点进行预测；例如，在站点 1、32、50 等处预测变量 11

我们可以看到，对于给定站点，可能需要预测不同的变量。例如，站点 50 需要变量 11、3 和 4

我们可以将小目标数据集保存到一个名为“targets.txt”的文件中，并将其加载以进行快速分析。

运行示例会打印唯一变量和站点的数量。

我们可以看到 39 个目标变量远少于 (12*14) 168 个，如果我们要预测所有站点所有变量的话。

让我们仔细看看目标变量的数据。

块的目标时间结构

我们可以从查看每个块目标的结构和分布开始。

前几个包含八天观测值的块的 chunkId 分别是 1、3 和 5。

我们可以枚举所有目标列，并为每个列创建一个线图。这将为每个目标变量创建一个时间序列线图，以粗略了解它随时间的变化。

我们可以对几个块重复此操作，以粗略了解时间结构在块之间可能如何变化。

下面的函数 plot_chunk_targets() 以块格式获取数据和要绘制的块 ID 列表。它将创建一个包含 39 个线图的图形，每个目标变量一个，每个图 n 条线，每个块一条。

完整的示例如下所示。

运行示例将为块标识符“1”创建一个包含 39 条线图的单个图形。

这些图很小，但可以粗略了解变量的时间结构。

我们可以看到，这个块中有很多变量没有数据。这些变量不能直接预测，可能也无法间接预测。

这表明，除了并非所有站点都有所有变量外，即使列标题中指定的变量也可能在某些块中不存在。

我们还可以看到一些序列中由于缺失值而出现中断。这表明，即使我们可能在块内每个时间步都有观测值，但我们可能无法在块内所有变量上都获得连续序列。

许多图都具有周期性结构。大多数都有八个峰值，很可能对应于块内的八天观测值。这种季节性结构可以直接建模，或许可以在建模时从数据中删除，并在预测区间中添加回来。

该序列似乎没有任何趋势。

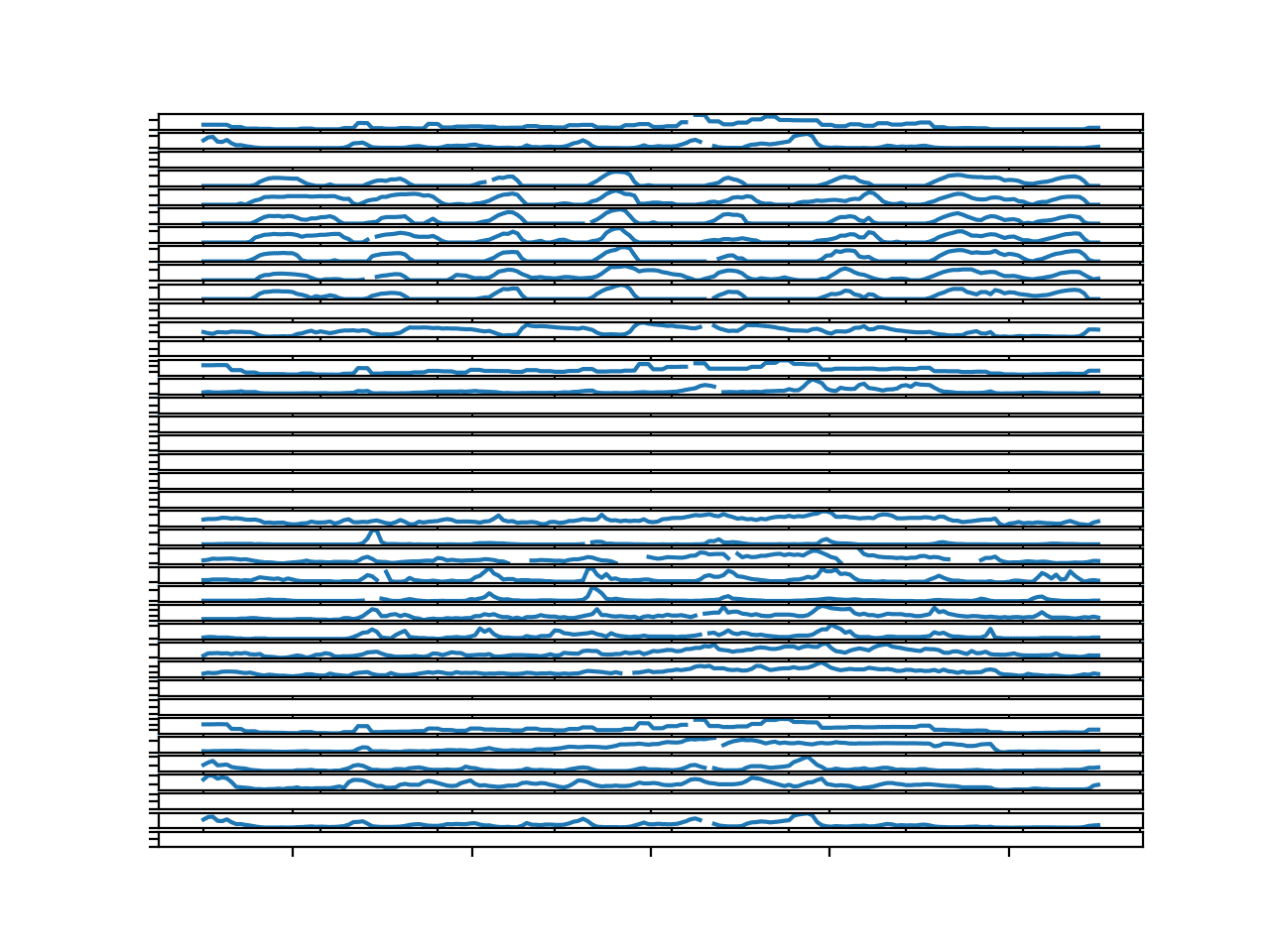
一个块所有目标变量的并行时间序列线图

我们可以重新运行示例，并绘制前三个具有完整数据的块的目标变量。

运行示例会创建一个包含 39 个图和每个图三条时间序列（每个块的目标对应一条）的图形。

该图内容较多，您可能需要增大图窗的大小才能更好地查看目标变量在不同块之间的比较。

对于许多具有循环每日结构的变量，我们可以在各个块中看到重复的结构。

这令人鼓舞，因为它表明为某个站点建模变量可能有助于跨块进行建模。

此外，图 3 到 10 对应于跨越七个不同站点的变量 11。这些图在时间结构上的字符串相似性表明，按变量对数据进行建模（该变量在不同站点使用）可能是有益的。

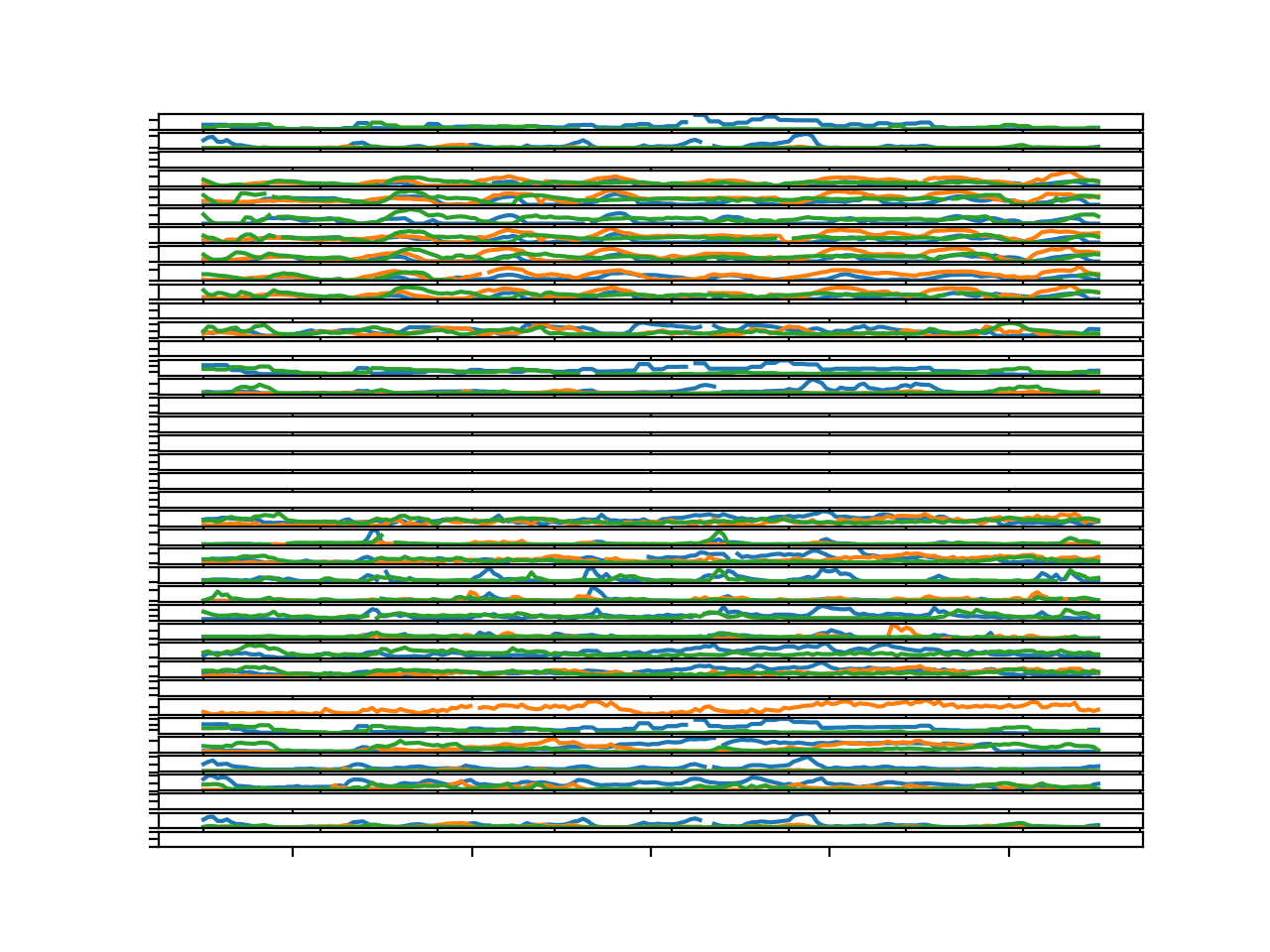
三个块所有目标变量的并行时间序列线图

目标变量的箱线图分布

查看目标变量的分布也很有用。

我们可以从查看一个块中每个目标变量的分布开始，方法是为每个目标变量创建箱线图。

可以为每个目标变量并排创建单独的箱线图，以便在相同比例下直接比较值的形状和范围。

完整的示例如下所示。

运行示例将创建一个包含 39 个箱线图的图形，每个箱线图对应第一个块中的 39 个目标变量之一。

我们可以看到许多变量的中位数接近零或一；我们还可以看到大多数变量存在较大的不对称分布，这表明这些变量可能存在偏斜和异常值。

令人鼓舞的是，变量 11 在七个站点上的箱线图 4-10 显示出相似的分布。这进一步支持了数据可以按变量分组并用于拟合可在不同站点使用的模型的证据。

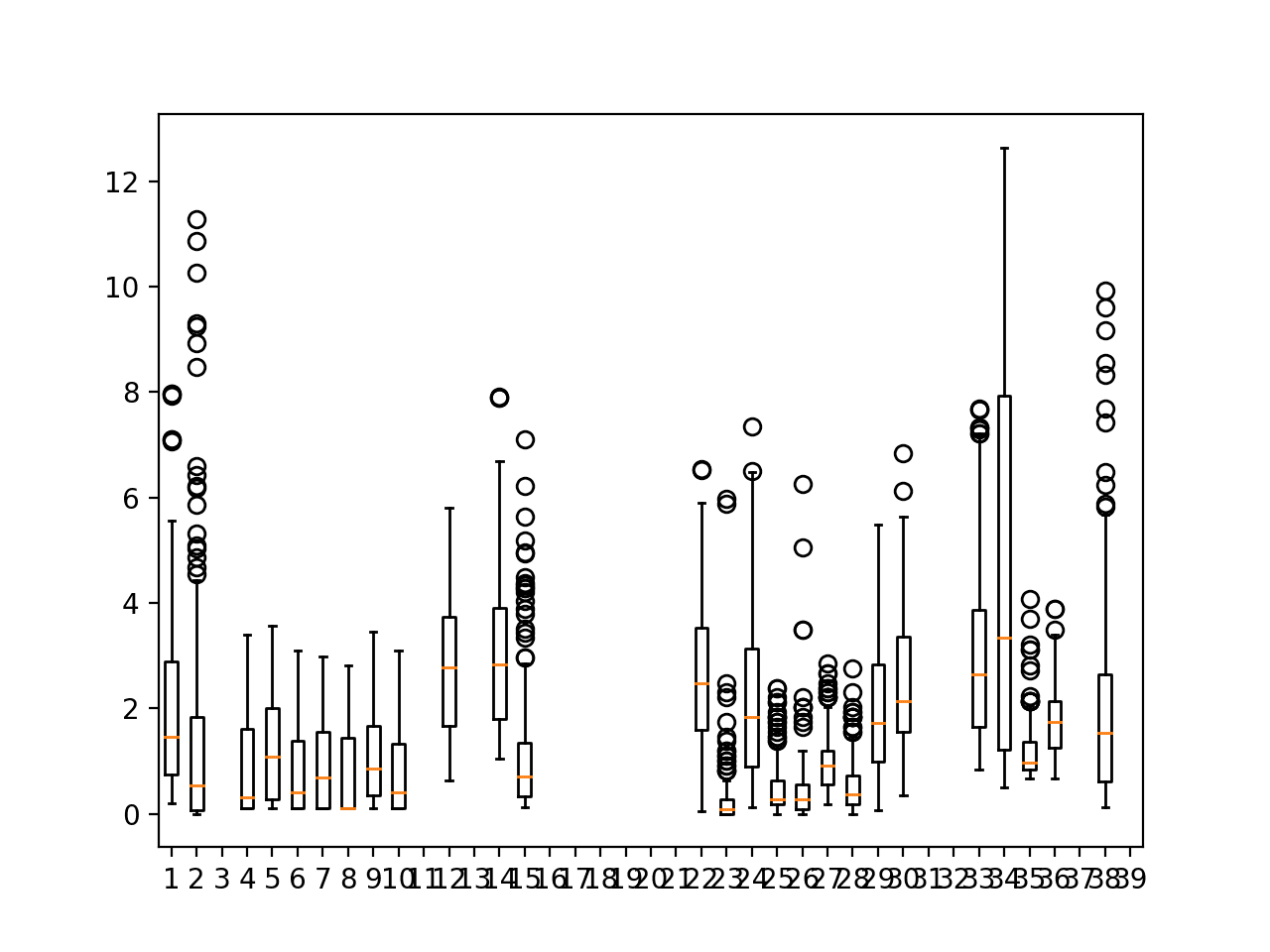
一个块目标变量的箱线图

我们可以使用所有块的数据重新创建此图，以查看数据集范围内的模式。

完整的示例如下所示。

运行示例会创建一个新图，显示整个训练数据集的 39 个箱线图，不考虑块。

这有点混乱，圆形异常值模糊了主要数据分布。

我们可以看到异常值确实延伸到 5 到 10 个单位的范围。这表明在建模时对目标进行标准化和/或重新缩放可能有用。

也许最有用的发现是，有些目标无论块如何，都没有任何（或很少）数据。这些列可能应该从数据集中排除。

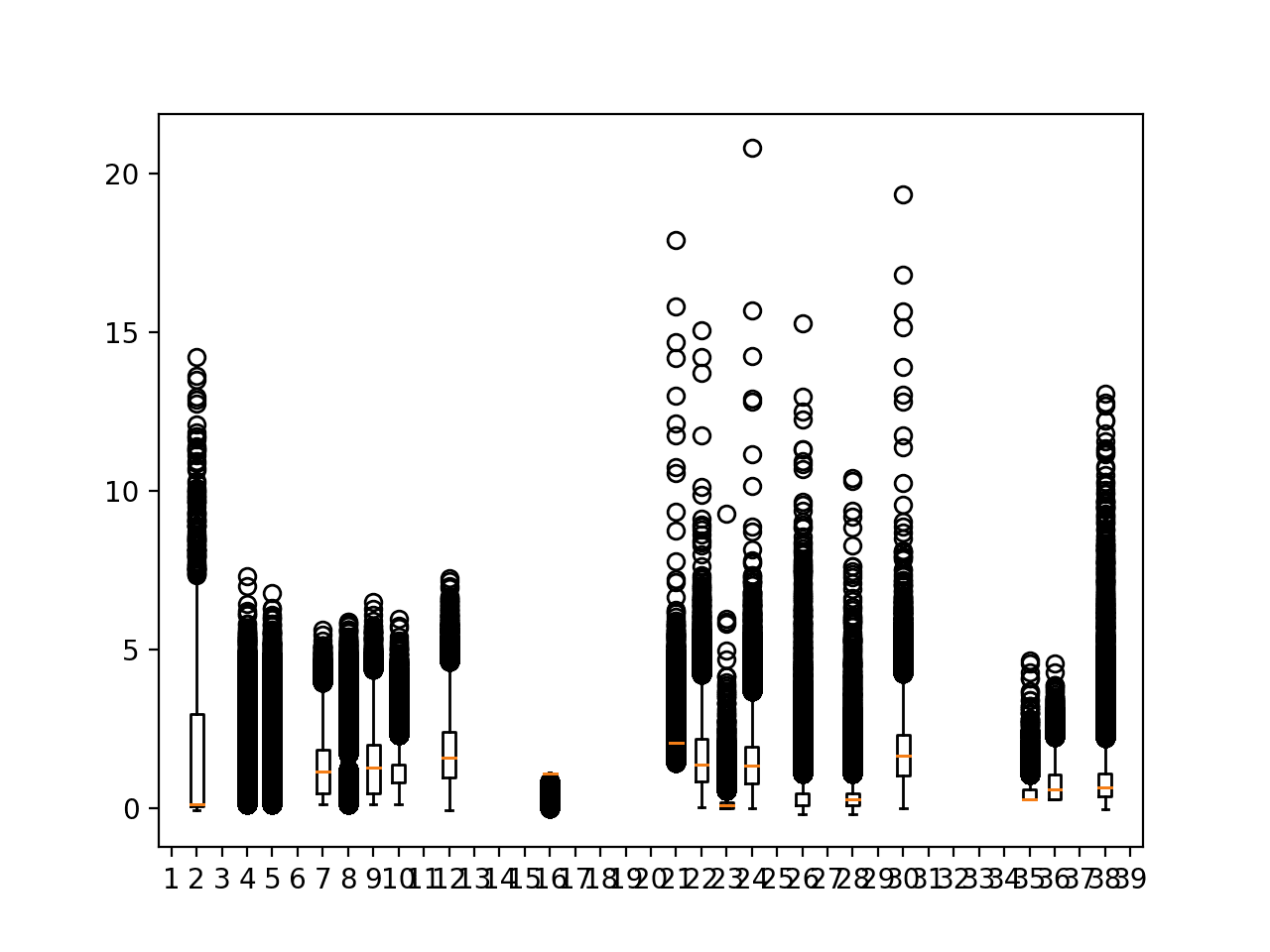
所有训练数据目标变量的箱线图

显然为空的目标列

我们可以通过创建每列缺失数据比率的条形图来进一步调查明显的缺失数据，不包括开头的元数据列（例如前五列）。

下面的 plot_col_percentage_missing() 函数实现了这一点。

完整的示例如下所示。

运行示例首先打印列 ID（零偏移量）和缺失数据比率，如果比率高于 90%。

我们可以看到实际上没有列包含零非 NaN 数据，但大约有二十几列（12 列）的缺失数据高于 90%。

有趣的是，其中七个是目标变量（索引 56 或更高）。

创建了一个柱状图，显示列索引号与缺失数据比率的关系。

我们可以看到缺失数据的比率可能存在一些分层，一簇低于 10%，一簇在 70% 左右，一簇高于 90%。

我们还可以看到输入变量和目标变量之间存在分离，前者非常规律，因为它们显示了在不同站点测量的相同变量类型。

一些目标变量如此少量的数据表明需要利用除了过去观测值之外的其他因素来进行预测。

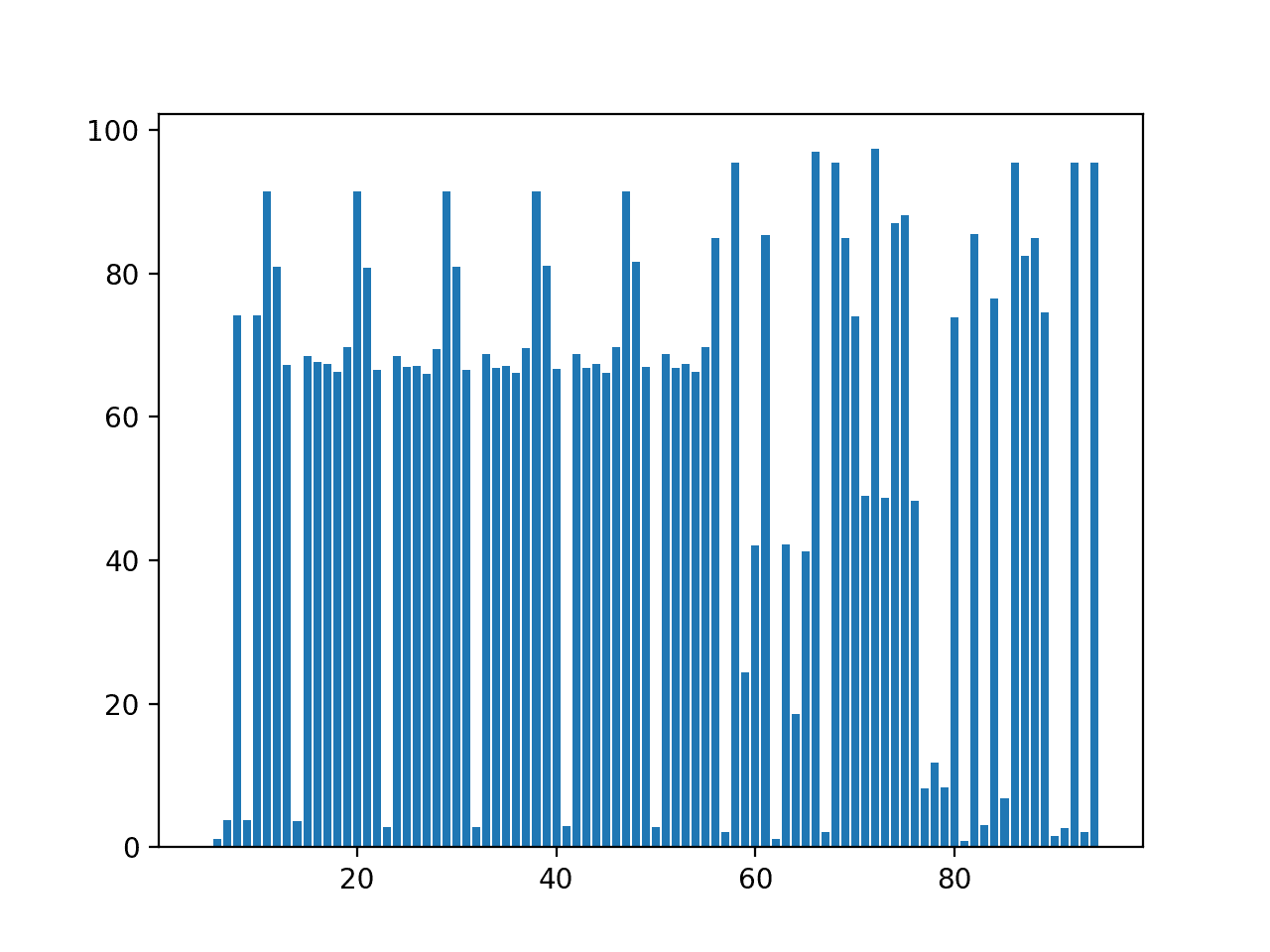
每列缺失数据百分比的条形图

目标变量的直方图分布

目标变量的分布不整齐，可能至少是非高斯分布，最坏情况下是高度多模态分布。

我们可以通过查看单个块数据的目标变量直方图来检查这一点。

matplotlib 中的 hist() 函数存在一个问题，即它对 NaN 值不健壮。我们可以通过在绘图前检查每列是否有非 NaN 值并排除带有 NaN 值的行来克服这个问题。

下面的函数完成了这项工作，并为一个或多个块的每个目标变量创建了一个直方图。

完整的示例如下所示。

运行示例将创建一个包含 39 个直方图的图形，每个直方图对应第一个块中的一个目标变量。

该图难以阅读，但大量的箱子确实显示了变量的分布。

可以公平地说，也许没有任何目标变量具有明显的高斯分布。许多可能具有长右尾的偏斜分布。

其他变量具有看起来非常离散的分布，这可能是所选测量设备或测量尺度的产物。

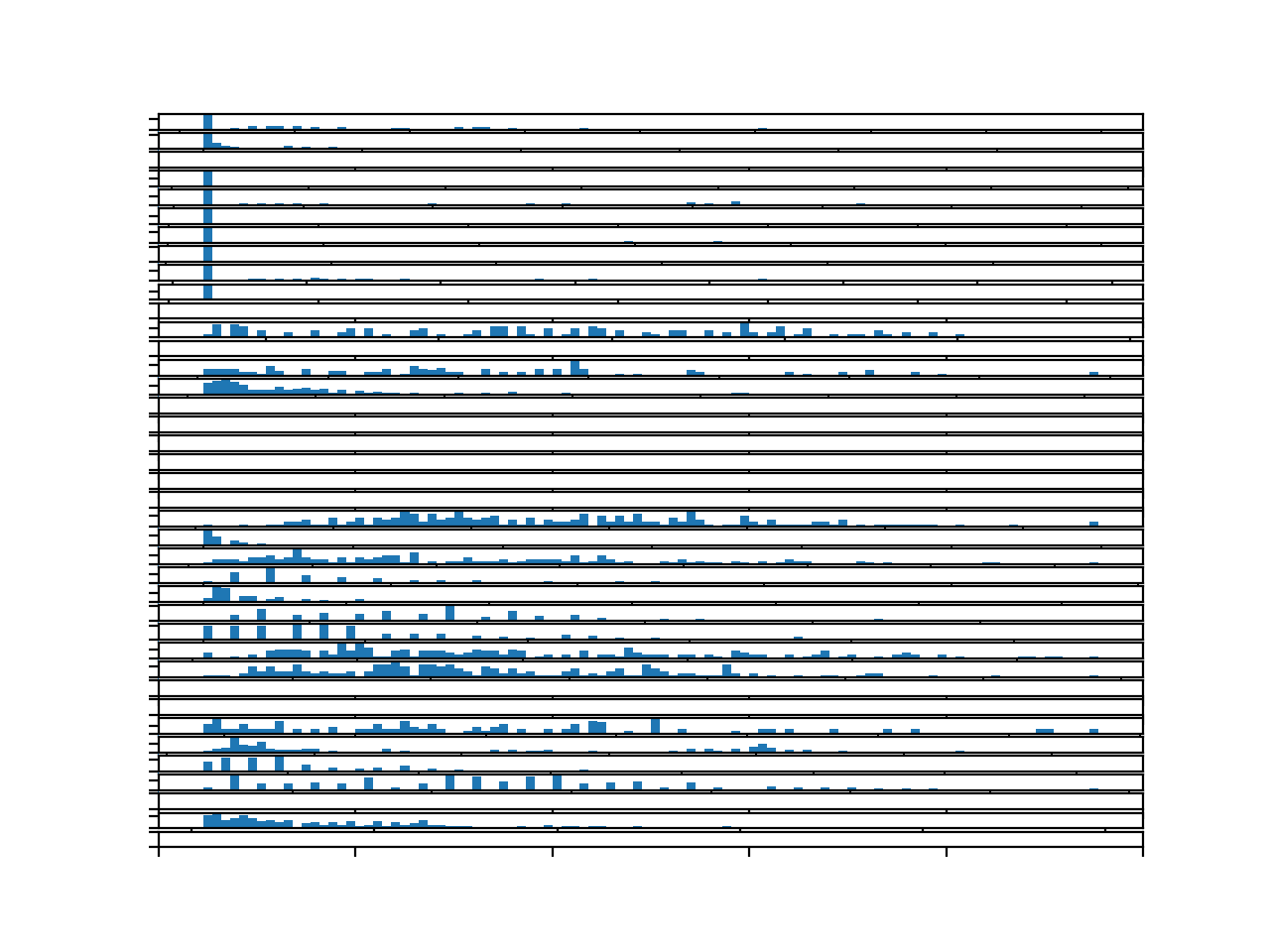
一个块中每个目标变量的直方图

我们可以用所有块的目标变量重新创建相同的图。

完整的示例如下所示。

运行示例将创建一个包含 39 个直方图的图形，每个直方图对应训练数据集中的一个目标变量。

我们可以看到更完整的分布，这更具洞察力。

最初的几个图可能显示高度偏斜的分布，其核心可能高斯也可能不是高斯。

我们可以看到许多类似高斯分布的带有间隙的分布，这表明离散测量强加于高斯分布的连续变量上。

我们还可以看到一些变量显示出指数分布。

总而言之，这表明可以使用幂变换来探索将数据重塑为更接近高斯分布，和/或使用不依赖于变量高斯分布的非参数建模方法。例如，经典的线性方法可能会遇到困难。

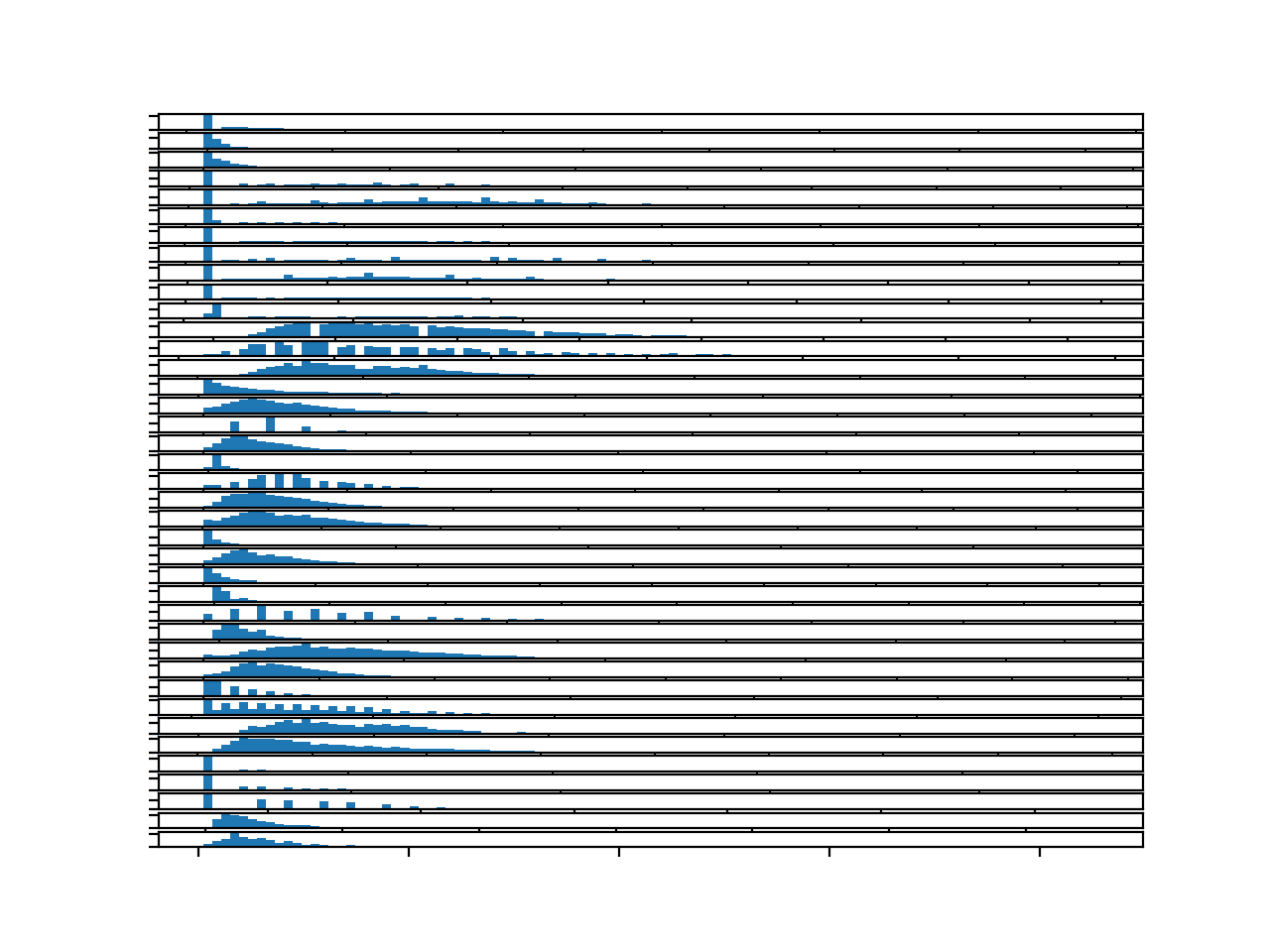
整个训练数据集中每个目标变量的直方图

目标变量的一个难题

比赛结束后，数据提供者 David Chudzicki 总结了 12 个输出变量的真实含义。

这在一篇题为“目标变量的真实含义”的论坛帖子中提供，部分摘录如下

这很有趣，因为我们可以看到目标变量在性质上是气象的，并且与空气质量相关，正如竞赛名称所示。

问题是，数据集中有 15 个变量，但只有 12 种不同类型的目标变量。

造成此问题的原因是数据集中相同的目标变量可能用于表示不同的目标变量。具体来说

• 目标 8 可能是“一氧化碳”或“硫酸盐 PM2.5 LC”的数据。
• 目标 4 可能是“二氧化硫”或“PM2.5 原始数据”的数据。
• 目标 3 可能是“SO2 最大 5 分钟平均值”或“PM2.5 AQI & 形态质量”的数据。

从变量名称来看，将数据重复到相同目标变量中是针对化学性质甚至测量方法不同的变量进行的，例如，这似乎是偶然而非策略性的。

目前尚不清楚，但很可能一个目标在一个块内表示一个变量，但在不同块之间可能表示不同的变量。或者，也可能变量在每个块内不同站点之间存在差异。在前一种情况下，这意味着期望这些目标变量在块之间保持一致性的模型（这是一个非常合理的假设）可能会遇到困难。在后一种情况下，模型可以将变量-站点组合视为不同的变量。

可以通过比较这些变量在不同块之间的分布和尺度来区分差异。

这令人失望，并且取决于其对建模技能的影响程度，可能需要从数据集中删除这些变量，这涉及到许多目标变量（39 个中的 20 个）。

建模思考

在本节中，我们将利用我们所发现的问题，并提出一些建模此问题的方法。

我喜欢这个数据集；它杂乱、真实，并且抵制了简单的处理方法。

本节分为四个部分；它们是

• 框架。
• 数据准备。
• 建模。
• 评估。

框架

该问题通常被构架为多元多步时间序列预测问题。

此外，需要在多个站点预测多个变量，这是时间序列预测问题常见的结构分解，例如在商店或站点等不同物理位置预测变量。

让我们来看看一些可能的数据框架。

按变量和站点进行单变量分析

初步方法可能是将每个站点上的每个变量视为一个单变量时间序列预测问题。

模型接收一个变量的八天每小时观测值，并被要求预测三天，从中选取特定子集的预测提前期并使用或评估。

在少数选定的情况下可能是可行的，这可以通过进一步的数据分析来确认。

然而，数据通常不符合这种框架，因为并非所有块都包含每个目标变量的八天观测值。此外，目标变量的时间序列可能严重不连续，甚至大部分（90% 到 95%）不完整。

我们可以放宽对模型所需先前数据结构和数量的期望，设计模型以利用可用的任何数据。

这种方法每个块需要 39 个模型，总共需要 (208 * 39) 即 8,112 个单独的模型。这听起来可行，但从工程角度来看，可能不如我们所期望的那样可扩展。

变量-站点组合可以在不同块之间建模，只需要 39 个模型。

按变量单变量

目标变量可以跨站点聚合。

我们还可以放宽用于进行预测的滞后提前期，并呈现可用数据，无论是使用零填充还是对缺失值进行插补，甚至是不考虑提前期的滞后观测值。

然后，我们可以将问题框架为：给定某个变量的一些先验观测值，预测接下来的三天。

模型可能有更多可处理的数据，但会忽略基于站点的任何变量差异。这可能或可能没有理由，可以通过比较站点之间的变量分布来检查。

有 12 个独特的变量。

我们可以对每个块的每个变量进行建模，得到 (208 * 12) 或 2,496 个模型。对 12 个变量跨块进行建模可能更有意义，只需要 12 个模型。

多变量模型

也许一个或多个目标变量依赖于一个或多个气象变量，甚至依赖于其他目标变量。

这可以通过调查每个目标变量与每个输入变量以及与其他目标变量之间的相关性来探索。

如果存在这种依赖关系，或者可以假设存在这种依赖关系，那么不仅可以预测数据更完整的变量，还可以预测缺失数据超过 90% 的目标变量。

此类模型可以使用先前的气象观测值和/或目标变量观测值的子集作为输入。数据的不连续性可能需要放宽输入变量的传统滞后时间结构，允许模型使用特定预测可用的任何数据。

数据准备

根据模型的选择，输入和目标变量可能会受益于一些数据准备，例如

• 标准化。
• 归一化。
• 幂变换，如果为高斯分布。
• 季节性差分，如果存在季节性结构。

为了解决缺失数据问题，在某些情况下可能需要使用简单的持久性或平均值进行插补。

在其他情况下，并且根据模型的选择，可以直接从 NaN 值中学习作为观测值（例如 XGBoost 可以做到这一点），或者用 0 值填充并屏蔽输入（例如 LSTM 可以做到这一点）。

研究将输入下采样到 2、4 或 12 小时数据或类似数据以尝试填补不连续数据中的空白可能会很有趣，例如，从 12 小时数据预测每小时数据。

建模

建模可能需要一些原型设计来发现哪些方法和选择的输入观测值效果良好。

经典方法

在极少数情况下，如果块数据完整，可以使用 ETS 或 SARIMA 等经典方法进行单变量预测。

总的来说，这个问题不适合使用经典方法。

机器学习

一个好的选择是使用非线性机器学习方法，这些方法与输入数据的时间结构无关，并利用可用的一切。

此类模型可以采用递归或直接策略来预测提前期。直接策略可能更有意义，每个所需的提前期使用一个模型。

有 10 个提前期和 39 个目标变量，在这种情况下，直接策略将需要 (39 * 10) 或 390 个模型。

直接建模方法的一个缺点是模型无法利用预测区间中目标变量之间的任何依赖关系，特别是在站点之间、变量之间或提前期之间。如果存在这些依赖关系（其中一些肯定存在），则可以通过使用第二层集成模型来添加它们的一些特征。

特征选择可用于发现可能对预测每个目标变量和提前期最有价值的变量和/或滞后提前期。

这种方法将提供很大的灵活性，正如竞赛中所示，决策树集成模型在几乎不进行调优的情况下表现良好。

深度学习

与机器学习方法一样，深度学习方法可能能够使用任何可用的多变量数据来进行预测。

值得探索的两种神经网络类别是：

• 卷积神经网络（CNN）。
• 循环神经网络，特别是长短期记忆网络（LSTM）。

卷积神经网络（CNN）能够将长序列的多元输入时间序列数据提炼成小型特征图，并从序列中学习最相关的预测特征。它们处理噪声和输入序列中特征不变性的能力可能很有用。与其他神经网络一样，CNN 可以输出向量来预测预测提前期。

LSTMs 旨在处理序列数据，并可以通过掩码直接支持缺失数据。它们也能够从长输入序列中自动学习特征，并且单独或与 CNN 结合使用时可能在此问题上表现良好。结合编码器-解码器架构，LSTM 网络可以原生预测多个提前期。

评估 (Evaluation)

一种反映竞赛中使用的朴素方法可能是评估模型的最佳选择。

也就是说，将每个块分成训练集和测试集，在这种情况下，使用前五天的数据进行训练，其余三天用于测试。

通过在整个数据集上训练模型并将其预测结果提交到 Kaggle 网站，以便在保留的测试数据集上进行评估，这可能是可行且有趣的。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

• 一个标准的多变量、多步、多站点时间序列预测问题
• EMC数据科学全球黑客马拉松（空气质量预测）
• 将所有内容扔进随机森林：本·哈姆纳谈赢得空气质量预测黑客马拉松
• EMC数据科学全球黑客马拉松（空气质量预测）的获胜代码
• 划分模型的一般方法？

总结

在本教程中，您发现并探索了空气质量预测数据集，它代表了一个具有挑战性的多元、多站点和多步时间序列预测问题。

具体来说，你学到了：

• 如何加载和探索数据集的块结构。
• 如何探索和可视化数据集的输入和目标变量。
• 如何利用新理解来概述一套用于构建问题、准备数据和建模数据集的方法。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

立即开发时间序列深度学习模型！

在几分钟内开发您自己的预测模型

...只需几行python代码

在我的新电子书中探索如何实现
用于时间序列预测的深度学习

它提供关于以下主题的自学教程：
CNN、LSTM、多元预测、多步预测等等...

最终将深度学习应用于您的时间序列预测项目

跳过学术理论。只看结果。

查看内容