人类活动识别是指将由专用安全带或智能手机记录的加速度计数据序列分类为已知的、定义明确的运动的问题。
鉴于每秒产生的大量观测数据、观测数据的时间性质以及缺乏将加速度计数据与已知运动关联起来的明确方法,这是一个具有挑战性的问题。
解决该问题的经典方法包括根据固定大小的窗口从时间序列数据中手动创建特征,并训练机器学习模型,例如决策树集成。困难在于这种特征工程需要该领域的深厚专业知识。
最近,深度学习方法,如循环神经网络和一维卷积神经网络(或CNN),已被证明在具有挑战性的活动识别任务中,在很少或没有数据特征工程的情况下,提供了最先进的结果。
在本教程中,您将发现用于时间序列分类的“智能手机活动识别”数据集,以及如何加载和探索该数据集以使其为预测建模做好准备。
完成本教程后,您将了解:
- 如何下载和加载数据集到内存。
- 如何使用线图、直方图和箱线图来更好地理解运动数据的结构。
- 如何对问题进行建模,包括框架、数据准备、建模和评估。
通过我的新书《时间序列预测深度学习》**启动您的项目**,其中包括**分步教程**和所有示例的**Python源代码**文件。
让我们开始吧。

如何根据智能手机数据为人类活动建模
摄影师拍摄,保留部分权利。
教程概述
本教程分为10个部分;它们是
- 人类活动识别
- 使用智能手机数据集进行活动识别
- 下载数据集
- 加载数据
- 活动类别的平衡
- 绘制一个受试者的时间序列数据
- 绘制每个受试者的直方图
- 绘制每个活动的直方图
- 绘制活动持续时间箱线图
- 建模方法
1. 人类活动识别
人类活动识别,简称HAR,是根据传感器记录的人体运动轨迹预测其正在做什么的问题。
运动通常是正常的室内活动,例如站立、坐着、跳跃和上楼梯。
传感器通常放置在受试者身上,例如智能手机或背心,并且通常以三个维度(x,y,z)记录加速度计数据。
人类活动识别(HAR)旨在根据对个人及其周围环境的一组观测来识别其所进行的动作。识别可以通过利用从各种来源(例如环境或穿戴式传感器)检索到的信息来完成。
——《使用智能手机进行人类活动识别的公共领域数据集》,2013年。
这个想法是,一旦识别并知道了受试者的活动,智能计算机系统就可以提供帮助。
这是一个具有挑战性的问题,因为没有明确的分析方法可以以普遍的方式将传感器数据与特定动作关联起来。从技术上讲,它具有挑战性,因为收集了大量传感器数据(例如,每秒数十或数百个观测值),并且在开发预测模型时,经典方法是手动从这些数据中提取特征和启发式方法。
最近,深度学习方法已成功应用于HAR问题,因为它们能够自动学习高阶特征。
基于传感器的活动识别旨在从大量低级传感器读数中获取关于人类活动的深刻高级知识。传统的模式识别方法在过去几年中取得了巨大进展。然而,这些方法通常严重依赖启发式手动特征提取,这可能会阻碍其泛化性能。 […] 最近,深度学习的最新进展使得自动进行高级特征提取成为可能,从而在许多领域取得了可喜的性能。
时间序列深度学习需要帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
2. 使用智能手机数据集进行活动识别
一个标准的人类活动识别数据集是2012年发布的“智能手机活动识别”数据集。
该数据集由意大利热那亚大学的Davide Anguita等人准备并提供,其详细信息在其2013年的论文《A Public Domain Dataset for Human Activity Recognition Using Smartphones》中作了完整描述。该数据集在其2012年的论文《Human Activity Recognition on Smartphones using a Multiclass Hardware-Friendly Support Vector Machine》中使用了机器学习算法进行建模。
该数据集已发布,可从UCI机器学习库免费下载
数据收集自30名年龄在19至48岁之间的受试者,他们佩戴腰部智能手机,记录运动数据,并执行6种标准活动之一。每位受试者执行活动时都录制了视频,并根据这些视频手动标注了运动数据。
下面是受试者执行活动并记录运动数据的示例视频。
执行的六项活动如下:
- 步行
- 上楼梯
- 下楼梯
- 坐着
- 站立
- 躺着
记录的运动数据是智能手机(特指三星Galaxy S II)的x、y、z加速度计数据(线性加速度)和陀螺仪数据(角速度)。
观测数据以50赫兹(即每秒50个数据点)的频率记录。每个受试者都执行了两次活动序列,一次将设备放在左侧,另一次将设备放在右侧。
为此任务选择了30名年龄在19至48岁之间的志愿者。每个人都被指示遵循一项活动协议,同时佩戴腰部安装的三星Galaxy S II智能手机。选择的六项ADL是站立、坐下、躺下、行走、下楼和上楼。每个受试者都执行了两次协议:第一次试验中智能手机固定在皮带的左侧,第二次则由用户自行放置。
——《使用智能手机进行人类活动识别的公共领域数据集》,2013年。
原始数据不可用。相反,提供的是一个经过预处理的数据集版本。
预处理步骤包括
- 使用噪声滤波器预处理加速度计和陀螺仪。
- 将数据分割成2.56秒(128个数据点)的固定窗口,重叠率为50%。
- 将加速度计数据分解为重力(总)和身体运动分量。
这些信号使用中值滤波器和带有20赫兹截止频率的三阶低通巴特沃斯滤波器进行噪声降噪预处理。 […] 具有重力和身体运动分量的加速度信号,使用另一个巴特沃斯低通滤波器分离为身体加速度和重力。
——《使用智能手机进行人类活动识别的公共领域数据集》,2013年。
对窗口数据应用特征工程,并提供了一份包含这些工程特征的数据副本。
从每个窗口中提取了人类活动识别领域常用的时间和频率特征。结果是生成了一个包含561个元素的特征向量。
数据集根据受试者的数据分为训练集(70%)和测试集(30%),例如21名受试者用于训练,9名受试者用于测试。
这表明,问题可以这样构建:将一系列运动活动作为输入,预测当前正在进行的活动部分(2.56秒),其中使用在已知受试者上训练的模型来从新受试者的运动中预测活动。
早期使用适用于智能手机的支持向量机(例如,定点运算)进行的实验结果显示,在测试数据集上的预测准确率为89%,与未经修改的SVM实现取得了相似的结果。
此方法改进了标准的支持向量机(SVM),并利用定点算术来降低计算成本。与传统SVM的比较显示,在计算成本方面有显著改进,同时保持了相似的准确性 […]
— 《使用多类硬件友好型支持向量机进行智能手机上的人类活动识别》,2012年。
现在我们熟悉了预测问题,接下来我们将了解如何加载和探索这个数据集。
3. 下载数据集
该数据集可免费从UCI机器学习库下载。
数据以一个大小约为58兆字节的zip文件提供。直接下载链接如下:
下载数据集并将所有文件解压到当前工作目录中名为“HARDataset”的新目录中。
检查解压后的内容,你会注意到几件事:
- 包含用于建模的数据(例如70%/30%)的“train”和“test”文件夹。
- 一个“README.txt”文件,其中包含数据集和解压文件的详细技术说明。
- 一个“features.txt”文件,其中包含工程特征的技术描述。
“train”和“test”文件夹的内容相似(例如文件夹和文件名),但在它们包含的具体数据上有所不同。
检查“train”文件夹,显示了几个重要元素:
- 一个“Inertial Signals”文件夹,其中包含预处理过的数据。
- “X_train.txt”文件,其中包含用于拟合模型的工程特征。
- “y_train.txt”文件,其中包含每个观测的类别标签(1-6)。
- “subject_train.txt”文件,其中包含数据文件中每行与其受试者标识符(1-30)的映射。
每个文件的行数匹配,表明每个数据文件中的一行是一个记录。
“Inertial Signals”目录包含9个文件。
- x、y、z轴的**重力加速度**数据文件:*total_acc_x_train.txt*、*total_acc_y_train.txt*、*total_acc_z_train.txt*。
- x、y、z轴的**身体加速度**数据文件:*body_acc_x_train.txt*、*body_acc_y_train.txt*、*body_acc_z_train.txt*。
- x、y、z轴的**身体陀螺仪**数据文件:*body_gyro_x_train.txt*、*body_gyro_y_train.txt*、*body_gyro_z_train.txt*。
“test”目录的结构与此相同。
我们将把注意力集中在“Inertial Signals”中的数据上,因为这对于开发能够学习合适表示的机器学习模型最有趣,而不是使用特定领域的特征工程。
检查数据文件显示列由空格分隔,值似乎已缩放到 -1 到 1 的范围。此缩放可通过数据集提供的 *README.txt* 文件中的注释得到确认。
现在我们知道了有哪些数据,我们可以找出如何将其加载到内存中。
4. 加载数据
在本节中,我们将开发一些代码来将数据集加载到内存中。
首先,我们需要加载一个文件。
我们可以使用Pandas函数`read_csv()`来加载单个数据文件,并指定文件没有标题,且使用空格分隔列。
|
1 |
dataframe = read_csv(filepath, header=None, delim_whitespace=True) |
我们可以将其封装在一个名为 `load_file()` 的函数中。此函数的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 |
# 加载数据集 from pandas import read_csv # 将单个文件加载为numpy数组 def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values data = load_file('HARDataset/train/Inertial Signals/total_acc_y_train.txt') print(data.shape) |
运行示例加载文件“total_acc_y_train.txt”,返回一个NumPy数组,并打印该数组的形状。
我们可以看到,训练数据由7,352行或数据窗口组成,每个窗口有128个观测值。
|
1 |
(7352, 128) |
接下来,加载一组文件(例如所有身体加速度数据文件)作为一个单独的组会很有用。
理想情况下,在处理多变量时间序列数据时,将数据结构化为以下格式会很有用:
|
1 |
[样本数, 时间步数, 特征数] |
这有助于分析,也是卷积神经网络和循环神经网络等深度学习模型的预期。
我们可以通过多次调用上述 `load_file()` 函数来实现,每次调用加载一个组中的一个文件。
一旦我们将每个文件加载为NumPy数组,我们就可以将所有三个数组组合或堆叠在一起。我们可以使用dstack() NumPy函数来确保每个数组以这样一种方式堆叠,即特征在第三维中分离,正如我们所希望的那样。
函数 `load_group()` 为文件列表实现了此行为,如下所示。
|
1 2 3 4 5 6 7 8 9 |
# 加载文件列表,例如给定变量的x、y、z数据 def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # 堆叠组,使特征成为第三维度 loaded = dstack(loaded) return loaded |
我们可以通过加载所有总加速度文件来演示此函数。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 加载数据集 from numpy import dstack from pandas import read_csv # 将单个文件加载为numpy数组 def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # 加载文件列表,例如给定变量的x、y、z数据 def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # 堆叠组,使特征成为第三维度 loaded = dstack(loaded) return loaded # 加载所有加速度数据 filenames = ['total_acc_x_train.txt', 'total_acc_y_train.txt', 'total_acc_z_train.txt'] total_acc = load_group(filenames, prefix='HARDataset/train/Inertial Signals/') print(total_acc.shape) |
运行该示例会打印返回的NumPy数组的形状,显示了数据集中预期的样本数、时间步长以及x、y和z三个特征。
|
1 |
(7352, 128, 3) |
最后,我们可以使用到目前为止开发的两个函数来加载训练集和测试集的所有数据。
鉴于训练文件夹和测试文件夹的并行结构,我们可以开发一个新函数来加载给定文件夹的所有输入和输出数据。该函数可以构建一个包含所有9个数据文件的列表,将它们加载为一个包含9个特征的NumPy数组,然后加载包含输出类别的数据文件。
下面的 `load_dataset()` 函数实现了这种行为。它可以用于“train”组或“test”组,作为字符串参数传递。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 加载数据集组,例如训练集或测试集 def load_dataset(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # 将所有9个文件加载为单个数组 filenames = list() # 总加速度 filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # 身体加速度 filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # 身体陀螺仪 filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # 加载输入数据 X = load_group(filenames, filepath) # 加载类别输出 y = load_file(prefix + group + '/y_'+group+'.txt') return X, y |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
# 加载数据集 from numpy import dstack from pandas import read_csv # 将单个文件加载为numpy数组 def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # 加载文件列表,例如给定变量的x、y、z数据 def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # 堆叠组,使特征成为第三维度 loaded = dstack(loaded) return loaded # 加载数据集组,例如训练集或测试集 def load_dataset(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # 将所有9个文件加载为单个数组 filenames = list() # 总加速度 filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # 身体加速度 filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # 身体陀螺仪 filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # 加载输入数据 X = load_group(filenames, filepath) # 加载类别输出 y = load_file(prefix + group + '/y_'+group+'.txt') 返回 X, y # 加载所有训练数据 trainX, trainy = load_dataset('train', 'HARDataset/') print(trainX.shape, trainy.shape) # 加载所有测试数据 testX, testy = load_dataset('test', 'HARDataset/') print(testX.shape, testy.shape) |
运行示例会加载训练集和测试集。
我们可以看到,测试数据集有2,947行窗口数据。正如预期的那样,训练集和测试集中的窗口大小匹配,并且训练集和测试集中输出(y)的大小与样本数量匹配。
|
1 2 |
(7352, 128, 9) (7352, 1) (2947, 128, 9) (2947, 1) |
既然我们知道如何加载数据,我们就可以开始探索它了。
5. 活动类别的平衡
对数据进行一个很好的初步检查是调查每个活动的平衡情况。
我们相信30个受试者中的每个都执行了六项活动中的每一项。
确认这一预期既可以检查数据是否确实平衡,使其更容易建模,也可以确认我们正在正确加载和解释数据集。
我们可以开发一个函数来总结输出变量(即y变量)的细分情况。
下面的 `class_breakdown()` 函数实现了这种行为,它首先将提供的 NumPy 数组封装在 DataFrame 中,然后根据类别值对行进行分组,并计算每个组的大小(行数)。最后,总结结果,包括计数和百分比。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 总结输出变量列中的类别平衡情况 def class_breakdown(data): # 将numpy数组转换为dataframe df = DataFrame(data) # 按类值分组数据并计算行数 counts = df.groupby(0).size() # 检索原始行 counts = counts.values # 总结 for i in range(len(counts)): percent = counts[i] / len(df) * 100 print('Class=%d, total=%d, percentage=%.3f' % (i+1, counts[i], percent)) |
总结训练集和测试集中类别的分布情况可能会很有用,以确保它们具有相似的分布,然后将结果与合并数据集的分布情况进行比较。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
# 总结类别平衡 from numpy import array from numpy import vstack from pandas import read_csv from pandas import DataFrame # 将单个文件加载为numpy数组 def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # 总结输出变量列中的类别平衡情况 def class_breakdown(data): # 将numpy数组转换为dataframe df = DataFrame(data) # 按类值分组数据并计算行数 counts = df.groupby(0).size() # 检索原始行 counts = counts.values # 总结 for i in range(len(counts)): percent = counts[i] / len(df) * 100 print('Class=%d, total=%d, percentage=%.3f' % (i+1, counts[i], percent)) # 加载训练文件 trainy = load_file('HARDataset/train/y_train.txt') # 总结类别分布 print('Train Dataset') class_breakdown(trainy) # 加载测试文件 testy = load_file('HARDataset/test/y_test.txt') # 总结类别分布 print('Test Dataset') class_breakdown(testy) # 总结合并后的类别分布 print('Both') combined = vstack((trainy, testy)) class_breakdown(combined) |
运行示例首先总结了训练集的细分情况。我们可以看到每个类别的分布非常相似,都在数据集的13%到19%之间。
测试集和两个数据集合并后的结果看起来非常相似。
假设每个训练集和测试集中的类别分布以及每个受试者的类别分布都是平衡的,那么处理这个数据集应该是安全的。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
训练数据集 类别=1,总计=1226,百分比=16.676 类别=2,总计=1073,百分比=14.595 类别=3,总计=986,百分比=13.411 类别=4,总计=1286,百分比=17.492 类别=5,总计=1374,百分比=18.689 类别=6,总计=1407,百分比=19.138 测试数据集 类别=1,总计=496,百分比=16.831 类别=2,总计=471,百分比=15.982 类别=3,总计=420,百分比=14.252 类别=4,总计=491,百分比=16.661 类别=5,总计=532,百分比=18.052 类别=6,总计=537,百分比=18.222 两者 类别=1,总计=1722,百分比=16.720 类别=2,总计=1544,百分比=14.992 类别=3,总计=1406,百分比=13.652 类别=4,总计=1777,百分比=17.254 类别=5,总计=1906,百分比=18.507 类别=6,总计=1944,百分比=18.876 |
6. 绘制一个受试者的时间序列数据
我们正在处理时间序列数据,因此一个重要的检查是创建原始数据的线图。
原始数据由每个变量的时间序列数据窗口组成,并且这些窗口有50%的重叠。这意味着除非去除重叠,否则线图可能会显示一些观测数据的重复。
我们可以通过使用上面开发的函数加载训练数据集来开始。
|
1 2 |
# 加载数据 trainX, trainy = load_dataset('train', 'HARDataset/') |
接下来,我们可以加载“`train`”目录中的“`subject_train.txt`”,该文件提供了行到其所属主题的映射。
我们可以使用 `load_file()` 函数加载此文件。加载后,我们还可以使用 `unique()` NumPy 函数检索训练数据集中唯一主题的列表。
|
1 2 3 |
sub_map = load_file('HARDataset/train/subject_train.txt') train_subjects = unique(sub_map) print(train_subjects) |
接下来,我们需要一种方法来检索单个受试者的所有行,例如受试者编号1。
我们可以通过找到属于给定主题的所有行号,并使用这些行号从训练数据集中加载的X和y数据中选择样本来实现。
下面的 `data_for_subject()` 函数实现了这种行为。它将获取加载的训练数据、行号到受试者的加载映射以及我们感兴趣的受试者的受试者识别号,并仅返回该受试者的 `X` 和 `y` 数据。
|
1 2 3 4 5 6 |
# 获取一个主题的所有数据 def data_for_subject(X, y, sub_map, sub_id): # 获取主题ID的行索引 ix = [i for i in range(len(sub_map)) if sub_map[i]==sub_id] # 返回选定的样本 return X[ix, :, :], y[ix] |
现在我们有了一个受试者的数据,我们可以绘制它。
数据由重叠的窗口组成。我们可以编写一个函数来消除这种重叠,并将给定变量的窗口压缩成一个可以直接绘制为线图的长序列。
下面的 `to_series()` 函数为给定变量(例如,窗口数组)实现了此行为。
|
1 2 3 4 5 6 7 8 9 |
# 将一系列窗口转换为一维列表 def to_series(windows): series = list() for window in windows: # 移除窗口中的重叠部分 half = int(len(window) / 2) - 1 for value in window[-half:]: series.append(value) return series |
最后,我们有足够的条件来绘制数据。我们可以依次绘制该受试者的九个变量,并最后绘制活动水平。
每个序列都具有相同数量的时间步(x轴长度),因此,为每个变量创建子图并垂直对齐所有图表以比较每个变量上的运动可能会很有用。
下面的 `plot_subject()` 函数为单个受试者的 `X` 和 `y` 数据实现了此行为。该函数假定变量(第3轴)的顺序与在 `load_dataset()` 函数中加载的顺序相同。每个图表还添加了一个粗略的标题,这样我们就不容易混淆我们正在看的是什么。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
# 绘制一个主题的数据 def plot_subject(X, y): pyplot.figure() # 确定总图数 n, off = X.shape[2] + 1, 0 # 绘制总加速度 for i in range(3): pyplot.subplot(n, 1, off+1) pyplot.plot(to_series(X[:, :, off])) pyplot.title('total acc '+str(i), y=0, loc='left') off += 1 # 绘制身体加速度 for i in range(3): pyplot.subplot(n, 1, off+1) pyplot.plot(to_series(X[:, :, off])) pyplot.title('body acc '+str(i), y=0, loc='left') off += 1 # 绘制身体陀螺仪 for i in range(3): pyplot.subplot(n, 1, off+1) pyplot.plot(to_series(X[:, :, off])) pyplot.title('body gyro '+str(i), y=0, loc='left') off += 1 # 绘制活动 pyplot.subplot(n, 1, n) pyplot.plot(y) pyplot.title('activity', y=0, loc='left') pyplot.show() |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 |
# 绘制一个主题的所有变量 from numpy import array from numpy import dstack from numpy import unique from pandas import read_csv from matplotlib import pyplot # 将单个文件加载为numpy数组 def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # 加载文件列表,例如给定变量的x、y、z数据 def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # 堆叠组,使特征成为第三维度 loaded = dstack(loaded) return loaded # 加载数据集组,例如训练集或测试集 def load_dataset(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # 将所有9个文件加载为单个数组 filenames = list() # 总加速度 filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # 身体加速度 filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # 身体陀螺仪 filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # 加载输入数据 X = load_group(filenames, filepath) # 加载类别输出 y = load_file(prefix + group + '/y_'+group+'.txt') 返回 X, y # 获取一个主题的所有数据 def data_for_subject(X, y, sub_map, sub_id): # 获取主题ID的行索引 ix = [i for i in range(len(sub_map)) if sub_map[i]==sub_id] # 返回选定的样本 return X[ix, :, :], y[ix] # 将一系列窗口转换为一维列表 def to_series(windows): series = list() for window in windows: # 移除窗口中的重叠部分 half = int(len(window) / 2) - 1 for value in window[-half:]: series.append(value) return series # 绘制一个主题的数据 def plot_subject(X, y): pyplot.figure() # 确定总图数 n, off = X.shape[2] + 1, 0 # 绘制总加速度 for i in range(3): pyplot.subplot(n, 1, off+1) pyplot.plot(to_series(X[:, :, off])) pyplot.title('total acc '+str(i), y=0, loc='left') off += 1 # 绘制身体加速度 for i in range(3): pyplot.subplot(n, 1, off+1) pyplot.plot(to_series(X[:, :, off])) pyplot.title('body acc '+str(i), y=0, loc='left') off += 1 # 绘制身体陀螺仪 for i in range(3): pyplot.subplot(n, 1, off+1) pyplot.plot(to_series(X[:, :, off])) pyplot.title('body gyro '+str(i), y=0, loc='left') off += 1 # 绘制活动 pyplot.subplot(n, 1, n) pyplot.plot(y) pyplot.title('activity', y=0, loc='left') pyplot.show() # 加载数据 trainX, trainy = load_dataset('train', 'HARDataset/') # 加载行到主题的映射 sub_map = load_file('HARDataset/train/subject_train.txt') train_subjects = unique(sub_map) print(train_subjects) # 获取一个主题的数据 sub_id = train_subjects[0] subX, suby = data_for_subject(trainX, trainy, sub_map, sub_id) print(subX.shape, suby.shape) # 绘制主题数据 plot_subject(subX, suby) |
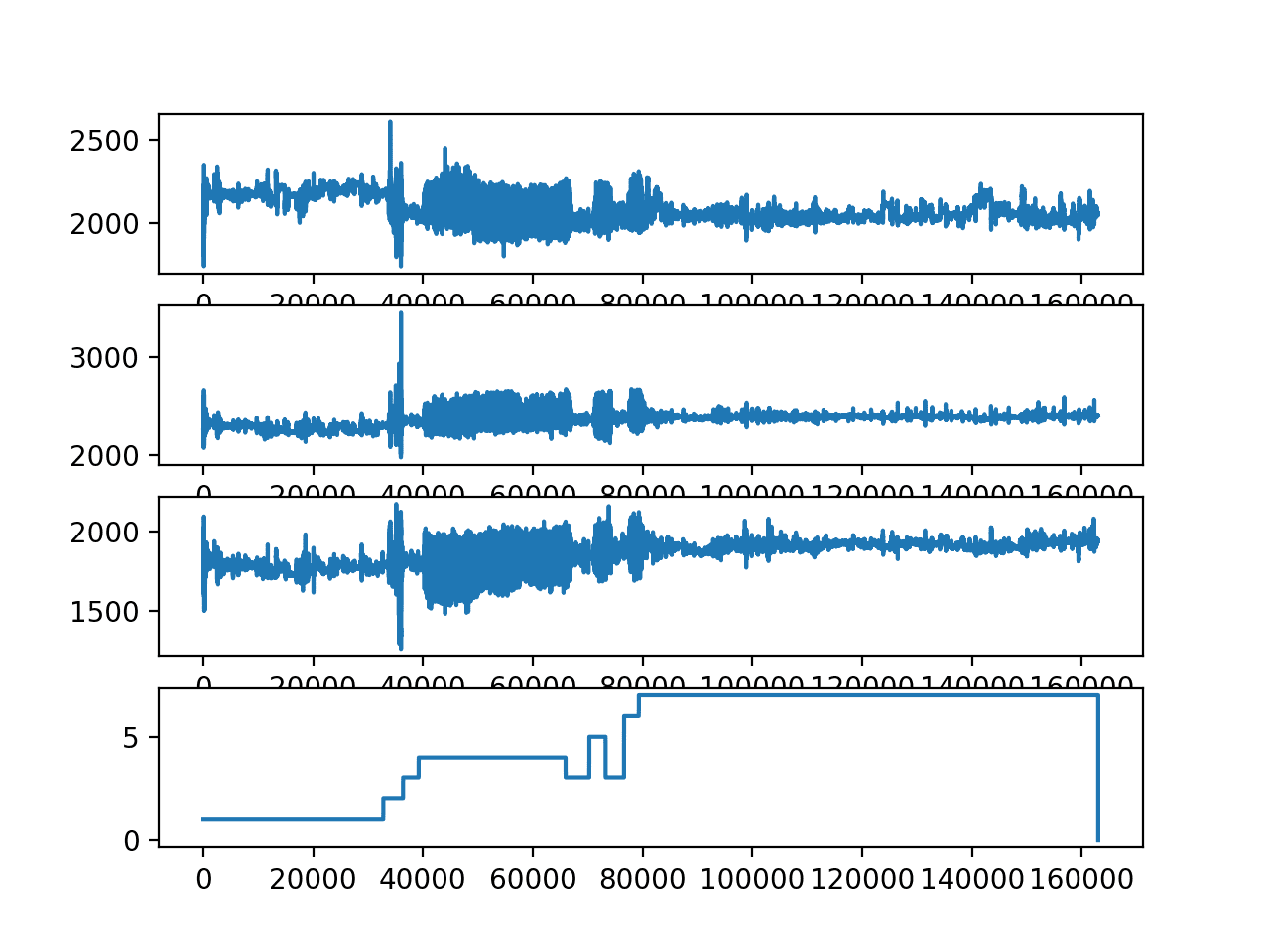
运行示例会打印训练数据集中的唯一主题,第一个主题的数据样本,并创建一个包含10个图的图形,其中9个用于输入变量,1个用于输出类别。
|
1 2 |
[ 1 3 5 6 7 8 11 14 15 16 17 19 21 22 23 25 26 27 28 29 30] (341, 128, 9) (341, 1) |
在图中,我们可以看到与活动1、2和3(步行活动)相对应的大幅度运动时期。我们还可以看到活动4、5和6(坐、站和躺)的活动量明显减少(即相对笔直的线条)。
这很好地证实了我们正确加载和解释了原始数据集。
我们可以看到这个受试者已经两次执行了相同的总体活动序列,并且有些活动执行了两次以上。这表明对于一个给定的受试者,我们不应该对其可能执行的活动或它们的顺序做出假设。
我们还可以看到一些相对较大的运动,即使在一些静止活动中,例如躺着。这些可能是异常值或与活动转换有关。通过平滑或移除这些观测值,可以将其视为异常值。
最后,我们看到九个变量之间存在许多共性。很可能只需要这些轨迹的一个子集就可以开发预测模型。
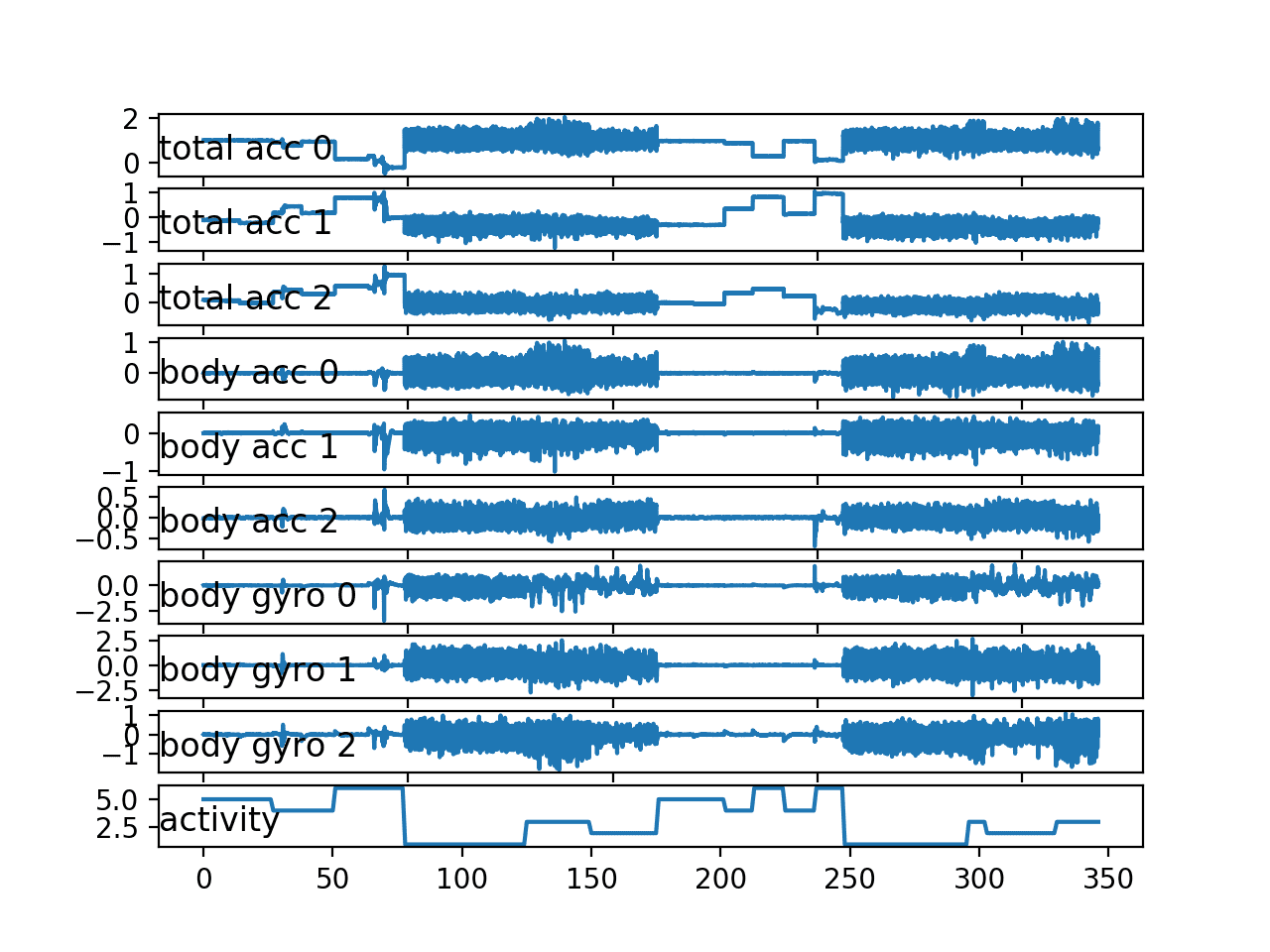
单个受试者所有变量的线图
我们可以通过进行一个小改动来重新运行另一个受试者的示例,例如选择训练数据集中第二个受试者的标识符。
|
1 2 |
# 获取一个主题的数据 sub_id = train_subjects[1] |
第二个受试者的图显示了类似的行为,没有意外。
活动的双重序列确实比第一个受试者看起来更规律。
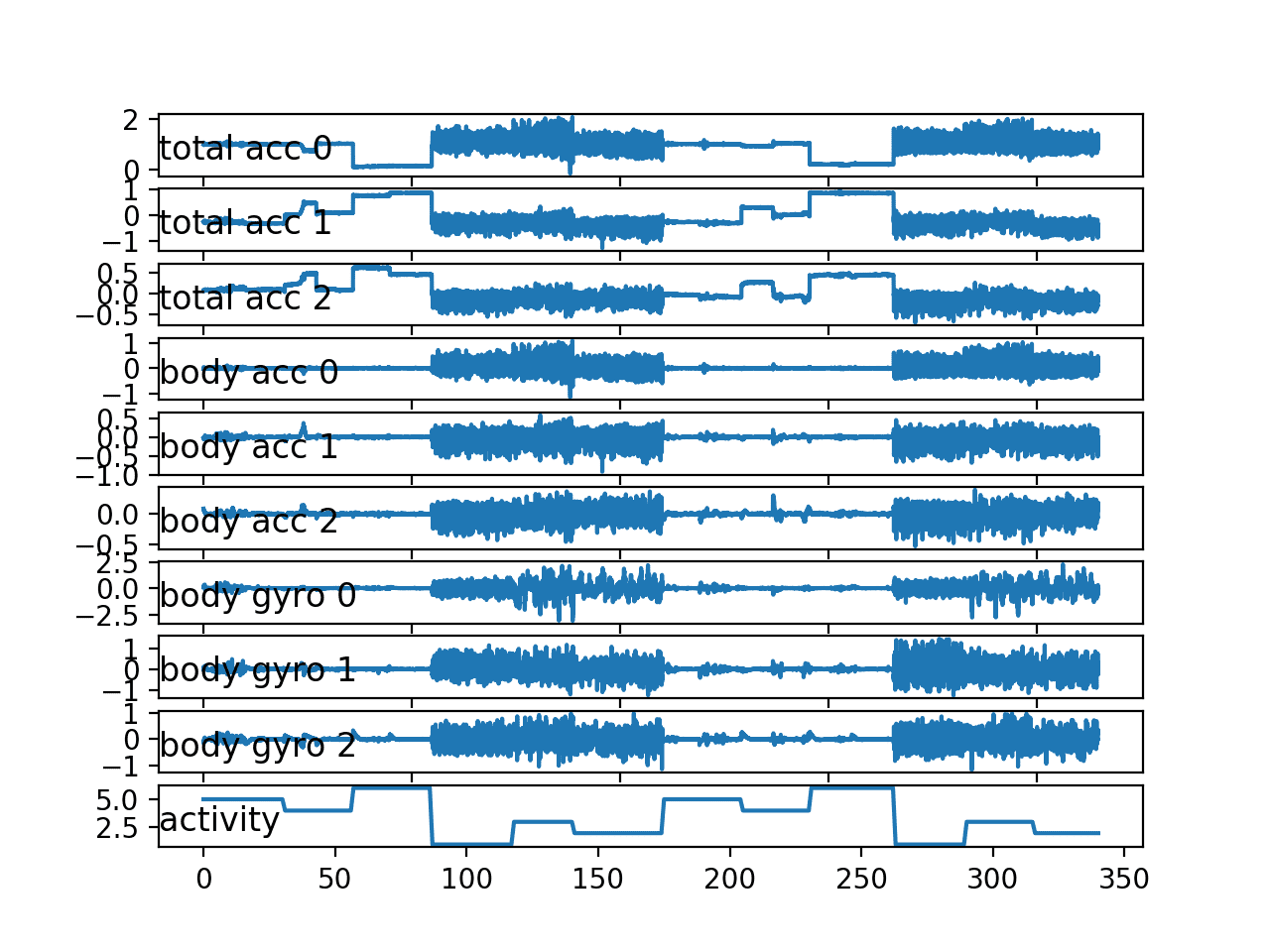
第二个单一受试者所有变量的线图
7. 绘制每个受试者的直方图
问题的框架是,我们有兴趣使用某些受试者的运动数据来预测其他受试者的活动。
这表明运动数据在各个受试者之间必然具有规律性。我们知道数据已缩放到-1到1之间,大概是针对每个受试者进行的,这表明检测到的运动的幅度将相似。
鉴于他们执行了相同的动作,我们还预计运动数据的分布在受试者之间是相似的。
我们可以通过绘制和比较各个受试者运动数据的直方图来检查这一点。一个有用的方法是为每个受试者创建一个图,并绘制给定数据(例如,总加速度)的所有三个轴,然后对多个受试者重复此操作。可以修改图以使用相同的轴并水平对齐,以便比较各个变量在受试者之间的分布。
下面的 `plot_subject_histograms()` 函数实现了此行为。该函数接受已加载的数据集和行到主题的映射,以及要绘制的最大主题数,默认设置为10。
为每个受试者创建了一个图,并将一种数据类型的三个变量绘制为包含100个 bin 的直方图,以帮助使分布更清晰。每个图共享相同的轴,该轴固定在 -1 和 1 的边界。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 绘制多个主题的直方图 def plot_subject_histograms(X, y, sub_map, n=10): pyplot.figure() # 获取唯一主题 subject_ids = unique(sub_map[:,0]) # 枚举主题 xaxis = None for k in range(n): sub_id = subject_ids[k] # 获取一个主题的数据 subX, _ = data_for_subject(X, y, sub_map, sub_id) # 总加速度 for i in range(3): ax = pyplot.subplot(n, 1, k+1, sharex=xaxis) ax.set_xlim(-1,1) if k == 0: xaxis = ax pyplot.hist(to_series(subX[:,:,i]), bins=100) pyplot.show() |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |
# 绘制多个主题的直方图 from numpy import array from numpy import unique from numpy import dstack from pandas import read_csv from matplotlib import pyplot # 将单个文件加载为numpy数组 def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # 加载文件列表,例如给定变量的x、y、z数据 def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # 堆叠组,使特征成为第三维度 loaded = dstack(loaded) return loaded # 加载数据集组,例如训练集或测试集 def load_dataset(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # 将所有9个文件加载为单个数组 filenames = list() # 总加速度 filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # 身体加速度 filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # 身体陀螺仪 filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # 加载输入数据 X = load_group(filenames, filepath) # 加载类别输出 y = load_file(prefix + group + '/y_'+group+'.txt') 返回 X, y # 获取一个主题的所有数据 def data_for_subject(X, y, sub_map, sub_id): # 获取主题ID的行索引 ix = [i for i in range(len(sub_map)) if sub_map[i]==sub_id] # 返回选定的样本 return X[ix, :, :], y[ix] # 将一系列窗口转换为一维列表 def to_series(windows): series = list() for window in windows: # 移除窗口中的重叠部分 half = int(len(window) / 2) - 1 for value in window[-half:]: series.append(value) return series # 绘制多个主题的直方图 def plot_subject_histograms(X, y, sub_map, n=10): pyplot.figure() # 获取唯一主题 subject_ids = unique(sub_map[:,0]) # 枚举主题 xaxis = None for k in range(n): sub_id = subject_ids[k] # 获取一个主题的数据 subX, _ = data_for_subject(X, y, sub_map, sub_id) # 总加速度 for i in range(3): ax = pyplot.subplot(n, 1, k+1, sharex=xaxis) ax.set_xlim(-1,1) if k == 0: xaxis = ax pyplot.hist(to_series(subX[:,:,i]), bins=100) pyplot.show() # 加载训练数据集 X, y = load_dataset('train', 'HARDataset/') # 加载行到主题的映射 sub_map = load_file('HARDataset/train/subject_train.txt') # 绘制主题直方图 plot_subject_histograms(X, y, sub_map) |
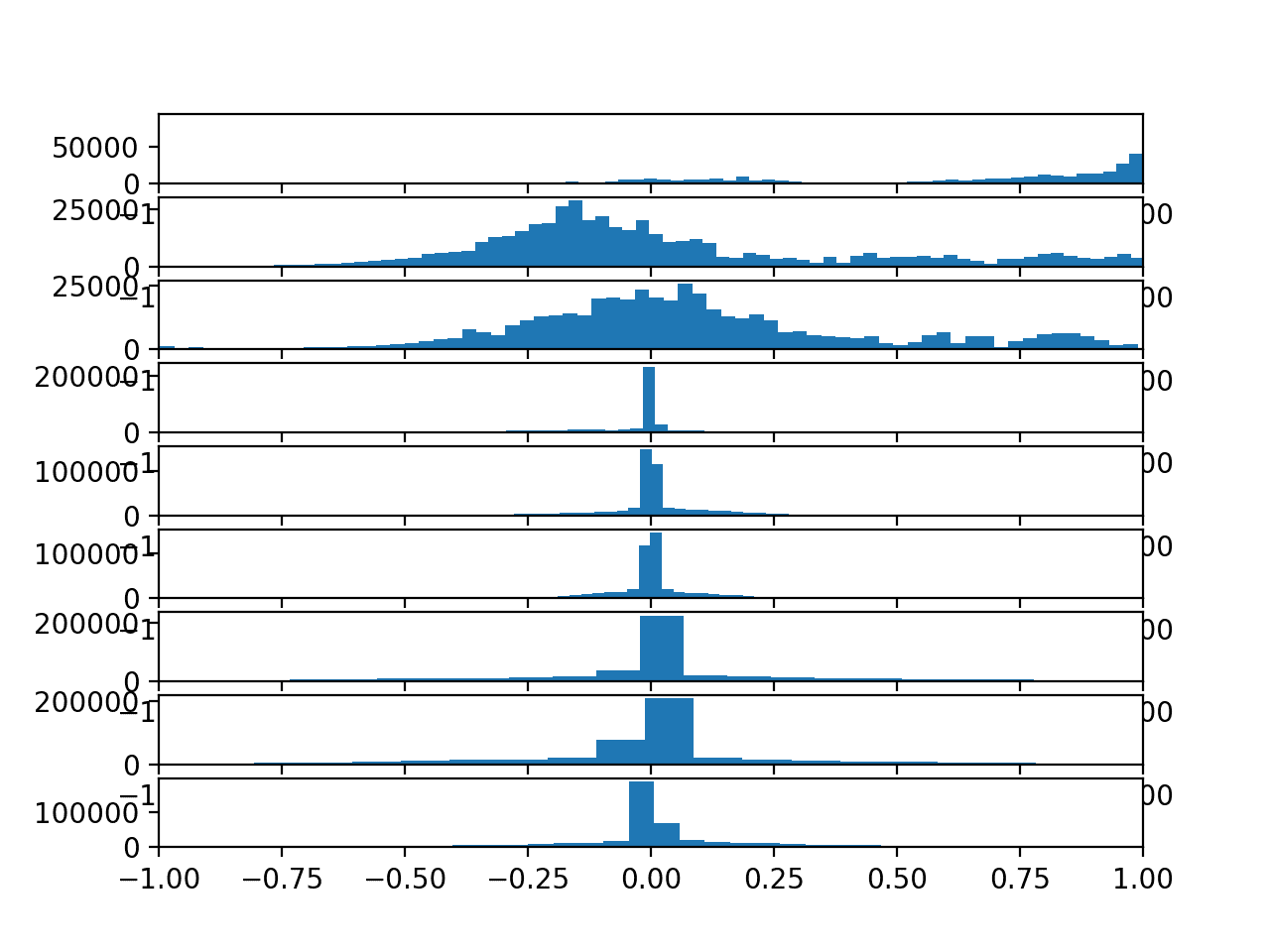
运行该示例会生成一个包含10个图的单个图形,其中包含总加速度数据的三个轴的直方图。
给定图上的三个轴分别具有不同的颜色,特别是x、y和z分别为蓝色、橙色和绿色。
我们可以看到,给定轴的分布确实呈现高斯分布,并伴随着大的独立数据组。
我们可以看到一些分布对齐(例如,中间主要组在0.0附近),这表明运动数据在受试者之间可能存在一定的连续性,至少对于此数据而言。
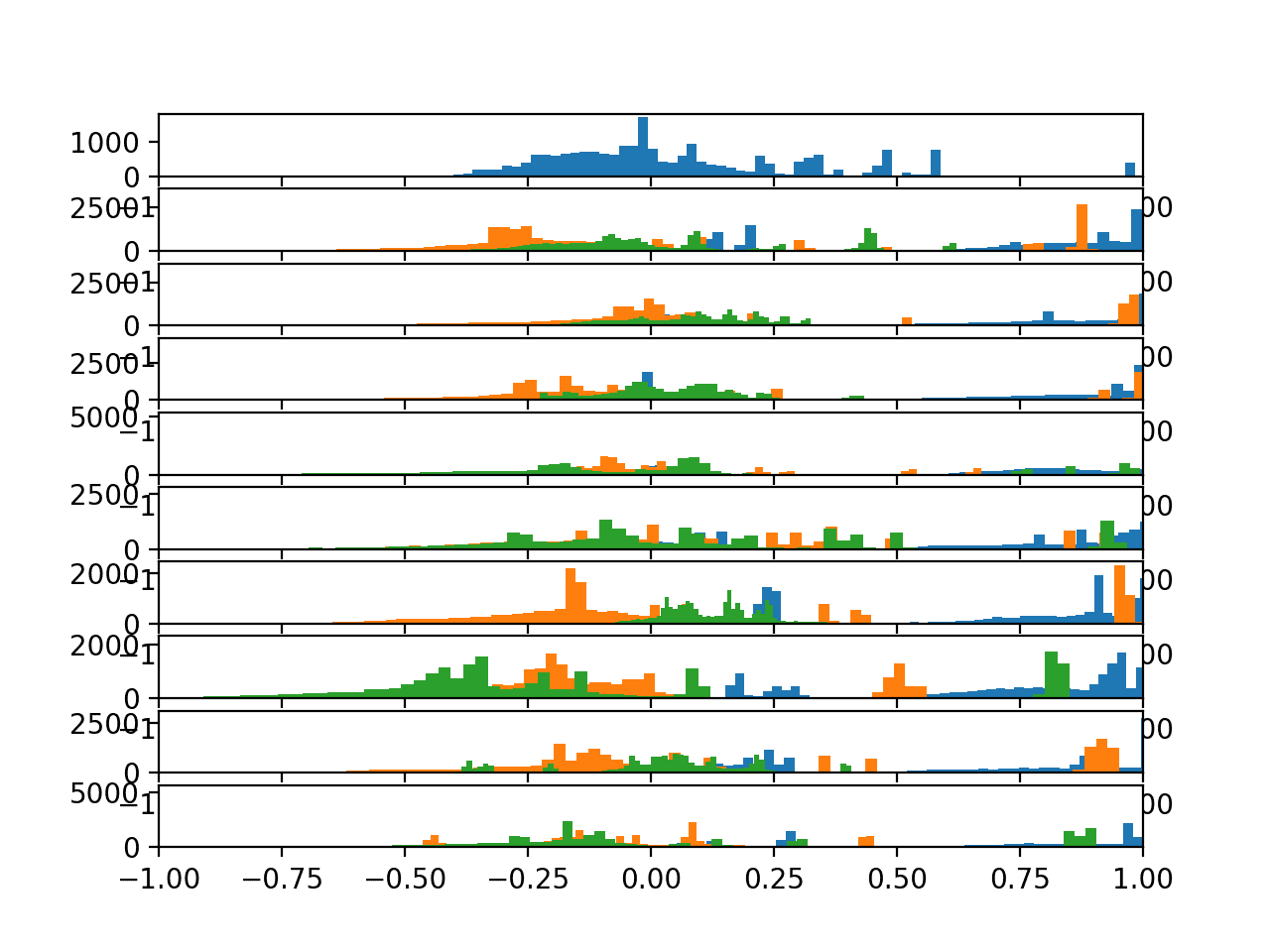
10名受试者总加速度数据的直方图
我们可以更新 `plot_subject_histograms()` 函数,接下来绘制身体加速度的分布图。更新后的函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 绘制多个主题的直方图 def plot_subject_histograms(X, y, sub_map, n=10): pyplot.figure() # 获取唯一主题 subject_ids = unique(sub_map[:,0]) # 枚举主题 xaxis = None for k in range(n): sub_id = subject_ids[k] # 获取一个主题的数据 subX, _ = data_for_subject(X, y, sub_map, sub_id) # 身体加速度 for i in range(3): ax = pyplot.subplot(n, 1, k+1, sharex=xaxis) ax.set_xlim(-1,1) if k == 0: xaxis = ax pyplot.hist(to_series(subX[:,:,3+i]), bins=100) pyplot.show() |
运行更新后的示例会生成相同的图,但结果截然不同。
在这里,我们可以看到所有数据都集中在0.0附近,跨轴在受试者内部以及跨受试者。这表明数据可能已经居中(零均值)。这种在受试者之间的高度一致性可能有助于建模,并可能表明总加速度数据中受试者之间的差异可能不那么有用。
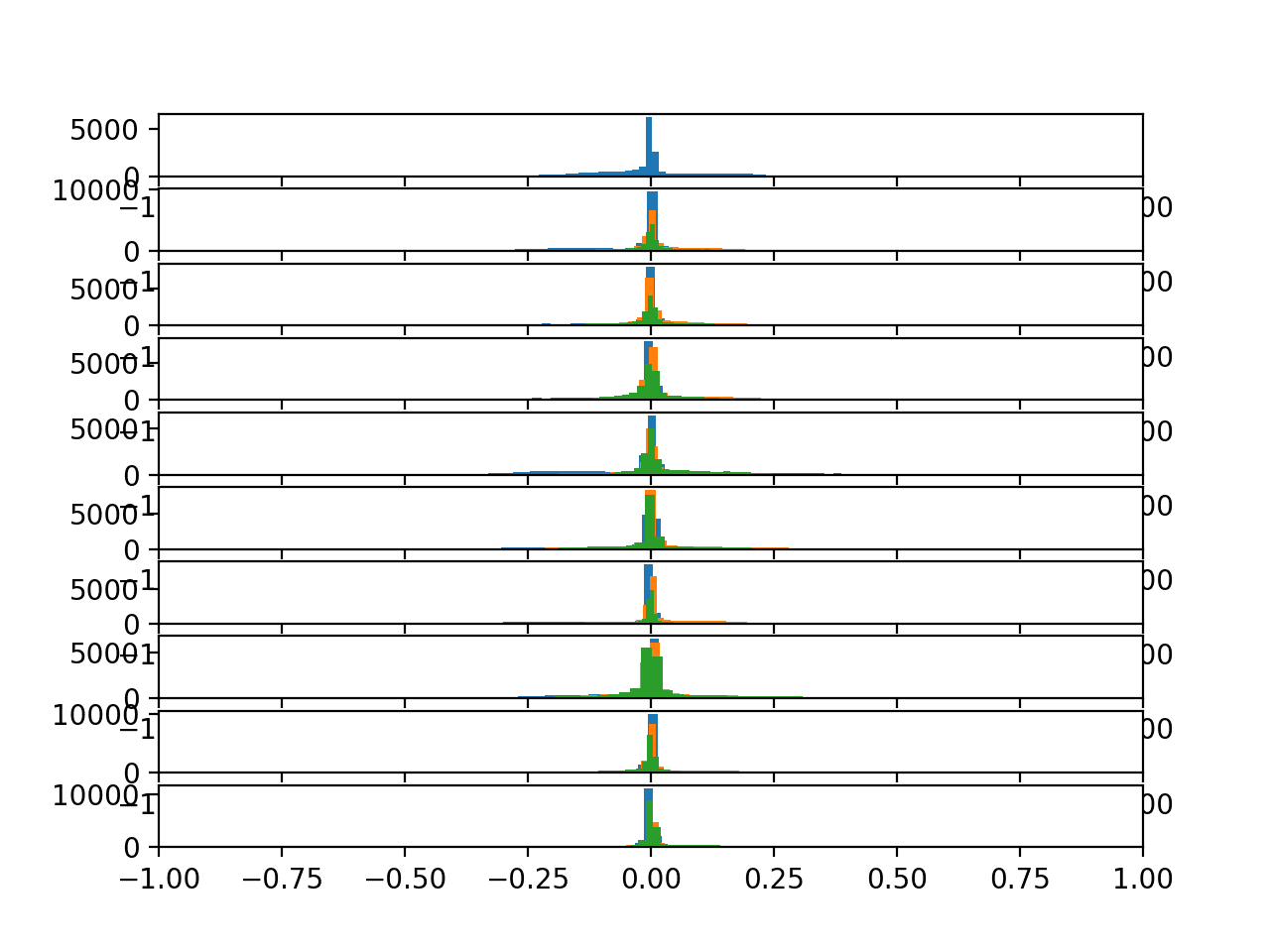
10名受试者身体加速度数据的直方图
最后,我们可以为陀螺仪数据生成一个最终的图。
更新后的函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 绘制多个主题的直方图 def plot_subject_histograms(X, y, sub_map, n=10): pyplot.figure() # 获取唯一主题 subject_ids = unique(sub_map[:,0]) # 枚举主题 xaxis = None for k in range(n): sub_id = subject_ids[k] # 获取一个主题的数据 subX, _ = data_for_subject(X, y, sub_map, sub_id) # 身体加速度 for i in range(3): ax = pyplot.subplot(n, 1, k+1, sharex=xaxis) ax.set_xlim(-1,1) if k == 0: xaxis = ax pyplot.hist(to_series(subX[:,:,6+i]), bins=100) pyplot.show() |
运行该示例显示了与身体加速度数据非常相似的结果。
我们看到每个轴在高斯分布的中心0.0处具有很高的可能性,并且每个受试者都如此。分布稍宽,并显示出更厚的尾部,但对于跨受试者的运动数据建模来说,这是一个令人鼓舞的发现。
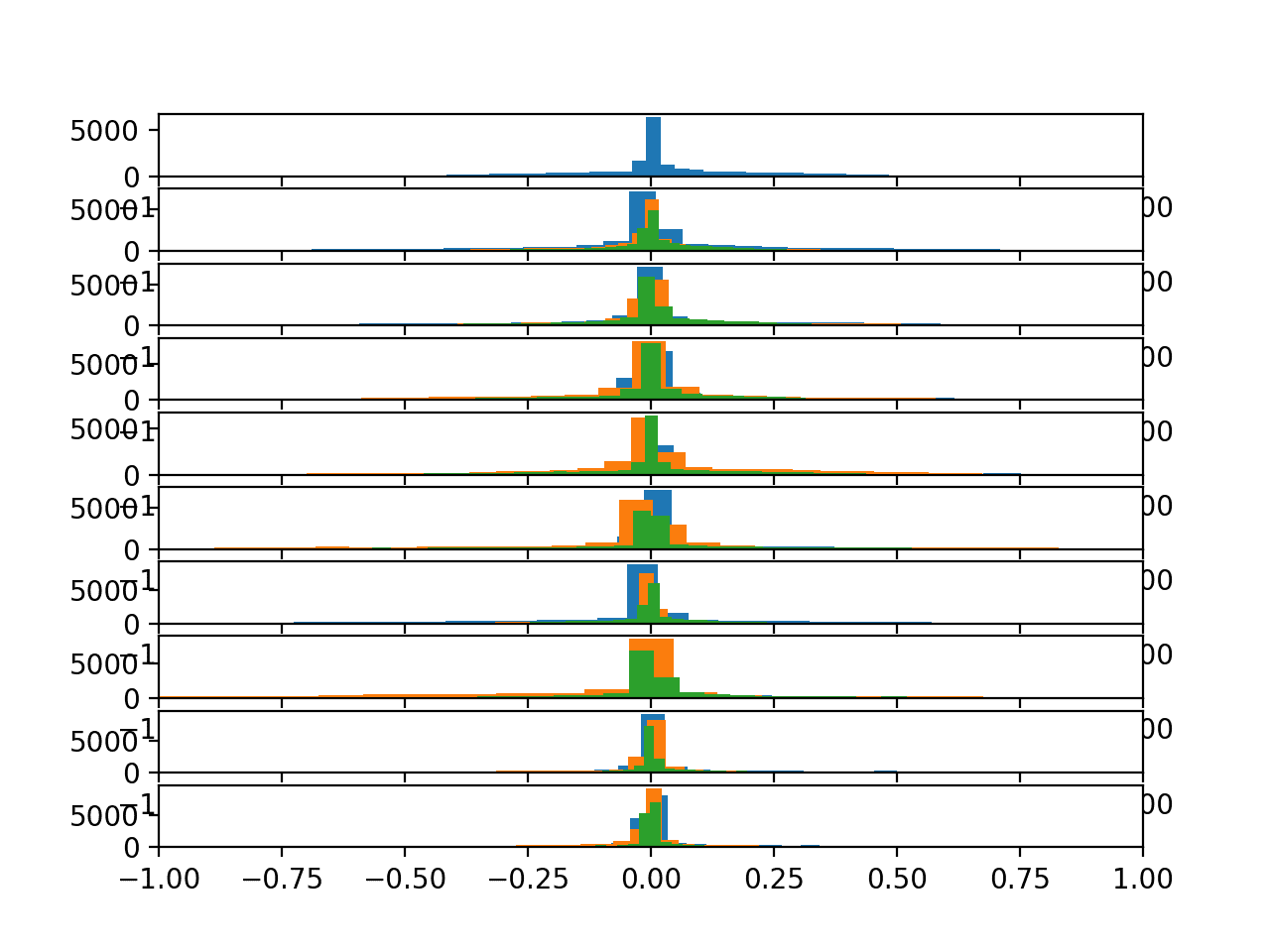
10名受试者身体陀螺仪数据的直方图
8. 绘制每个活动的直方图
我们有兴趣根据活动数据来区分不同的活动。
最简单的情况是区分单个受试者的活动。调查此问题的一种方法是查看单个受试者不同活动的运动数据分布。我们预期会看到单个受试者不同活动的运动数据分布存在一些差异。
我们可以通过为每个活动创建直方图图,并在每个图上显示给定数据类型的所有三个轴来查看此内容。同样,这些图可以水平排列,以比较每个活动的数据轴的分布。我们预计会看到不同活动在图中的分布存在差异。
首先,我们必须按活动对受试者的轨迹进行分组。下面的 `data_by_activity()` 函数实现了此行为。
|
1 2 3 4 |
# 按活动分组数据 def data_by_activity(X, y, activities): # 按活动分组窗口 return {a:X[y[:,0]==a, :, :] for a in activities} |
我们现在可以为给定受试者创建每个活动的图。
下面的 `plot_activity_histograms()` 函数为给定受试者的轨迹数据实现了此功能。
首先,数据按活动分组,然后为每个活动创建一个子图,并将数据类型的每个轴添加为直方图。该函数仅枚举数据的前三个特征,即总加速度变量。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 绘制一个主题的每个活动的直方图 def plot_activity_histograms(X, y): # 获取主题的唯一活动列表 activity_ids = unique(y[:,0]) # 按活动分组窗口 grouped = data_by_activity(X, y, activity_ids) # 按活动绘制,每个轴的直方图 pyplot.figure() xaxis = None for k in range(len(activity_ids)): act_id = activity_ids[k] # 总加速度 for i in range(3): ax = pyplot.subplot(len(activity_ids), 1, k+1, sharex=xaxis) ax.set_xlim(-1,1) if k == 0: xaxis = ax pyplot.hist(to_series(grouped[act_id][:,:,i]), bins=100) pyplot.title('activity '+str(act_id), y=0, loc='left') pyplot.show() |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 |
# 绘制一个主题的每个活动的直方图 from numpy import array from numpy import dstack from numpy import unique from pandas import read_csv from matplotlib import pyplot # 将单个文件加载为numpy数组 def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # 加载文件列表,例如给定变量的x、y、z数据 def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # 堆叠组,使特征成为第三维度 loaded = dstack(loaded) return loaded # 加载数据集组,例如训练集或测试集 def load_dataset(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # 将所有9个文件加载为单个数组 filenames = list() # 总加速度 filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # 身体加速度 filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # 身体陀螺仪 filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # 加载输入数据 X = load_group(filenames, filepath) # 加载类别输出 y = load_file(prefix + group + '/y_'+group+'.txt') 返回 X, y # 获取一个主题的所有数据 def data_for_subject(X, y, sub_map, sub_id): # 获取主题ID的行索引 ix = [i for i in range(len(sub_map)) if sub_map[i]==sub_id] # 返回选定的样本 return X[ix, :, :], y[ix] # 将一系列窗口转换为一维列表 def to_series(windows): series = list() for window in windows: # 移除窗口中的重叠部分 half = int(len(window) / 2) - 1 for value in window[-half:]: series.append(value) return series # 按活动分组数据 def data_by_activity(X, y, activities): # 按活动分组窗口 return {a:X[y[:,0]==a, :, :] for a in activities} # 绘制一个主题的每个活动的直方图 def plot_activity_histograms(X, y): # 获取主题的唯一活动列表 activity_ids = unique(y[:,0]) # 按活动分组窗口 grouped = data_by_activity(X, y, activity_ids) # 按活动绘制,每个轴的直方图 pyplot.figure() xaxis = None for k in range(len(activity_ids)): act_id = activity_ids[k] # 总加速度 for i in range(3): ax = pyplot.subplot(len(activity_ids), 1, k+1, sharex=xaxis) ax.set_xlim(-1,1) if k == 0: xaxis = ax pyplot.hist(to_series(grouped[act_id][:,:,i]), bins=100) pyplot.title('activity '+str(act_id), y=0, loc='left') pyplot.show() # 加载数据 trainX, trainy = load_dataset('train', 'HARDataset/') # 加载行到主题的映射 sub_map = load_file('HARDataset/train/subject_train.txt') train_subjects = unique(sub_map) # 获取一个主题的数据 sub_id = train_subjects[0] subX, suby = data_for_subject(trainX, trainy, sub_map, sub_id) # 绘制主题数据 plot_activity_histograms(subX, suby) |
运行示例会生成一个包含六个子图的图,每个子图对应训练数据集中第一个受试者的一个活动。总加速度数据的x、y和z轴分别用蓝色、橙色和绿色直方图表示。
我们可以看到每个活动都有不同的数据分布,其中大幅度运动(前三个活动)与静止活动(后三个活动)之间存在显著差异。前三个活动的数据分布看起来是高斯分布,可能具有不同的均值和标准差。后几个活动的分布看起来是多峰的(即有多个峰值)。
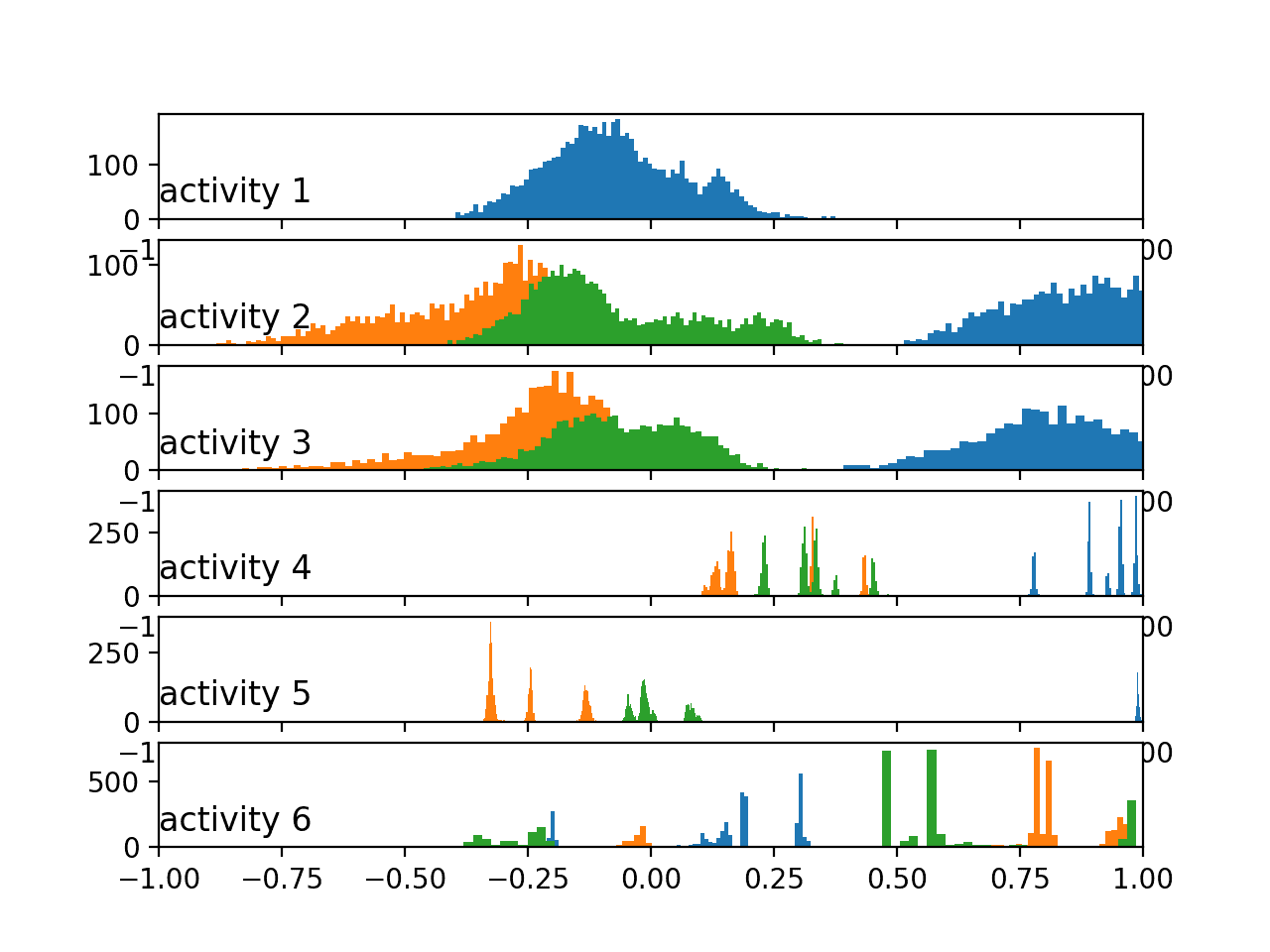
按活动划分的总加速度数据直方图
我们可以使用 `plot_activity_histograms()` 函数的更新版本重新运行相同的示例,该版本将绘制身体加速度数据。
更新后的函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 绘制一个主题的每个活动的直方图 def plot_activity_histograms(X, y): # 获取主题的唯一活动列表 activity_ids = unique(y[:,0]) # 按活动分组窗口 grouped = data_by_activity(X, y, activity_ids) # 按活动绘制,每个轴的直方图 pyplot.figure() xaxis = None for k in range(len(activity_ids)): act_id = activity_ids[k] # 总加速度 for i in range(3): ax = pyplot.subplot(len(activity_ids), 1, k+1, sharex=xaxis) ax.set_xlim(-1,1) if k == 0: xaxis = ax pyplot.hist(to_series(grouped[act_id][:,:,3+i]), bins=100) pyplot.title('activity '+str(act_id), y=0, loc='left') pyplot.show() |
运行更新后的示例会创建一个新的图。
在这里,我们可以看到运动中活动与静止活动之间的活动分布更相似。数据在运动中活动的情况下看起来是双峰的,而在静止活动的情况下可能是高斯分布或指数分布。
我们看到的总加速度与身体加速度按活动分布的模式,与上一节中不同主体相同数据类型所呈现的模式相似。也许总加速度数据是区分活动的关键。
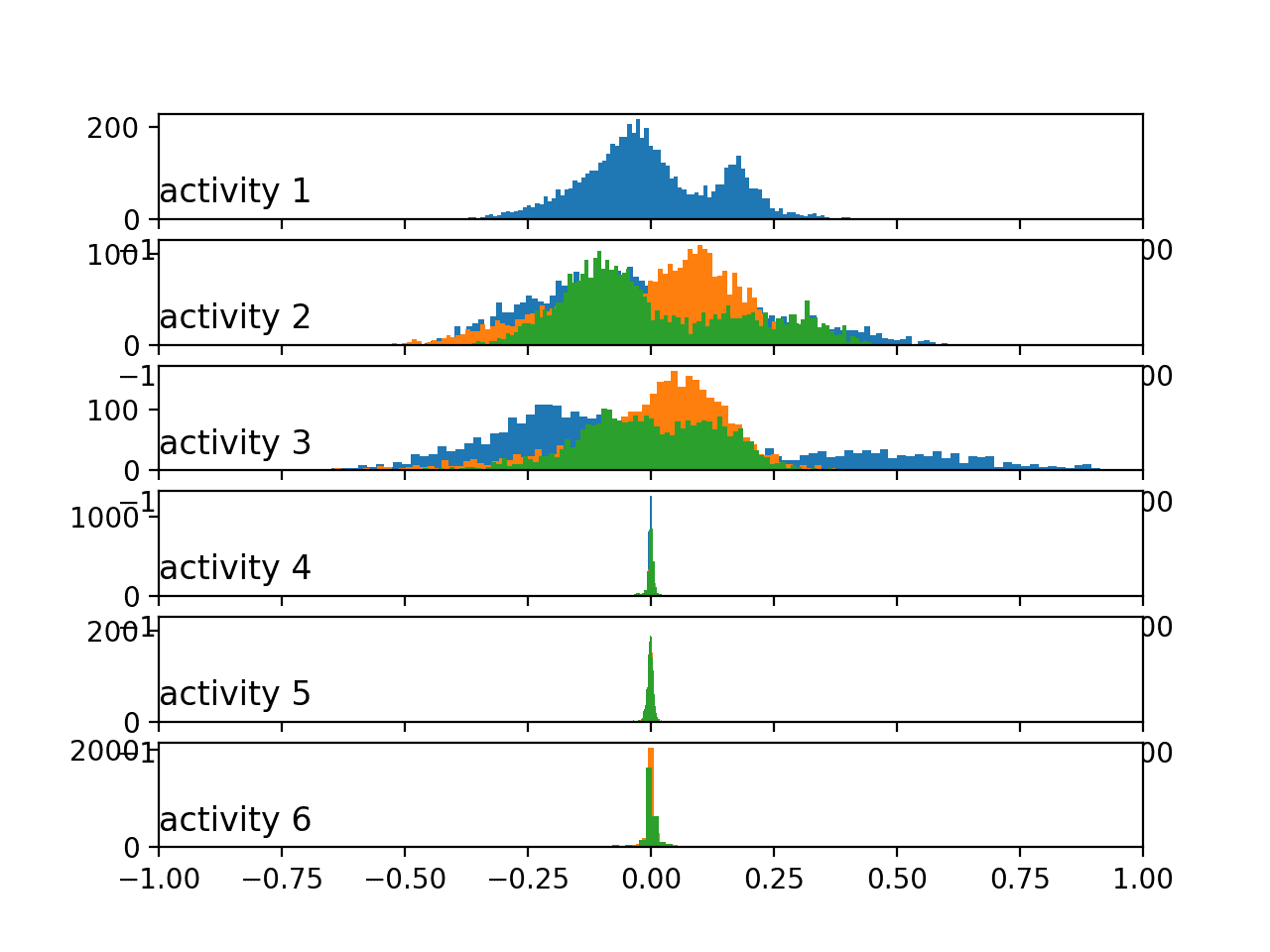
按活动划分的身体加速度数据直方图
最后,我们可以再次更新示例,绘制陀螺仪数据每个活动的直方图。
更新后的函数如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 绘制一个主题的每个活动的直方图 def plot_activity_histograms(X, y): # 获取主题的唯一活动列表 activity_ids = unique(y[:,0]) # 按活动分组窗口 grouped = data_by_activity(X, y, activity_ids) # 按活动绘制,每个轴的直方图 pyplot.figure() xaxis = None for k in range(len(activity_ids)): act_id = activity_ids[k] # 总加速度 for i in range(3): ax = pyplot.subplot(len(activity_ids), 1, k+1, sharex=xaxis) ax.set_xlim(-1,1) if k == 0: xaxis = ax pyplot.hist(to_series(grouped[act_id][:,:,6+i]), bins=100) pyplot.title('activity '+str(act_id), y=0, loc='left') pyplot.show() |
运行示例会创建与身体加速度数据相似模式的图表,尽管运动中活动可能显示的是肥尾高斯分布而非双峰分布。
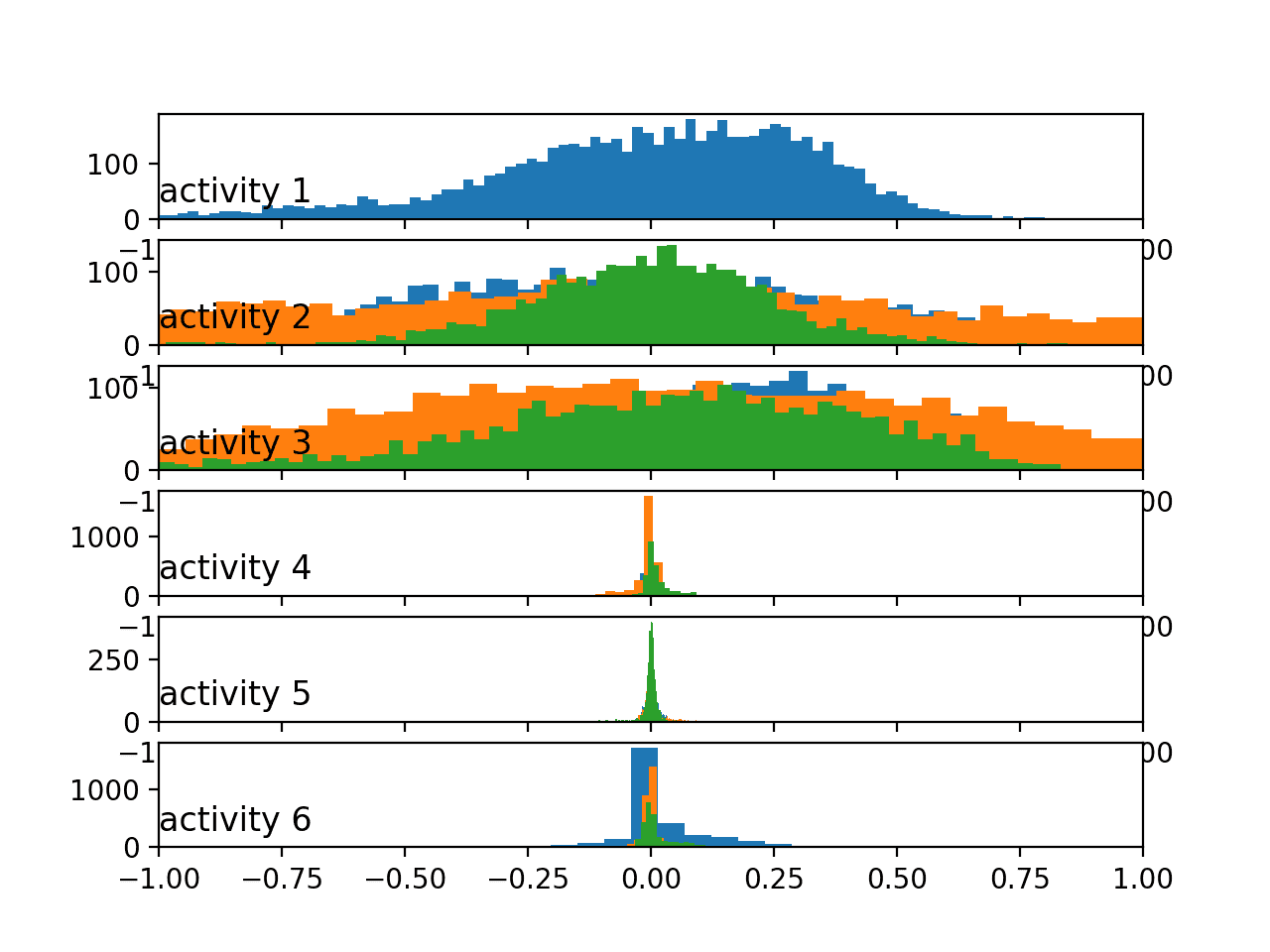
按活动划分的身体陀螺仪数据直方图
所有这些图都是为第一个受试者创建的,我们期望其他受试者的运动数据在不同活动中也会显示相似的分布和关系。
9. 绘制活动持续时间箱线图
最后要考虑的一个方面是受试者在每个活动上花费的时间。
这与类别的平衡密切相关。如果活动(类别)在一个数据集中通常是平衡的,那么我们期望一个给定受试者在其轨迹过程中活动的平衡也会相对较好。
我们可以通过计算每个受试者在每个活动上花费的时间(以样本或行数计)并查看每个活动持续时间的分布来证实这一点。
查看这些数据的一个便捷方式是将分布总结为箱线图,显示中位数(线)、中间 50%(箱体)、数据的一般范围作为四分位距(触须),以及异常值(点)。
下面的函数 plot_activity_durations_by_subject() 通过首先按受试者分割数据集,然后按活动分割受试者数据并计算每个活动上花费的行数,最后为每个活动的持续时间测量值创建箱线图来实现此行为。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 绘制按受试者划分的活动持续时间 def plot_activity_durations_by_subject(X, y, sub_map): # 获取唯一的受试者和活动 subject_ids = unique(sub_map[:,0]) activity_ids = unique(y[:,0]) # 枚举主题 activity_windows = {a:list() for a in activity_ids} for sub_id in subject_ids: # 获取一个主题的数据 _, subj_y = data_for_subject(X, y, sub_map, sub_id) # 按活动计数窗口 for a in activity_ids: activity_windows[a].append(len(subj_y[subj_y[:,0]==a])) # 将持续时间组织成列表的列表 durations = [activity_windows[a] for a in activity_ids] pyplot.boxplot(durations, labels=activity_ids) pyplot.show() |
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
# 绘制每个活动按受试者划分的持续时间 from numpy import array from numpy import dstack from numpy import unique from pandas import read_csv from matplotlib import pyplot # 将单个文件加载为numpy数组 def load_file(filepath): dataframe = read_csv(filepath, header=None, delim_whitespace=True) return dataframe.values # 加载文件列表,例如给定变量的x、y、z数据 def load_group(filenames, prefix=''): loaded = list() for name in filenames: data = load_file(prefix + name) loaded.append(data) # 堆叠组,使特征成为第三维度 loaded = dstack(loaded) return loaded # 加载数据集组,例如训练集或测试集 def load_dataset(group, prefix=''): filepath = prefix + group + '/Inertial Signals/' # 将所有9个文件加载为单个数组 filenames = list() # 总加速度 filenames += ['total_acc_x_'+group+'.txt', 'total_acc_y_'+group+'.txt', 'total_acc_z_'+group+'.txt'] # 身体加速度 filenames += ['body_acc_x_'+group+'.txt', 'body_acc_y_'+group+'.txt', 'body_acc_z_'+group+'.txt'] # 身体陀螺仪 filenames += ['body_gyro_x_'+group+'.txt', 'body_gyro_y_'+group+'.txt', 'body_gyro_z_'+group+'.txt'] # 加载输入数据 X = load_group(filenames, filepath) # 加载类别输出 y = load_file(prefix + group + '/y_'+group+'.txt') 返回 X, y # 获取一个主题的所有数据 def data_for_subject(X, y, sub_map, sub_id): # 获取主题ID的行索引 ix = [i for i in range(len(sub_map)) if sub_map[i]==sub_id] # 返回选定的样本 return X[ix, :, :], y[ix] # 将一系列窗口转换为一维列表 def to_series(windows): series = list() for window in windows: # 移除窗口中的重叠部分 half = int(len(window) / 2) - 1 for value in window[-half:]: series.append(value) return series # 按活动分组数据 def data_by_activity(X, y, activities): # 按活动分组窗口 return {a:X[y[:,0]==a, :, :] for a in activities} # 绘制按受试者划分的活动持续时间 def plot_activity_durations_by_subject(X, y, sub_map): # 获取唯一的受试者和活动 subject_ids = unique(sub_map[:,0]) activity_ids = unique(y[:,0]) # 枚举主题 activity_windows = {a:list() for a in activity_ids} for sub_id in subject_ids: # 获取一个主题的数据 _, subj_y = data_for_subject(X, y, sub_map, sub_id) # 按活动计数窗口 for a in activity_ids: activity_windows[a].append(len(subj_y[subj_y[:,0]==a])) # 将持续时间组织成列表的列表 durations = [activity_windows[a] for a in activity_ids] pyplot.boxplot(durations, labels=activity_ids) pyplot.show() # 加载训练数据集 X, y = load_dataset('train', 'HARDataset/') # 加载行到主题的映射 sub_map = load_file('HARDataset/train/subject_train.txt') # 绘制持续时间 plot_activity_durations_by_subject(X, y, sub_map) |
运行该示例会创建六个箱线图,每个活动一个。
每个箱线图总结了训练数据集中的受试者在每项活动上花费的时间(以行数或窗口数表示)。
我们可以看到,受试者在静止活动(4、5 和 6)上花费的时间更多,而在运动活动(1、2 和 3)上花费的时间更少,其中活动 3 的分布最小,或者说花费的时间最少。
各项活动之间的差异不大,表明无需裁剪持续时间较长的活动,也无需对运动中的活动进行过采样。尽管如此,如果预测模型在运动中的活动上的技能普遍较差,这些方法仍然可用。
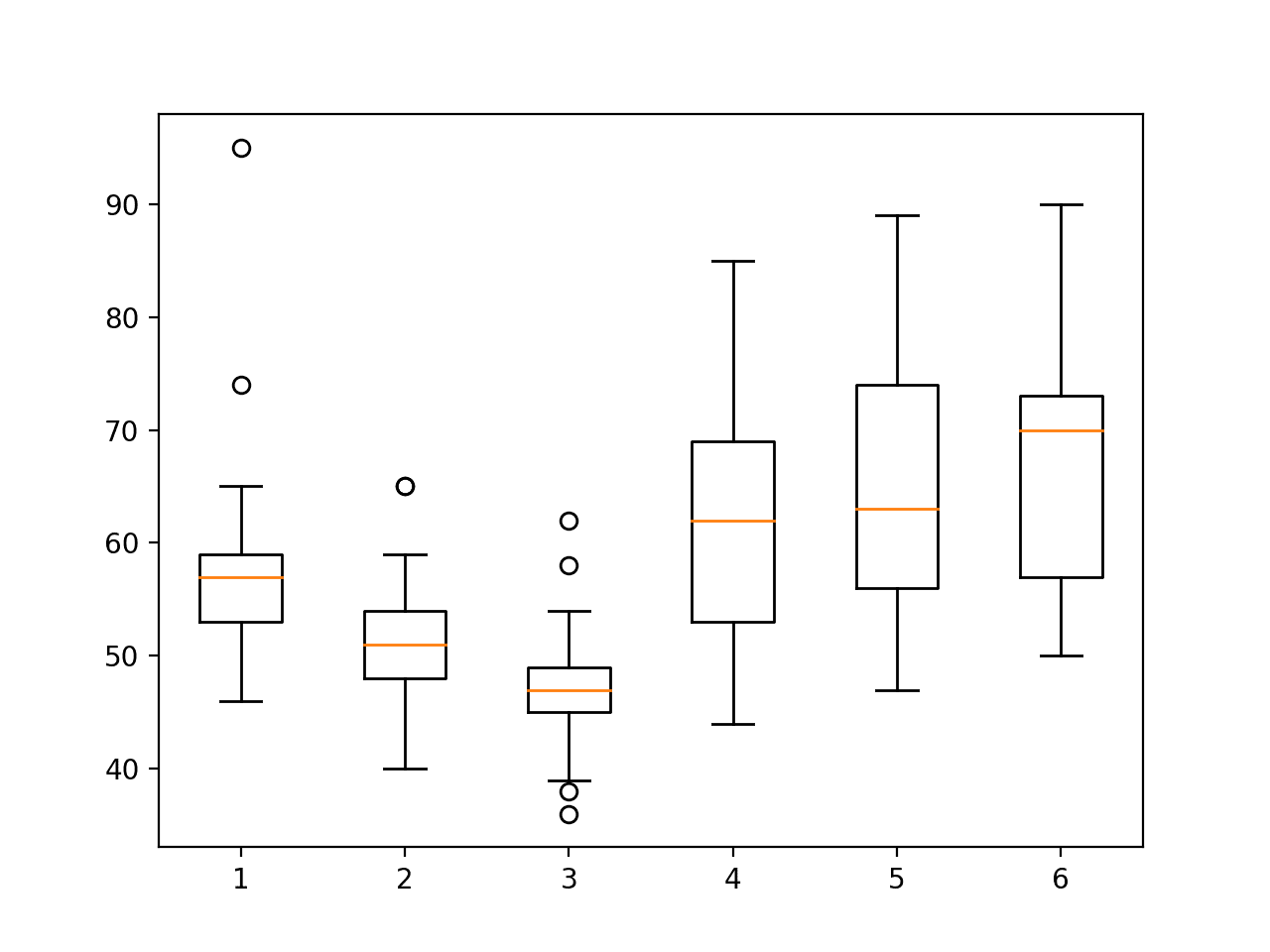
训练集上每个受试者的活动持续时间箱线图
我们可以为训练数据创建一个类似的箱线图,并添加以下行。
|
1 2 3 4 5 6 |
# 加载测试数据集 X, y = load_dataset('test', 'HARDataset/') # 加载行到主题的映射 sub_map = load_file('HARDataset/test/subject_test.txt') # 绘制持续时间 plot_activity_durations_by_subject(X, y, sub_map) |
运行更新后的示例显示了活动之间相似的关系。
这令人鼓舞,表明测试和训练数据集确实能很好地代表整个数据集。
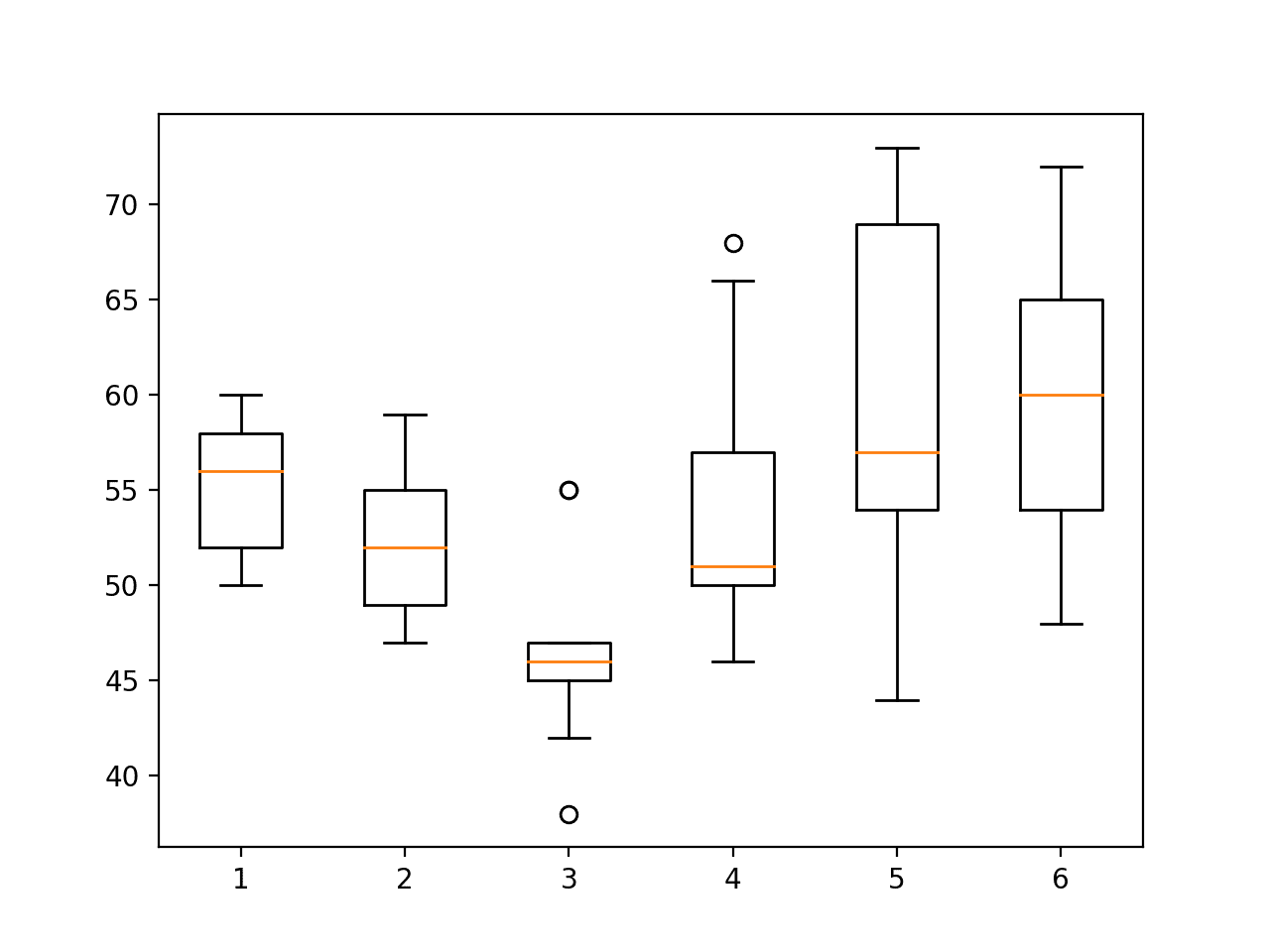
测试集上每个受试者的活动持续时间箱线图
现在我们已经探索了数据集,我们可以提出一些关于如何对其进行建模的想法。
10. 建模方法
在本节中,我们总结了一些用于活动识别数据集建模的方法。
这些想法分为项目的主要主题。
问题构建
第一个重要的考虑是预测问题的框架。
原始工作中描述的问题框架是根据已知受试者的运动数据和活动,预测新受试者的活动。
我们可以将其总结为
- 给定运动数据窗口,预测活动。
这是一个合理且有用的问题框架。
将提供的数据框架为预测问题的一些其他可能方式包括以下几种
- 给定一个时间步的运动数据,预测活动。
- 给定多个运动数据窗口,预测活动。
- 给定多个运动数据窗口,预测活动序列。
- 给定预分段活动的一系列运动数据,预测活动。
- 给定一个时间步的运动数据,预测活动停止或转换。
- 给定运动数据窗口,预测静止或非静止活动
其中一些框架可能过于具有挑战性或过于简单。
尽管如此,这些框架提供了额外的方法来探索和理解数据集。
数据准备
在使用原始数据训练模型之前,可能需要进行一些数据准备。
数据似乎已经被缩放到 [-1,1] 范围。
在建模之前可以执行的一些额外数据转换包括
- 跨受试者归一化。
- 按受试者标准化。
- 跨受试者标准化。
- 轴特征选择。
- 数据类型特征选择。
- 信号异常值检测和去除。
- 移除过度表示活动的窗口。
- 对未充分表示活动的窗口进行过采样。
- 将信号数据下采样至部分数据的 1/4、1/2、1、2 或其他分数。
预测建模
通常,该问题是一个时间序列多类分类问题。
如我们所见,它也可以被框定为二元分类问题和多步时间序列分类问题。
原始论文探索了在数据集的一个版本上使用经典机器学习算法,其中从每个数据窗口中提取了特征。具体来说,是一个改进的支持向量机。
SVM 在特征工程版本数据集上的结果可能为问题提供性能基线。
在此基础上,对该版本数据集上的多个线性、非线性和集成机器学习算法进行评估,可能会提供改进的基准。
问题的重点可能在于数据集的未处理或原始版本。
在这里,可以探索模型复杂度的进展,以确定最适合该问题的模型;一些可供探索的候选模型包括
- 常见的线性、非线性和集成机器学习算法。
- 多层感知器。
- 卷积神经网络,特别是1D CNN。
- 循环神经网络,特别是LSTMs。
- CNN和LSTM的混合模型,如CNN-LSTM和ConvLSTM。
模型评估
原始论文中的模型评估涉及使用按受试者划分的70%和30%比例的数据进行训练/测试拆分。
对这种预定义的数据分割的探索表明,两组数据都能很好地代表整个数据集。
另一种替代方法可能是对每个受试者使用留一交叉验证 (LOOCV)。除了让每个受试者的数据都有机会被用作保留的测试集外,该方法还将提供一个包含 30 个分数的集合,这些分数可以进行平均和总结,从而可能提供更稳健的结果。
模型性能使用分类准确率和混淆矩阵进行展示,两者都适用于预测问题的多类性质。
具体而言,混淆矩阵将有助于确定某些类别是否比其他类别更容易或更具挑战性,例如静止活动与涉及运动的活动。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
API
文章
总结
在本教程中,您了解了用于时间序列分类的智能手机活动识别数据集,以及如何加载和探索该数据集,以便为预测建模做好准备。
具体来说,你学到了:
- 如何下载和加载数据集到内存。
- 如何使用线图、直方图和箱线图来更好地理解运动数据的结构。
- 如何对问题进行建模,包括框架、数据准备、建模和评估。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



Jason,一如既往的精彩作品。我只希望你能提供与手机(例如安卓)通信的代码,而不是加载采样数据。
谢谢。
好建议!
有几个开源演示了如何从手机收集数据(参见 github)。
在我的应用程序(开发中)中,我正在收集加速度数据(使用 10 秒的滑动窗口),并在某些触发器触发后保存到临时文件并上传到谷歌云。由于所有烦人的安全问题,这不是一项简单的任务。
如果有人对此感兴趣,请告诉我,我将尝试开发一个示例应用程序。
听起来是个挑战性问题!
请帮我了解如何通过应用程序识别活动
我对此非常感兴趣。我正在做一个学校项目,这是一个六学分的课程。我一直在阅读关于人类活动识别的资料,并将其选为我的主题。我甚至已经开始开发移动应用程序。我卡在了如何使用所需的滑动窗口收集加速度计和陀螺仪数据以及如何使用这些数据进行预测上。
我认为首先通过手机收集数据,然后根据需要将其重构为滑动窗口。
嗨,先生
我热衷于开发一个安卓应用程序(人类活动识别),通过手机获取数据。
请帮我了解如何从中获取数据
抱歉,我不了解安卓系统。
非常感谢,
如果您有关于活动识别或活动异常检测的任何文章,请告诉我,再次感谢。
我将发布几篇关于活动识别的帖子。
我还在本书中详细介绍了该主题
https://machinelearning.org.cn/deep-learning-for-time-series-forecasting/
谢谢分享。
不客气。
谢谢你,Jason。
不客气。
是否有类似的摔倒数据集?我发现很多关于老年人跌倒检测的参考文献,但没有关于年轻人(20-60 岁)的。具体来说,我想识别骑行时的跌倒(这并不像人们预期的那样容易,因为我没有速度数据)。
感谢您的博客文章!
我预计有,我不知道,也许试着搜索一下?
我使用 Keras 实现了一个模型,用于对同一个问题进行 LSTM 建模,你可以在 https://github.com/servomac/Human-Activity-Recognition 查看。
干得好!
嗨
我有一个问题:如果研究对实际数据感兴趣,为什么研究人员要转换数据。转换有不同的模式和模型。
是的,我们转换数据是为了更好地向学习算法展示数据中模式的结构。没有其他原因。
关于人类活动识别的精彩文章。
谢谢约翰!
我需要在智能手机上实时识别人类活动?请帮帮我。
抱歉,我没有在智能手机上运行的示例。
嘿!
我正在使用无线传感器数据挖掘 (WISDM) 数据集,其中包括
http://www.cis.fordham.edu/wisdm/dataset.php
示例数:1,098,207
属性数:6
班级分布
步行:424,400 (38.6%)
慢跑:342,177 (31.2%)
上楼:122,869 (11.2%)
下楼:100,427 (9.1%)
坐:59,939 (5.5%)
站立:48,395 (4.4%)
我的问题是关于这个数据集的数据准备。
我将使用 CONV2D-LSTM 网络,所以我选择 90x3 的大小。
我这样做的方式是,将一个 90x3 的窗口以 45 步垂直地移动到数据上。
首先,这种重叠(45)有帮助吗?
然后我选择 60% 的数据用于训练,20% 用于测试,20% 用于验证。这样做是为了确保每个人(36 人)在训练、测试和验证中都有自己的份额。
我的想法对吗?
谢谢
我对这个数据集不熟悉,抱歉。我建议进行实验并确认您选择的配置是稳定的。
谢谢。
这是我的硕士论文,我把你的回答看作一个很好的观点。
我很感激
作为一名专业人士,您对这种数据和活动适合多少层有什么想法?我正在使用 CONV2D(作为特征提取器)和 LSTM。
我建议测试一系列网络配置/层数,以查看哪种最适合您的特定数据集。
嗨,Jason,
令人惊叹的作品。有没有关于信号处理部分(与去除噪声相关)的链接?像三阶中值滤波器和三阶低通巴特沃斯滤波器(截止频率 = 20Hz)这样的滤波器是如何工作的?这里的归一化又是如何完成的?
抱歉,我没有关于这些主题的教程。也许可以查阅一些DSP库?即使是scipy也能实现其中一部分功能。
先生,您好,
请帮我解释一下数据集,我很难理解它……
我来告诉您我理解了什么:::
我们有来自加速度计和陀螺仪传感器的 6 个时间序列。
对于每个时间序列,我们将其划分为每个包含 128 个样本的窗口……我们总共有 7352 个点,每个点对应一个活动。
数据集描述中还提到:“从每个活动窗口中提取了总共 561 个特征” 我在这里感到困惑……每个窗口有 128 个样本,每个窗口代表 561 个特征……在这里我感到困惑。
是的。
提取的特征是数据集的一部分,但我们不必使用它们,实际上,我在大多数示例中都没有使用它们。
先生,您好,
“10个受试者总加速度数据直方图”中的Y轴代表什么?
比如2500,5000等等?…X轴是从-1到1,因为数据是缩放过的…Y轴呢?
好问题,回想一下,直方图计算X轴上观测值的频率。
你好先生,
我从两个传感器“加速度计”和“陀螺仪”收集了数据。我想用这些数据训练一个单一模型。能否指导我如何构建我的数据集,例如“UCI”或任何其他能完成我任务的方法。谢谢
也许你可以以UCI数据集的示例作为起点,并根据你的需求进行调整?
但是加速度计和“陀螺仪”给我不同的值。加速度计每秒给我 12 个值,而陀螺仪给我 24 个值。所以我无法像 UCI 那样映射和构建数据集。所以请指导我如何解决这个问题。谢谢
我还没有找到能帮助我构建像UCI传感器数据集那样的资源。
你可能需要编写自定义代码来完成这项工作。慢慢来,并尝试利用准备其他数据集的代码。
如果太具挑战性,也许可以雇佣一个开发人员来做你需要的事情?比如在upwork.com上?
也许你需要缩放数据?
好的
我已经在 50 Hz 数据集上训练了一个 LSTM 模型,用于“加速度计”和“陀螺仪”。现在我想部署这个模型来获取预测。为了训练,我设置了
TIME_STEP = 100
SEGMENT_TIME_SIZE = 180
现在我正在思考如何准确地将测试数据集传递给训练好的模型以获取预测。哪种方法能准确地获取预测并避免错误结果?
以下是该项目的存储库链接
https://github.com/bartkowiaktomasz/har-wisdm-lstm-rnns
如果你不理解我的问题……我可以重复一遍
您可以调用 model.predict() 对新数据进行预测。
也许这会有帮助。
https://machinelearning.org.cn/how-to-make-classification-and-regression-predictions-for-deep-learning-models-in-keras/
好的,我明白了
谢谢!
但是,就像在 LSTM 中一样,您以定义的段大小传递数据,并且它在预测后返回该段的结果。所以我正在思考如何准确地传递段大小,以便获得准确的结果。
抱歉,我没听懂你的问题。你能详细说明一下吗?
您好,您是否有通过 python 代码从原始数据中计算窗口的示例?另外,您是否有从原始数据计算手工特征的示例?
是的,也许从这里开始
https://machinelearning.org.cn/start-here/#deep_learning_time_series
谢谢。我能问您另一个问题并验证我的直觉吗?如果知道数据是以 50 赫兹在 10 秒内采集的,我如何定义窗口的持续时间?我参考了文献(可能在 1 到 2 秒之间),然后我选择了,比如 2 秒?这样我的 2 秒窗口中将有 100 个样本。
该模型与时间无关,它只知道输入样本。
也许可以在您的输入数据上测试不同的窗口大小并比较结果?
谢谢,Jason。您了解深度学习中的隐私技术吗?差分隐私或联邦学习?
没有,抱歉。
大家好,我刚开始学习机器学习,我需要一些帮助来执行 CSV 文件数据(我用智能手机记录的加速度计的 Z 轴)的 EMD 分解
什么是EMD分解?
先生,我正在用从三星 Galaxy Note3 收集的原始加速度计数据进行实验。哪种滤波器最适合在 Python 中预处理数据。感谢并致敬
也许可以尝试几种方法,然后选择对您的特定数据集性能最佳的方法。
先生,你好
我使用智能手机收集了数据,我想根据正常和异常运动这两种类型对数据进行标注
你能帮我如何标注输出以及如何过滤噪声吗
谢谢你
也许最初手动标注,然后看看如何实现自动化。
嗨!请提供我如何找出人类识别准确率的代码。
也许从这里开始
https://machinelearning.org.cn/how-to-develop-rnn-models-for-human-activity-recognition-time-series-classification/
Jason Brownlee 博士,感谢您所有这些精彩的教程。我明白了您是如何通过为每个轴创建单独的分布来比较每个活动的三个轴(x、y、z)的数据的,但是如果我有来自两个不同设备的加速度计数据,并且我想比较这两个设备的数据分布,是否可以将三个轴(x、y、z)组合成一个代表设备收集的数据的分布?我能否以某种方式将所有活动和三个轴的数据总结成一个与设备对应的分布?
我认为将两组观测值合并没有意义。如果需要,您可以将它们都输入模型。
感谢您的回复,Jason 博士。抱歉造成困惑,我的问题不是将数据输入模型,而是比较两种不同设备(智能手机或智能手表)的加速度计数据分布。基本上,我试图通过视觉解释为什么模型性能在一种设备上开发后部署到另一种新设备上会下降。我根据这篇文章的想法是平均三个轴数据的幅度,然后为每个设备计算直方图或箱线图。您认为这有意义吗?您有什么建议?
比较两个样本分布听起来是一个很好的开始,例如通过统计假设检验。
是的,我想统计测试在我的案例中会更有意义。谢谢你的提示 🙂
那么,HAR 如何通过给定的数据集进行预测?
这里有一个例子
https://machinelearning.org.cn/cnn-models-for-human-activity-recognition-time-series-classification/
嗨,Jason 教授,我总是从您的教程中受益匪浅。这些天,我正在做一个关于人类活动识别的项目,我使用了一些滤波器来过滤时间序列数据,并做了一些变换,如 FFT、PSD 等。同时,我将数据切片成窗口,但没有对其进行归一化,然后我在 sklearn 中导入了 MLP。然而,我发现它在时间序列上的表现比在特征提取数据上的表现更好。这真的让我很困惑,这是否意味着我的特征提取方法是错误的?非常感谢您的时间,如果您能回复我,我将不胜感激。
这可能是您的数据集和所选模型的特性。
您可以尝试探索替代模型和数据准备,以了解更多关于您的数据集的信息。
尊敬的布朗利博士,请您解释一下关于“6. 绘制一个受试者的时间序列数据”,341这个值代表什么(以及为什么时间序列x轴会达到350)——并且它会因受试者而异。我的理解是这个轴将始终是128个数据点?
此致!
我相信我们正在绘制所有数据或大部分数据,并已移除重叠部分。
你好,
我有一个很大的pandas数据框数据。
像这样
数据('x', 'y', 'z', '标签数据')
我想在这个数据框上应用一个50%重叠的滑动窗口。然后我想从每个窗口中提取共同特征(均值、标准差、方差)特征。
请给我一些例子,帮助我解决这个问题。
看这里
https://machinelearning.org.cn/convert-time-series-supervised-learning-problem-python/
Jason 教授您好
我想问一下 X_train 和惯性信号之间有什么区别,以及为什么您加载了惯性信号而没有加载 X_train?
我猜 X_train 是经过 3 阶巴特沃斯滤波器分离之前的数据,不是吗?
从帖子中:”
“惯性信号”文件夹,其中包含预处理过的数据。
X_train 是什么意思?它包含什么?“READ ME.txt”文件包含 561 个工程特征。所以这意味着 X_train 是预处理“raw_data”之前的数据,不是吗?
训练数据集。
先生,实际上我没明白。我知道训练集是什么意思。
但 X_train 和 inertial_Signals 之间的核心区别究竟是什么?
inertial_Signals 是对训练集进行预处理的结果吗?
X_train 和 inertial_Signals 之间有什么关系?
内部信号包含预处理过的(原始)数据——这是我们在本教程中使用的。
X_train.txt 和 y_train.txt 包含工程特征——这些我们没有在本教程中使用。
区别在“3. 下载数据集”一节中有所描述。
我认为他们对惯性信号进行了不同的计算来提取训练集。
对吗?
内部信号是原始数据。
如果你仍然有困难,也许可以阅读原始论文。
解释得很精彩,先生,如果您有类似的视频链接,请附上。
谢谢。
我没有视频。
布朗利博士,您好,
感谢您提供这篇信息丰富且结构清晰的文章。我目前正在从事一个项目,我需要实际预测单次举重练习的质量性能(5 个质量等级)。
我正在使用原始传感器数据,并计划将该项目框定为在给定运动数据时间步的情况下预测活动质量。这也应该被视为时间序列吗?
我随机将数据分为验证集和训练集,使用随机森林模型获得了约 97% 的高准确率,但我明白这并不意味着我的决策是正确的
是的,听起来像是时间序列。
如果观测结果是按时间顺序排列的,您必须使用前向验证或类似方法评估模型
https://machinelearning.org.cn/backtest-machine-learning-models-time-series-forecasting/
谢谢您!
不客气!
你好 Jason,
首先,我要感谢您与我们分享这篇帖子。
我想问一下每个活动的传感器直方图——为什么在所有三个信号(total_acc、body_acc 和 body_gyro)中,y 轴和 z 轴信号(绿色和橙色)都缺少活动 1(步行)。似乎只有 x 轴信号(蓝色)是活动的。
谢谢,
嗨……谢谢你的提问。我们会审查直方图。你执行代码了吗?如果是,你的直方图有什么不同吗?
嗨 James,
我执行了代码,得到了相同的结果。
但至少据我理解,x 和 y 确实有值,这些值应该出现在活动 #1 的直方图中。
我还没有机会尝试找到解决方案。
如果您已经找到了,或者您认为当前的直方图是正确的,我将很乐意听到。
谢谢,