统计学领域有很大一部分关注的是那些假设数据符合高斯分布(熟悉的钟形曲线)的方法。
如果你的数据符合高斯分布,参数化方法就非常强大且易于理解。如果可能,这会激励你去使用它们。即使你的数据不符合高斯分布。
你的数据可能看起来不像高斯分布,或者未能通过正态性检验,但通过变换可以使其符合高斯分布。如果你熟悉生成观测值的过程,并认为它是一个高斯过程,或者分布看起来接近高斯分布,只是有些失真,那么这种情况更有可能发生。
在本教程中,你将了解高斯状分布可能失真的原因以及可用于使数据样本更接近正态分布的技术。
完成本教程后,您将了解:
- 如何考虑样本量以及大数定律是否能帮助改善样本的分布。
- 如何识别和去除分布中的极端值和长尾。
- 功率变换和 Box-Cox 变换,可用于控制二次或指数分布。
启动你的项目,阅读我的新书《机器学习统计学》,其中包含分步教程以及所有示例的Python源代码文件。
让我们开始吧。

如何转换数据以更好地适应正态分布
照片由 duncan_idaho_2007 提供,保留部分权利。
教程概述
本教程分为7个部分;它们是:
- 高斯和类高斯
- 样本大小
- 数据分辨率
- 极端值
- 长尾
- 幂变换
- 仍可使用
需要机器学习统计学方面的帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
高斯和类高斯
当你处理非高斯分布但希望使用参数统计方法而非非参数方法时,可能会遇到这种情况。
例如,你的数据样本可能具有熟悉的钟形,意味着它看起来像高斯分布,但未能通过一项或多项统计正态性检验。这表明数据可能是类高斯分布。在这种情况下,你会更倾向于使用参数统计,因为它们具有更好的统计功效,并且数据本身就是高斯分布,或者经过正确的 数据转换后可以变为高斯分布。
数据集在技术上可能不符合高斯分布的原因有很多。在本文中,我们将介绍一些简单技术,你可以使用这些技术将具有类高斯分布的数据样本转换为高斯分布。
这个过程没有万能药;可能需要一些实验和判断。
样本大小
数据样本非高斯分布的一个常见原因是样本量太小。
许多统计方法是在数据稀缺的时代开发的。因此,许多方法的最小样本数可能低至 20 或 30 个观测值。
尽管如此,考虑到数据中的噪声,你可能无法看到熟悉的钟形,或者在拥有 50 或 100 个样本的适中样本量下未能通过正态性检验。如果是这种情况,也许你可以收集更多数据。得益于大数定律,你收集的数据越多,就越有可能描述底层总体分布。
为了具体说明,下面是一个从均值为 100,标准差为 50 的高斯分布中提取的 50 个观测值的小样本的示例图。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 小样本的直方图绘制 from numpy.random import seed from numpy.random import randn from matplotlib import pyplot # 为随机数生成器设置种子 seed(1) # 生成单变量数据样本 data = 50 * randn(50) + 100 # 直方图 pyplot.hist(数据) pyplot.show() |
运行该示例会生成数据的直方图,显示没有明显的高斯分布,甚至不是类高斯分布。
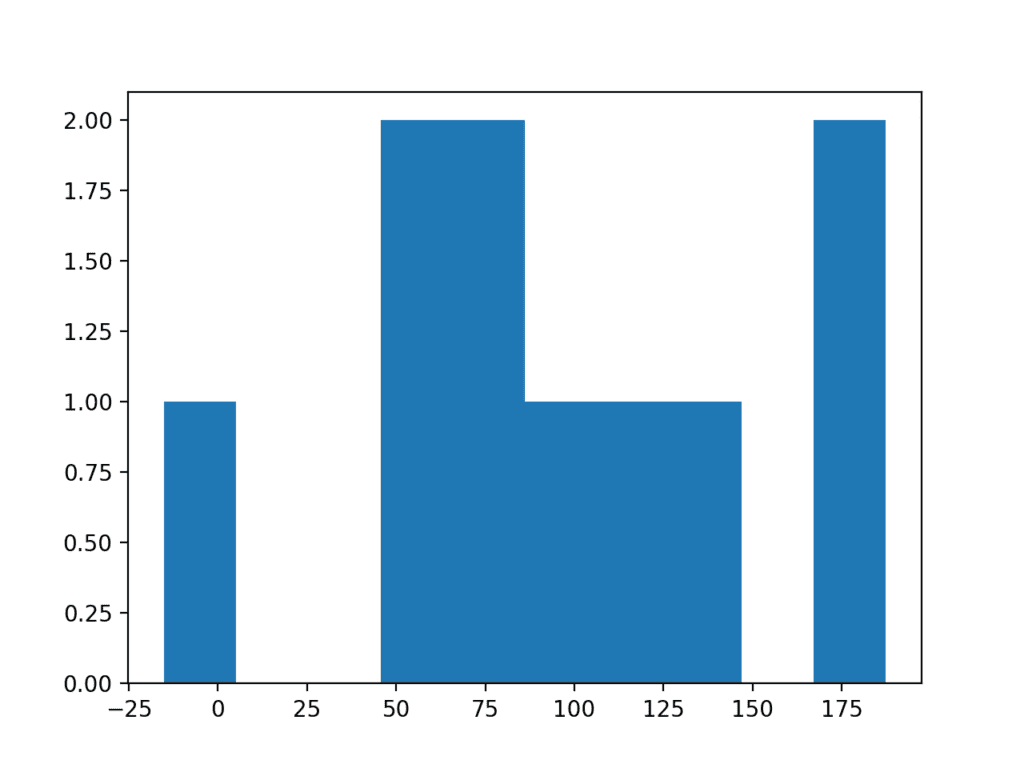
极小样本量数据直方图
将样本量从 50 增加到 100 有助于更好地揭示数据分布的高斯形状。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 小样本的直方图绘制 from numpy.random import seed from numpy.random import randn from matplotlib import pyplot # 为随机数生成器设置种子 seed(1) # 生成单变量数据样本 data = 50 * randn(100) + 100 # 直方图 pyplot.hist(数据) pyplot.show() |
运行示例,我们可以更好地看到数据的正态分布,这些数据可以通过统计检验和肉眼检查。
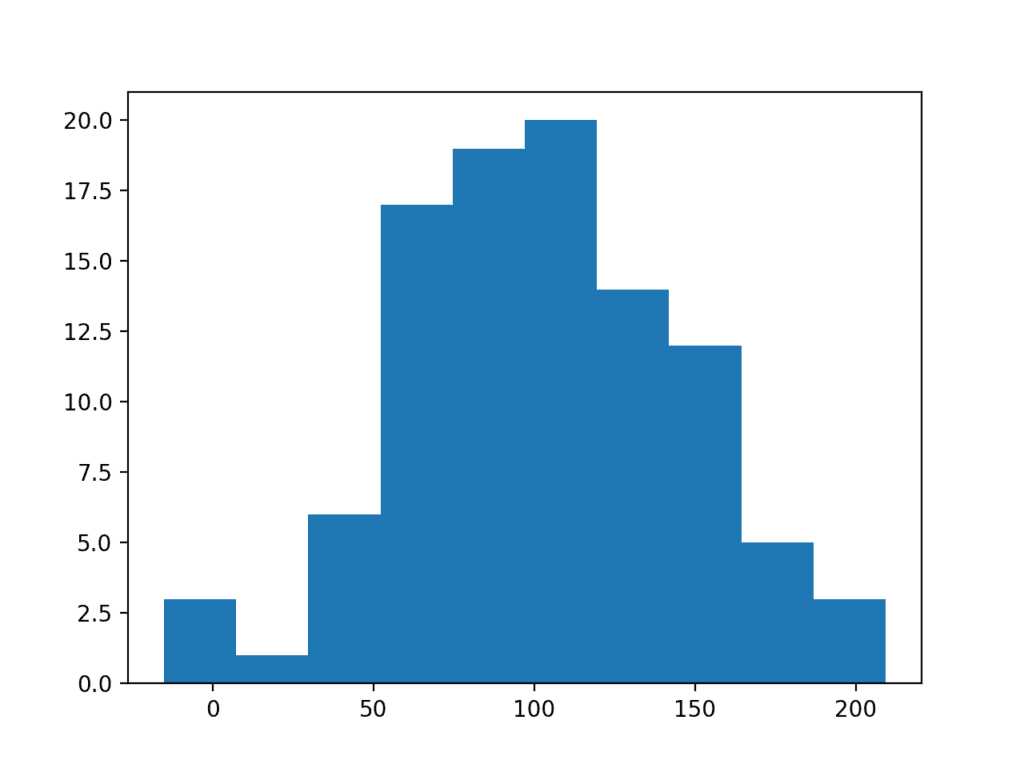
较大样本量数据直方图
数据分辨率
也许你预期数据是高斯分布,但无论你收集多少样本量,结果都不尽如人意。
一个常见的原因是你收集观测值所使用的分辨率。数据的分布可能被所选的数据分辨率或观测值的保真度所掩盖。在建模之前,数据分辨率可能被修改的原因有很多,例如:
- 生成观测值的机制的配置。
- 数据经过了质量控制流程。
- 用于存储数据的数据库的分辨率。
为了具体说明,我们可以生成一个具有均值为 0、标准差为 1 的 100 个随机高斯数样本,并去除所有小数位。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 低分辨率样本的直方图绘制 from numpy.random import seed from numpy.random import randn from matplotlib import pyplot # 为随机数生成器设置种子 seed(1) # 生成单变量数据样本 data = randn(100) # 去除小数部分 data = data.round(0) # 直方图 pyplot.hist(数据) pyplot.show() |
运行示例后,得到的分布看起来是离散的,尽管是类高斯分布。将分辨率加回到观测值中将得到一个更完整的数据分布。
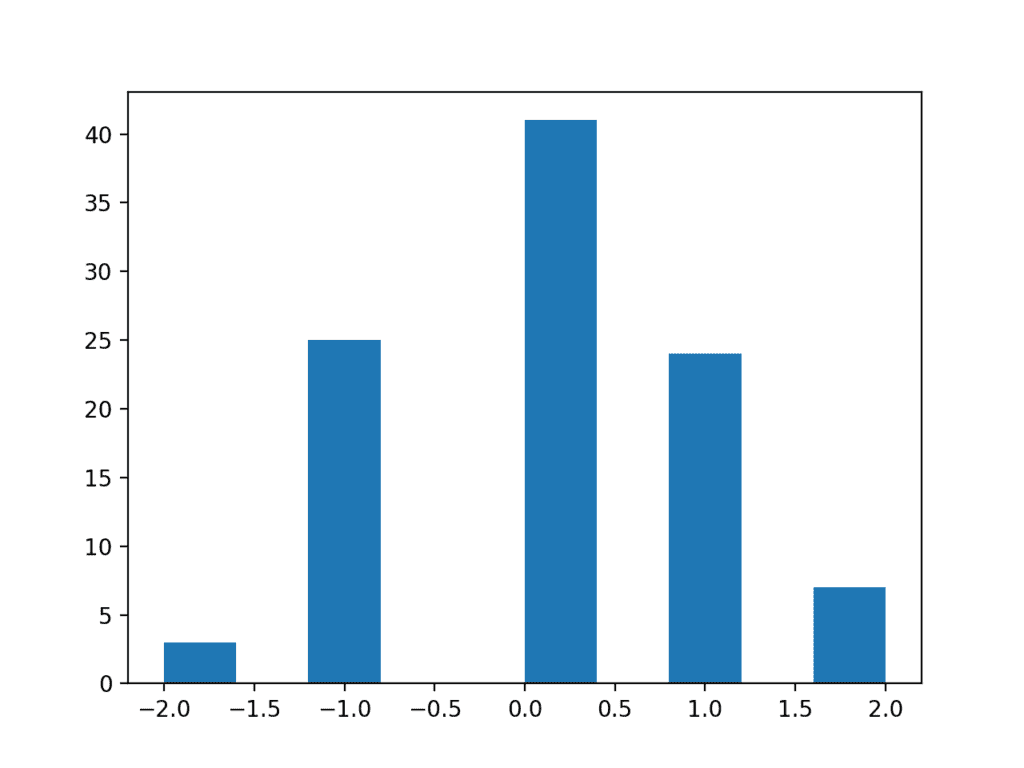
低分辨率数据样本直方图
极端值
数据样本可能具有高斯分布,但可能因多种原因而失真。
一个常见的原因是分布边缘存在极端值。极端值可能存在的原因有很多,例如:
- 测量误差。
- 缺失数据。
- 数据损坏。
- 罕见事件。
在这种情况下,可以识别并移除极端值,以使分布更符合高斯分布。这些极端值通常被称为异常值。
这可能需要领域专业知识或与领域专家的咨询,以便设计识别异常值的标准,然后将其从数据样本以及你或你的模型期望在未来处理的所有数据样本中删除。
我们可以演示极端值如何轻易地破坏数据分布。
下面的示例创建了一个具有 100 个随机高斯数的数据样本,其均值为 10,标准差为 5。然后向分布中添加了 10 个值为零的观测值。如果缺失或损坏的值被赋值为零,就会发生这种情况。这在公开可用的机器学习数据集中很常见;例如。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 带有异常值的数据直方图绘制 from numpy.random import seed from numpy.random import randn from numpy import zeros from numpy import append from matplotlib import pyplot # 为随机数生成器设置种子 seed(1) # 生成单变量数据样本 data = 5 * randn(100) + 10 # 添加极端值 data = append(data, zeros(10)) # 直方图 pyplot.hist(数据) pyplot.show() |
运行示例会创建并绘制数据样本。你可以清楚地看到零值观测值的高意外频率如何破坏了分布。
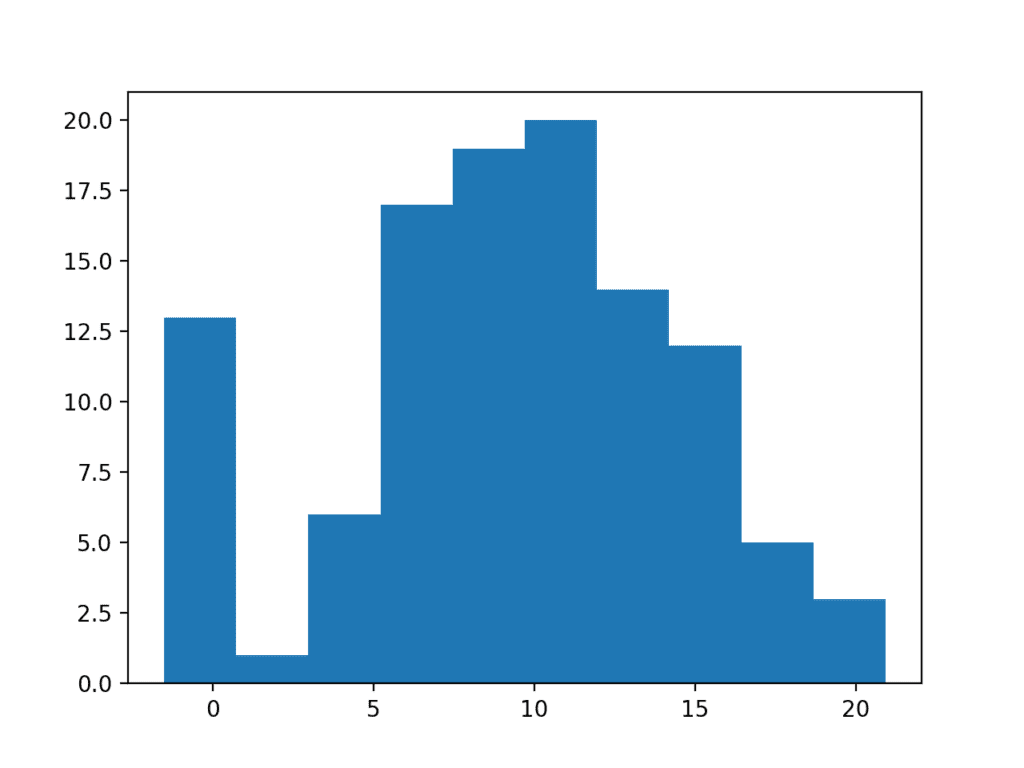
带有极端值的数据样本直方图
长尾
极端值可能以多种方式出现。除了分布边缘存在大量罕见事件外,你可能还会看到分布在一侧或两侧出现长尾。
在图中,这可能会使分布看起来像指数分布,而实际上它可能是高斯分布,在一侧有大量罕见事件。
你可以使用简单的阈值,例如距离均值标准差的倍数,来识别和删除长尾值。
我们可以通过一个人为设计的示例来演示这一点。数据样本包含 100 个均值为 10、标准差为 5 的高斯随机数。另外添加了 50 个在 10 到 110 范围内的均匀分布的随机值。这会在分布中造成一个长尾。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 带有长尾的数据直方图绘制 from numpy.random import seed from numpy.random import randn from numpy.random import rand from numpy import append from matplotlib import pyplot # 为随机数生成器设置种子 seed(1) # 生成单变量数据样本 data = 5 * randn(100) + 10 tail = 10 + (rand(50) * 100) # 添加长尾 data = append(data, tail) # 直方图 pyplot.hist(数据) pyplot.show() |
运行示例,你可以看到长尾如何扭曲高斯分布,使其看起来像指数分布,或者甚至像双峰分布(两个峰)。
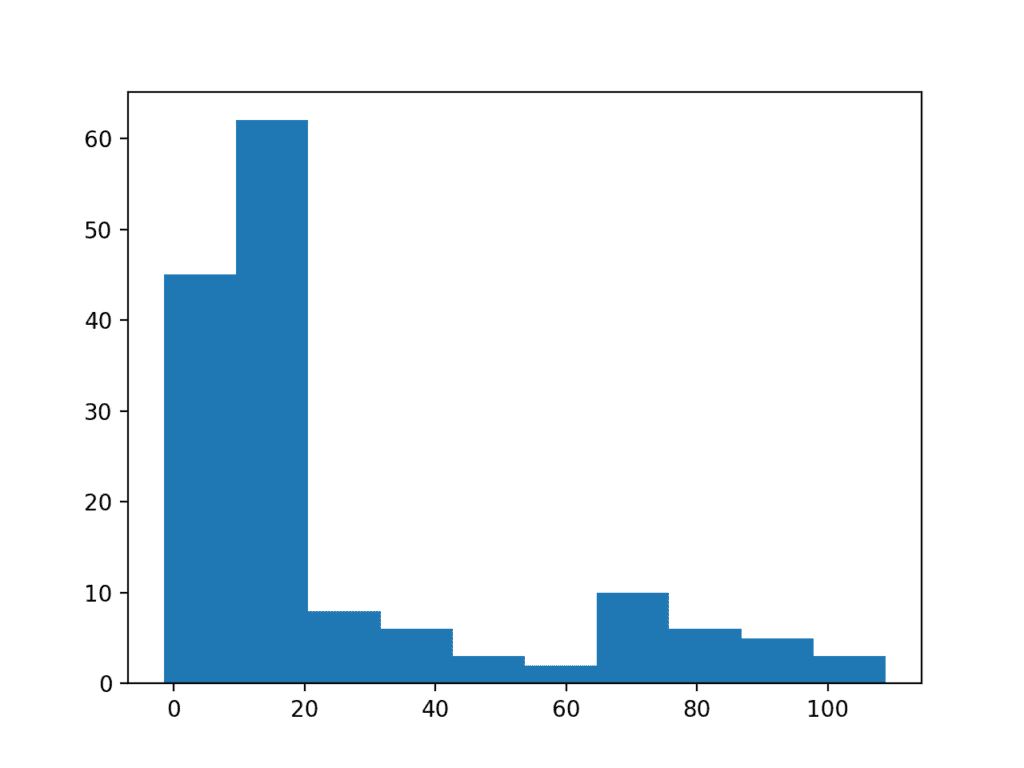
带有长尾的数据样本直方图
我们可以对这个数据集使用一个简单的阈值,例如 25,作为截止点,并删除所有高于此阈值的观测值。我们选择这个阈值是基于对数据样本如何被构造的先验知识,但你可以想象在自己的数据集中测试不同的阈值并评估它们的效果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 带有长尾的数据直方图绘制 from numpy.random import seed from numpy.random import randn from numpy.random import rand from numpy import append from matplotlib import pyplot # 为随机数生成器设置种子 seed(1) # 生成单变量数据样本 data = 5 * randn(100) + 10 tail = 10 + (rand(10) * 100) # 添加长尾 data = append(data, tail) # 修剪值 data = [x for x in data if x < 25] # 直方图 pyplot.hist(数据) pyplot.show() |
运行代码显示,这种简单的修剪长尾的方法将数据恢复为高斯分布。
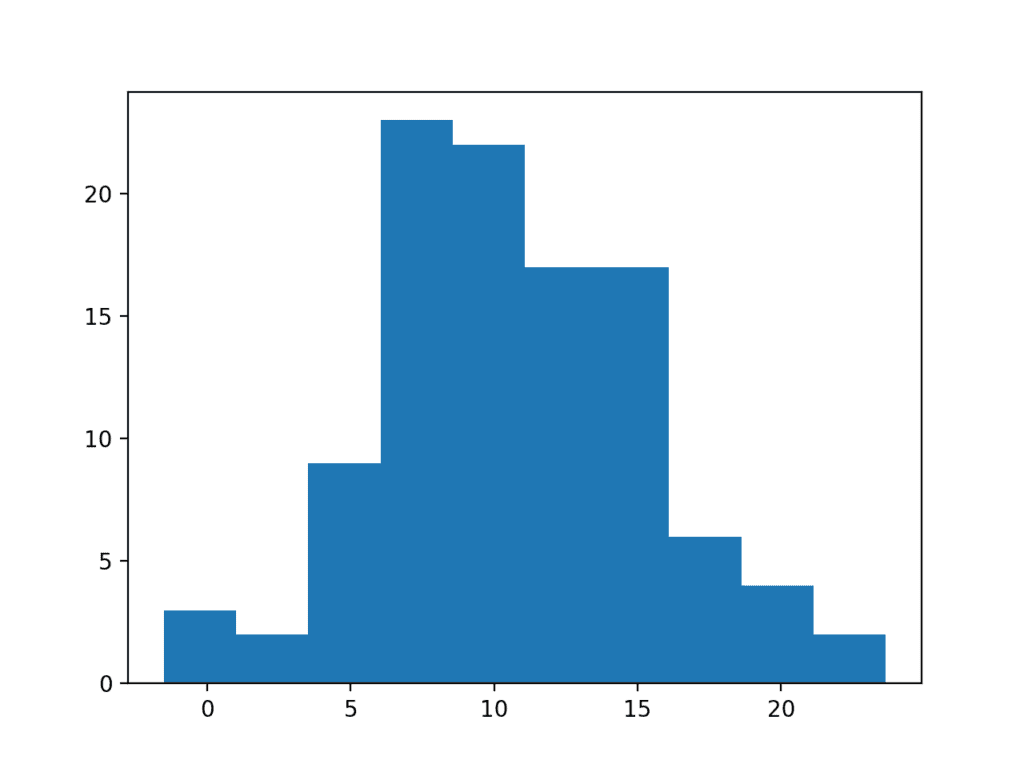
截断长尾的数据样本直方图
幂变换
数据的分布可能是正态的,但数据可能需要进行转换才能更好地揭示它。
例如,数据可能存在偏斜,这意味着钟形曲线的钟可能偏向一侧或另一侧。在某些情况下,可以通过对观测值计算平方根来转换数据来纠正这一点。
或者,分布可能是指数分布,但如果将观测值进行对数转换(取自然对数),则可能看起来像正态分布。具有这种分布的数据称为对数正态分布。
为了具体说明,下面是一个将高斯数样本转换为指数分布的示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 对数正态分布 from numpy.random import seed from numpy.random import randn from numpy import exp from matplotlib import pyplot # 为随机数生成器设置种子 seed(1) # 生成两组单变量观测值 data = 5 * randn(100) + 50 # 转换为指数分布 data = exp(data) # 直方图 pyplot.hist(数据) pyplot.show() |
运行示例会生成一个显示指数分布的直方图。事实上,数据是对数正态分布的这一点并不明显。
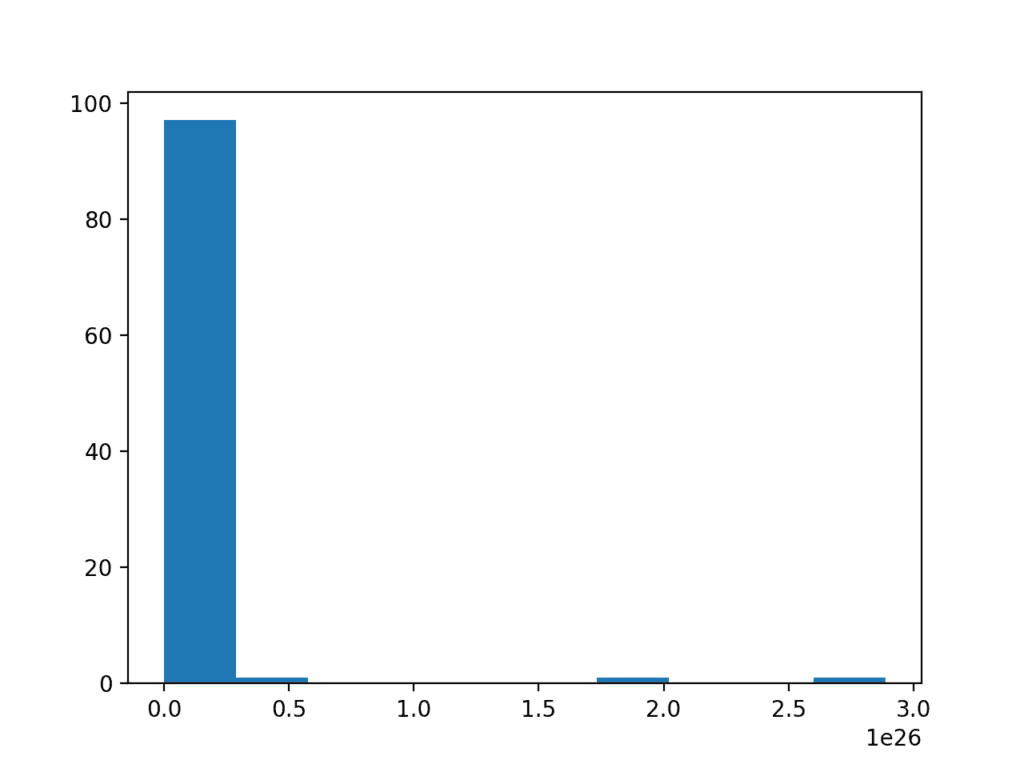
对数正态分布的直方图
为了使分布正态而取观测值的平方根和对数属于一类称为幂变换的变换。Box-Cox 方法是一种数据转换方法,能够执行一系列幂变换,包括对数变换和平方根变换。该方法以 George Box 和 David Cox 的名字命名。
更重要的是,它可以配置为自动评估一系列变换并选择最佳拟合。它可以被视为一种强大的工具,可以消除数据样本中基于幂的偏差。得到的数据样本可能更线性,并且能更好地表示潜在的非幂分布,包括高斯分布。
SciPy 的 boxcox() 函数实现了 Box-Cox 方法。它有一个名为 lambda 的参数,该参数控制要执行的变换类型。
以下是 lambda 的一些常见值
- lambda = -1:倒数变换。
- lambda = -0.5:倒数平方根变换。
- lambda = 0.0:对数变换。
- lambda = 0.5:平方根变换。
- lambda = 1.0:无变换。
例如,因为我们知道数据是对数正态分布的,我们可以通过将 lambda 显式设置为 0 来使用 Box-Cox 执行对数变换。
|
1 2 |
# 幂变换 data = boxcox(data, 0) |
对指数数据样本应用 Box-Cox 变换的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# Box-Cox 变换 from numpy.random import seed from numpy.random import randn from numpy import exp from scipy.stats import boxcox from matplotlib import pyplot # 为随机数生成器设置种子 seed(1) # 生成两组单变量观测值 data = 5 * randn(100) + 100 # 转换为指数分布 data = exp(data) # 幂变换 data = boxcox(data, 0) # 直方图 pyplot.hist(数据) pyplot.show() |
运行示例后,对数据样本执行 Box-Cox 变换并绘制结果,清楚地显示了高斯分布。
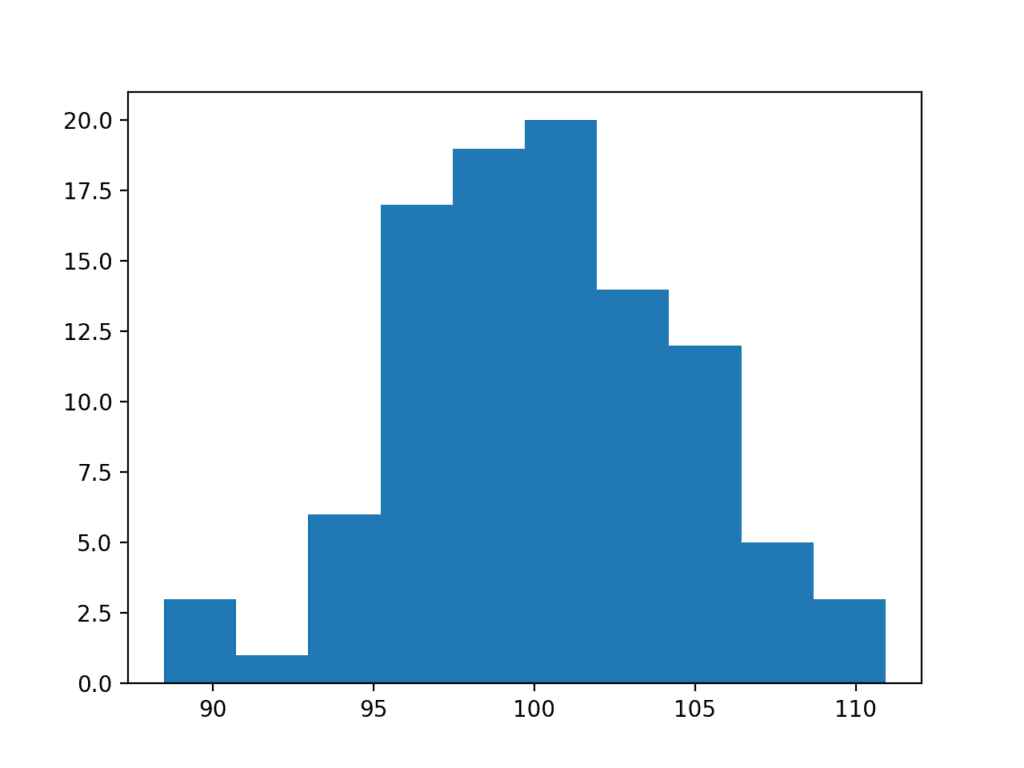
Box Cox 变换后的指数数据样本直方图
Box-Cox 变换的一个限制是它假设数据样本中的所有值都是正数。
Yeo-Johnson 变换是一种不作此假设的替代方法。
仍可使用
最后,你可能希望仍然将数据视为高斯分布,特别是如果数据已经是类高斯分布。
在某些情况下,例如使用参数统计方法,这可能会导致过于乐观的发现。
在其他情况下,例如对输入数据做出高斯期望的机器学习方法,你仍然可能获得良好的结果。
这是一个你可以做出的选择,只要你意识到潜在的缺点。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 列出高斯分布可能失真的 3 种可能附加方式
- 开发一个数据样本,并尝试 Box-Cox 变换的 5 个常见 lambda 值。
- 加载一个至少有一个变量具有类高斯分布的机器学习数据集并进行实验。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
文章
API
- numpy.random.seed() API
- numpy.random.randn() API
- numpy.random.rand() API
- matplotlib.pyplot.hist() API
- scipy.stats.boxcox() API
文章
总结
在本教程中,你了解了类高斯分布可能失真的原因以及可用于使数据样本更接近正态分布的技术。
具体来说,你学到了:
- 如何考虑样本量以及大数定律是否能帮助改善样本的分布。
- 如何识别和去除分布中的极端值和长尾。
- 功率变换和 Box-Cox 变换,可用于控制二次或指数分布。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。




尊敬的Jason博士,
数据转换后是否需要进行进一步的测试?
假设对数据进行了 Box-Cox 变换,使其具有对称的高斯外观。要确保转换后的数据是高斯分布,还需要进行哪些进一步的测试?
另一个问题是,泊松分布是离散值而不是连续值的分布。泊松分布可以具有对称的直方图。依赖数据为高斯分布假设的机器学习技术是否适用于泊松分布?
谢谢你,
来自令人兴奋的Belfield的Anthony
你可以使用这些测试。
https://machinelearning.org.cn/a-gentle-introduction-to-normality-tests-in-python/
泊松分布并不总是对称的。在对称的情况下,许多假设高斯分布的算法足够稳健,可以在不严重失败的情况下与其他对称分布一起工作。
解释得很好。
非常感谢 Jason 先生。
谢谢。
正如 Ravi 所说,解释得非常到位!
现在,如果我想将此方法应用于真实世界数据,我是否需要查看每个特征的分布,并尝试使用这些方法将其转换为高斯分布?
谢谢!
这取决于建模方法,是的。
由于朴素贝叶斯假设分布为高斯分布,那么在这种情况下是否必须转换为高斯分布?
高斯朴素贝叶斯假设高斯分布,在这种情况下,确保你的数据是高斯分布是个好主意。
否则,你可以使用任何分布,包括经验分布。
Brownlee 先生您好。
我正在尝试用 Python 编写一个算法,从名为 “NGC5055_HI_lab.fits” 的 fits 文件中提取数据
并将其另存为另一个 fits 文件,例如 “test.fits”。
到目前为止,我什么都没做。
我的算法到目前为止是这样的…
from matplotlib import pyplot as mp
import numpy as np
import astropy.io.fits as af
cube=af.open (‘NGC5055_HI_lab.fits’)[0]
mo=np.mean(cube.data)
s=np.var(cube.data)
σ=np.std(cube.data)
amp=1/(σ*np.sqrt(2*3.14))
cube.data=amp*np.exp(-np.power(cube.data-mo,2.)/(2*np.power(s,2.)))
cube.writeto(‘test.fits, overwrite=True)
你能帮忙吗?
这听起来像个编程问题,而不是机器学习问题。我建议在 Stack Overflow 上提问。
我是否可以将所有特征转换为高斯分布以进行线性分布?
抱歉,是线性回归。
可能可以,使用类似分位数变换的方法。但是为什么要这样做呢?
嗨,Brownlee先生,
首先,非常感谢您撰写的有帮助的博文。
我有一个关于我的特征变量的具体问题,希望您能帮助我。我有多个特征作为机器学习的输入。然而,我的特征具有非常不同的分布。其中一些是正态分布的,但有些是高度偏斜的。对不同特征应用不同类型的变换是否有效?例如,一些特征将被对数转换,而另一些我可以保留原始值?
非常感谢。
是的,如果需要,请单独准备每个特征。
您好,一切都非常有帮助,非常感谢。我有一个与此主题相关的疑问。如果变量在所有组中都没有正态分布,我们应该怎么办?例如,男性数据已经是正态的,而女性数据不是。但在变换之后,情况却相反,那么我是否可以根据组分别转换变量?
希望我能解释我的问题。
谢谢你
也许可以探索一下,将变换应用于整体数据、分组数据或原始数据这几种情况,对模型性能有何影响。
希望你一切安好。
我正在尝试应用一个需要值呈正态分布的统计归一化。
我准备了一个简短的笔记本,其中包含所有详细信息。
https://nbviewer.jupyter.org/github/diallobakary4/bioinformatics/blob/master/Normatily_test.ipynb
如果有人能帮我解决这个问题,那就太好了。
谢谢
抱歉,我没有能力审查代码,也许你可以用一两句话概括一下问题?
我有一个非正态分布的数据。如果我运行 Pandas Spearman 相关性,它会自动将数据转换为有序数据,还是我需要先将数据转换为有序数据?
不,您可以直接将 Spearman 相关性应用于实际值。
我要感谢您不仅提供本教程,还感谢您发布的许多其他教程,从中我获益良多。
我肯定很快就会购买您的书。
谢谢,我真的很感谢您的支持!
亲爱的 Jason 先生,
在 Python 中是否有将数据转换为对数正态分布并将其逆转的函数?
自然对数和指数是彼此的逆函数。
更多信息在这里
https://en.wikipedia.org/wiki/Log-normal_distribution
嗨,Jason,
我是在阅读了您关于 Python Mastery 的书后才来到这个页面的,我必须说这本书太棒了。感谢您创作如此清晰的电子书。
我是数据科学的初学者,有一个基本问题。如果我们想构建多个模型以根据准确性选择最佳模型,是否需要将所有输入变量转换为正态分布?我打算在数据上使用各种线性和非线性算法,如逻辑回归、SVM、NN、DT 等。如果是,我们在选择正态分布变量时应该选择哪些算法?
谢谢并致以问候,
Heramb
谢谢!
这真的取决于您使用的模型。也许可以尝试在转换后和转换前分别拟合,然后比较模型的性能?
嗨,Jason,
从这篇帖子中学到了一两点。
有没有一种方法可以转换具有负值和正值的特征?我尝试使用 boxcox 函数,但它不支持负值。
谢谢
您可以将数据缩放到正数,或者使用 Yeo-Johnson 变换。
嗨,Jason,
这是一个非常好的解释,感谢您花时间详细说明。我有一个问题,您如何知道数据是对数正态分布的(在对数正态分布的直方图图像附近)?请详细说明。
好问题,一种方法是取数据的对数,然后查看 Q-Q 图或只是数据的直方图。
感谢您提供的详细解释。我发现这篇文章对于选择适合您情况/倾斜程度的转换非常简洁:https://www.anatomisebiostats.com/biostatistics-blog/transforming-skewed-data
它清晰地切中要点。我发现当您必须为特定数据做出最佳选择时,这个主题可能会有点混乱。
感谢分享。
老师您好。
请问,如果我使用对数等变换某些输入变量(X)和/或使用对数或其他函数变换目标变量(Y),在用 fit 训练模型并进行 predict 等预测之后,我是否需要使用反函数(对数/指数)来反转预测结果?
提前非常感谢。
是的,在计算误差或使用预测结果之前反转变换是个好主意——以便将其恢复到原始单位。
好的。谢谢。还有一个问题请教。
我能否将幂变换(对数/指数/等等)与缩放变换(归一化/标准化)结合使用?
如果可以,那么在预测后我是否需要同时使用这两种反变换来获得“真实”误差等?
提前非常感谢。
是的,变换及其反变换的顺序在此
https://machinelearning.org.cn/machine-learning-data-transforms-for-time-series-forecasting/
好的。明白了。我做到了。谢谢!
您能否帮我检查一下我的“管道”的顺序是否正确?我的意思是,在流程结束时计算正确的/真实的 RMSE。
1. 数据集:X, y
2. 分割:X_train, X_test, y_train, y_test
3. Y 的幂变换 BOXCOX:y_train_BC, y_test_BC
4. Y 的归一化 MINMAXSCALER:y_train_BC_MMS, y_test_BC_MMS
5. X 的归一化 MINMAXSCALER:X_train_MMS, X_test_MMS
6. 定义/编译/拟合/评估模型:X_train_MMS, y_train_BC_MMS
7. 预测 X_test_MMS:preds_test
8. 反转 Y 归一化 preds_test:preds_inverse_MMS
9. 反转 X 归一化:X_test_inverse_MMS
10. 反转 Y 归一化:Y_test_inverse_MMS
11. 反转 Y BoxCox preds_inverse_MMS:preds_inverse_BC
12. 反转 Y BoxCox Y_test_inverse_MMS:Y_test_inverse_BC
13. 计算真实 RMSE:Y_test_inverse_BC, preds_inverse_BC
提前非常感谢!
抱歉,我没有能力审查和调试您的工作。
或许可以测试一下看看?
好的。我测试了一下,似乎还可以。我得到了一些比之前更好的 RMSE。
我只想确保我的变换和反变换的顺序是正确的。
我遵循了您下面的链接,所以我想它们是正确的……
https://machinelearning.org.cn/machine-learning-data-transforms-for-time-series-forecasting/
非常感谢,并致以最诚挚的问候!
做得好,很高兴听到这个!
顺便说一句/及时
我是否/能否为每个输入变量 (X) 使用不同的幂变换和/或不同的缩放变换?
或者我是否必须为所有输入变量 (X) 使用相同的幂变换和/或相同的缩放变换?
提前非常感谢。
很好的问题!
是的,请单独处理每个变量。
好的。完成了。但这并没有提高我在上一步中得到的 RMSE,当时我只对输出变量 (y) 进行了幂变换,并对 X 和 y 都进行了缩放变换。
很好的发现。
大家好,
我有一组传感器值 [x y]= [467021 478610], [464025 479352], [465688 478515], [464025 478610] 等等,围绕着一个地面真值 [x y]= [466111 478611]。我需要找出“传感器周围点的分布”是如何围绕着地面真值的。哪种分布有用?
我计划使用期望最大化(EM)和高斯混合模型(GMM)算法进行聚类。
在应用 EM/ GMM 算法之前,我是否需要通过应用归一化或任何幂变换技术将输入传感器值转换为高斯分布?
或者
我是否可以直接使用相同的 [x y] 值用于 EM/GMM 算法,而不使用归一化/标准化技术,因为这两个值几乎在同一尺度上?
我是这个领域的新手。请帮帮我……
您可以假设目标是高斯分布的均值,而点是与高斯分布的某个标准差,作为建模练习。
但是您到底想实现什么?您在预测什么?
非常感谢您的回复!
实际上,我想找出传感器输出遵循的“点的分布”(关于哪个分布)。我也拥有地面真值。来自传感器的值散布在地面真值周围。我需要找出传感器输出遵循哪种分布。有了这些信息,我必须创建一个 ML 模型来预测与地面真值最接近的传感器值。
希望您能帮助我。
也许您可以使用高斯过程来模拟观测点密度?
这可能会给你一些想法
https://machinelearning.org.cn/probability-density-estimation/
嗨,Jason,
这篇帖子太棒了。我喜欢它!
我有一个关于处理非高斯分布变量/特征的问题,当涉及到构建 ML 模型时。
假设我有一些非正态分布的特征,为什么这会成为问题?(例如,它会导致残差非正态分布吗?)
我们是否应该首选将这些变量转换为正态分布?
例如
使用对数缩放处理偏斜变量是一种好/流行的做法,我知道这确实能使这些变量正态分布,但为什么它对特定 ML 算法(例如 RandomForest)更好?
我认为我缺少其中的直觉……如果您能帮助我,我将不胜感激!
谢谢!
这取决于模型。如果您使用的模型假定高斯分布,您可能会得到较差或更差的结果——并且它会是一个平缓的衰减。
否则,也许影响很小或没有影响。RF 不在乎。
感谢您的快速回复!
那么您的意思是,不对这些变量进行变换对残差没有影响吗?
我只是说缩放不会提高某些算法的性能,而像 RF 这样的算法对于输入的线性缩放是无关的。
谢谢,这很棒。我注意到 scp.boxcox() 如果您将变量留空,它会选择 lambda 的最大似然估计值。虽然这确实为最初从 exponential() 分布抽取的数据产生了一个相当奇怪的直方图。
谢谢!
是的。有意思。
你好,Jason!
您能给我一些假设因变量或预测变量正态分布的模型示例吗?
线性回归仅假设残差的正态性,而不假设底层数据的正态性。逻辑回归对自变量的分布不做任何假设。树基回归方法也是如此。即使是像 t 检验这样的统计检验,也不假设样本分布是正态的(只有当 n 很小时才假设总体分布是正态的,但否则由于中心极限定理,实际上不需要任何分布)。
(希望您能提供一些额外的材料供我进一步阅读!)
uniforme distribution to normal? i m reading about the box miller transform but its somehow not working on my data..
Hi Vanetoj…Please describe in detail what is “not working” so that we may better assist you.
Hi the 1st and 2nd pictures are no showing currently. Can you fix it?
Hi Hue…We do not see any issues on our side. Perhaps you could try another browser.
Hi! Thanks for an awesome tutorial and your amazing books.
I have a question regarding this specific tutorial about making data more normal.
You’ve touched on the topic of zero-inflated data and emphasized that this often occurs in publicly available datasets. Yet, I haven’t grasped from the tutorial how to make such data fit the normal distribution in an optimal way.
Could you please clarify this bit in more detail?
Hi Pavlo…Thank you for your feedback! Please clarify what may be lacking from the procedure presented in the tutorial that is not meeting your needs so that we may better assist you.
Hello can you elaborate data resolution/discrimination?
I can not find relatives articles about this subject…have you got references to look up on?
Hi Mpampis…The concept of **data resolution/discrimination** pertains to the granularity or precision of the data, which can impact its ability to approximate a normal distribution or other target distributions. Let’s explore what this means, its relevance to transforming data, and potential references or resources to dive deeper into the subject.
—
### **1. What is Data Resolution/Discrimination?**
– **Resolution** refers to the smallest measurable unit or increment in your data. For instance
– A scale that measures weight in kilograms has a resolution of 1 kg.
– A scale that measures to the nearest gram has a resolution of 0.001 kg.
– **Discrimination** often relates to the sensitivity of the measurement system to distinguish between data points. Low discrimination results in “chunky” or discrete-looking data, which may not fit a continuous distribution well (like the normal distribution).
—
### **2. Relevance to Normal Distribution**
– **Low resolution or discrimination can introduce artifacts:**
– Data may appear “binned” or quantized (e.g., scores that only take values like 1, 2, or 3 on a scale).
– This can create a pseudo-discrete effect that reduces the visual and statistical resemblance to a continuous normal distribution.
– **Improving resolution can help:**
– When data resolution is increased, the granularity improves, making the distribution smoother and more likely to approximate a continuous normal distribution.
—
### **3. Transforming Data for Better Normality**
If poor resolution is an issue, these strategies can help
– **Aggregation**: Combining multiple low-resolution measurements to form a composite score (central limit theorem effect).
– **Smoothing or Interpolation**: Using techniques like kernel density estimation or spline interpolation to create a continuous representation of discrete data.
– **Transformations**: Applying common transforms (e.g., log, square root, Box-Cox) can sometimes mitigate issues caused by resolution.
—
### **4. References and Resources**
Since “data resolution/discrimination” might not be a standalone research topic, it is often embedded within broader discussions on measurement precision, data preprocessing, and statistical modeling. Here are some related areas and references
#### **Textbooks:**
1. **”Statistical Methods for the Social Sciences” by Agresti and Finlay**
– Focuses on measurement precision and its implications for statistical models.
2. **”Practical Data Analysis” by Hector Cuesta**
– Covers data preprocessing and techniques for transforming and improving data quality.
#### **Research Articles and Keywords:**
1. **Key Search Terms:**
– Data resolution and statistical analysis
– Measurement precision and normality
– Impact of quantization on data modeling
2. **Example Articles:**
– “Effects of Measurement Precision on Statistical Inference” in *Journal of Applied Statistics*.
– “The Role of Data Granularity in Distribution Fitting” in *Computational Statistics*.
#### **Online Resources:**
1. **Kaggle Discussions and Notebooks:**
– Search for preprocessing methods to address data granularity or quantization issues.
2. **Statistical Modeling Blogs:**
– Explore articles on data transformations and normality checks (e.g., CrossValidated on StackExchange).
—
### **Practical Example in Python**
Here’s how you might analyze and adjust data resolution programmatically
pythonimport numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
# Simulate low-resolution data
low_res_data = np.round(np.random.normal(loc=50, scale=10, size=1000), decimals=0)
# Plot low-resolution data
plt.hist(low_res_data, bins=20, alpha=0.6, color='b', density=True)
# Generate smooth, continuous data for comparison
x = np.linspace(20, 80, 100)
y = norm.pdf(x, loc=50, scale=10)
plt.plot(x, y, 'k--', label="Ideal Normal")
plt.legend()
plt.show()
—