Nelder-Mead 优化算法是一种广泛用于非可微目标函数的处理方法。
因此,它通常被称为模式搜索算法,并用作局部或全局搜索程序,用于挑战非线性、可能带有噪声且具有多模态函数的最优化问题。
在本教程中,您将了解 Nelder-Mead 优化算法。
完成本教程后,您将了解:
- Nelder-Mead 优化算法是一种模式搜索,不使用函数梯度。
- 如何在 Python 中应用 Nelder-Mead 算法进行函数优化。
- 如何解释 Nelder-Mead 算法在带有噪声和多模态目标函数上的结果。
通过我的新书《机器学习优化》,其中包含分步教程和所有示例的Python 源代码文件,开启您的项目。
让我们开始吧。
如何在 Python 中使用 Nelder-Mead 优化方法
照片由 Don Graham 拍摄,部分权利保留。
教程概述
本教程分为三个部分;它们是:
- Nelder-Mead 算法
- Python 中的 Nelder-Mead 示例
- Nelder-Mead 在挑战性函数上的应用
- 噪声优化问题
- 多模态优化问题
Nelder-Mead 算法
Nelder-Mead 是一种以该技术开发者 John Nelder 和 Roger Mead 命名的优化算法。
该算法在其 1965 年的论文《A Simplex Method For Function Minimization》(一种用于函数最小化的单纯形方法)中进行了描述,并已成为函数优化中的标准且广泛使用的技术。
它适用于具有数值输入的单变量或多变量函数。
Nelder-Mead 是一种 模式搜索优化算法,这意味着它不需要或不使用函数梯度信息,并且适用于梯度未知或无法合理计算的优化问题。
它通常用于多维非线性函数优化问题,尽管它可能会陷入局部最优解。
Nelder–Mead 算法的实际性能通常是合理的,尽管已观察到其会在非最优点停滞。当检测到停滞时,可以使用重新启动。
— 第 239 页,《Numerical Optimization》,2006 年。
算法必须提供一个起始点,该点可以是另一个全局优化算法的终点,也可以是从域中随机抽取的点。
鉴于算法可能会陷入停滞,它可能受益于使用不同的起始点进行多次重启。
Nelder-Mead 单纯形方法使用一个单纯形在空间中遍历以寻找最小值。
— 第 105 页,《Algorithms for Optimization》,2019 年。
该算法通过使用一个由 n + 1 个点(顶点)组成的形状结构(称为单纯形)来工作,其中 n 是函数输入的维度数。
例如,在一个二维问题中,该问题可以绘制为曲面,其形状结构将由三个点组成,表示为一个三角形。
Nelder-Mead 方法使用一系列规则来决定如何根据其顶点处目标函数的评估来更新单纯形。
— 第 106 页,《Algorithms for Optimization》,2019 年。
形状结构中的点会被评估,并使用简单的规则根据它们相对的评估结果来决定如何移动形状的点。这包括诸如单纯形形状在目标函数曲面上的“反射”、“扩张”、“收缩”和“缩小”等操作。
在 Nelder-Mead 算法的单次迭代中,我们试图去除具有最差函数值的顶点,并用一个具有更好值的点替换它。新点是通过沿着连接最差顶点和其余顶点质心的线反射、扩张或收缩单纯形获得的。如果我们无法通过这种方式找到一个更好的点,我们将只保留具有最佳函数值的顶点,并通过将所有其他顶点移向该值来收缩单纯形。
— 第 238 页,《Numerical Optimization》,2006 年。
当点收敛于最优解、观察到评估之间的最小差异或执行了最大数量的函数评估时,搜索将停止。
现在我们对算法的工作原理有了大致了解,让我们看看如何在实践中使用它。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
Python 中的 Nelder-Mead 示例
可以通过 minimize() 函数 在 Python 中使用 Nelder-Mead 优化算法。
此函数要求将“method”参数设置为“nelder-mead”以使用 Nelder-Mead 算法。它接受要最小化的目标函数和搜索的初始点。
|
1 2 3 |
... # 执行搜索 result = minimize(objective, pt, method='nelder-mead') |
结果是一个 OptimizeResult 对象,其中包含有关优化结果的信息,可以通过键进行访问。
例如,“success”布尔值指示搜索是否成功完成,“message”提供了关于搜索成功或失败的易于理解的消息,而“nfev”键表示执行的函数评估次数。
重要的是,“x”键指定了如果成功,搜索找到的最优解的输入值。
|
1 2 3 4 5 |
... # 总结结果 print('Status : %s' % result['message']) print('Total Evaluations: %d' % result['nfev']) print('Solution: %s' % result['x']) |
我们可以演示 Nelder-Mead 优化算法在良好行为函数上的应用,以表明它可以在不使用任何函数导数信息的情况下快速有效地找到最优解。
在这种情况下,我们将使用二维的 x^2 函数,定义在 -5.0 到 5.0 的范围内,已知最优解为 [0.0, 0.0]。
我们可以在下面定义 *objective()* 函数。
|
1 2 3 |
# 目标函数 def objective(x): return x[0]**2.0 + x[1]**2.0 |
我们将使用定义域内的随机点作为搜索的起始点。
|
1 2 3 4 5 |
... # 定义输入范围 r_min, r_max = -5.0, 5.0 # 将起始点定义为从域中随机采样 pt = r_min + rand(2) * (r_max - r_min) |
然后可以执行搜索。我们使用通过“maxiter”设置的最大函数评估次数,该次数设置为 N*200,其中 N 是输入变量的数量,在本例中为 2,例如 400 次评估。
|
1 2 3 |
... # 执行搜索 result = minimize(objective, pt, method='nelder-mead') |
搜索完成后,我们将报告找到最优解所用的总函数评估次数以及搜索的成功消息,我们预计在这种情况下将是积极的。
|
1 2 3 4 |
... # 总结结果 print('Status : %s' % result['message']) print('Total Evaluations: %d' % result['nfev']) |
最后,我们将检索找到的最优解的输入值,使用目标函数对其进行评估,并以人类可读的方式报告两者。
|
1 2 3 4 5 |
... # 评估解 solution = result['x'] evaluation = objective(solution) print('Solution: f(%s) = %.5f' % (solution, evaluation)) |
将这些内容整合起来,下面列出了在简单的凸目标函数上使用 Nelder-Mead 优化算法的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# 凸函数的 nelder-mead 优化 from scipy.optimize import minimize from numpy.random import rand # 目标函数 def objective(x): return x[0]**2.0 + x[1]**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 将起始点定义为从域中随机采样 pt = r_min + rand(2) * (r_max - r_min) # 执行搜索 result = minimize(objective, pt, method='nelder-mead') # 总结结果 print('Status : %s' % result['message']) print('Total Evaluations: %d' % result['nfev']) # 评估解 solution = result['x'] evaluation = objective(solution) print('Solution: f(%s) = %.5f' % (solution, evaluation)) |
运行该示例会执行优化,然后报告结果。
注意:鉴于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。请尝试运行示例几次并比较平均结果。
在这种情况下,我们可以看到搜索已成功完成,正如我们预期的那样,并且在 88 次函数评估后完成。
我们可以看到,最优解是在输入非常接近 [0,0] 的情况下找到的,其目标值为 0.0。
|
1 2 3 |
状态:优化成功终止。 总评估次数:88 解:f([ 2.25680716e-05 -3.87021351e-05]) = 0.00000 |
既然我们已经看到了如何成功使用 Nelder-Mead 优化算法,那么让我们来看一些它表现不佳的示例。
Nelder-Mead 在挑战性函数上的应用
Nelder-Mead 优化算法适用于一系列具有挑战性的非线性且不可微的目标函数。
尽管如此,它可能会在多模态优化问题和带有噪声的问题上陷入停滞。
为了具体说明这一点,让我们来看每个方面的示例。
噪声优化问题
噪声目标函数是指每次评估相同的输入时给出不同答案的函数。
我们可以通过在输入评估之前向输入添加小的乘法高斯随机数来人为地使目标函数产生噪声。
例如,我们可以定义 x^2 函数的一维版本,并使用 randn() 函数 将均值为 0.0、标准差为 0.3 的小高斯随机数添加到输入中。
|
1 2 3 |
# 目标函数 def objective(x): return (x + randn(len(x))*0.3)**2.0 |
噪声将使该函数对算法的优化变得困难,并且它很可能找不到 x=0.0 处的最小值。
下面列出了使用 Nelder-Mead 优化带噪声目标函数的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 带噪声的一维凸函数的 nelder-mead 优化 from scipy.optimize import minimize from numpy.random import rand from numpy.random import randn # 目标函数 def objective(x): return (x + randn(len(x))*0.3)**2.0 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 将起始点定义为从域中随机采样 pt = r_min + rand(1) * (r_max - r_min) # 执行搜索 result = minimize(objective, pt, method='nelder-mead') # 总结结果 print('Status : %s' % result['message']) print('Total Evaluations: %d' % result['nfev']) # 评估解 solution = result['x'] evaluation = objective(solution) print('Solution: f(%s) = %.5f' % (solution, evaluation)) |
运行该示例会执行优化,然后报告结果。
注意:鉴于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。请尝试运行示例几次并比较平均结果。
在这种情况下,算法不会收敛,而是使用了最大函数评估次数,即 200 次。
|
1 2 3 |
状态:已超出最大函数评估次数。 总评估次数:200 解:f([-0.6918238]) = 0.79431 |
该算法可能在运行代码时收敛,但会收敛到一个偏离最优解的点。
多模态优化问题
许多非线性目标函数可能具有多个最优解,这称为多模态问题。
问题可能被构造为具有多个全局最优解,这些解具有等效的函数评估值,或者具有一个全局最优解和多个局部最优解,而像 Nelder-Mead 这样的算法可能会在寻找局部最优解时陷入其中。
the Ackley 函数是后者的一个例子。它是一个二维目标函数,在 [0,0] 处具有全局最优解,但有许多局部最优解。
下面的示例实现了 Ackley 函数,并创建了一个三维图,显示了全局最优解和多个局部最优解。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# ackley 多峰函数 from numpy import arange from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行该示例会创建 Ackley 函数的曲面图,显示大量的局部最优解。
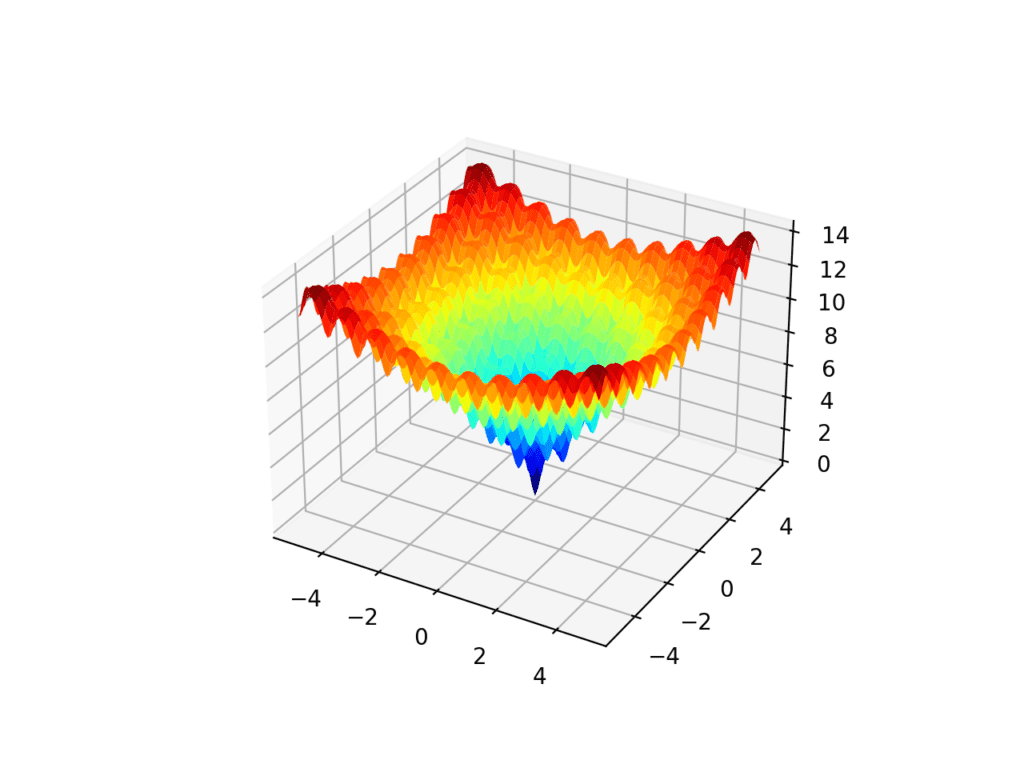
Ackley 多峰函数的三维曲面图
我们期望 Nelder-Mead 函数在寻找全局最优解的过程中会陷入一个局部最优解。
最初,当单纯形较大时,算法可能会跳过许多局部最优解,但随着其收缩,它会陷入停滞。
我们可以通过下面演示 Nelder-Mead 算法在 Ackley 函数上应用的示例来探讨这一点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# 用于多模态函数优化的 nelder-mead from scipy.optimize import minimize from numpy.random import rand from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi # 目标函数 def objective(v): x, y = v return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 将起始点定义为从域中随机采样 pt = r_min + rand(2) * (r_max - r_min) # 执行搜索 result = minimize(objective, pt, method='nelder-mead') # 总结结果 print('Status : %s' % result['message']) print('Total Evaluations: %d' % result['nfev']) # 评估解 solution = result['x'] evaluation = objective(solution) print('Solution: f(%s) = %.5f' % (solution, evaluation)) |
运行该示例会执行优化,然后报告结果。
注意:鉴于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。请尝试运行示例几次并比较平均结果。
在这种情况下,我们可以看到搜索成功完成,但未能找到全局最优解。它陷入了局部最优解。
每次运行示例时,由于搜索的随机起始点不同,我们将找到一个不同的局部最优解。
|
1 2 3 |
状态:优化成功终止。 总评估次数:62 解:f([-4.9831427 -3.98656015]) = 11.90126 |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 一种用于函数最小化的单纯形方法, 1965.
书籍
API
- Nelder-Mead 单纯形算法(method=’Nelder-Mead’)
- scipy.optimize.minimize API.
- scipy.optimize.OptimizeResult API.
- numpy.random.randn API.
文章
总结
在本教程中,您了解了 Nelder-Mead 优化算法。
具体来说,你学到了:
- Nelder-Mead 优化算法是一种模式搜索,不使用函数梯度。
- 如何在 Python 中应用 Nelder-Mead 算法进行函数优化。
- 如何解释 Nelder-Mead 算法在带有噪声和多模态目标函数上的结果。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。




嗨,Jason,
您是否计划撰写一本实用的优化书籍?
Matthew
我希望如此。
我看不出您为什么说 Nelder Mead 算法具有随机成分。它不是像模拟退火这样的随机算法。因此,如果您从同一点开始,您应该始终获得相同的结果。
只是搜索的起始点。
使用过此方法。如提到的,可能会陷入局部最小值。如果初始条件是另一个优化算法(如粒子群优化)的结果,有时会很有用。
完全同意!!!
Jason,这一行是否应为“...意味着它*不*需要或不使用函数梯度...
“Nelder-Mead 是一种模式搜索优化算法,这意味着它需要或不使用函数梯度信息,并且适用于函数梯度未知或无法合理计算的优化问题。”
当然,谢谢,已修复。
尊敬的Jason博士,
Nelder-Mead 优化方法可用于非可微方程。
非可微函数的示例,y = |x|,y = x**0.5 和 x**0.3333333,来源,https://ocw.mit.edu/ans7870/18/18.013a/textbook/HTML/chapter06/section03.html。
这意味着 Nelder-Mead 优化可能适用。
问题——当涉及到真实数据时,如何知道真实数据可能属于一个非可微函数,以便应用 Nelder Mead 优化?
谢谢你,
悉尼的Anthony
是的,当您没有导数时,可以使用它。
在真实项目中,您将知道您的目标是否可微,如果您不确定,可以尝试自动微分方法来确认。
通常我们没有方程,只有一个模拟(它不可微)。
尊敬的Jason博士,
感谢您的回复。
请问:当您说“...您将知道您的目标函数是否可微...”时,是指通过查看真实数据的图形并检查图形,查看拐点是否找不到切线?
再次感谢您,
悉尼的Anthony
不,抱歉。我的意思是您要么有方程,要么没有。如果您有一个方程,您可以推导出导数函数,或者不能。
尊敬的Jason博士,
如果您没有方程,但有真实数据,并且数据绘制在图上,而该图看起来像一个不可微的函数。
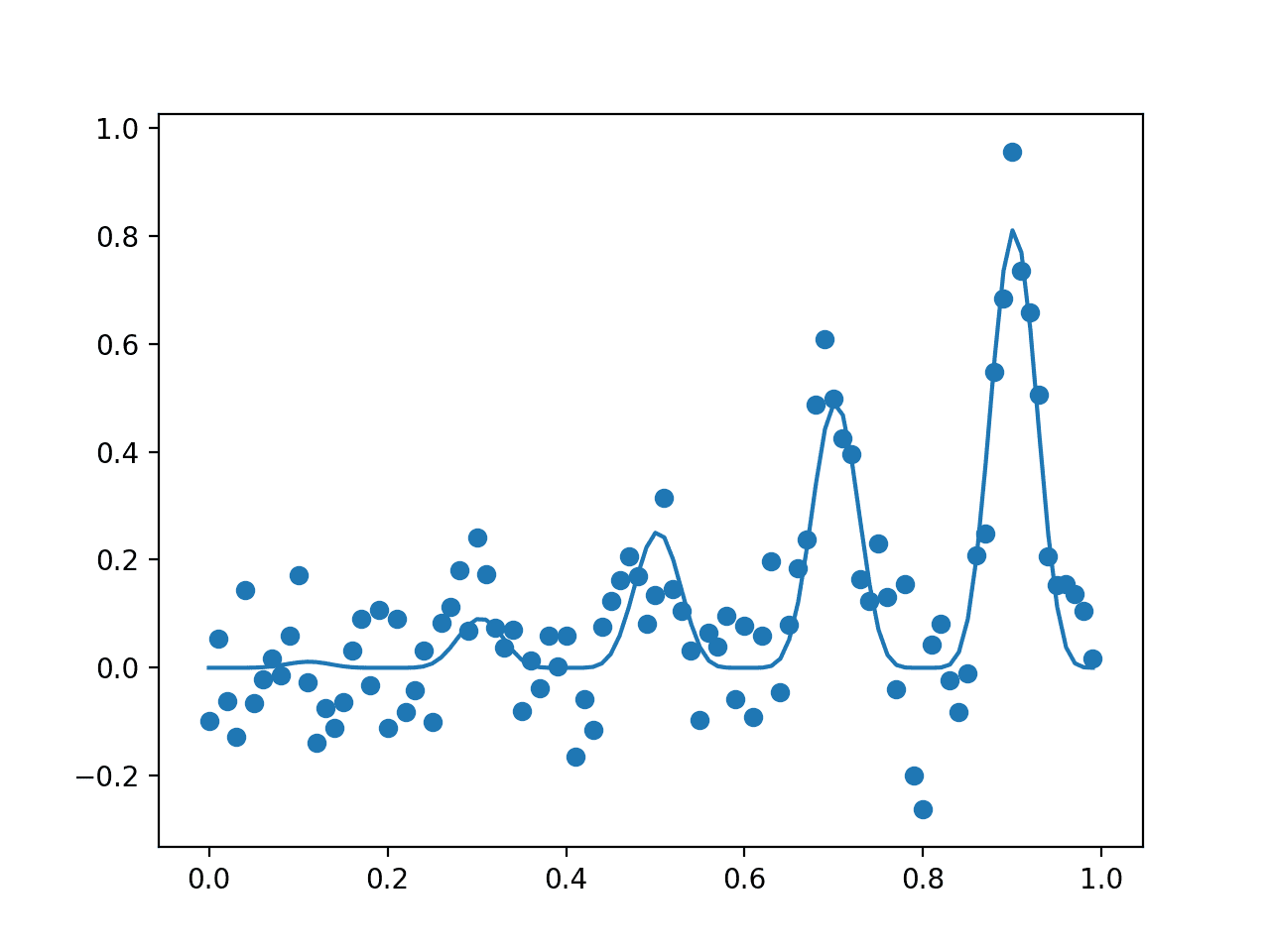
这是一个 y = |x| + 噪声的例子
假设这是真实数据。我们如何确定真实数据是否遵循一个不可微分的函数?
谢谢你,
悉尼的Anthony
这比这更复杂。
考虑您正在用数据训练神经网络的情况。
通过链式法则,损失函数可微于模型权重
https://en.wikipedia.org/wiki/Chain_rule
对于上面的代码中的第 25 行,
替换
用
谢谢你,
悉尼的Anthony
这是一个对整个乐观世界的精彩介绍!我有时觉得你读了我的谷歌搜索并给我发了答案。我前几天还在研究这个课题!再次感谢。
谢谢!
对于有兴趣了解实现细节的人:我第一次看到该算法的实现(用 Pascal 编写)以及很好的解释是在 Byte Magazine 1984 年 5 月刊,第 9 卷第 5 期,第 340 页。
“Fitting Curves to Data” 作者:M.S. Cacechi 和 W.P. Cacheris。
可在 Byte 档案中找到
https://vintageapple.org/byte/pdf/198405_Byte_Magazine_Vol_09-05_Computers_and_the_Professions.pdf
https://archive.org/details/byte-magazine-1984-05/page/n347/mode/2up
我想这个参考把我牢牢地定位在了侏罗纪前时代 :)
Jason 引用的维基百科文章有一个不错的动画。
感谢分享!
感谢您的信息和知识分享
不客气!
谢谢你写了一篇好文章。
一个问题:你知道在 Python 中使用 nelder mead 时如何获得置信区间吗?
谢谢你。
也许可以从许多不同的起点运行,并根据所有最终得分定义一个区间。
你好,我正在做我的大学本科项目,并试图将 MATLAB 的混合函数转换为 python。我计划使用混合遗传算法(GA+nelder-mead from scipy)来评估一些基准函数,例如 rosenbrock、rastrigin、griewack、ackley、schewefel。是否可以在 Python 中做到这一点?就像我们在 matlab 中做的那样?谢谢
如果可以,我需要先运行 GA,然后在它终止后运行 scipy,还是需要修改我的 GA?
非常感谢,我对优化非常陌生。
我相信是的。
这可能对 GA 有帮助
https://machinelearning.org.cn/simple-genetic-algorithm-from-scratch-in-python/
感谢 Jason 的分享。
我是机器学习方面的新手,目前正在做一个个人项目。我正在使用线性回归、基于树的模型(决策树和随机森林)以及人工神经网络来解决回归问题。我有 11 个数值预测变量。
我想使用这种方法来优化所有这些模型,但我有一些问题。
1.这种方法可以用于上面列出的所有模型吗?
2.我如何知道我正在处理的优化类型(即它是凸的、多峰的、噪声的)?
3.既然我已经有了一个训练好的模型,我想它将是我的目标函数。
4.我如何指定 r min、r max 和 pt?
(1) Nelder-Mead 用于优化函数。如果您将模型包装成一个函数,您就可以应用这种方法。
(2) 您永远不知道模型是否过于复杂。
(3) 如果您已经有一个训练好的模型,那么您就没有目标函数了,因为没有什么可以为您调整。
(4) 您必须做出这些假设。
Nelder-Mead 的一个问题是经常需要大量的迭代。R 默认为 500,对于高维情况,这可能不够。在许多情况下,初始的 n+1 个起始位置需要随机生成,因此这种多面体可能是退化的——一个简单的例子是三角形,其中 2 个顶点非常接近。所以:
1) 生成 > n+1(例如 2n)个随机位置。
2) 计算每对顶点之间的单位向量。
3) 按其对应的函数结果排序。
3) 从“最佳”顶点开始,计算其余顶点之间每对单位向量的点积,即角度的余弦。
4) 如果点积高于临界值(例如 0.8),则丢弃较差的 2 个顶点。
5) 当有 n+1 个“良好”位置时终止。
偶尔需要生成另一批顶点。
这比试图确保多面体是凸的,或者估计超体积与超球体进行比较要简单得多,而且我发现 NM 在最多 40 维的问题中只需要 50-120 次迭代就能收敛。
感谢您的反馈 John!我们很感激!
你好,谢谢你的例子。
它需要更新
MatplotlibDeprecationWarning: Calling gca() with keyword arguments was deprecated in Matplotlib 3.4. Starting two minor releases later, gca() will take no keyword arguments. The gca() function should only be used to get the current axes, or if no axes exist, create new axes with default keyword arguments. To create a new axes with non-default arguments, use plt.axes() or plt.subplot().
axis = figure.gca(projection=’3d’)
没有参数
axis.plot_surface(x, y, results, cmap=’jet’)
AttributeError: ‘AxesSubplot’ object has no attribute ‘plot_surface’
我对 matplotlib 还不熟悉……
感谢您的反馈 Sihir!