用于比较机器学习算法的假设检验

作者 Jason Brownlee 于 2020年9月1日在统计学 43

机器学习模型是根据它们的平均性能选择的，通常使用 k 折交叉验证计算。

平均性能最佳的算法预计会优于平均性能较差的算法。但如果平均性能的差异是由统计上的偶然因素造成的呢？

解决方案是使用 **统计假设检验** 来评估任意两个算法之间的平均性能差异是真实的还是虚假的。

在本教程中，您将了解如何使用统计假设检验来比较机器学习算法。

完成本教程后，您将了解：

基于平均模型性能进行模型选择可能会产生误导。
对修改后的 Student's t-Test 进行五次重复的两次交叉验证是比较机器学习算法的一个好方法。
如何使用 MLxtend 机器学习通过统计假设检验来比较算法。

开始您的项目，阅读我的新书《机器学习统计学》，其中包括分步教程和所有示例的Python源代码文件。

让我们开始吧。

Hypothesis Test for Comparing Machine Learning Algorithms

用于比较机器学习算法的假设检验
照片由 Frank Shepherd 拍摄，部分权利保留。

教程概述

本教程分为三个部分；它们是：

比较算法的假设检验
5×2 程序配合 MLxtend
比较分类器算法

比较算法的假设检验

模型选择涉及评估一套不同的机器学习算法或建模流程，并根据它们的性能进行比较。

然后，根据您的性能指标选择达到最佳性能的模型或建模流程，作为您可以用于在新数据上进行预测的最终模型。

这适用于经典的机器学习算法和深度学习的回归和分类预测建模任务。过程始终相同。

问题是，您如何知道两个模型之间的差异是真实的，而不仅仅是统计上的偶然因素？

这个问题可以通过统计假设检验来解决。

一种方法是在数据的同一 k 折交叉验证分割上评估每个模型（例如，在每种情况下使用相同的随机数种子来分割数据），并为每个分割计算一个分数。这会得到 10 折交叉验证的一个分数样本。然后可以使用配对统计假设检验来比较这些分数，因为每种算法用于得出每个分数的处理（数据行）是相同的。可以使用配对 Student's t-Test。

在这种情况下，使用配对 Student's t-Test 的一个问题是，每个模型的评估都不是独立的。这是因为相同的数据行被多次用于训练数据——实际上，除了数据行用于保留测试折之外，每次都使用。这种评估中的非独立性意味着配对 Student's t-Test 存在乐观偏差。

可以调整此统计检验以考虑非独立性。此外，还可以配置折数和程序重复次数，以实现对模型性能的良好采样，使其能够很好地推广到各种问题和算法。具体来说，是五次重复的两次交叉验证，即所谓的 5×2 折交叉验证。

这种方法由 Thomas Dietterich 在他 1998 年的论文《Approximate Statistical Tests for Comparing Supervised Classification Learning Algorithms》中提出。

欲了解更多关于此主题的信息，请参阅教程

用于比较机器学习算法的统计显著性检验

幸运的是，我们无需自己实现此过程。

5×2 程序配合 MLxtend

由 Sebastian Raschka 开发的 MLxtend 库通过 `paired_ttest_5x2cv()` 函数提供了实现。

首先，您必须安装 mlxtend 库，例如

sudo pip install mlxtend

1	sudo pip install mlxtend

要使用该评估，您必须先加载数据集，然后定义要比较的两个模型。

...
# load data
X, y = ....
# define models
model1 = ...
model2 = ...

...

# 加载数据

X, y = ....

# 定义模型

model1 = ...

model2 = ...

然后，您可以调用 `paired_ttest_5x2cv()` 函数，传入您的数据和模型，它将报告 t 统计量值和 p 值，以确定两个算法的性能差异是否具有统计学意义。

...
# compare algorithms
t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y)

...

# 比较算法

t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y)

p 值必须使用 alpha 值来解释，alpha 是您愿意接受的显著性水平。

如果 p 值小于或等于选定的 alpha，我们就拒绝原假设（即模型具有相同的平均性能），这意味着差异很可能是真实的。如果 p 值大于 alpha，我们就无法拒绝原假设（即模型具有相同的平均性能），任何观察到的平均准确度差异都可能是统计上的偶然因素。

alpha 值越小越好，通常的值是 5% (0.05)。

...
# interpret the result
if p <= 0.05:
	print('Difference between mean performance is probably real')
else:
	print('Algorithms probably have the same performance')

...

# 解释结果

if p <= 0.05:

print('平均性能差异可能真实存在')

else:

print('算法可能具有相同的性能')

现在我们熟悉了如何使用假设检验来比较算法，让我们看一些例子。

比较分类器算法

在本节中，我们将比较两个机器学习算法在二分类任务上的性能，然后检查观察到的差异是否具有统计学意义。

首先，我们可以使用 make_classification() 函数创建一个具有 1000 个样本和 20 个输入变量的合成数据集。

下面的示例创建了数据集并总结了其形状。

# create classification dataset
from sklearn.datasets import make_classification
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)
# summarize the dataset
print(X.shape, y.shape)

# 创建分类数据集

from sklearn.datasets import make_classification

# 定义数据集

X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)

# 汇总数据集

print(X.shape, y.shape)

运行示例会创建数据集并总结行数和列数，确认了我们的预期。

我们可以使用此数据作为比较两个算法的基础。

(1000, 10) (1000,)

1	(1000, 10) (1000,)

我们将在此数据集上比较两种线性算法的性能。具体来说，是逻辑回归算法和线性判别分析 (LDA) 算法。

我喜欢的方法是使用重复分层 k 折交叉验证，10 折，3 次重复。我们将使用此过程来评估每个算法，并返回和报告平均分类准确度。

完整的示例如下所示。

# compare logistic regression and lda for binary classification
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from matplotlib import pyplot
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)
# evaluate model 1
model1 = LogisticRegression()
cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)
print('LogisticRegression Mean Accuracy: %.3f (%.3f)' % (mean(scores1), std(scores1)))
# evaluate model 2
model2 = LinearDiscriminantAnalysis()
cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)
print('LinearDiscriminantAnalysis Mean Accuracy: %.3f (%.3f)' % (mean(scores2), std(scores2)))
# plot the results
pyplot.boxplot([scores1, scores2], labels=['LR', 'LDA'], showmeans=True)
pyplot.show()

# 比较逻辑回归和 LDA 进行二分类

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.linear_model import LogisticRegression

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from matplotlib import pyplot

# 定义数据集

X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)

# 评估模型 1

model1 = LogisticRegression()

cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)

print('逻辑回归平均准确率: %.3f (%.3f)' % (mean(scores1), std(scores1)))

# 评估模型 2

model2 = LinearDiscriminantAnalysis()

cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)

print('线性判别分析平均准确率: %.3f (%.3f)' % (mean(scores2), std(scores2)))

# 绘制结果图

pyplot.boxplot([scores1, scores2], labels=['LR', 'LDA'], showmeans=True)

pyplot.show()

运行示例首先报告了每个算法的平均分类准确率。

注意：您的结果可能有所不同，因为算法或评估过程的随机性，或数值精度的差异。考虑多次运行示例并比较平均结果。

在这种情况下，如果我们仅查看平均分数：逻辑回归为 89.2%，LDA 为 89.3%，结果表明 LDA 具有更好的性能。

LogisticRegression Mean Accuracy: 0.892 (0.036)
LinearDiscriminantAnalysis Mean Accuracy: 0.893 (0.033)

1 2	逻辑回归平均准确率: 0.892 (0.036) 线性判别分析平均准确率: 0.893 (0.033)

还创建了一个箱线图，总结了准确度分数的分布。

这个图表支持我选择 LDA 而不是 LR 的决定。

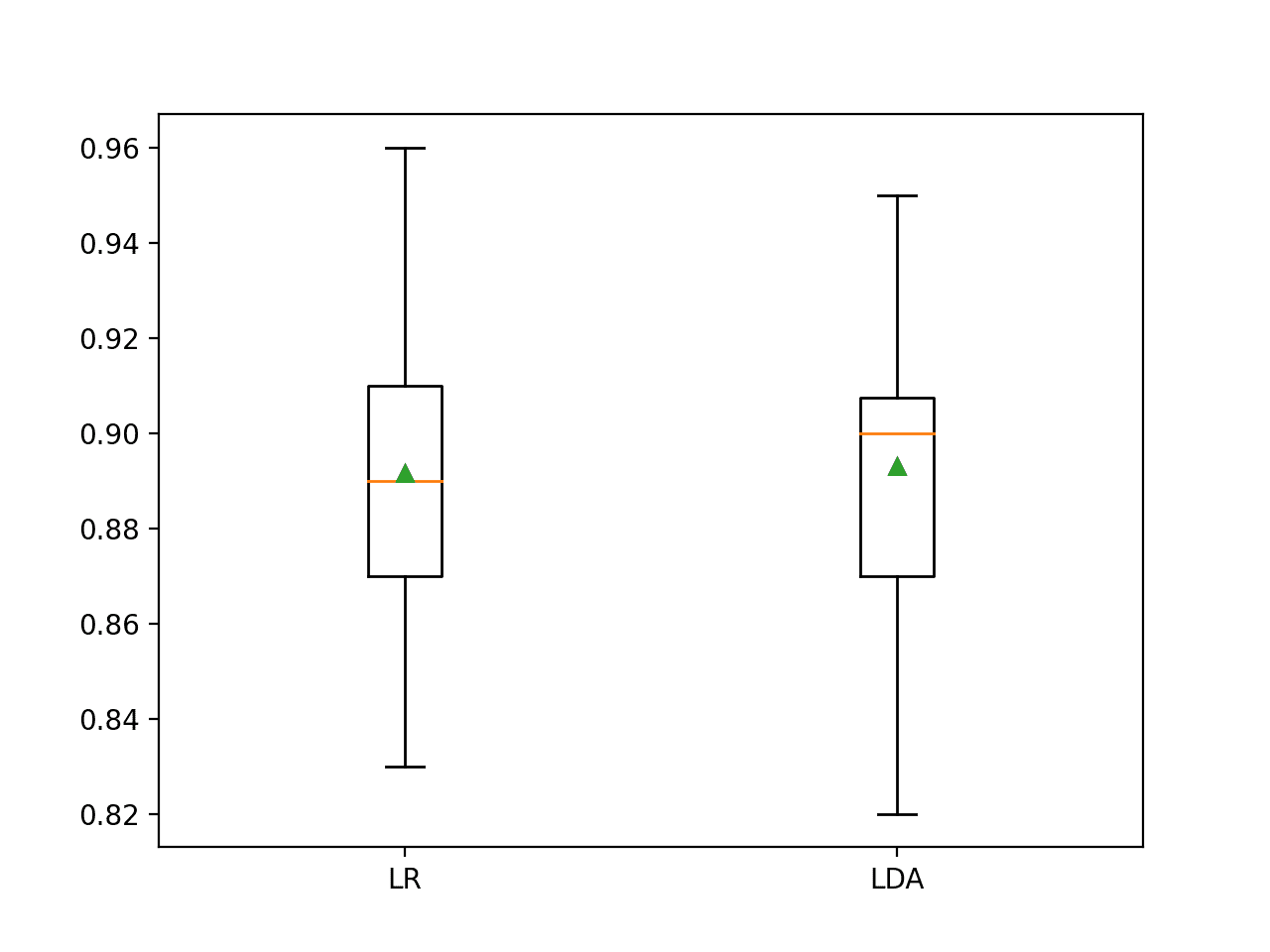
Box and Whisker Plot of Classification Accuracy Scores for Two Algorithms

两个算法的分类准确度分数的箱线图

现在我们可以使用假设检验来查看观察到的结果是否具有统计学意义。

首先，我们将使用 5×2 程序来评估算法，并计算 p 值和检验统计量值。

...
# check if difference between algorithms is real
t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)
# summarize
print('P-value: %.3f, t-Statistic: %.3f' % (p, t))

...

# 检查算法之间的差异是否真实

t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)

# 总结

print('P值: %.3f, t统计量: %.3f' % (p, t))

然后，我们可以使用 5% 的 alpha 值来解释 p 值。

...
# interpret the result
if p <= 0.05:
	print('Difference between mean performance is probably real')
else:
	print('Algorithms probably have the same performance')

...

# 解释结果

if p <= 0.05:

print('平均性能差异可能真实存在')

else:

print('算法可能具有相同的性能')

将这些结合起来，完整的示例列在下面。

# use 5x2 statistical hypothesis testing procedure to compare two machine learning algorithms
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from mlxtend.evaluate import paired_ttest_5x2cv
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)
# evaluate model 1
model1 = LogisticRegression()
cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)
print('LogisticRegression Mean Accuracy: %.3f (%.3f)' % (mean(scores1), std(scores1)))
# evaluate model 2
model2 = LinearDiscriminantAnalysis()
cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)
print('LinearDiscriminantAnalysis Mean Accuracy: %.3f (%.3f)' % (mean(scores2), std(scores2)))
# check if difference between algorithms is real
t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)
# summarize
print('P-value: %.3f, t-Statistic: %.3f' % (p, t))
# interpret the result
if p <= 0.05:
	print('Difference between mean performance is probably real')
else:
	print('Algorithms probably have the same performance')

# 使用 5x2 统计假设检验程序比较两个机器学习算法

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.linear_model import LogisticRegression

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from mlxtend.evaluate import paired_ttest_5x2cv

# 定义数据集

X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)

# 评估模型 1

model1 = LogisticRegression()

cv1 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)

print('逻辑回归平均准确率: %.3f (%.3f)' % (mean(scores1), std(scores1)))

# 评估模型 2

model2 = LinearDiscriminantAnalysis()

cv2 = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)

scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)

print('线性判别分析平均准确率: %.3f (%.3f)' % (mean(scores2), std(scores2)))

# 检查算法之间的差异是否真实

t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)

# 总结

print('P值: %.3f, t统计量: %.3f' % (p, t))

# 解释结果

if p <= 0.05:

print('平均性能差异可能真实存在')

else:

print('算法可能具有相同的性能')

运行示例，我们首先评估算法，然后报告统计假设检验的结果。

注意：您的结果可能有所不同，因为算法或评估过程的随机性，或数值精度的差异。考虑多次运行示例并比较平均结果。

在这种情况下，我们可以看到 p 值约为 0.3，远大于 0.05。这导致我们无法拒绝原假设，表明算法之间观察到的任何差异可能都不是真实的。

我们可以选择逻辑回归或 LDA，平均而言，两者表现都差不多。

这凸显了仅基于平均性能进行模型选择可能不足够。

LogisticRegression Mean Accuracy: 0.892 (0.036)
LinearDiscriminantAnalysis Mean Accuracy: 0.893 (0.033)
P-value: 0.328, t-Statistic: 1.085
Algorithms probably have the same performance

逻辑回归平均准确率: 0.892 (0.036)

线性判别分析平均准确率: 0.893 (0.033)

P值: 0.328, t统计量: 1.085

算法可能具有相同的性能

回想一下，我们使用与用于估计统计检验中性能的过程（5×2 CV）不同的过程（3×10 CV）来报告性能。也许如果我们查看使用五次重复的两次交叉验证的分数，结果会有所不同？

下面的示例已更新，使用 5×2 CV 为两种算法报告分类准确度。

# use 5x2 statistical hypothesis testing procedure to compare two machine learning algorithms
from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from mlxtend.evaluate import paired_ttest_5x2cv
# define dataset
X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)
# evaluate model 1
model1 = LogisticRegression()
cv1 = RepeatedStratifiedKFold(n_splits=2, n_repeats=5, random_state=1)
scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)
print('LogisticRegression Mean Accuracy: %.3f (%.3f)' % (mean(scores1), std(scores1)))
# evaluate model 2
model2 = LinearDiscriminantAnalysis()
cv2 = RepeatedStratifiedKFold(n_splits=2, n_repeats=5, random_state=1)
scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)
print('LinearDiscriminantAnalysis Mean Accuracy: %.3f (%.3f)' % (mean(scores2), std(scores2)))
# check if difference between algorithms is real
t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)
# summarize
print('P-value: %.3f, t-Statistic: %.3f' % (p, t))
# interpret the result
if p <= 0.05:
	print('Difference between mean performance is probably real')
else:
	print('Algorithms probably have the same performance')

# 使用 5x2 统计假设检验程序比较两个机器学习算法

from numpy import mean

from numpy import std

from sklearn.datasets import make_classification

from sklearn.model_selection import cross_val_score

from sklearn.model_selection import RepeatedStratifiedKFold

from sklearn.linear_model import LogisticRegression

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis

from mlxtend.evaluate import paired_ttest_5x2cv

# 定义数据集

X, y = make_classification(n_samples=1000, n_features=10, n_informative=10, n_redundant=0, random_state=1)

# 评估模型 1

model1 = LogisticRegression()

cv1 = RepeatedStratifiedKFold(n_splits=2, n_repeats=5, random_state=1)

scores1 = cross_val_score(model1, X, y, scoring='accuracy', cv=cv1, n_jobs=-1)

print('逻辑回归平均准确率: %.3f (%.3f)' % (mean(scores1), std(scores1)))

# 评估模型 2

model2 = LinearDiscriminantAnalysis()

cv2 = RepeatedStratifiedKFold(n_splits=2, n_repeats=5, random_state=1)

scores2 = cross_val_score(model2, X, y, scoring='accuracy', cv=cv2, n_jobs=-1)

print('线性判别分析平均准确率: %.3f (%.3f)' % (mean(scores2), std(scores2)))

# 检查算法之间的差异是否真实

t, p = paired_ttest_5x2cv(estimator1=model1, estimator2=model2, X=X, y=y, scoring='accuracy', random_seed=1)

# 总结

print('P值: %.3f, t统计量: %.3f' % (p, t))

# 解释结果

if p <= 0.05:

print('平均性能差异可能真实存在')

else:

print('算法可能具有相同的性能')

运行示例报告了两种算法的平均准确率以及统计检验的结果。

注意：您的结果可能有所不同，因为算法或评估过程的随机性，或数值精度的差异。考虑多次运行示例并比较平均结果。

在这种情况下，我们可以看到两种算法的平均性能差异更大，逻辑回归为 89.4%，LDA 为 89.0%，这与 3×10 CV 的情况相反。

LogisticRegression Mean Accuracy: 0.894 (0.012)
LinearDiscriminantAnalysis Mean Accuracy: 0.890 (0.013)
P-value: 0.328, t-Statistic: 1.085
Algorithms probably have the same performance

逻辑回归平均准确率: 0.894 (0.012)

线性判别分析平均准确率: 0.890 (0.013)

P值: 0.328, t统计量: 1.085

算法可能具有相同的性能

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

教程

论文

用于比较监督分类学习算法的近似统计检验, 1998.

API

总结

在本教程中，您了解了如何使用统计假设检验来比较机器学习算法。

具体来说，你学到了：

基于平均模型性能进行模型选择可能会产生误导。
对修改后的 Student's t-Test 进行五次重复的两次交叉验证是比较机器学习算法的一个好方法。
如何使用 MLxtend 机器学习通过统计假设检验来比较算法。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息

如何使用 Python 计算偏差-方差权衡

如何在 NumPy 中设置行和列的轴

对《比较机器学习算法的假设检验》的 43 条回复

Peter 2020年8月21日上午6:38 #

谢谢分享！！

另一个可能的选择是通过 BEST 进行贝叶斯方法

https://best.readthedocs.io/en/latest/

回复
- Jason Brownlee 2020年8月21日上午6:45 #
  
  感谢分享！
  
  回复
Dipti 2020年8月22日晚上11:26 #

真的很好……对于那些没有 proper 知识的人来说很容易理解。我是一名统计学副教授，在一家享有盛誉的理学院工作。

回复
- Jason Brownlee 2020年8月23日上午6:25 #
  
  谢谢！
  
  回复

Anthony The Koala 2020年8月23日下午1:47 #

尊敬的Jason博士，
我已将上述准确率扩展到 https://machinelearning.org.cn/calculate-the-bias-variance-trade-off/#comment-550512 中使用的模型。也就是说，我已经将该网站和本网站的模型进行了成对组合，并产生了以下结果。

这包含统计上显著和不显著的比较

comparing  LogisticRegression()  with  KNeighborsClassifier()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
P-value: 0.131, t-Statistic: -1.802
not statistically significant

------------------------------
comparing  LogisticRegression()  with  DecisionTreeClassifier()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.035)
P-value: 0.004, t-Statistic: 5.098
statistically significant

------------------------------
comparing  LogisticRegression()  with  SVC()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.003, t-Statistic: -5.318
statistically significant

------------------------------
comparing  LogisticRegression()  with  GaussianNB()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.368, t-Statistic: 0.988
not statistically significant

------------------------------
comparing  LogisticRegression()  with  LinearDiscriminantAnalysis()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.328, t-Statistic: 1.085
not statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  DecisionTreeClassifier()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
DecisionTreeClassifier() Mean Accuracy: 0.832 (0.033)
P-value: 0.007, t-Statistic: 4.420
statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  SVC()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.028, t-Statistic: -3.062
statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  GaussianNB()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.211, t-Statistic: 1.434
not statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  LinearDiscriminantAnalysis()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.136, t-Statistic: 1.777
not statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  SVC()
DecisionTreeClassifier() Mean Accuracy: 0.829 (0.040)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.002, t-Statistic: -5.782
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  GaussianNB()
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.036)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.041, t-Statistic: -2.732
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  LinearDiscriminantAnalysis()
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.034)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.002, t-Statistic: -6.124
statistically significant

------------------------------
comparing  SVC()  with  GaussianNB()
SVC() Mean Accuracy: 0.952 (0.021)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.018, t-Statistic: 3.467
statistically significant

------------------------------
comparing  SVC()  with  LinearDiscriminantAnalysis()
SVC() Mean Accuracy: 0.952 (0.021)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.003, t-Statistic: 5.191
statistically significant

------------------------------
comparing  GaussianNB()  with  LinearDiscriminantAnalysis()
GaussianNB() Mean Accuracy: 0.866 (0.039)<p
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.450, t-Statistic: -0.819
not statistically significant

------------------------------

100

101

102

103

104

105

比较 LogisticRegression() 与 KNeighborsClassifier()

LogisticRegression() 平均准确率: 0.892 (0.034)

KNeighborsClassifier() 平均准确率: 0.942 (0.022)

P-value: 0.131, t-Statistic: -1.802

不统计上显著

------------------------------

比较 LogisticRegression() 与 DecisionTreeClassifier()

LogisticRegression() 平均准确率: 0.892 (0.034)

DecisionTreeClassifier() 平均准确率: 0.831 (0.035)

P-value: 0.004, t-Statistic: 5.098

统计上显著

------------------------------

比较 LogisticRegression() 与 SVC()

LogisticRegression() 平均准确率: 0.892 (0.034)

SVC() 平均准确率: 0.952 (0.021)

P-value: 0.003, t-Statistic: -5.318

统计上显著

------------------------------

比较 LogisticRegression() 与 GaussianNB()

LogisticRegression() 平均准确率: 0.892 (0.034)

GaussianNB() 平均准确率: 0.866 (0.039)

P-value: 0.368, t-Statistic: 0.988

不统计上显著

------------------------------

比较 LogisticRegression() 与 LinearDiscriminantAnalysis()

LogisticRegression() 平均准确率: 0.892 (0.034)

LinearDiscriminantAnalysis() 平均准确率: 0.894 (0.031)

P-value: 0.328, t-Statistic: 1.085

不统计上显著

------------------------------

比较 KNeighborsClassifier() 与 DecisionTreeClassifier()

KNeighborsClassifier() 平均准确率: 0.942 (0.022)

DecisionTreeClassifier() 平均准确率: 0.832 (0.033)

P-值: 0.007, t-统计量: 4.420

统计上显著

------------------------------

比较 KNeighborsClassifier() 与 SVC()

KNeighborsClassifier() 平均准确率: 0.942 (0.022)

SVC() 平均准确率: 0.952 (0.021)

P-值: 0.028, t-统计量: -3.062

统计上显著

------------------------------

比较 KNeighborsClassifier() 与 GaussianNB()

KNeighborsClassifier() 平均准确率: 0.942 (0.022)

GaussianNB() 平均准确率: 0.866 (0.039)

P-值: 0.211, t-统计量: 1.434

不统计上显著

------------------------------

比较 KNeighborsClassifier() 与 LinearDiscriminantAnalysis()

KNeighborsClassifier() 平均准确率: 0.942 (0.022)

LinearDiscriminantAnalysis() 平均准确率: 0.894 (0.031)

P-值: 0.136, t-统计量: 1.777

不统计上显著

------------------------------

比较 DecisionTreeClassifier() 与 SVC()

DecisionTreeClassifier() 平均准确率: 0.829 (0.040)

SVC() 平均准确率: 0.952 (0.021)

P-值: 0.002, t-统计量: -5.782

统计上显著

------------------------------

比较 DecisionTreeClassifier() 与 GaussianNB()

DecisionTreeClassifier() 平均准确率: 0.831 (0.036)

GaussianNB() 平均准确率: 0.866 (0.039)

P-值: 0.041, t-统计量: -2.732

统计上显著

------------------------------

比较 DecisionTreeClassifier() 与 LinearDiscriminantAnalysis()

DecisionTreeClassifier() 平均准确率: 0.831 (0.034)

LinearDiscriminantAnalysis() 平均准确率: 0.894 (0.031)

P-值: 0.002, t-统计量: -6.124

统计上显著

------------------------------

比较 SVC() 与 GaussianNB()

SVC() 平均准确率: 0.952 (0.021)

GaussianNB() 平均准确率: 0.866 (0.039)

P-值: 0.018, t-统计量: 3.467

统计上显著

------------------------------

比较 SVC() 与 LinearDiscriminantAnalysis()

SVC() 平均准确率: 0.952 (0.021)

LinearDiscriminantAnalysis() 平均准确率: 0.894 (0.031)

P-值: 0.003, t-统计量: 5.191

统计上显著

------------------------------

比较 GaussianNB() 与 LinearDiscriminantAnalysis()

GaussianNB() 平均准确率: 0.866 (0.039)<p

LinearDiscriminantAnalysis() 平均准确率: 0.894 (0.031)

P-值: 0.450, t-统计量: -0.819

不统计上显著

------------------------------

统计学上显著的模型是

comparing  LogisticRegression()  with  DecisionTreeClassifier()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.035)
P-value: 0.004, t-Statistic: 5.098
statistically significant

------------------------------
comparing  LogisticRegression()  with  SVC()
LogisticRegression() Mean Accuracy: 0.892 (0.034)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.003, t-Statistic: -5.318
statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  DecisionTreeClassifier()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
DecisionTreeClassifier() Mean Accuracy: 0.832 (0.033)
P-value: 0.007, t-Statistic: 4.420
statistically significant

------------------------------
comparing  KNeighborsClassifier()  with  SVC()
KNeighborsClassifier() Mean Accuracy: 0.942 (0.022)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.028, t-Statistic: -3.062
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  SVC()
DecisionTreeClassifier() Mean Accuracy: 0.829 (0.040)
SVC() Mean Accuracy: 0.952 (0.021)
P-value: 0.002, t-Statistic: -5.782
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  GaussianNB()
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.036)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.041, t-Statistic: -2.732
statistically significant

------------------------------
comparing  DecisionTreeClassifier()  with  LinearDiscriminantAnalysis()
DecisionTreeClassifier() Mean Accuracy: 0.831 (0.034)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.002, t-Statistic: -6.124
statistically significant

------------------------------
comparing  SVC()  with  GaussianNB()
SVC() Mean Accuracy: 0.952 (0.021)
GaussianNB() Mean Accuracy: 0.866 (0.039)
P-value: 0.018, t-Statistic: 3.467
statistically significant

------------------------------
comparing  SVC()  with  LinearDiscriminantAnalysis()
SVC() Mean Accuracy: 0.952 (0.021)
LinearDiscriminantAnalysis() Mean Accuracy: 0.894 (0.031)
P-value: 0.003, t-Statistic: 5.191
statistically significant

比较 LogisticRegression() 与 DecisionTreeClassifier()

LogisticRegression() 平均准确率: 0.892 (0.034)

DecisionTreeClassifier() 平均准确率: 0.831 (0.035)

P-value: 0.004, t-Statistic: 5.098

统计上显著

------------------------------

比较 LogisticRegression() 与 SVC()

LogisticRegression() 平均准确率: 0.892 (0.034)

SVC() 平均准确率: 0.952 (0.021)

P-value: 0.003, t-Statistic: -5.318

统计上显著

------------------------------

比较 KNeighborsClassifier() 与 DecisionTreeClassifier()

KNeighborsClassifier() 平均准确率: 0.942 (0.022)

DecisionTreeClassifier() 平均准确率: 0.832 (0.033)

P-值: 0.007, t-统计量: 4.420

统计上显著

------------------------------

比较 KNeighborsClassifier() 与 SVC()

KNeighborsClassifier() 平均准确率: 0.942 (0.022)

SVC() 平均准确率: 0.952 (0.021)

P-值: 0.028, t-统计量: -3.062

统计上显著

------------------------------

比较 DecisionTreeClassifier() 与 SVC()

DecisionTreeClassifier() 平均准确率: 0.829 (0.040)

SVC() 平均准确率: 0.952 (0.021)

P-值: 0.002, t-统计量: -5.782

统计上显著

------------------------------

比较 DecisionTreeClassifier() 与 GaussianNB()

DecisionTreeClassifier() 平均准确率: 0.831 (0.036)

GaussianNB() 平均准确率: 0.866 (0.039)

P-值: 0.041, t-统计量: -2.732

统计上显著

------------------------------

比较 DecisionTreeClassifier() 与 LinearDiscriminantAnalysis()

DecisionTreeClassifier() 平均准确率: 0.831 (0.034)

LinearDiscriminantAnalysis() 平均准确率: 0.894 (0.031)

P-值: 0.002, t-统计量: -6.124

统计上显著

------------------------------

比较 SVC() 与 GaussianNB()

SVC() 平均准确率: 0.952 (0.021)

GaussianNB() 平均准确率: 0.866 (0.039)

P-值: 0.018, t-统计量: 3.467

统计上显著

------------------------------

比较 SVC() 与 LinearDiscriminantAnalysis()

SVC() 平均准确率: 0.952 (0.021)

LinearDiscriminantAnalysis() 平均准确率: 0.894 (0.031)

P-值: 0.003, t-统计量: 5.191

统计上显著

结论
在统计学上显著的模型中，SVC的准确率为0.952，高于LDA的0.894。P值为0.003。

谢谢你，
悉尼的Anthony

Anthony The Koala 2020年8月23日下午1:57 #

尊敬的Jason博士，
抱歉，我忘记考虑SVC和KNeighborsClassifier的比较，它们的平均值为0.952和0.942，P值为0.028，是显著的。

进一步结论
尽管SVC和KNeighborsClassifier之间的准确率差异很小，但对于由X和y组成的特定数据集，SVC似乎是最适合的方法。

因此，如果有人要为给定的数据集X、y做预测，SVC很可能是首选模型。

谢谢你，
悉尼的Anthony

回复
- Jason Brownlee 2020年8月24日上午6:15 #
  
  很好，谢谢分享。
  
  回复

Jason Brownlee 2020年8月24日上午6:13 #

干得好！

展示成对假设检验的一个好方法是使用一个矩阵，算法沿着两个轴排列，并在矩阵的每个单元格中显示显著的真/假值。

Anthony The Koala 2020年8月24日下午12:22 #

尊敬的Jason博士，
谢谢你的回复。
当你说“展示成对假设检验的一个好方法是使用一个矩阵”时，你能详细说明一下吗？你是指成对箱线图，还是散点图对？

是否存在一个散点图矩阵，可以让你从散点图切换到成对箱线图的比较？

谢谢你，
悉尼的Anthony

Jason Brownlee 2020年8月24日下午1:55 #

不，不是图，而是一个矩阵或表格，其中包含指示每对算法之间是否存在显著差异的真/假值。

然后可以查看每种算法的实际平均值，并忽略其余部分。

也可以使用一对列表。

Anthony The Koala 2020年8月24日下午2:21 #

尊敬的Jason博士，
谢谢你。
你是指这样的表格吗

Model Combination Pair.      Model1  score1 std1  Model2 score2 std1  sig/no diff
LDA()  SVC()                       LDA       0.894   0.03  SVC     0.952  0.021 sig
...........................
...........................
DTC() LDA()                        DTC      0.831   0.03  LDA      0.894 0.031 sig

模型组合对. 模型1 score1 std1 模型2 score2 std1 sig/无差

LDA() SVC() LDA 0.894 0.03 SVC 0.952 0.021 sig

...........................

DTC() LDA() DTC 0.831 0.03 LDA 0.894 0.031 sig

请指教。
谢谢你，
悉尼的Anthony

Jason Brownlee 2020年8月25日上午6:34 #

我不这么认为。那是我博士时期做的事情。
Anthony The Koala 2020年8月24日下午2:24 #

尊敬的Jason博士，
请扩大上述“表格”的显示范围，它显示了

Model, Combination Pair, model1, score1,std1, model2, score2,std2, sig/not sig

1

模型, 组合对, model1, score1,std1, model2, score2,std2, sig/否 sig

谢谢你，
悉尼的Anthony

Anthony The Koala 2020年8月24日下午4:05 #

尊敬的Jason博士，
对程序的一项修改产生了以下列表

model pairs, model1, mean, std, model2, mean, std, sig/not sig
lr & cart,     lr, 0.89, 0.03,  cart, 0.83, 0.03,   sig
lr & svm,     lr, 0.89, 0.03,  svm, 0.95, 0.02,   sig
knn & cart,     knn, 0.94, 0.02,  cart, 0.83, 0.03,   sig
knn & svm,     knn, 0.94, 0.02,  svm, 0.95, 0.02,   sig
cart & svm,     cart, 0.83, 0.03,  svm, 0.95, 0.02,   sig
cart & bayes,     cart, 0.83, 0.04,  bayes, 0.87, 0.04,   sig
cart & lda,     cart, 0.83, 0.04,  lda, 0.89, 0.03,   sig
svm & bayes,     svm, 0.95, 0.02,  bayes, 0.87, 0.04,   sig
svm & lda,     svm, 0.95, 0.02,  lda, 0.89, 0.03,   sig

模型对, model1, mean, std, model2, mean, std, sig/否 sig

lr & cart, lr, 0.89, 0.03, cart, 0.83, 0.03, sig

lr & svm, lr, 0.89, 0.03, svm, 0.95, 0.02, sig

knn & cart, knn, 0.94, 0.02, cart, 0.83, 0.03, sig

knn & svm, knn, 0.94, 0.02, svm, 0.95, 0.02, sig

cart & svm, cart, 0.83, 0.03, svm, 0.95, 0.02, sig

cart & bayes, cart, 0.83, 0.04, bayes, 0.87, 0.04, sig

cart & lda, cart, 0.83, 0.04, lda, 0.89, 0.03, sig

svm & bayes, svm, 0.95, 0.02, bayes, 0.87, 0.04, sig

svm & lda, svm, 0.95, 0.02, lda, 0.89, 0.03, sig

你的意思是像上面那样的东西吗？
如果是这样，有没有办法以一种美观的方式显示文本，使文本对齐得很好？

谢谢你，
悉尼的Anthony

Jason Brownlee 2020年8月25日上午6:38 #

干得好！

Anthony The Koala 2020年8月24日下午7:00 #

尊敬的Jason博士，
这是使用“prettyable”包的文本图输出，来自https://pypi.ac.cn/project/PrettyTable/

pip install prettytable --upgrade

1	pip install prettytable --upgrade

一些演示实现的示例代码

from prettytable import PrettyTable
................
................
#values of the *_values determined elsewhere................
x = PrettyTable()
column_names = ["model pairs", "model1", "mean1", "std", "model2", "mean", "std", "sig/not sig"]x.add_column(column_names[0],models_values)
x.add_column(column_names[1],model_values)
x.add_column(column_names[2],mean1_values)
x.add_column(column_names[3],std1_values)
x.add_column(column_names[4],model_values)
x.add_column(column_names[5],mean2_values)
x.add_column(column_names[6],std2_values)
x.add_column(column_names[7],sig_values)
print(x)

from prettytable import PrettyTable

................

# *_values 的值已在别处确定................

x = PrettyTable()

column_names = ["模型对", "模型1", "mean1", "std", "模型2", "mean", "std", "sig/not sig"]x.add_column(column_names[0],models_values)

x.add_column(column_names[1],model_values)

x.add_column(column_names[2],mean1_values)

x.add_column(column_names[3],std1_values)

x.add_column(column_names[4],model_values)

x.add_column(column_names[5],mean2_values)

x.add_column(column_names[6],std2_values)

x.add_column(column_names[7],sig_values)

print(x)

输出 – 将鼠标悬停在此输出的顶部以查看完整视图，从而扩展页面宽度。

+--------------+--------+-------+-------+--------+-------+-------+-------------+
| model pairs  | model1 | mean1 |  std  | model2 |  mean |  std  | sig/not sig |
+--------------+--------+-------+-------+--------+-------+-------+-------------+
|  lr & cart   |   lr   | 0.892 | 0.034 |  cart  | 0.828 | 0.037 |     sig     |
|   lr & svm   |   lr   | 0.892 | 0.034 |  svm   | 0.952 | 0.021 |     sig     |
|  knn & cart  |  knn   | 0.942 | 0.022 |  cart  | 0.832 | 0.039 |     sig     |
|  knn & svm   |  knn   | 0.942 | 0.022 |  svm   | 0.952 | 0.021 |     sig     |
|  cart & svm  |  cart  | 0.830 | 0.033 |  svm   | 0.952 | 0.021 |     sig     |
| cart & bayes |  cart  | 0.832 | 0.038 | bayes  | 0.866 | 0.039 |     sig     |
|  cart & lda  |  cart  | 0.830 | 0.039 |  lda   | 0.894 | 0.031 |     sig     |
| svm & bayes  |  svm   | 0.952 | 0.021 | bayes  | 0.866 | 0.039 |     sig     |
|  svm & lda   |  svm   | 0.952 | 0.021 |  lda   | 0.894 | 0.031 |     sig     |
+--------------+--------+-------+-------+--------+-------+-------+-------------+

+--------------+--------+-------+-------+--------+-------+-------+-------------+

+--------------+--------+-------+-------+--------+-------+-------+-------------+

| lr & cart | lr | 0.892 | 0.034 | cart | 0.828 | 0.037 | sig |

| lr & svm | lr | 0.892 | 0.034 | svm | 0.952 | 0.021 | sig |

| knn & cart | knn | 0.942 | 0.022 | cart | 0.832 | 0.039 | sig |

| knn & svm | knn | 0.942 | 0.022 | svm | 0.952 | 0.021 | sig |

| cart & svm | cart | 0.830 | 0.033 | svm | 0.952 | 0.021 | sig |

| cart & bayes | cart | 0.832 | 0.038 | bayes | 0.866 | 0.039 | sig |

| cart & lda | cart | 0.830 | 0.039 | lda | 0.894 | 0.031 | sig |

| svm & bayes | svm | 0.952 | 0.021 | bayes | 0.866 | 0.039 | sig |

| svm & lda | svm | 0.952 | 0.021 | lda | 0.894 | 0.031 | sig |

+--------------+--------+-------+-------+--------+-------+-------+-------------+

谢谢你，

悉尼的Anthony

Jason Brownlee 2020年8月25日上午6:40 #

太棒了。

Weka 似乎也这样做，并为主平均值添加了一个*，以使表格更容易扫描。

Anthony The Koala 2020年8月25日 12:31 AM #

尊敬的Jason博士，
上面的表格是ASCII文本表格。下面的两个是使用plotly和matplotlib实现的图形。

#This is the graphical implementation of the table using plotly and matplotlib

#column names and labels calculated earlier.
column_names = ["model pairs", "model1", "mean1", "std", "model2", "mean2", "std", "sig/not sig"]
columns = [models,model1,mean1,std1,model2,mean2,std2,sig]

#Graphical implementation using plotly
import plotly.graph_objects as go
fig = go.Figure(data=[go.Table(header=dict(values=column_names), cells=dict(values=columns))])
fig.show()

#Graphical implementation using matplotlib 
from matplotlib import pyplot
fig = pyplot.figure()
ax = fig.add_subplot(111)
ax.axis('off')
the_table = ax.table(cellText= array(columns).T,colLabels=column_names,loc='center')
pyplot.show()

#这是使用plotly和matplotlib实现的表格图形化表示

#前面计算出的列名和标签。

column_names = ["模型对", "模型1", "均值1", "标准差", "模型2", "均值2", "标准差", "有/无显著性"]

columns = [models,model1,mean1,std1,model2,mean2,std2,sig]

#使用plotly进行图形化实现

import plotly.graph_objects as go

fig = go.Figure(data=[go.Table(header=dict(values=column_names), cells=dict(values=columns))])

fig.show()

#使用matplotlib进行图形化实现

from matplotlib import pyplot

fig = pyplot.figure()

ax = fig.add_subplot(111)

ax.axis('off')

the_table = ax.table(cellText= array(columns).T,colLabels=column_names,loc='center')

pyplot.show()

谢谢你，
悉尼的Anthony

Jason Brownlee 2020年8月25日 6:42 AM #

太棒了！

Anthony The Koala 2020年8月25日 2:03 PM #

尊敬的Jason博士，
你提到“……我相信Weka也是这样做的，并且会在较大的数字旁边添加一个*，使表格更容易扫描。”

我花了两分钟额外修改了python中的代码。

        #mean1 and mean2 are numeric that is converted to a string.
        #asterisk is added to string whether mean1 > mean2 and vice versa
	temp_mean1 = "%.3f"%mean1 
	temp_mean2 = "%.3f"%mean2
	if mean1 > mean2:
		temp_mean1 = temp_mean1 + "*"
	else:	
		temp_mean2 = temp_mean2 + "*"

#mean1和mean2是数字，转换为字符串。

#如果mean1 > mean2，则向字符串中添加星号，反之亦然

temp_mean1 = "%.3f"%mean1

temp_mean2 = "%.3f"%mean2

if mean1 > mean2:

temp_mean1 = temp_mean1 + "*"

else:

temp_mean2 = temp_mean2 + "*"

这是结果

+--------------+--------+--------+-------+--------+--------+-------+-------------+
| model pairs  | model1 | mean1  |  std  | model2 | mean2  |  std  | sig/not sig |
+--------------+--------+--------+-------+--------+--------+-------+-------------+
|  lr & cart   |   lr   | 0.892* | 0.034 |  cart  | 0.831  | 0.039 |     sig     |
|   lr & svm   |   lr   | 0.892  | 0.034 |  svm   | 0.952* | 0.021 |     sig     |
|  knn & cart  |  knn   | 0.942* | 0.022 |  cart  | 0.831  | 0.039 |     sig     |
|  knn & svm   |  knn   | 0.942  | 0.022 |  svm   | 0.952* | 0.021 |     sig     |
|  cart & svm  |  cart  | 0.832  | 0.036 |  svm   | 0.952* | 0.021 |     sig     |
|  cart & lda  |  cart  | 0.830  | 0.036 |  lda   | 0.894* | 0.031 |     sig     |
| svm & bayes  |  svm   | 0.952* | 0.021 | bayes  | 0.866  | 0.039 |     sig     |
|  svm & lda   |  svm   | 0.952* | 0.021 |  lda   | 0.894  | 0.031 |     sig     |
+--------------+--------+--------+-------+--------+--------+-------+-------------+

+--------------+--------+--------+-------+--------+--------+-------+-------------+

| 模型对 | 模型1 | 均值1 | 标准差 | 模型2 | 均值2 | 标准差 | 显著性/不显著性 |

+--------------+--------+--------+-------+--------+--------+-------+-------------+

| lr & cart | lr | 0.892* | 0.034 | cart | 0.831 | 0.039 | 显著 |

| lr & svm | lr | 0.892 | 0.034 | svm | 0.952* | 0.021 | 显著 |

| knn & cart | knn | 0.942* | 0.022 | cart | 0.831 | 0.039 | 显著 |

| knn & svm | knn | 0.942 | 0.022 | svm | 0.952* | 0.021 | 显著 |

| cart & svm | cart | 0.832 | 0.036 | svm | 0.952* | 0.021 | 显著 |

| cart & lda | cart | 0.830 | 0.036 | lda | 0.894* | 0.031 | 显著 |

| svm & bayes | svm | 0.952* | 0.021 | bayes | 0.866 | 0.039 | 显著 |

| svm & lda | svm | 0.952* | 0.021 | lda | 0.894 | 0.031 | 显著 |

+--------------+--------+--------+-------+--------+--------+-------+-------------+

谢谢你，
悉尼的Anthony

Jason Brownlee 2020年8月26日 6:43 AM #

Anthony，这真是太棒了！

Anthony The Koala 2020年8月28日 2:40 AM #

尊敬的Jason博士，
上面的表格使用了prettytable包。
不幸的是，你无法使用prettytable包添加标题。
如果你想添加一个标题，就像下面的表格一样

+--------------------------------------------------------------------------------+
|                    Pairwise comparison of scores for models                    |
+--------------+--------+--------+-------+--------+--------+-------+-------------+
| model pairs  | model1 | mean1  |  std  | model2 | mean2  |  std  | sig/not sig |
+--------------+--------+--------+-------+--------+--------+-------+-------------+
|  lr & cart   |   lr   | 0.892* | 0.034 |  cart  | 0.834  | 0.037 |     sig     |
|   lr & svm   |   lr   | 0.892  | 0.034 |  svm   | 0.952* | 0.021 |     sig     |
|  knn & cart  |  knn   | 0.942* | 0.022 |  cart  | 0.832  | 0.034 |     sig     |
|  knn & svm   |  knn   | 0.942  | 0.022 |  svm   | 0.952* | 0.021 |     sig     |
|  cart & svm  |  cart  | 0.830  | 0.035 |  svm   | 0.952* | 0.021 |     sig     |
|  cart & lda  |  cart  | 0.831  | 0.032 |  lda   | 0.894* | 0.031 |     sig     |
| svm & bayes  |  svm   | 0.952* | 0.021 | bayes  | 0.866  | 0.039 |     sig     |
|  svm & lda   |  svm   | 0.952* | 0.021 |  lda   | 0.894  | 0.031 |     sig     |
+--------------+--------+--------+-------+--------+--------+-------+-------------+

+--------------------------------------------------------------------------------+

| 模型得分的两两比较模型 |

+--------------+--------+--------+-------+--------+--------+-------+-------------+

| 模型对 | 模型1 | 均值1 | 标准差 | 模型2 | 均值2 | 标准差 | 显著性/不显著性 |

+--------------+--------+--------+-------+--------+--------+-------+-------------+

| lr & cart | lr | 0.892* | 0.034 | cart | 0.834 | 0.037 | 显著 |

| lr & svm | lr | 0.892 | 0.034 | svm | 0.952* | 0.021 | 显著 |

| knn & cart | knn | 0.942* | 0.022 | cart | 0.832 | 0.034 | 显著 |

| knn & svm | knn | 0.942 | 0.022 | svm | 0.952* | 0.021 | 显著 |

| cart & svm | cart | 0.830 | 0.035 | svm | 0.952* | 0.021 | 显著 |

| cart & lda | cart | 0.831 | 0.032 | lda | 0.894* | 0.031 | 显著 |

| svm & bayes | svm | 0.952* | 0.021 | bayes | 0.866 | 0.039 | 显著 |

| svm & lda | svm | 0.952* | 0.021 | lda | 0.894 | 0.031 | 显著 |

+--------------+--------+--------+-------+--------+--------+-------+-------------+

使用pytable包。首先卸载prettytable，然后安装pytable。

rem in your dos window

pip uninstall prettytable

pip uninstall ptable --upgrade

rem 在你的dos 窗口中

pip uninstall prettytable

pip uninstall ptable --upgrade

在你的python程序中，像导入prettytable一样导入ptable包。

在这个例子中，你添加了另一行

x.title = "Pairwise comparison of scores for models"

1	x.title = "Pairwise comparison of scores for models"

代码如下：

from prettytable import PrettyTable
x = PrettyTable()
column_names = ["model pairs", "model1", "mean1", "std", "model2", "mean", "std", "sig/not sig"]x.add_column(column_names[0],models_values)
x.title = "Pairwise comparison of scores for models  "
x.add_column(column_names[1],model_values)
x.add_column(column_names[2],mean1_values)
x.add_column(column_names[3],std1_values)
x.add_column(column_names[4],model_values)
x.add_column(column_names[5],mean2_values)
x.add_column(column_names[6],std2_values)
x.add_column(column_names[7],sig_values)
print(x)

from prettytable import PrettyTable

x = PrettyTable()

column_names = ["模型对", "模型1", "mean1", "std", "模型2", "mean", "std", "sig/not sig"]x.add_column(column_names[0],models_values)

x.title = "Pairwise comparison of scores for models "

x.add_column(column_names[1],model_values)

x.add_column(column_names[2],mean1_values)

x.add_column(column_names[3],std1_values)

x.add_column(column_names[4],model_values)

x.add_column(column_names[5],mean2_values)

x.add_column(column_names[6],std2_values)

x.add_column(column_names[7],sig_values)

print(x)

谢谢你，
悉尼的Anthony

Jason Brownlee 2020年8月28日 6:53 AM #

干得不错。

Anthony The Koala 2020年8月28日 11:03 PM #

尊敬的Jason博士，
从我对你关于比较模型得分的教程的改进中，我展示了如何制作一个表格，列出一模型与另一模型之间存在显著关系的列表。

本教程展示了比较模型时的得分箱线图。

在不展示完整代码的情况下，我将重点介绍使用matplotlib、matplotlib和seaborn（它使用matplotlib）绘制箱线图数据的核心内容。请注意，我没有意外地写两次matplotlib。有两种方法。

我将把这个与教程联系起来。

假设包已在程序顶部声明。

这被呈现为一种“概念性”方法，但没有细节。

首先是matplotlib，其中subplots使用行数和列数进行实例化。

#This is matplotlib using rows and cols method
fig, ax = pyplot.subplots(vert,horiz)
fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')
fig.tight_layout()
index_limit = len(data from an array containing model1 and model2 )
counter = 0; #Use this to access an array containing model1 and model2 data. and other arrays such as whether the relationship between the two models is sig or not sig
for i in range(vert):
	for j in range(horiz):
           ............
           ............
          model1_scores = data from an array containing model1 and model2 [counter];#conceptual
          model2_scores = data from an array containing model1 and model2 [counter];#conceptual
          ax[i,j].boxplot([model1_scores,model2_scores],showmeans=True)
          .........
         ..........
         counter +=1;# for use in accessing other arrays su
         if counter  == index_limit:
              ax[i,j+1].set_axis_off(); #ensure that you don't have an empty graph
              break

#这是使用行和列方法的matplotlib

fig, ax = pyplot.subplots(vert,horiz)

fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')

fig.tight_layout()

index_limit = len(包含model1和model2的数组数据 )

counter = 0; #用于访问包含model1和model2数据的数组。以及其他数组，例如两个模型之间的关系是否显著

for i in range(vert):

for j in range(horiz):

............

model1_scores = 包含model1和model2的数组 [counter];#概念性

model2_scores = 包含model1和model2的数组 [counter];#概念性

ax[i,j].boxplot([model1_scores,model2_scores],showmeans=True)

.........

..........

counter +=1;# 用于访问其他数组

if counter == index_limit:

ax[i,j+1].set_axis_off(); #确保没有空的图

break

这使用了matplotlib：比较这两个示例中subplots的实例化差异。

fig = pyplot.figure()
fig.subplots_adjust(hspace=0.7,wspace = 0.3)
fig.tight_layout()
fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')
counter = 0; #Use this to access an array containing model1 and model2 data. and other arrays such as whether the relationship between the two models is sig or not sig
for item in data from an array containing model1 and model2 :
	ax = fig.add_subplot(int(vert),int(horiz),int(item[0]+1))
	
        model1_scores = data from an array containing model1 and model2 [counter];#conceptual
       model2_scores = data from an array containing model1 and model2 [counter];#conceptual

       ax.boxplot([model1_scores,model2_scores],showmeans=True)
       counter += 1; #the counter in this instance may be used to get other arrays associated with model1 and model2

fig = pyplot.figure()

fig.subplots_adjust(hspace=0.7,wspace = 0.3)

fig.tight_layout()

fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')

counter = 0; #用于访问包含model1和model2数据的数组。以及其他数组，例如两个模型之间的关系是否显著

for item in 包含model1和model2的数组 :

ax = fig.add_subplot(int(vert),int(horiz),int(item[0]+1))

model1_scores = 包含model1和model2的数组 [counter];#概念性

model2_scores = 包含model1和model2的数组 [counter];#概念性

ax.boxplot([model1_scores,model2_scores],showmeans=True)

counter += 1; #在此实例中使用计数器获取与model1和model2相关的其他数组

本示例使用seaborn和matplotlib。

seaborn中的箱线图需要 (i) 一个DataFrame，以及 (ii) 将model1和model2这两个变量重塑为一个数组。seaborn中的箱线图做到了这一点，但不是。

 import seaborn as sns
#This shows difference between matplotlib's boxplot using variables model1 and model2
pyplot.boxplot([model1, model2], showmeans=True)
#This won't display properly - you'll get len(model1) boxplots!
sns.boxplot([model1,model2],showmeans=True)

import seaborn as sns

#这显示了matplotlib的箱线图使用model1和model2变量之间的区别

pyplot.boxplot([model1, model2], showmeans=True)

#这不会正确显示——您将得到 len(model1) 个箱线图！

sns.boxplot([model1,model2],showmeans=True)

Seaborn 的 boxplot 需要两个变量：一个用于识别 model1 和 model2 的分类变量，以及另一个包含 model1 和 model2 值堆叠的数组。

单独的分类变量和值数组的生成是通过 pandas 的 melt 和 DataFrame 函数自动完成的。

import seaborn as sns
from pandas import DataFrame
from pandas import melt
#This is matplotlib using rows and cols method
fig, ax = pyplot.subplots(vert,horiz)
fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')
fig.tight_layout()
index_limit = len(data from an array containing model1 and model2 )
counter = 0; #Use this to access an array containing model1 and model2 data.
for i in range(vert):
	for j in range(horiz):
           ............
           ............
          model1_scores = data from an array containing model1 and model2 [counter];#conceptual
          model2_scores = data from an array containing model1 and model2 [counter];#conceptual

         labels = (str(type(list_of_models[0]).__name__) , str(type(list_of_models[1]).__name__))
         model1_scores = data from an array containing model1 and model2  
	 model1_scores = data from an array containing model1 and model2 
        #sns requires all data to be in a DataFrame
        temp_array = array([x1,x2]).T    
        # The column names will show the paritcular model pair's names, eg LDA and SVC
        tempdf = DataFrame(temp_array,columns=array(labels))
        # This next procedure generates two columns
        # one column containing the hidden array of labels and the other model1 and model2
        tempdf = melt(tempdf)
        # By DEFAULT tempdf has two columns of data, named 'variable' and 'value'
        # Let's rename the labels, 'models' for the x axis and 'scores' for the y axis
	templabel = ['models','scores']
	tempdf.columns = templabel
     	ax[i,j].set_ylabel("scores",fontsize=8)
       # I choose not to display xlabel as the tick labels are self-explanatory
       ax[i,j].set_xlabel("")
       sns.boxplot(x=tempdf.columns[0],y=tempdf.columns[1], data=tempdf, width=0.2, showmeans=True, color='white' ,ax=ax[i,j])
	.........
         ..........
         counter +=1
         if counter  == index_limit:
              ax[i,j+1].set_axis_off(); #ensure that you don't have an empty graph
              break

import seaborn as sns

from pandas import DataFrame

from pandas import melt

#这是使用行和列方法的matplotlib

fig, ax = pyplot.subplots(vert,horiz)

fig.suptitle("Pairwise comparison of scores for models",fontsize=14, fontweight='bold')

fig.tight_layout()

index_limit = len(包含model1和model2的数组数据 )

counter = 0; # 用于访问包含 model1 和 model2 数据的数组。

for i in range(vert):

for j in range(horiz):

............

model1_scores = 包含model1和model2的数组 [counter];#概念性

model2_scores = 包含model1和model2的数组 [counter];#概念性

labels = (str(type(list_of_models[0]).__name__) , str(type(list_of_models[1]).__name__))

model1_scores = data from an array containing model1 and model2

# sns 需要所有数据都在 DataFrame 中

temp_array = array([x1,x2]).T

# 列名将显示特定模型对的名称，例如 LDA 和 SVC

tempdf = DataFrame(temp_array,columns=array(labels))

# 下面的过程生成两列

# 一列包含隐藏的标签数组，另一列包含 model1 和 model2

tempdf = melt(tempdf)

# 默认情况下，tempdf 有两列数据，名为“variable”和“value”

# 我们将标签重命名为 x 轴的“models”，y 轴的“scores”

templabel = ['models','scores']

tempdf.columns = templabel

ax[i,j].set_ylabel("scores",fontsize=8)

# 我选择不显示 x 轴标签，因为刻度标签本身就说明了一切

ax[i,j].set_xlabel("")

sns.boxplot(x=tempdf.columns[0],y=tempdf.columns[1], data=tempdf, width=0.2, showmeans=True, color='white' ,ax=ax[i,j])

.........

..........

counter +=1

if counter == index_limit:

ax[i,j+1].set_axis_off(); #确保没有空的图

break

一个加分项。
您可以结合使用 DataFrame 和 melt 方法来生成一个与另一“数组”数据关联的分类变量数组。

分类变量是在初始化 DataFrame 时派生的。

df = DataFrame([model1_scores, model2_scores],columns = labels, .....)
#df has the labels for the columns
df = melt(df) ; # df generates one column of categories based on the value of labels (of the columns)
df.columns = ['category', 'scores']
category = df.values[:,0]
values = df.values[:,1]

df = DataFrame([model1_scores, model2_scores],columns = labels, .....)

# df 有列的标签

df = melt(df) ; # df 根据列的标签值生成一列类别

df.columns = ['category', 'scores']

category = df.values[:,0]

values = df.values[:,1]

谢谢你，
悉尼的Anthony

Jason Brownlee 2020年8月29日上午8:01 #

干得好，感谢分享！

回复

Aaron Yeardley 2020年9月23日下午8:39 #

嗨，Jason，
这是一篇非常有意思的文章，对我的博士论文工作帮助很大，非常感谢。
我想请教一下，如果我想在多个数据集上测试多个机器学习算法，您会给出什么建议？

我正在考虑通过交叉验证来测试每个数据集，然后得到每个机器学习算法的结果表，以便进行假设检验。下面是一个示例表格，展示了各种机器学习算法的标准RMSE。

数据集 | GP1 | GP2 | ANN | 线性回归
Ishigami | 0.21 | 0.16 | 0.19 | 0.32
Sobol | blah | blah | blah | blah
....
....

等等。

那么，在这种情况下，是否有推荐的假设检验方法来比较回归技术？您是否推荐任何文献让我进一步研究？您对此类分析有什么看法？

我的问题是，我发现的大部分文献都是将两种机器学习技术作为最佳，但只针对一个数据集。而我想为多个数据集找到一个总体上更好的技术。

谢谢，
Aaron

回复
- Jason Brownlee 2020年9月24日上午6:13 #
  
  也许是所有情况之间的成对检验。
  
  回复
- Sadegh 2022年8月17日下午10:02 #
  
  你好 Aaron，我希望你现在已经找到了答案，但我可以分享一本非常棒的书，它深入探讨了这个领域，那就是：“Evaluating Learning Algorithms A Classification Perspective”，作者是“NATHALIE JAPKOWICZ, University of Ottawa”和“MOHAK SHAH, McGill University”。
  希望这个参考能帮助你和其他人解决这些问题。
  
  回复
Kasia 2021年3月11日下午7:51 #

有人知道如何计算这种检验的功效吗？🙂

回复
- Jason Brownlee 2021年3月12日上午4:54 #
  
  这篇教程中的参考文献或许能帮到你
  https://machinelearning.org.cn/statistical-power-and-power-analysis-in-python/
  
  回复
Laura 2021年5月7日凌晨3:44 #

嗨，Jason，

感谢您的文章！确实非常有帮助！

我能问一下，在使用大型数据集时，您建议使用什么方法？交叉验证会非常耗时，所以也许有什么其他方法可以考虑？

谢谢，
Laura

回复
- Jason Brownlee 2021年5月7日凌晨6:30 #
  
  对于非常大的数据集，也许可以采用 train/test split 和 McNemar 检验
  https://machinelearning.org.cn/mcnemars-test-for-machine-learning/
  
  回复
  - Silvia 2022年8月8日凌晨2:38 #
    
    当模型在同一个 train/test split 上训练了 k（例如 5）次时（这是一个基准测试），是否有推荐的检验方法？这不完全是交叉验证（数据分割没有变异性），而是由于模型本身的随机性而产生的多次运行。
    
    回复
vvv 2021年7月2日凌晨1:52 #

当我进行这个测试时，我应该在测试之前对数据进行预处理，还是没有必要？

回复
- Jason Brownlee 2021年7月2日凌晨5:21 #
  
  没必要。
  
  回复
ds 2021年7月12日凌晨7:36 #

如果我比较 ML 和 DL 分类器，DL 中的 cross val score 是如何编写的？

回复
- Jason Brownlee 2021年7月13日凌晨5:13 #
  
  也许你可以使用标准的测试框架，如交叉验证。
  https://machinelearning.org.cn/repeated-k-fold-cross-validation-with-python/
  
  回复
Shruti 2022年1月5日凌晨3:10 #

你好，我偶然发现了这篇论文，它似乎与你的文章非常相似。我不知道它是否是抄袭的，但想提请你注意。

https://www.spu.edu.iq/kjar/index.php/kjar/article/view/630/333

回复
- James Carmichael 2022年1月5日凌晨6:54 #
  
  感谢 Shruti 的反馈！
  
  回复
Michael 2022年2月26日晚上10:07 #

你好 Jason。只有一个小问题。你为什么定义 cv 和 cv2？这是否意味着这两个模型将在不同的数据分割中进行训练和评估？如果只使用一个 cv 是否是错误的？

回复
- Gabriel Leite 2022年3月23日凌晨8:37 #
  
  我也只用了一个。
  
  回复
carol 2023年3月8日凌晨9:05 #

你好 Jason，感谢你这篇精彩的文章。我想问一个关于比较两个深度学习模型（如 u-net 和 attention u-net）的问题。是否可以将数据集固定（添加 10% 的数据用于测试，其余用于训练），然后在固定数据集上使用一组相同的超参数训练这两个模型？然后，对获得的结果使用假设检验？

回复
- James Carmichael 2023年3月8日凌晨9:17 #
  
  你好 Carol…非常欢迎！你的理解是正确的！你也可以尝试在新的数据上运行各种模型，并比较它们各自的均方根误差。
  
  https://machinelearning.org.cn/regression-metrics-for-machine-learning/
  
  这里还提供了其他想法
  
  https://machinelearning.org.cn/evaluate-performance-deep-learning-models-keras/
  
  回复

导航

用于比较机器学习算法的假设检验

教程概述

比较算法的假设检验

5×2 程序配合 MLxtend

比较分类器算法

进一步阅读

教程

论文

API

总结

掌握机器学习统计学！

培养对统计学的实用理解

探索如何将数据转化为知识

关于此主题的更多信息

对《比较机器学习算法的假设检验》的 43 条回复

留下回复点击此处取消回复。

导航

教程概述

比较算法的假设检验

5×2 程序配合 MLxtend

比较分类器算法

进一步阅读

教程

论文

API

总结

掌握机器学习统计学！

培养对统计学的实用理解

探索如何将数据转化为知识

关于此主题的更多信息

对《比较机器学习算法的假设检验》的 43 条回复

留下回复 点击此处取消回复。

留下回复点击此处取消回复。