许多不平衡分类任务需要一个能够预测清晰类别标签的熟练模型,其中两个类别都同样重要。
在卫星图像中检测溢油或油膜是一个不平衡分类问题的例子,在该问题中需要类别标签且两个类别都同样重要。溢油的检测需要动员昂贵的响应,而错过一次事件同样昂贵,会造成环境损害。
评估预测清晰标签的不平衡分类模型的一种方法是计算对阳性类别和阴性类别的单独准确率,分别称为灵敏度和特异度。然后可以使用几何平均数将这两个度量值相加,称为 G-均值,它对倾斜的类别分布不敏感,并正确报告了模型在两个类别上的熟练程度。
在本教程中,您将学习如何开发模型来预测卫星图像中是否存在溢油,并使用 G-均值指标对其进行评估。
完成本教程后,您将了解:
- 如何加载和探索数据集,并为数据准备和模型选择提供思路。
- 如何评估一组概率模型并通过适当的数据准备来提高其性能。
- 如何拟合最终模型并使用它来预测特定案例的类别标签。
开始您的项目,阅读我的新书《Python 不平衡分类》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
- 2021 年 1 月更新:更新了 API 文档链接。

开发不平衡分类模型以检测溢油
照片作者:Lenny K Photography,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 溢油数据集
- 探索数据集
- 模型测试和基线结果
- 评估模型
- 评估概率模型
- 评估平衡逻辑回归
- 评估带概率模型的重采样
- 对新数据进行预测
溢油数据集
在此项目中,我们将使用一个标准的不平衡机器学习数据集,称为“溢油”数据集,“油膜”数据集或简单称为“油”。
该数据集由 Miroslav Kubat 等人在 1998 年的论文“使用机器学习检测卫星雷达图像中的溢油”中首次提出。该数据集通常归功于该论文的合著者 Robert Holte。
该数据集是通过从包含溢油和不包含溢油的海洋卫星图像开始开发的。图像被分割成若干部分,并使用计算机视觉算法进行处理,为描述图像部分或块的内容提供一个特征向量。
输入到[系统]的是来自雷达卫星的原始像素图像。使用图像处理技术 [...] 图像处理的输出是每个可疑区域的固定长度特征向量。在正常操作期间,这些特征向量被馈送到分类器,以决定要向人工检查呈现哪些图像以及图像中的哪些区域。
— 使用机器学习检测卫星雷达图像中的溢油, 1998。
任务是给定一个描述卫星图像块内容的向量,然后预测该块是否包含溢油,例如,是否是由于非法或意外倾倒在海洋中的石油。
共有 937 个样本。每个样本由 48 个数字计算机视觉派生特征、一个图像块编号和一个类别标签组成。
总共处理了九张卫星图像以生成图像块。数据集中的样本按图像排序,数据集的第一列代表图像的图像块编号。这提供是为了估计每张图像的模型性能。在这种情况下,我们不关心图像或图像块编号,可以删除第一列。
正常情况是没有溢油,分配的类别标签为 0,而溢油则用类别标签 1 表示。没有溢油的案例有 896 个,溢油的案例有 41 个。
溢油领域的第二个关键特征可以称为不平衡的训练集:比阳性样本油膜的负性样本类似物多得多。与 41 个阳性样本相比,我们有 896 个负性样本,因此多数类占数据的近 96%。
— 使用机器学习检测卫星雷达图像中的溢油, 1998。
我们无法访问用于从卫星图像准备计算机视觉特征的程序,因此我们仅限于使用收集并提供的提取特征。
接下来,我们仔细看看数据。
想要开始学习不平衡分类吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
探索数据集
首先,下载数据集并将其保存在当前工作目录中,文件名为“oil-spill.csv”。
查看文件内容。
文件的前几行应如下所示
|
1 2 3 4 5 6 |
1,2558,1506.09,456.63,90,6395000,40.88,7.89,29780,0.19,214.7,0.21,0.26,0.49,0.1,0.4,99.59,32.19,1.84,0.16,0.2,87.65,0,0.47,132.78,-0.01,3.78,0.22,3.2,-3.71,-0.18,2.19,0,2.19,310,16110,0,138.68,89,69,2850,1000,763.16,135.46,3.73,0,33243.19,65.74,7.95,1 2,22325,79.11,841.03,180,55812500,51.11,1.21,61900,0.02,901.7,0.02,0.03,0.11,0.01,0.11,6058.23,4061.15,2.3,0.02,0.02,87.65,0,0.58,132.78,-0.01,3.78,0.84,7.09,-2.21,0,0,0,0,704,40140,0,68.65,89,69,5750,11500,9593.48,1648.8,0.6,0,51572.04,65.73,6.26,0 3,115,1449.85,608.43,88,287500,40.42,7.34,3340,0.18,86.1,0.21,0.32,0.5,0.17,0.34,71.2,16.73,1.82,0.19,0.29,87.65,0,0.46,132.78,-0.01,3.78,0.7,4.79,-3.36,-0.23,1.95,0,1.95,29,1530,0.01,38.8,89,69,1400,250,150,45.13,9.33,1,31692.84,65.81,7.84,1 4,1201,1562.53,295.65,66,3002500,42.4,7.97,18030,0.19,166.5,0.21,0.26,0.48,0.1,0.38,120.22,33.47,1.91,0.16,0.21,87.65,0,0.48,132.78,-0.01,3.78,0.84,6.78,-3.54,-0.33,2.2,0,2.2,183,10080,0,108.27,89,69,6041.52,761.58,453.21,144.97,13.33,1,37696.21,65.67,8.07,1 5,312,950.27,440.86,37,780000,41.43,7.03,3350,0.17,232.8,0.15,0.19,0.35,0.09,0.26,289.19,48.68,1.86,0.13,0.16,87.65,0,0.47,132.78,-0.01,3.78,0.02,2.28,-3.44,-0.44,2.19,0,2.19,45,2340,0,14.39,89,69,1320.04,710.63,512.54,109.16,2.58,0,29038.17,65.66,7.35,0 ... |
我们可以看到第一列包含图像块编号的整数。我们还可以看到,计算机视觉派生的特征是实值,具有不同的尺度,例如第二列中的千位数字,以及其他列中的分数。
所有输入变量都是数字的,并且没有用“?”字符标记的缺失值。
首先,我们可以加载 CSV 数据集并确认行数和列数。
可以使用read_csv() Pandas 函数将数据集加载为 DataFrame,指定位置和没有标题行。
|
1 2 3 4 5 |
... # 定义数据集位置 filename = 'oil-spill.csv' # 将csv文件加载为数据框 dataframe = read_csv(filename, header=None) |
加载后,我们可以通过打印DataFrame的形状来总结行数和列数。
|
1 2 3 |
... # 总结数据集的形状 print(dataframe.shape) |
我们还可以使用Counter对象总结每个类别的示例数量。
|
1 2 3 4 5 6 7 |
... # 总结类别分布 target = dataframe.values[:,-1] counter = Counter(target) for k,v in counter.items(): per = v / len(target) * 100 print('Class=%d, Count=%d, Percentage=%.3f%%' % (k, v, per)) |
总而言之,下面列出了加载和汇总数据集的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 加载并汇总数据集 from pandas import read_csv from collections import Counter # 定义数据集位置 filename = 'oil-spill.csv' # 将csv文件加载为数据框 dataframe = read_csv(filename, header=None) # 总结数据集的形状 print(dataframe.shape) # 总结类别分布 target = dataframe.values[:,-1] counter = Counter(target) for k,v in counter.items(): per = v / len(target) * 100 print('Class=%d, Count=%d, Percentage=%.3f%%' % (k, v, per)) |
运行示例,首先加载数据集并确认行数和列数。
然后汇总类别分布,确认溢油和非溢油的数量以及少数类和多数类中的样本百分比。
|
1 2 3 |
(937, 50) Class=1, Count=41, Percentage=4.376% Class=0, Count=896, Percentage=95.624% |
我们还可以通过为每个变量创建直方图来查看其分布。
有 50 个变量,这有很多图,但我们可能会发现一些有趣的模式。此外,由于图太多,我们必须关闭坐标轴标签和图标题以减少混乱。完整的示例列出如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 创建每个变量的直方图 from pandas import read_csv from matplotlib import pyplot # 定义数据集位置 filename = 'oil-spill.csv' # 将csv文件加载为数据框 dataframe = read_csv(filename, header=None) # 创建每个变量的直方图 ax = dataframe.hist() # 禁用坐标轴标签 for axis in ax.flatten(): axis.set_title('') axis.set_xticklabels([]) axis.set_yticklabels([]) pyplot.show() |
运行示例后,会创建带有 50 个变量的直方图子图的图形。
我们可以看到许多不同的分布,有些具有类高斯分布,有些则具有似乎是指数或离散的分布。
根据建模算法的选择,我们预计将分布缩放到相同的范围将是有用的,并且可能需要使用一些幂变换。
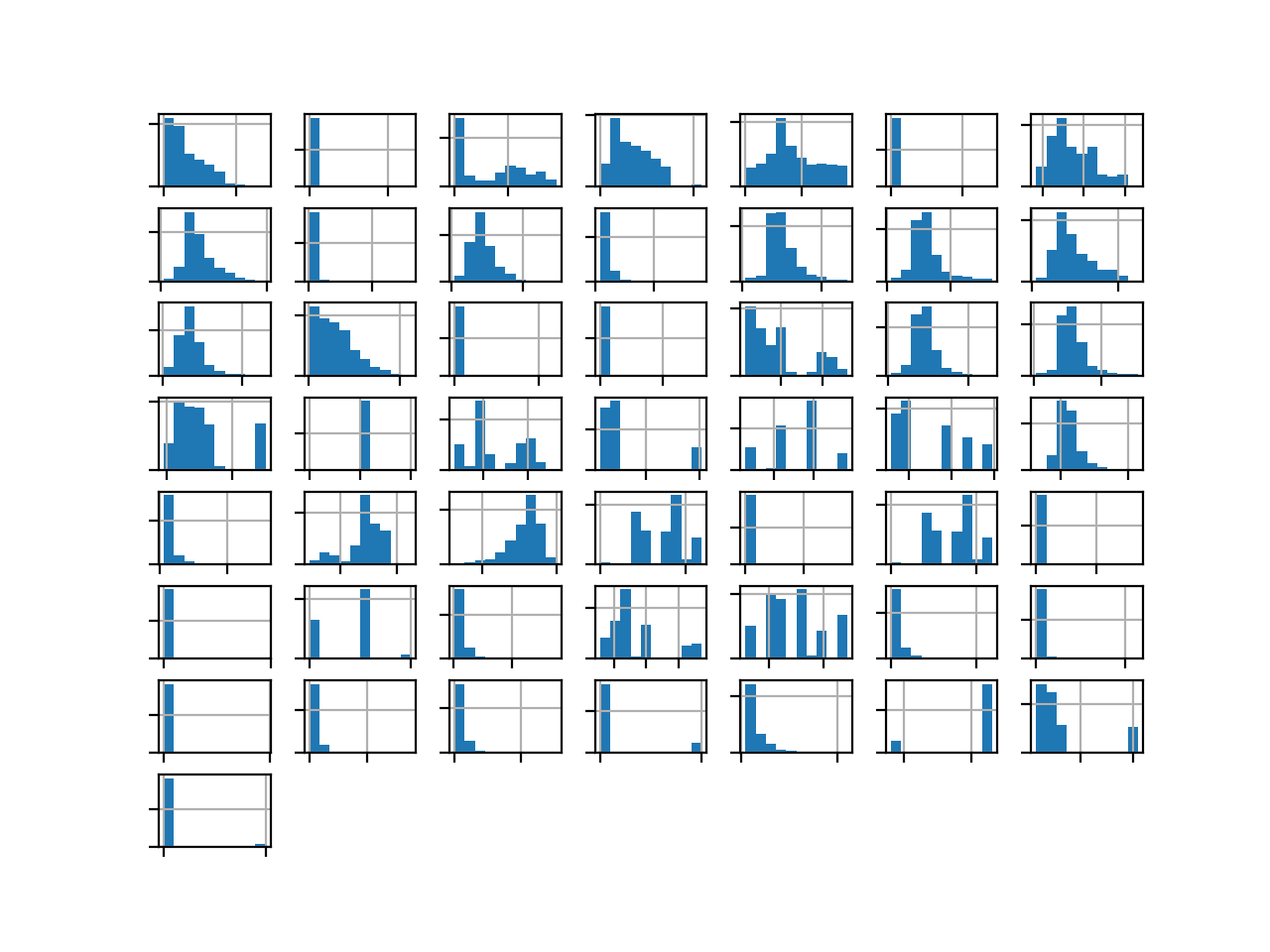
溢油数据集各变量的直方图
现在我们已经审阅了数据集,接下来我们将开发一个测试工具来评估候选模型。
模型测试和基线结果
我们将使用重复分层 k 折交叉验证来评估候选模型。
k 折交叉验证程序提供了一个良好的模型性能总体估计,至少与单个训练-测试分割相比,它不会过于乐观地偏倚。我们将使用 k=10,这意味着每个折叠大约包含 937/10 或约 94 个样本。
分层意味着每个折叠将包含相同比例的样本,即约 96% 的非溢油和 4% 的溢油。重复意味着将执行多次评估过程,以帮助避免偶然结果并更好地捕捉所选模型的方差。我们将使用三次重复。
这意味着一个模型将进行 10 * 3 = 30 次拟合和评估,并将报告这些运行的平均值和标准差。
这可以通过使用RepeatedStratifiedKFold scikit-learn 类来实现。
我们正在预测卫星图像块是否包含溢油的类别标签。我们可以使用许多度量,尽管该论文的作者选择报告灵敏度、特异度和两者得分的几何平均值,称为 G-均值。
为此,我们主要使用了几何平均数(g-mean)[...] 该度量具有独立于类别间样本分布的独特属性,因此在分布可能随时间变化或在训练集和测试集中不同的情况下是稳健的。
— 使用机器学习检测卫星雷达图像中的溢油, 1998。
回想一下,灵敏度是衡量阳性类别准确率的度量,而特异度是衡量阴性类别准确率的度量。
- 灵敏度 = 真阳性 / (真阳性 + 假阴性)
- 特异度 = 真阴性 / (真阴性 + 假阳性)
G-均值寻求这些得分的平衡,即几何平均数,其中一个或另一个的性能不佳会导致 G-均值得分较低。
- G-Mean = sqrt(灵敏度 * 特异性)
我们可以使用 imbalanced-learn 库提供的geometric_mean_score() 函数来计算模型所做预测集 G-均值。
首先,我们可以定义一个函数来加载数据集并将列分割成输入和输出变量。我们还将删除第 22 列,因为该列包含一个单值,以及定义图像块编号的第一列。下面的 `load_dataset()` 函数实现了这一点。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) return X, y |
然后,我们可以定义一个函数,该函数将在数据集上评估给定的模型,并返回每次重复和每次折叠的 G-均值得分列表。
下面的 evaluate_model() 函数实现了这一点,它将数据集和模型作为参数,并返回分数列表。
|
1 2 3 4 5 6 7 8 9 |
# 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) return scores |
最后,我们可以使用这个测试工具评估数据集上的基线模型。
预测所有样本的多数类标签(0)或少数类标签(1)的模型将导致 G-均值为零。因此,一个好的默认策略是随机预测一个类标签或另一个类标签,概率为 50%,目标 G-均值为 0.5 左右。
可以使用 scikit-learn 库中的DummyClassifier 类,并将“strategy”参数设置为‘uniform’来实现这一点。
|
1 2 3 |
... # 定义参考模型 model = DummyClassifier(strategy='uniform') |
模型评估后,我们可以直接报告 G-均值得分的平均值和标准差。
|
1 2 3 4 5 |
... # 评估模型 result_m, result_s = evaluate_model(X, y, model) # 总结性能 print('Mean G-Mean: %.3f (%.3f)' % (result_m, result_s)) |
将所有内容结合起来,加载数据集、评估基线模型和报告性能的完整示例列于下文。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
# 测试框架和基线模型评估 from collections import Counter from numpy import mean from numpy import std from pandas import read_csv from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from imblearn.metrics import geometric_mean_score from sklearn.metrics import make_scorer from sklearn.dummy import DummyClassifier # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义数据集位置 full_path = 'oil-spill.csv' # 加载数据集 X, y = load_dataset(full_path) # 总结已加载的数据集 print(X.shape, y.shape, Counter(y)) # 定义参考模型 model = DummyClassifier(strategy='uniform') # 评估模型 scores = evaluate_model(X, y, model) # 总结性能 print('Mean G-Mean: %.3f (%.3f)' % (mean(scores), std(scores))) |
运行示例首先加载并总结数据集。
我们可以看到已加载正确的行数,并且有 47 个计算机视觉派生的输入变量,已删除常量值列(索引 22)和图像块编号列(索引 0)。
重要的是,我们可以看到类别标签已正确映射到整数,其中 0 代表多数类,1 代表少数类,这对于不平衡二元分类数据集来说是惯例。
接下来,报告 G-均值得分的平均值。
在这种情况下,我们可以看到基线算法实现了约 0.47 的 G-均值,接近理论最大值 0.5。该分数提供了模型技能的下限;任何实现平均 G-均值高于约 0.47(或者真正高于 0.5)的模型都具有技能,而实现低于该值得分的模型在此数据集上不具备技能。
|
1 2 |
(937, 47) (937,) Counter({0: 896, 1: 41}) Mean G-Mean: 0.478 (0.143) |
值得注意的是,该论文报告的一个良好 G-均值约为 0.811,尽管模型评估过程不同。这为在该数据集上获得“良好”性能提供了一个大致的目标。
现在我们有了测试工具和性能基线,我们可以开始评估该数据集上的一些模型。
评估模型
在本节中,我们将使用上一节中开发的测试工具,评估数据集上的一系列不同技术。
目标是演示如何系统地解决问题,并展示一些针对不平衡分类问题设计的技术的能力。
报告的性能良好,但尚未高度优化(例如,超参数未进行调整)。
你能得到什么分数?如果您可以使用相同的测试框架获得更好的 G-均值性能,我很想知道。请在下面的评论中告知我。
评估概率模型
让我们开始在数据集上评估一些概率模型。
概率模型是在概率框架下拟合到数据中的模型,并且通常在不平衡分类数据集方面表现良好。
我们将使用默认超参数在数据上评估以下概率模型:
- 逻辑回归 (LR)
- 线性判别分析 (LDA)
- 高斯朴素贝叶斯 (NB)
LR 和 LDA 都对输入变量的尺度敏感,并且通常期望或在输入变量尺度不同时进行标准化或归一化作为预处理步骤,效果会更好。
在这种情况下,我们将在拟合每个模型之前对数据集进行标准化。这将使用Pipeline和StandardScaler类来实现。使用 Pipeline 可确保 StandardScaler 在训练数据集上进行拟合,并在每个 k 折交叉验证评估中应用于训练集和测试集,从而避免任何可能导致乐观结果的数据泄露。
我们可以定义一个模型列表,以便在我们的测试框架中进行评估,如下所示:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
... # 定义模型 models, names, results = list(), list(), list() # LR models.append(Pipeline(steps=[('t', StandardScaler()),('m',LogisticRegression(solver='liblinear'))])) names.append('LR') # LDA models.append(Pipeline(steps=[('t', StandardScaler()),('m',LinearDiscriminantAnalysis())])) names.append('LDA') # NB models.append(GaussianNB()) names.append('NB') |
定义后,我们可以枚举列表并逐一评估。在评估过程中可以打印 G-均值得分的平均值和标准差,并且可以存储得分样本。
可以根据其平均 G-均值得分直接比较算法。
|
1 2 3 4 5 6 7 8 |
... # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) |
在运行结束时,我们可以使用得分来为每个算法创建箱线图。
并排创建图形可以比较分布,包括平均得分和 25% 到 75% 分位数之间的中位数 50% 的分布。
|
1 2 3 4 |
... # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
将所有内容结合起来,使用测试框架在溢油数据集上比较三个概率模型的完整示例列于下文。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
# 在溢油数据集上比较概率模型 from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import make_scorer from sklearn.linear_model import LogisticRegression from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.naive_bayes import GaussianNB from imblearn.metrics import geometric_mean_score from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义数据集位置 full_path = 'oil-spill.csv' # 加载数据集 X, y = load_dataset(full_path) # 定义模型 models, names, results = list(), list(), list() # LR models.append(Pipeline(steps=[('t', StandardScaler()),('m',LogisticRegression(solver='liblinear'))])) names.append('LR') # LDA models.append(Pipeline(steps=[('t', StandardScaler()),('m',LinearDiscriminantAnalysis())])) names.append('LDA') # NB models.append(GaussianNB()) names.append('NB') # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行示例会在数据集上评估每个概率模型。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑运行示例几次并比较平均结果。
您可能会看到 LDA 算法的一些警告,例如“变量是共线的”。目前可以安全地忽略它们,但这表明该算法可以通过特征选择来去除一些变量。
在这种情况下,我们可以看到每个算法都有技能,平均 G-均值高于 0.5。结果表明 LDA 可能是测试模型中性能最佳的。
|
1 2 3 |
>LR 0.621 (0.261) >LDA 0.741 (0.220) >NB 0.721 (0.197) |
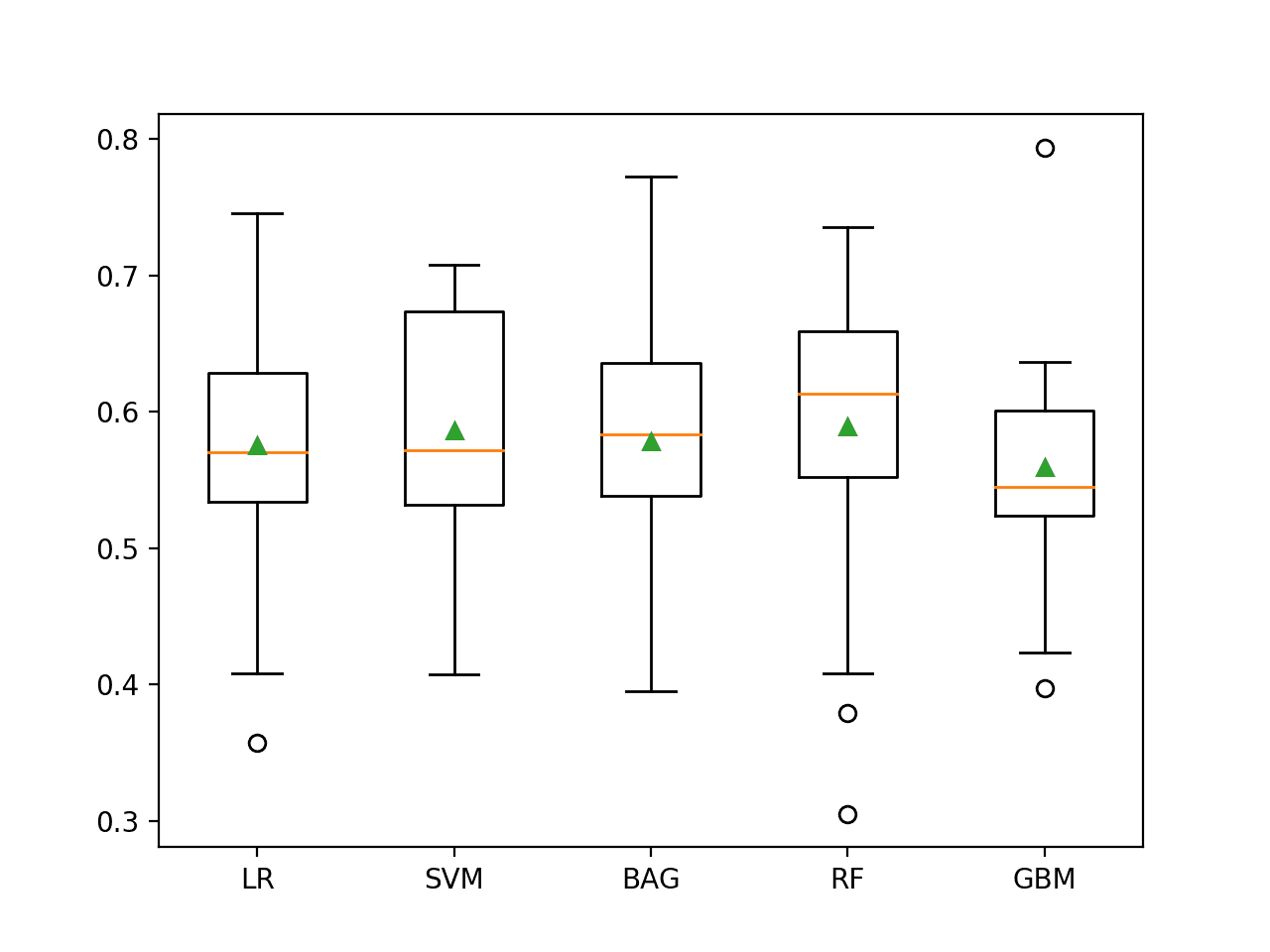
G-均值得分的分布通过带有每个算法的箱线图的图形进行汇总。我们可以看到 LDA 和 NB 的分布都很紧凑且具有技能,而 LR 在运行期间可能有一些性能不佳的结果,从而降低了分布。
这说明在选择模型时,不仅要考虑平均性能,还要考虑模型的稳定性。

不平衡溢油数据集上概率模型的箱线图
我们开了一个好头,但我们可以做得更好。
评估平衡逻辑回归
逻辑回归算法支持一项修改,该修改将分类错误的权重调整为与类别权重成反比。
这使得模型能够更好地学习有利于少数类的类边界,这可能有助于提高整体 G-均值性能。通过将LogisticRegression的“class_weight”参数设置为‘balanced’来实现这一点。
|
1 2 |
... LogisticRegression(solver='liblinear', class_weight='balanced') |
如前所述,逻辑回归对输入变量的尺度敏感,使用归一化或标准化的输入可以获得更好的性能;因此,对于给定的数据集,测试这两种方法是一个好主意。此外,还可以使用幂分布来分散每个输入变量的分布,并使具有类似高斯分布的变量更接近高斯分布。这可以使像逻辑回归这样的模型受益,这些模型对输入变量的分布做出假设。
幂变换将使用支持正向和负向输入的 Yeo-Johnson 方法,但我们也会在变换之前对数据进行归一化。此外,用于变换的 PowerTransformer 类将在变换后对每个变量进行标准化。
我们将比较一个具有平衡类权重的LogisticRegression模型与具有三种不同数据准备方案(即归一化、标准化和幂变换)的相同算法。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
... # 定义模型 models, names, results = list(), list(), list() # LR 平衡 models.append(LogisticRegression(solver='liblinear', class_weight='balanced')) names.append('Balanced') # LR 平衡 + 归一化 models.append(Pipeline(steps=[('t', MinMaxScaler()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Norm') # LR 平衡 + 标准化 models.append(Pipeline(steps=[('t', StandardScaler()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Std') # LR 平衡 + 幂变换 models.append(Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Power') |
总而言之,下面列出了平衡逻辑回归与不同数据准备方案的比较。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
# 在溢油数据集上比较平衡逻辑回归 from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import make_scorer from sklearn.linear_model import LogisticRegression from imblearn.metrics import geometric_mean_score from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler 从 sklearn.预处理 导入 MinMaxScaler from sklearn.preprocessing import PowerTransformer # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义数据集位置 full_path = 'oil-spill.csv' # 加载数据集 X, y = load_dataset(full_path) # 定义模型 models, names, results = list(), list(), list() # LR 平衡 models.append(LogisticRegression(solver='liblinear', class_weight='balanced')) names.append('Balanced') # LR 平衡 + 归一化 models.append(Pipeline(steps=[('t', MinMaxScaler()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Norm') # LR 平衡 + 标准化 models.append(Pipeline(steps=[('t', StandardScaler()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Std') # LR 平衡 + 幂变换 models.append(Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()),('m', LogisticRegression(solver='liblinear', class_weight='balanced'))])) names.append('Balanced-Power') # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行示例将评估平衡逻辑回归模型的每个版本在数据集上的表现。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑运行示例几次并比较平均结果。
您可能会看到第一个平衡 LR 模型的一些警告,例如“Liblinear 未收敛”。这些警告目前可以安全地忽略,但表明该算法可以从特征选择中受益,以去除一些变量。
在这种情况下,我们可以看到,平衡版本的逻辑回归比上一节评估的所有概率模型都要好得多。
结果表明,在数据归一化作为预处理的情况下使用平衡 LR 可能在此数据集上表现最佳,平均 G-mean 得分为约 0.852。这与 1998 年论文中报告的结果在同一范围内或更好。
|
1 2 3 4 |
>平衡 0.846 (0.142) >平衡-归一化 0.852 (0.119) >平衡-标准化 0.843 (0.124) >平衡-幂变换 0.847 (0.130) |
创建了一个包含每种算法箱须图的图形,允许比较结果的分布。
我们可以看到,与上一节的非平衡版本相比,平衡 LR 的分布总体上更紧凑。我们还可以看到,归一化版本的其中位数结果(橙色线)高于平均值,超过 0.9,这令人印象深刻。平均值与中位数不同,表明结果分布偏斜,少数糟糕的结果会拉低平均值。

不平衡溢油数据集上平衡逻辑回归模型的箱须图
我们现在已经取得了很好的结果,工作量也很少;看看我们能否更进一步。
评估概率模型的数据采样
数据采样是在拟合模型之前对不平衡训练数据集进行更好准备的一种方法。
也许最流行的数据采样技术是 SMOTE 过采样技术,用于为少数类创建新的合成样本。这可以与 编辑最近邻 (ENN) 算法配对,该算法将定位并删除数据集中含糊不清的样本,从而使模型更容易学习区分两个类别。
这种组合称为 SMOTE-ENN,可以使用 imbalanced-learn 库中的 SMOTEENN 类来实现;例如:
|
1 2 3 |
... # 定义 SMOTE-ENN 数据采样方法 e = SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))) |
SMOTE 和 ENN 在输入数据事先缩放后效果更好。这是因为这两种技术内部都使用了最近邻算法,而该算法对具有不同尺度的输入变量敏感。因此,我们将要求数据首先进行归一化,然后进行采样,然后用作(不平衡)逻辑回归模型的输入。
因此,我们可以使用 imbalanced-learn 库提供的 Pipeline 类来创建数据变换序列,包括数据采样方法,并以逻辑回归模型结束。
我们将比较四种数据采样逻辑回归模型变体,具体是:
- SMOTEENN + LR
- 归一化 + SMOTEENN + LR
- 标准化 + SMOTEENN + LR
- 归一化 + 幂变换 + SMOTEENN + LR
预期是 LR 配合 SMOTEENN 会表现更好,而 SMOTEENN 配合标准化或归一化会表现更好。最后一种情况做了很多工作,首先归一化数据集,然后应用幂变换,标准化结果(回想一下 PowerTransformer 类默认会标准化输出),应用 SMOTEENN,然后最后拟合逻辑回归模型。
这些组合可以定义如下:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
... # SMOTEENN models.append(Pipeline(steps=[('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('LR') # SMOTEENN + 归一化 models.append(Pipeline(steps=[('t', MinMaxScaler()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Norm') # SMOTEENN + 标准化 models.append(Pipeline(steps=[('t', StandardScaler()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Std') # SMOTEENN + 幂变换 models.append(Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Power') |
将这些结合起来,完整的示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
# 在溢油数据集上比较数据采样与逻辑回归 from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import LabelEncoder from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import make_scorer from sklearn.linear_model import LogisticRegression from imblearn.metrics import geometric_mean_score from sklearn.preprocessing import PowerTransformer from sklearn.preprocessing import StandardScaler 从 sklearn.预处理 导入 MinMaxScaler from imblearn.pipeline import Pipeline from imblearn.combine import SMOTEENN from imblearn.under_sampling import EditedNearestNeighbours # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # drop unused columns data.drop(22, axis=1, inplace=True) data.drop(0, axis=1, inplace=True) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # define the model evaluation metric metric = make_scorer(geometric_mean_score) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义数据集位置 full_path = 'oil-spill.csv' # 加载数据集 X, y = load_dataset(full_path) # 定义模型 models, names, results = list(), list(), list() # SMOTEENN models.append(Pipeline(steps=[('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('LR') # SMOTEENN + 归一化 models.append(Pipeline(steps=[('t', MinMaxScaler()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Norm') # SMOTEENN + 标准化 models.append(Pipeline(steps=[('t', StandardScaler()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Std') # SMOTEENN + 幂变换 models.append(Pipeline(steps=[('t1', MinMaxScaler()), ('t2', PowerTransformer()), ('e', SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority'))), ('m', LogisticRegression(solver='liblinear'))])) names.append('Power') # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) # 总结并存储 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) results.append(scores) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行示例将评估 SMOTEENN 与逻辑回归模型的每个版本在数据集上的表现。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑运行示例几次并比较平均结果。
在这种情况下,我们可以看到 SMOTEENN 的加入提高了默认 LR 算法的性能,平均 G-mean 达到 0.852,而第一组实验结果中为 0.621。这甚至比上一节中没有数据缩放的平衡 LR(G-mean 约为 0.846)还要好。
结果表明,最后一种组合(归一化、幂变换和标准化)可能比默认 LR 配合 SMOTEENN 获得了略好的得分,G-mean 约为 0.873,尽管警告消息表明存在一些需要解决的问题。
|
1 2 3 4 |
>LR 0.852 (0.105) >归一化 0.838 (0.130) >标准化 0.849 (0.113) >幂变换 0.873 (0.118) |
可以使用箱须图比较结果的分布。我们可以看到所有分布的大致分布范围相同,并且结果的平均值差异可用于选择模型。

不平衡溢油数据集上逻辑回归模型与数据采样模型的箱须图
对新数据进行预测
直接在逻辑回归中使用 SMOTEENN,而无需任何数据缩放,可能是最简单且性能良好的模型,可以用于未来。
该模型在我们的测试框架上的平均 G-mean 约为 0.852。
我们将以此作为我们的最终模型,并用它来对新数据进行预测。
首先,我们可以将模型定义为管道。
|
1 2 3 4 5 |
... # 定义模型 smoteenn = SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority')) model = LogisticRegression(solver='liblinear') pipeline = Pipeline(steps=[('e', smoteenn), ('m', model)]) |
定义好后,我们就可以在整个训练数据集上对其进行拟合。
|
1 2 3 |
... # 拟合模型 pipeline.fit(X, y) |
拟合后,我们可以通过调用 predict() 函数来使用它对新数据进行预测。这将返回 0(无溢油)或 1(有溢油)的类别标签。
例如
|
1 2 3 4 5 6 7 |
... # 定义一行数据 row = [...] # 进行预测 yhat = pipeline.predict([row]) # 获取标签 label = yhat[0] |
为了说明这一点,我们可以使用拟合的模型来预测一些已知没有溢油的情况和一些已知有溢油的情况的标签。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
# 拟合模型并对溢油数据集进行预测 from pandas import read_csv from sklearn.preprocessing import LabelEncoder from sklearn.linear_model import LogisticRegression from imblearn.pipeline import Pipeline from imblearn.combine import SMOTEENN from imblearn.under_sampling import EditedNearestNeighbours # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, 1:-1], data[:, -1] # 对目标变量进行标签编码,使其具有类别0和1 y = LabelEncoder().fit_transform(y) 返回 X, y # 定义数据集位置 full_path = 'oil-spill.csv' # 加载数据集 X, y = load_dataset(full_path) # 定义模型 smoteenn = SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy='majority')) model = LogisticRegression(solver='liblinear') pipeline = Pipeline(steps=[('e', smoteenn), ('m', model)]) # 拟合模型 pipeline.fit(X, y) # 评估一些无溢油情况(已知类别 0) print('无溢油情况:') data = [[329,1627.54,1409.43,51,822500,35,6.1,4610,0.17,178.4,0.2,0.24,0.39,0.12,0.27,138.32,34.81,2.02,0.14,0.19,75.26,0,0.47,351.67,0.18,9.24,0.38,2.57,-2.96,-0.28,1.93,0,1.93,34,1710,0,25.84,78,55,1460.31,710.63,451.78,150.85,3.23,0,4530.75,66.25,7.85], [3234,1091.56,1357.96,32,8085000,40.08,8.98,25450,0.22,317.7,0.18,0.2,0.49,0.09,0.41,114.69,41.87,2.31,0.15,0.18,75.26,0,0.53,351.67,0.18,9.24,0.24,3.56,-3.09,-0.31,2.17,0,2.17,281,14490,0,80.11,78,55,4287.77,3095.56,1937.42,773.69,2.21,0,4927.51,66.15,7.24], [2339,1537.68,1633.02,45,5847500,38.13,9.29,22110,0.24,264.5,0.21,0.26,0.79,0.08,0.71,89.49,32.23,2.2,0.17,0.22,75.26,0,0.51,351.67,0.18,9.24,0.27,4.21,-2.84,-0.29,2.16,0,2.16,228,12150,0,83.6,78,55,3959.8,2404.16,1530.38,659.67,2.59,0,4732.04,66.34,7.67]] for row in data: # 进行预测 yhat = pipeline.predict([row]) # 获取标签 label = yhat[0] # 总结 print('>预测=%d (预期为 0)' % (label)) # 评估一些溢油情况(已知类别 1) print('溢油情况:') data = [[2971,1020.91,630.8,59,7427500,32.76,10.48,17380,0.32,427.4,0.22,0.29,0.5,0.08,0.42,149.87,50.99,1.89,0.14,0.18,75.26,0,0.44,351.67,0.18,9.24,2.5,10.63,-3.07,-0.28,2.18,0,2.18,164,8730,0,40.67,78,55,5650.88,1749.29,1245.07,348.7,4.54,0,25579.34,65.78,7.41], [3155,1118.08,469.39,11,7887500,30.41,7.99,15880,0.26,496.7,0.2,0.26,0.69,0.11,0.58,118.11,43.96,1.76,0.15,0.18,75.26,0,0.4,351.67,0.18,9.24,0.78,8.68,-3.19,-0.33,2.19,0,2.19,150,8100,0,31.97,78,55,3471.31,3059.41,2043.9,477.23,1.7,0,28172.07,65.72,7.58], [115,1449.85,608.43,88,287500,40.42,7.34,3340,0.18,86.1,0.21,0.32,0.5,0.17,0.34,71.2,16.73,1.82,0.19,0.29,87.65,0,0.46,132.78,-0.01,3.78,0.7,4.79,-3.36,-0.23,1.95,0,1.95,29,1530,0.01,38.8,89,69,1400,250,150,45.13,9.33,1,31692.84,65.81,7.84]] for row in data: # 进行预测 yhat = pipeline.predict([row]) # 获取标签 label = yhat[0] # 总结 print('>预测=%d (预期为 1)' % (label)) |
首先运行示例,在整个训练数据集上拟合模型。
然后使用拟合的模型对已知没有溢油的案例(从数据集文件中选取)进行预测,看是否能预测出溢油标签。我们可以看到所有案例都得到了正确预测。
然后将实际溢油案例作为输入模型,并预测标签。正如我们所期望的那样,再次预测了正确的标签。
|
1 2 3 4 5 6 7 8 |
无溢油情况 >预测值=0(期望值 0) >预测值=0(期望值 0) >预测值=0(期望值 0) 溢油情况 >预测值=1(期望值 1) >预测值=1(期望值 1) >预测值=1(期望值 1) |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 卫星雷达图像中的溢油检测机器学习, 1998.
API
- pandas.read_csv API.
- sklearn.model_selection.RepeatedStratifiedKFold API.
- sklearn.dummy.DummyClassifier API.
- imblearn.metrics.geometric_mean_score API.
- sklearn.pipeline.Pipeline API.
- sklearn.linear_model.LogisticRegression API.
- imblearn.combine.SMOTEENN API.
文章
总结
在本教程中,您学习了如何开发一个模型来预测卫星图像中是否存在溢油,并使用 G-mean 指标进行评估。
具体来说,你学到了:
- 如何加载和探索数据集,并为数据准备和模型选择提供思路。
- 如何评估一组概率模型并通过适当的数据准备来提高其性能。
- 如何拟合最终模型并使用它来预测特定案例的类别标签。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



嗨,Jason,
您的文章非常出色。
祝贺您。
谢谢。
嗨,Jason,
感谢这篇文章。
我需要购买哪本书的帮助。
我有一个经典的失衡问题:为大型公司预测信用违约。
但我不想用经典方法(如逻辑回归或 LDA)来处理这个问题。
我在一篇文章中看到,异质数据集(中等权重数据集)在类似问题上表现出色。
哪本书最值得推荐?
谢谢你。
#异质集成(加权平均集成)
这本。
https://machinelearning.org.cn/imbalanced-classification-with-python/
出色的工作!我爱死它了 😀
您好 sir…在机器学习领域做得很好…我目前正在攻读博士学位…能否请您为我提供一些研究课题,以便我进行研究工作……
这是我在这里回答的一个常见问题
https://machinelearning.org.cn/faq/single-faq/what-research-topic-should-i-work-on
嘿,Jason Brownlee
您能否就自然语言处理的文本摘要写一篇详细的文章。
感谢您的建议。
我想知道如何处理非正态分布的数据用于回归任务。例如价格预测,数据不是正态分布的。我们该如何处理?
尝试直接将其作为基线进行建模。然后可以尝试幂变换和其他变换,并查看性能是否有任何变化/提升。
smoteenn 代码中似乎有拼写错误
SMOTEENN(enn=EditedNearestNeighbours(sampling_strategy=’minority’))
谢谢,确切的拼写错误是什么?
嗨,Jason,
再次感谢您对构建模型的每个步骤的详细而出色的解释。
您选择逻辑回归模型是为了方便与论文复现吗?只是好奇,如果使用提升算法是否能获得更高的准确率。
谢谢!
卡洛斯。
不,我测试了大量的算法,发现它的表现很好。
感谢您的演示。
我对于使用重采样数据集来估计性能感到非常不适。我的意思是使用文章中重采样函数(Smoteenn)的输出数据集。我宁愿使用原始数据。
尽管如此,如果我们期望估计函数的平滑边界,重采样会使边界更加“可见”,但也可能更具噪声。
另一方面,smoteenn的一个优势是移除步骤,它近似地将重采样数据集保持在一个凸空间(几乎)。
仍然,我对这个问题没有清晰的认识,您有吗?
谢谢,
Jérémie
我认为您误解了数据重采样。
我们在重采样数据上进行拟合,但在原始数据上进行估计。
我同意这个策略:在重采样数据上拟合,在原始数据上估计。
但是,我不明白在“Evaluate Data Sampling With Probabilistic Models”这一部分的整个代码中,性能估计是如何仅在原始数据上计算的。
在“cross_val_score”的交叉验证循环中,您将原始数据(X,y)提供给包含重采样方法的管道。您的意思是cross_val_score仅在训练步骤中应用重采样,而在预测/评估时保留原始数据吗?我认为不是这样的。
谢谢!
是的,本教程枚举了不同的策略,以便发现哪种策略最适合此数据集。
是的,我们使用Pipeline的原因是它知道在交叉验证期间仅对训练数据执行数据重采样转换,而对测试数据不执行。在此处了解更多信息
https://imbalanced-learn.readthedocs.io/en/stable/generated/imblearn.pipeline.Pipeline.html
事实上,我在imbalearn库的pipeline.py代码中看到了这一点:https://github.com/scikit-learn-contrib/imbalanced-learn/blob/12b2e0d2858a30d4687fbf910372b8f416b33998/imblearn/pipeline.py#L319
谢谢!
不客气。
一如既往的精彩教程!
我有一个关于管道中PowerTransformer步骤的问题。
我设想只有部分特征,而不是全部,需要这种转换才能具有更“类高斯”的分布。
当我们将此转换应用于整个数据集时,是否会损害其他特征?
在管道中,是否有办法告诉PowerTransformer仅将转换应用于某些特征而不是其他特征?
更新:我尝试通过定义一个自定义函数来实现这一点,该函数仅将转换器拟合到选定的列。我不确定这是否有意义。它对分数没有任何影响……
def powtransf()
pt = PowerTransformer()
columns=[0,1,2,4,7,9,15,16,21,26,30,32,33,38,39,40,41,42,43,44,45,46]
return pt.fit(X[:,columns])
[…]
models.append(Pipeline(steps=[(‘t’, MinMaxScaler()),(‘p’,powtransf()),(‘m’, LogisticRegression(solver=’liblinear’, class_weight = ‘balanced’))]))
如果对分数没有影响,那么在此任务中就不需要它,但可能在其他项目中很有用……
很有可能。
理想情况下,我们会逐一检查每个特征。
您好,我想问一下,什么是数字化的图像特征?我找不到50多个,您是如何获得这么多数字特征的?
您可以在教程中找到链接的论文“Machine Learning for the Detection of Oil Spills in Satellite Radar Images”,其中解释了数据。
您好,感谢分享,我是机器学习新手。我的问题是:如何将此模型应用于新图像?我不太明白特征是什么,以及如何将卫星图像转换为使用此模型。
您需要从新图像中提取特征,然后将这些特征输入模型。
在这种情况下,我们没有用于从图像中提取特征的工具。