欺诈是信用卡公司面临的一个主要问题,这既是因为每天完成的交易量很大,也是因为许多欺诈交易看起来与正常交易非常相似。
识别欺诈性信用卡交易是一种常见的不平衡二元分类类型,其中重点是积极类别(是否为欺诈)类别。
因此,诸如精确率和召回率之类的指标可用于总结模型在类别标签方面的性能,而精确率-召回率曲线可用于总结模型在概率阈值范围内的性能,当将预测概率映射到类别标签时。
这使模型运算符能够控制预测的生成方式,例如偏向于模型产生的假阳性或假阴性类型的错误。
在本教程中,您将了解如何为不平衡的信用卡欺诈数据集开发和评估模型。
完成本教程后,您将了解:
- 如何加载和探索数据集,并为数据准备和模型选择提供思路。
- 如何使用稳健的测试框架系统地评估一套机器学习模型。
- 如何拟合最终模型并使用它来预测特定案例的欺诈概率。
让我们开始吧。

如何预测欺诈性信用卡交易的概率
照片作者:Andrea Schaffer,部分权利保留。
教程概述
本教程分为五个部分;它们是:
- 信用卡欺诈数据集
- 探索数据集
- 模型测试和基线结果
- 评估模型
- 在新数据上进行预测
信用卡欺诈数据集
在此项目中,我们将使用一个标准的不平衡机器学习数据集,称为“信用卡欺诈检测”数据集。
这些数据代表了2013年9月两天内欧洲持卡人发生的信用卡交易。
该数据集归功于布鲁塞尔自由大学机器学习小组(Université Libre de Bruxelles)以及Andrea Dal Pozzolo等人的系列出版物。
所有持卡人的详细信息都已通过主成分分析(PCA)转换进行匿名化。相反,提供了这些匿名特征的总共28个主成分。此外,还提供了交易之间的秒数以及购买金额(可能是欧元)。
每条记录被分类为正常(类别“0”)或欺诈(类别“1”),交易严重偏向正常。具体来说,在总共284,807笔交易中,有492笔欺诈性信用卡交易,占所有交易的大约0.172%。
它包含两天内发生的在线交易的子集,其中284,807笔交易中有492笔欺诈。该数据集高度不平衡,积极类别(欺诈)占所有交易的0.172%……
— Calibrating Probability with Undersampling for Unbalanced Classification,2015。
一些出版物使用ROC曲线下面积指标,尽管数据集网站建议使用精确率-召回率曲线下面积指标,因为类别不平衡严重。
鉴于类别不平衡比率,我们建议使用精确率-召回率曲线下面积(AUPRC)来衡量准确性。
— 信用卡欺诈检测,Kaggle。
接下来,我们仔细看看数据。
探索数据集
首先,下载并解压数据集,并将其保存在当前工作目录中,文件名为“creditcard.csv”。
查看文件内容。
文件的前几行应如下所示
|
1 2 3 4 5 6 |
0,-1.3598071336738,-0.0727811733098497,2.53634673796914,1.37815522427443,-0.338320769942518,0.462387777762292,0.239598554061257,0.0986979012610507,0.363786969611213,0.0907941719789316,-0.551599533260813,-0.617800855762348,-0.991389847235408,-0.311169353699879,1.46817697209427,-0.470400525259478,0.207971241929242,0.0257905801985591,0.403992960255733,0.251412098239705,-0.018306777944153,0.277837575558899,-0.110473910188767,0.0669280749146731,0.128539358273528,-0.189114843888824,0.133558376740387,-0.0210530534538215,149.62,"0" 0,1.19185711131486,0.26615071205963,0.16648011335321,0.448154078460911,0.0600176492822243,-0.0823608088155687,-0.0788029833323113,0.0851016549148104,-0.255425128109186,-0.166974414004614,1.61272666105479,1.06523531137287,0.48909501589608,-0.143772296441519,0.635558093258208,0.463917041022171,-0.114804663102346,-0.183361270123994,-0.145783041325259,-0.0690831352230203,-0.225775248033138,-0.638671952771851,0.101288021253234,-0.339846475529127,0.167170404418143,0.125894532368176,-0.00898309914322813,0.0147241691924927,2.69,"0" 1,-1.35835406159823,-1.34016307473609,1.77320934263119,0.379779593034328,-0.503198133318193,1.80049938079263,0.791460956450422,0.247675786588991,-1.51465432260583,0.207642865216696,0.624501459424895,0.066083685268831,0.717292731410831,-0.165945922763554,2.34586494901581,-2.89008319444231,1.10996937869599,-0.121359313195888,-2.26185709530414,0.524979725224404,0.247998153469754,0.771679401917229,0.909412262347719,-0.689280956490685,-0.327641833735251,-0.139096571514147,-0.0553527940384261,-0.0597518405929204,378.66,"0" 1,-0.966271711572087,-0.185226008082898,1.79299333957872,-0.863291275036453,-0.0103088796030823,1.24720316752486,0.23760893977178,0.377435874652262,-1.38702406270197,-0.0549519224713749,-0.226487263835401,0.178228225877303,0.507756869957169,-0.28792374549456,-0.631418117709045,-1.0596472454325,-0.684092786345479,1.96577500349538,-1.2326219700892,-0.208037781160366,-0.108300452035545,0.00527359678253453,-0.190320518742841,-1.17557533186321,0.647376034602038,-0.221928844458407,0.0627228487293033,0.0614576285006353,123.5,"0" 2,-1.15823309349523,0.877736754848451,1.548717846511,0.403033933955121,-0.407193377311653,0.0959214624684256,0.592940745385545,-0.270532677192282,0.817739308235294,0.753074431976354,-0.822842877946363,0.53819555014995,1.3458515932154,-1.11966983471731,0.175121130008994,-0.451449182813529,-0.237033239362776,-0.0381947870352842,0.803486924960175,0.408542360392758,-0.00943069713232919,0.79827849458971,-0.137458079619063,0.141266983824769,-0.206009587619756,0.502292224181569,0.219422229513348,0.215153147499206,69.99,"0" ... |
请注意,此版本的数据集已删除标题行。如果您从Kaggle下载数据集,则必须先删除标题行。
我们可以看到第一列是时间,这是一个整数,倒数第二列是购买金额。最后一列包含类别标签。我们可以看到PCA转换后的特征是正数和负数,并且包含很多浮点精度。
时间列可能没有用,可能可以删除。PCA变量与美元金额之间的尺度差异表明,数据缩放应该用于对输入变量尺度敏感的算法。
可以使用Pandas的read_csv()函数将数据集加载为DataFrame,指定位置和列名,因为没有标题行。
|
1 2 3 4 5 |
... # 定义数据集位置 filename = 'creditcard.csv' # 将csv文件加载为数据框 dataframe = read_csv(filename, header=None) |
加载后,我们可以通过打印DataFrame的形状来总结行数和列数。
|
1 2 3 |
... # 总结数据集的形状 print(dataframe.shape) |
我们还可以使用Counter对象总结每个类别的示例数量。
|
1 2 3 4 5 6 7 |
... # 总结类别分布 target = dataframe.values[:,-1] counter = Counter(target) for k,v in counter.items(): per = v / len(target) * 100 print('Class=%d, Count=%d, Percentage=%.3f%%' % (k, v, per)) |
总而言之,下面列出了加载和汇总数据集的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
# 加载并汇总数据集 from pandas import read_csv from collections import Counter # 定义数据集位置 filename = 'creditcard.csv' # 将csv文件加载为数据框 dataframe = read_csv(filename, header=None) # 总结数据集的形状 print(dataframe.shape) # 总结类别分布 target = dataframe.values[:,-1] counter = Counter(target) for k,v in counter.items(): per = v / len(target) * 100 print('Class=%d, Count=%d, Percentage=%.3f%%' % (k, v, per)) |
运行示例首先加载数据集并确认行数和列数,即284,807行和30个输入变量,1个目标变量。
然后对类别分布进行汇总,确认类别分布的严重倾斜,其中约99.827%的交易被标记为正常,约0.173%被标记为欺诈。这通常与论文中数据集的描述相符。
|
1 2 3 |
(284807, 31) Class=0, Count=284315, Percentage=99.827% Class=1, Count=492, Percentage=0.173% |
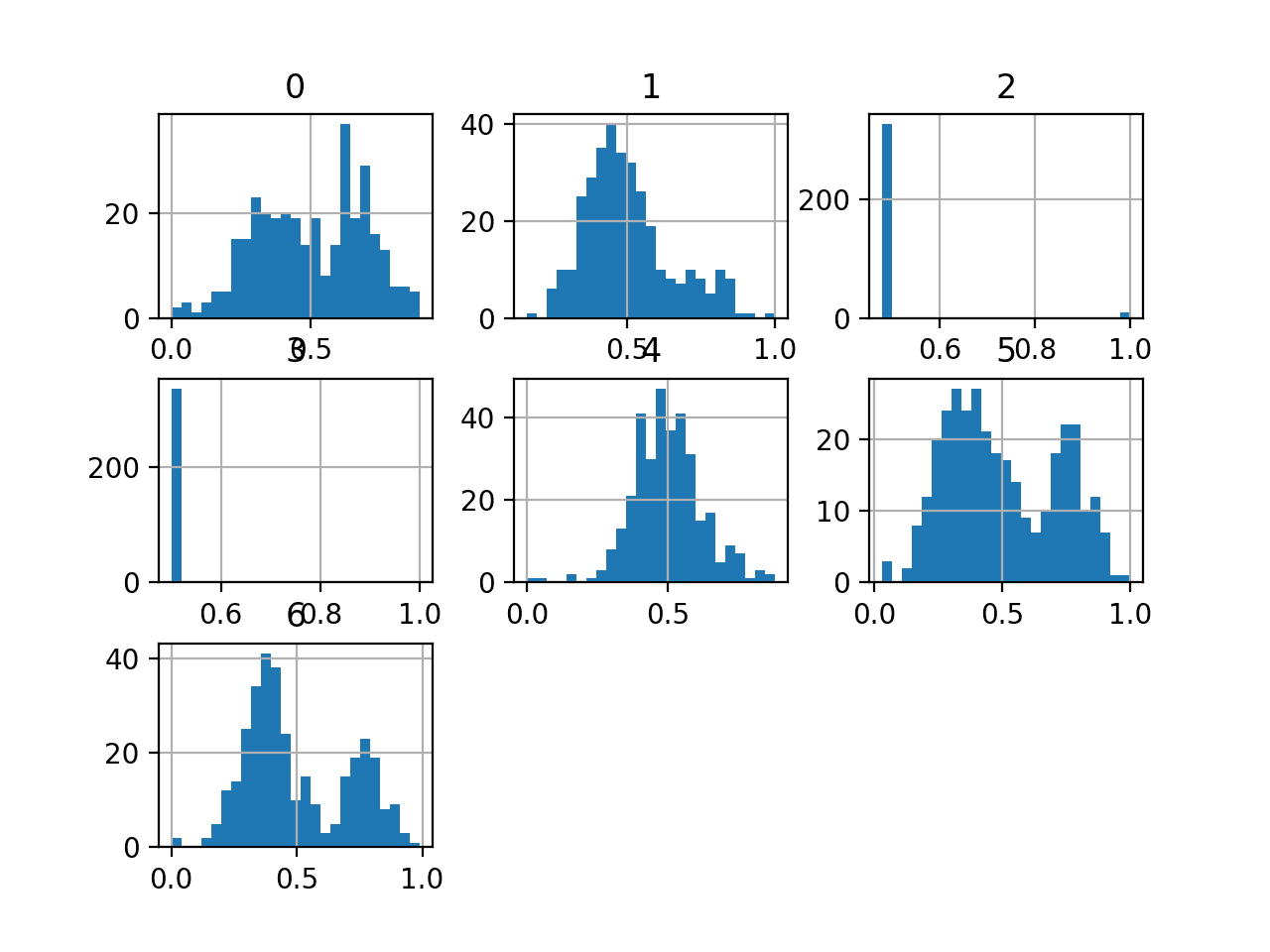
我们还可以通过为每个变量创建直方图来查看输入变量的分布。
由于变量数量众多,绘图可能会显得杂乱。因此,我们将禁用轴标签,以便我们专注于直方图。我们还将增加每个直方图中使用的箱数,以帮助更好地查看数据分布。
创建所有输入变量直方图的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# create histograms of input variables from pandas import read_csv from matplotlib import pyplot # 定义数据集位置 filename = 'creditcard.csv' # 将csv文件加载为数据框 df = read_csv(filename, header=None) # drop the target variable df = df.drop(30, axis=1) # 为每个数值变量创建直方图 ax = df.hist(bins=100) # disable axis labels to avoid the clutter for axis in ax.flatten(): axis.set_xticklabels([]) axis.set_yticklabels([]) # 显示绘图 pyplot.show() |
我们可以看到,大多数PCA分量的分布是高斯分布,并且许多可能以零为中心,这表明变量在PCA转换过程中已进行标准化。
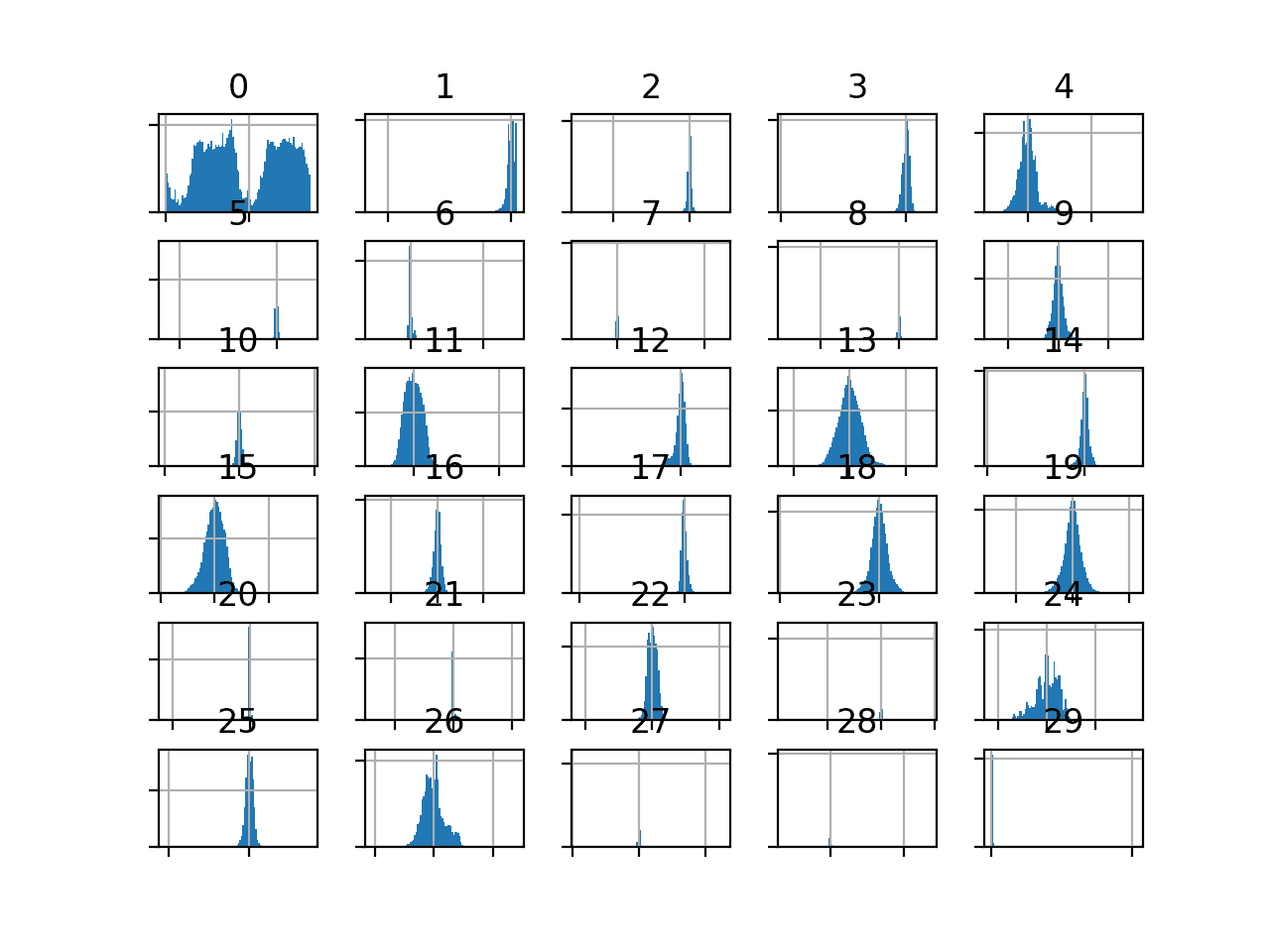
信用卡欺诈数据集输入变量的直方图
金额变量可能很有趣,并且没有出现在直方图中。
这表明金额值的分布可能偏斜。我们可以创建此变量的5数汇总,以更好地了解交易规模。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 |
# summarize the amount variable from pandas import read_csv # 定义数据集位置 filename = 'creditcard.csv' # 将csv文件加载为数据框 df = read_csv(filename, header=None) # summarize the amount variable. print(df[29].describe()) |
运行示例,我们可以看到大多数金额都很小,平均值为88左右,中间50%的观测值在5到77之间。
最大值为25,691左右,这会拉高分布,并且可能是异常值(例如,有人在信用卡上购买了汽车)。
|
1 2 3 4 5 6 7 8 9 |
count 284807.000000 mean 88.349619 std 250.120109 min 0.000000 25% 5.600000 50% 22.000000 75% 77.165000 max 25691.160000 Name: 29, dtype: float64 |
现在我们已经审阅了数据集,接下来我们将开发一个测试工具来评估候选模型。
模型测试和基线结果
我们将使用重复分层 k 折交叉验证来评估候选模型。
k折交叉验证过程提供了对模型性能的良好一般估计,该估计不太可能过于乐观地偏倚,至少与单次训练-测试分割相比是如此。我们将使用k=10,这意味着每个折叠将包含大约284807/10或28,480个示例。
分层意味着每个折叠将包含相同的示例混合,即约99.8%到0.2%的正常交易和欺诈交易。重复意味着将执行多次评估过程,以帮助避免偶然结果并更好地捕捉所选模型的方差。我们将使用3次重复。
这意味着一个模型将被拟合和评估10 * 3或30次,并将报告这些运行的均值和标准差。
这可以通过使用RepeatedStratifiedKFold scikit-learn 类来实现。
我们将使用推荐的指标,即精确率-召回率曲线下面积或PR AUC。
这要求给定算法首先预测概率或类似概率的度量。然后,使用不同阈值下的精确率和召回率来评估预测的精确率-召回率曲线,这些阈值用于将概率映射到类别标签,并将这些曲线下的面积报告为模型的性能。
此指标侧重于积极类别,这对于如此严重的类别不平衡是有益的。它还允许最终模型的运算符选择一个阈值,用于将概率映射到类别标签(欺诈或非欺诈交易),该阈值可以最好地平衡最终模型的精确率和召回率。
我们可以定义一个函数来加载数据集并将列分割成输入和输出变量。下面的load_dataset()函数实现了这一点。
|
1 2 3 4 5 6 7 8 9 |
# 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] return X, y |
然后,我们可以定义一个函数来计算给定预测集上的精确率-召回率曲线下面积。
这涉及到首先通过precision_recall_curve()函数计算精确率-召回率曲线。然后,可以将每个阈值的输出召回率和精确率值作为参数传递给auc()以计算曲线下面积。下面的pr_auc()函数实现了这一点。
|
1 2 3 4 5 6 |
# calculate precision-recall area under curve def pr_auc(y_true, probas_pred): # calculate precision-recall curve p, r, _ = precision_recall_curve(y_true, probas_pred) # calculate area under curve return auc(r, p) |
然后,我们可以定义一个函数来评估给定数据集上的模型,并返回每个折叠和重复的PR AUC分数列表。
下面的evaluate_model()函数实现了这一点,它以数据集和模型作为参数,并返回分数列表。使用make_scorer()函数来定义精确率-召回率AUC指标,并指示模型必须预测概率才能进行评估。
|
1 2 3 4 5 6 7 8 9 |
# 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(pr_auc, needs_proba=True) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) return scores |
最后,我们可以使用这个测试工具评估数据集上的基线模型。
预测所有样本的积极类别(类别1)的模型将提供精确率-召回率曲线下面积指标的基线性能。
这可以通过scikit-learn库中的DummyClassifier类来实现,并将“strategy”参数设置为‘constant’,并将“constant”参数设置为‘1’来预测积极类别。
|
1 2 3 |
... # 定义参考模型 model = DummyClassifier(strategy='constant', constant=1) |
模型评估完成后,我们可以直接报告PR AUC分数的平均值和标准差。
|
1 2 3 4 5 |
... # 评估模型 scores = evaluate_model(X, y, model) # 总结性能 print('Mean PR AUC: %.3f (%.3f)' % (mean(scores), std(scores))) |
总而言之,加载数据集、评估基线模型和报告性能的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
# test harness and baseline model evaluation for the credit dataset from collections import Counter from numpy import mean from numpy import std from pandas import read_csv from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import precision_recall_curve from sklearn.metrics import auc from sklearn.metrics import make_scorer from sklearn.dummy import DummyClassifier # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] 返回 X, y # calculate precision-recall area under curve def pr_auc(y_true, probas_pred): # calculate precision-recall curve p, r, _ = precision_recall_curve(y_true, probas_pred) # calculate area under curve return auc(r, p) # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(pr_auc, needs_proba=True) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义数据集位置 full_path = 'creditcard.csv' # 加载数据集 X, y = load_dataset(full_path) # 总结已加载的数据集 print(X.shape, y.shape, Counter(y)) # 定义参考模型 model = DummyClassifier(strategy='constant', constant=1) # 评估模型 scores = evaluate_model(X, y, model) # 总结性能 print('Mean PR AUC: %.3f (%.3f)' % (mean(scores), std(scores))) |
运行示例首先加载并总结数据集。
我们可以看到加载的行数正确,并且有30个输入变量。
接下来,报告PR AUC分数的平均值。
在这种情况下,我们可以看到基线算法的平均PR AUC约为0.501。
该分数提供了模型技能的下限;任何平均PR AUC高于0.5的模型都具有技能,而分数低于此值的模型在此数据集上不具有技能。
|
1 2 |
(284807, 30) (284807,) Counter({0.0: 284315, 1.0: 492}) Mean PR AUC: 0.501 (0.000) |
现在我们有了测试工具和性能基线,我们可以开始评估该数据集上的一些模型。
评估模型
在本节中,我们将使用上一节中开发的测试工具,评估数据集上的一系列不同技术。
目标是演示如何系统地解决问题,并展示一些针对不平衡分类问题设计的技术的能力。
报告的性能良好,但未进行高度优化(例如,未调整超参数)。
你能做得更好吗?如果你能使用相同的测试方法取得更好的PR AUC性能,我很想听听。请在下面的评论中告诉我。
评估机器学习算法
让我们开始在数据集上评估一系列机器学习模型。
最好在数据集上对一系列不同的非线性算法进行抽样检查,以便快速了解哪些效果好且值得进一步关注,哪些效果不好。
我们将对信用卡欺诈数据集评估以下机器学习模型:
- 决策树(CART)
- k-近邻(KNN)
- 装袋决策树(BAG)
- 随机森林 (RF)
- 极端随机树(ET)
我们将使用大多数默认模型超参数,除了集成算法中的树数量,我们将将其设置为合理的默认值100。我们还将在将输入变量提供给KNN算法之前对其进行标准化。
我们将依次定义每个模型并将它们添加到一个列表中,以便我们可以按顺序评估它们。下面的 get_models() 函数定义了要评估的模型列表,以及用于稍后绘制结果的模型简称列表。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 定义要测试的模型 定义 获取_模型(): models, names = list(), list() # CART models.append(DecisionTreeClassifier()) names.append('CART') # KNN steps = [('s',StandardScaler()),('m',KNeighborsClassifier())] models.append(Pipeline(steps=steps)) names.append('KNN') # Bagging models.append(BaggingClassifier(n_estimators=100)) names.append('BAG') # RF models.append(RandomForestClassifier(n_estimators=100)) names.append('RF') # ET models.append(ExtraTreesClassifier(n_estimators=100)) names.append('ET') return models, names |
然后我们可以依次枚举模型列表并评估每个模型,存储分数以供后续评估。
|
1 2 3 4 5 6 7 8 9 10 11 |
... # 定义模型 models, names = get_models() results = list() # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结性能 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) |
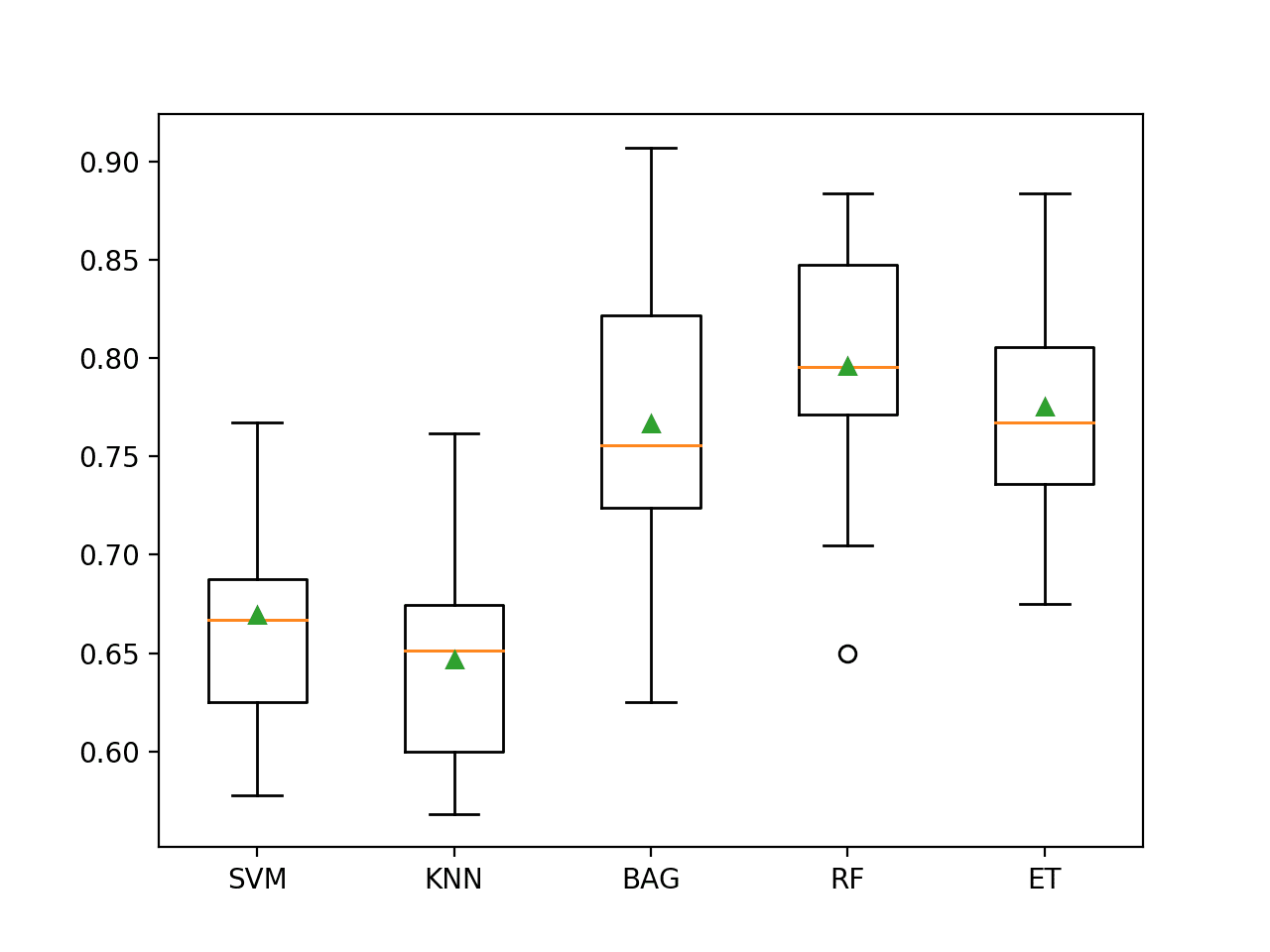
在运行结束时,我们可以将每个样本的分数绘制成箱须图,并具有相同的比例,以便直接比较其分布。
|
1 2 3 4 |
... # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
总而言之,在信用卡欺诈数据集上评估一系列机器学习算法的完整示例列在下面。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
# spot check machine learning algorithms on the credit card fraud dataset from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.preprocessing import StandardScaler from sklearn.pipeline import Pipeline from sklearn.model_selection import cross_val_score from sklearn.model_selection import RepeatedStratifiedKFold from sklearn.metrics import precision_recall_curve from sklearn.metrics import auc from sklearn.metrics import make_scorer from sklearn.tree import DecisionTreeClassifier from sklearn.neighbors import KNeighborsClassifier from sklearn.ensemble import RandomForestClassifier from sklearn.ensemble import ExtraTreesClassifier from sklearn.ensemble import BaggingClassifier # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] 返回 X, y # calculate precision-recall area under curve def pr_auc(y_true, probas_pred): # calculate precision-recall curve p, r, _ = precision_recall_curve(y_true, probas_pred) # calculate area under curve return auc(r, p) # 评估模型 def evaluate_model(X, y, model): # 定义评估过程 cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1) # 定义模型评估指标 metric = make_scorer(pr_auc, needs_proba=True) # 评估模型 scores = cross_val_score(model, X, y, scoring=metric, cv=cv, n_jobs=-1) 返回 分数 # 定义要测试的模型 定义 获取_模型(): models, names = list(), list() # CART models.append(DecisionTreeClassifier()) names.append('CART') # KNN steps = [('s',StandardScaler()),('m',KNeighborsClassifier())] models.append(Pipeline(steps=steps)) names.append('KNN') # Bagging models.append(BaggingClassifier(n_estimators=100)) names.append('BAG') # RF models.append(RandomForestClassifier(n_estimators=100)) names.append('RF') # ET models.append(ExtraTreesClassifier(n_estimators=100)) names.append('ET') return models, names # 定义数据集位置 full_path = 'creditcard.csv' # 加载数据集 X, y = load_dataset(full_path) # 定义模型 models, names = get_models() results = list() # 评估每个模型 for i in range(len(models)): # 评估模型并存储结果 scores = evaluate_model(X, y, models[i]) results.append(scores) # 总结性能 print('>%s %.3f (%.3f)' % (names[i], mean(scores), std(scores))) # 绘制结果图 pyplot.boxplot(results, labels=names, showmeans=True) pyplot.show() |
运行示例将依次评估每个算法,并报告平均和标准差PR AUC。
注意:鉴于算法或评估过程的随机性,或者数值精度的差异,您的结果可能会有所不同。请考虑运行示例几次,并比较平均结果。
在这种情况下,我们可以看到所有测试过的算法都有技能,PR AUC高于默认值0.5。结果表明,决策树算法的集成在数据集上都表现良好,尽管经过标准化处理的KNN似乎平均表现最好。
|
1 2 3 4 5 |
>CART 0.771 (0.049) >KNN 0.867 (0.033) >BAG 0.846 (0.045) >RF 0.855 (0.046) >ET 0.864 (0.040) |
创建了一个图,显示每个算法样本结果的箱须图。箱子显示了数据的中间50%,每个箱子中间的橙色线显示了样本的中位数,每个箱子中的绿色三角形显示了样本的平均值。
我们可以看到,KNN和决策树集成的分数分布紧密,并且平均值似乎与中位数一致,这表明分布可能是对称的,并且可能是高斯分布,并且分数可能相当稳定。
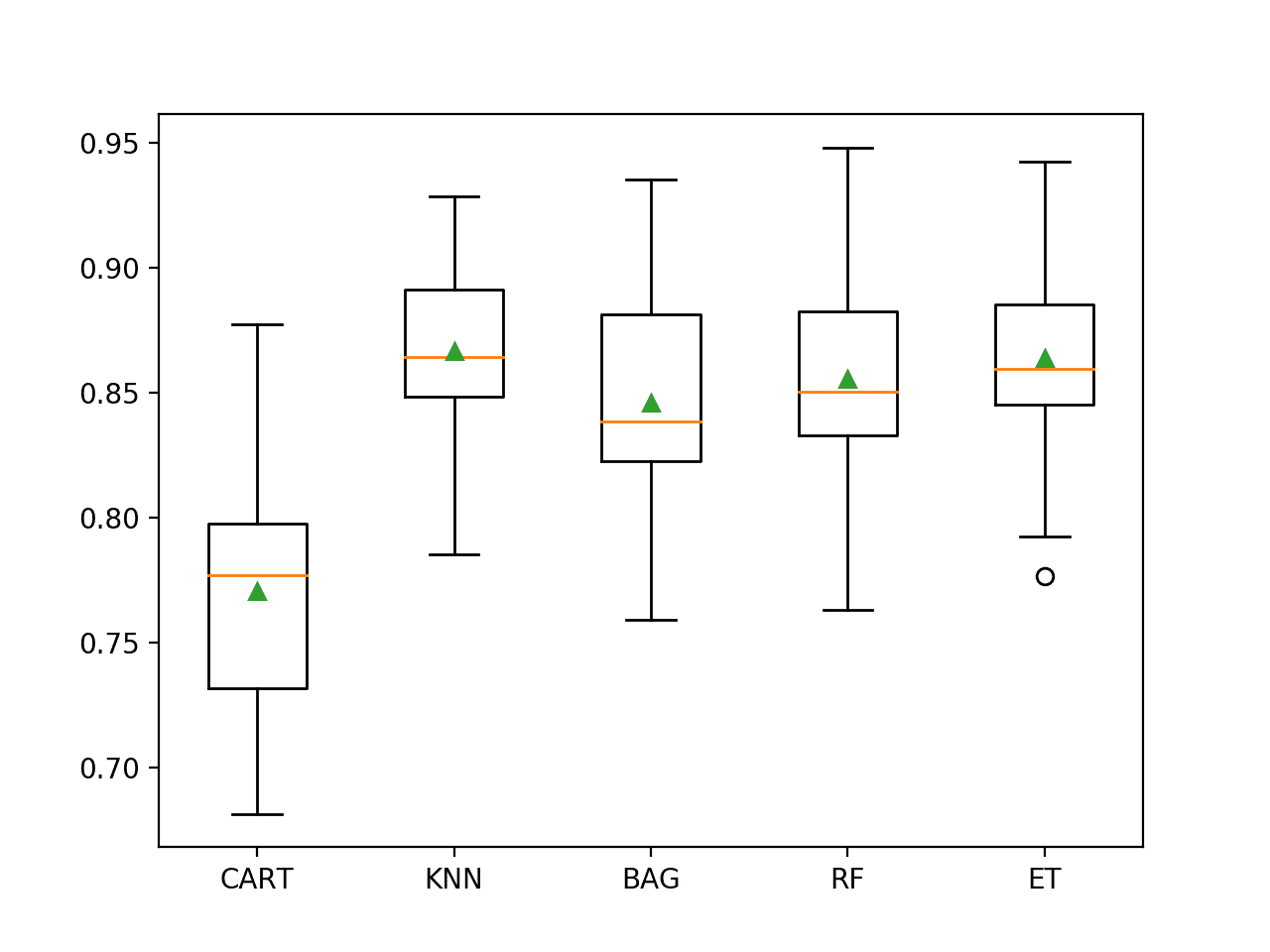
不平衡信用卡欺诈数据集上机器学习模型的箱须图
现在我们已经了解了如何在此数据集上评估模型,接下来看看如何使用最终模型进行预测。
对新数据进行预测
在本节中,我们可以拟合最终模型并使用它来预测单行数据。
我们将使用KNN模型作为我们的最终模型,该模型实现了约0.867的PR AUC。拟合最终模型涉及定义一个Pipeline,在拟合模型之前对数值变量进行缩放。
然后,可以使用Pipeline直接对新数据进行预测,并且它将自动使用与训练数据集上执行的相同操作来缩放新数据。
首先,我们可以将模型定义为管道。
|
1 2 3 4 5 |
... # 定义要评估的模型 model = KNeighborsClassifier() # scale, then fit model pipeline = Pipeline(steps=[('s',StandardScaler()), ('m',model)]) |
定义好后,我们就可以在整个训练数据集上对其进行拟合。
|
1 2 3 |
... # 拟合模型 pipeline.fit(X, y) |
拟合后,我们可以通过调用predict_proba()函数来使用它对新数据进行预测。这将返回每个类别的概率。
我们可以检索积极类别的预测概率,模型运算符可以使用该概率来解释预测。
例如
|
1 2 3 4 5 6 |
... # 定义一行数据 row = [...] yhat = pipeline.predict_proba([row]) # get the probability for the positive class result = yhat[0][1] |
为了演示这一点,我们可以使用已训练好的模型来预测一些已知结果的案例的标签。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
# fit a model and make predictions for the on the credit card fraud dataset from pandas import read_csv from sklearn.preprocessing import StandardScaler from sklearn.neighbors import KNeighborsClassifier from sklearn.pipeline import Pipeline # 加载数据集 def load_dataset(full_path): # 将数据集加载为numpy数组 data = read_csv(full_path, header=None) # 检索numpy数组 data = data.values # 分割为输入和输出元素 X, y = data[:, :-1], data[:, -1] 返回 X, y # 定义数据集位置 full_path = 'creditcard.csv' # 加载数据集 X, y = load_dataset(full_path) # 定义要评估的模型 model = KNeighborsClassifier() # scale, then fit model pipeline = Pipeline(steps=[('s',StandardScaler()), ('m',model)]) # 拟合模型 pipeline.fit(X, y) # evaluate on some normal cases (known class 0) print('Normal cases:') data = [[0,-1.3598071336738,-0.0727811733098497,2.53634673796914,1.37815522427443,-0.338320769942518,0.462387777762292,0.239598554061257,0.0986979012610507,0.363786969611213,0.0907941719789316,-0.551599533260813,-0.617800855762348,-0.991389847235408,-0.311169353699879,1.46817697209427,-0.470400525259478,0.207971241929242,0.0257905801985591,0.403992960255733,0.251412098239705,-0.018306777944153,0.277837575558899,-0.110473910188767,0.0669280749146731,0.128539358273528,-0.189114843888824,0.133558376740387,-0.0210530534538215,149.62], [0,1.19185711131486,0.26615071205963,0.16648011335321,0.448154078460911,0.0600176492822243,-0.0823608088155687,-0.0788029833323113,0.0851016549148104,-0.255425128109186,-0.166974414004614,1.61272666105479,1.06523531137287,0.48909501589608,-0.143772296441519,0.635558093258208,0.463917041022171,-0.114804663102346,-0.183361270123994,-0.145783041325259,-0.0690831352230203,-0.225775248033138,-0.638671952771851,0.101288021253234,-0.339846475529127,0.167170404418143,0.125894532368176,-0.00898309914322813,0.0147241691924927,2.69], [1,-1.35835406159823,-1.34016307473609,1.77320934263119,0.379779593034328,-0.503198133318193,1.80049938079263,0.791460956450422,0.247675786588991,-1.51465432260583,0.207642865216696,0.624501459424895,0.066083685268831,0.717292731410831,-0.165945922763554,2.34586494901581,-2.89008319444231,1.10996937869599,-0.121359313195888,-2.26185709530414,0.524979725224404,0.247998153469754,0.771679401917229,0.909412262347719,-0.689280956490685,-0.327641833735251,-0.139096571514147,-0.0553527940384261,-0.0597518405929204,378.66]] for row in data: # 进行预测 yhat = pipeline.predict_proba([row]) # get the probability for the positive class result = yhat[0][1] # 总结 print('>Predicted=%.3f (expected 0)' % (result)) # evaluate on some fraud cases (known class 1) print('Fraud cases:') data = [[406,-2.3122265423263,1.95199201064158,-1.60985073229769,3.9979055875468,-0.522187864667764,-1.42654531920595,-2.53738730624579,1.39165724829804,-2.77008927719433,-2.77227214465915,3.20203320709635,-2.89990738849473,-0.595221881324605,-4.28925378244217,0.389724120274487,-1.14074717980657,-2.83005567450437,-0.0168224681808257,0.416955705037907,0.126910559061474,0.517232370861764,-0.0350493686052974,-0.465211076182388,0.320198198514526,0.0445191674731724,0.177839798284401,0.261145002567677,-0.143275874698919,0], [7519,1.23423504613468,3.0197404207034,-4.30459688479665,4.73279513041887,3.62420083055386,-1.35774566315358,1.71344498787235,-0.496358487073991,-1.28285782036322,-2.44746925511151,2.10134386504854,-4.6096283906446,1.46437762476188,-6.07933719308005,-0.339237372732577,2.58185095378146,6.73938438478335,3.04249317830411,-2.72185312222835,0.00906083639534526,-0.37906830709218,-0.704181032215427,-0.656804756348389,-1.63265295692929,1.48890144838237,0.566797273468934,-0.0100162234965625,0.146792734916988,1], [7526,0.00843036489558254,4.13783683497998,-6.24069657194744,6.6757321631344,0.768307024571449,-3.35305954788994,-1.63173467271809,0.15461244822474,-2.79589246446281,-6.18789062970647,5.66439470857116,-9.85448482287037,-0.306166658250084,-10.6911962118171,-0.638498192673322,-2.04197379107768,-1.12905587703585,0.116452521226364,-1.93466573889727,0.488378221134715,0.36451420978479,-0.608057133838703,-0.539527941820093,0.128939982991813,1.48848121006868,0.50796267782385,0.735821636119662,0.513573740679437,1]] for row in data: # 进行预测 yhat = pipeline.predict_proba([row]) # get the probability for the positive class result = yhat[0][1] # 总结 print('>Predicted=%.3f (expected 1)' % (result)) |
首先运行示例,在整个训练数据集上拟合模型。
然后使用拟合模型来预测数据集中选择的正常案例的标签。我们可以看到所有案例都得到了正确预测。
然后将一些欺诈案例作为输入提供给模型并预测标签。正如我们所希望的,大多数示例都通过默认阈值得到了正确预测。这突显了模型用户需要选择一个合适的概率阈值。
正常案例
|
1 2 3 4 5 6 7 |
>Predicted=0.000 (expected 0) >Predicted=0.000 (expected 0) >Predicted=0.000 (expected 0) 欺诈案例 >Predicted=1.000 (expected 1) >Predicted=0.400 (expected 1) >Predicted=1.000 (expected 1) |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 针对不平衡分类校准概率与欠采样, 2015.
API
- pandas.read_csv API.
- sklearn.metrics.precision_recall_curve API.
- sklearn.metrics.auc API.
- sklearn.metrics.make_scorer API.
- sklearn.dummy.DummyClassifier API.
数据集 (Dataset)
总结
在本教程中,您了解了如何为不平衡的信用卡欺诈分类数据集开发和评估模型。
具体来说,你学到了:
- 如何加载和探索数据集,并为数据准备和模型选择提供思路。
- 如何使用稳健的测试框架系统地评估一套机器学习模型。
- 如何拟合最终模型并使用它来预测特定案例的欺诈概率。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。



Jason,一如既往地,这篇文章写得非常好。您不认为如果您的模型使用了 class_weights,结果会更好吗?
谢谢。
试试看,看看是否能获得更好的结果。
Jason,这个教程非常有帮助!请帮助我将 pr_auc 和 evaluate_model 函数改编为多类别(少数类别)分类的情况。
感谢您的建议。
非常棒,谢谢!
谢谢!
Jason
虽然我的 SKFold PR AUC 分数通常与您的相似:KNN 0.869 (0.042),ET 0.862 (0.043),RF(带平衡类别权重)0.858 (0.046),但当 RF 和 ET 在 80/20 的数据集拆分上进行训练/测试时,它们都优于 KNN。RF 达到了 0.845 的 PR AUC 分数和 0.75 的欺诈类别召回率(精度为 0.94);ET 达到了 0.838 的 PR AUC 分数,也达到了 0.75 的召回率(精度为 0.93)。相比之下,KNN 的 PR AUC 分数为 0.807,召回率为 0.69(精度为 0.92)。让我惊讶的是,这三种模型在此数据集上的表现基本相当。
干得好!
谢谢。
另一个不错的可用数据集是 Databricks 汽车保险索赔欺诈检测集:https://databricks-prod-cloudfront.cloud.databricks.com/public/4027ec902e239c93eaaa8714f173bcfc/4954928053318020/1058911316420443/167703932442645/latest.html
使用 LR、ET 或 RF 结合 SMOTEENN 可以实现高于 0.950 的召回率。Ron
感谢分享。
Jason,您在这里似乎没有使用您在之前帖子中讨论过的成本敏感算法。有什么不在这里使用的想法或策略吗?
是的,我使用了一个合适的指标,然后我无法在该指标下获得比使用标准模型更好的性能。
如果您能在相同的测试环境中做得更好,请分享您的结果。
Jason,好文章!
我很难理解 DummyClassifier 如何能带来 0.501 的 PR AUC。它应该具有 100% 的固定召回率和 0.2% 的精度,无论阈值如何。我是否遗漏了什么?
谢谢
这可能有帮助
https://machinelearning.org.cn/naive-classifiers-imbalanced-classification-metrics/
有关此主题的更多研究工作,请参阅 https://www.researchgate.net/project/Fraud-detection-with-machine-learning
感谢分享。
感谢 Jason 提供如此简洁而又解释得很好的帖子。我想问一个问题,为什么在数据倾斜且欺诈交易非常少的情况下,没有进行欠采样或过采样?谢谢!!
不客气。
在此问题上没有帮助。
我的结果比算法简单得多。
SVM:99.93504441557529
随机森林:99.96137776061234
决策树:99.92275552122467
KNN:99.95611109160492
逻辑回归:99.91748885221726
梯度增强分类器:99.77177767634564
哇,你使用了和上面一样的评估程序吗?
我也是...
我在数据集上以 100% 的数据进行训练,并在相同的数据上进行测试,获得了 99% 以上的准确率。但是,当我尝试将 50% 的数据用于训练,50% 用于测试时,结果却非常糟糕。
也许应该使用重复的 k 折交叉验证来估计模型性能,而不是简单的训练/测试拆分。
嗨,Jason,
您能否针对没有先前标签的数据集进行异常检测的博客文章?另外,如果您有资源,请指向流式异常检测实现。非常感谢。
是的,这些算法可以在没有标签的情况下使用
https://machinelearning.org.cn/model-based-outlier-detection-and-removal-in-python/
Jason,感谢您的发布!
快速提问 – 为什么我们要使用“constant”策略,而对于 PR-AUC 指标,它应该是“stratified”?我是否遗漏了什么?
我想您在您的一篇文章中提到过这一点
“预测一个常量值,如多数类或少数类,将导致无效的 PR 曲线(例如,一个点),进而导致无效的 PR AUC 分数。应忽略预测常量值的模型的得分。”
谢谢
也许我写这篇教程之前写了那篇教程
https://machinelearning.org.cn/naive-classifiers-imbalanced-classification-metrics/
好的,感谢您的回复!那么,正确的采样策略应该是分层的,对吗?
总的来说,是的。
Jason,好文章!
我从您那里学到了很多!非常有用的文章。
有一个问题,我认为当您对无标签数据集进行预测时,假阳性的数量会非常多,我没有看到您提到这一点。
我这样说是因为我正在做一个垃圾电话预测项目,我的数据集与您的相似。
谢谢!
也许您需要一个替代的数据准备/模型/模型配置?
也许您用于评估模型的测试环境不可靠?例如,尝试重复分层 10 折交叉验证?
Jason,干得好!我是该数据集在 Kaggle 上发布的这个研究团队的成员。对于验证部分,我们认为一种更好的方法是顺序验证,因为用于测试的交易应该发生在用于训练的交易之后 – https://fraud-detection-handbook.github.io/fraud-detection-handbook/Chapter_5_ModelValidationAndSelection/ValidationStrategies.html。您可能还对使用我们在此处提出的模拟数据集感兴趣 https://fraud-detection-handbook.github.io/fraud-detection-handbook/Chapter_3_GettingStarted/SimulatedDataset.html,它比 Kaggle 数据集更大,更易于解释。
感谢分享。
你好 Jason,
非常有信息量的帖子!在文章的结尾,您提到预测正类是由用户选择合适的概率阈值。我想知道是否有办法找到最佳阈值?还是更多的是试错法?
Robert……你确实提出了一个有趣的问题!我不知道有什么方法可以确定最佳阈值,但是你可以收集足够多的历史数据,并通过统计方法确定最可能的阈值。
你好,快速提问,为了编码这些信息,您使用了什么 IDE?Atom、Visual Studio Code、IDLE 等?
感谢您的时间和专业知识,
Grace
你好,快速提问,为了编码这些信息,您使用了什么 IDE?Atom、Visual Studio Code、IDLE 等?
感谢您的时间和专业知识,
Grace
Grace 你好……不推荐使用 IDE。对于所提供的示例,命令行就足够了。
你好。我们应该何时应用过采样或欠采样技术,何时继续处理不平衡数据集?非常感谢您在博客上分享的所有信息。