如何用 Python 从零开始实现决策树算法

决策树是一种强大的预测方法，并且非常受欢迎。

它们之所以受欢迎，是因为最终模型对于实践者和领域专家来说都非常容易理解。最终的决策树可以精确地解释为什么会做出某个特定的预测，这使得它在实际应用中极具吸引力。

决策树也为更高级的集成方法（如装袋法、随机森林和梯度提升）奠定了基础。

在本教程中，您将学习如何使用Python从零开始实现分类和回归树算法。

完成本教程后，您将了解：

• 如何计算和评估数据中的候选分割点。
• 如何将分割组织成决策树结构。
• 如何将分类和回归树算法应用于实际问题。

启动您的项目，阅读我的新书《从零开始的机器学习算法》，其中包含分步教程以及所有示例的Python源代码文件。

让我们开始吧。

• 更新于 2017 年 1 月：更改了 `cross_validation_split()` 中 `fold_size` 的计算，使其始终为整数。修复了 Python 3 的问题。
• 2017 年 2 月更新：修复了 build_tree 中的一个 bug。
• 2017 年 8 月更新：修复了 Gini 计算中的一个 bug，添加了按组大小对组 Gini 分数进行加权的功能（感谢 Michael！）。
• 2018 年 8 月更新：测试并更新以与 Python 3.6 配合使用。

如何用 Python 从零开始实现决策树算法
照片由 Martin Cathrae 拍摄，保留部分权利。

描述

本节简要介绍了分类和回归树算法以及本教程使用的纸币数据集。

分类与回归树

分类和回归树，简称 CART，是 Leo Breiman 提出的一个缩写，用于指代可用于分类或回归预测建模问题的决策树算法。

在本教程中，我们将专注于使用 CART 进行分类。

CART模型的表示是一个二叉树。这与算法和数据结构中的二叉树相同，没有什么特别之处（每个节点可以有零个、一个或两个子节点）。

节点代表一个输入变量（X）以及该变量上的一个分割点，假设该变量是数值型的。树的叶节点（也称为终端节点）包含一个输出变量（y），用于进行预测。

一旦创建，就可以使用新的数据行导航树，沿着每个分支直到做出最终预测。

创建二叉决策树实际上是一个分割输入空间的过程。一种被称为递归二分分割的贪婪方法用于分割空间。这是一个数值过程，所有值都被排列起来，并使用成本函数尝试和测试不同的分割点。

根据成本函数选择成本最低的分割点。所有输入变量和所有可能的分割点都被贪婪地评估和选择，基于成本函数。

• 回归：为了选择分割点而最小化的成本函数是落在矩形内的所有训练样本的总平方误差。
• 分类：使用 Gini 成本函数，它指示了节点的纯度，其中节点纯度是指分配到每个节点的训练数据混合程度。

分割持续进行，直到节点包含最少数量的训练样本或达到最大树深度。

纸币数据集

纸币数据集涉及根据从照片中获取的若干测量值来预测给定纸币是否是真实的。

该数据集包含 1,372 行，具有 5 个数值变量。这是一个二分类问题（二元分类）。

下面列出了数据集中五个变量的列表。

1. 小波变换图像的方差（连续）。
2. 小波变换图像的偏度（连续）。
3. 图像的峰度（连续）。
4. 图像的熵（连续）。
5. 类别（整数）。

下面是数据集中前 5 行的样本

使用零规则算法预测最常见的类别值，该问题的基线准确率为 50% 左右。

您可以从 UCI 机器学习库了解更多信息并下载该数据集。

下载数据集并将其保存在当前工作目录中，文件名为 data_banknote_authentication.csv。

教程

本教程分为 5 部分

1. Gini 指数。
2. 创建分割。
3. 构建树。
4. 进行预测。
5. 纸币案例研究。

这些步骤将为您提供从零开始实现 CART 算法并将其应用于您自己的预测建模问题的基础。

1. Gini 指数

Gini 指数是用于评估数据集中分割的成本函数的名称。

数据集中的分割涉及一个输入属性和一个该属性的值。它可用于将训练样本分成两组行。

Gini 分数通过分割创建的两组类别混合程度来表明分割的好坏。完美分离的结果是 Gini 分数为 0，而最差的分割结果是每组 50/50 类别，则 Gini 分数为 0.5（对于 2 类问题）。

通过示例可以最好地演示 Gini 的计算。

我们有两个数据组，每个组有 2 行。第一组中的行都属于类别 0，第二组中的行都属于类别 1，所以这是一个完美的分割。

我们首先需要计算每个组中类别的比例。

此示例的比例将是

然后，Gini 的计算方法如下：

然后，每个组的 Gini 指数必须按该组的大小相对于父节点中所有样本的比例进行加权，例如，当前正在分组的所有样本。我们可以按如下方式将此加权添加到组的 Gini 计算中：

在此示例中，每个组的 Gini 分数计算如下：

然后，这些分数按每个子节点在分割点处进行加总，以获得分割点的最终 Gini 分数，该分数可以与其他候选分割点进行比较。

此分割点的 Gini 将为 0.0 + 0.0，即完美的 Gini 分数 0.0。

下面是一个名为 gini_index() 的函数，它计算一组组和一组已知类别值的 Gini 指数。

您可以看到其中有一些安全检查，以避免空组的除以零错误。

我们可以用上面计算的例子来测试这个函数。我们也可以测试每个组中 50/50 分割的最坏情况。完整的示例如下所示。

运行示例将打印两个 Gini 分数，首先是最坏情况下的 0.5，然后是最佳情况下的 0.0。

现在我们知道如何评估分割结果了，让我们看看如何创建分割。

2. 创建分割

分割由数据中的一个属性和一个值组成。

我们可以将其概括为要分割的属性的索引以及用于分割该属性行的值。这只是对数据行进行索引的一种便捷的简写。

创建分割包括三个部分，第一个部分我们已经看过了，那就是计算 Gini 分数。其余两个部分是：

1. 分割数据集。
2. 评估所有分割。

让我们逐一查看。

2.1. 分割数据集

分割数据集意味着根据属性的索引和该属性的分割值，将数据集分成两行列表。

一旦我们有了这两组，我们就可以使用上面的 Gini 分数来评估分割的成本。

分割数据集包括遍历每一行，检查属性值是否小于或大于分割值，并分别将其分配到左组或右组。

下面是一个名为 test_split() 的函数，它实现了这个过程。

没什么特别的。

请注意，右组包含所有在索引处值大于或等于分割值的行。

2.2. 评估所有分割

有了上面的 Gini 函数和测试分割函数，我们现在拥有了评估分割所需的一切。

给定一个数据集，我们必须将属性上的每个值作为候选分割进行检查，评估分割的成本，并找到我们可以进行的最优分割。

一旦找到最佳分割，我们就可以将其作为决策树中的一个节点。

这是一个穷举的贪婪算法。

我们将使用字典来表示决策树中的节点，因为我们可以按名称存储数据。在选择最佳分割并将其用作树的新节点时，我们将存储所选属性的索引、用于分割该属性的值以及通过所选分割点分割的两组数据。

每组数据都是一个小的数据集，只包含通过分割过程分配到左组或右组的那些行。您可以想象我们如何递归地再次分割每个组，同时构建我们的决策树。

下面是一个名为 get_split() 的函数，它实现了这个过程。您可以看到它遍历每个属性（除类别值外），然后遍历该属性的每个值，在遍历过程中进行分割和评估。

最佳分割会被记录下来，并在所有检查完成后返回。

我们可以构造一个小型数据集来测试这个函数和我们整个数据集的分割过程。

我们可以使用每种类别的不同颜色来绘制此数据集。您可以看到，手动选择 X1 的值（图上的 x 轴）来分割此数据集并不难。

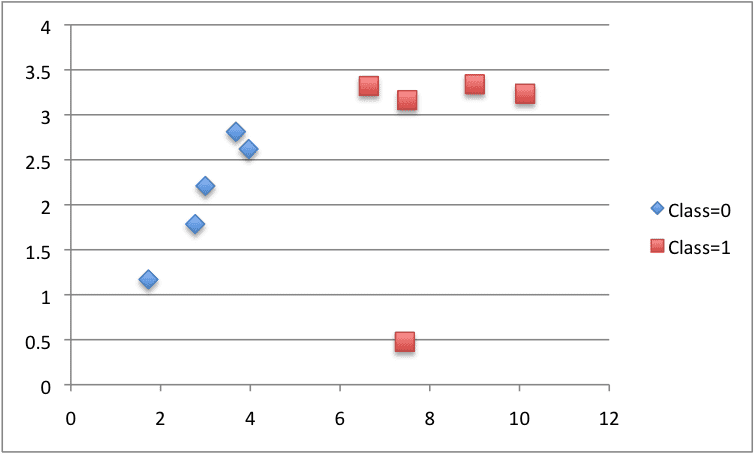
CART 构造的数据集

下面的示例将所有这些内容整合在一起。

get_split() 函数已被修改，可以在评估过程中打印每个分割点及其 Gini 指数。

运行示例将打印所有 Gini 分数，然后打印最佳分割分数，即 X1 < 6.642，Gini 指数为 0.0，即完美分割。

现在我们知道了如何在数据或行列表中找到最佳分割点，让我们看看如何使用它来构建决策树。

3. 构建树

创建树的根节点很简单。

我们使用上面的 get_split() 函数并传入整个数据集。

向树中添加更多节点更有趣。

构建树可能分为 3 个主要部分：

1. 终端节点。
2. 递归分割。
3. 构建树。

3.1. 终端节点

我们需要决定何时停止生长树。

我们可以通过树的深度和节点在训练数据集中负责的行数来做到这一点。

• 最大树深度。这是从树根节点开始的最大节点数。一旦达到树的最大深度，我们就必须停止分割并添加新节点。更深的树更复杂，并且更有可能过拟合训练数据。
• 最小节点记录数。这是给定节点负责的最少训练样本数。一旦达到或低于此最小值，我们就必须停止分割并添加新节点。负责的训练样本太少的节点预计会过于具体，并且很可能过拟合训练数据。

这两种方法将是我们的树构建过程的用户指定参数。

还有一种情况。有可能选择一个分割，其中所有行都属于一个组。在这种情况下，我们将无法继续分割和添加子节点，因为我们将在某一边或另一边没有记录可供分割。

现在我们对何时停止生长树有了一些想法。当我们停止在给定点生长时，该节点称为终端节点，并用于做出最终预测。

这是通过获取分配给该节点的行组并选择组中最常见的类别值来完成的。这将用于进行预测。

下面是一个名为 to_terminal() 的函数，它将为一组行选择一个类别值。它返回列表中行中最常见的输出值。

3.2. 递归分割

我们知道如何以及何时创建终端节点，现在我们可以构建我们的树。

构建决策树涉及反复调用上面开发的 get_split() 函数来处理为每个节点创建的组。

添加到现有节点的新节点称为子节点。一个节点可以有零个子节点（终端节点），一个子节点（一个分支直接进行预测）或两个子节点。在给定节点的字典表示中，我们将子节点称为左节点和右节点。

一旦创建了一个节点，我们就可以通过再次调用相同的函数来递归地在分割产生的每个数据组上创建子节点。

下面是一个实现此递归过程的函数。它将一个节点作为参数，以及最大深度、节点中的最小样本数和节点的当前深度。

您可以想象如何首次调用它，传入根节点和深度 1。这个函数最好分步解释：

1. 首先，提取节点分割的两个数据组以供使用，并从节点中删除。在我们处理这些组时，节点不再需要访问这些数据。
2. 接下来，我们检查左组或右组是否为空，如果是，我们使用我们拥有的记录来创建终端节点。
3. 然后我们检查是否已达到最大深度，如果是，我们创建终端节点。
4. 然后，我们处理左子节点，如果行组太小，则创建一个终端节点，否则，以深度优先的方式创建并添加左节点，直到达到该分支的树底。然后以相同的方式处理右侧，当我们重新上升到树的根节点时。
5. 然后在构建的树中，我们向上回溯到根节点。

3.3. 构建树

现在我们可以将所有部分组合在一起。

构建树的过程包括创建根节点并调用 split() 函数，然后该函数递归地调用自身来构建整棵树。

下面是实现此过程的小型 build_tree() 函数。

我们可以使用上面构造的小数据集来测试整个过程。

下面是完整的示例。

还包含一个小型 print_tree() 函数，该函数递归地打印决策树的节点，每个节点占一行。虽然它不像真正的决策树图那样醒目，但它能让我们了解树的结构和所做的决策。

我们可以通过改变 build_tree() 函数调用的第二个参数（最大深度）来测试此过程，并观察对打印树的影响。

当最大深度为 1 时，我们可以看到树使用了我们在上一节中发现的完美分割。这是一棵只有一个节点的树，也称为决策桩。

将最大深度增加到 2，我们会强制树进行分割，即使没有必要。根节点的左子节点和右子节点再次使用 X1 属性来分割已经完美混合的类别。

最后，也是反常地，我们可以强制再增加一个分割级别，最大深度为 3。

这些测试表明，有很大的空间来改进实现，以避免不必要的分割。这留作扩展。

既然我们已经能够创建决策树，让我们看看如何使用它来对新数据进行预测。

4. 进行预测

使用决策树进行预测涉及使用专门提供的行数据来导航树。

同样，我们可以使用递归函数来实现这一点，其中根据分割如何影响提供的数据，将相同的预测例程递归地调用到左子节点或右子节点。

我们必须检查子节点是应作为预测返回的终端值，还是包含要考虑的树的另一个级别的字典节点。

下面是实现此过程的 predict() 函数。您可以看到给定节点中的索引和值

您可以看到给定节点中的索引和值如何用于评估提供的数据行是落在分割的左侧还是右侧。

我们可以使用我们构造的数据集来测试此函数。下面是一个示例，该示例使用硬编码的决策树，其中包含一个最佳分割数据的节点（决策桩）。

该示例对数据集中每一行都进行预测。

运行示例，结果如预期，对每一行都打印了正确的预测。

现在我们知道了如何创建决策树以及如何使用它进行预测。接下来，让我们将其应用于实际数据集。

5. 纸币案例研究

本节将 CART 算法应用于纸币数据集。

第一步是加载数据集，并将加载的数据转换为我们可以用来计算分割点的数字。为此，我们将使用辅助函数 load_csv() 来加载文件，并使用 str_column_to_float() 将字符串数字转换为浮点数。

我们将使用 k 折交叉验证（k=5）来评估该算法。这意味着每折将使用 1372/5 = 274.4，即略多于 270 条记录。我们将使用辅助函数 evaluate_algorithm() 和 accuracy_metric() 来评估交叉验证算法并计算预测的准确性。

开发了一个名为 decision_tree() 的新函数来管理 CART 算法的应用，首先从训练数据集中创建树，然后使用该树对测试数据集进行预测。

完整的示例如下所示。

该示例使用 5 层最大树深度和每节点最小行数为 10。CART 的这些参数是通过一些实验选择的，但绝非最优。

运行示例将打印出每折的平均分类准确率以及所有折的平均性能。

您可以看到，CART 和所选配置实现了大约 97% 的平均分类准确率，这比仅获得 50% 准确率的零规则算法有了显著提高。

扩展

本节列出了本教程的扩展内容，您可能希望进行探索。

• 算法调优。CART 在纸币数据集上的应用尚未进行调优。尝试不同的参数值，看看是否可以获得更好的性能。
• 交叉熵。另一个用于评估分割的成本函数是交叉熵（对数损失）。您可以实现并尝试此替代成本函数。
• 树剪枝。减少训练数据集过拟合的重要技术是剪枝树。研究并实现树剪枝方法。
• 分类数据集。该示例专为具有数值或有序输入属性的输入数据而设计，尝试使用分类输入数据和可能使用相等性而不是排秩的分割。
• 回归。使用不同的成本函数和创建终端节点的方法来调整树以用于回归。
• 更多数据集。将算法应用于 UCI 机器学习存储库上的更多数据集。

您是否探索过这些扩展？
在下面的评论中分享您的经验。

回顾

在本教程中，您学习了如何从头开始使用 Python 实现决策树算法。

具体来说，你学到了：

• 如何选择和评估训练数据集中的分割点。
• 如何从多个分割递归地构建决策树。
• 如何将 CART 算法应用于现实世界的分类预测建模问题。

你有什么问题吗？
请在下方评论中提问，我将尽力回答。

了解如何从零开始编写算法！

没有库，只有 Python 代码。

...附带真实世界数据集的逐步教程

在我的新电子书中探索如何实现
从零开始实现机器学习算法

它涵盖了 18 个教程，包含 12 种顶级算法的所有代码，例如
线性回归、k-近邻、随机梯度下降等等……

最后，揭开
机器学习算法的神秘面纱

跳过学术理论。只看结果。

查看内容