如何在 Python 中从头实现线性回归

作者 Jason Brownlee 于 2019年8月13日分类于从零开始的代码算法 111

许多机器学习算法的核心是优化。

机器学习算法使用优化算法，在给定训练数据集的情况下，找到一组好的模型参数。

机器学习中最常用的优化算法是随机梯度下降。

在本教程中，您将学习如何从零开始使用Python实现随机梯度下降来优化线性回归算法。

完成本教程后，您将了解：

如何使用随机梯度下降估计线性回归系数。
如何对多元线性回归进行预测。
如何使用随机梯度下降实现线性回归，以对新数据进行预测。

快速启动您的项目，阅读我的新书《从零开始的机器学习算法》，其中包含分步教程以及所有示例的Python源代码文件。

让我们开始吧。

更新于 2017 年 1 月：更改了 `cross_validation_split()` 中 `fold_size` 的计算，使其始终为整数。修复了 Python 3 的问题。
2018 年 8 月更新：测试并更新以与 Python 3.6 配合使用。

How to Implement Linear Regression With Stochastic Gradient Descent From Scratch With Python

如何用Python从零开始实现带随机梯度下降的线性回归
照片由 star5112 提供，保留部分权利。

描述

在本节中，我们将介绍线性回归、随机梯度下降技术以及本教程中使用的葡萄酒质量数据集。

多元线性回归

线性回归是一种预测实值的技术。

令人困惑的是，这些需要预测实值的问题被称为回归问题。

线性回归是一种使用直线来模拟输入和输出值之间关系的技术。在多于两个维度的情况下，这条直线可以被认为是平面或超平面。

预测是通过输入值的组合来预测输出值。

每个输入属性（x）都通过一个系数（b）进行加权，学习算法的目标是找到一组能够产生良好预测（y）的系数。

1	y = b0 + b1 * x1 + b2 * x2 + ...

可以使用随机梯度下降来找到系数。

随机梯度下降

梯度下降是通过沿着成本函数的梯度来最小化函数的过程。

这涉及知道成本的形式以及其导数，以便从给定点知道梯度并可以朝该方向移动，例如朝向最小值向下移动。

在机器学习中，我们可以使用一种称为随机梯度下降的技术，它在每次迭代时评估和更新系数，以最小化模型在训练数据上的误差。

该优化算法的工作方式是，每个训练实例一次显示给模型。模型为训练实例做出预测，计算误差，然后更新模型，以便为下一次预测减少误差。这个过程会重复固定次数的迭代。

此过程可用于在模型中找到一组系数，这些系数可使模型在训练数据上的误差最小。每次迭代，机器学习语言中的系数（b）将使用以下公式进行更新：

1	b = b - learning_rate * error * x

其中 b 是正在优化的系数或权重，learning_rate 是您必须配置的学习率（例如 0.01），error 是模型在训练数据上因权重引起的预测误差，而 x 是输入值。

葡萄酒质量数据集

在我们开发了带随机梯度下降的线性回归算法后，我们将使用它来建模葡萄酒质量数据集。

该数据集包含 4,898 种白葡萄酒的详细信息，包括酸度和 pH 值等测量数据。目标是利用这些客观测量值来预测葡萄酒在 0 到 10 之间的质量。

下面是该数据集的前 5 条记录的样本。

7,0.27,0.36,20.7,0.045,45,170,1.001,3,0.45,8.8,6

6.3,0.3,0.34,1.6,0.049,14,132,0.994,3.3,0.49,9.5,6

8.1,0.28,0.4,6.9,0.05,30,97,0.9951,3.26,0.44,10.1,6

7.2,0.23,0.32,8.5,0.058,47,186,0.9956,3.19,0.4,9.9,6

数据集必须在 0 到 1 之间进行归一化，因为每个属性都有不同的单位和不同的尺度。

通过预测归一化数据集上的均值（零规则算法），可以达到 0.148 的基线均方根误差（RMSE）。

您可以在 UCI 机器学习知识库上了解更多关于该数据集的信息。

您可以下载数据集并将其保存在当前工作目录中，文件名为 winequality-white.csv。您必须删除文件开头的标题信息，并将“;”值分隔符转换为“,”以符合 CSV 格式。

教程

本教程分为 3 部分

进行预测。
估计系数。
葡萄酒质量预测。

这将为您提供在您自己的预测建模问题上实现和应用带随机梯度下降的线性回归所需的基础。

1. 进行预测

第一步是开发一个能够进行预测的函数。

这在随机梯度下降中评估候选系数时以及在模型最终确定后我们希望开始对测试数据或新数据进行预测时都会用到。

下面是一个名为 predict() 的函数，它给定一组系数，为一行预测输出值。

第一个系数始终是截距，也称为偏差或 b0，因为它独立存在，不负责特定的输入值。

# 用系数进行预测

def predict(row, coefficients):

yhat = coefficients[0]

for i in range(len(row)-1):

yhat += coefficients[i + 1] * row[i]

return yhat

我们可以构造一个小型数据集来测试我们的预测函数。

x, y

1, 1

2, 3

4, 3

3, 2

5, 5

下面是这个数据集的图。

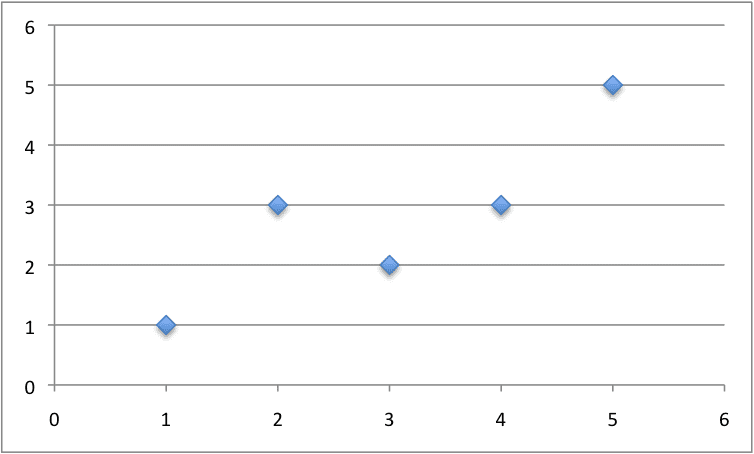
Small Contrived Dataset For Simple Linear Regression

用于线性回归的小型构造数据集

我们还可以使用预先准备好的系数来为这个数据集进行预测。

将所有内容放在一起，我们可以在下面测试我们的 predict() 函数。

# 用系数进行预测

def predict(row, coefficients):

yhat = coefficients[0]

for i in range(len(row)-1):

yhat += coefficients[i + 1] * row[i]

return yhat

dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]

coef = [0.4, 0.8]

for row in dataset:

yhat = predict(row, coef)

print("Expected=%.3f, Predicted=%.3f" % (row[-1], yhat))

有一个输入值（x）和两个系数（b0 和 b1）。我们为此问题建模的预测方程是：

1	y = b0 + b1 * x

或者，使用我们手工选择的特定系数：

1	y = 0.4 + 0.8 * x

运行此函数，我们得到的预测值与预期输出（y）值相当接近。

预期=1.000, 预测=1.200

预期=3.000, 预测=2.000

预期=3.000, 预测=3.600

预期=2.000, 预测=2.800

预期=5.000, 预测=4.400

现在我们准备实现随机梯度下降来优化我们的系数。

2. 估计系数

我们可以使用随机梯度下降来估计训练数据的系数。

随机梯度下降需要两个参数

学习率：用于限制每次更新系数时修正的量。
轮数（Epochs）：在更新系数时遍历训练数据的次数。

这些参数以及训练数据将是函数的参数。

函数中需要进行 3 次循环

遍历每个周期。
遍历训练数据中的每一行以进行一个周期。
针对一个轮次中的一行，循环遍历每个系数并更新它。

正如您所见，在每个轮次中，我们都会为训练数据中的每一行更新每个系数。

系数根据模型犯的错误进行更新。误差计算为使用候选系数进行的预测与预期输出值之间的差值。

1	error = prediction - expected

每个输入属性都有一个系数来加权，这些系数以一致的方式更新，例如：

1	b1(t+1) = b1(t) - learning_rate * error(t) * x1(t)

列表开头的特殊系数，也称为截距或偏差，其更新方式类似，只是没有输入，因为它不与特定输入值关联。

1	b0(t+1) = b0(t) - learning_rate * error(t)

现在我们可以将所有这些整合起来。下面是一个名为 coefficients_sgd() 的函数，它使用随机梯度下降为训练数据集计算系数。

# 使用随机梯度下降估计线性回归系数

def coefficients_sgd(train, l_rate, n_epoch):

coef = [0.0 for i in range(len(train[0]))]

for epoch in range(n_epoch):

sum_error = 0

for row in train:

yhat = predict(row, coef)

error = yhat - row[-1]

sum_error += error**2

coef[0] = coef[0] - l_rate * error

for i in range(len(row)-1):

coef[i + 1] = coef[i + 1] - l_rate * error * row[i]

print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))

return coef

您可以看到，此外，我们还跟踪每个轮次的平方误差之和（一个正值），以便在外部循环中打印出一条有用的消息。

我们可以对上面相同的、经过设计的示例数据集进行测试。

# 用系数进行预测

def predict(row, coefficients):

yhat = coefficients[0]

for i in range(len(row)-1):

yhat += coefficients[i + 1] * row[i]

return yhat

# 使用随机梯度下降估计线性回归系数

def coefficients_sgd(train, l_rate, n_epoch):

coef = [0.0 for i in range(len(train[0]))]

for epoch in range(n_epoch):

sum_error = 0

for row in train:

yhat = predict(row, coef)

error = yhat - row[-1]

sum_error += error**2

coef[0] = coef[0] - l_rate * error

for i in range(len(row)-1):

coef[i + 1] = coef[i + 1] - l_rate * error * row[i]

print('>epoch=%d, lrate=%.3f, error=%.3f' % (epoch, l_rate, sum_error))

return coef

# 计算系数

dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]

l_rate = 0.001

n_epoch = 50

coef = coefficients_sgd(dataset, l_rate, n_epoch)

print(coef)

我们使用 0.001 的小学习率，并训练模型 50 个轮次，即让系数暴露于整个训练数据集 50 次。

运行示例会为每个轮次打印一条消息，其中包含该轮次的平方误差总和以及最终的系数集。

>epoch=45, lrate=0.001, error=2.650

>epoch=46, lrate=0.001, error=2.627

>epoch=47, lrate=0.001, error=2.607

>epoch=48, lrate=0.001, error=2.589

>epoch=49, lrate=0.001, error=2.573

[0.22998234937311363, 0.8017220304137576]

您可以看到，即使在最后一个轮次中，误差也在继续下降。我们也许可以训练更长时间（更多的轮次）或者增加每次迭代中系数的更新量（更高的学习率）。

进行实验，看看您能得出什么结果。

现在，让我们将此算法应用于真实数据集。

3. 葡萄酒质量预测

在本节中，我们将使用随机梯度下降在葡萄酒质量数据集上训练一个线性回归模型。

示例假定数据集的 CSV 副本位于当前工作目录中，文件名为 winequality-white.csv。

首先加载数据集，将字符串值转换为数字，并对每一列进行 0 到 1 之间的归一化。这是通过辅助函数 load_csv() 和 str_column_to_float() 来加载和准备数据集，以及 dataset_minmax() 和 normalize_dataset() 来进行归一化来实现的。

我们将使用 k 折交叉验证来估计模型在未见过的数据上的性能。这意味着我们将构建和评估 k 个模型，并将性能估计为平均模型误差。均方根误差将用于评估每个模型。这些行为由 cross_validation_split()、rmse_metric() 和 evaluate_algorithm() 辅助函数提供。

我们将使用上面创建的 predict()、coefficients_sgd() 和 linear_regression_sgd() 函数来训练模型。

下面是完整的示例。

# Linear Regression With Stochastic Gradient Descent for Wine Quality
from random import seed
from random import randrange
from csv import reader
from math import sqrt

# Load a CSV file
def load_csv(filename):
	dataset = list()
	with open(filename, 'r') as file:
		csv_reader = reader(file)
		for row in csv_reader:
			if not row:
				continue
			dataset.append(row)
	return dataset

# Convert string column to float
def str_column_to_float(dataset, column):
	for row in dataset:
		row[column] = float(row[column].strip())

# Find the min and max values for each column
def dataset_minmax(dataset):
	minmax = list()
	for i in range(len(dataset[0])):
		col_values = [row[i] for row in dataset]
		value_min = min(col_values)
		value_max = max(col_values)
		minmax.append([value_min, value_max])
	return minmax

# Rescale dataset columns to the range 0-1
def normalize_dataset(dataset, minmax):
	for row in dataset:
		for i in range(len(row)):
			row[i] = (row[i] - minmax[i][0]) / (minmax[i][1] - minmax[i][0])

# Split a dataset into k folds
def cross_validation_split(dataset, n_folds):
	dataset_split = list()
	dataset_copy = list(dataset)
	fold_size = int(len(dataset) / n_folds)
	for i in range(n_folds):
		fold = list()
		while len(fold) < fold_size:
			index = randrange(len(dataset_copy))
			fold.append(dataset_copy.pop(index))
		dataset_split.append(fold)
	return dataset_split

# Calculate root mean squared error
def rmse_metric(actual, predicted):
	sum_error = 0.0
	for i in range(len(actual)):
		prediction_error = predicted[i] - actual[i]
		sum_error += (prediction_error ** 2)
	mean_error = sum_error / float(len(actual))
	return sqrt(mean_error)

# Evaluate an algorithm using a cross validation split
def evaluate_algorithm(dataset, algorithm, n_folds, *args):
	folds = cross_validation_split(dataset, n_folds)
	scores = list()
	for fold in folds:
		train_set = list(folds)
		train_set.remove(fold)
		train_set = sum(train_set, [])
		test_set = list()
		for row in fold:
			row_copy = list(row)
			test_set.append(row_copy)
			row_copy[-1] = None
		predicted = algorithm(train_set, test_set, *args)
		actual = [row[-1] for row in fold]
		rmse = rmse_metric(actual, predicted)
		scores.append(rmse)
	return scores

# Make a prediction with coefficients
def predict(row, coefficients):
	yhat = coefficients[0]
	for i in range(len(row)-1):
		yhat += coefficients[i + 1] * row[i]
	return yhat

# Estimate linear regression coefficients using stochastic gradient descent
def coefficients_sgd(train, l_rate, n_epoch):
	coef = [0.0 for i in range(len(train[0]))]
	for epoch in range(n_epoch):
		for row in train:
			yhat = predict(row, coef)
			error = yhat - row[-1]
			coef[0] = coef[0] - l_rate * error
			for i in range(len(row)-1):
				coef[i + 1] = coef[i + 1] - l_rate * error * row[i]
			# print(l_rate, n_epoch, error)
	return coef

# Linear Regression Algorithm With Stochastic Gradient Descent
def linear_regression_sgd(train, test, l_rate, n_epoch):
	predictions = list()
	coef = coefficients_sgd(train, l_rate, n_epoch)
	for row in test:
		yhat = predict(row, coef)
		predictions.append(yhat)
	return(predictions)

# Linear Regression on wine quality dataset
seed(1)
# load and prepare data
filename = 'winequality-white.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])):
	str_column_to_float(dataset, i)
# normalize
minmax = dataset_minmax(dataset)
normalize_dataset(dataset, minmax)
# evaluate algorithm
n_folds = 5
l_rate = 0.01
n_epoch = 50
scores = evaluate_algorithm(dataset, linear_regression_sgd, n_folds, l_rate, n_epoch)
print('Scores: %s' % scores)
print('Mean RMSE: %.3f' % (sum(scores)/float(len(scores))))

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

# 带随机梯度下降的线性回归用于葡萄酒质量

from random import seed

from random import randrange

from csv import reader

from math import sqrt

# 加载 CSV 文件

def load_csv(filename):

dataset = list()

with open(filename, 'r') as file:

csv_reader = reader(file)

for row in csv_reader:

if not row:

continue

dataset.append(row)

return dataset

# 将字符串列转换为浮点数

def str_column_to_float(dataset, column):

for row in dataset:

row[column] = float(row[column].strip())

# 查找每列的最小值和最大值

def dataset_minmax(dataset):

minmax = list()

for i in range(len(dataset[0])):

col_values = [row[i] for row in dataset]

value_min = min(col_values)

value_max = max(col_values)

minmax.append([value_min, value_max])

return minmax

# 将数据集列重新缩放到 0-1 范围

def normalize_dataset(dataset, minmax):

for row in dataset:

for i in range(len(row)):

row[i] = (row[i] - minmax[i][0]) / (minmax[i][1] - minmax[i][0])

# 将数据集分成 k 折

def cross_validation_split(dataset, n_folds):

dataset_split = list()

dataset_copy = list(dataset)

fold_size = int(len(dataset) / n_folds)

for i in range(n_folds):

fold = list()

while len(fold) < fold_size:

index = randrange(len(dataset_copy))

fold.append(dataset_copy.pop(index))

dataset_split.append(fold)

return dataset_split

# 计算均方根误差

def rmse_metric(actual, predicted):

sum_error = 0.0

for i in range(len(actual)):

prediction_error = predicted[i] - actual[i]

sum_error += (prediction_error ** 2)

mean_error = sum_error / float(len(actual))

return sqrt(mean_error)

# 使用交叉验证分割评估算法

def evaluate_algorithm(dataset, algorithm, n_folds, *args):

folds = cross_validation_split(dataset, n_folds)

scores = list()

for fold in folds:

train_set = list(folds)

train_set.remove(fold)

train_set = sum(train_set, [])

test_set = list()

for row in fold:

row_copy = list(row)

test_set.append(row_copy)

row_copy[-1] = None

predicted = algorithm(train_set, test_set, *args)

actual = [row[-1] for row in fold]

rmse = rmse_metric(actual, predicted)

scores.append(rmse)

返回分数

# 用系数进行预测

def predict(row, coefficients):

yhat = coefficients[0]

for i in range(len(row)-1):

yhat += coefficients[i + 1] * row[i]

return yhat

# 使用随机梯度下降估计线性回归系数

def coefficients_sgd(train, l_rate, n_epoch):

coef = [0.0 for i in range(len(train[0]))]

for epoch in range(n_epoch):

for row in train:

yhat = predict(row, coef)

error = yhat - row[-1]

coef[0] = coef[0] - l_rate * error

for i in range(len(row)-1):

coef[i + 1] = coef[i + 1] - l_rate * error * row[i]

# print(l_rate, n_epoch, error)

return coef

# 带随机梯度下降的线性回归算法

def linear_regression_sgd(train, test, l_rate, n_epoch):

predictions = list()

coef = coefficients_sgd(train, l_rate, n_epoch)

for row in test:

yhat = predict(row, coef)

predictions.append(yhat)

return(predictions)

# Wine quality dataset 的线性回归

seed(1)

# 加载并准备数据

filename = 'winequality-white.csv'

dataset = load_csv(filename)

for i in range(len(dataset[0])):

str_column_to_float(dataset, i)

# 归一化

minmax = dataset_minmax(dataset)

normalize_dataset(dataset, minmax)

# 评估算法

n_folds = 5

l_rate = 0.01

n_epoch = 50

scores = evaluate_algorithm(dataset, linear_regression_sgd, n_folds, l_rate, n_epoch)

print('Scores: %s' % scores)

print('Mean RMSE: %.3f' % (sum(scores)/float(len(scores))))

在交叉验证中使用了5个k值，每个折叠每次迭代有4,898/5 = 979.6或不到1000条记录进行评估。经过一些实验，选择了0.01的学习率和50个训练周期。

You can try your own configurations and see if you can beat my score.

运行此示例将打印5个交叉验证折叠的得分，然后打印平均RMSE。

我们可以看到，RMSE（在标准化数据集上）为0.126，低于如果我们仅预测平均值（使用零规则算法）的基线值0.148。

1 2	Scores: [0.12248058224159092, 0.13034017509167112, 0.12620370547483578, 0.12897687952843237, 0.12446990678682233] Mean RMSE: 0.126

扩展

本节列出了本教程的一些扩展，您可能希望考虑进行探索。

调整示例。调整学习率、周期数甚至数据准备方法，以在葡萄酒质量数据集上获得更好的得分。
批量随机梯度下降。更改随机梯度下降算法，以累积每个周期的更新，并在周期结束时仅以批量方式更新系数。
其他回归问题。将该技术应用于UCI机器学习存储库上的其他回归问题。

您是否探索过这些扩展？
Let me know about it in the comments below.

回顾

在本教程中，您将学习如何从头开始使用Python实现随机梯度下降的线性回归。

You learned.

如何为多元线性回归问题进行预测。
如何使用随机梯度下降优化一组系数。
如何将该技术应用于真实的回归预测建模问题。

你有什么问题吗？
在下面的评论中提出您的问题，我将尽力回答。

关于此主题的更多信息

如何从头开始实现简单线性回归（Python）

如何从头开始用Python实现逻辑回归

111条对如何从头开始用Python实现线性回归的回复

Blessing Ojeme 2016年10月28日上午11:41 #

感谢Jason，使它尽可能简单明了。本教程非常有帮助。

回复
- Jason Brownlee 2016年10月28日上午12:00 #
  
  我很高兴听到这个消息，Blessing。
  
  回复
Arvind Ganesh 2017年3月12日下午8:47 #

你是手动选择系数，以便为训练提供依据吗？为什么不直接使用随机值作为系数，然后直接进行梯度下降？

回复
- Jason Brownlee 2017年3月13日上午7:41 #
  
  在最后的示例（教程的末尾）中，我使用了“0”的初始系数，并使用SGD来搜索最适合数据的系数。
  
  回复
  - Christian Picon Calderon 2019年9月10日下午1:33 #
    
    你正在用测试集的标签喂给sdg（第70-74行）。
    
    for row in fold: row_copy = list(row) test_set.append(row_copy) row_copy[-1] = None <<<<-- it must before
    
    1
    2
    3
    4
    
    for row in fold:
    row_copy = list(row)
    test_set.append(row_copy)
    row_copy[-1] = None <<<<-- it must before
    
    回复
    - Jason Brownlee 2019年9月10日下午2:22 #
      
      我不这么认为，我们正在操作碰巧在测试集列表中的列表。
      
      例如，列表的引用。
      
      回复
klaas 2017年3月18日下午10:24 #

嗨，Jason，

这个博客真的很棒，我读得越多，问题越多。例如，我在这里不明白为什么葡萄酒数据集被标记为回归问题？我们有固定的类别标签，所以它应该是分类分类，对吧？
我还想知道您是否会建议也标准化标签，或者仅对特征进行标准化是否足够？谷歌对此并不完全清楚，所以我更喜欢专家的意见。谢谢

回复
- Jason Brownlee 2017年3月19日上午6:11 #
  
  你可以将这个问题视为分类问题，尝试一下看看（使用不同的算法）。
  
  标准化会有帮助。再次在你的问题上尝试一下看看。
  
  回复
Nandhini 2017年4月9日下午4:54 #

嗨，Jason，
关于寻找最优系数的问题。根据我从梯度下降方程中理解的
coeff(0) = coeff(0) – l_rate *1\m*errors
coeff(1) = coeff(1) – l_rate * 1\m * errors * X[i]
其中 m 是训练行的数量。

但是在我上面的代码中，我找不到1\m部分。你能解释一下我的梯度下降方程理解有什么错误吗？

回复
- Jason Brownlee 2017年4月10日上午7:37 #
  
  我没有包含缩放项1/m。你可以加上它，如果你愿意的话。
  
  回复
  - Adarsh 2017年9月13日上午1:58 #
    
    当我加入1/m时，我的系数和总误差值似乎不同。应该这样吗？
    
    回复
    - Jason Brownlee 2017年9月13日下午12:32 #
      
      是的，请看这篇文章
      https://machinelearning.org.cn/randomness-in-machine-learning/
      
      回复
  - Gonzalo A. Aranda 2020年10月15日下午8:54 #
    
    问题在于误差的定义……这不正确！
    
    它定义为yhat – y……这意味着2个误差为+1和-1的示例可以总结为0误差。
    
    正确的定义应该是1/2 (yhat – y)^2……并且在更新中，推导包含X_i……。
    
    回复
Kirill 2017年4月13日上午1:40 #

你好 Jason,
你在这里解决的问题是寻找拟合直线到数据的系数。但是如何可视化这个算法的结果，有可能吗？

回复
- Jason Brownlee 2017年4月13日上午10:06 #
  
  是的，你可以将每个可能的输入变量（x）输入到学习到的模型中并收集输出变量（y），然后绘制x，y点。
  
  回复
Sri 2017年5月28日上午3:54 #

当处理许多输入（>3）时，我们如何可视化数据，因为在葡萄酒质量数据集中有11个特征/输入？

回复
- Jason Brownlee 2017年6月2日下午12:05 #
  
  您可以使用成对散点图。
  
  回复
Kay 2017年6月17日上午7:47 #

嗨，Jason，

我正在处理一个包含6列每行的数据集，其中前5个值（例如，a,b,c,d,e）是输入变量，产生第6个值作为输出（例如，y）。现在，如果我想利用上面实现的SGD来找到一组使y最大化（最小化1-y）的a,b,c,d,e，我该怎么做？感谢您的教程，它们对刚入门的人非常有帮助！

回复
- Jason Brownlee 2017年6月18日上午6:28 #
  
  您可能需要从Weka这样的标准工具开始
  https://machinelearning.org.cn/start-here/#weka
  
  回复
Jason L 2017年6月20日上午6:23 #

嗨，Jason，

我正在将您的教程应用于一个有5个输入、1个输出的建模场景，输入和输出变量的尺度在10^4到10^5的范围内（这是一个媒体建模示例，用于估算成本效益，我们通常在预处理中不进行归一化）。在比较您的方法和SKlearn线性回归时，我发现使用您的方法很难准确估算截距，我的系数和截距都收敛到一些合理的小且相似的值（初始化所有系数为0）。当将截距项初始化为与SKlearn线性回归截距结果相似时，您的方法就收敛到SKlearn线性回归的精确结果。您认为您的方法是否依赖于系数的初始化，这是您以前遇到过的现象吗？我想知道我是否忽略了什么，或者这是否取决于数据的尺度，或者这是数据具有明显的大截距的结果？

回复
- Jason L 2017年6月20日上午6:42 #
  
  我还要指出，当将您的方法与没有截距的SKlearn线性回归进行比较时，它是完美的。
  
  回复
- Jason Brownlee 2017年6月20日上午6:44 #
  
  梯度下降更适用于无法使用linalg方法（如sklearn）的情况，这些方法需要所有数据都能放入内存。
  
  GD方法可能需要根据您的问题进行调整，例如学习率、批量大小等。
  
  回复
nenduru 2017年7月5日下午2:14 #

嗨 Jason

感谢您提供这些很棒的教程，
您是否在下面的代码中将coef[0]和coef[1]初始化为0？
通过for循环调试很令人困惑

coef = [0.0 for i in range(len(train[0]))]

回复
- Jason Brownlee 2017年7月6日上午10:21 #
  
  是的，零初始化。
  
  回复
Mohit Garg 2017年8月10日上午12:05 #

非常感谢您的努力……
先生，您能告诉我如何省略csv文件的第一行吗？

回复
- Jason Brownlee 2017年8月10日上午6:58 #
  
  一些想法
  
  – 手动删除它
  – 使用read_csv加载时跳过它
  – 加载它，然后稍后使用pandas从数据框中删除，或使用numpy从数组中删除。
  
  希望这些能作为一个开始有所帮助。
  
  回复
mohit garg 2017年8月11日上午3:23 #

先生，当我调用ds.info时，它显示它读取为单个列，请问您能告诉我如何解决这个问题吗？

这是代码

df=pd.read_csv(‘wine1.csv’)
df.info()

OUTPUT
class ‘pandas.core.frame.DataFrame’>
RangeIndex: 4898 entries, 0 to 4897
Data columns (total 1 columns)
fixed acidity;”volatile acidity”;”citric acid”;”residual sugar”;”chlorides”;”free sulfur dioxide”;”total sulfur dioxide”;”density”;”pH”;”sulphates”;”alcohol”;”quality” 4898 non-null object
dtypes: object(1)
memory usage: 38.3+ KB

回复
- Jason Brownlee 2017年8月11日上午6:45 #
  
  您可能需要配置加载，以便按“;”而不是“,”分隔列。
  
  请参阅此处的API
  https://pandas.ac.cn/pandas-docs/stable/generated/pandas.read_csv.html
  
  回复
Arthur Grisel-DAvy 2017年8月12日下午8:32 #

很棒的教程，谢谢。
但是，我遇到了一个问题。葡萄酒数据集中的一个值（总二氧化硫）远大于其他值，这造成了一个不稳定的情况，即误差和系数飙升，从正数变为负数，导致溢出。我甚至无法处理数据集中的200行。我检查了我的代码并复制了您的代码，但没有改变。
这是一个常见问题吗？有什么简单的解决方案吗？

回复
- Jason Brownlee 2017年8月13日上午9:53 #
  
  听到这个消息我很难过。
  
  也许您可以识别该示例并从数据集中删除它？
  
  回复
neha 2017年8月16日上午5:28 #

嗨，Jason，
我正在从事活动分析，并在Python中使用线性回归，然后进行交叉验证，SGD。以前，我使用80%训练集和20%测试集进行线性回归，我得到预测并根据十分位数进行推荐。而在此技术中，您推荐的，我如何将数据集划分为十分位数并进行推荐？

回复
- Jason Brownlee 2017年8月16日上午6:41 #
  
  这是两种不同的估计模型在未知数据上技能的方法。
  
  使用能给出最少偏差估计的方法。
  
  回复
  - nehasharma 2017年8月16日下午5:43 #
    
    因此，如果我采用您的交叉验证方法，我会得到5行系数，因为fold=5。对于我的最终线性回归方程，我应该选择哪些系数来完成我的方程，然后推导出十分位数分割以进行推荐？
    
    回复
    - Jason Brownlee 2017年8月17日上午6:37 #
      
      一旦您选择了一个模型配置，您就可以在所有数据上拟合一个最终模型并用它进行预测。
      
      关于开发最终模型的更多信息
      https://machinelearning.org.cn/train-final-machine-learning-model/
      
      回复
      - nehasharma 2017年8月17日下午11:31 #
        
        谢谢您的回复！您真的帮到我了！
      - Jason Brownlee 2017年8月18日上午6:21 #
        
        很高兴听到这个消息。
KUNAL SARKAR 2017年8月21日下午12:37 #

嗨，Jason，
您在这里是在每次样本后更新权重，但根据SGD，它应该在批处理处理后更新。您能解释一下吗？

回复
- Jason Brownlee 2017年8月21日下午4:24 #
  
  每次示例后更新称为“随机梯度下降”。
  
  在样本批次后更新称为“小批量梯度下降”。
  
  在此处了解更多关于差异的信息
  https://machinelearning.org.cn/gentle-introduction-mini-batch-gradient-descent-configure-batch-size/
  
  回复
Shinichi 2017年9月2日下午8:29 #

如何在此处添加正则化，其中正则化范数是1<=p<=2（p=1为Lasso，p=2为Ridge）的通用p范数？

回复
- Jason Brownlee 2017年9月3日上午5:42 #
  
  更新损失函数以考虑组合系数的幅度。
  
  抱歉，我还没有工作示例（）。
  
  回复
Ami Tabak 2017年10月25日下午11:38 #

(minmax[i][1] – minmax[i][0]) 是否会导致0除法？

回复
- Jason Brownlee 2017年10月26日上午5:29 #
  
  为什么？
  
  回复
  - Ami Tabak 2017年10月27日下午8:26 #
    
    File “C:/tutorials/pure-python-lessons/linear-regression/stochastic-regression-protect-nan.py”, line 37, in normalize_dataset
    row[i] = (row[i] – minmax[i][0]) / (minmax[i][1] – minmax[i][0])
    
    ZeroDivisionError: float division by zero
    
    csv文件是
    
    7,0.27,0.36,20.7,0.045,45,170,1.001,3,0.45,8.8,6
    6.3,0.3,0.34,1.6,0.049,14,132,0.994,3.3,0.49,9.5,6
    8.1,0.28,0.4,6.9,0.05,30,97,0.9951,3.26,0.44,10.1,6
    7.2,0.23,0.32,8.5,0.058,47,186,0.9956,3.19,0.4,9.9,6
    7.2,0.23,0.32,8.5,0.058,47,186,0.9956,3.19,0.4,9.9,6
    
    回复
    - Jason Brownlee 2017年10月28日上午5:12 #
      
      这表明您的一列中的所有值可能相同。也许您可以删除这一列？
      
      回复
      - Ami tabak 2017年10月28日下午5:12 #
        
        嗨 Jason
        我使用的数据来自这个页面。您将其发布为葡萄酒质量统计数据。
        事实上，当我进行更改，使最后一列不再是相同的时，错误就不再出现了。
        
        但当然，这种情况也可能发生在其他数据集中。
        将代码更改为以下内容是否正确？
        
        def normalize_dataset(dataset, minmax)
        for row in dataset
        for i in range(len(row))
        if minmax[i][1] == minmax[i][0]
        row[i] = 0
        else
        row[i] = (row[i] – minmax[i][0]) / (minmax[i][1] – minmax[i][0])
      - Jason Brownlee 2017年10月29日上午5:51 #
        
        通常我们会删除像您描述的没有信息量的列。
Imtithal Saeed 2018年5月23日上午12:41 #

嗨，Jason，

那么为什么要使用随机梯度下降呢？而不是其他方法？例如，使用最小二乘法的梯度下降？

回复
- Jason Brownlee 2018年5月23日上午6:27 #
  
  主要原因是当输入数据的矩阵无法放入内存时，无法计算linalg解决方案。
  
  回复
Prabhu 2018年6月4日上午3:36 #

ValueError: could not convert string to float: fixed acidity;”volatile acidity”;”citric acid”;”residual sugar”;”chlorides”;”free sulfur dioxide”;”total sulfur dioxide”;”density”;”pH”;”sulphates”;”alcohol”;”quality”

回复
- Jason Brownlee 2018年6月4日上午6:34 #
  
  看起来您正在处理一个不同的数据集，可能需要先进行处理。
  
  回复
- Guardiana 2018年7月2日下午11:09 #
  
  嘿，我遇到了同样的问题。问题在于csv文件中的分隔符。您只需要将第11行从
  csv_reader = reader(file)
  推广到
  csv_reader = reader(file,delimiter=’;’)
  
  回复
Guardiana 2018年7月3日上午12:48 #

嗨，Jason，

在第47行，您使用来自数据集的随机索引条目填充了fold列表。这意味着某些点会在一个折叠中出现多次，而并非每个点都被使用，对吗？难道不应该使用每个点更好吗？
提前感谢！

回复
- Jason Brownlee 2018年7月3日上午6:27 #
  
  不完全是，您可以在此处了解更多关于交叉验证的信息
  https://machinelearning.org.cn/k-fold-cross-validation/
  
  回复
vince 2018年8月13日上午1:14 #

嗨，Jason，

我尝试了您的示例，一切正常。但是，我尝试使用该函数来估计具有负关系（预测变量和目标变量之间）的不同数据集的系数，而该函数似乎不提供任何负系数。我尝试了不同的学习率，但不是这个问题。

希望您能指出我哪里错了。

我使用的数据集是mtcars数据集，其中disp和hp是与mpg负相关的列的示例。

回复
- Jason Brownlee 2018年8月13日上午6:18 #
  
  也许可以尝试在拟合模型之前对数据进行缩放？
  
  回复
vincent 2018年8月23日下午2:26 #

嗨，Jason，
感谢您提供的精彩教程。
我正在尝试使用您的SGD处理我的数据集。我的数据集有6个特征a、b、c、d、e、f，g是目标结果，我需要预测它。我的数据集中的一些行如下所示：
a b c d e f g
8 20 2 8 1 0 162401
7 30 2 16 1 0 157731
7 30 2 10 1 0 174087
7 30 2 14 1 0 175439
7 30 2 11 1 0 137424
所以，我的问题是，如果我像本教程那样标准化数据，我也必须标准化g列。然后，在我获得系数向量后，我如何用我的测试数据预测结果？因为系数向量中的元素值非常小。另一方面，g列的实际结果非常大。

回复
- Jason Brownlee 2018年8月24日上午6:06 #
  
  您也必须使用训练数据的min/max来标准化测试数据。
  
  回复
dohye 2018年9月11日下午10:08 #

你好，Jason。感谢您的解释。

但我有一个问题。你能告诉我为什么你使用误差而不是梯度吗？
我期待您的回答。
谢谢 🙂

回复
- Jason Brownlee 2018年9月12日上午8:11 #
  
  我们沿着误差梯度向下导航。
  
  回复
Ken Stpnecipher 2018年9月24日下午2:50 #

Jason，您从哪里得到0.148这个数字？

我们可以看到，RMSE（在标准化数据集上）为0.126，低于如果我们仅预测平均值（使用零规则算法）的基线值0.148。

谢谢

肯

回复
- Jason Brownlee 2018年9月25日上午6:16 #
  
  我事先在数据集上运行了zeror。
  
  在教程的前面我曾提到
  
  通过预测归一化数据集上的均值（零规则算法），可以达到 0.148 的基线均方根误差（RMSE）。
  
  回复
Muath Kefayah 2018年10月19日下午7:02 #

嗨，Jason，

在您的教程中，您将哪个特征视为响应变量（目标）？

提前感谢

回复
- Jason Brownlee 2018年10月20日上午5:53 #
  
  葡萄酒质量。
  
  回复
sandy 2018年10月26日下午10:43 #

为什么不使用sklearn模型。为什么您使用常规程序代码。它们和任何复杂性之间有什么区别吗？

回复
- Jason Brownlee 2018年10月27日上午6:01 #
  
  我通常推荐使用sklearn。
  
  我仅作为学习练习展示如何从头开始编写。
  
  回复
Manjunath 2018年12月27日下午5:29 #

你好，
我尝试运行或遵循您的步骤，但遇到了以下错误：
OverflowError: (34, ‘Numerical result out of range’)
在 evaluate_algorithm(dataset, algorithm, n_folds, *args)中
12 test_set.append(row_copy)
13 row_copy[-1] = None
—> 14 predicted = algorithm(train_set, test_set, *args)
15 actual = [row[-1] for row in fold]
16 rmse = rmse_metric(actual, predicted)

在 linear_regression_sgd(train, test, l_rate, n_epoch) 中
21 def linear_regression_sgd(train, test, l_rate, n_epoch)
22 predictions = list()
—> 23 coef = coefficients_sgd(train, l_rate, n_epoch)
24 for row in test
25 yhat = predict(row, coef)

在 coefficients_sgd(train, l_rate, n_epoch) 中
35 yhat = predict(row, coef)
36 error = yhat – row[-1]
—> 37 sum_error += error**2
38 coef[0] = coef[0] – l_rate * error
39 for i in range(len(row)-1)

回复
- Jason Brownlee 2018年12月28日上午5:53 #
  
  我在这里有一些建议
  https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
  
  回复
Saitejapsk 2019年3月20日下午9:31 #

你好，我将使用sklearn的波士顿数据集将SGD应用于线性回归，您能否分享一些像您一样的好的资源？

回复
- Jason Brownlee 2019年3月21日上午8:09 #
  
  这篇帖子（上面）是你真正需要并且是一个很好的起点。
  
  回复
Toni 2019年4月26日上午7:17 #

你好Jason！感谢您的工作。我是ML算法方面（尤其是数学部分）的初学者。我整天都在想您是如何推导出误差函数的。据我所知，代码中的误差函数是（error = yhat – row(-1）），而yhat是从predict函数中获取的。据我理解，predict函数在数学上类似（f(x) = x0 + n – 1
Σ
i = 1
xi * d(i-1)
其中d是数据，n是长度。我尝试得到导数函数，但看起来我弄错了。

回复
- Jason Brownlee 2019年4月26日上午8:40 #
  
  我没有推导误差函数，我使用的是一本书中的推导。
  
  回复
  - Toni 2019年4月27日下午5:15 #
    
    非常感谢您的回复！我（经过深思熟虑）得出结论，代码中推导的部分不是
    error * row(i)
    而是仅仅
    row(i)
    基于直线函数的推导
    f'(x) (a + bx – y) = b
    并得出结论，梯度下降算法通过从系数中减去
    error * derivation * lrate
    而不是
    derivation * lrate
    但在此教程的“估计系数”部分，如果我将第19行更改为
    coef(i + 1) = coef(i + 1) – l_rate * row(i)
    最终结果是
    epoch = 50, lRate = 0.01, error = 1043.0016830658
    16.8916015949 -7.5
    这表明代码中的“* error”部分是有充分理由存在的，而不是随意尝试的，我可能弄错了，但我会继续尝试理解。
    抱歉回复太长，但我开始根据网络上的一些代码从头开始实现神经网络，现在我正在分析它，我认为神经网络使用的优化算法，尤其是其推导部分，非常重要，我不想在没有充分理解的情况下继续。
    
    回复
    - Toni 2019年5月4日上午2:36 #
      
      你好！我明白了为什么代码中的推导是这样描述的，我会和你分享。我将用b表示coef[0]，用mi表示其他coef，用xi表示数据。
      代码中的误差实际上是SSE函数对b的导数除以2，即2*error = ∂[SSE]/∂[b]。SSE函数对mi的导数就是SSE函数对b的导数*xi（即代码中的xi * error部分）。作者可能为了简化或因为2只是一个常数，其影响可以通过调整l_rate的值来轻松替代，因此省略了导数中的“* 2”部分。
      
      回复
      - Jason Brownlee 2019年5月4日上午7:13 #
        
        谢谢。
shriya 2019年9月26日上午1:40 #

1. epoch数与误差（成本）的图
2. 10种不同学习率与误差（成本）的图
3. 10种不同参数值（θ0和θ1）与误差（成本）的图
4. 梯度下降算法应该停止运行，而不是运行到最后一个epoch，当误差
（成本）与前几个epoch相比没有明显下降时。
5. 数据集应随机划分，例如70%用于训练，30%用于测试，因此算法
应该只使用70%的数据计算参数（θ0和θ1）值，并找到训练
误差（成本）和测试误差（成本）。

回复
- Jason Brownlee 2019年9月26日上午6:43 #
  
  有什么我可以帮忙的问题吗？
  
  回复
daniel 2019年11月19日下午2:25 #

分数代表什么？是R平方值吗？

回复
- Jason Brownlee 2019年11月20日上午6:07 #
  
  它们是交叉验证中每个折叠的RMSE分数。
  
  回复
Nikhil Parmar 2019年12月9日下午6:12 #

先生，感谢您提供的精彩文章。我刚开始学习机器学习。
我对以上实现有一个疑问。我读过，对于SGD更新，我们需要获取1.损失函数“L”关于“W”的导数，称之为“dLW”，以及
2.损失函数“L”关于“b”的导数，称之为“dLb”。

然后

设“j”为迭代次数，则更新如下：
W(j+1)=W(j)-LearningRate(r)*dWL
b(j+1)=b(j)-LearningRate(r)*dLb

先生，您能否重定向我到代码中执行这些导数步骤的地方？
抱歉，我是新手，从您那里学到了很多。
谢谢你

回复
- Jason Brownlee 2019年12月10日上午7:29 #
  
  请参见coefficients_sgd()函数。
  
  回复
  - Berke Cesur 2020年3月9日上午5:30 #
    
    布朗利先生，在函数内部，我们在每个epoch结束时将学习率乘以计算出的误差。我们不是应该使用偏导数来计算新系数吗？这个过程只在ANN中使用吗？
    
    回复
    - Jason Brownlee 2020年3月9日上午7:18 #
      
      类似。
      
      回复
Mike Mawira 2020年3月12日上午9:25 #

你好，Jason。我们能否像示例1那样，在进行葡萄酒质量预测时，同时获得预测值和期望值？

回复
- Jason Brownlee 2020年3月12日下午1:41 #
  
  是的，您可以拟合模型并调用预测，然后输出期望值与预测值的示例。
  
  这可以通过调整教程中的最后一个示例来实现。
  
  回复
  - Mike Mawira 2020年3月13日上午2:35 #
    
    谢谢你。
    
    回复
    - Jason Brownlee 2020年3月13日上午8:21 #
      
      不客气。
      
      回复
Nancy 2020年6月18日下午7:52 #

你好，Jason。当我使用代码训练我的数据集时，出现了一些错误。这是错误：
train_set.remove(fold)
ValueError：包含多个元素的数组的真值不明确。请使用 a.any() 或 a.all()
我不知道如何处理，您能告诉我问题是什么以及我应该如何修改吗？

回复
- Jason Brownlee 2020年6月19日上午6:11 #
  
  很抱歉听到这个消息，也许可以确认您的数据是否已正确加载。
  
  或者直接使用scikit-learn
  https://machinelearning.org.cn/spot-check-regression-machine-learning-algorithms-python-scikit-learn/
  
  回复
Nancy 2020年7月8日下午6:35 #

谢谢，我已经解决了问题，我想问一下，‘coef[i + 1] = coef[i + 1] – l_rate * error * row[i]’中的参数是否代表梯度？因为我最近才学到，所以理解得不是很好。

回复
- Jason Brownlee 2020年7月9日上午6:38 #
  
  是的，误差梯度。
  
  回复
  - Nancy 2020年7月20日下午7:43 #
    
    谢谢，如果我想将随机梯度下降改为批量随机梯度下降，我该如何修改？我的想法是使用每个用户的数据来计算系数，然后计算平均系数。这是对的吗？如果不对，我该如何修改？希望您能给我一些想法。
    
    回复
    - Jason Brownlee 2020年7月21日上午6:00 #
      
      对所有示例的误差进行平均，然后在数据集末尾对系数执行一次更新，然后重复n个epoch。
      
      回复
Nancy 2020年7月21日下午5:25 #

这是关于最小批量梯度下降的问题，我找到了：
β(t+1) = β(t) -γt · 1/|G| ∑|G| i=1 ∇l(i)
参数∇l(i)是否等于代码中的变量‘error’？

回复
- Jason Brownlee 2020年7月22日上午5:27 #
  
  可能。
  
  回复
Nancy 2020年7月31日下午5:51 #

你好，Jason。我想问一下，如果我想添加正则化因子，我应该如何更新系数？我只需要将其乘以正则化因子吗？

回复
- Jason Brownlee 2020年8月1日上午6:09 #
  
  您可以将预测误差乘以一个惩罚项。
  
  回复
  - Nancy 2020年8月1日下午5:41 #
    
    感谢您的回答。顺便问一下，我想实现逻辑回归和SVM，就像您介绍的线性回归一样，您有没有类似这篇文章中示例描述的例子？
    
    回复
    - Jason Brownlee 2020年8月2日上午5:40 #
      
      是的，您可以在博客上找到示例，请使用搜索框。
      
      回复
Gideon Aswani 2020年9月6日上午7:25 #

嗨 Jason

我已在Jupyter笔记本中实现了此教程中的代码，效果非常好。该模型会预测葡萄酒质量（yhat），这些预测值是归一化后的值。我该如何将归一化后的预测值转换回int64或float64？

再次感谢您的分享。

Gideon Aswani

回复
- Jason Brownlee 2020年9月7日上午8:20 #
  
  您可以直接在Python中转换值，例如：
  
  value = 11 newvalue = float(value)
  
  1
  2
  
  value = 11
  newvalue = float(value)
  
  回复
  - Gideon Aswani 2020年9月7日下午3:23 #
    
    你好Jason，也许我没有正确地表述我的问题。load_csv()、str_column_to_float()、dataset_minmax()和normalize_dataset()函数将字符串值转换为数字并将列归一化到0到1的范围。预测（that）也是用此范围内的值进行的。我的问题是，我们如何将这些预测转换回字符串值或数值，即“反归一化yhats”。
    
    回复
    - Jason Brownlee 2020年9月8日上午6:46 #
      
      您可以编写代码来记住映射并进行反向操作。
      
      或者，您可以使用scikit-learn的transform对象并调用inverse_transform()。
      
      回复
      - Gideon Aswani 2020年9月8日下午2:58 #
        
        我实际上写了几行代码来逆转归一化过程，并且成功地将预测值转换到了1到10的尺度上。我会尝试scikit-learn的inverse_transform()方法。
      - Jason Brownlee 2020年9月9日上午6:42 #
        
        干得好！
Gideon Aswani 2020年9月8日下午6:49 #

你好Jason，在教程中您提到“我们可以看到，RMSE（在归一化数据集上）是0.126，低于如果我们只预测均值（使用零规则算法）的基线值0.148。我使用了整个数据集（winequality-white.csv）的目标（归一化后）作为我的训练集来确定使用零规则算法的基线值，我得到的预测值为0.479651558459236，而不是0.148。这是什么原因造成的？

同样，在保险教程中，使用零规则算法处理整个数据集（insurance.csv），我得到98.18730158730159作为预测值，而不是81千克朗。如何解释这种差异？

回复
- Jason Brownlee 2020年9月9日上午6:46 #
  
  好问题，请看这个
  https://machinelearning.org.cn/faq/single-faq/why-do-i-get-different-results-each-time-i-run-the-code
  
  回复
Casey 2020年9月22日上午2:53 #

先生，是否必须归一化数据集？因为当我尝试使用sklearn的load_boston数据集时，它返回了一个nan的错误值。

回复
- Jason Brownlee 2020年9月22日上午6:53 #
  
  不一定。某些数据和某些模型可能受益于缩放。
  
  回复
constantin 2021年12月2日下午11:06 #

嗨 Jason

我在Jupyter笔记本中实现了此教程中的代码，并出现此错误：

无法将字符串转换为浮点数：“fixed acidity”

你能帮我吗？

回复
- Adrian Tam 2021年12月8日上午6:26 #
  
  请跳过CSV文件中的第一行。那是列标题。
  
  回复
- James Carmichael 2021年12月22日上午9:48 #
  
  Constantin你好…请尝试在您的计算机上本地安装Python，根据以下资源：
  
  https://machinelearning.org.cn/setup-python-environment-machine-learning-deep-learning-anaconda/
  
  然后尝试运行您的代码，如果仍有问题，请告诉我。
  
  此致，
  
  回复

导航

如何在 Python 中从头实现线性回归

描述

多元线性回归

随机梯度下降

葡萄酒质量数据集

教程

1. 进行预测

2. 估计系数

3. 葡萄酒质量预测

扩展

回顾

了解如何从零开始编写算法！

没有库，只有 Python 代码。

最后，揭开
机器学习算法的神秘面纱

关于此主题的更多信息

111条对如何从头开始用Python实现线性回归的回复

留下回复点击此处取消回复。

导航

描述

多元线性回归

随机梯度下降

葡萄酒质量数据集

教程

1. 进行预测

2. 估计系数

3. 葡萄酒质量预测

扩展

回顾

了解如何从零开始编写算法！

没有库，只有 Python 代码。

最后，揭开机器学习算法的神秘面纱

关于此主题的更多信息

111条对如何从头开始用Python实现线性回归的回复

留下回复 点击此处取消回复。

最后，揭开
机器学习算法的神秘面纱

留下回复点击此处取消回复。