如何使用 Python 从零开始实现简单线性回归

作者 Jason Brownlee 于 2020 年 5 月 11 日在代码从零开始算法 168

线性回归是一种已有 200 多年历史的预测方法。

简单线性回归是一种很好的入门机器学习算法，因为它需要您从训练数据集中估计属性，但对于初学者来说足够简单。

在本教程中，您将学习如何使用 Python 从零开始实现简单线性回归算法。

完成本教程后，您将了解

如何从训练数据中估计统计量。
如何从数据中估计线性回归系数。
如何使用线性回归对新数据进行预测。

通过我的新书《从零开始的机器学习算法》开启您的项目，其中包括逐步教程和所有示例的 Python 源代码文件。

让我们开始吧。

2018 年 8 月更新：测试并更新以与 Python 3.6 配合使用。
2019 年 2 月更新：对保险数据集的预期默认 RMSE 进行了小幅更新。

How To Implement Simple Linear Regression From Scratch With Python

如何使用 Python 从零开始实现简单线性回归
照片来源 Kamyar Adl，保留部分权利。

描述

本节分为两部分，即简单线性回归技术的描述和我们稍后将应用它的数据集的描述。

简单线性回归

线性回归假设输入变量 (X) 和单个输出变量 (y) 之间存在线性或直线关系。

更具体地说，输出 (y) 可以通过输入变量 (X) 的线性组合计算得出。当存在单个输入变量时，该方法称为简单线性回归。

在简单线性回归中，我们可以使用训练数据上的统计量来估计模型所需的系数，以对新数据进行预测。

简单线性回归模型的直线可以写成

y = b0 + b1 * x

1	y = b0 + b1 * x

其中 b0 和 b1 是我们必须从训练数据中估计的系数。

一旦知道系数，我们就可以使用这个方程来估计给定 x 的新输入示例的 y 输出值。

它要求您计算数据的统计属性，例如均值、方差和协方差。

所有的代数问题都已解决，我们剩下一些算术运算来实现，以估计简单线性回归系数。

简而言之，我们可以按如下方式估计系数

B1 = sum((x(i) - mean(x)) * (y(i) - mean(y))) / sum( (x(i) - mean(x))^2 )
B0 = mean(y) - B1 * mean(x)

1 2	B1 = sum((x(i) - mean(x)) * (y(i) - mean(y))) / sum( (x(i) - mean(x))^2 ) B0 = mean(y) - B1 * mean(x)

其中 i 指的是输入 x 或输出 y 的第 i 个值。

如果现在还不清楚，请不要担心，这些是本教程中将实现的函数。

瑞典保险数据集

我们将使用真实数据集来演示简单线性回归。

该数据集称为“瑞典汽车保险”数据集，涉及根据索赔总数 (x) 预测所有索赔的总付款（以千瑞典克朗计）(y)。

这意味着对于新的索赔数量 (x)，我们将能够预测索赔的总付款 (y)。

以下是数据集前 5 条记录的小样本。

108,392.5
19,46.2
13,15.7
124,422.2
40,119.4

108,392.5

19,46.2

13,15.7

124,422.2

40,119.4

使用零规则算法（预测平均值）预计均方根误差 (RMSE) 约为 81（千克朗）。

以下是整个数据集的散点图。

瑞典保险数据集

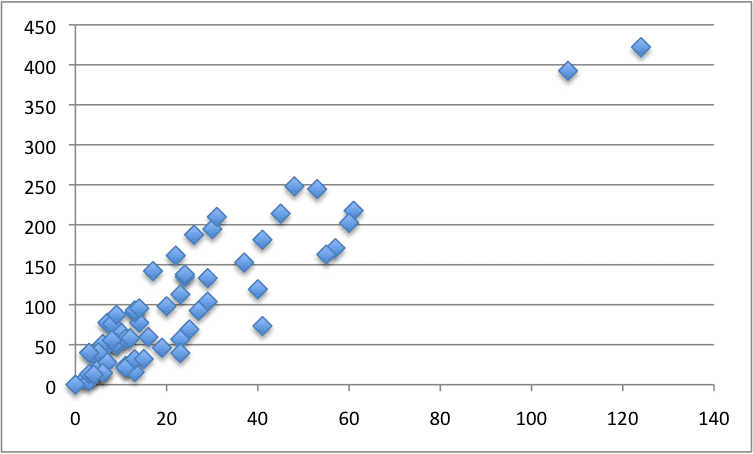
您可以从此处或此处下载原始数据集。

将其保存到本地工作目录中名为“insurance.csv”的 CSV 文件。

请注意，您可能需要将欧洲的“,”转换为十进制的“.”。您还需要将文件从空格分隔变量更改为 CSV 格式。

教程

本教程分为五部分

计算均值和方差。
计算协方差。
估计系数。
进行预测。
预测保险。

这些步骤将为您提供实现和训练简单线性回归模型以解决您自己的预测问题所需的基础。

1. 计算均值和方差

第一步是根据训练数据估计输入变量和输出变量的均值和方差。

数字列表的均值可以计算为

mean(x) = sum(x) / count(x)

1	mean(x) = sum(x) / count(x)

下面是一个名为 mean() 的函数，它实现了数字列表的此行为。

# Calculate the mean value of a list of numbers
def mean(values):
	return sum(values) / float(len(values))

# 计算数字列表的平均值

def mean(values):

return sum(values) / float(len(values))

方差是每个值与平均值的平方差之和。

数字列表的方差可以计算为

variance = sum( (x - mean(x))^2 )

1	方差 = sum( (x - mean(x))^2 )

下面是一个名为 variance() 的函数，它计算数字列表的样本方差（注意，我们有意计算与均值的平方差之和，而不是与均值的平均平方差）。它需要将列表的均值作为参数提供，这样我们就不必计算多次。

# Calculate the variance of a list of numbers
def variance(values, mean):
	return sum([(x-mean)**2 for x in values])

# 计算数字列表的方差

def variance(values, mean):

return sum([(x-mean)**2 for x in values])

我们可以将这两个函数组合在一起，并在一个小的人为数据集上测试它们。

下面是一个包含 x 和 y 值的小数据集。

注意：如果要将此数据保存到 .CSV 文件以用于最终代码示例，请删除列标题。

x, y
1, 1
2, 3
4, 3
3, 2
5, 5

x，y

1, 1

2, 3

4, 3

3, 2

5, 5

我们可以在散点图上绘制此数据集，如下所示

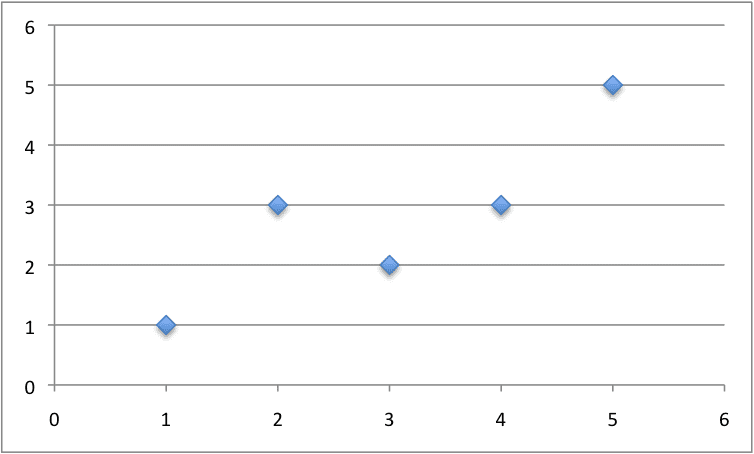
Small Contrived Dataset For Simple Linear Regression

用于简单线性回归的小型人为数据集

在下面的示例中，我们可以计算 x 和 y 值的均值和方差。

# Estimate Mean and Variance

# Calculate the mean value of a list of numbers
def mean(values):
	return sum(values) / float(len(values))

# Calculate the variance of a list of numbers
def variance(values, mean):
	return sum([(x-mean)**2 for x in values])

# calculate mean and variance
dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]
x = [row[0] for row in dataset]
y = [row[1] for row in dataset]
mean_x, mean_y = mean(x), mean(y)
var_x, var_y = variance(x, mean_x), variance(y, mean_y)
print('x stats: mean=%.3f variance=%.3f' % (mean_x, var_x))
print('y stats: mean=%.3f variance=%.3f' % (mean_y, var_y))

# 估计均值和方差

# 计算数字列表的平均值

def mean(values):

return sum(values) / float(len(values))

# 计算数字列表的方差

def variance(values, mean):

return sum([(x-mean)**2 for x in values])

# 计算均值和方差

dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]

x = [row[0] for row in dataset]

y = [row[1] for row in dataset]

mean_x, mean_y = mean(x), mean(y)

var_x, var_y = variance(x, mean_x), variance(y, mean_y)

print('x stats: mean=%.3f variance=%.3f' % (mean_x, var_x))

print('y stats: mean=%.3f variance=%.3f' % (mean_y, var_y))

运行此示例将打印出两列的均值和方差。

x stats: mean=3.000 variance=10.000
y stats: mean=2.800 variance=8.800

1 2	x 统计：均值=3.000 方差=10.000 y 统计：均值=2.800 方差=8.800

这是我们的第一步，接下来我们需要利用这些值来计算协方差。

2. 计算协方差

两组数字的协方差描述了这些数字如何一起变化。

协方差是相关性的推广。相关性描述了两组数字之间的关系，而协方差可以描述两组或更多组数字之间的关系。

此外，协方差可以标准化以产生相关值。

尽管如此，我们可以按如下方式计算两个变量之间的协方差

covariance = sum((x(i) - mean(x)) * (y(i) - mean(y)))

1	协方差 = sum((x(i) - mean(x)) * (y(i) - mean(y)))

下面是一个名为 covariance() 的函数，它实现了这个统计量。它建立在前面的步骤之上，并将 x 和 y 值的列表以及这些值的均值作为参数。

# Calculate covariance between x and y
def covariance(x, mean_x, y, mean_y):
	covar = 0.0
	for i in range(len(x)):
		covar += (x[i] - mean_x) * (y[i] - mean_y)
	return covar

# 计算 x 和 y 之间的协方差

def covariance(x, mean_x, y, mean_y):

covar = 0.0

for i in range(len(x)):

covar += (x[i] - mean_x) * (y[i] - mean_y)

return covar

我们可以在与上一节相同的小人为数据集上测试协方差的计算。

将所有内容组合在一起，我们得到以下示例。

# Calculate Covariance

# Calculate the mean value of a list of numbers
def mean(values):
	return sum(values) / float(len(values))

# Calculate covariance between x and y
def covariance(x, mean_x, y, mean_y):
	covar = 0.0
	for i in range(len(x)):
		covar += (x[i] - mean_x) * (y[i] - mean_y)
	return covar

# calculate covariance
dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]
x = [row[0] for row in dataset]
y = [row[1] for row in dataset]
mean_x, mean_y = mean(x), mean(y)
covar = covariance(x, mean_x, y, mean_y)
print('Covariance: %.3f' % (covar))

# 计算协方差

# 计算数字列表的平均值

def mean(values):

return sum(values) / float(len(values))

# 计算 x 和 y 之间的协方差

def covariance(x, mean_x, y, mean_y):

covar = 0.0

for i in range(len(x)):

covar += (x[i] - mean_x) * (y[i] - mean_y)

return covar

# 计算协方差

dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]

x = [row[0] for row in dataset]

y = [row[1] for row in dataset]

mean_x, mean_y = mean(x), mean(y)

covar = covariance(x, mean_x, y, mean_y)

print('协方差: %.3f' % (covar))

运行此示例会打印 x 和 y 变量的协方差。

Covariance: 8.000

协方差：8.000

现在我们已经具备了计算模型系数的所有要素。

3. 估计系数

我们必须在简单线性回归中估计两个系数的值。

第一个是 B1，可以估计为

B1 = sum((x(i) - mean(x)) * (y(i) - mean(y))) / sum( (x(i) - mean(x))^2 )

1	B1 = sum((x(i) - mean(x)) * (y(i) - mean(y))) / sum( (x(i) - mean(x))^2 )

我们已经学习了一些东西，可以简化这个算术为

B1 = covariance(x, y) / variance(x)

1	B1 = covariance(x, y) / variance(x)

我们已经有计算 covariance() 和 variance() 的函数。

接下来，我们需要估计 B0 的值，也称为截距，因为它控制着直线与 y 轴相交的起点。

B0 = mean(y) - B1 * mean(x)

1	B0 = mean(y) - B1 * mean(x)

同样，我们知道如何估计 B1，并且我们有一个函数可以估计 mean()。

我们可以将所有这些组合成一个名为 coefficients() 的函数，该函数将数据集作为参数并返回系数。

# Calculate coefficients
def coefficients(dataset):
	x = [row[0] for row in dataset]
	y = [row[1] for row in dataset]
	x_mean, y_mean = mean(x), mean(y)
	b1 = covariance(x, x_mean, y, y_mean) / variance(x, x_mean)
	b0 = y_mean - b1 * x_mean
	return [b0, b1]

# 计算系数

def coefficients(dataset):

x = [row[0] for row in dataset]

y = [row[1] for row in dataset]

x_mean, y_mean = mean(x), mean(y)

b1 = covariance(x, x_mean, y, y_mean) / variance(x, x_mean)

b0 = y_mean - b1 * x_mean

return [b0, b1]

我们可以将此与前两个步骤中的所有函数结合起来，并测试系数的计算。

# Calculate Coefficients

# Calculate the mean value of a list of numbers
def mean(values):
	return sum(values) / float(len(values))

# Calculate covariance between x and y
def covariance(x, mean_x, y, mean_y):
	covar = 0.0
	for i in range(len(x)):
		covar += (x[i] - mean_x) * (y[i] - mean_y)
	return covar

# Calculate the variance of a list of numbers
def variance(values, mean):
	return sum([(x-mean)**2 for x in values])

# Calculate coefficients
def coefficients(dataset):
	x = [row[0] for row in dataset]
	y = [row[1] for row in dataset]
	x_mean, y_mean = mean(x), mean(y)
	b1 = covariance(x, x_mean, y, y_mean) / variance(x, x_mean)
	b0 = y_mean - b1 * x_mean
	return [b0, b1]

# calculate coefficients
dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]
b0, b1 = coefficients(dataset)
print('Coefficients: B0=%.3f, B1=%.3f' % (b0, b1))

# 计算系数

# 计算数字列表的平均值

def mean(values):

return sum(values) / float(len(values))

# 计算 x 和 y 之间的协方差

def covariance(x, mean_x, y, mean_y):

covar = 0.0

for i in range(len(x)):

covar += (x[i] - mean_x) * (y[i] - mean_y)

return covar

# 计算数字列表的方差

def variance(values, mean):

return sum([(x-mean)**2 for x in values])

# 计算系数

def coefficients(dataset):

x = [row[0] for row in dataset]

y = [row[1] for row in dataset]

x_mean, y_mean = mean(x), mean(y)

b1 = covariance(x, x_mean, y, y_mean) / variance(x, x_mean)

b0 = y_mean - b1 * x_mean

return [b0, b1]

# 计算系数

dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]

b0, b1 = coefficients(dataset)

print('系数: B0=%.3f, B1=%.3f' % (b0, b1))

运行此示例会计算并打印系数。

Coefficients: B0=0.400, B1=0.800

1	系数：B0=0.400，B1=0.800

既然我们知道如何估计系数，下一步就是使用它们。

4. 进行预测

简单线性回归模型是由从训练数据中估计的系数定义的直线。

一旦估计了系数，我们就可以使用它们进行预测。

使用简单线性回归模型进行预测的方程如下

y = b0 + b1 * x

1	y = b0 + b1 * x

下面是一个名为 simple_linear_regression() 的函数，它实现了预测方程，以对测试数据集进行预测。它还将上述步骤中训练数据上的系数估计联系起来。

从训练数据准备的系数用于对测试数据进行预测，然后返回这些预测。

def simple_linear_regression(train, test):
	predictions = list()
	b0, b1 = coefficients(train)
	for row in test:
		yhat = b0 + b1 * row[0]
		predictions.append(yhat)
	return predictions

def simple_linear_regression(train, test):

predictions = list()

b0, b1 = coefficients(train)

for row in test:

yhat = b0 + b1 * row[0]

predictions.append(yhat)

return predictions

让我们整合我们所学的一切，为我们简单的人为数据集进行预测。

作为此示例的一部分，我们还将添加一个函数来管理预测的评估，称为 evaluate_algorithm()，以及另一个函数来估计预测的均方根误差，称为 rmse_metric()。

完整的示例如下所示。

# Standalone simple linear regression example
from math import sqrt

# Calculate root mean squared error
def rmse_metric(actual, predicted):
	sum_error = 0.0
	for i in range(len(actual)):
		prediction_error = predicted[i] - actual[i]
		sum_error += (prediction_error ** 2)
	mean_error = sum_error / float(len(actual))
	return sqrt(mean_error)

# Evaluate regression algorithm on training dataset
def evaluate_algorithm(dataset, algorithm):
	test_set = list()
	for row in dataset:
		row_copy = list(row)
		row_copy[-1] = None
		test_set.append(row_copy)
	predicted = algorithm(dataset, test_set)
	print(predicted)
	actual = [row[-1] for row in dataset]
	rmse = rmse_metric(actual, predicted)
	return rmse

# Calculate the mean value of a list of numbers
def mean(values):
	return sum(values) / float(len(values))

# Calculate covariance between x and y
def covariance(x, mean_x, y, mean_y):
	covar = 0.0
	for i in range(len(x)):
		covar += (x[i] - mean_x) * (y[i] - mean_y)
	return covar

# Calculate the variance of a list of numbers
def variance(values, mean):
	return sum([(x-mean)**2 for x in values])

# Calculate coefficients
def coefficients(dataset):
	x = [row[0] for row in dataset]
	y = [row[1] for row in dataset]
	x_mean, y_mean = mean(x), mean(y)
	b1 = covariance(x, x_mean, y, y_mean) / variance(x, x_mean)
	b0 = y_mean - b1 * x_mean
	return [b0, b1]

# Simple linear regression algorithm
def simple_linear_regression(train, test):
	predictions = list()
	b0, b1 = coefficients(train)
	for row in test:
		yhat = b0 + b1 * row[0]
		predictions.append(yhat)
	return predictions

# Test simple linear regression
dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]
rmse = evaluate_algorithm(dataset, simple_linear_regression)
print('RMSE: %.3f' % (rmse))

# 独立的简单线性回归示例

from math import sqrt

# 计算均方根误差

def rmse_metric(actual, predicted):

sum_error = 0.0

for i in range(len(actual)):

prediction_error = predicted[i] - actual[i]

sum_error += (prediction_error ** 2)

mean_error = sum_error / float(len(actual))

return sqrt(mean_error)

# 在训练数据集上评估回归算法

def evaluate_algorithm(dataset, algorithm):

test_set = list()

for row in dataset:

row_copy = list(row)

row_copy[-1] = None

test_set.append(row_copy)

predicted = algorithm(dataset, test_set)

print(predicted)

actual = [row[-1] for row in dataset]

rmse = rmse_metric(actual, predicted)

return rmse

# 计算数字列表的平均值

def mean(values):

return sum(values) / float(len(values))

# 计算 x 和 y 之间的协方差

def covariance(x, mean_x, y, mean_y):

covar = 0.0

for i in range(len(x)):

covar += (x[i] - mean_x) * (y[i] - mean_y)

return covar

# 计算数字列表的方差

def variance(values, mean):

return sum([(x-mean)**2 for x in values])

# 计算系数

def coefficients(dataset):

x = [row[0] for row in dataset]

y = [row[1] for row in dataset]

x_mean, y_mean = mean(x), mean(y)

b1 = covariance(x, x_mean, y, y_mean) / variance(x, x_mean)

b0 = y_mean - b1 * x_mean

return [b0, b1]

# 简单线性回归算法

def simple_linear_regression(train, test):

predictions = list()

b0, b1 = coefficients(train)

for row in test:

yhat = b0 + b1 * row[0]

predictions.append(yhat)

return predictions

# 测试简单线性回归

dataset = [[1, 1], [2, 3], [4, 3], [3, 2], [5, 5]]

rmse = evaluate_algorithm(dataset, simple_linear_regression)

print('RMSE: %.3f' % (rmse))

运行此示例会显示以下输出，首先列出预测和这些预测的 RMSE。

[1.1999999999999995, 1.9999999999999996, 3.5999999999999996, 2.8, 4.3999999999999995]
RMSE: 0.693

1 2	[1.1999999999999995, 1.9999999999999996, 3.5999999999999996, 2.8, 4.3999999999999995] RMSE：0.693

最后，我们可以将预测绘制成一条线，并将其与原始数据集进行比较。

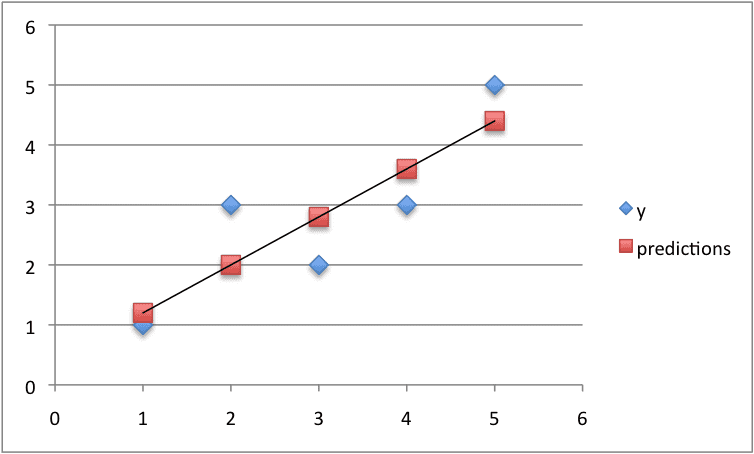
Predictions For Small Contrived Dataset For Simple Linear Regression

用于简单线性回归的小型人为数据集的预测

5. 预测保险

我们现在知道如何实现简单线性回归模型。

让我们将其应用于瑞典保险数据集。

本节假设您已将数据集下载到文件 insurance.csv 中，并且它在当前工作目录中可用。

我们将为前几步中的简单线性回归添加一些便利函数。

具体来说，一个加载 CSV 文件的函数，名为 load_csv()，一个将加载的数据集转换为数字的函数，名为 str_column_to_float()，一个使用训练集和测试集评估算法的函数，名为 train_test_split()，一个计算 RMSE 的函数，名为 rmse_metric()，以及一个评估算法的函数，名为 evaluate_algorithm()。

完整的示例如下所示。

使用 60% 的数据作为训练数据集来准备模型，并在剩余的 40% 上进行预测。

# Simple Linear Regression on the Swedish Insurance Dataset
from random import seed
from random import randrange
from csv import reader
from math import sqrt

# Load a CSV file
def load_csv(filename):
	dataset = list()
	with open(filename, 'r') as file:
		csv_reader = reader(file)
		for row in csv_reader:
			if not row:
				continue
			dataset.append(row)
	return dataset

# Convert string column to float
def str_column_to_float(dataset, column):
	for row in dataset:
		row[column] = float(row[column].strip())

# Split a dataset into a train and test set
def train_test_split(dataset, split):
	train = list()
	train_size = split * len(dataset)
	dataset_copy = list(dataset)
	while len(train) < train_size:
		index = randrange(len(dataset_copy))
		train.append(dataset_copy.pop(index))
	return train, dataset_copy

# Calculate root mean squared error
def rmse_metric(actual, predicted):
	sum_error = 0.0
	for i in range(len(actual)):
		prediction_error = predicted[i] - actual[i]
		sum_error += (prediction_error ** 2)
	mean_error = sum_error / float(len(actual))
	return sqrt(mean_error)

# Evaluate an algorithm using a train/test split
def evaluate_algorithm(dataset, algorithm, split, *args):
	train, test = train_test_split(dataset, split)
	test_set = list()
	for row in test:
		row_copy = list(row)
		row_copy[-1] = None
		test_set.append(row_copy)
	predicted = algorithm(train, test_set, *args)
	actual = [row[-1] for row in test]
	rmse = rmse_metric(actual, predicted)
	return rmse

# Calculate the mean value of a list of numbers
def mean(values):
	return sum(values) / float(len(values))

# Calculate covariance between x and y
def covariance(x, mean_x, y, mean_y):
	covar = 0.0
	for i in range(len(x)):
		covar += (x[i] - mean_x) * (y[i] - mean_y)
	return covar

# Calculate the variance of a list of numbers
def variance(values, mean):
	return sum([(x-mean)**2 for x in values])

# Calculate coefficients
def coefficients(dataset):
	x = [row[0] for row in dataset]
	y = [row[1] for row in dataset]
	x_mean, y_mean = mean(x), mean(y)
	b1 = covariance(x, x_mean, y, y_mean) / variance(x, x_mean)
	b0 = y_mean - b1 * x_mean
	return [b0, b1]

# Simple linear regression algorithm
def simple_linear_regression(train, test):
	predictions = list()
	b0, b1 = coefficients(train)
	for row in test:
		yhat = b0 + b1 * row[0]
		predictions.append(yhat)
	return predictions

# Simple linear regression on insurance dataset
seed(1)
# load and prepare data
filename = 'insurance.csv'
dataset = load_csv(filename)
for i in range(len(dataset[0])):
	str_column_to_float(dataset, i)
# evaluate algorithm
split = 0.6
rmse = evaluate_algorithm(dataset, simple_linear_regression, split)
print('RMSE: %.3f' % (rmse))

# 瑞典保险数据集上的简单线性回归

from random import seed

from random import randrange

from csv import reader

from math import sqrt

# 加载 CSV 文件

def load_csv(filename):

dataset = list()

with open(filename, 'r') as file:

csv_reader = reader(file)

for row in csv_reader:

if not row:

continue

dataset.append(row)

return dataset

# 将字符串列转换为浮点数

def str_column_to_float(dataset, column):

for row in dataset:

row[column] = float(row[column].strip())

# 将数据集拆分为训练集和测试集

def train_test_split(dataset, split):

train = list()

train_size = split * len(dataset)

dataset_copy = list(dataset)

while len(train) < train_size:

index = randrange(len(dataset_copy))

train.append(dataset_copy.pop(index))

return train, dataset_copy

# 计算均方根误差

def rmse_metric(actual, predicted):

sum_error = 0.0

for i in range(len(actual)):

prediction_error = predicted[i] - actual[i]

sum_error += (prediction_error ** 2)

mean_error = sum_error / float(len(actual))

return sqrt(mean_error)

# 使用训练/测试拆分评估算法

def evaluate_algorithm(dataset, algorithm, split, *args):

train, test = train_test_split(dataset, split)

test_set = list()

for row in test:

row_copy = list(row)

row_copy[-1] = None

test_set.append(row_copy)

predicted = algorithm(train, test_set, *args)

actual = [row[-1] for row in test]

rmse = rmse_metric(actual, predicted)

return rmse

# 计算数字列表的平均值

def mean(values):

return sum(values) / float(len(values))

# 计算 x 和 y 之间的协方差

def covariance(x, mean_x, y, mean_y):

covar = 0.0

for i in range(len(x)):

covar += (x[i] - mean_x) * (y[i] - mean_y)

return covar

# 计算数字列表的方差

def variance(values, mean):

return sum([(x-mean)**2 for x in values])

# 计算系数

def coefficients(dataset):

x = [row[0] for row in dataset]

y = [row[1] for row in dataset]

x_mean, y_mean = mean(x), mean(y)

b1 = covariance(x, x_mean, y, y_mean) / variance(x, x_mean)

b0 = y_mean - b1 * x_mean

return [b0, b1]

# 简单线性回归算法

def simple_linear_regression(train, test):

predictions = list()

b0, b1 = coefficients(train)

for row in test:

yhat = b0 + b1 * row[0]

predictions.append(yhat)

return predictions

# 瑞典保险数据集上的简单线性回归

seed(1)

# 加载并准备数据

filename = 'insurance.csv'

dataset = load_csv(filename)

for i in range(len(dataset[0])):

str_column_to_float(dataset, i)

# 评估算法

split = 0.6

rmse = evaluate_algorithm(dataset, simple_linear_regression, split)

print('RMSE: %.3f' % (rmse))

运行算法会打印出训练模型在训练数据集上的 RMSE。

得分约为 33（千克朗），远优于零规则算法在同一问题上获得的约 81（千克朗）的得分。

RMSE: 33.630

1	RMSE：33.630

扩展

本教程最好的扩展是在更多问题上尝试该算法。

只有输入 (x) 和输出 (y) 列的小数据集在统计书籍和课程中很受欢迎。这些数据集中的许多都可以在线获取。

寻找更多小型数据集，并使用简单线性回归进行预测。

您是否将简单线性回归应用于另一个数据集？
在下面的评论中分享您的经验。

回顾

在本教程中，您学习了如何使用 Python 从零开始实现简单线性回归算法。

具体来说，你学到了：

如何从训练数据集估计统计量，如均值、方差和协方差。
如何估计模型系数并使用它们进行预测。
如何使用简单线性回归对真实数据集进行预测。

你有什么问题吗？
在下面的评论中提出您的问题，我将尽力回答。

关于此主题的更多信息

如何使用 Python 从零开始创建算法测试框架

如何在 Python 中从零开始实现线性回归

对如何使用 Python 从零开始实现简单线性回归的 168 条回复

Vineeth 2016 年 10 月 27 日下午 7:28 #

嗨，Jason，

我已下载 csv 文件，但当我尝试对该文件运行脚本时，出现以下错误

” 无法将字符串转换为浮点数：’X’ ”

此脚本在函数 def train_test_split(dataset, split) 处停止

您能确认您的 csv 文件结构吗？

此致
Vineeth

回复
- Jason Brownlee 2016 年 10 月 28 日上午 9:08 #
  
  很抱歉听到这个消息，Vineeth。
  
  完全是我的错误，请勿在小的人为数据集中包含列标题。删除第一行。
  
  我将更新示例。
  
  回复
  - En-wai 2016 年 10 月 30 日上午 7:58 #
    
    嗨，Jason……我已删除了列标题 X 和 Y 以及文件中的所有其他描述性信息，但我仍然收到此错误
    
    ” ValueError: 无法将字符串转换为浮点数: i”
    
    这是我的 csv 文件在删除空格（将其替换为逗号）并将欧洲的“,”更改为十进制的“.”后的前 5 个值
    
    108,392.5
    19,46.2
    13,15.7
    124,422.2
    40,119.4
    
    回复
    - Jason Brownlee 2016 年 10 月 30 日上午 8:59 #
      
      您的文件看起来很完美。
      
      确认文件末尾没有空行。
      
      回复
    - ajay rana 2020 年 12 月 29 日下午 6:50 #
      
      您应该怎么做，将列作为数组提取
      
      x = np.array(data[['column']] )
      
      像这样提取两列
      它会工作
      
      回复
  - Adeel 2021 年 12 月 3 日上午 12:54 #
    
    我在哪里可以找到 csv 文件？
    
    回复
    - Adrian Tam 2021 年 12 月 8 日上午 6:30 #
      
      链接在帖子中
      
      回复
    - James Carmichael 2021 年 12 月 22 日上午 9:45 #
      
      嗨，Adeel……引用的数据可以在以下链接中找到
      
      https://college.cengage.com/mathematics/brase/understandable_statistics/7e/students/datasets/slr/frames/slr06.html
      
      到达此位置后，选择 .xls 文件，下载并将其保存为 .csv 文件。
      
      如果您需要进一步澄清，请告诉我。
      
      此致，
      
      回复
Adrian Moldovan 2016 年 10 月 27 日下午 9:20 #

太棒了！
感谢您花时间讲解所有步骤，并逐字逐句解释……所有内容。

回复
- Jason Brownlee 2016 年 10 月 28 日上午 9:09 #
  
  不客气，Adrian，很高兴您觉得它有价值。
  
  回复
Nelson Silva 2016 年 10 月 28 日上午 2:11 #

你好 Jason，
很棒的教程！
如果您还提供 Python 中相应绘图的代码，那就太好了！
特别是数据集的绘图 🙂

谢谢你。

回复
- Jason Brownlee 2016 年 10 月 28 日上午 9:16 #
  
  好建议，Nelson，谢谢。
  
  我打算将库的使用量降到最低（例如，没有 matplotlib 或 seaborn）。
  
  回复
- Rahul Sharma 2017 年 6 月 13 日上午 5:46 #
  
  嗨，Nelson，您可以使用 pyplotlib 库创建这种散点图
  
  请使用此代码实现散点图
  
  import pyplotlib.pyplot as py
  py.scatter(x_axis_value,y_axis_value,color='black')
  py.show()
  
  希望这有帮助！
  
  回复
venkat dabbara 2016 年 10 月 28 日上午 4:58 #

predicted = algorithm(dataset, test_set)

algorithm 在哪里定义？？？

回复
- Jason Brownlee 2016 年 10 月 28 日上午 9:18 #
  
  好问题，Venkat。
  
  evaluate_algorithm() 函数中的“algorithm”参数是一个函数名。我们将函数名作为“simple_linear_regression”传入。这意味着当我们在 evaluate_algorithm() 中执行 algorithm() 进行预测时，我们实际上正在调用 simple_linear_regression() 函数。
  
  我这样做是为了将算法评估与算法实现分开，以便相同的测试工具可以用于许多不同的算法。
  
  回复
En-wai 2016 年 10 月 28 日下午 9:14 #

在第 2 节“计算协方差”中，我认为这两个含义不是很清楚。请检查。

“事实上，协方差是相关性的一种推广，它仅限于两个变量。而协方差可以在两个或多个变量之间计算。”？？？？？？？

回复
- Jason Brownlee 2016 年 10 月 29 日上午 7:42 #
  
  谢谢 En-wai，我已更新措辞。
  
  我试图评论协方差是如何将相关性从 2 组数字抽象到 2 组以上数字的。
  
  回复
Ram 2016 年 10 月 29 日上午 1:06 #

你好，

我对线性回归有了清晰的了解。谢谢。

我们使用 SciPi 库计算线性回归，如下所示。

regr = linear_model.LinearRegression()

regr.fit(X_train, y_train)。

请澄清，当我们调用上述代码时，所有这些计算是否会在后台发生。

回复
- Jason Brownlee 2016 年 10 月 29 日上午 9:25 #
  
  你好，Ram，
  
  有更有效的方法可以使用线性代数来实现这些算法。我预计这些更有效的方法正在幕后使用。
  
  实现算法对于学习它们的工作原理非常有用，但不建议在生产中使用这些从零开始的实现。
  
  回复
Aliyu A. Aziz 2016 年 10 月 29 日下午 6:03 #

嗨，Jason，

非常感谢这个易于理解的从零开始的 LR。我注意到第 9 行

file = open(filename, "rb")

正在以文本模式打开文件，导致“错误：迭代器应返回字符串，而不是字节（您是否以文本模式打开文件？）”

将 'rb' 更改为 'rt' 或 'r'
file = open(filename, "rt")

修复了错误。

此致

回复
- Jason Brownlee 2016 年 10 月 30 日上午 8:54 #
  
  太棒了，谢谢 Aliyu。
  
  它在我的平台上确实有效，但我将使示例更具可移植性。
  
  回复
saimadhu 2016 年 11 月 3 日下午 6:06 #

你好，
Jason Brownlee

非常感谢您关于简单线性回归的精彩文章。这篇文章是了解简单线性回归分析的最佳教程，我觉得这篇文章是学习多重回归分析之前必读的文章。

回复
- Jason Brownlee 2016 年 11 月 4 日上午 9:06 #
  
  谢谢 saimadhu，很高兴您觉得它有用。
  
  回复
Johnny 2016 年 12 月 13 日上午 4:45 #

又一篇精彩的文章，我喜欢这些基础文章。此外，您直接进入了步骤/核心内容，并且没有遗漏修饰——只是在最后巧妙地总结了它们。谢谢您，先生。

我希望看到/研究针对基本业务类型的数据集的相同类型流程。具体来说，如何生成好的数据集并正确地为业务构建问题区域。您有什么推荐的书籍吗？

回复
- Jason Brownlee 2016 年 12 月 13 日上午 8:09 #
  
  谢谢 Johnny。
  
  抱歉，我不知道有这样的好书。这是一项经验性的追求——更像是一门手艺。最好的教育是实践。
  
  回复
Aslam 2017 年 3 月 12 日上午 4:39 #

我是一个初学者，觉得这很有用。

谢谢您，先生！

回复
- Jason Brownlee 2017 年 3 月 12 日上午 8:28 #
  
  很高兴听到这个消息！
  
  回复
Girish 2017 年 3 月 25 日上午 2:58 #

我们如何使用代码绘制图表

回复
- Jason Brownlee 2017 年 3 月 25 日上午 7:39 #
  
  您可以使用 matplotlib
  
  from matplotlib import pyplot pyplot.plot(x, y) pyplot.show()
  
  1
  2
  3
  
  from matplotlib import pyplot
  pyplot.plot(x, y)
  pyplot.show()
  
  回复
  - Tamil 2019 年 1 月 3 日上午 1:27 #
    
    我试过这个，但它给出了一个空图表。
    
    回复
Nemanja 2017 年 4 月 2 日上午 5:33 #

你好，我们如何在图表上绘制回归线？我们如何减少 rmse？谢谢

回复
- Jason Brownlee 2017 年 4 月 2 日上午 6:33 #
  
  您可以评估每个 epoch/迭代的 RMSE，将 RMSE 值保存在一个数组中，并使用 matplotlib 绘制该数组。
  
  回复
Sean 2017 年 4 月 3 日上午 4:36 #

numpy.cov()、numpy.var() 方法和您的 covariance()、variance() 计算之间有什么关系？我发现两者之间有很大的不同。

谢谢

回复
- Daniel L 2018 年 4 月 27 日下午 12:08 #
  
  协方差和方差都应该除以“n”（由于某种原因他没有这样做），但它在评估 b1 [ b1= cov/var ] 时失去了其重要性。
  
  回复
  - Aiden 2020 年 4 月 10 日上午 5:59 #
    
    仍然是不良做法……您同意吗，Jason？
    
    回复
    - Mahaprasad 2023 年 6 月 19 日下午 6:07 #
      
      嘿，Jason，你能验证一下吗？
      
      方差不应该在公式中除以 N 吗？
      
      这些数据的方差：[1,2,3,4,5] 怎么会是 10？
      这没有意义。
      
      回复
      - James Carmichael 2023 年 6 月 20 日上午 9:55 #
        
        嗨 Mahaprasad……以下资源可能会帮助您澄清
        
        https://www.wikihow.com/Calculate-Variance
Abhishek 2017 年 4 月 28 日下午 3:25 #

这是一篇很棒的文章，感谢您的帮助……

回复
- Jason Brownlee 2017 年 4 月 29 日上午 7:21 #
  
  谢谢 Abhishek，很高兴您觉得它有用。
  
  回复
Nuwan C 2017 年 5 月 4 日下午 1:30 #

嗨，Jason，
感谢您的又一篇精彩教程。
零基算法是做什么的，为什么在这里使用它？

谢谢你

回复
- Jason Brownlee 2017 年 5 月 5 日上午 7:28 #
  
  您是指零规则算法吗？
  
  请参阅此帖子了解描述和工作示例
  https://machinelearning.org.cn/implement-baseline-machine-learning-algorithms-scratch-python/
  
  回复
John David Kromkowski 2017 年 5 月 5 日上午 2:28 #

做得好

可能有个小错字

covariance = sum((x(i) – mean(x)) * (y – mean(y)))

应该是

covariance = sum((x(i) – mean(x)) * (y(i) – mean(y)))

您在实际代码中是正确的

回复
- Jason Brownlee 2017 年 5 月 5 日上午 7:32 #
  
  谢谢约翰。已修复。
  
  回复
Etienne 2017 年 5 月 20 日下午 6:35 #

Jason 您好

我的模型是 y = b0 + (b1 * x) – (b2 / (b3+x))，这在絮凝过程中给出了一个渐近方法。虽然我使用 scipy curve_fit 例程获得了良好的数据拟合，但我不知道如何获得杠杆，即帽子矩阵 H 的对角线元素。而在您的模型中，X 系统矩阵将被表示为

^y = H.y

其中 H 是 X(XT.X)**-1.XT，其中 XT 是 X 的转置

在您的模型中 X.^b 将是

[ 1 x0 ] [b0]
[ 1 x1 ] [b1]
[ 1 x2 ] 。
[ 1 x3 ]
[ .. .. ]

但我的情况会怎样？

另一个问题是如何求解 H，这样我就可以得到对角线元素 hii。

任何帮助将不胜感激。

回复
suguna 2017 年 5 月 24 日上午 4:45 #

我从 csv 文件（保险 CSV）中删除了列标题

然后我收到以下错误

ValueError: 无法将字符串转换为浮点数: female

回复
- Rahul Sharma 2017 年 6 月 13 日上午 5:47 #
  
  suguna，您需要删除 csv 文件中所有存在的空单元格。这就是导致此错误的原因
  
  回复
Rahul Sharma 2017 年 6 月 14 日上午 2:21 #

嗨，Jason，

根据推导：https://en.wikipedia.org/wiki/Standard_deviation

方差 = 平均值 (xi – xMean)^2

但在此算法中，您将其用作：sum([(x-mean)**2 for x in values])

这不是平均值，而只是平方差之和。这是一种修改吗？

回复
- Rahul Sharma 2017 年 6 月 15 日下午 10:12 #
  
  嗨，Jason。您能澄清这个疑问吗。
  
  回复
Digvijay Rana 2017 年 6 月 15 日上午 5:10 #

非常感谢您，先生，
我一直在寻找一个可以自己开始实现算法的地方。这是我读过的最好的教程。期待其他算法的简单实现。

回复
- Jason Brownlee 2017 年 6 月 15 日上午 8:53 #
  
  谢谢，听到这个我很高兴。
  
  我这里有很多
  https://machinelearning.org.cn/machine-learning-algorithms-from-scratch/
  
  回复
- noname 2017 年 6 月 24 日下午 3:13 #
  
  太晚了，Digvijay……赶不上 ML 的班车了……
  
  回复
  - Jason Brownlee 2017 年 6 月 25 日上午 5:58 #
    
    永远不会太晚。
    
    回复
Vaibhav 2017 年 6 月 17 日下午 11:08 #

非常感谢，先生！这是迄今为止最好的描述。

回复
- Jason Brownlee 2017 年 6 月 18 日上午 6:31 #
  
  很高兴听到这个消息。
  
  回复
Kris 2017 年 7 月 6 日下午 11:20 #

我对协方差的定义感到困惑。通常它最终除以 (n - 1)，其中 n 是样本数，而整个代码中没有进行这种操作。您能澄清一下吗？

回复

Soumik Rakshit 2017 年 7 月 13 日上午 1:45 #

我无法将数据集下载为 csv 文件。有人能帮我吗？？？

Jason Brownlee 2017 年 7 月 13 日上午 9:57 #

这是原始文件

Auto Insurance in Sweden

In the following data
X = number of claims
Y = total payment for all the claims in thousands of Swedish Kronor
for geographical zones in Sweden
Reference: Swedish Committee on Analysis of Risk Premium in Motor Insurance
http://college.hmco.com/mathematics/brase/understandable_statistics/7e/students/datasets/
       slr/frames/frame.html

X	Y
108	392,5
19	46,2
13	15,7
124	422,2
40	119,4
57	170,9
23	56,9
14	77,5
45	214
10	65,3
5	20,9
48	248,1
11	23,5
23	39,6
7	48,8
2	6,6
24	134,9
6	50,9
3	4,4
23	113
6	14,8
9	48,7
9	52,1
3	13,2
29	103,9
7	77,5
4	11,8
20	98,1
7	27,9
4	38,1
0	0
25	69,2
6	14,6
5	40,3
22	161,5
11	57,2
61	217,6
12	58,1
4	12,6
16	59,6
13	89,9
60	202,4
41	181,3
37	152,8
55	162,8
41	73,4
11	21,3
27	92,6
8	76,1
3	39,9
17	142,1
13	93
13	31,9
15	32,1
8	55,6
29	133,3
30	194,5
24	137,9
9	87,4
31	209,8
14	95,5
53	244,6
26	187,5

瑞典的汽车保险

在以下数据中

X = 索赔数量

Y = 所有索赔的总付款（以千瑞典克朗计）

适用于瑞典的地理区域

参考: 瑞典机动车保险风险溢价分析委员会

http://college.hmco.com/mathematics/brase/understandable_statistics/7e/students/datasets/

slr/frames/frame.html

X Y

108 392,5

19 46,2

13 15,7

124 422,2

40 119,4

57 170,9

23 56,9

14 77,5

45 214

10 65,3

5 20,9

48 248,1

11 23,5

23 39,6

7 48,8

2 6,6

24 134,9

6 50,9

3 4,4

23 113

6 14,8

9 48,7

9 52,1

3 13,2

29 103,9

7 77,5

4 11,8

20 98,1

7 27,9

4 38,1

0 0

25 69,2

6 14,6

5 40,3

22 161,5

11 57,2

61 217,6

12 58,1

4 12,6

16 59,6

13 89,9

60 202,4

41 181,3

37 152,8

55 162,8

41 73,4

11 21,3

27 92,6

8 76,1

3 39,9

17 142,1

13 93

13 31,9

15 32,1

8 55,6

29 133,3

30 194,5

24 137,9

9 87,4

31 209,8

14 95,5

53 244,6

26 187,5

您需要将“,”转换为“.”，并将列之间的空格替换为“,”。

uma maheswari 2017 年 7 月 16 日下午 9:09 #

嗨，jason

你能告诉我如何对图像数据集进行线性回归吗

回复
- Jason Brownlee 2017 年 7 月 17 日上午 8:46 #
  
  也许线性回归不适合图像数据。
  
  卷积神经网络在图像数据方面非常流行
  https://machinelearning.org.cn/crash-course-convolutional-neural-networks/
  
  回复
Pierce Ng 2017 年 7 月 31 日上午 1:39 #

嗨，Jason，

太棒了！感谢您的阐述。

我实现了一个不进行打乱的 train_test_split 版本，它始终将前 38 个条目作为训练数据，后 25 个条目作为测试数据。程序给出的 RMSE 为 45.23。

您的 RMSE 38.339 是来自 train_test_split 中使用 seed(1) 的随机化。如果我尝试使用 seed(2)，则 RMSE 为 37.734。

不同 RMSE 值下一步是什么？

回复
- Jason Brownlee 2017 年 7 月 31 日上午 8:16 #
  
  这是该方法的方差。
  
  理想情况下，我们会多次评估算法，并报告模型的平均值和标准差。
  
  这有帮助吗？
  
  回复
  - Pierce Ng 2017年8月6日下午3:20 #
    
    确实如此，谢谢。
    
    我将您的Python代码移植到Pharo Smalltalk并写了一篇博客文章。请参阅http://www.samadhiweb.com/blog/2017.08.06.dataframe.html。
    
    回复
    - Jason Brownlee 2017年8月7日上午8:39 #
      
      非常酷，皮尔斯。干得好！
      
      我以前和一个非常喜欢Smalltalk的开发者合作过。
      
      回复
Eoin Kenny 2017年8月11日上午3:14 #

那不是方差的公式……你应该除以n或n-1，这是怎么回事？

回复
- Jason Brownlee 2017年8月11日上午6:43 #
  
  可能是总体方差与样本方差的差异。
  
  回复
Tanmay 2017年9月1日上午2:42 #

你好 Jason，evaluate_algorithm 函数中的 *args 参数是做什么用的？

回复
- Jason Brownlee 2017年9月1日上午6:49 #
  
  这样我们就可以为算法向 evaluate_algorithm() 函数提供可变数量的参数。
  
  它对不同的算法是通用的。
  
  回复
vedang 2017年9月15日上午2:19 #

给定 x，我们如何预测 y 的值？另外，如何获得准确性？

回复
- Jason Brownlee 2017年9月15日下午12:16 #
  
  这就是应用机器学习的全部内容。
  
  也许你最好从Weka开始
  https://machinelearning.org.cn/start-here/#weka
  
  回复
Barrys 2017年9月15日下午1:27 #

嗨，Jason，

感谢您的精彩文章。它们对我很有帮助。

有些地方我不清楚。我们为什么要计算RMSE，它到底意味着什么？我原以为您会像在KNN文章中那样，计算测试数据的预测准确性。

谢谢。

回复
- Jason Brownlee 2017年9月16日上午8:36 #
  
  RMSE 是均方根误差，是预测误差，其单位与输出变量相同。
  
  你无法计算回归问题的准确性。准确性是指所有标签预测中正确标签预测的百分比。在回归中，我们不预测标签，我们预测数量。
  
  回复
  - Barrys 2017年9月16日下午1:28 #
    
    所以我们需要运行另一种算法来预测其标签？如何在不知道其标签的情况下使用给定 x 的 y 值（据我理解，这就是线性回归）？线性回归解决哪种问题？
    
    最好在文档中解释 RMSE 以及我们为什么计算它？它被提及但没有解释。
    
    回复
    - Jason Brownlee 2017年9月17日上午5:25 #
      
      线性回归用于需要预测数量的问题，称为回归问题。
      
      如果您有一个需要预测标签的数据集，则不能使用线性回归。您将需要另一种算法，例如逻辑回归。
      
      回复
Rizvi 2017年10月11日下午9:23 #

嗨，Jason，

对于初学者来说，这是一篇很棒的文章。

目前，我们正在用两个系数拟合一个多项式到数据。如果我们将这种方法扩展到更高阶的多项式，这是否属于非线性回归的范畴？此外，增加多项式阶数会提高估计精度吗？

回复
- Jason Brownlee 2017年10月12日上午5:28 #
  
  它可能会提高准确性，也可能会过拟合数据。试试看吧。
  
  使用可靠的测试工具，确保你不会欺骗自己。
  
  回复
Melina 2017年10月17日上午12:08 #

很棒的教程！谢谢你 🙂

我正在准备一个简单的线性回归演示，我打算使用 sklearn 来展示代码，并将其与您修改过的“自己的”回归算法代码进行比较！

我被您的代码中的一件事卡住了，那就是方差公式/方程。
* 您正在使用：方差 = Sum( (x – mean(x))^2 )
* 它不应该是：方差 = Sum( (x – mean(x))^2 ) / N

我可能只是搞混了，如果我错了，请纠正我的思路。

回复
- Jason Brownlee 2017年10月17日上午5:49 #
  
  它没有标准化。更多信息请参见此处
  https://en.wikipedia.org/wiki/Simple_linear_regression
  
  回复
Adilah 2017年12月6日上午12:46 #

嗨，Jason，这种方法可以用来预测客户对某种产品的消费量吗？（我的英语不好，抱歉）

回复
- Jason Brownlee 2017年12月6日上午9:04 #
  
  我建议您使用此流程系统地解决您的问题
  https://machinelearning.org.cn/start-here/#process
  
  回复
Ronnie Mukherjee 2017年12月16日下午10:01 #

有没有人有整个瑞典保险数据集用于训练和测试（用于验证）的 RMSE？

谢谢

回复
Himsikha hazarika 2018年1月10日下午8:55 #

数据集已经是浮点格式了。所以，我注释掉了

# 将字符串列转换为浮点数
”’def str_column_to_float(dataset, column)
for row in dataset
row[column] = float(row[column].strip())”’
_______________________
X Y
108 392.5
19 46.2
13 15.7
124 422.2
40 119.4
;;;;;;_
______________________________

但是我得到了以下错误

回溯（最近一次调用）
File “linear.py”, line 97, in
rmse = evaluate_algorithm(dataset, simple_linear_regression, split)
File “linear.py”, line 50, in evaluate_algorithm
predicted = algorithm(train, test_set, *args)
File “linear.py”, line 82, in simple_linear_regression
b0, b1 = coefficients(train)
File “linear.py”, line 74, in coefficients
x_mean, y_mean = mean(x), mean(y)
File “linear.py”, line 57, in mean
return sum(values) / float(len(values))
TypeError: 不支持的运算符类型(s) +: ‘int’ 和 ‘str’

回复
- Jason Brownlee 2018年1月11日上午5:49 #
  
  抱歉，我不知道您错误的原因。
  
  回复
  - Gosia 2019年3月15日上午1:49 #
    
    您需要将数据框转换为列表
    
    回复
Faraz 2018年1月22日上午2:20 #

谁能帮我把“,”转换成“.”，并把列之间的空格替换成“,”？如果你能上传代码就太好了！

回复
- Jason Brownlee 2018年1月22日上午4:46 #
  
  抱歉，也许从基础编程课程开始是个不错的选择。
  
  回复
- Shashank 2018年4月23日下午8:09 #
  
  使用linux 🙂 Sed 命令可以一次性帮你搞定 😀
  
  回复
Shashank 2018年4月23日下午8:08 #

嗨，Jason，您能帮我解释一下代码第50行中的 algorithm() 函数吗？它在任何地方都没有定义……？它是一个预定义函数吗……我认为它只是 simple_linear_regression() 函数，因为用后者替换它，我得到了相同的结果 🙂 请协助。

回复
- Jason Brownlee 2018年4月24日上午6:33 #
  
  这是一个函数引用，我们将其作为参数传入。具体来说，它正在执行 simple_linear_regression()
  
  如果你是 Python 编程新手，也许可以从这里开始
  https://machinelearning.org.cn/faq/single-faq/how-do-i-get-started-with-python-programming
  
  回复
Aarabhi Putty 2018年4月27日下午6:38 #

非常感谢你，Jason。它非常有用且易于理解。

回复
- Jason Brownlee 2018年4月28日上午5:26 #
  
  很高兴它有帮助。
  
  回复
ranjan 2018年5月3日下午7:06 #

嗨，Jason，

感谢您的代码并使其易于理解。我编辑了代码，并从末尾选择了后半部分作为训练集，RMSE 为 35.365。

而我看到您的代码会任意选择 60% 的值作为训练集，并给出 RMSE 输出为 38.339。

问：这两种方法中哪种是正确的方法？

回复
- Jason Brownlee 2018年5月4日上午7:39 #
  
  这是一个臆造的例子，我们可以编造它。
  
  通常，训练集和测试集的选择取决于问题的类型以及对数据的了解。
  
  这可能会给你一些想法
  https://machinelearning.org.cn/faq/single-faq/how-do-i-evaluate-a-machine-learning-algorithm
  
  回复
Balghari 2018年5月8日上午6:05 #

如何找到多元线性回归中的 beta_0 和 beta 值？请指导我

回复
- Jason Brownlee 2018年5月8日上午6:18 #
  
  通过优化过程，例如线性代数公式或梯度下降中使用的方法。
  
  回复
manohar 2018年5月14日下午3:02 #

您如何使用零规则算法为保险数据集获得 RMSE 72.251

我正在使用您下面的帖子

https://machinelearning.org.cn/implement-baseline-machine-learning-algorithms-scratch-python/

这是一个回归问题，所以我正在使用回归零规则算法
对于您的帖子我没有得到

例如

108,392.5
19,46.2
13,15.7
124,422.2
40,119.4

这是一个保险数据集，您如何使用零规则算法获得 RMSE 72.251
您能帮忙解决一下吗？

回复
- Jason Brownlee 2018年5月15日上午7:50 #
  
  你到底遇到了什么问题？
  
  回复
manohar palanisamy 2018年5月15日下午6:38 #

实际上，我不知道您如何使用零规则算法获得前五次观测的 RMSE 72.251

108+19+13+124+40=304

平均值 = 304/5 = 60.8

根据您在回归部分提到的以下链接，我得到 60.8

https://machinelearning.org.cn/implement-baseline-machine-learning-algorithms-scratch-python/

回复
- Jason Brownlee 2018年5月16日上午6:00 #
  
  零规则将计算训练数据集中所有值的平均值，以便对测试数据集进行预测。
  
  回复
manohar palanisamy 2018年5月15日下午6:39 #

请告诉我？

回复
Harshit Jain 2018年6月9日下午8:44 #

梯度下降法和解析法在现实世界中没有实现吗？

回复
- Jason Brownlee 2018年6月10日上午6:03 #
  
  线性代数方法是大多数库解决线性回归方程的方式，但它们要求所有数据都在内存中，并且符合该方法的预期（高斯分布，不相关变量等）。
  
  回复
Gourav Singh Bais 2018年6月15日下午2:55 #

如何绘制 x 和 y 的散点图以及所有预测值？

回复
- Jason Brownlee 2018年6月16日上午7:23 #
  
  您可以使用 matplotlib 的 scatter() 函数。
  
  回复
Boris 2018年7月3日下午10:51 #

嗨 Jason
我是机器学习新手。很棒的例子和教程。如果 X 部分有多列，例如有 6 列，代码应该怎么写？谢谢

回复
- Jason Brownlee 2018年7月4日上午8:23 #
  
  您可以修改代码以支持多个输入，或使用 sklearn 等库。
  
  回复
Betaman 2018年7月12日上午12:44 #

我不明白这段代码的重要性
能不能一次性把代码发过来

不过帖子很棒

回复
- Jason Brownlee 2018年7月12日上午6:26 #
  
  如果本教程不适合您，请尝试在 Google 上搜索其他教程？
  
  回复
Prajna p n 2018年7月12日下午4:57 #

根据您在文章中提供的方差公式
方差 = sum( (x – mean(x))^2 ) ..但理想情况下，根据公式，方差 = sum( (x – mean(x))^2 )/(n-1)。

回复
Aditi 2018年8月12日下午10:59 #

你好 Jason，

我尝试运行程序。它给我以下错误。你能告诉我这里出了什么问题吗？

ipython-input-4-eae09e62a94d> in load_csv(filename)
6 if not row
7 continue
—-> 8 dataset.append()
9 return dataset
10

TypeError: append() 恰好接受一个参数（给定 0 个）

回复
- Jason Brownlee 2018年8月13日上午6:17 #
  
  或许确认您正在使用 Python 2.7？
  
  回复
  - mrunal 2018年8月22日下午4:40 #
    
    这是一个很棒的教程。我非常喜欢它。我的回归分析已经通过您的教程解决了。此外，我有 4000 个数据集的 6 个输入和 6 个输出。您能提供给我 Python 中的神经网络拟合代码吗？
    
    回复
    - Jason Brownlee 2018年8月23日上午6:12 #
      
      干得好。
      
      是的，您可以有一个向量输出。我推荐使用 Keras
      https://machinelearning.org.cn/start-here/#deeplearning
      
      回复
Narender 2018年8月23日上午3:03 #

很棒的网站和宝贵的资源。谢谢 Jason！

回复
- Jason Brownlee 2018年8月23日上午6:15 #
  
  谢谢，希望它有帮助。
  
  回复
Syed Fakhar Alam 2018年9月3日下午11:42 #

嗨 Jason，我如何使用 tensorflow 在 python 中实现 svm 模型？

回复
- Jason Brownlee 2018年9月4日上午6:07 #
  
  抱歉，我没有任何关于 TensorFlow 的教程。
  
  我建议使用 sklearn 来实现 SVM 模型
  https://machinelearning.org.cn/start-here/#python
  
  回复
Karthik Kolle 2019年2月17日上午2:21 #

嗨
我是机器学习新手。

这可能听起来像一个愚蠢的问题，但我还是要问。

屏幕上打印的最终值到底代表什么？

另外，如果我要包含绘图，我该如何进行？

回复
- Jason Brownlee 2019年2月17日上午6:35 #
  
  在这个例子中，我们学习了如何预测一个小规模的虚构问题中的输出，给定一个输入。
  
  你可以像我一样在 Excel 中创建一个图表，显示输入和输出之间的原始关系，以及输入和预测之间的关系。
  
  回复
Suchha 2019年3月29日下午5:48 #

嗨，Jason，

这是一篇很棒的帖子。我对回归代码的搜索到此结束。
我非常感谢你的耐心。你已经回复了迄今为止的每一条评论……
向你致敬。愿上帝保佑你……

回复
- Jason Brownlee 2019年3月30日上午6:24 #
  
  乐意效劳。
  
  回复
Laxmikant 2019年5月28日下午9:31 #

只是一个建议，您可以制作一个视频，其中可能包含所有答案。🙂 这会节省我们阅读您的宝贵博客的时间 😛

顺便说一句，我发现您的帖子内容丰富，对初学者来说是很好的文章。非常感谢 🙂

回复
- Jason Brownlee 2019年5月29日上午8:42 #
  
  感谢您的建议。
  
  我发现视频不是一种好的教学媒介。太被动了。
  
  我们在应用机器学习中通过实践学习。这包括阅读、写作、编码、实验等。
  
  回复
Red 2019年8月11日下午10:43 #

非常感谢 Jason，
您的帖子信息量很大，很有帮助。您有没有关于 Huber 回归的类似帖子？

回复
- Jason Brownlee 2019年8月12日上午6:37 #
  
  谢谢。
  
  目前还没有，谢谢您的建议！
  
  回复
v.c 2019年9月25日上午4:31 #

嗨，Jason，

感谢您的精彩博客，参考您的博客，我用 C 语言实现了同样的功能。可以在 https://github.com/novice-programmer/numerical-programing/tree/master/simple_linear_regression 找到。如果有任何建议，请分享。

回复
- Jason Brownlee 2019年9月25日上午6:04 #
  
  干得好！
  
  回复
Shoumitra Bala 2019年10月19日上午10:18 #

非常有帮助且内容丰富，适合机器学习初学者入门

回复
- Jason Brownlee 2019年10月20日上午6:14 #
  
  谢谢！
  
  回复
lavanya 2019年10月21日下午9:03 #

你好 jason,

它真的很有用。

你能帮助我们理解线性回归的假设以及实现这些假设的方法，比如误差的正态分布、等方差、独立性吗？

提前感谢

回复
- Jason Brownlee 2019年10月22日上午5:47 #
  
  我相信维基百科有一个很好的线性回归假设列表
  https://zh.wikipedia.org/wiki/线性回归#假设
  
  回复
Ashish 2019年11月15日上午7:30 #

嗨，Jason，

请您帮忙解决以下疑问。

1) 这个完整的过程与 Sklearn LinearRegression() 有何不同？

2) 我们如何确定我们获得了最适合我们模型的最佳最优线，即我们的模型成本已尽可能最小化。就像我们在 MLE 和梯度下降中获得的那样。

3) 这种方法最适合大型数据集吗？

谢谢

阿希什·阿罗拉

回复
- Jason Brownlee 2019年11月15日上午7:58 #
  
  Sklearn 将使用分析解，例如线性代数。
  
  最小化 MSE 将实现模型的“最优”拟合，它可能或可能不是数据集的最佳模型。
  
  此方法仅适用于两个变量（一个输入，一个输出），并且当相关系数可以计算或估计时。
  
  回复
chase 2019年12月10日上午10:35 #

嗨 Jason，如果我只是想测试线性回归函数而不使用 RMSE，我该怎么做？谢谢

回复
- Jason Brownlee 2019年12月10日下午1:36 #
  
  你具体指的是什么？
  
  回复
  - Chase 2019年12月10日下午1:53 #
    
    如何在不使用“evaluate_algorithm”和“rmse_metric”函数的情况下测试 simple_linear_regression 函数？或者那是不可能的？
    
    回复
    - Jason Brownlee 2019年12月11日上午6:46 #
      
      是的，您可以训练系数并直接使用它们进行预测。
      
      回复
Abhishek Panchal 2019年12月26日下午10:51 #

我运行代码时遇到此错误
—————————————————————————
ValueError 回溯 (最近一次调用)
in
1 split = 0.6
—-> 2 rmse = evaluate_algorithm(dataset, simple_linear_regression, split)

在 evaluate_algorithm(dataset, algorithm, split, *args)
1 def evaluate_algorithm(dataset, algorithm, split, *args)
—-> 2 train, test = train_test_split(dataset, split)
3 test_set = list()
4 for row in test
5 row_copy = list(row)

在 train_test_split(dataset, split)
4 dataset_copy = list(dataset)
5 while len(train) 6 index = randrange(len(dataset_copy))
7 train.append(dataset_copy.pop(index))
8 return train, dataset_copy

~\Anaconda3\lib\random.py in randrange(self, start, stop, step, _int)
188 if istart > 0
189 return self._randbelow(istart)
–> 190 raise ValueError(“randrange() 的范围为空”)
191
192 # 提供了 stop 参数。

ValueError: randrange() 的范围为空

有什么想法为什么它不工作吗？

回复
- Jason Brownlee 2019年12月27日上午6:34 #
  
  很抱歉听到这个消息，我在这里有一些建议。
  https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
  
  回复
DM 2020年3月28日上午9:24 #

预测点的输出数组不是一个错误吗？
1.1999999999999995,
1.9999999999999996,
3.5999999999999996,
2.8,
4.3999999999999995

看起来第3和第4个元素混淆了。

回复
- Jason Brownlee 2020年3月29日上午5:48 #
  
  怎么会呢？
  
  回复
Siddharth Singh 2020年6月3日下午11:25 #

嗨，Jason，
帮助我理解
row_copy[-1] = None 和
actual = [row[-1] for row in dataset]
来自函数 evaluate_algorithm()

回复
- Jason Brownlee 2020年6月4日上午6:23 #
  
  第一个将列表中的最后一个值设置为 None，即输出值，这样我们就不会作弊。
  
  第二个检索数据集中每行的最后一个值，即创建一个仅包含预测的列表。
  
  回复
Siddharth Singh 2020年6月5日上午2:51 #

谢谢你，Jason

回复
- Jason Brownlee 2020年6月5日上午8:17 #
  
  不客气。
  
  回复
Oleg 2020年6月19日上午9:03 #

谢谢你，Jason！这是一个很棒的例子。
澄清一下，这里我们训练了算法，然后测试了它。
那么，如果我有一个只有“X”值的列表，如何将它们传递给函数以获取输出“Y”值？假设我有 200 个索赔，我需要它的总付款？
谢谢你

回复
- Jason Brownlee 2020年6月19日下午1:11 #
  
  您可以在最后一个示例中看到进行预测的示例，例如使用一行数据
  
  yhat = b0 + b1 * row[0]
  
  1
  
  yhat = b0 + b1 * row[0]
  
  回复
Gideon Aswani 2020年9月2日下午9:38 #

嗨 Jason

感谢分享。这是一个很棒的教程。我能够在 Jupyter Notebook 中顺利地跟随并实现它。我将尝试不同的数据集，并对代码进行适当的更改。再次感谢。

回复
- Jason Brownlee 2020年9月3日上午6:06 #
  
  不客气，干得好！
  
  回复
Santosh Khanal 2020年9月7日下午4:51 #

C:\Users\99193942\AppLockerExceptions\PycharmProject\Simple_linear_regression\venv\Scripts\python.exe C:/Users/99193942/AppLockerExceptions/PycharmProject/Simple_linear_regression/Predict_insurance.py
回溯（最近一次调用）
File “C:/Users/99193942/AppLockerExceptions/PycharmProject/Simple_linear_regression/Predict_insurance.py”, line 98, in
rmse = evaluate_algorithm(dataset, simple_linear_regression, split)
File “C:/Users/99193942/AppLockerExceptions/PycharmProject/Simple_linear_regression/Predict_insurance.py”, line 50, in evaluate_algorithm
predicted = algorithm(train, test_set, *args)
File “C:/Users/99193942/AppLockerExceptions/PycharmProject/Simple_linear_regression/Predict_insurance.py”, line 83, in simple_linear_regression
for row in test
NameError: 名称“test”未定义

回复
- Jason Brownlee 2020年9月8日上午6:47 #
  
  很抱歉您遇到问题，这些提示可能会有所帮助
  https://machinelearning.org.cn/faq/single-faq/why-does-the-code-in-the-tutorial-not-work-for-me
  
  回复
  - Robin 2020年11月14日下午10:09 #
    
    嗨，Jason，
    
    我刚开始深度学习硕士课程，我正在做一个模型来检测工业领域中使用的 Modbus 协议中的恶意行为，您有什么可以开始的吗，请给我您的建议
    
    回复
    - Jason Brownlee 2020年11月15日上午6:25 #
      
      也许这个过程会帮助您完成您的项目
      https://machinelearning.org.cn/start-here/#process
      
      回复
Fahmi 2020年12月2日下午12:47 #

你好，Jason……
我们如何通过代码从上面保险数据集的简单线性回归预测结果中绘制图表？
非常感谢

回复
- Jason Brownlee 2020年12月2日下午1:20 #
  
  本教程提供了绘制回归模型线的示例
  https://machinelearning.org.cn/robust-regression-for-machine-learning-in-python/
  
  回复
Trupt 2021年9月2日下午7:28 #

嗨，Jason

杰作。

我只是想知道你是如何得到 B0 和 B1 的这些起始值的

B1 = sum((x(i) – mean(x)) * (y(i) – mean(y))) / sum( (x(i) – mean(x))^2 )
B0 = mean(y) – B1 * mean(x)

，我很好奇……

回复
- Jason Brownlee 2021年9月3日上午5:30 #
  
  谢谢！
  
  任意的。实际上，从零或一个小的随机数开始。
  
  回复
Sobia murtaza 2021年9月27日下午3:50 #

使用此代码我可以获得线性回归来查找任何数据集的成本函数吗？我应该遵循所有这些步骤来查找成本函数吗？

回复
- Adrian Tam 2021年9月28日上午9:32 #
  
  通常成本函数是你在进行回归之前就决定的。例如，对于 y=f(X) 的线性回归，使用均方误差作为成本。
  
  回复
alifiya 2021年10月18日上午10:13 #

我的 RMSE 值是 104，这可能吗（因为该值应该在 0~1 之间），原因可能是什么

回复
- Adrian Tam 2021年10月20日上午9:16 #
  
  可能。但这表示你的模型非常糟糕。这样想，你的输出 y 的范围是 0 到 1，因此标准差不应大于 1。你犯的误差是标准差的 100 倍。
  
  回复
Alina 2022年3月24日下午12:47 #

你好，
当我运行代码时，它给我一个浮点对象不可下标的错误。错误发生在系数函数中，当尝试获取数据的系数时。你知道这个问题的解决方案吗？

回复
- James Carmichael 2022年3月25日下午1:51 #
  
  嗨 Alina……谢谢提问。
  
  我很想帮忙，但我实在没有能力为您调试代码。
  
  我很乐意提出一些建议
  
  考虑将代码积极削减到最低要求。这将帮助您隔离问题并专注于它。
  考虑将问题简化为一个或几个简单的例子。
  考虑寻找其他可行的类似代码示例，并慢慢修改它们以满足您的需求。这可能会暴露您的失误。
  考虑在 StackOverflow 上发布您的问题和代码。
  
  回复
Burhan Bilen 2022年4月22日下午6:44 #

你好 Jason，感谢你的解释和代码。我想知道为什么有些人使用梯度下降来优化成本，而另一些人则不使用（在我的案例中，我也没有使用，只使用了基本公式）。它们之间有什么区别吗？

回复
- James Carmichael 2022年4月24日上午3:35 #
  
  嗨 Burhan……是的，梯度下降可以按如下方式使用
  
  https://machinelearning.org.cn/a-gentle-introduction-to-optimization-mathematical-programming/
  
  回复
ankit 2023年2月22日上午1:52 #

嘿，感谢您的精彩博客，您有没有关于实现多项式回归的类似博客，实际上我有 5 个候选多项式回归模型，我必须估计它们的参数

回复
- James Carmichael 2023年2月22日上午8:23 #
  
  嗨 Ankit……以下资源可能会引起您的兴趣
  
  https://medium.com/analytics-vidhya/understanding-polynomial-regression-5ac25b970e18
  
  回复
Vinícius Jean Ferreira 2023年8月1日上午12:10 #

你好，詹姆斯。
好帖子！我只是很难理解：线性回归真的就这么简单，还是算法中有更多迭代来寻找最佳系数？我的意思是……它应该使用梯度下降函数来评估误差并最小化它，还是我错了？

谢谢？

回复
- James Carmichael 2023年8月1日上午9:10 #
  
  嗨 Vincius……是的，梯度下降可以如下使用
  
  https://machinelearning.org.cn/a-gentle-introduction-to-gradient-descent-procedure/
  
  回复

导航

如何使用 Python 从零开始实现简单线性回归

描述

简单线性回归

瑞典保险数据集

教程

1. 计算均值和方差

2. 计算协方差

3. 估计系数

4. 进行预测

5. 预测保险

扩展

回顾

了解如何从零开始编写算法！

没有库，只有 Python 代码。

最后，揭开
机器学习算法的神秘面纱

关于此主题的更多信息

对如何使用 Python 从零开始实现简单线性回归的 168 条回复

发表评论点击此处取消回复。

导航

描述

简单线性回归

瑞典保险数据集

教程

1. 计算均值和方差

2. 计算协方差

3. 估计系数

4. 进行预测

5. 预测保险

扩展

回顾

了解如何从零开始编写算法！

没有库，只有 Python 代码。

最后，揭开机器学习算法的神秘面纱

关于此主题的更多信息

对如何使用 Python 从零开始实现简单线性回归的 168 条回复

发表评论 点击此处取消回复。

最后，揭开
机器学习算法的神秘面纱

发表评论点击此处取消回复。