
Python 中逐步实现高级特征缩放技术
图片作者 | ChatGPT
在本文中,您将学习到:
- 为什么标准缩放方法有时不够用,以及何时应使用高级技术。
- 四种高级策略的概念:分位数转换、幂转换、鲁棒缩放和单位向量缩放。
- 如何使用 Python 的 scikit-learn 库逐步实现这些技术。
引言
特征缩放是最常用的数据预处理技术之一,其应用范围从统计建模到分析、机器学习、数据可视化和数据叙事。尽管在大多数项目和用例中,我们通常会采用一些最流行的方法——如归一化和标准化——但在某些情况下,这些基本技术可能不够用。例如,当数据是偏斜的、充满异常值,或者不遵循或不接近高斯分布时。在这些情况下,可能需要采用更高级的缩放技术,能够将数据转换为更能反映下游算法或分析技术假设的形式。这些高级技术包括分位数转换、幂转换、鲁棒缩放和单位向量缩放。
本文旨在提供高级特征缩放技术的实用概述,描述每种技术的工作原理,并展示每种技术的 Python 实现。
四种高级特征缩放策略
在接下来的章节中,我们将通过基于 Python 的示例介绍和展示如何使用以下四种特征缩放技术
- 分位数转换
- 幂转换
- 鲁棒缩放
- 单位向量缩放
让我们开始吧。
1. 分位数转换
分位数转换将输入数据的分位数(按特征)映射到目标分布的分位数,通常是均匀分布或正态分布。该方法不就数据的真实分布做出硬性假设,而是关注与观测数据点相关的经验分布。它的一个主要优点是对于异常值具有鲁棒性,这在将数据映射到均匀分布时特别有用,因为它会展开常见值并压缩极端值。
本示例展示了如何将分位数转换应用于小型数据集,并使用正态分布作为输出分布
|
1 2 3 4 5 6 7 8 9 10 |
from sklearn.preprocessing import QuantileTransformer import numpy as np X = np.array([[10], [200], [30], [40], [5000]]) qt = QuantileTransformer(output_distribution='normal', random_state=0) X_trans = qt.fit_transform(X) print("Original Data:\n", X.ravel()) print("Quantile Transformed (Normal):\n", X_trans.ravel()) |
其机制与大多数 scikit-learn 类相似。我们使用实现了转换的 QuantileTransformer 类,在初始化缩放器时指定所需的输出分布,然后对数据应用 fit_transform 方法。
输出
|
1 2 3 4 |
原始数据: [ 10 200 30 40 5000] 分位数转换( (正态): [-5.19933758 0.67448975 -0.67448975 0. 5.19933758] |
如果我们想按分位数将数据映射到均匀分布,只需将 output_distribution 设置为 'uniform' 即可。
2. 幂转换
众所周知,许多机器学习算法、分析技术和假设检验方法都假定数据服从正态分布。幂转换有助于使非正态数据看起来更像正态分布。要应用的具体转换取决于参数 $λ$,其值通过最大似然估计等优化方法确定,该方法试图找到能产生最正态映射的原始数据值的 $λ$。称为Box-Cox 幂转换的基本方法仅适用于处理正值。称为Yeo-Johnson 幂转换的替代方法在存在正值、负值以及零值时更可取。
|
1 2 3 4 5 6 7 8 9 10 |
from sklearn.preprocessing import PowerTransformer import numpy as np X = np.array([[1.0], [2.0], [3.0], [4.0], [5.0]]) pt = PowerTransformer(method='box-cox', standardize=True) X_trans = pt.fit_transform(X) print("Original Data:\n", X.ravel()) print("Power Transformed (Box-Cox):\n", X_trans.ravel()) |
输出
|
1 2 3 4 |
原始数据: [1. 2. 3. 4. 5.] 幂转换( (Box-Cox): [-1.50121999 -0.64662521 0.07922595 0.73236192 1.33625733] |
如果数据集中包含零值或负值,您可以通过将 method 设置为 'yeo-johnson' 来使用 Yeo-Johnson 转换。
3. 鲁棒缩放
当数据包含异常值或不服从正态分布时,鲁棒缩放器是标准化的一个有趣替代方案。标准化将数据围绕均值居中并根据标准差进行缩放,而鲁棒缩放使用对异常值鲁棒的统计量。具体来说,它通过减去中位数来居中数据,然后除以四分位距(IQR)来缩放数据,遵循以下公式
$X_{scaled} = \frac{X – \text{Median}(X)}{\text{IQR}(X)}$
Python 实现很简单
|
1 2 3 4 5 6 7 8 9 10 |
from sklearn.preprocessing import RobustScaler import numpy as np X = np.array([[10], [20], [30], [40], [1000]]) scaler = RobustScaler() X_trans = scaler.fit_transform(X) print("Original Data:\n", X.ravel()) print("Robust Scaled:\n", X_trans.ravel()) |
输出
|
1 2 3 4 |
原始数据: [ 10 20 30 40 1000] 鲁棒缩放: [-1. -0.5 0. 0.5 48.5] |
鲁棒缩放的价值在于能够提供更可靠的数据分布表示,尤其是在存在像上面示例中的 1000 这样极端异常值的情况下。
4. 单位向量缩放
单位向量缩放,也称为归一化,将每个样本(即数据矩阵中的每一行)缩放到具有单位范数(长度为 1)。它通过将样本中的每个元素除以该样本的范数来实现。有两种常见的范数:L1 范数,即元素绝对值之和;L2 范数,即平方和的平方根。使用其中一种或另一种取决于您是想关注数据稀疏性(L1)还是保留几何距离(L2)。
本示例将单位向量缩放应用于两个样本,将每一行转换为基于 L2 范数的单位向量(将参数更改为 'l1' 以使用 L1 范数)
|
1 2 3 4 5 6 7 8 9 10 |
从 sklearn.预处理 导入 Normalizer import numpy as np X = np.array([[1, 2, 3], [4, 5, 6]]) normalizer = Normalizer(norm='l2') X_trans = normalizer.transform(X) print("Original Data:\n", X) print("L2 Normalized:\n", X_trans) |
输出
|
1 2 3 4 5 6 |
原始数据: [[1 2 3] [4 5 6]] L2归一化: [[0.26726124 0.53452248 0.80178373] [0.45584231 0.56980288 0.68376346]] |
总结
本文介绍了四种高级特征缩放技术,它们在处理极端异常值、非正态分布数据等方面非常有用。通过代码示例,我们展示了在 Python 中使用这些特征缩放技术的具体方法。
作为最后的总结,下表将重点介绍数据问题以及可以考虑使用每种特征缩放技术的示例实际场景
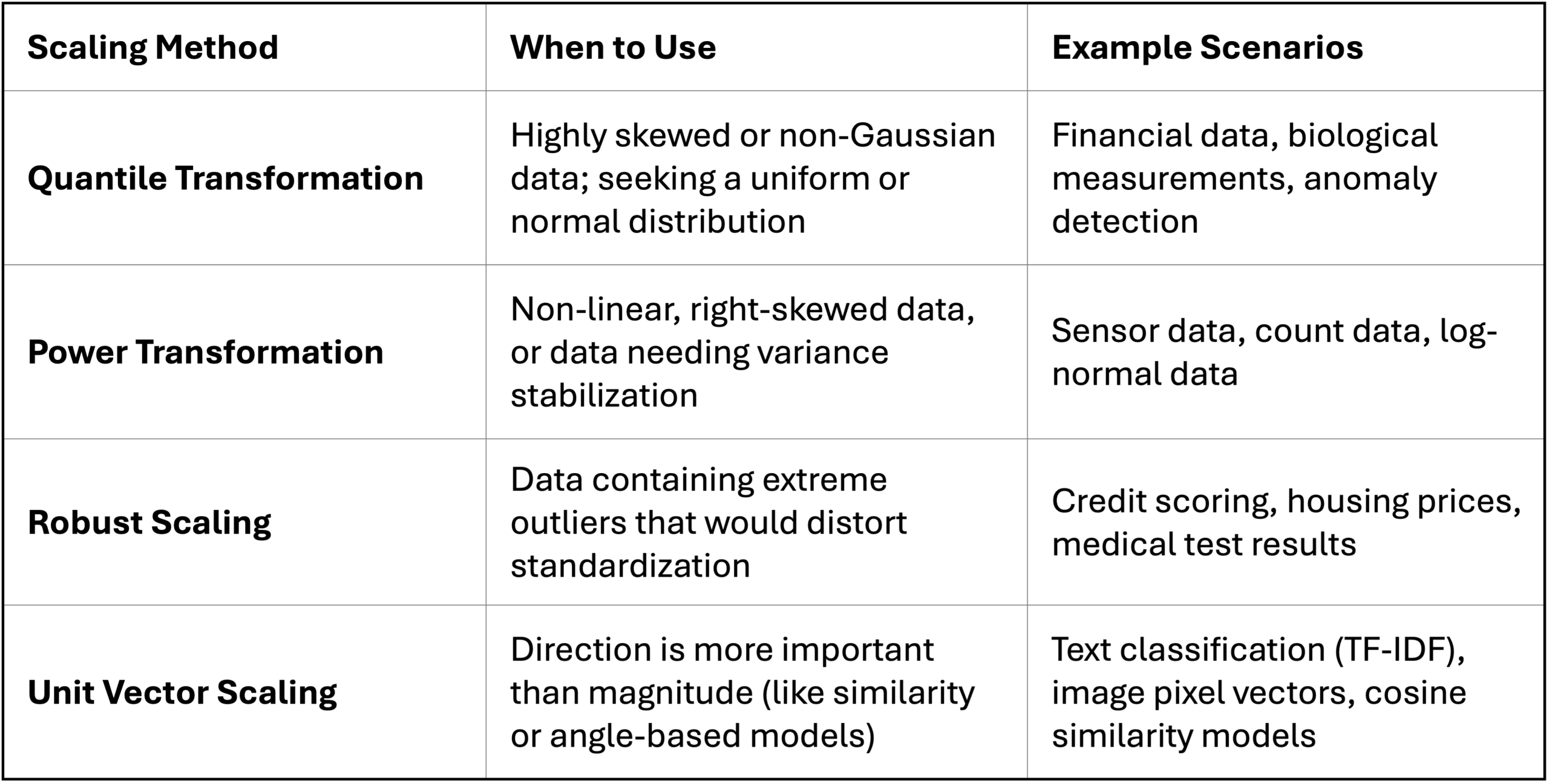






暂无评论。