梯度下降算法是训练深度神经网络最流行的技术之一。它在计算机视觉、语音识别和自然语言处理等领域有许多应用。虽然梯度下降的概念已经存在了几十年,但直到最近才应用于深度学习相关的应用。
梯度下降是一种迭代优化方法,通过在每一步迭代地更新值来找到目标函数的最小值。每次迭代,它都会朝着所需方向迈出小步,直到收敛或满足停止条件。
在本教程中,您将使用两个可训练参数训练一个简单的线性回归模型,并探索梯度下降的工作原理以及如何在 PyTorch 中实现它。特别是,您将学习到
- 梯度下降算法及其在 PyTorch 中的实现
- 批量梯度下降及其在 PyTorch 中的实现
- 随机梯度下降及其在 PyTorch 中的实现
- 批量梯度下降和随机梯度下降有何不同
- 在训练过程中,批量梯度下降和随机梯度下降的损失如何降低
通过我的《用PyTorch进行深度学习》一书来启动你的项目。它提供了包含可用代码的自学教程。
那么,让我们开始吧。

在 PyTorch 中实现梯度下降。
图片来自 Michael Behrens。保留部分权利。
概述
本教程分为四个部分;它们是:
- 准备数据
- 批量梯度下降
- 随机梯度下降
- 绘制图表进行比较
准备数据
为了使模型简单易懂,我们将沿用上一个教程中的线性回归问题。数据是合成的,生成方式如下:
|
1 2 3 4 5 6 7 8 9 10 |
import torch import numpy as np import matplotlib.pyplot as plt # 创建一个斜率为 -5 的函数 f(X) X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X # 将高斯噪声添加到函数 f(X) 并将其保存在 Y 中 Y = func + 0.4 * torch.randn(X.size()) |
与之前的教程一样,我们初始化了一个变量`X`,其值范围从-5到5,并创建了一个斜率为-5的线性函数。然后,添加高斯噪声以创建变量`Y`。
我们可以使用 matplotlib 绘制数据以可视化模式
|
1 2 3 4 5 6 7 8 9 |
... # 绘制并可视化蓝色数据点 plt.plot(X.numpy(), Y.numpy(), 'b+', label='Y') plt.plot(X.numpy(), func.numpy(), 'r', label='func') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid('True', color='y') plt.show() |
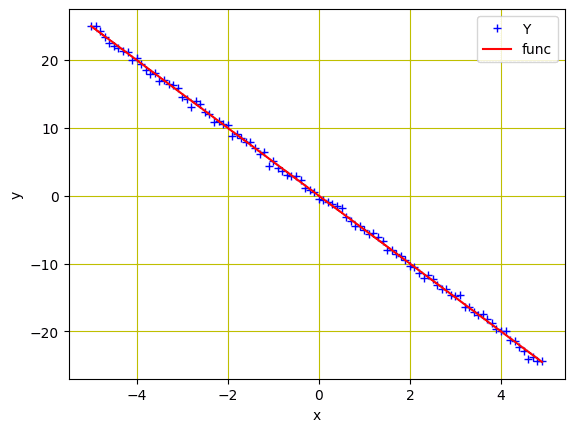
回归模型的数据点
想开始使用PyTorch进行深度学习吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
批量梯度下降
现在我们已经为模型创建了数据,接下来我们将根据一个简单的线性回归方程构建一个前向函数。我们将训练模型以确定两个参数($w$ 和 $b$)。我们还需要一个损失准则函数。因为它是一个连续值的回归问题,所以 MSE 损失是合适的。
|
1 2 3 4 5 6 7 8 |
... # 定义用于预测的前向传播函数 def forward(x): return w * x + b # 使用均方误差 (MSE) 评估数据点 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) |
在我们训练模型之前,让我们了解一下**批量梯度下降**。在批量梯度下降中,训练数据中的所有样本都只考虑一个步骤。通过计算所有训练示例的平均梯度来更新参数。换句话说,在一个 epoch 中只有一步梯度下降。
虽然批量梯度下降对于平滑误差流形是最佳选择,但它相对较慢且计算复杂,特别是当您有更大的数据集进行训练时。
使用批量梯度下降进行训练
让我们随机初始化可训练参数 $w$ 和 $b$,并定义一些训练参数,例如学习率或步长、一个用于存储损失的空列表以及训练的 epoch 数。
|
1 2 3 4 5 6 |
w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) step_size = 0.1 loss_BGD = [] n_iter = 20 |
我们将使用以下代码行训练模型 20 个 epoch。在这里,`forward()`函数生成预测,而`criterion()`函数测量损失并将其存储在`loss`变量中。`backward()`方法执行梯度计算,更新后的参数存储在`w.data`和`b.data`中。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
for i in range (n_iter): # 使用前向传播进行预测 Y_pred = forward(X) # 计算原始数据点和预测数据点之间的损失 loss = criterion(Y_pred, Y) # 将计算出的损失存储在列表中 loss_BGD.append(loss.item()) # 反向传播,计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() # 打印值以便理解 print('{}, \t{}, \t{}, \t{}'.format(i, loss.item(), w.item(), b.item())) |
以下是应用批量梯度下降后,每次 epoch 结束时输出和参数的更新方式。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
0, 596.7191162109375, -1.8527469635009766, -16.062074661254883 1, 343.426513671875, -7.247585773468018, -12.83026123046875 2, 202.7098388671875, -3.616910219192505, -10.298759460449219 3, 122.16651153564453, -6.0132551193237305, -8.237251281738281 4, 74.85094451904297, -4.394278526306152, -6.6120076179504395 5, 46.450958251953125, -5.457883358001709, -5.295622825622559 6, 29.111614227294922, -4.735295295715332, -4.2531514167785645 7, 18.386211395263672, -5.206836700439453, -3.4119482040405273 8, 11.687058448791504, -4.883906364440918, -2.7437009811401367 9, 7.4728569984436035, -5.092618465423584, -2.205873966217041 10, 4.808231830596924, -4.948029518127441, -1.777699589729309 11, 3.1172332763671875, -5.040188312530518, -1.4337140321731567 12, 2.0413269996643066, -4.975278854370117, -1.159447193145752 13, 1.355530858039856, -5.0158305168151855, -0.9393846988677979 14, 0.9178376793861389, -4.986582279205322, -0.7637402415275574 15, 0.6382412910461426, -5.004333972930908, -0.6229321360588074 16, 0.45952412486076355, -4.991086006164551, -0.5104631781578064 17, 0.34523946046829224, -4.998797416687012, -0.42035552859306335 18, 0.27213525772094727, -4.992753028869629, -0.3483465909957886 19, 0.22536347806453705, -4.996064186096191, -0.2906789183616638 |
总而言之,以下是完整的代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
import torch import numpy as np import matplotlib.pyplot as plt X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X Y = func + 0.4 * torch.randn(X.size()) # 定义用于预测的前向传播函数 def forward(x): return w * x + b # 使用均方误差 (MSE) 评估数据点 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) step_size = 0.1 loss_BGD = [] n_iter = 20 for i in range (n_iter): # 使用前向传播进行预测 Y_pred = forward(X) # 计算原始数据点和预测数据点之间的损失 loss = criterion(Y_pred, Y) # 将计算出的损失存储在列表中 loss_BGD.append(loss.item()) # 反向传播,计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() # 打印值以便理解 print('{}, \t{}, \t{}, \t{}'.format(i, loss.item(), w.item(), b.item())) |
上面的 for 循环每 epoch 打印一行,如下所示
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
0, 596.7191162109375, -1.8527469635009766, -16.062074661254883 1, 343.426513671875, -7.247585773468018, -12.83026123046875 2, 202.7098388671875, -3.616910219192505, -10.298759460449219 3, 122.16651153564453, -6.0132551193237305, -8.237251281738281 4, 74.85094451904297, -4.394278526306152, -6.6120076179504395 5, 46.450958251953125, -5.457883358001709, -5.295622825622559 6, 29.111614227294922, -4.735295295715332, -4.2531514167785645 7, 18.386211395263672, -5.206836700439453, -3.4119482040405273 8, 11.687058448791504, -4.883906364440918, -2.7437009811401367 9, 7.4728569984436035, -5.092618465423584, -2.205873966217041 10, 4.808231830596924, -4.948029518127441, -1.777699589729309 11, 3.1172332763671875, -5.040188312530518, -1.4337140321731567 12, 2.0413269996643066, -4.975278854370117, -1.159447193145752 13, 1.355530858039856, -5.0158305168151855, -0.9393846988677979 14, 0.9178376793861389, -4.986582279205322, -0.7637402415275574 15, 0.6382412910461426, -5.004333972930908, -0.6229321360588074 16, 0.45952412486076355, -4.991086006164551, -0.5104631781578064 17, 0.34523946046829224, -4.998797416687012, -0.42035552859306335 18, 0.27213525772094727, -4.992753028869629, -0.3483465909957886 19, 0.22536347806453705, -4.996064186096191, -0.2906789183616638 |
随机梯度下降
正如我们所知,当训练数据量巨大时,批量梯度下降并不是一个合适的选择。然而,深度学习算法对数据有很高的要求,通常需要大量数据进行训练。例如,如果使用批量梯度下降,一个拥有数百万训练样本的数据集将要求模型在单个步骤中计算所有数据的梯度。
这似乎不是一种有效的方法,替代方案是**随机梯度下降** (SGD)。随机梯度下降一次只考虑训练数据中的一个样本,计算梯度并迈出一步,然后更新权重。因此,如果训练数据中有 N 个样本,每个 epoch 将有 N 个步骤。
使用随机梯度下降进行训练
为了使用随机梯度下降训练我们的模型,我们将随机初始化可训练参数 $w$ 和 $b$,就像我们为上述批量梯度下降所做的那样。在这里,我们将定义一个空列表来存储随机梯度下降的损失,并训练模型 20 个 epoch。以下是根据先前示例修改后的完整代码。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
import torch import numpy as np import matplotlib.pyplot as plt X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X Y = func + 0.4 * torch.randn(X.size()) # 定义用于预测的前向传播函数 def forward(x): return w * x + b # 使用均方误差 (MSE) 评估数据点 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) step_size = 0.1 loss_SGD = [] n_iter = 20 for i in range (n_iter): # 计算真实损失并存储 Y_pred = forward(X) # 将损失存储在列表中 loss_SGD.append(criterion(Y_pred, Y).tolist()) for x, y in zip(X, Y): # 进行前向传播预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 反向传播,计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() # 打印值以便理解 print('{}, \t{}, \t{}, \t{}'.format(i, loss.item(), w.item(), b.item())) |
这会打印出一长串值,如下所示
|
1 2 3 4 5 6 7 8 9 |
0, 24.73763084411621, -5.02630615234375, -20.994739532470703 0, 455.0946960449219, -25.93259620666504, -16.7281494140625 0, 6968.82666015625, 54.207733154296875, -33.424049377441406 0, 97112.9140625, -238.72393798828125, 28.901844024658203 .... 19, 8858971136.0, -1976796.625, 8770213.0 19, 271135948800.0, -1487331.875, 8874354.0 19, 3010866446336.0, -3153109.5, 8527317.0 19, 47926483091456.0, 3631328.0, 9911896.0 |
绘制图表进行比较
现在我们已经使用批量梯度下降和随机梯度下降训练了我们的模型,让我们可视化在模型训练过程中两种方法的损失是如何降低的。因此,批量梯度下降的图表看起来像这样。
|
1 2 3 4 5 6 |
... plt.plot(loss_BGD, label="Batch Gradient Descent") plt.xlabel('Epoch') plt.ylabel('Cost/Total loss') plt.legend() plt.show() |
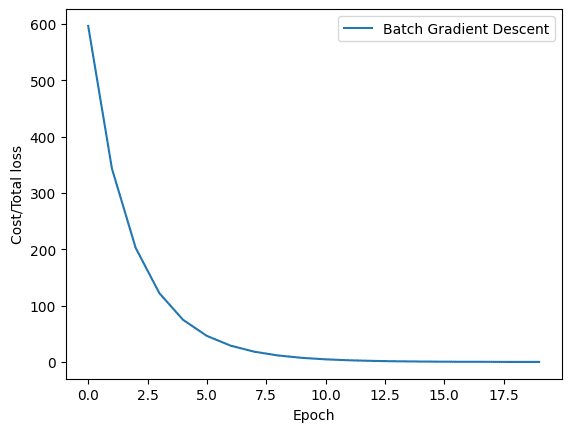
批量梯度下降的损失历史
同样,随机梯度下降的图表如下所示。
|
1 2 3 4 5 |
plt.plot(loss_SGD,label="Stochastic Gradient Descent") plt.xlabel('Epoch') plt.ylabel('Cost/Total loss') plt.legend() plt.show() |
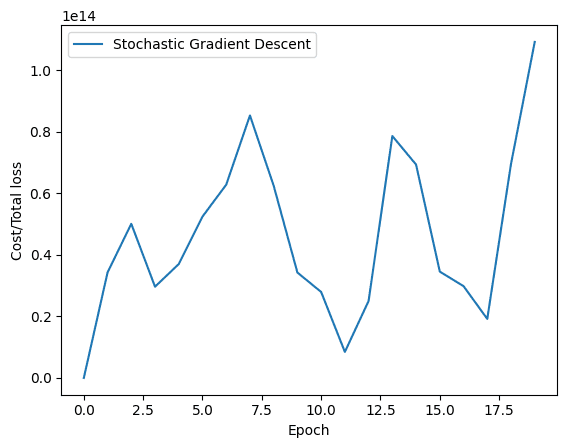
随机梯度下降的损失历史
如您所见,批量梯度下降的损失平稳下降。另一方面,您会观察到随机梯度下降的图表出现波动。正如前面提到的,原因很简单。在批量梯度下降中,损失是在处理完所有训练样本后才更新的,而随机梯度下降则是在训练数据中的每个训练样本之后更新损失的。
综上所述,以下是完整的代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 |
import torch import numpy as np import matplotlib.pyplot as plt # 创建一个斜率为 -5 的函数 f(X) X = torch.arange(-5, 5, 0.1).view(-1, 1) func = -5 * X # 将高斯噪声添加到函数 f(X) 并将其保存在 Y 中 Y = func + 0.4 * torch.randn(X.size()) # 绘制并可视化蓝色数据点 plt.plot(X.numpy(), Y.numpy(), 'b+', label='Y') plt.plot(X.numpy(), func.numpy(), 'r', label='func') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid('True', color='y') plt.show() # 定义用于预测的前向传播函数 def forward(x): return w * x + b # 使用均方误差 (MSE) 评估数据点 def criterion(y_pred, y): return torch.mean((y_pred - y) ** 2) # 批量梯度下降 w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) step_size = 0.1 loss_BGD = [] n_iter = 20 for i in range (n_iter): # 使用前向传播进行预测 Y_pred = forward(X) # 计算原始数据点和预测数据点之间的损失 loss = criterion(Y_pred, Y) # 将计算出的损失存储在列表中 loss_BGD.append(loss.item()) # 反向传播,计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() # 打印值以便理解 print('{}, \t{}, \t{}, \t{}'.format(i, loss.item(), w.item(), b.item())) # 随机梯度下降 w = torch.tensor(-10.0, requires_grad=True) b = torch.tensor(-20.0, requires_grad=True) step_size = 0.1 loss_SGD = [] n_iter = 20 for i in range(n_iter): # 计算真实损失并存储 Y_pred = forward(X) # 将损失存储在列表中 loss_SGD.append(criterion(Y_pred, Y).tolist()) for x, y in zip(X, Y): # 进行前向传播预测 y_hat = forward(x) # 计算原始数据点和预测数据点之间的损失 loss = criterion(y_hat, y) # 反向传播,计算损失相对于可学习参数的梯度 loss.backward() # 每次迭代后更新参数 w.data = w.data - step_size * w.grad.data b.data = b.data - step_size * b.grad.data # 每次迭代后将梯度清零 w.grad.data.zero_() b.grad.data.zero_() # 打印值以便理解 print('{}, \t{}, \t{}, \t{}'.format(i, loss.item(), w.item(), b.item())) # 绘制图表 plt.plot(loss_BGD, label="Batch Gradient Descent") plt.xlabel('Epoch') plt.ylabel('Cost/Total loss') plt.legend() plt.show() plt.plot(loss_SGD,label="Stochastic Gradient Descent") plt.xlabel('Epoch') plt.ylabel('Cost/Total loss') plt.legend() plt.show() |
总结
在本教程中,您了解了梯度下降,它的一些变体,以及如何在 PyTorch 中实现它们。特别是,您学习了
- 梯度下降算法及其在 PyTorch 中的实现
- 批量梯度下降及其在 PyTorch 中的实现
- 随机梯度下降及其在 PyTorch 中的实现
- 批量梯度下降和随机梯度下降有何不同
- 在训练过程中,批量梯度下降和随机梯度下降的损失如何降低





感谢您的代码,它对我的学习非常有帮助。不幸的是,SGD 不起作用。
但我建议进行一些修正
1) 第 10 行只是为了美化:Y = func + torch.randn(X.size())
2) 为了让 SGD 工作(这里它不收敛):仅对 SGD 设置 step_size=0.001
3) 为了让 SGD 符合维基百科的描述,在每个 epoch 之前打乱数据
在内部循环之前添加
idx = torch.randperm(Y.shape[0])
X = X[idx].view(X.size())
Y = Y[idx].view(Y.size())
你好 Evgeny…非常欢迎!请详细说明为什么 SGD 对您的模型不够用。
您可以尝试 Adam
https://machinelearning.org.cn/adam-optimization-algorithm-for-deep-learning/
对于线性回归问题使用随机梯度下降法有点牵强,因为线性回归问题存在闭式解……为什么不用另一个简单的问题来做呢,比如逻辑回归?