
图片作者 | Canva
毫无疑问,搜索是计算中最基本的问题之一。无论您是在计算机上查找文件、在 Google 上查找任何内容,还是使用简单的 find 命令,您实际上都在依赖某种形式的搜索引擎。以前,这些方法大多基于关键词搜索。但随着语言和数据的演变,这些方法开始力不从心。它们通过计算单词出现的频率及其在数据集中的稀有程度来对文档进行排名,但它们非常字面化。我来解释一下。如果您搜索“汽车维修”,但文档中写的是“车辆保养”,系统可能会完全遗漏,因为它没有匹配到确切的词语。
用户所说和用户实际意思之间的这种差距,催生了对更智能的、能够理解不同上下文的搜索系统的需求。这就是 **向量搜索** 的由来。
您可能最近才开始听说向量搜索,尤其是在 RAG(检索增强生成)兴起之后,但它已经存在相当长一段时间了。**向量搜索不匹配精确的词语,而是匹配含义**。它将查询和文档都转换为数值向量——捕获文本语义本质的高维数组。然后,它在该空间中找到最接近查询向量的向量,返回结果不仅在关键词上相似,而且在上下文上也相关。您会在任何地方找到这种解释。但您找不到的是它的内部工作原理。*您能从头开始构建一个向量搜索引擎吗?* 我们通常被教授概念和理论,但一旦被要求自己构建类似的东西,我们就会遇到困难。这正是我喜欢创建教程来向您展示如何从头开始编写代码的原因。
在本文中,我将引导您完成从生成向量表示到使用余弦相似度进行搜索的每一个步骤,我们甚至还会可视化幕后发生的事情。到最后,您不仅会理解向量搜索的工作原理,还将拥有一个可以继续改进的工作实现。那么,让我们开始吧。
向量搜索是如何工作的?
其核心是,向量搜索涉及三个步骤:
- **向量表示:** 使用词嵌入或神经网络等技术将数据(例如文本、图像)转换为数值向量。每个向量在高维空间中表示数据。
- **相似度计算:** 使用余弦相似度或欧氏距离等指标,测量查询向量与其他向量在数据集中的“接近”程度。越接近的向量表示越高的相似度。
- **检索:** 根据相似度得分返回最相似的 top-k 个项。
例如,如果您正在搜索关于“机器学习”的文档,则查询“机器学习”将被转换为一个向量,系统会查找其向量最接近该向量的文档,即使这些文档使用了“人工智能”或“深度学习”等相关术语。
现在,让我们用 Python 从头开始构建一个向量搜索系统。我们将使用一个玩具数据集的句子,将它们转换为向量(为简单起见,通过平均词向量),并实现一个搜索函数。我们还将可视化向量,看看它们如何在空间中聚类。
第一步:设置环境
为了保持简单,我们将使用 NumPy 进行向量运算,并使用 Matplotlib 进行可视化。我们将避免使用 FAISS 或 spaCy 等外部库,以专注于从头开始的实现。对于向量表示,我们将用一个小的、预定义的字典来模拟词嵌入,但实际上,您会使用 Word2Vec、GloVe 或 BERT 等模型。
让我们安装所需的包(如果需要),并进行导入设置。
|
1 2 3 4 |
import numpy as np import matplotlib.pyplot as plt from collections import defaultdict import re |
我们将使用 NumPy 进行向量数学运算,Matplotlib 进行绘图,以及基本的 Python 进行文本处理。re 模块有助于分词。
第二步:创建玩具数据集和词嵌入
在本教程中,我们将处理一个关于技术的简短句子数据集。为了将词语表示为向量,我们将创建一个简化的词嵌入字典,其中每个词语映射到一个 2D 向量(以便于可视化)。这些向量是任意的,但设计用于将相关词语聚类(例如,“machine”和“neural”是接近的)。实际上,您会加载一个预训练的嵌入模型,但这使我们的实现是自包含的。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# 玩具数据集的句子 documents = [ "Machine learning is powerful", "Artificial intelligence advances rapidly", "Deep learning transforms technology", "Data science drives innovation", "Neural networks power AI" ] # 简化的 2D 词嵌入(实际上,请使用预训练的嵌入) word_embeddings = { "machine": [0.8, 0.2], "learning": [0.7, 0.3], "powerful": [0.6, 0.4], "artificial": [0.9, 0.1], "intelligence": [0.85, 0.15], "advances": [0.5, 0.5], "rapidly": [0.4, 0.6], "deep": [0.75, 0.25], "transforms": [0.65, 0.35], "technology": [0.7, 0.4], "data": [0.3, 0.7], "science": [0.35, 0.65], "drives": [0.4, 0.6], "innovation": [0.45, 0.55], "neural": [0.8, 0.2], "networks": [0.78, 0.22], "power": [0.6, 0.4], "ai": [0.9, 0.1] } |
第三步:将句子转换为向量
为了搜索文档,我们需要将每个句子转换为一个单独的向量。一种简单的方法是平均句子中所有词语的词向量(在分词并去除停用词后)。这可以捕获句子的“平均含义”。如果一个词语不在 word_embeddings 中,我们将使用零向量(但实际上,您可能会以不同的方式处理未知词语)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
def tokenize(text): """将文本转换为小写并拆分成单词。""" return re.findall(r'\b\w+\b', text.lower()) def sentence_to_vector(sentence, embeddings): """通过平均词嵌入将句子转换为向量。""" words = tokenize(sentence) vectors = [embeddings.get(word, [0, 0]) for word in words] vectors = [v for v in vectors if sum(v) != 0] # 移除未知词语 if not vectors: return np.zeros(2) # 如果没有有效词语,则返回零向量 return np.mean(vectors, axis=0) # 将所有文档转换为向量 doc_vectors = [sentence_to_vector(doc, word_embeddings) for doc in documents] |
第四步:实现余弦相似度
余弦相似度是向量搜索的常用指标,因为它衡量向量之间的角度,忽略了它们的幅度。这使其非常适合比较词嵌入中的语义相似度。它计算为两个向量的点积除以它们范数的乘积。如果任一向量为零(例如,没有有效词语),我们返回 0 以避免除以零。此函数将比较查询向量与文档向量。
|
1 2 3 4 5 6 7 8 |
def cosine_similarity(vec1, vec2): """计算两个向量之间的余弦相似度。""" dot_product = np.dot(vec1, vec2) norm1 = np.linalg.norm(vec1) norm2 = np.linalg.norm(vec2) if norm1 == 0 or norm2 == 0: return 0.0 return dot_product / (norm1 * norm2) |
第五步:构建向量搜索函数
现在,让我们实现核心的向量搜索函数,它接受一个查询,将其转换为向量,计算与每个文档向量的余弦相似度,并返回 top-k 个文档及其相似度得分。我们使用 np.argsort 对文档按相似度进行排名,并过滤掉得分不为零的结果(例如,如果查询没有有效词语)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def vector_search(query, documents, embeddings, top_k=3): """执行向量搜索并返回 top-k 个相似文档。""" query_vector = sentence_to_vector(query, embeddings) similarities = [cosine_similarity(query_vector, doc_vec) for doc_vec in doc_vectors] # 获取 top-k 相似度的索引 ranked_indices = np.argsort(similarities)[::-1][:top_k] results = [ (documents[i], similarities[i]) for i in ranked_indices if similarities[i] > 0 ] return results # 示例查询 query = "Machine learning technology" results = vector_search(query, documents, word_embeddings) print("Query:", query) print("Top results:") for doc, score in results: print(f"Score: {score:.3f}, Document: {doc}") |
|
1 2 3 4 5 6 |
<strong>输出:</strong> Query: Machine learning technology Top results: Score: 1.000, Document: Machine learning is powerful Score: 0.999, Document: Deep learning transforms technology Score: 0.997, Document: Artificial intelligence advances rapidly |
正如您所见,该函数成功地检索了与查询最相关的文档。即使它们都不包含“machine learning technology”这个确切的短语,但它们的含义却非常接近,这就是基于向量搜索的强大之处。
第六步:可视化向量
为了理解向量搜索的工作原理,让我们在 2D 空间中可视化文档和查询向量。这将显示相似的项目如何聚类在一起。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
def plot_vectors(doc_vectors, documents, query, query_vector): """在 2D 空间中绘制文档和查询向量。""" plt.figure(figsize=(8, 6)) # 绘制文档向量 doc_x, doc_y = zip(*doc_vectors) plt.scatter(doc_x, doc_y, c='blue', label='Documents', s=100) for i, doc in enumerate(documents): plt.annotate(doc[:20] + "...", (doc_x[i], doc_y[i])) # 绘制查询向量 plt.scatter(query_vector[0], query_vector[1], c='red', label='Query', s=200, marker='*') plt.annotate(query[:20], (query_vector[0], query_vector[1]), color='red') plt.title('Vector Search: Document and Query Vectors') plt.xlabel('Dimension 1') plt.ylabel('Dimension 2') plt.legend() plt.grid(True) plt.show() plt.close() # 生成图表 query_vector = sentence_to_vector(query, word_embeddings) plot_vectors(doc_vectors, documents, query, query_vector) |
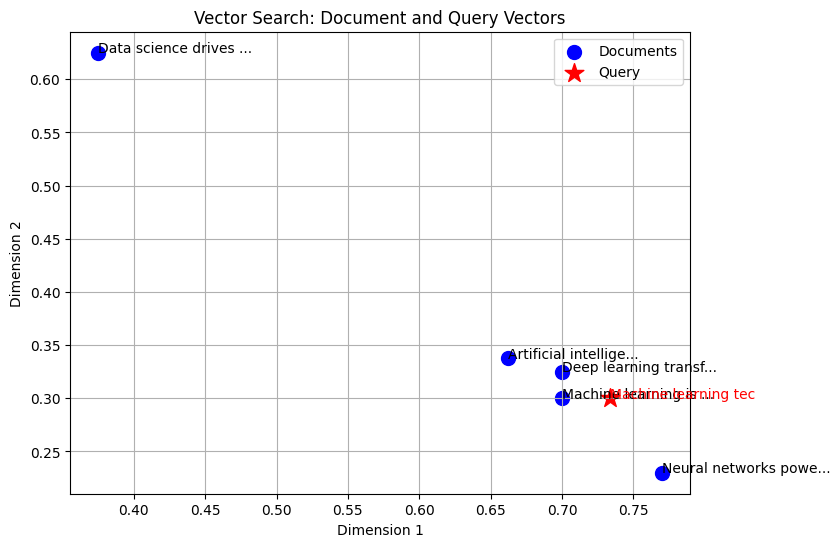
蓝点代表文档向量,红星代表查询向量。注解显示了每个文档和查询的前 20 个字符。您还可以看到,越接近查询向量的文档越相似,直观地证实了向量搜索的工作原理。
为什么这对 RAG 很重要
在 RAG 中,向量搜索是检索步骤的支柱。通过将文档和查询转换为向量,RAG 能够获取上下文相关的信息,即使是复杂的查询。我们简单的实现模拟了这一过程:查询向量检索语义上相近的文档,然后语言模型可以使用这些文档生成响应。将其扩展到实际应用涉及更高维度的嵌入和优化的搜索算法(如 HNSW 或 IVF),但核心思想保持不变。
结论
在本教程中,我们使用 Python 从头开始实现了向量搜索。您可以通过使用真实的词嵌入(例如,来自 Hugging Face 的 Transformers)或使用近似最近邻技术优化搜索来扩展此实现。尝试使用不同的查询或数据集进行实验,以加深您对向量搜索的理解!





暂无评论。