室内移动预测涉及利用无线传感器强度数据来预测建筑物内主体的位置和运动。
这是一个具有挑战性的问题,因为没有直接的分析模型可以将来自多个传感器的可变长度信号强度数据转换为用户行为。
“室内用户移动”数据集是一个标准且免费的时间序列分类问题。
在本教程中,您将了解室内移动预测时间序列分类问题,以及如何为该问题设计特征和评估机器学习算法。
完成本教程后,您将了解:
- 根据传感器强度预测房间之间移动的时间序列分类问题。
- 如何调查数据以更好地理解问题,以及如何从原始数据中为预测建模设计特征。
- 如何对一套分类算法进行抽查,并调整一个算法以进一步提升该问题的性能。
通过我的新书《时间序列预测深度学习》来**启动您的项目**,其中包括**分步教程**和所有示例的**Python 源代码**文件。
让我们开始吧。
- 2018 年 9 月更新:添加了数据集镜像的链接。

使用机器学习算法进行室内移动时间序列分类
图片由 Nola Tularosa 拍摄,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 室内用户移动预测
- 室内移动预测数据集
- 模型评估
- 数据准备
- 算法抽查
室内用户移动预测
“室内用户移动”预测问题涉及根据环境中无线探测器测量的信号强度变化来判断个人是否在房间之间移动。
该数据集由意大利比萨大学的 Davide Bacciu 等人收集并提供,并首次在其 2011 年的论文“通过储备池计算预测异构室内环境中的用户移动”中描述,作为探索一种类似于循环神经网络的方法(称为“储备池计算”)的数据集。
该问题是预测室内用户定位和移动模式这一更通用问题的一个特例。
数据通过在环境中放置四个无线传感器和一个在主体身上进行收集。主体在环境中移动,同时四个无线传感器检测并记录传感器强度的时间序列。
结果是一个包含可变长度时间序列的数据集,其中有四个变量描述了通过一个明确定义的静态环境的轨迹,以及对主体是否在环境中更换房间的分类。
这是一个具有挑战性的问题,因为没有明显且通用的方法可以将信号强度数据与环境中的主体位置关联起来。
RSS 和跟踪对象位置之间的关系无法轻易地用分析模型来表示,因为它强烈依赖于环境的特性以及所涉及的无线设备。I
— 通过储备池计算预测异构室内环境中的用户移动,2011 年。
数据是在受控实验条件下收集的。
传感器被放置在三对由典型办公室家具连接的房间中。每对房间的角落各放置两个传感器,主体沿着六条预设路径之一穿过房间。预测在每条路径上可能导致或不导致房间更换的某个点进行。
下图清晰地展示了传感器位置 (A1-A4)、六条可能的路径以及进行预测的两个点 (M)。
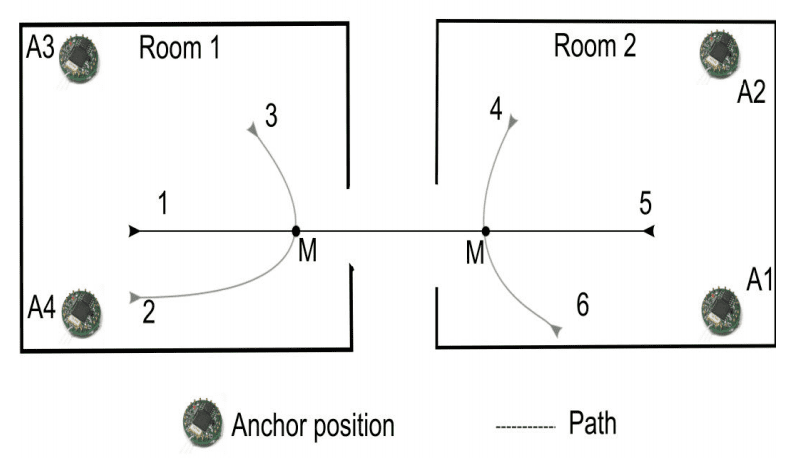
两间房、传感器位置和 6 条预定义路径概览。
摘自“通过储备池计算预测异构室内环境中的用户移动”。
从三对房间收集了三个数据集,在这些房间中进行了路径行走和传感器测量,分别称为数据集 1、数据集 2 和数据集 3。
下表摘自论文,总结了每个数据集中行走的路径数量、房间转换和非房间转换的总数(类别标签)以及时间序列输入的长度。
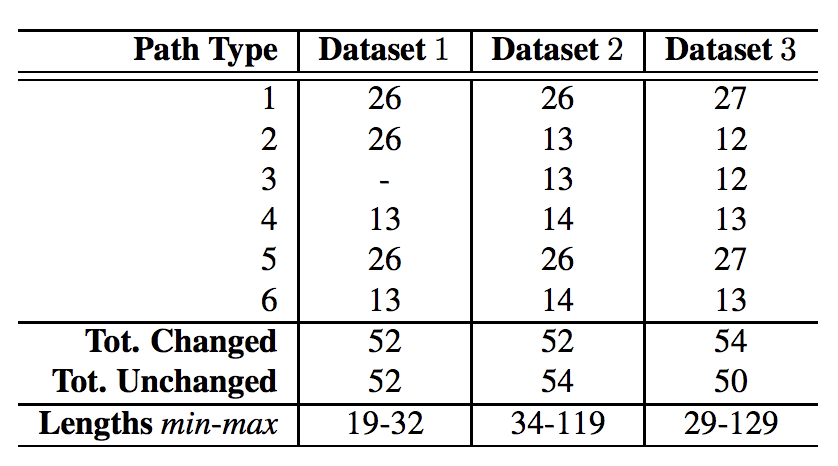
从三对房间收集的传感器数据摘要。
摘自“通过储备池计算预测异构室内环境中的用户移动”。
从技术上讲,数据由多元时间序列输入和分类输出组成,可以描述为时间序列分类问题。
来自四个锚点的 RSS 值被组织成不同长度的序列,对应于从起点到标记 M 的轨迹测量。每个输入序列都关联一个目标分类标签,以指示用户是否即将改变其位置(房间)。
— 通过储备池计算预测异构室内环境中的用户移动,2011 年。
时间序列深度学习需要帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
室内移动预测数据集
该数据集可从 UCI 机器学习存储库免费获取。
万一上述网站出现故障(这可能会发生),这里有一个指向数据集镜像的直接链接
数据可下载为 .zip 文件,其中包含以下重要文件:
- dataset/MovementAAL_RSS_???.csv 每个移动的 RSS 轨迹,文件名中的“???”表示轨迹编号从 1 到 311。
- dataset/MovementAAL_target.csv 轨迹编号到输出类值或目标的映射。
- groups/MovementAAL_DatasetGroup.csv 轨迹编号到数据集组 1、2 或 3 的映射,标记记录轨迹的房间对。
- groups/MovementAAL_Paths.csv 轨迹编号到路径类型(1-6)的映射,如上图所示。
提供的数据已归一化。
具体来说,每个输入变量在每个数据集(房间对)中都被归一化到 [-1,1] 范围,输出类别变量被标记为 -1 表示房间之间没有过渡,+1 表示通过房间的过渡。
[...] 输入数据包含 4 维 RSS 测量值(NU = 4)的时间序列,对应于 4 个锚点 [...] 独立地针对每个数据集归一化到 [−1, 1] 范围
— 通过储备池计算预测异构室内环境中的用户移动,2011 年。
如果数据集之间预归一化的分布差异很大,那么按数据集进行数据缩放可能会(或可能不会)在组合观测值时引入额外的挑战。
给定轨迹文件中的一个轨迹的时间序列按时间顺序提供,其中一行记录一个时间步的观测值。数据以 8Hz 记录,这意味着数据中每八个时间步过去一秒钟的实时时间。
下面是一个轨迹示例,取自“_dataset/MovementAAL_RSS_1.csv_”,其输出目标为“1”(发生了房间转换),来自第 1 组(第一对房间),是路径 1(在房间之间从左到右的直线)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
#RSS_anchor1, RSS_anchor2, RSS_anchor3, RSS_anchor4 -0.90476,-0.48,0.28571,0.3 -0.57143,-0.32,0.14286,0.3 -0.38095,-0.28,-0.14286,0.35 -0.28571,-0.2,-0.47619,0.35 -0.14286,-0.2,0.14286,-0.2 -0.14286,-0.2,0.047619,0 -0.14286,-0.16,-0.38095,0.2 -0.14286,-0.04,-0.61905,-0.2 -0.095238,-0.08,0.14286,-0.55 -0.047619,0.04,-0.095238,0.05 -0.19048,-0.04,0.095238,0.4 -0.095238,-0.04,-0.14286,0.35 -0.33333,-0.08,-0.28571,-0.2 -0.2381,0.04,0.14286,0.35 0,0.08,0.14286,0.05 -0.095238,0.04,0.095238,0.1 -0.14286,-0.2,0.14286,0.5 -0.19048,0.04,-0.42857,0.3 -0.14286,-0.08,-0.2381,0.15 -0.33333,0.16,-0.14286,-0.8 -0.42857,0.16,-0.28571,-0.1 -0.71429,0.16,-0.28571,0.2 -0.095238,-0.08,0.095238,0.35 -0.28571,0.04,0.14286,0.2 0,0.04,0.14286,0.1 0,0.04,-0.047619,-0.05 -0.14286,-0.6,-0.28571,-0.1 |
如第一篇论文所述,这些数据集以两种特定方式(实验设置或 ES)用于评估预测模型的性能,分别指定为 ES1 和 ES2。
- ES1:结合数据集 1 和 2,将其分为训练集(80%)和测试集(20%)来评估模型。
- ES2:结合数据集 1 和 2 作为训练集(66%),数据集 3 作为测试集(34%)来评估模型。
ES1 情况评估了模型在两个已知房间(即具有已知几何形状的房间)内概括移动的能力。ES2 情况试图将移动从两个房间概括到第三个未见的房间:这是一个更困难的问题。
这篇 2011 年的论文报告称,ES1 的分类准确率约为 95%,ES2 约为 89%,在我自己测试了一套算法之后,这个结果非常令人印象深刻。
加载并探索数据集
在本节中,我们将数据加载到内存中,并通过摘要和可视化来探索它,以帮助更好地理解如何对问题进行建模。
首先,下载数据集并将其解压缩到您当前的工作目录中。
加载数据集
目标、组和路径文件可以直接作为 Pandas DataFrame 加载。
|
1 2 3 4 5 |
# 加载映射文件 from pandas import read_csv target_mapping = read_csv('dataset/MovementAAL_target.csv', header=0) group_mapping = read_csv('groups/MovementAAL_DatasetGroup.csv', header=0) paths_mapping = read_csv('groups/MovementAAL_Paths.csv', header=0) |
信号强度轨迹存储在 dataset/ 目录中的单独文件中。
这些可以通过迭代目录中的所有文件并直接加载序列来加载。由于每个序列的长度可变(行数可变),我们可以将每个轨迹的 NumPy 数组存储在一个列表中。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 将序列和目标加载到内存中 from pandas import read_csv from os import listdir sequences = list() directory = 'dataset' target_mapping = None for name in listdir(directory): filename = directory + '/' + name if filename.endswith('_target.csv'): continue df = read_csv(filename, header=0) values = df.values sequences.append(values) |
我们可以将所有这些组合成一个名为 `load_dataset()` 的函数,并将数据加载到内存中。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
# 将用户移动数据集加载到内存中 from pandas import read_csv from os import listdir # 返回轨迹列表,以及目标、组和路径的数组 def load_dataset(prefix=''): grps_dir, data_dir = prefix+'groups/', prefix+'dataset/' # 加载映射文件 targets = read_csv(data_dir + 'MovementAAL_target.csv', header=0) groups = read_csv(grps_dir + 'MovementAAL_DatasetGroup.csv', header=0) paths = read_csv(grps_dir + 'MovementAAL_Paths.csv', header=0) # 加载轨迹 sequences = list() target_mapping = None for name in listdir(data_dir): filename = data_dir + name if filename.endswith('_target.csv'): continue df = read_csv(filename, header=0) values = df.values sequences.append(values) return sequences, targets.values[:,1], groups.values[:,1], paths.values[:,1] # 加载数据集 sequences, targets, groups, paths = load_dataset() # 总结加载数据的形状 print(len(sequences), targets.shape, groups.shape, paths.shape) |
运行示例会加载数据并显示 314 条轨迹已正确从磁盘加载,以及它们相关的输出(目标为 -1 或 +1)、数据集编号(组为 1、2 或 3)和路径编号(路径为 1-6)。
|
1 |
314 (314,) (314,) (314,) |
基本信息
现在我们可以更仔细地查看已加载的数据,以更好地理解或确认我们对问题的理解。
我们从论文中得知,该数据集在两类方面是合理平衡的。我们可以通过汇总所有观测值的类别分类来证实这一点。
|
1 2 3 4 |
# 总结类别分类 class1,class2 = len(targets[targets==-1]), len(targets[targets==1]) print('Class=-1: %d %.3f%%' % (class1, class1/len(targets)*100)) print('Class=+1: %d %.3f%%' % (class2, class2/len(targets)*100)) |
接下来,我们可以通过绘制每个四个锚点的原始值的直方图来回顾传感器强度值的分布。
这要求我们创建一个包含所有观测行的一维数组,以便我们可以绘制每列的分布。NumPy 的 `vstack()` 函数将为我们完成这项工作。
|
1 2 3 4 5 6 7 8 |
# 每个锚点的直方图 all_rows = vstack(sequences) pyplot.figure() variables = [0, 1, 2, 3] for v in variables: pyplot.subplot(len(variables), 1, v+1) pyplot.hist(all_rows[:, v], bins=20) pyplot.show() |
最后,另一个有趣的方面是轨迹长度的分布。
我们可以用直方图来总结这个分布。
|
1 2 3 4 |
# 轨迹长度直方图 trace_lengths = [len(x) for x in sequences] pyplot.hist(trace_lengths, bins=50) pyplot.show() |
将所有这些整合在一起,下面列出了加载和汇总数据的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
# 汇总用户移动数据的简单信息 from os import listdir from numpy import array from numpy import vstack from pandas import read_csv from matplotlib import pyplot # 返回轨迹列表,以及目标、组和路径的数组 def load_dataset(prefix=''): grps_dir, data_dir = prefix+'groups/', prefix+'dataset/' # 加载映射文件 targets = read_csv(data_dir + 'MovementAAL_target.csv', header=0) groups = read_csv(grps_dir + 'MovementAAL_DatasetGroup.csv', header=0) paths = read_csv(grps_dir + 'MovementAAL_Paths.csv', header=0) # 加载轨迹 sequences = list() target_mapping = None for name in listdir(data_dir): filename = data_dir + name if filename.endswith('_target.csv'): continue df = read_csv(filename, header=0) values = df.values sequences.append(values) return sequences, targets.values[:,1], groups.values[:,1], paths.values[:,1] # 加载数据集 sequences, targets, groups, paths = load_dataset() # 总结类别分类 class1,class2 = len(targets[targets==-1]), len(targets[targets==1]) print('Class=-1: %d %.3f%%' % (class1, class1/len(targets)*100)) print('Class=+1: %d %.3f%%' % (class2, class2/len(targets)*100)) # 每个锚点的直方图 all_rows = vstack(sequences) pyplot.figure() variables = [0, 1, 2, 3] for v in variables: pyplot.subplot(len(variables), 1, v+1) pyplot.hist(all_rows[:, v], bins=20) pyplot.show() # 轨迹长度直方图 trace_lengths = [len(x) for x in sequences] pyplot.hist(trace_lengths, bins=50) pyplot.show() |
运行示例首先总结观测值的类别分布。
结果证实了我们对整个数据集在两种类别结果的观测值方面几乎完美平衡的预期。
|
1 2 |
类别=-1:156 49.682% 类别=+1:158 50.318% |
接下来,为每个锚点创建传感器强度的直方图,总结数据分布。
我们可以看到每个变量的分布都接近正态,呈现出高斯状的形状。我们还可以看到,在 -1 附近观测值可能过多。这可能表明一个通用的“无强度”观测值,可以标记或甚至从序列中过滤掉。
研究分布是否随路径类型甚至数据集编号而变化可能会很有趣。
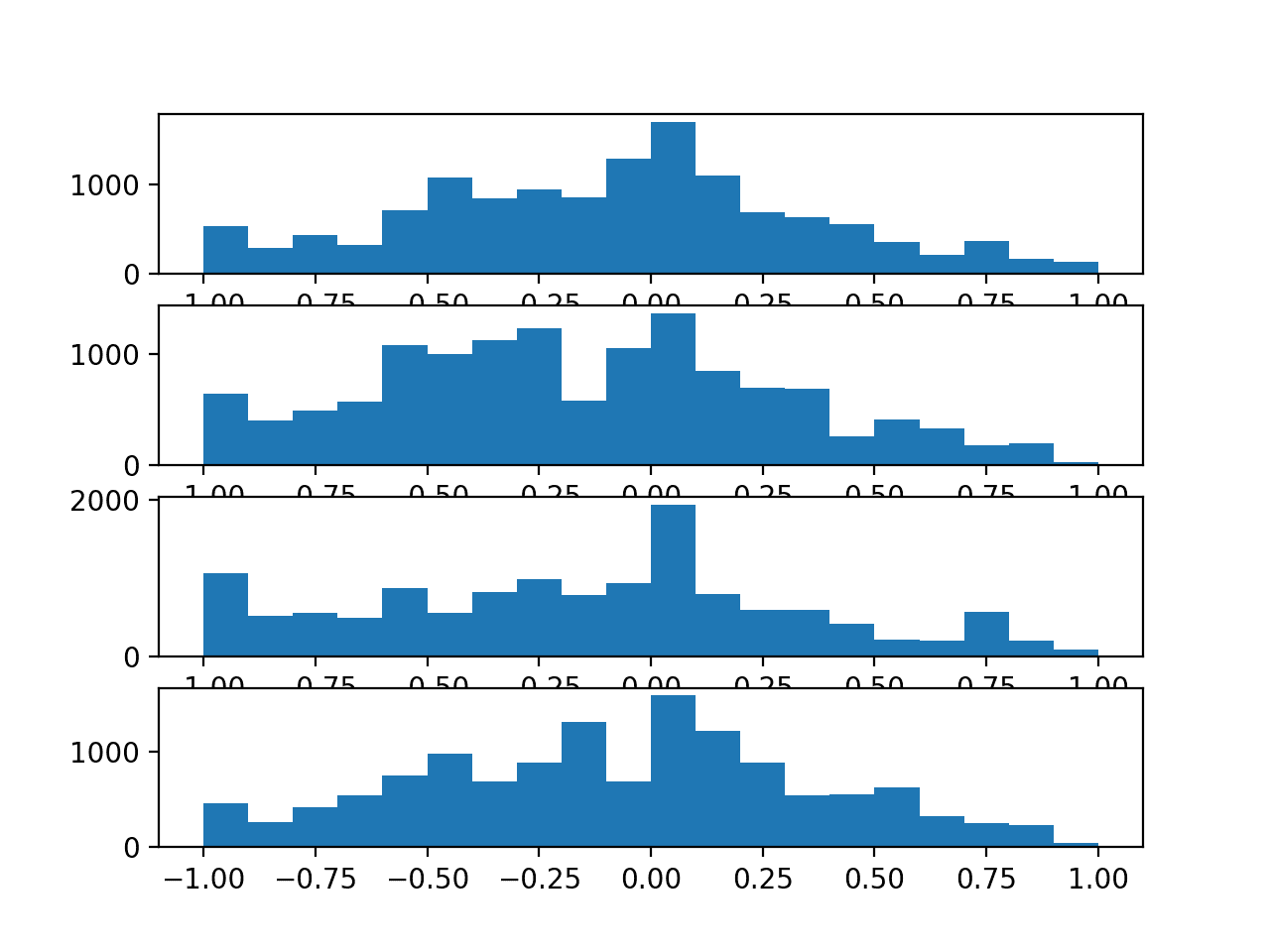
每个锚点传感器强度值的直方图
最后,创建序列长度的直方图。
我们可以看到长度约为 25、40 和 60 的序列簇。我们还可以看到,如果我们要截断长序列,那么最大长度为 70 个时间步可能比较合适。最小长度似乎是 19。
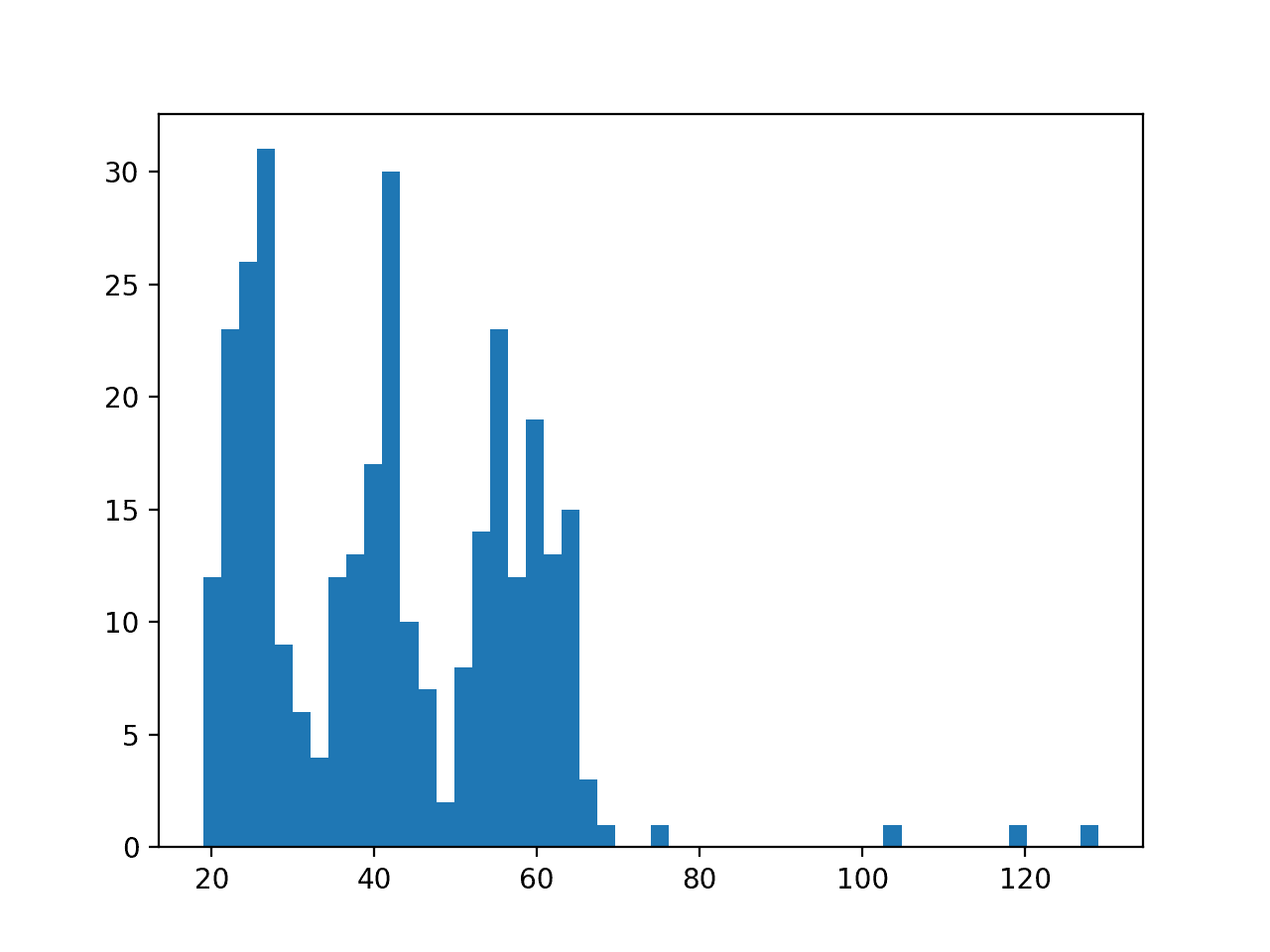
传感器强度序列长度直方图
时间序列图
我们正在处理时间序列数据,因此回顾一些序列示例非常重要。
我们可以按路径对轨迹进行分组,并为每条路径绘制一个轨迹示例。期望是不同路径的轨迹在某种程度上可能看起来不同。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 按路径分组序列 paths = [1,2,3,4,5,6] seq_paths = dict() for path in paths: seq_paths[path] = [sequences[j] for j in range(len(paths)) if paths[j]==path] # 绘制每条路径的一个轨迹示例 pyplot.figure() for i in paths: pyplot.subplot(len(paths), 1, i+1) # 绘制每个变量的线图 for j in [0, 1, 2, 3]: pyplot.plot(seq_paths[i][0][:, j], label='Anchor ' + str(j+1)) pyplot.title('Path ' + str(i), y=0, loc='left') pyplot.show() |
我们还可以绘制一个轨迹中的每个系列,以及线性回归模型预测的趋势。这将使系列中的任何趋势变得明显。
我们可以使用 `lstsq()` NumPy 函数为给定序列拟合线性回归。
下面的 `regress()` 函数将一个单变量序列作为输入,通过最小二乘法拟合一个线性回归模型,并预测每个时间步的输出,返回一个捕获数据趋势的序列。
|
1 2 3 4 5 6 7 8 9 |
# 拟合线性回归函数并返回序列的预测值 def regress(y): # 将输入定义为时间步 X = array([i for i in range(len(y))]).reshape(len(y), 1) # 通过最小二乘法拟合线性回归 b = lstsq(X, y)[0][0] # 预测时间步的趋势 yhat = b * X[:,0] return yhat |
我们可以使用该函数绘制单个轨迹中每个变量的时间序列趋势。
|
1 2 3 4 5 6 7 8 9 10 11 |
# 绘制带有趋势的单个轨迹的系列图 seq = sequences[0] variables = [0, 1, 2, 3] pyplot.figure() for i in variables: pyplot.subplot(len(variables), 1, i+1) # 绘制序列 pyplot.plot(seq[:,i]) # 绘制趋势 pyplot.plot(regress(seq[:,i])) pyplot.show() |
将所有这些联系在一起,完整的示例如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
# 绘制序列数据 from os import listdir from numpy import array from numpy import vstack from numpy.linalg import lstsq from pandas import read_csv from matplotlib import pyplot # 返回轨迹列表,以及目标、组和路径的数组 def load_dataset(prefix=''): grps_dir, data_dir = prefix+'groups/', prefix+'dataset/' # 加载映射文件 targets = read_csv(data_dir + 'MovementAAL_target.csv', header=0) groups = read_csv(grps_dir + 'MovementAAL_DatasetGroup.csv', header=0) paths = read_csv(grps_dir + 'MovementAAL_Paths.csv', header=0) # 加载轨迹 sequences = list() target_mapping = None for name in listdir(data_dir): filename = data_dir + name if filename.endswith('_target.csv'): continue df = read_csv(filename, header=0) values = df.values sequences.append(values) return sequences, targets.values[:,1], groups.values[:,1], paths.values[:,1] # 拟合线性回归函数并返回序列的预测值 def regress(y): # 将输入定义为时间步 X = array([i for i in range(len(y))]).reshape(len(y), 1) # 通过最小二乘法拟合线性回归 b = lstsq(X, y)[0][0] # 预测时间步的趋势 yhat = b * X[:,0] return yhat # 加载数据集 sequences, targets, groups, paths = load_dataset() # 按路径分组序列 paths = [1,2,3,4,5,6] seq_paths = dict() for path in paths: seq_paths[path] = [sequences[j] for j in range(len(paths)) if paths[j]==path] # 绘制每条路径的一个轨迹示例 pyplot.figure() for i in paths: pyplot.subplot(len(paths), 1, i+1) # 绘制每个变量的线图 for j in [0, 1, 2, 3]: pyplot.plot(seq_paths[i][0][:, j], label='Anchor ' + str(j+1)) pyplot.title('Path ' + str(i), y=0, loc='left') pyplot.show() # 绘制带有趋势的单个轨迹的系列图 seq = sequences[0] variables = [0, 1, 2, 3] pyplot.figure() for i in variables: pyplot.subplot(len(variables), 1, i+1) # 绘制序列 pyplot.plot(seq[:,i]) # 绘制趋势 pyplot.plot(regress(seq[:,i])) pyplot.show() |
运行示例会创建一个包含六个图形的图表,每个图形对应六条路径中的一条。给定图形显示了一个轨迹的线图,其中包含该轨迹的四个变量,每个锚点一个。
也许所选轨迹能代表每条路径,也许不能。
我们可以看到一些明显的区别:
- **变量随时间的分组**。在给定时间,变量可能成对分组,也可能所有变量都分组在一起。
- **变量随时间的趋势**。变量趋于在中间聚集或向极端扩散。
理想情况下,如果这些行为变化具有预测性,则预测模型必须提取这些特征,或者以这些特征的摘要作为输入呈现。
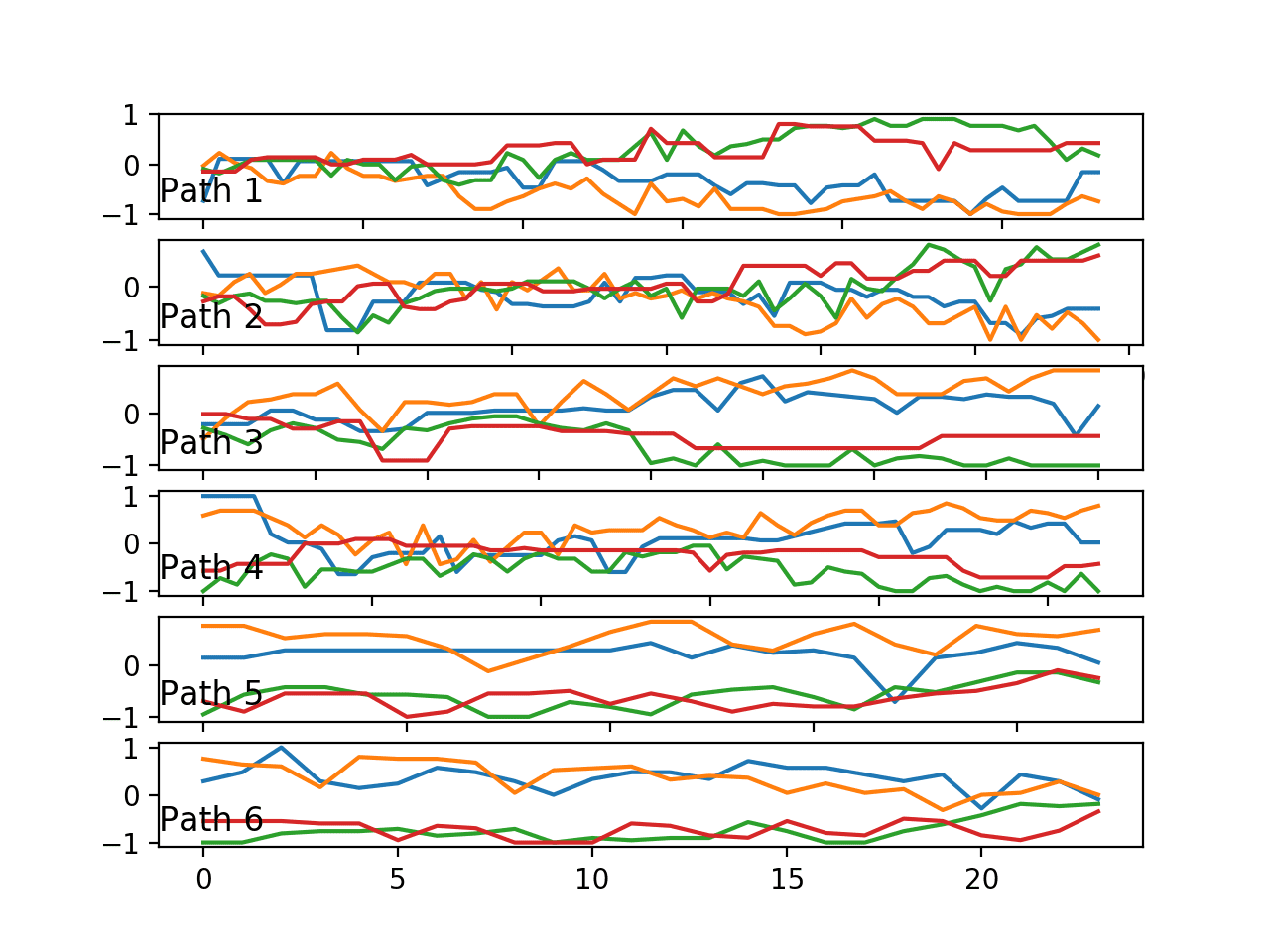
每条六条路径的一个轨迹(4 个变量)的线图。
创建了第二个图,显示了单个轨迹中四个时间序列的线图以及趋势线。
我们可以看到,至少对于这个轨迹,当用户在环境中移动时,传感器强度数据存在明显的趋势。这可能表明有机会在建模之前使数据平稳,或者将轨迹中每个序列的趋势(观测值或系数)用作预测模型的输入。
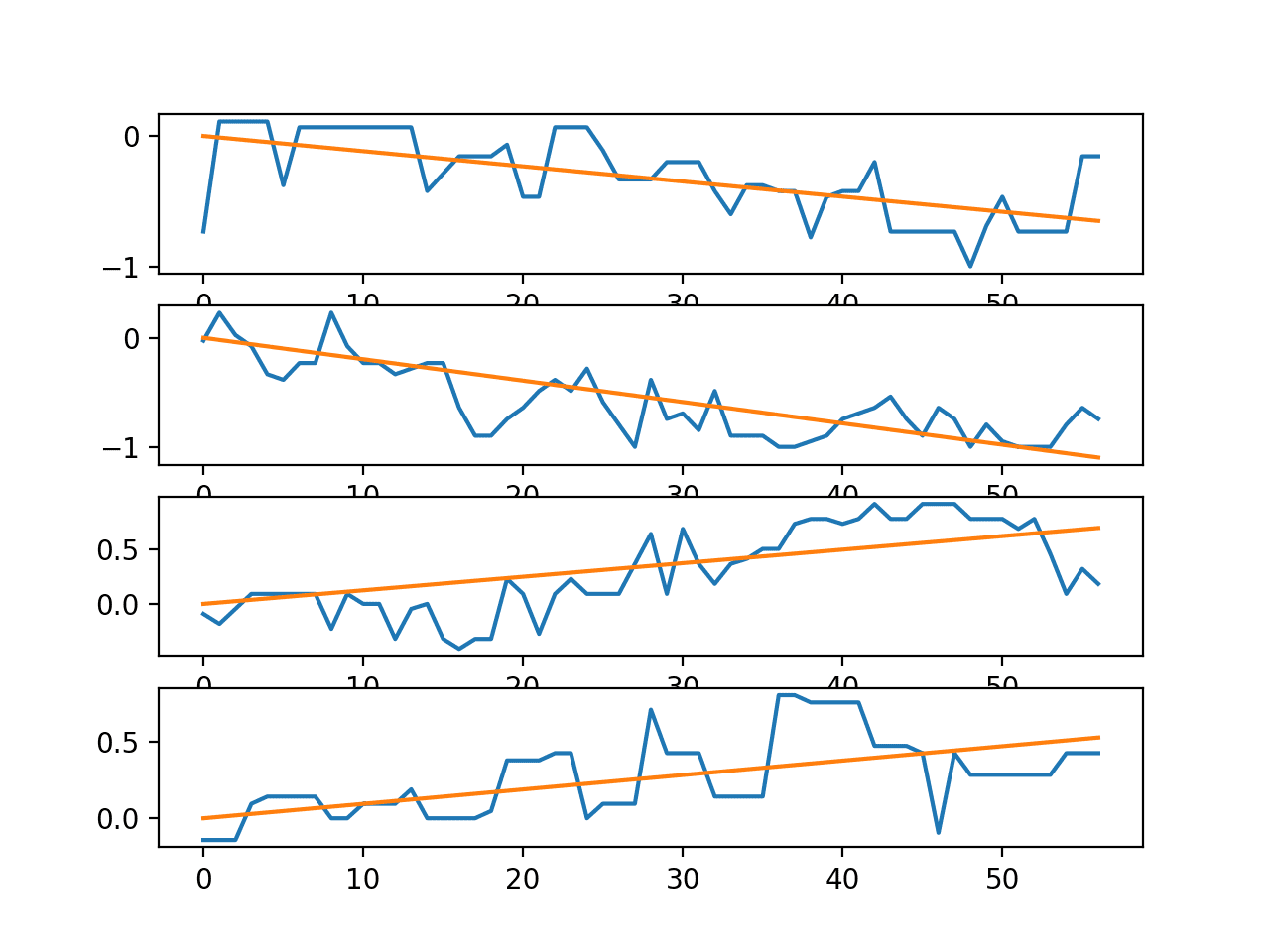
单个轨迹中时间序列的线图和趋势线
模型评估
有很多方法可以拟合和评估此数据上的模型。
考虑到类别的平衡性,分类准确率似乎是一个不错的初步评估指标。将来可以通过预测概率和探索 ROC 曲线上的阈值来寻求更多的细微差别。
我看到使用此数据有两个主要主题
- **同一房间**:在同一房间的轨迹上训练的模型能否预测该房间中新轨迹的结果?
- **不同房间**:在一个或两个房间的轨迹上训练的模型能否预测不同房间中新轨迹的结果?
论文中描述并总结的 ES1 和 ES2 情况探讨了这些问题,并提供了一个有用的起点。
首先,我们必须将加载的轨迹和目标分成三个组。
|
1 2 3 4 5 6 7 8 9 10 |
# 分离轨迹 seq1 = [sequences[i] for i in range(len(groups)) if groups[i]==1] seq2 = [sequences[i] for i in range(len(groups)) if groups[i]==2] seq3 = [sequences[i] for i in range(len(groups)) if groups[i]==3] print(len(seq1),len(seq2),len(seq3)) # 分离目标 targets1 = [targets[i] for i in range(len(groups)) if groups[i]==1] targets2 = [targets[i] for i in range(len(groups)) if groups[i]==2] targets3 = [targets[i] for i in range(len(groups)) if groups[i]==3] print(len(targets1),len(targets2),len(targets3)) |
在 ES1 的情况下,我们可以使用 k=5 的 k 折交叉验证,以与论文相同的比例进行,重复评估提供了一些评估的鲁棒性。
我们可以使用 scikit-learn 的 `cross_val_score()` 函数来评估模型,然后计算分数的平均值和标准差。
|
1 2 3 4 5 6 7 |
# 评估 ES1 模型 from numpy import mean from numpy import std from sklearn.model_selection import cross_val_score ... scores = cross_val_score(model, X, y, scoring='accuracy', cv=5, n_jobs=-1) m, s = mean(scores), std(scores) |
在 ES2 的情况下,我们可以直接在数据集 1 和 2 上拟合模型,并在数据集 3 上测试模型技能。
数据准备
输入数据在预测问题中的框架方式是灵活的。
有两种方法:
- **自动特征学习**。深度神经网络能够自动学习特征,循环神经网络可以直接支持多元多步输入数据。可以使用循环神经网络,例如 LSTM 或 1D CNN。序列可以填充到相同的长度,例如 70 个时间步,并且可以使用遮蔽层来忽略填充的时间步。
- **特征工程**。或者,可以将可变长度序列汇总为单个固定长度向量,并将其提供给标准机器学习模型进行预测。这将需要仔细的特征工程,以便为模型提供对轨迹的充分描述,以学习到输出类别的映射。
这两种方法都很有趣。
作为第一步,我们将通过手动特征工程准备更传统的固定长度向量输入。
以下是一些可以包含在向量中的特征的想法:
- 变量的第一个、中间或最后 n 个观测值。
- 变量的第一个、中间或最后 n 个观测值的均值或标准差。
- 最后 n 个观测值与第一个 n 个观测值之间的差值
- 变量的第一个、中间或最后 n 个观测值的差分。
- 变量的所有、第一个、中间或最后 n 个观测值的线性回归系数。
- 变量的第一个、中间或最后 n 个观测值的线性回归预测趋势。
此外,原始值可能不需要进行数据缩放,因为数据已经缩放到了 -1 到 1 的范围。如果添加了具有不同单位的新特征,则可能需要进行缩放。
一些变量确实显示出一些趋势,这表明变量的差分可能有助于提取信号。
每个变量的分布接近高斯分布,因此一些算法可能会受益于标准化,甚至 Box-Cox 变换。
算法抽查
在本节中,我们将对一系列标准机器学习算法的默认配置进行抽查,并使用不同的工程特征集。
抽查是一种有用的技术,可以快速发现输入和输出之间是否存在任何可学习的信号,因为大多数测试方法都会检测到一些东西。该方法还可以建议值得进一步研究的方法。
一个缺点是,每种方法都没有获得其最佳机会(配置)来展示其在该问题上的能力,这意味着任何进一步研究的方法都将受到初步结果的偏见。
在这些测试中,我们将考察六种不同类型的算法,具体如下:
- 逻辑回归。
- k-近邻。
- 决策树。
- 支持向量机。
- 随机森林。
- 梯度提升机。
我们将测试这些方法的默认配置,关注时间序列变量的末端特征,因为它们很可能对房间转换是否发生最具预测性。
最后 n 个观测值
最后 n 个观测值很可能预测移动是否会导致房间转换。
轨迹数据中的最小时间步数为 19,因此我们将使用 n=19 作为起点。
下面名为 `create_dataset()` 的函数将使用每个轨迹的最后 n 个观测值创建一个扁平的一维固定长度向量,然后将目标作为向量的最后一个元素添加。
简单机器学习算法需要对轨迹数据进行扁平化处理。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# 为每个带有输出变量的轨迹创建一个固定的一维向量 def create_dataset(sequences, targets): # 创建转换后的数据集 transformed = list() n_vars = 4 n_steps = 19 # 依次处理每个轨迹 for i in range(len(sequences)): seq = sequences[i] vector = list() # 最后 n 个观测值 for row in range(1, n_steps+1): for col in range(n_vars): vector.append(seq[-row, col]) # 添加输出 vector.append(targets[i]) # 存储 transformed.append(vector) # 准备数组 transformed = array(transformed) transformed = transformed.astype('float32') return transformed |
我们可以像以前一样加载数据集,并将其分类到“模型评估”部分所述的数据集 1、2 和 3 中。
然后,我们可以调用 `create_dataset()` 函数来创建 ES1 和 ES2 情况所需的数据集,具体来说,ES1 结合了数据集 1 和 2,而 ES2 使用数据集 1 和 2 作为训练集,数据集 3 作为测试集。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
# 准备固定长度向量数据集 from os import listdir from numpy import array from numpy import savetxt from pandas import read_csv # 返回轨迹列表,以及目标、组和路径的数组 def load_dataset(prefix=''): grps_dir, data_dir = prefix+'groups/', prefix+'dataset/' # 加载映射文件 targets = read_csv(data_dir + 'MovementAAL_target.csv', header=0) groups = read_csv(grps_dir + 'MovementAAL_DatasetGroup.csv', header=0) paths = read_csv(grps_dir + 'MovementAAL_Paths.csv', header=0) # 加载轨迹 sequences = list() target_mapping = None for name in listdir(data_dir): filename = data_dir + name if filename.endswith('_target.csv'): continue df = read_csv(filename, header=0) values = df.values sequences.append(values) return sequences, targets.values[:,1], groups.values[:,1], paths.values[:,1] # 为每个带有输出变量的轨迹创建一个固定的一维向量 def create_dataset(sequences, targets): # 创建转换后的数据集 transformed = list() n_vars = 4 n_steps = 19 # 依次处理每个轨迹 for i in range(len(sequences)): seq = sequences[i] vector = list() # 最后 n 个观测值 for row in range(1, n_steps+1): for col in range(n_vars): vector.append(seq[-row, col]) # 添加输出 vector.append(targets[i]) # 存储 transformed.append(vector) # 准备数组 transformed = array(transformed) transformed = transformed.astype('float32') return transformed # 加载数据集 sequences, targets, groups, paths = load_dataset() # 分离轨迹 seq1 = [sequences[i] for i in range(len(groups)) if groups[i]==1] seq2 = [sequences[i] for i in range(len(groups)) if groups[i]==2] seq3 = [sequences[i] for i in range(len(groups)) if groups[i]==3] # 分离目标 targets1 = [targets[i] for i in range(len(groups)) if groups[i]==1] targets2 = [targets[i] for i in range(len(groups)) if groups[i]==2] targets3 = [targets[i] for i in range(len(groups)) if groups[i]==3] # 创建 ES1 数据集 es1 = create_dataset(seq1+seq2, targets1+targets2) print('ES1: %s' % str(es1.shape)) savetxt('es1.csv', es1, delimiter=',') # 创建 ES2 数据集 es2_train = create_dataset(seq1+seq2, targets1+targets2) es2_test = create_dataset(seq3, targets3) print('ES2 Train: %s' % str(es2_train.shape)) print('ES2 Test: %s' % str(es2_test.shape)) savetxt('es2_train.csv', es2_train, delimiter=',') savetxt('es2_test.csv', es2_test, delimiter=',') |
运行示例会创建三个新的 CSV 文件,分别是用于 ES1 和 ES2 情况的“_es1.csv_”、“_es2_train.csv_”和“_es2_test.csv_”。
这些数据集的形状也进行了汇总。
|
1 2 3 |
ES1:(210,77) ES2 训练集:(210,77) ES2 测试集:(104,77) |
接下来,我们可以评估 ES1 数据集上的模型。
经过一些测试,似乎标准化数据集对于依赖距离值的方法(KNN 和 SVM)会产生更好的模型技能,并且通常对其他方法没有影响。因此,管道用于评估每个算法,该算法首先标准化数据集。
下面列出了在新数据集上抽查算法的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# ES1 抽查 from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.model_selection import cross_val_score from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.tree import DecisionTreeClassifier from sklearn.svm import SVC from sklearn.ensemble import RandomForestClassifier from sklearn.ensemble import GradientBoostingClassifier # 加载数据集 dataset = read_csv('es1.csv', header=None) # 分割输入和输出 values = dataset.values X, y = values[:, :-1], values[:, -1] # 创建要评估的模型列表 models, names = list(), list() # 逻辑回归 models.append(LogisticRegression()) names.append('LR') # knn models.append(KNeighborsClassifier()) names.append('KNN') # cart models.append(DecisionTreeClassifier()) names.append('CART') # svm models.append(SVC()) names.append('SVM') # 随机森林 models.append(RandomForestClassifier()) names.append('RF') # gbm models.append(GradientBoostingClassifier()) names.append('GBM') # 评估模型 all_scores = list() for i in range(len(models)): # 为模型创建一个管道 s = StandardScaler() p = Pipeline(steps=[('s',s), ('m',models[i])]) scores = cross_val_score(p, X, y, scoring='accuracy', cv=5, n_jobs=-1) all_scores.append(scores) # 总结 m, s = mean(scores)*100, std(scores)*100 print('%s %.3f%% +/-%.3f' % (names[i], m, s)) # 绘图 pyplot.boxplot(all_scores, labels=names) pyplot.show() |
运行该示例将打印每个算法的估计性能,包括通过5折交叉验证获得的平均值和标准差。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。
结果表明,SVM在58%的准确率下可能值得更详细地研究。
|
1 2 3 4 5 6 |
LR 55.285% +/-5.518 KNN 50.897% +/-5.310 CART 50.501% +/-10.922 SVM 58.551% +/-7.707 RF 50.442% +/-6.355 GBM 55.749% +/-5.423 |
结果还以箱线图的形式呈现,显示了分数的分布。
再次,SVM似乎具有良好的平均性能和紧密的方差。
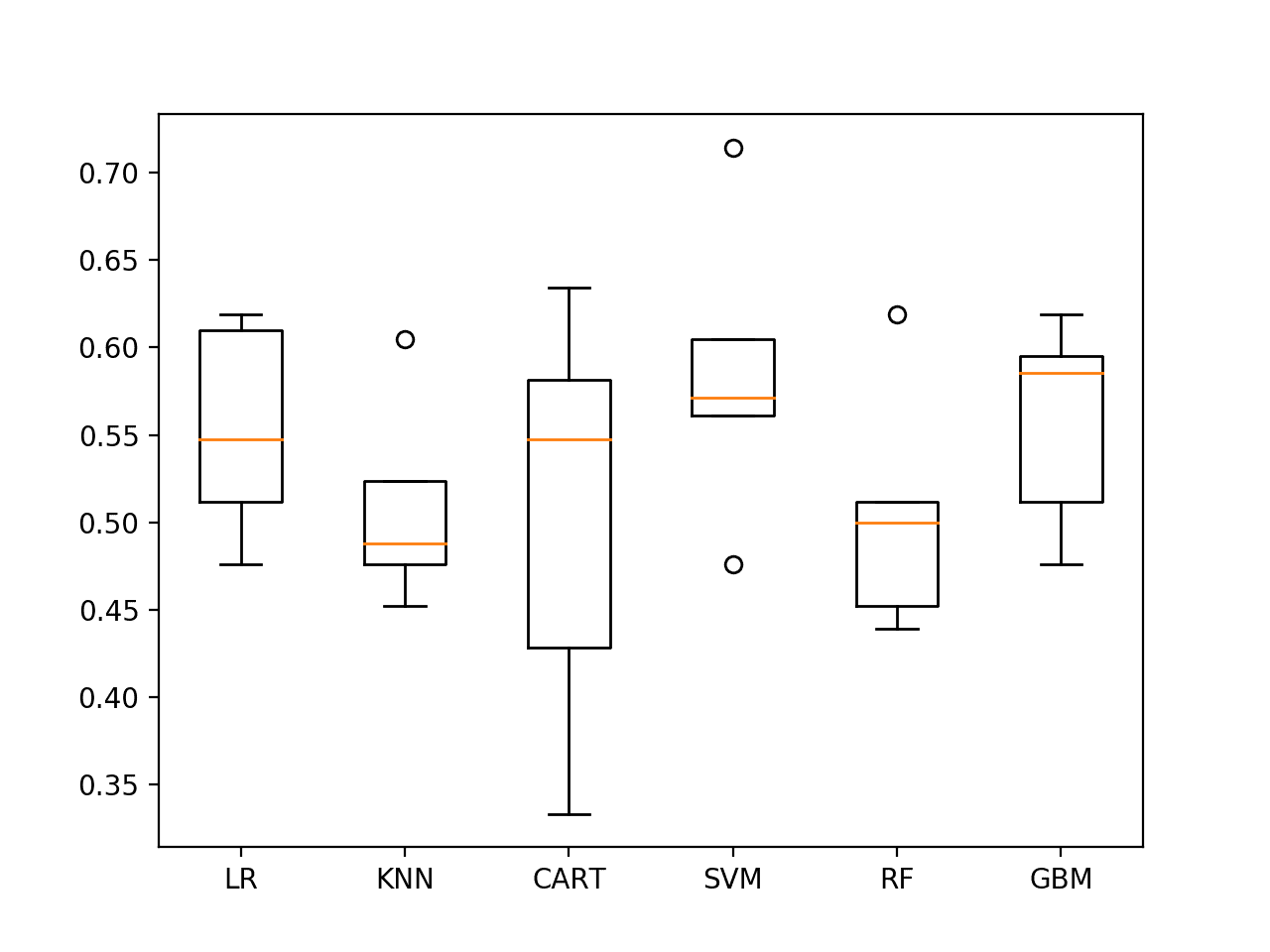
使用最后19个观测值对ES1进行抽查算法
带填充的最后n个观测值
我们可以将每个轨迹填充到固定长度。
这将提供灵活性,以在每个序列中包含更多之前的n个观测值。n的选择还必须与添加到较短序列中的填充值增加量相平衡,这反过来可能会对模型在这些序列上的性能产生负面影响。
我们可以通过在每个变量序列的开头添加0.0值来填充每个序列,直到达到最大长度,例如200个时间步。我们可以使用pad() NumPy函数来完成此操作。
|
1 2 3 4 5 |
from numpy import pad ... # 填充序列 max_length = 200 seq = pad(seq, ((max_length-len(seq),0),(0,0)), 'constant', constant_values=(0.0)) |
下面是支持填充的更新版create_dataset()函数。
我们将尝试使用n=25,在每个向量的每个序列中包含最后25个观测值。这个值是通过一些反复试验得到的,尽管您可能希望探索其他配置是否能带来更好的技能。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 为每个带有输出变量的轨迹创建一个固定的一维向量 def create_dataset(sequences, targets): # 创建转换后的数据集 transformed = list() n_vars, n_steps, max_length = 4, 25, 200 # 依次处理每个轨迹 for i in range(len(sequences)): seq = sequences[i] # 填充序列 seq = pad(seq, ((max_length-len(seq),0),(0,0)), 'constant', constant_values=(0.0)) vector = list() # 最后 n 个观测值 for row in range(1, n_steps+1): for col in range(n_vars): vector.append(seq[-row, col]) # 添加输出 vector.append(targets[i]) # 存储 transformed.append(vector) # 准备数组 transformed = array(transformed) transformed = transformed.astype('float32') return transformed |
再次运行带有新函数的脚本会创建更新的CSV文件。
|
1 2 3 |
ES1: (210, 101) ES2 训练集: (210, 101) ES2 测试集: (104, 101) |
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。
再次,重新运行数据上的抽查脚本,结果是SVM的模型技能略有提升,也表明KNN可能值得进一步研究。
|
1 2 3 4 5 6 |
LR 54.344% +/-6.195 KNN 58.562% +/-4.456 CART 52.837% +/-7.650 SVM 59.515% +/-6.054 RF 50.396% +/-7.069 GBM 50.873% +/-5.416 |
KNN和SVM的箱线图显示了良好的性能和相对紧凑的标准差。
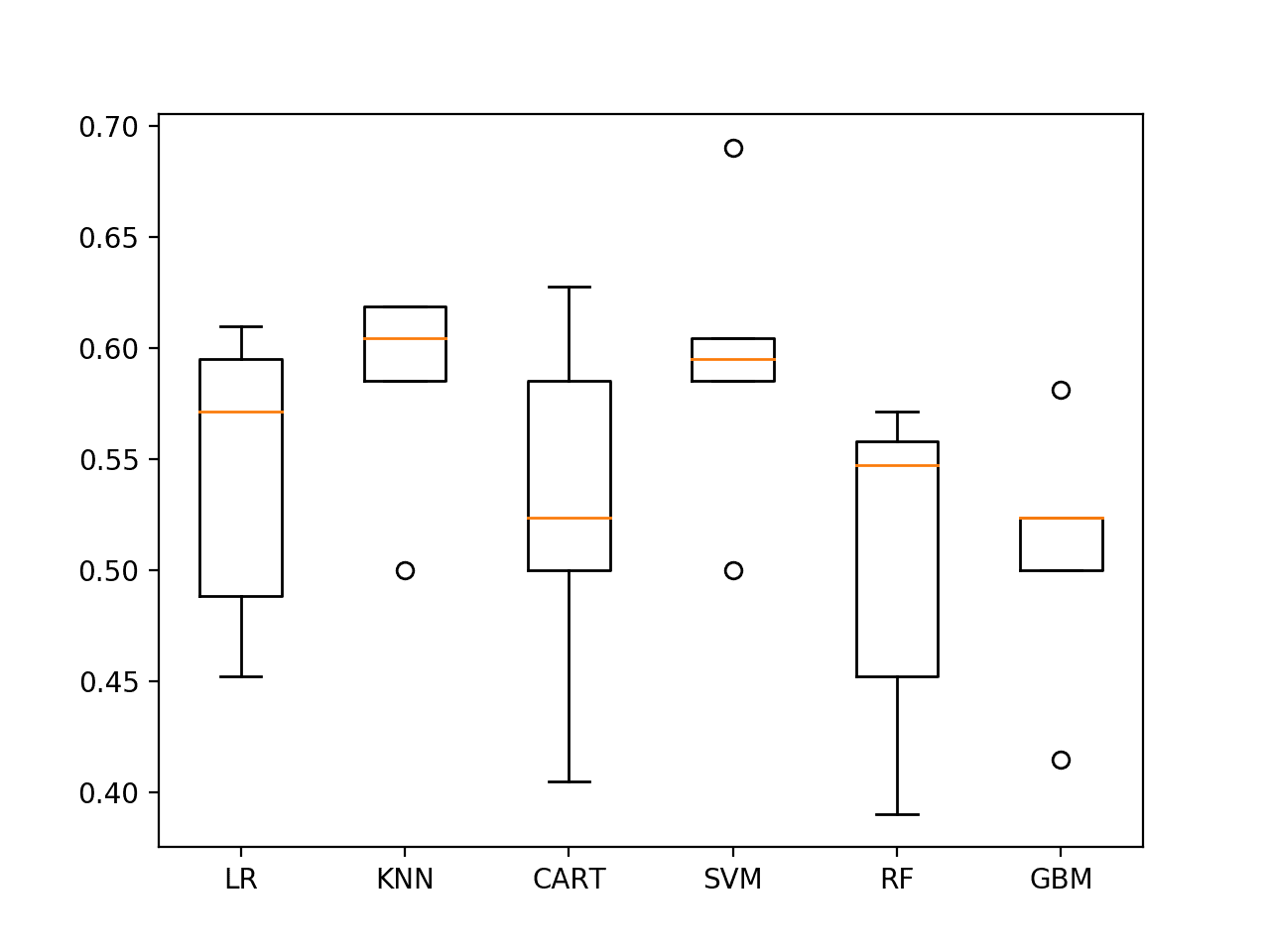
使用最后25个观测值对ES1上的算法进行抽查
我们可以更新抽查,为KNN算法进行一系列k值的网格搜索,看看是否可以通过少量调优进一步提高模型的技能。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
# ES1 抽查 from numpy import mean from numpy import std from pandas import read_csv from matplotlib import pyplot from sklearn.model_selection import cross_val_score from sklearn.neighbors import KNeighborsClassifier from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler # 加载数据集 dataset = read_csv('es1.csv', header=None) # 分割输入和输出 values = dataset.values X, y = values[:, :-1], values[:, -1] # 尝试一系列k值 all_scores, names = list(), list() for k in range(1,22): # 评估 scaler = StandardScaler() model = KNeighborsClassifier(n_neighbors=k) pipeline = Pipeline(steps=[('s',scaler), ('m',model)]) names.append(str(k)) scores = cross_val_score(pipeline, X, y, scoring='accuracy', cv=5, n_jobs=-1) all_scores.append(scores) # 总结 m, s = mean(scores)*100, std(scores)*100 print('k=%d %.3f%% +/-%.3f' % (k, m, s)) # 绘图 pyplot.boxplot(all_scores, labels=names) pyplot.show() |
运行该示例将打印k值从1到21的准确度的平均值和标准差。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。
我们可以看到,k=7达到了62.872%的最佳技能。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
k=1 49.534% +/-4.407 k=2 49.489% +/-4.201 k=3 56.599% +/-6.923 k=4 55.660% +/-6.600 k=5 58.562% +/-4.456 k=6 59.991% +/-7.901 k=7 62.872% +/-8.261 k=8 59.538% +/-5.528 k=9 57.633% +/-4.723 k=10 59.074% +/-7.164 k=11 58.097% +/-7.583 k=12 58.097% +/-5.294 k=13 57.179% +/-5.101 k=14 57.644% +/-3.175 k=15 59.572% +/-5.481 k=16 59.038% +/-1.881 k=17 59.027% +/-2.981 k=18 60.490% +/-3.368 k=19 60.014% +/-2.497 k=20 58.562% +/-2.018 k=21 58.131% +/-3.084 |
k值的准确度得分的箱线图显示,k值在七左右,例如五和六,在数据集上也能产生稳定且表现良好的模型。
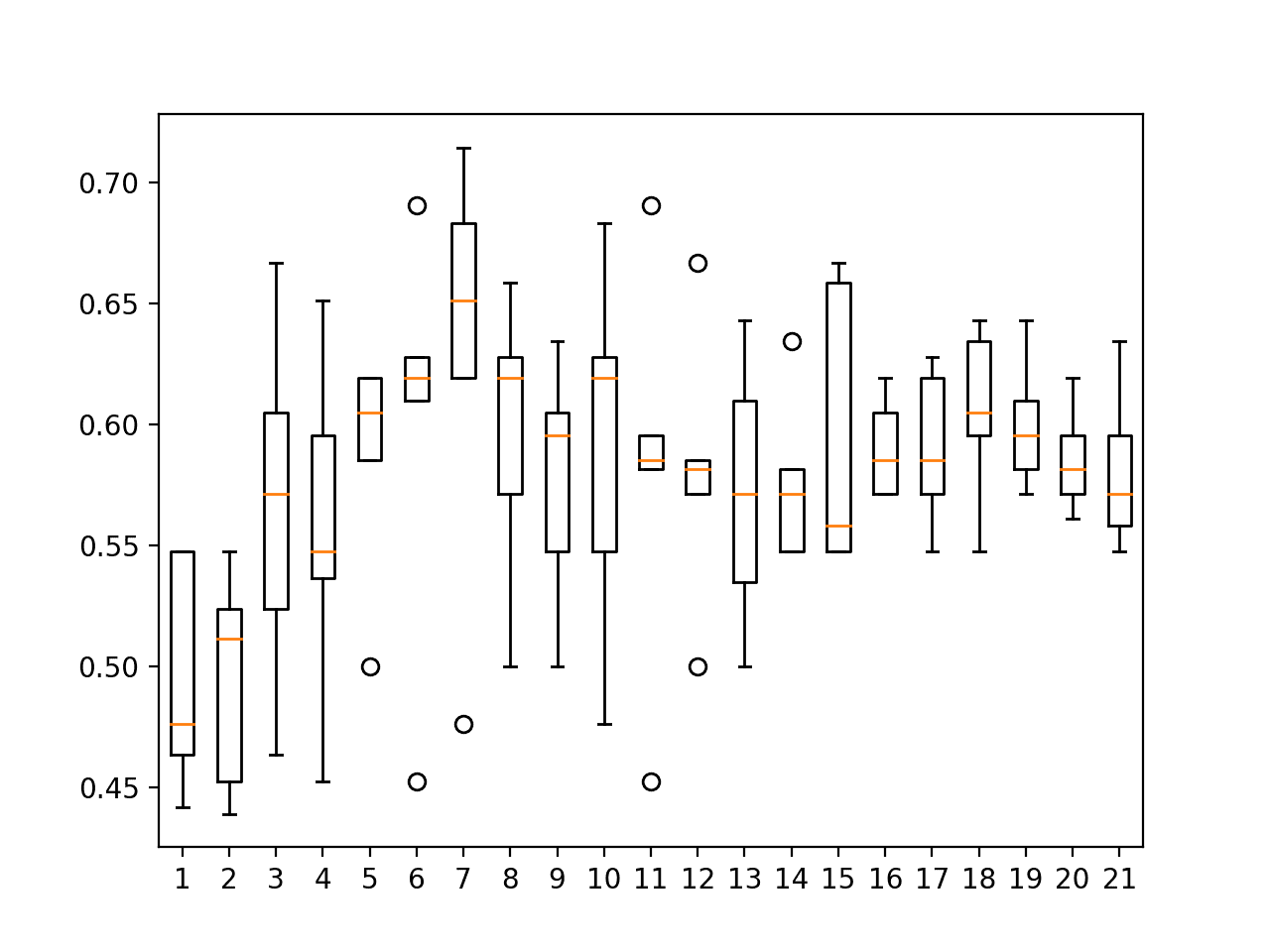
使用最后25个观测值对ES1上的KNN邻居进行抽查
评估ES2上的KNN
既然我们对某个表示(n=25)和某个模型(KNN,k=7)相对于随机预测有一些技能,我们就可以在更难的ES2数据集上测试该方法。
每个模型都在数据集1和2的组合上进行训练,然后在数据集3上进行评估。不使用k折交叉验证过程,因此我们预计分数会比较嘈杂。
下面列出了ES2算法的完整抽查结果。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
# ES2的抽查 from pandas import read_csv from matplotlib import pyplot from sklearn.metrics import accuracy_score from sklearn.linear_model import LogisticRegression from sklearn.neighbors import KNeighborsClassifier from sklearn.tree import DecisionTreeClassifier from sklearn.svm import SVC from sklearn.ensemble import RandomForestClassifier from sklearn.ensemble import GradientBoostingClassifier from sklearn.pipeline import Pipeline from sklearn.preprocessing import StandardScaler # 加载数据集 train = read_csv('es2_train.csv', header=None) test = read_csv('es2_test.csv', header=None) # 分割输入和输出 trainX, trainy = train.values[:, :-1], train.values[:, -1] testX, testy = test.values[:, :-1], test.values[:, -1] # 创建要评估的模型列表 models, names = list(), list() # 逻辑回归 models.append(LogisticRegression()) names.append('LR') # knn models.append(KNeighborsClassifier()) names.append('KNN') # knn models.append(KNeighborsClassifier(n_neighbors=7)) names.append('KNN-7') # cart models.append(DecisionTreeClassifier()) names.append('CART') # svm models.append(SVC()) names.append('SVM') # 随机森林 models.append(RandomForestClassifier()) names.append('RF') # gbm models.append(GradientBoostingClassifier()) names.append('GBM') # 评估模型 all_scores = list() for i in range(len(models)): # 为模型创建一个管道 scaler = StandardScaler() model = Pipeline(steps=[('s',scaler), ('m',models[i])]) # 拟合 # model = models[i] model.fit(trainX, trainy) # 预测 yhat = model.predict(testX) # 评估 score = accuracy_score(testy, yhat) * 100 all_scores.append(score) # 总结 print('%s %.3f%%' % (names[i], score)) # 绘图 pyplot.bar(names, all_scores) pyplot.show() |
运行该示例将报告ES2场景下的模型准确率。
注意:由于算法或评估过程的随机性,或数值精度的差异,您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。
我们可以看到KNN表现良好,并且在ES1上表现良好的七个邻居的KNN在ES2上也表现良好。
|
1 2 3 4 5 6 7 |
LR 45.192% KNN 54.808% KNN-7 57.692% CART 53.846% SVM 51.923% RF 53.846% GBM 52.885% |
准确率得分的条形图有助于更清楚地显示不同方法之间的相对性能差异。
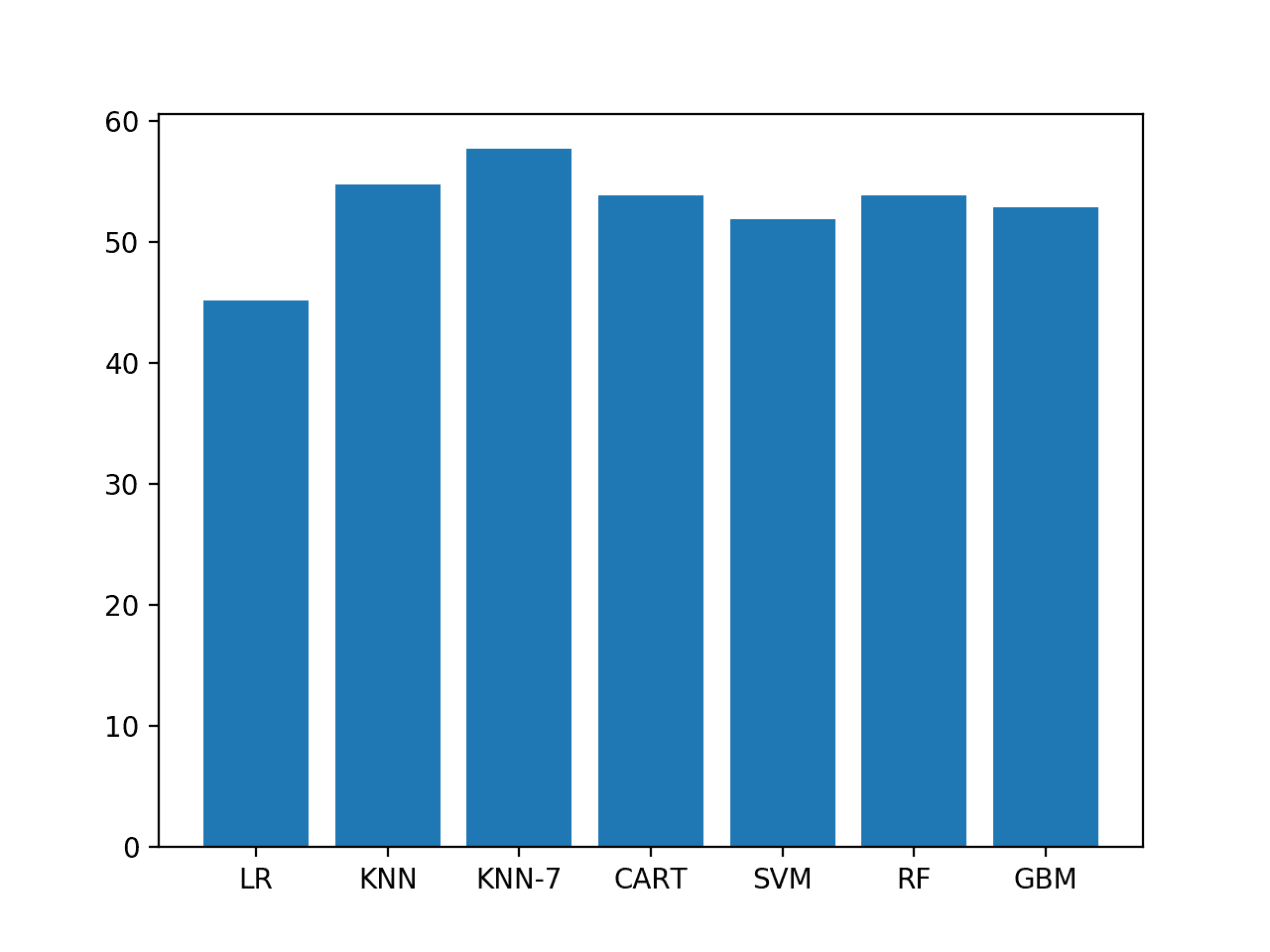
ES2模型准确率的条形图
所选择的表示和模型配置确实比50%准确率的朴素预测具有更好的技能。
进一步的调优可能会带来具有更好技能的模型,而且我们离论文中报道的ES1和ES2分别达到95%和89%的准确率还有很长的路要走。
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 数据准备。有很多机会可以探索更多的数据准备方法,例如归一化、差分和幂变换。
- 特征工程。进一步的特征工程可能会带来表现更好的模型,例如每个序列的开始、中间和结束的统计数据以及趋势信息。
- 调优。只有KNN算法得到了调优的机会;其他模型,如梯度提升,可能受益于超参数的精细调优。
- RNNs。这个序列分类任务似乎非常适合循环神经网络,如支持可变长度多变量输入的LSTM。对这个数据集(我自己)进行的一些初步测试显示结果非常不稳定,但更广泛的调查可能会给出更好甚至更优的结果。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
论文
- 通过水库计算预测异构室内环境中的用户移动, 2011.
- 环境辅助生活应用中水库计算的实验特征, 2014.
API
文章
- 来自 RSS 数据的室内用户移动预测数据集,UCI 机器学习存储库
- 通过水库计算预测异构室内环境中的用户移动,Paolo Barsocchi 主页.
- 室内用户移动预测 RSS 数据集,Laurae [法语]。
总结
在本教程中,您了解了室内移动预测时间序列分类问题,以及如何为该问题进行特征工程和评估机器学习算法。
具体来说,你学到了:
- 根据传感器强度预测房间之间移动的时间序列分类问题。
- 如何调查数据以更好地理解问题,以及如何从原始数据中为预测建模设计特征。
- 如何对一套分类算法进行抽查,并调整一个算法以进一步提升该问题的性能。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。







你好,Jason。
非常感谢这个很棒且有用的教程。
我阅读了Davide Bacciu等人的论文(2011年)“通过储层计算预测异构室内环境中的用户移动”。他的方法包括储层计算和LI-ESN,似乎效率惊人。
你认为有机会在Python中实现这种方法吗?
祝好,
雷米
目前不行。我怀疑大多数论文中的结果是否能够重现。
你好 Jason,
关于多变量时间序列和LSTM的精彩教程;我非常喜欢阅读它们,学到了很多。我是这个领域的新手(还在上在线深度学习课程),有一个普遍的问题(我最好说我需要一个普遍的建议)。假设我有一个多变量时间序列数据,我想构建一个分类器模型(三类分类,值为0、1或2)。解决这个问题的最佳方法是什么?LSTM还是多通道CNN?你还写过其他教程吗?
谢谢
我建议测试一系列方法,以发现最适合您的特定数据集的方法。
数据集的链接似乎对我不起作用。有人能确认网站是否还在运行吗?
网站似乎已关闭,有时会这样。非常抱歉!
我在这里创建了一个镜像
https://raw.githubusercontent.com/jbrownlee/Datasets/master/IndoorMovement.zip
谢谢你!很棒的工作,谢谢分享。
谢谢。
嗨,Jason,
请问,这与人类活动识别是相似的话题吗?
祝好,
艾伦
不太一样,HAR是关于“根据传感器数据,人在做什么”,室内移动是关于“根据传感器数据,人在建筑物中的位置”。
嗨,Jason,教程非常棒!
我不明白为什么你在准备数据集时使用“ -row” 在 vector.append(seq[-row, col]) 中。
我们正在添加最后的“n”个观测值,从数据集的末尾向后工作。
好的,但是你颠倒了值的顺序。为什么选择这样做?
是的,对于无状态机器学习算法,顺序并不重要——它们都被视为输入变量。
嗨,Jason,我不知道为什么,但是当我使用create_dataset函数时,我得到以下输出
ES1: (1L, 77L)
ES2 训练: (1L, 77L)
ES2 测试: (1L, 77L)
而不是
ES1:(210,77)
ES2 训练集:(210,77)
ES2 测试集:(104,77)
您能确认您正在使用 Python 3.5+ 并且您的库是最新的吗?
是的,我尝试了 python 2.7 和 3.6。但是,问题出在转换为 float32
transformed = transformed.astype(‘float32′)
我通过在转换为 numpy 数组时直接转换数据来解决这个问题
transformed = np.array(transformed,dtype=’float32’)
干得好!
嗨 Jason
当我为ES1任务运行cross_val_score()时,我遇到了这个错误。
TypeError(“unbound method new_CreateProcess() 必须使用 _winapi 实例作为第一个参数调用(得到 str 实例代替)”,)
您的Python环境可能出现了一些奇怪的问题。
您确定是在命令行运行,而不是在某些引入新问题的笔记本或IDE中运行吗?
我正在使用 Visual Studio 运行。问题出在使用了 n_jobs=-1。
也许尝试将 n_jobs 设置为 1。
你好,Jason。
仅供参考,我使用朴素高斯在ES1上获得了最佳性能
干得好!
嗨,Jacob,
根据过去20个时间观测值对未来5个样本进行分类。我想知道是否可以进行多步时间序列分类。如果可以,您能给我指出任何例子吗?
谢谢你。
我写这个问题的时候正在和雅各布说话……显然不能同时写作和说话……对不起,Jason 🙂
没问题,我一点也不介意!
是的,你可以根据需要调整问题。
抱歉,我没有这方面的例子。
嗨,Jason,
很棒的帖子!我有个问题想问你。我什么时候应该对时间序列数据进行归一化?假设我正在使用KNN,我应该总是进行归一化吗?
谢谢。
当它能提高模型技能时。
嗨,Jason,
使用tslearn库中的TimeSeriesResampler进行特征工程怎么样?
使用此函数将序列重采样为相同长度。有什么优点和缺点?
https://tslearn.readthedocs.io/en/latest/gen_modules/preprocessing/tslearn.preprocessing.TimeSeriesResampler.html#tslearn.preprocessing.TimeSeriesResampler
谢谢
感谢您的建议。
亲爱的 Jason,
很抱歉打扰,但可能发现了一些错误。
也许您的脚本在读取文件时丢失了正确的ID序列。在这种情况下,文件读取的顺序与文件名中的正确ID序列不对应。正确的ID序列已放入文件名中。
感谢您的关注。
感谢分享。
嗨 Jason
在机器人上使用Wifi RSS指纹进行室内定位时,实施kNN方法是否正确?我已经完成了映射,现在可以通过三角测量/三边测量和指纹识别进行定位。我现在想基于AI实施定位。我使用相同的数据集与随机森林,但结果不够好。
也许可以尝试一下,并与其他方法的结果进行比较。
嗨,Jason,
做得好。请问,以下用例是否可行?
一个模型,用于使用多个患者的ICU临床时间序列数据预测心脏病发作。我需要根据过去的临床数据对患者进行分类。使用多变量数据对多个患者进行二元分类。
提前感谢。
您好,Vanitha……我们无法为您在项目上采取的具体路径提供建议,但我们有内容可以帮助您为模型选择正确的路径。
您似乎有多种目标……时间序列预测、聚类和二元分类。我们有内容可以帮助您理解每个概念。
以下是所有内容的绝佳起点
https://machinelearning.org.cn/start-here/