在浩瀚的数据宇宙中,重要的往往不是你所能看到的,而是你所能推断的。置信区间作为推断统计学的基石,使你能够根据样本数据对更大的人口做出有根据的猜测。利用艾姆斯(Ames)住房数据集,让我们揭示置信区间的概念,看看它们如何为房地产市场提供可操作的见解。
让我们开始吧。

推断性洞察:置信区间如何阐明艾姆斯房地产市场。
图片由Jonathan Klok提供。保留部分权利。
概述
本文包含以下部分:
- 推断统计学的核心
- 什么是置信区间?
- 用置信区间估计销售价格
- 理解置信区间背后的假设
推断统计学的核心
推断统计学使用数据样本对来自该样本的总体进行推断。主要组成部分包括:
- 置信区间:总体参数可能所在的范围。
- 假设检验:对总体参数进行推断的过程。
当研究整个总体不切实际,需要从代表性样本中得出见解时,推断统计学是不可或缺的,例如艾姆斯(Ames)房产数据集的情况。
通过我的书《数据科学新手指南》启动您的项目。它提供了带有工作代码的自学教程。
什么是置信区间?
想象一下,你从一个城市随机抽取了一些房屋样本,并计算出平均销售价格。虽然这为你提供了一个单一的估计值,但如果能有一个范围,让你知道整个城市的真实平均销售价格可能落在哪里,会不会更有信息量?这个范围估计就是置信区间所提供的。本质上,置信区间为我们提供了一个值范围,我们可以在其中合理地确信(例如,95%的置信度)真实的总体参数(如均值或比例)位于该范围内。
用置信区间估计销售价格
虽然像均值和中位数这样的点估计给了我们关于集中趋势的概念,但它们没有告诉我们真实总体参数可能所在的范围。置信区间弥补了这一差距。例如,如果你想估计艾姆斯所有房屋的平均销售价格,你可以使用数据集计算平均销售价格的95%置信区间。这个区间将给我们一个范围,我们有95%的信心艾姆斯所有房屋的真实平均销售价格位于其中。
你将使用t-分布找到置信区间
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
# 导入必要的库并加载数据 import scipy.stats as stats import pandas as pd Ames = pd.read_csv('Ames.csv') #定义置信水平和自由度 confidence_level = 0.95 degrees_freedom = Ames['SalePrice'].count() - 1 #计算“SalePrice”的置信区间 confidence_interval = stats.t.interval(confidence_level, degrees_freedom, loc=Ames['SalePrice'].mean(), scale=Ames['SalePrice'].sem()) # 打印出包含置信区间数字的句子 print(f"艾姆斯所有房屋真实平均销售价格的95%置信区间" f"介于 \${confidence_interval[0]:.2f} 和 \${confidence_interval[1]:.2f} 之间。") |
|
1 2 |
The 95% confidence interval for the true mean sales price of all houses in Ames is between $175155.78 and $180951.11. |
置信区间提供了一个范围,我们有一定程度的信心,认为该范围包含真实的总体参数。解释这个范围可以帮助我们理解估计的变异性和精确度。如果均值“SalePrice”的95%置信区间是($175,156, $180,951),那么我们有95%的信心认为艾姆斯所有房产的真实平均销售价格介于$175,156和$180,951之间。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 导入其他库 import matplotlib.pyplot as plt # 绘制主直方图 plt.figure(figsize=(10, 7)) plt.hist(Ames['SalePrice'], bins=30, color='lightblue', edgecolor='black', alpha=0.5, label='Sales Prices Distribution') # 调整样式后的样本均值和置信区间的垂直线 plt.axvline(Ames['SalePrice'].mean(), color='blue', linestyle='-', label=f'Mean: ${Ames["SalePrice"].mean():,.2f}') plt.axvline(confidence_interval[0], color='red', linestyle='--', label=f'Lower 95% CI: ${confidence_interval[0]:,.2f}') plt.axvline(confidence_interval[1], color='green', linestyle='--', label=f'Upper 95% CI: ${confidence_interval[1]:,.2f}') # 注释和标签 plt.title('销售价格分布与置信区间', fontsize=20) plt.xlabel('销售价格', fontsize=16) plt.ylabel('频率', fontsize=16) plt.xlim([min(Ames['SalePrice']) - 5000, max(Ames['SalePrice']) + 5000]) plt.legend() plt.grid(axis='y') plt.show() |
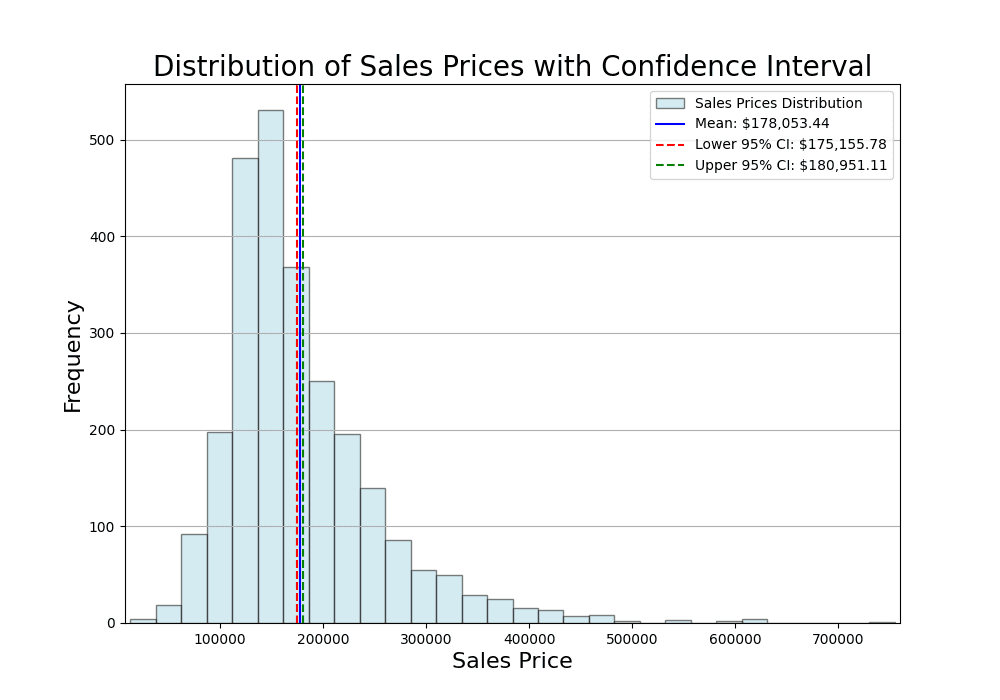
销售价格分布与均值
在上面的可视化中,直方图表示艾姆斯(Ames)住房数据集中的销售价格分布。蓝色垂直线对应于样本均值,提供了平均销售价格的点估计。虚线红色和绿色线分别代表95%的下限和上限置信区间。
让我们深入探讨150,000美元至200,000美元之间的价格范围。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 创建第二个图,重点关注均值和置信区间 plt.figure(figsize=(10, 7)) plt.hist(Ames['SalePrice'], bins=30, color='lightblue', edgecolor='black' alpha=0.5, label='Sales Prices') # 放大到均值和置信区间附近 plt.xlim([150000, 200000]) # 调整样式后的样本均值和置信区间的垂直线 plt.axvline(Ames['SalePrice'].mean(), color='blue', linestyle='-', label=f'Mean: ${Ames["SalePrice"].mean():,.2f}') plt.axvline(confidence_interval[0], color='red', linestyle='--', label=f'Lower 95% CI: ${confidence_interval[0]:,.2f}') plt.axvline(confidence_interval[1], color='green', linestyle='--', label=f'Upper 95% CI: ${confidence_interval[1]:,.2f}') # 放大图的注释和标签 plt.title('均值和置信区间放大视图', fontsize=20) plt.xlabel('销售价格', fontsize=16) plt.ylabel('频率', fontsize=16) plt.legend() plt.grid(axis='y') plt.show() |
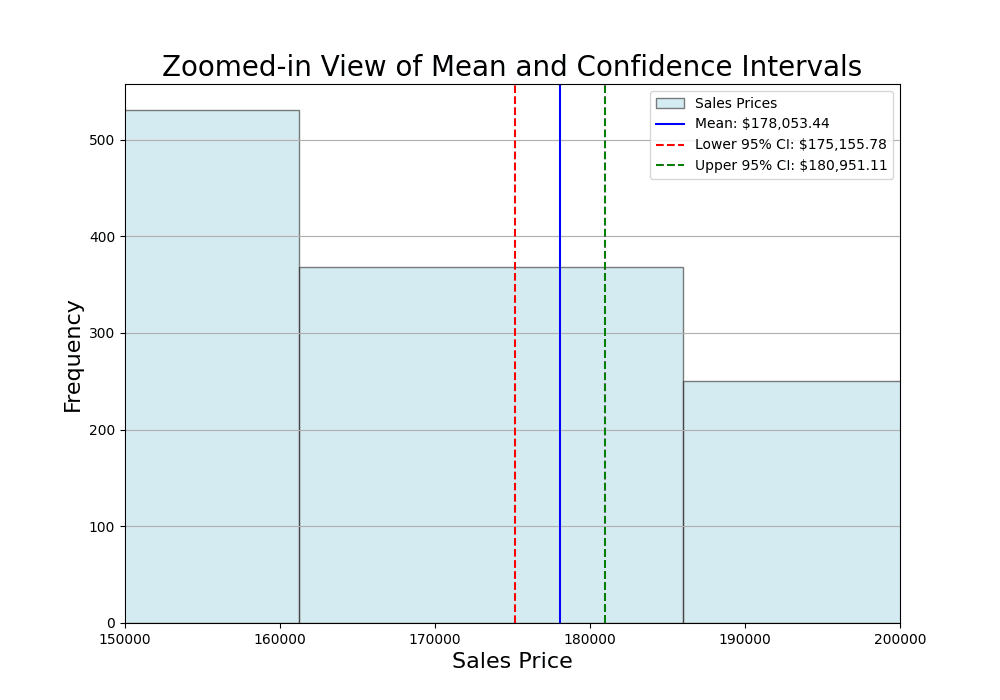
置信区间的解释如下:我们有95%的信心认为艾姆斯所有房屋的真实平均销售价格介于下限置信水平175,156美元和上限置信水平180,951美元之间。这个范围考虑了从样本估计总体参数时固有的变异性。从收集到的样本计算出的平均值为178,053美元,但整个总体的实际值可能不同。换句话说,由于它是从大量样本中计算出来的,所以这个区间很窄。
想开始学习数据科学新手指南吗?
立即参加我的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
理解置信区间背后的假设
为了在艾姆斯房地产市场动态多变的环境中熟练应用置信区间,理解我们分析所依据的基本假设至关重要。
假设1:随机抽样。 我们的分析假设数据是通过随机抽样过程收集的,确保艾姆斯的每个房产都有平等的机会被纳入。这种随机性增强了我们的发现对整个房地产市场的普遍性。
假设2:中心极限定理(CLT)和大样本。 我们分析中的一个关键假设是中心极限定理(CLT),它允许在计算置信区间时使用t-分布。CLT认为,对于大样本,样本均值的抽样分布近似于正态分布,无论总体分布如何。在我们的案例中,有2,579个观测值,CLT得到了强有力的满足。
假设3:独立性。 我们假设单个房屋的销售价格彼此独立。这个假设至关重要,它确保一栋房屋的销售价格不影响另一栋房屋的销售价格。这在艾姆斯多元化的房地产市场中尤为重要。
假设4:已知或估计的总体标准差(用于Z区间)。 虽然我们的主要方法涉及使用t分布,但值得注意的是,置信区间也可以使用Z分数计算,这需要知道或可靠地估计总体标准差。然而,我们的分析倾向于t分布,它在处理较小的样本量或总体标准差未知时更具鲁棒性。
假设5:连续数据。 置信区间应用于连续数据。在我们的背景下,艾姆斯房屋的销售价格是连续变量,这使得置信区间适合于估计总体参数。
这些假设构成了我们分析的基础,认识到它们的作用并评估其有效性对于可靠且富有洞察力的房地产市场分析至关重要。违反这些假设可能会损害我们结论的可靠性。总而言之,我们以t分布为基础的方法论利用这些假设,为艾姆斯的市场趋势和房产价值提供了细致入微的见解。
进一步阅读
教程
- 置信区间教程
- scipy.stats.t API
资源
总结
具体来说,你学到了:
- 推断统计学中置信区间的基础概念。
- 如何估计和解释艾姆斯(Ames)房地产市场平均销售价格的95%置信区间。
- 置信区间计算的关键假设。
您有任何问题吗?请在下面的评论中提出您的问题,我将尽力回答。







暂无评论。