机器学习中的信息增益与互信息

信息增益计算通过以某种方式转换数据集来减少熵或惊喜。

它常用于从训练数据集中构建决策树，通过评估每个变量的信息增益，并选择使信息增益最大的变量，从而最小化熵并最佳地将数据集分割成用于有效分类的组。

信息增益也可用于特征选择，通过在目标变量的背景下评估每个变量的增益。在此略有不同的用法中，该计算被称为两个随机变量之间的互信息。

在本文中，您将了解机器学习中的信息增益和互信息。

阅读本文后，你将了解：

• 信息增益是通过转换数据集来减少熵或惊喜，并且通常用于训练决策树。
• 信息增益的计算方法是比较转换前后数据集的熵。
• 互信息计算两个变量之间的统计依赖性，当应用于变量选择时，它被称为信息增益。

开始您的项目，阅读我的新书 机器学习概率，其中包含分步教程和所有示例的Python源代码文件。

让我们开始吧。

• 更新 2019年11月：改进了信息/熵基础的描述（感谢HR）。
• 更新 2020年8月：为公式添加了缺失的括号（感谢David）。

什么是机器学习的信息增益和互信息
照片由 Giuseppe Milo 拍摄，保留部分权利。

概述

本教程分为五个部分；它们是：

1. 什么是信息增益？
2. 信息增益计算的实例
3. 机器学习中信息增益的示例
4. 什么是互信息？
5. 信息增益和互信息之间有什么关系？

什么是信息增益？

信息增益，简称 IG，衡量通过根据随机变量的给定值分割数据集来减少熵或惊喜。

更大的信息增益表明样本组的熵更低或惊喜更少。

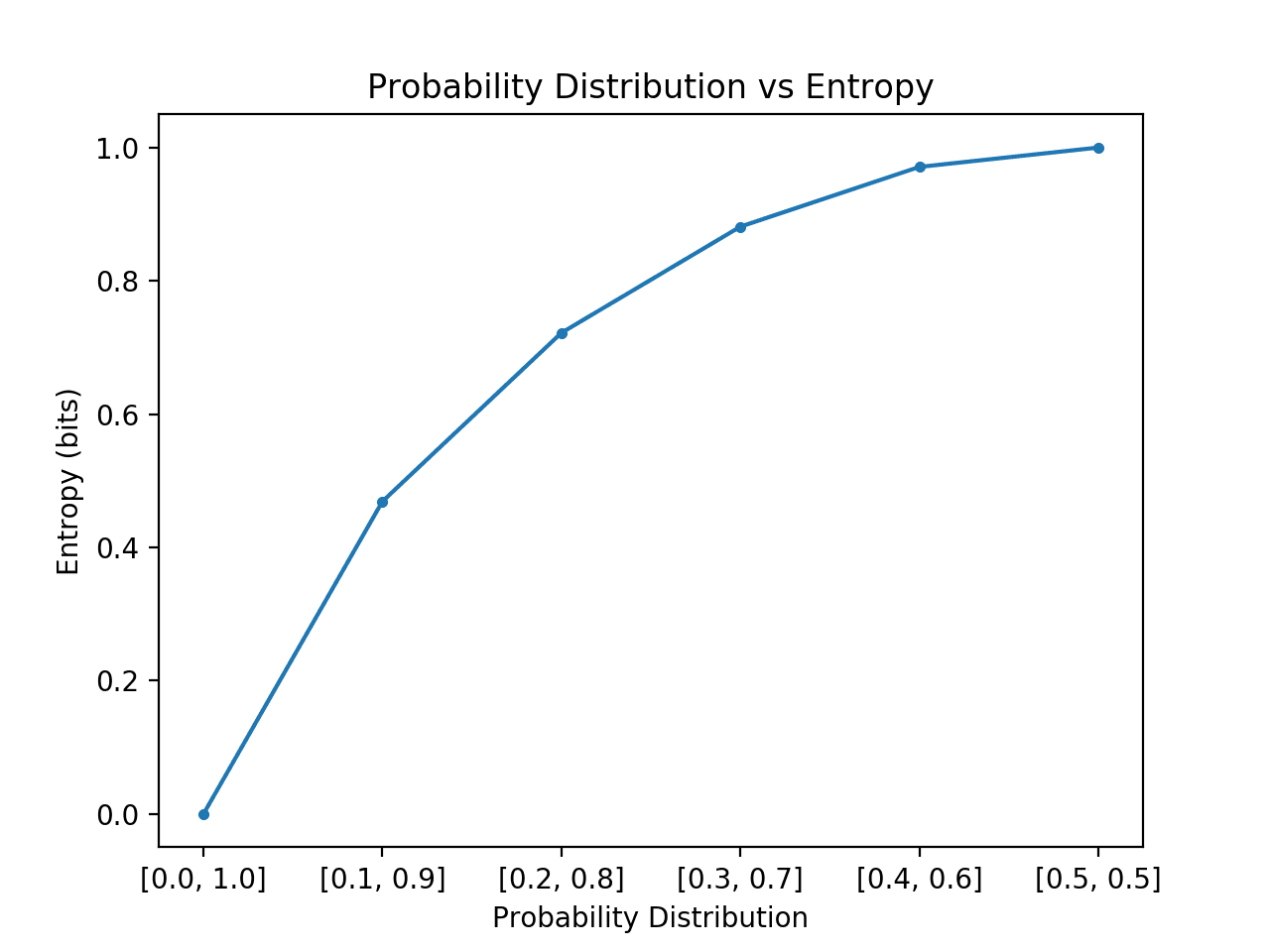
您可能还记得，信息量化了事件在比特中的惊喜程度。低概率事件具有更多信息，高概率事件具有更少信息。熵量化了随机变量中存在多少信息，或者更具体地说，它的概率分布。倾斜的分布具有低熵，而事件概率相等的分布具有更大的熵。

在信息论中，我们喜欢描述事件的“惊喜”。低概率事件更令人惊喜，因此具有更多的信息。而事件概率相等的概率分布更令人惊喜，具有更大的熵。

• 偏斜的概率分布（不令人意外）：低熵。
• 均衡的概率分布（令人意外）：高熵。

有关信息和熵基础知识的更多内容，请参阅教程

• 信息熵简明介绍

现在，让我们考虑数据集的熵。

我们可以从信息论的角度来考虑数据集的熵，即数据集中观测值属于一个类别或另一个类别的概率分布，例如二元分类数据集中的两个类别。

从信息论的角度来看，熵的一个解释是，它指定了编码S的任意成员（即，从S中随机抽取一个成员，具有均匀概率）的分类所需的最小比特信息。

— 第 58 页，机器学习，1997。

例如，在二元分类问题（两个类别）中，我们可以按如下方式计算样本集熵：

• 熵 = -(p(0) * log(P(0)) + p(1) * log(P(1)))

包含两个类别样本比例为 50/50 的数据集将具有最大熵（最大惊喜）1 比特，而比例为 10/90 的不平衡数据集将具有较小的熵，因为从数据集中随机抽取一个示例的惊喜会更少。

我们可以通过一个在 Python 中计算此不平衡数据集熵的示例来演示这一点。完整的示例列在下面。

运行该示例，我们可以看到二元分类数据集的熵小于 1 比特。也就是说，要对数据集中任意示例的类标签进行编码，只需不到 1 比特的信息。

通过这种方式，熵可以作为计算数据集纯度的度量，例如类别分布的均衡程度。

熵为 0 比特表示数据集中只包含一个类别；熵为 1 比特或更高表示平衡数据集的最大熵（取决于类别数量），中间值表示这些极端之间的水平。

信息增益提供了一种使用熵来计算数据集的更改如何影响数据集纯度（例如，类别分布）的方法。熵越小，纯度越高或惊喜越少。

…信息增益，就是通过根据该属性对示例进行划分所导致的熵的预期减少。

— 第 57 页，机器学习，1997。

例如，我们可能希望通过将数据集*S*按具有一系列值的随机变量进行划分来评估对纯度的影响。

这可以按如下方式计算：

• IG(S, a) = H(S) – H(S | a)

其中 *IG(S, a)* 是数据集 *S* 对变量 *a* 的信息，*H(S)* 是更改前的熵（如上所述），*H(S | a)* 是给定变量 *a* 的数据集的条件熵。

此计算描述了数据集 *S* 对变量 *a* 的增益。这是转换数据集时节省的比特数。

可以通过将数据集划分为变量 *a* 的每个观测值的组，并计算每个组中示例占整个数据集的比例乘以每个组的熵的总和来计算条件熵。

• H(S | a) = sum v in a Sa(v)/S * H(Sa(v))

其中 *Sa(v)/S* 是数据集中变量 *a* 取值为 *v* 的示例数量的比例，*H(Sa(v))* 是变量 *a* 取值为 *v* 的样本组的熵。

这听起来可能有点令人困惑。

我们可以通过一个实例来具体说明信息增益的计算。

信息增益计算的实例

在本节中，我们将通过一个实例来具体说明信息增益的计算。

我们可以定义一个函数来计算样本组的熵，该函数基于属于类别 0 和类别 1 的样本比例。

现在，考虑一个包含 20 个示例的数据集，其中 13 个是类别 0，7 个是类别 1。我们可以计算此数据集的熵，它将小于 1 比特。

现在，假设数据集中有一个变量有两个唯一值，例如“*value1*”和“*value2*”。我们对计算此变量的信息增益感兴趣。

假设如果我们按 value1 分割数据集，我们会得到一个包含七个类别 0 和一个类别 1 的八个样本的组。然后我们可以计算这个样本组的熵。

现在，假设我们按 value2 分割数据集；我们得到一个包含六个样本的组。我们预计此组的熵为 1。

最后，我们可以根据变量每个值创建的组以及计算出的熵来计算此变量的信息增益。

第一个变量导致了数据集中的八个示例组，第二个组包含数据集中剩余的 12 个样本。因此，我们拥有计算信息增益所需的一切。

在这种情况下，信息增益可以计算为：

• 熵(数据集) – (组1计数 / 数据集计数 * 熵(组1) + 组2计数 / 数据集计数 * 熵(组2))

或

• 熵(13/20, 7/20) – (8/20 * 熵(7/8, 1/8) + 12/20 * 熵(6/12, 6/12))

或在代码中：

将所有这些结合起来，完整的示例如下所示。

首先，数据集的熵计算结果略低于 1 比特。然后，第一组和第二组的熵分别计算为约 0.5 和 1 比特。

最后，该变量的信息增益计算为 0.117 比特。也就是说，通过选择的变量分割数据集所带来的增益是 0.117 比特。

机器学习中信息增益的示例

也许信息增益在机器学习中最受欢迎的应用是在 决策树 中。

例如，用于构建决策树的 Iterative Dichotomiser 3 算法，简称 ID3。

信息增益正是 ID3 在生长树的每个步骤中用于选择最佳属性的度量。

— 第 58 页，机器学习，1997。

为数据集中每个变量计算信息增益。信息增益最大的变量被选中用于分割数据集。通常，增益越大表示熵越小或惊喜越少。

请注意，最小化熵等同于最大化信息增益……

— 第 547 页，机器学习：概率视角，2012。

然后，该过程在每个创建的组上重复进行，排除已选定的变量。一旦达到所需的决策树深度或不再可能进行分割，该过程就会停止。

现在，为每个非终端后代节点重复选择新属性和划分训练示例的过程，这次仅使用与该节点关联的训练示例。已合并到树较高位置的属性将被排除，因此任何给定属性最多只能出现在树的任意路径上一次。

— 第 60 页，机器学习，1997。

信息增益可用作大多数现代决策树实现中的分割标准，例如 scikit-learn Python 机器学习库中用于分类的 DecisionTreeClassifier 类 中实现的分类和回归树 (CART) 算法。

通过在配置模型时将 criterion 参数设置为“*entropy*”来实现这一点；例如：

信息增益也可用于建模之前的特征选择。

它涉及计算目标变量与训练数据集中每个输入变量之间的信息增益。Weka 机器学习工作台通过 InfoGainAttributeEval 类提供了用于特征选择的信息增益实现。

在特征选择的背景下，信息增益可能被称为“*互信息*”，并计算两个变量之间的统计依赖性。使用信息增益（互信息）进行特征选择的一个例子是 mutual_info_classif() scikit-learn 函数。

什么是互信息？

互信息在两个变量之间计算，并衡量在已知另一个变量的值时，一个变量的不确定性减少的量。

一个称为互信息量的度量，衡量从一个随机变量可以获得关于另一个随机变量的信息量。

— 第 310 页，数据挖掘：实用机器学习工具与技术，第 4 版，2016。

两个随机变量 *X* 和 *Y* 之间的互信息可以正式表述如下：

• I(X ; Y) = H(X) – H(X | Y)

其中 *I(X ; Y)* 是 *X* 和 *Y* 的互信息，*H(X)* 是 *X* 的熵，*H(X | Y)* 是给定 *Y* 的 *X* 的条件熵。结果的单位是比特。

互信息是两个随机变量之间依赖性或“*相互依赖性*”的度量。因此，该度量是对称的，意味着 *I(X ; Y) = I(Y ; X)*。

它衡量了学习 *y* 的值所导致的关于 *x* 的不确定性的平均减少；或者反之，*x* 传达关于 *y* 的信息量。

— 第 139 页，信息论、推理与学习算法，2003。

Kullback-Leibler 散度，或 KL 散度，是一种度量，用于计算两个概率分布之间的差异。

互信息也可以计算为联合概率分布与每个变量的边际概率乘积之间的 KL 散度。

如果变量不独立，我们可以通过考虑联合分布与边际分布乘积之间的 Kullback-Leibler 散度来了解它们是否“接近”独立……这被称为变量之间的互信息。

— 第 57 页，模式识别与机器学习，2006。

这可以正式表述如下：

• I(X ; Y) = KL(p(X, Y) || p(X) * p(Y))

互信息总是大于或等于零，值越大，两个变量之间的关系越强。如果计算结果为零，则变量是独立的。

互信息通常用作相关系数的一般形式，例如衡量随机变量之间依赖性的度量。

它也用作某些机器学习算法的一个方面。一个常见的例子是 独立成分分析，简称 ICA，它提供了数据集统计独立成分的投影。

信息增益和互信息之间有什么关系？

互信息和信息增益是同一回事，尽管度量的上下文或用法经常导致不同的名称。

例如

• 数据集变换的影响（决策树）：信息增益。
• 变量之间的依赖性（特征选择）：互信息。

注意互信息的计算方式与信息增益的计算方式相似；它们是等效的。

• I(X ; Y) = H(X) – H(X | Y)

和

• IG(S, a) = H(S) – H(S | a)

因此，互信息有时用作信息增益的同义词。严格来说，如果应用于相同的数据，它们的计算量是相同的。

我们可以将两者之间的关系理解为：联合概率分布与边际概率分布之间的差异越大（互信息），信息增益就越大（信息增益）。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

• 信息论、推理与学习算法, 2003.
• 机器学习：概率视角, 2012.
• 模式识别与机器学习, 2006.
• 机器学习, 1997.
• 数据挖掘：实用机器学习工具与技术，第4版，2016年。

API

• scipy.stats.entropy API

文章

• 熵（信息论），维基百科.
• 决策树中的信息增益，维基百科.
• ID3 算法，维基百科.
• 信息增益率，维基百科.
• 互信息，维基百科.

总结

在本文中，您了解了机器学习中的信息增益和互信息。

具体来说，你学到了：

• 信息增益是通过转换数据集来减少熵或惊喜，并且通常用于训练决策树。
• 信息增益的计算方法是比较转换前后数据集的熵。
• 互信息计算两个变量之间的统计依赖性，当应用于变量选择时，它被称为信息增益。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

掌握机器学习中的概率！

增进你对概率的理解

...只需几行python代码

在我的新电子书中探索如何实现
机器学习概率

它提供了关于以下内容的自学教程和端到端项目：
贝叶斯定理、贝叶斯优化、分布、最大似然、交叉熵、校准模型
以及更多...

最终在你的项目中驾驭不确定性

跳过学术理论。只看结果。

查看内容