某些神经网络配置可能导致模型不稳定。
这会使它们难以表征,并且难以使用描述性统计与同一问题上的其他模型配置进行比较。
一个明显的模型不稳定的例子是,对状态LSTM(stateful LSTM)模型使用在线学习(批量大小为1)。
在本教程中,您将学习如何探索使用在线学习在标准时间序列预测问题上拟合的状态LSTM的结果。
完成本教程后,您将了解:
- 如何设计一个健壮的测试框架,用于评估时间序列预测问题的LSTM模型。
- 如何分析结果的分布,包括汇总统计、离散度和结果分布。
- 分析增加实验重复次数的影响。
开始您的项目,阅读我的新书《深度学习在时间序列预测中的应用》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。
- 2019 年 4 月更新:更新了数据集链接。

在线学习状态LSTM用于时间序列预测的不稳定性
照片由 Magnus Brath 拍摄,保留部分权利。
模型不稳定性
当您在相同数据上多次训练同一个网络时,您可能会得到非常不同的结果。
这是因为神经网络是随机初始化的,并且它们如何拟合训练数据的优化性质可能导致网络中最终权重不同。这些不同的网络反过来可能导致在给定相同输入数据时产生不同的预测。
因此,重要的是要多次重复神经网络的任何实验,以找到平均预期的性能。
有关像神经网络这样的机器学习算法的随机性质的更多信息,请参阅文章
神经网络中的批量大小定义了在给定训练数据集暴露后,网络内权重更新的频率。
批量大小为1意味着在每个单独的训练数据行后都会更新网络权重。这被称为在线学习。其结果是网络可以快速学习,但这种配置可能相当不稳定。
在本教程中,我们将探讨在时间序列预测中,状态LSTM配置的在线学习的不稳定性。
我们将通过查看LSTM配置在标准时间序列预测问题上的平均性能,以及实验重复次数的变化来探讨这一点。
也就是说,我们将对同一数据进行多次相同的模型配置重新训练,并查看模型在保留数据集上的性能,并回顾模型可能有多不稳定。
教程概述
本教程分为6个部分。它们是:
- 洗发水销售数据集
- 实验测试框架
- 代码和结果收集
- 结果的基本统计
- 重复次数与测试RMSE
- 结果回顾
环境
本教程假定您已安装 Python SciPy 环境。您可以使用 Python 2 或 3。
本教程假定您已安装 Keras v2.0 或更高版本,并使用 TensorFlow 或 Theano 后端。
本教程还假定您已安装 scikit-learn、Pandas、NumPy 和 Matplotlib。
接下来,让我们看看一个标准的时间序列预测问题,我们可以将其作为本次实验的背景。
如果您需要帮助设置 Python 环境,请参阅此帖子
时间序列深度学习需要帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
洗发水销售数据集
此数据集描述了 3 年期间洗发水月销量。
单位是销售计数,共有 36 个观测值。原始数据集归功于 Makridakis、Wheelwright 和 Hyndman (1998)。
以下示例加载并创建加载数据集的图表。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 加载并绘制数据集 from pandas import read_csv from pandas import datetime from matplotlib import pyplot # 加载数据集 def parser(x): return datetime.strptime('190'+x, '%Y-%m') series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) # 总结前几行 print(series.head()) # 线图 series.plot() pyplot.show() |
运行该示例将数据集作为 Pandas Series 加载并打印前 5 行。
|
1 2 3 4 5 6 7 |
月份 1901-01-01 266.0 1901-02-01 145.9 1901-03-01 183.1 1901-04-01 119.3 1901-05-01 180.3 名称:销售额,数据类型:float64 |
然后创建该系列的线图,显示出明显的上升趋势。
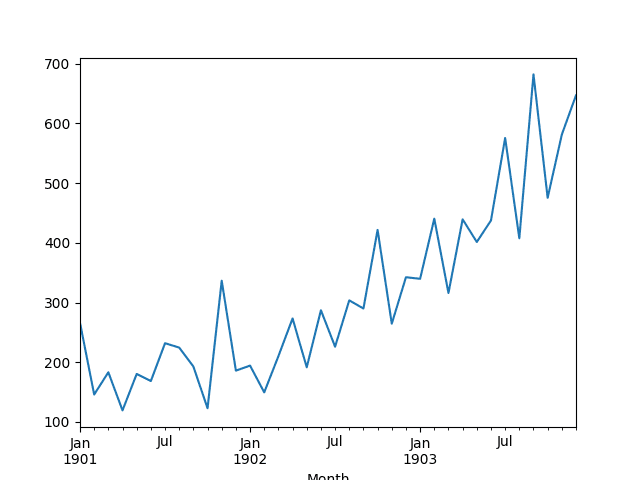
洗发水销售数据集的折线图
接下来,我们将看看实验中使用的LSTM配置和测试框架。
实验测试框架
本节将介绍本教程中使用的测试框架。
数据分割
我们将把洗发水销售数据集分为两部分:训练集和测试集。
前两年的数据将用于训练数据集,剩下的一年数据将用于测试集。
模型将使用训练数据集进行开发,并对测试数据集进行预测。
在测试数据集上的持久性预测(朴素预测)实现了136.761个月洗发水销量的误差。这为测试集上的性能提供了一个可接受的较低界限。
模型评估
将使用滚动预测方案,也称为向前验证模型。
测试数据集的每个时间步将逐一进行。模型将用于对时间步进行预测,然后将从测试集中获取实际预期值,并使其可用于模型对下一个时间步的预测。
这模拟了现实世界场景,其中每个月都会有新的洗发水销售观察值,并用于预测下个月。
这将通过训练和测试数据集的结构进行模拟。
将收集测试数据集上的所有预测,并计算一个误差分数来总结模型的技能。将使用均方根误差(RMSE),因为它会惩罚大的误差,并且其分数与预测数据单位相同,即月度洗发水销量。
数据准备
在我们使用 LSTM 模型拟合数据集之前,我们必须转换数据。
在拟合模型和进行预测之前,对数据集执行以下三种数据转换。
- 转换时间序列数据使其平稳。具体来说,进行滞后1的差分以消除数据中增加的趋势。
- 将时间序列转换为监督学习问题。具体来说,是将数据组织成输入和输出模式,其中先前时间步的观测值用作当前时间步观测值预测的输入。
- 转换观测值以具有特定比例。具体来说,将数据重新缩放到-1到1之间的值,以满足LSTM模型的默认双曲正切激活函数。
在计算误差分数之前,这些转换将被应用于预测中,以将它们恢复到其原始尺度。
LSTM 模型
我们将使用一个基础的状态LSTM模型,包含1个神经元,训练1000个周期。
由于我们将使用向前滚动验证,并且对最后12个月的测试数据进行单步预测,因此需要批量大小为1。
批量大小为1意味着模型将使用在线训练(而不是批量训练或小批量训练)进行拟合。因此,预计模型拟合会存在一些方差。
理想情况下,会使用更多的训练周期(例如1500个),但为了使运行时间合理,此处截断为1000个。
模型将使用高效的ADAM优化算法和均方误差损失函数进行拟合。
实验运行
每个实验场景将运行100次,并从每次运行结束时记录测试集上的RMSE分数。
所有测试RMSE分数都将被写入文件以供后续分析。
让我们开始实验。
代码和结果收集
完整的代码列表如下。
在现代硬件上,这可能需要几个小时才能运行。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 |
from pandas import DataFrame from pandas import Series 从 pandas 导入 concat from pandas import read_csv from pandas import datetime from sklearn.metrics import mean_squared_error 从 sklearn.预处理 导入 MinMaxScaler from keras.models import Sequential from keras.layers import Dense 从 keras.layers 导入 LSTM from math import sqrt import matplotlib import numpy from numpy import concatenate # 用于加载数据集的日期时间解析函数 def parser(x): return datetime.strptime('190'+x, '%Y-%m') # 将序列构造成监督学习问题 def timeseries_to_supervised(data, lag=1): df = DataFrame(data) columns = [df.shift(i) for i in range(1, lag+1)] columns.append(df) df = concat(columns, axis=1) return df # 创建差分序列 def difference(dataset, interval=1): diff = list() for i in range(interval, len(dataset)): value = dataset[i] - dataset[i - interval] diff.append(value) return Series(diff) # 反转差分值 def inverse_difference(history, yhat, interval=1): return yhat + history[-interval] # 将训练和测试数据缩放到 [-1, 1] def scale(train, test): # 拟合缩放器 scaler = MinMaxScaler(feature_range=(-1, 1)) scaler = scaler.fit(train) # 转换训练集 train = train.reshape(train.shape[0], train.shape[1]) train_scaled = scaler.transform(train) # 转换测试集 test = test.reshape(test.shape[0], test.shape[1]) test_scaled = scaler.transform(test) return scaler, train_scaled, test_scaled # 预测值的逆缩放 def invert_scale(scaler, X, yhat): new_row = [x for x in X] + [yhat] array = numpy.array(new_row) array = array.reshape(1, len(array)) inverted = scaler.inverse_transform(array) return inverted[0, -1] # 训练一个 LSTM 网络 def fit_lstm(train, batch_size, nb_epoch, neurons): X, y = train[:, 0:-1], train[:, -1] X = X.reshape(X.shape[0], 1, X.shape[1]) model = Sequential() model.add(LSTM(neurons, batch_input_shape=(batch_size, X.shape[1], X.shape[2]), stateful=True)) model.add(Dense(1)) model.compile(loss='mean_squared_error', optimizer='adam') for i in range(nb_epoch): model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False) model.reset_states() return model # 进行一步预测 def forecast_lstm(model, batch_size, X): X = X.reshape(1, 1, len(X)) yhat = model.predict(X, batch_size=batch_size) return yhat[0,0] # 运行重复实验 def experiment(repeats, series): # 将数据转换为平稳 raw_values = series.values diff_values = difference(raw_values, 1) # 将数据转换为监督学习 supervised = timeseries_to_supervised(diff_values, 1) supervised_values = supervised.values[1:,:] # 将数据分割成训练集和测试集 train, test = supervised_values[0:-12, :], supervised_values[-12:, :] # 转换数据尺度 scaler, train_scaled, test_scaled = scale(train, test) # 运行实验 error_scores = list() for r in range(repeats): # 拟合基础模型 lstm_model = fit_lstm(train_scaled, 1, 1000, 1) # 预测测试数据集 predictions = list() for i in range(len(test_scaled)): # 预测 X, y = test_scaled[i, 0:-1], test_scaled[i, -1] yhat = forecast_lstm(lstm_model, 1, X) # 反转缩放 yhat = invert_scale(scaler, X, yhat) # 反转差分 yhat = inverse_difference(raw_values, yhat, len(test_scaled)+1-i) # 存储预测 predictions.append(yhat) # 报告性能 rmse = sqrt(mean_squared_error(raw_values[-12:], predictions)) print('%d) Test RMSE: %.3f' % (r+1, rmse)) error_scores.append(rmse) return error_scores # 执行实验 def run(): # 加载数据集 series = read_csv('shampoo-sales.csv', header=0, parse_dates=[0], index_col=0, squeeze=True, date_parser=parser) # 实验 repeats = 100 results = DataFrame() # 运行实验 results['results'] = experiment(repeats, series) # 总结结果 print(results.describe()) # 保存结果 results.to_csv('experiment_stateful.csv', index=False) # 入口点 run() |
运行实验会将拟合模型在测试数据集上的 RMSE 分数保存下来。
结果保存在文件“experiment_stateful.csv”中。
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能有所不同。请考虑多次运行示例并比较平均结果。
下面提供了结果的截断列表。
|
1 2 3 4 5 6 7 8 9 10 11 |
... 116.39769471284067 105.0459745537738 93.57827109861229 128.973001927212 97.02915084460737 198.56877142225886 113.09568645243242 97.84127724751188 124.60413895331735 111.62139008607713 |
结果的基本统计
我们可以先计算 100 个测试 RMSE 分数总体的一些基本统计数据。
通常,我们期望机器学习结果呈现高斯分布。这使我们能够报告模型均值和标准差,并在对未见过的数据进行预测时,为模型指示一个置信区间。
下面的代码段加载结果文件并计算一些描述性统计数据。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
from pandas import DataFrame from pandas import read_csv from numpy import mean from numpy import std from matplotlib import pyplot # 加载结果文件 results = read_csv('experiment_stateful.csv', header=0) # 描述性统计 print(results.describe()) # 箱线图 results.boxplot() pyplot.show() |
运行示例会打印结果的描述性统计数据。
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能有所不同。请考虑多次运行示例并比较平均结果。
我们可以看到,平均而言,该配置实现的 RMSE 大约为每月洗发水销售额的 107,标准差约为 17。
我们还可以看到,观察到的最佳测试 RMSE 约为 90 次销售,而最差的则略低于 200,这是一个相当大的分数范围。
|
1 2 3 4 5 6 7 8 9 |
results count 100.000000 mean 107.051146 std 17.694512 min 90.407323 25% 96.630800 50% 102.603908 75% 111.199574 max 198.568771 |
为了更好地了解数据的分布情况,我们还创建了箱线图。
该图显示了中位数(绿线)、数据中间 50%(框)和异常值(点)。我们可以看到数据在向较差的 RMSE 分数方向有相当大的分散。
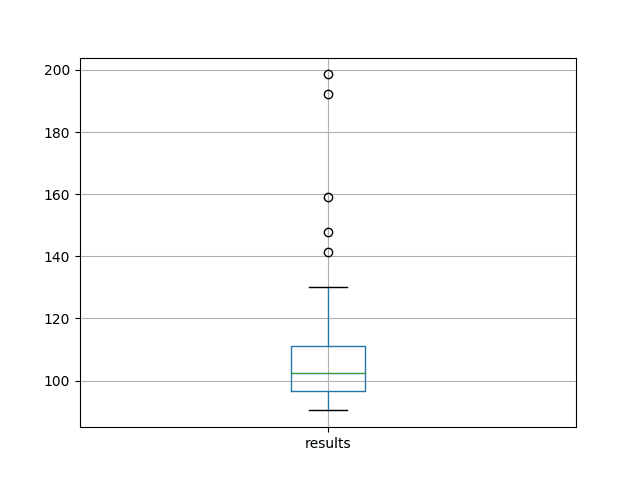
洗发水销售数据集上 100 个测试 RMSE 分数的箱线图
此外,我们还创建了原始结果值的直方图。
该图表明数据呈现偏斜分布甚至指数分布,在 RMSE 约为 100 时有一个质量集中,并在 RMSE 接近 200 时有一个长尾。
结果的分布明显不是高斯的。这很可惜,因为均值和标准差不能直接用于估计模型的置信区间(例如,95% 置信区间为均值周围的标准差的 2 倍)。
偏斜的分布也凸显了对于这些结果,中位数(第 50 百分位数)将比均值更能代表中心趋势。中位数应该比均值更能抵抗异常值结果。
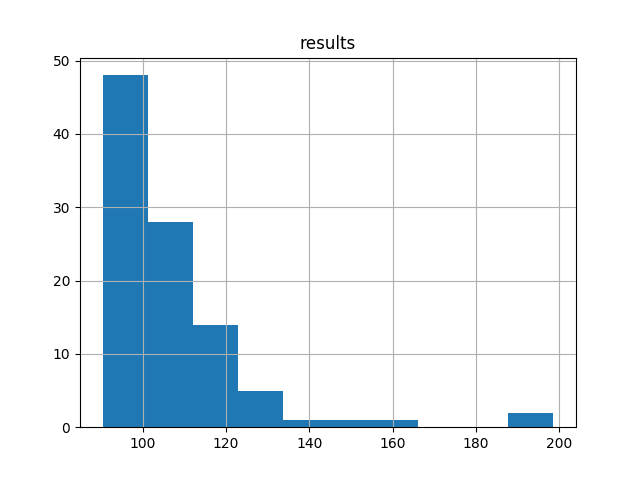
洗发水销售数据集测试 RMSE 分数直方图
重复次数与测试RMSE
我们可以开始查看随着重复次数从 1 增加到 100,实验的汇总统计数据如何变化。
我们可以累积测试 RMSE 分数并计算描述性统计数据。例如,一次重复的分数,前两次重复的分数,前 3 次重复的分数,依此类推,直到 100 次重复。
我们将通过折线图来回顾中心趋势随着重复次数的增加而如何变化。我们将同时查看均值和中位数。
通常,我们期望随着实验重复次数的增加,分布会越来越好地匹配底层分布,包括中心趋势,如均值。
完整的代码列表如下。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from pandas import DataFrame from pandas import read_csv from numpy import median from numpy import mean from matplotlib import pyplot import numpy # 加载结果文件 results = read_csv('experiment_stateful.csv', header=0) values = results.values # 收集累积统计 medians, means = list(), list() for i in range(1,len(values)+1): data = values[0:i, 0] mean_rmse, median_rmse = mean(data), median(data) means.append(mean_rmse) medians.append(median_rmse) print(i, mean_rmse, median_rmse) # 累积值的折线图 line1, = pyplot.plot(medians, label='中位数 RMSE') line2, = pyplot.plot(means, label='均值 RMSE') pyplot.legend(handles=[line1, line2]) pyplot.show() |
随着重复次数的增加,会打印出分布、均值和中位数的累积大小。
注意:由于算法或评估过程的随机性,或者数值精度的差异,您的结果可能有所不同。请考虑多次运行示例并比较平均结果。
下面列出了截断的输出。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
... 90 105.759546832 101.477640071 91 105.876449555 102.384620485 92 105.867422653 102.458057114 93 105.735281239 102.384620485 94 105.982491033 102.458057114 95 105.888245347 102.384620485 96 106.853667494 102.458057114 97 106.918018205 102.531493742 98 106.825398399 102.458057114 99 107.004981637 102.531493742 100 107.051145721 102.603907965 |
还创建了一个折线图,显示了均值和中位数随重复次数增加而变化的情况。
结果表明,正如预期的那样,均值比中位数更容易受到异常值结果的影响。
我们可以看到,中位数似乎相当稳定,大约在 99-100 左右。这在图的末尾跃升至 102,表明在后续的重复中出现了一系列较差的 RMSE 分数。
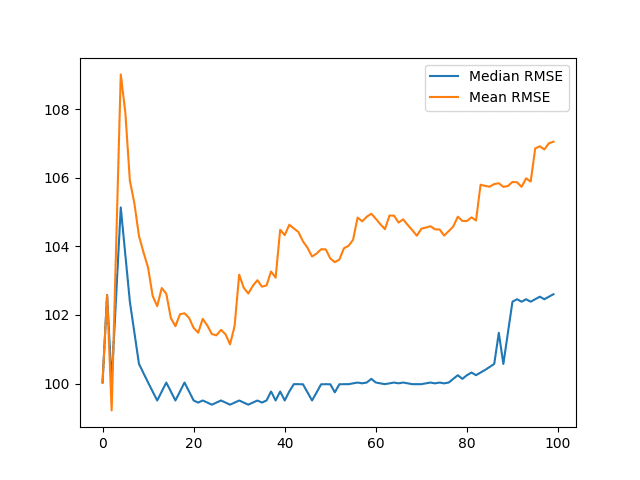
均值和中位数测试 RMSE 与重复次数的折线图
结果回顾
我们对在标准时间序列预测问题上对状态 LSTM 进行 100 次重复中获得了一些有用的观察。
具体来说:
- 我们观察到结果的分布不是高斯的。它可能是偏斜高斯或指数分布,具有长尾和异常值。
- 我们观察到,随着重复次数从 1 增加到 100,结果的分布并未稳定下来。
这些观察结果表明了一些重要的特性:
- 选择 LSTM 的在线学习以及问题导致模型相对不稳定。
- 选择的重复次数(100 次)可能不足以表征模型的行为。
这是一个有用的发现,因为基于 100 次或更少的实验重复对模型做出强有力的结论会是一个错误。
这是在描述您自己的机器学习结果时需要考虑的重要警告。
这提示了一些对该实验的扩展,例如:
- 探讨重复次数对更稳定的模型的影响,例如使用批处理或小批量学习的模型。
- 将重复次数增加到数千次或更多,以尝试解释模型在在线学习中的普遍不稳定性。
总结
在本教程中,您将了解如何分析使用在线学习拟合的 LSTM 模型的实验结果。
您学到了
- 如何为时间序列预测问题设计一个健壮的测试平台来评估 LSTM 模型。
- 如何分析实验结果,包括汇总统计。
- 如何分析增加实验重复次数的影响以及如何识别不稳定的模型。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。







亲爱的 Jason,
感谢您一直以来的帖子,它们非常有帮助。
我是一名机器学习初学者,我被一些问题困扰了很长时间。
1.什么是在线学习?批大小=1 是在线和动态的吗?
2.如何设置一个 LSTM 结构,能够每分钟动态添加新数据,并更新权重和偏差或其他东西。然后它就可以预测每一分钟的下一个数据。
再次感谢,Jason。
在线学习意味着模型在每个训练模式后都会被更新。
结构不会改变。您需要找到一个结构,能够解决您的问题。
亲爱的 Jason,
感谢分享您的知识!
您的 LSTM 是状态化的吗?
在我看来,您必须在第 66 行设置 stateful=True,或者当 batchsize=1 时会自动发生这种情况吗?
此致
抱歉,我没看到 stateful=True。
是的,这意味着状态仅在显式重置时才会被重置。
我看到你经常使用这种结构
for i in range(nb_epoch)
model.fit(X, y, epochs=1, batch_size=batch_size, verbose=0, shuffle=False)
model.reset_states()
我发现 Keras 中的回调函数可以代替将 fit() 包装在循环中。
# 定义回调类
class ModelStateReset(keras.callbacks.Callback)
def on_epoch_end(self, epoch, logs={})
self.model.reset_states()
reset = ModelStateReset()
# 在 fit 中使用 reset 回调实例
model.fit(x, y, epochs=i, batch_size=batch_size, shuffle=False, callbacks=[reset])
如果你错过了这一点,只是提醒一下。我个人更喜欢使用 fit() 的参数而不是循环 😉
感谢分享。
感谢您发表这篇帖子,Jason。您为我最初的 LSTM 测试研究结果中的困惑解除了疑虑。所有 LSTM 本质上都是随机的吗,因为权重初始化是随机的?
是的,请看这篇文章
https://machinelearning.org.cn/randomness-in-machine-learning/
嗨 Jason,
感谢您发表的精彩帖子!
我正在处理时间序列数据,并为此使用 LSTM。我正在使用状态 LSTM 对单变量序列进行在线学习(batch_size=1),并考虑 timesteps=200。
这是训练方式:
for i in range(NUM_EPOCHS)
print(“Epoch {:d}/{:d}”.format(i+1, NUM_EPOCHS))
model.fit(Xtrain, Ytrain, batch_size=BATCH_SIZE, epochs=1, verbose =1, callbacks=callbacks_list, shuffle=False)
model.reset_states()
其中 callbacks_list 仅用于提前停止和在平台时减少 LR。
并且用于预测:
predictions = model.predict(Xtest,batch_size=BATCH_SIZE)
由于我正在进行在线学习,因此当新数据到来时(假设每小时),我不想从头开始重新训练模型。想法是仅用新数据更新训练好的模型并为新数据进行预测。那么,我是否只需在拟合训练数据后保存权重,并在预测之前加载保存的权重?这样够吗?它是否也会保存状态,因为我正在使用状态 LSTM?您能否告诉我我是否想对了,或者有什么建议?
是的,您可以使用新数据更新权重。
总的来说,我鼓励您尝试其他方法,因为我发现与许多其他方法相比,LSTM 在时间序列预测方面表现非常差。
嗨,Jason,
感谢您的帖子。
您能否为我推荐一些时间序列预测的方法?
是的,尝试一套经典的 ARIMA 方法(SARIMA、ETC 等),一套机器学习方法(线性方法和非线性方法)以及一套深度学习方法(mlp、cnn、lstm 等)。
谢谢 Jason 的回答。
Hi Harsh,我正在进行一个与您类似的问题,使用 LSTM 进行在线时间序列预测。我想就我的问题征求您的意见和帮助。有没有一种好的方式可以联系到您?谢谢,Narendran。
我已经实现了 ARIMA,但是它太慢了,因为它每次有新数据进来时都需要重新训练。而且使用网格搜索找到 p 和 q 的值非常耗时。
这就是为什么我切换到状态 LSTM,并且令人惊讶的是,我用 LSTM 得到了更好的结果,而且速度也更快。
我还有一些问题:
1.我每次运行模型都会得到不同的预测。您知道如何获得一致的结果吗?我看到您使用了重复次数并取 RMSE 的平均值,但我不知道是否有办法获得相同的预测。
2.一旦我保存了拟合训练数据后的模型权重,并在预测之前加载权重,它是否也会加载保存权重时的状态?您是否有执行比基本 LSTM 示例更复杂的示例,例如如何在实际场景(端到端模型)中实现?
很高兴听到这个消息。
是的,这是神经网络的一个特性,您可以在这里了解更多信息:
https://machinelearning.org.cn/randomness-in-machine-learning/
如果状态很重要,您可以使用“热启动”,在预测新数据之前先在训练数据上进行预测,并且中间不重置状态。不过,我倒是会惊讶于状态会如此重要。
您不能使用 random_seed 来使您的模型确定性吗?
并非如此。
https://machinelearning.org.cn/reproducible-results-neural-networks-keras/
嗨,Jason,
一个已经训练好的稳定网络是否可以进行在线再训练,并且仍然保持稳定?因为权重将不再是随机的,而这就像是迁移学习。
我这样问是因为我正在处理一个已经训练好的 LSTM,但是,我遇到了概念漂移问题,并且被迫时不时地重新训练我的模型,以便预测保持对我的应用程序足够好。
它可以,也许可以尝试混合一些旧样本。
我在这里有更多关于这个主题的内容:
https://machinelearning.org.cn/gentle-introduction-concept-drift-machine-learning/
谢谢
嗨,Jason,
感谢您的精彩教程。
两个问题
– 从教程中,我假设此问题的解决方案是增加批次大小?您是否有使用批次大小 > 1 的状态 LSTM 网络教程?-
– 这里是否可以使用提前停止回调?-
– 如何将数据转换为高斯分布(如此处所述:https://machinelearning.org.cn/how-to-transform-data-to-fit-the-normal-distribution/)?
提前感谢!!!
是的,我有更多关于管理状态和更大批次大小的 LSTM 的示例。也许可以从这里开始:
https://machinelearning.org.cn/start-here/#lstm
如果手动循环 epoch,提前停止必须是手动进行的。
您可以转换数据。
太棒了!感谢您的及时回复!
您好,布朗利,
感谢您的提醒。我对在线训练和实时时间序列数据预测很感兴趣。
如果您的书中有,我希望得到它,并且可能需要一份循序渐进的指南,因为我对实时预测的权重更新概念相对较新。谢谢。
您所说的实时是什么意思?
您是指在每次新观测后重新拟合模型吗?
还是您只是指根据需要进行预测?
在关于“在线”的博客文章的背景下,“实时”意味着在每次新观测时进行预测,并在每次新观测后重新拟合模型。
我实际上没有太多关于用新样本更新模型的内容。
总的来说,这听起来很简单,只要您通过受控实验来验证您选择的更新计划是否能产生有技能的模型。如果模型(权重)更新不能提高性能,就没有意义。
Hi Jason,我从您的帖子中学到了很多东西,谢谢!!
关于这个主题:我有几个本地天气传感器,每 10 分钟获取一次数据,我想尝试测试一下,与预训练模型相比,增量学习对这些新流入数据可以得到什么样的结果。
1 – 我想做的是将新数据附加到大型数据集中,然后使用切片采样一个等于我的时间步长的预测集,只预测未来 1 步。(选择 10 分钟只是因为我将定期获得更多数据来测试。)然后将其显示在应用程序中。
2 – 在上一步之后,我创建一个单一的训练集:X[-60 :-1 , : ] 和 y[-1,0],并使用 Batch_size=1 拟合模型以获得最新的更新。
我将使用堆叠 LSTM。
我正在忙于设计/弄清楚如何设计它,但我想在走得太远之前获得现实的反馈,或者您是否有其他方法可以建议?
非常感谢。
我推荐这个框架来确认 LSTM 比线性模型更有价值。
https://machinelearning.org.cn/how-to-develop-a-skilful-time-series-forecasting-model/
Hi Jason,感谢您分享这些有价值的信息。如果您能回复我的问题,我将不胜感激。我的项目中,我将数据分为训练集、验证集和测试集。我很好奇在选择最适合我的问题的结构后(我用验证集做的),我是否应该重新训练模型,包括训练集和验证集数据?或者是否有办法在预测测试集之前包含验证数据来更新模型?这个问题一直困扰我,因为当我用选定的结构重新训练模型时,我感觉新数据会影响我之前获得的结果。
非常感谢您的博客,它对我的项目非常有帮助。
此致!
不客气。
好问题,理想情况下,如果您可以的话,您希望用所有可用数据训练最终模型。