机器学习中的矩阵和矩阵运算简介

作者： Jason Brownlee 发表于 2021年10月17日类别：线性代数 13

矩阵是线性代数的基础元素。

在机器学习领域中，矩阵被广泛用于描述算法和过程，例如训练算法时的输入数据变量（X）。

在本教程中，您将学习线性代数中的矩阵以及如何在 Python 中操作它们。

完成本教程后，您将了解：

什么是矩阵以及如何在 Python 中使用 NumPy 定义矩阵。
如何执行逐元素操作，如加法、减法和哈达玛乘积。
如何将矩阵相乘以及操作背后的直觉。

使用我的新书《机器学习的线性代数》启动您的项目，其中包括分步教程和所有示例的Python 源代码文件。

让我们开始吧。

2019年6月更新：修正了矩阵-向量乘法部分的一个错字（感谢 M. Vincent）。
2019年6月更新：修正了 Python 中矩阵描述的错字（感谢 Ari）。
2021年10月更新：添加了使用 @ 运算符进行矩阵-向量乘法的示例。

A Gentle Introduction to Matrices for Machine Learning

机器学习中的矩阵简介
图片来源：Maximiliano Kolus，保留部分权利。

教程概述

本教程分为6个部分；它们是

什么是矩阵？
定义矩阵
矩阵运算
矩阵-矩阵乘法（点积）
矩阵-向量乘法
矩阵-标量乘法

在机器学习线性代数方面需要帮助吗？

立即参加我为期7天的免费电子邮件速成课程（附示例代码）。

点击注册，同时获得该课程的免费PDF电子书版本。

什么是矩阵？

矩阵是具有一个或多个列和一个或多个行的二维标量数组。

矩阵是一个二维数组（一个数字表）。

—— 第 115 页，《线性代数无废话指南》，2017

矩阵的表示法通常是一个大写字母，例如 A，其条目通过行 (i) 和列 (j) 的二维下标来表示，例如 aij。例如：

A = ((a11, a12), (a21, 22), (a31, a32))

1	A = ((a11, a12), (a21, a22), (a31, a32))

更常见的是使用水平表示法定义矩阵。

     a11, a12
A = (a21, a22)
     a31, a32

a11, a12

A = (a21, a22)

a31, a32

您在机器学习中第一次遇到矩阵可能是在模型训练数据中，它由许多行和列组成，通常用大写字母“X”表示。

用于帮助理解向量及其某些运算的几何类比不适用于矩阵。此外，向量本身可以被视为一个具有一列和多行的矩阵。

矩阵的维度通常用 m 表示行数，用 n 表示列数。

既然我们知道什么是矩阵，那么让我们看看如何在 Python 中定义一个矩阵。

定义矩阵

我们可以使用二维 NumPy 数组在 Python 中表示一个矩阵。

NumPy 数组可以由列表的列表构造。例如，下面是一个 2 行 3 列的矩阵。

# create matrix
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)

# 创建矩阵

from numpy import array

A = array([[1, 2,3], [4, 5, 6]])

print(A)

运行示例将打印创建的矩阵，显示预期的结构。

[[1 2 3]
 [4 5 6]]

1 2	[[1 2 3] [4 5 6]]

矩阵运算

在本节中，我们将演示简单的矩阵-矩阵算术，其中所有操作都在两个相同大小的矩阵之间逐元素执行，从而得到一个相同大小的新矩阵。

矩阵加法

两个具有相同维度的矩阵可以相加，从而创建一个新的第三个矩阵。

C = A + B

C = A + B

结果矩阵中的标量元素通过将每个被相加矩阵中的元素相加来计算。

         a11 + b11, a12 + b12
A + B = (a21 + b21, a22 + b22)
         a31 + b31, a32 + b32

a11 + b11, a12 + b12

A + B = (a21 + b21, a22 + b22)

a31 + b31, a32 + b32

或者，换句话说

C[0,0] = A[0,0] + B[0,0]
C[1,0] = A[1,0] + B[1,0]
C[2,0] = A[2,0] + B[2,0]
C[0,1] = A[0,1] + B[0,1]
C[1,1] = A[1,1] + B[1,1]
C[2,1] = A[2,1] + B[2,1]

C[0,0] = A[0,0] + B[0,0]

C[1,0] = A[1,0] + B[1,0]

C[2,0] = A[2,0] + B[2,0]

C[0,1] = A[0,1] + B[0,1]

C[1,1] = A[1,1] + B[1,1]

C[2,1] = A[2,1] + B[2,1]

我们可以在 Python 中使用加号运算符直接在两个 NumPy 数组上实现这一点。

# add matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[1, 2, 3], [4, 5, 6]])
print(B)
C = A + B
print(C)

# 矩阵相加

from numpy import array

A = array([[1, 2,3], [4, 5, 6]])

print(A)

B = array([[1, 2,3], [4, 5, 6]])

print(B)

C = A + B

print(C)

此示例首先定义两个 2×3 矩阵，然后将它们相加。

运行示例首先打印两个父矩阵，然后打印它们相加的结果。

[[1 2 3]
 [4 5 6]]

[[1 2 3]
 [4 5 6]]

[[ 2  4  6]
 [ 8 10 12]]

[[1 2 3]

[4 5 6]]

[[1 2 3]

[4 5 6]]

[[ 2 4 6]

[ 8 10 12]]

矩阵减法

同样，一个矩阵可以从另一个具有相同维度的矩阵中减去。

C = A - B

C = A - B

结果矩阵中的标量元素通过将每个矩阵中的元素相减来计算。

         a11 - b11, a12 - b12
A - B = (a21 - b21, a22 - b22)
         a31 - b31, a32 - b32

a11 - b11, a12 - b12

A - B = (a21 - b21, a22 - b22)

a31 - b31, a32 - b32

或者，换句话说

C[0,0] = A[0,0] - B[0,0]
C[1,0] = A[1,0] - B[1,0]
C[2,0] = A[2,0] - B[2,0]
C[0,1] = A[0,1] - B[0,1]
C[1,1] = A[1,1] - B[1,1]
C[2,1] = A[2,1] - B[2,1]

C[0,0] = A[0,0] - B[0,0]

C[1,0] = A[1,0] - B[1,0]

C[2,0] = A[2,0] - B[2,0]

C[0,1] = A[0,1] - B[0,1]

C[1,1] = A[1,1] - B[1,1]

C[2,1] = A[2,1] - B[2,1]

我们可以在 Python 中使用减号运算符直接在两个 NumPy 数组上实现这一点。

# subtract matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[0.5, 0.5, 0.5], [0.5, 0.5, 0.5]])
print(B)
C = A - B
print(C)

# 矩阵相减

from numpy import array

A = array([[1, 2,3], [4, 5, 6]])

print(A)

B = array([[0.5, 0.5,0.5], [0.5, 0.5, 0.5]])

print(B)

C = A - B

print(C)

此示例首先定义两个 2×3 矩阵，然后将其中一个从另一个中减去。

运行示例首先打印两个父矩阵，然后从第二个矩阵中减去第一个矩阵的结果。

[[1 2 3]
 [4 5 6]]

[[ 0.5  0.5  0.5]
 [ 0.5  0.5  0.5]]

[[ 0.5  1.5  2.5]
 [ 3.5  4.5  5.5]]

[[1 2 3]

[4 5 6]]

[[ 0.5 0.5 0.5]

[ 0.5 0.5 0.5]]

[[ 0.5 1.5 2.5]

[ 3.5 4.5 5.5]]

矩阵乘法（哈达玛乘积）

两个相同大小的矩阵可以相乘，这通常被称为逐元素矩阵乘法或哈达玛乘积。

它不是指矩阵乘法时的典型操作，因此通常使用不同的运算符，例如圆圈“o”。

C = A o B

C = A o B

与逐元素减法和加法一样，逐元素乘法涉及将每个父矩阵中的元素相乘，以计算新矩阵中的值。

         a11 * b11, a12 * b12
A o B = (a21 * b21, a22 * b22)
         a31 * b31, a32 * b32

a11 * b11, a12 * b12

A o B = (a21 * b21, a22 * b22)

a31 * b31, a32 * b32

或者，换句话说

C[0,0] = A[0,0] * B[0,0]
C[1,0] = A[1,0] * B[1,0]
C[2,0] = A[2,0] * B[2,0]
C[0,1] = A[0,1] * B[0,1]
C[1,1] = A[1,1] * B[1,1]
C[2,1] = A[2,1] * B[2,1]

C[0,0] = A[0,0] * B[0,0]

C[1,0] = A[1,0] * B[1,0]

C[2,0] = A[2,0] * B[2,0]

C[0,1] = A[0,1] * B[0,1]

C[1,1] = A[1,1] * B[1,1]

C[2,1] = A[2,1] * B[2,1]

我们可以在 Python 中使用星号运算符直接在两个 NumPy 数组上实现这一点。

# element-wise multiply matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[1, 2, 3], [4, 5, 6]])
print(B)
C = A * B
print(C)

# 逐元素相乘矩阵

from numpy import array

A = array([[1, 2,3], [4, 5, 6]])

print(A)

B = array([[1, 2,3], [4, 5, 6]])

print(B)

C = A * B

print(C)

此示例首先定义两个 2×3 矩阵，然后将它们相乘。

运行示例首先打印两个父矩阵，然后打印它们通过哈达玛乘积相乘的结果。

[[1 2 3]
 [4 5 6]]

[[1 2 3]
 [4 5 6]]

[[ 1  4  9]
 [16 25 36]]

[[1 2 3]

[4 5 6]]

[[1 2 3]

[4 5 6]]

[[ 1 4 9]

[16 25 36]]

矩阵除法

一个矩阵可以被另一个具有相同维度的矩阵除。

C = A / B

C = A / B

结果矩阵中的标量元素通过将每个矩阵中的元素相除来计算。

         a11 / b11, a12 / b12
A / B = (a21 / b21, a22 / b22)
         a31 / b31, a32 / b32

a11 / b11, a12 / b12

A / B = (a21 / b21, a22 / b22)

a31 / b31, a32 / b32

或者，换句话说

C[0,0] = A[0,0] / B[0,0]
C[1,0] = A[1,0] / B[1,0]
C[2,0] = A[2,0] / B[2,0]
C[0,1] = A[0,1] / B[0,1]
C[1,1] = A[1,1] / B[1,1]
C[2,1] = A[2,1] / B[2,1]

C[0,0] = A[0,0] / B[0,0]

C[1,0] = A[1,0] / B[1,0]

C[2,0] = A[2,0] / B[2,0]

C[0,1] = A[0,1] / B[0,1]

C[1,1] = A[1,1] / B[1,1]

C[2,1] = A[2,1] / B[2,1]

我们可以在 Python 中使用除法运算符直接在两个 NumPy 数组上实现这一点。

# divide matrices
from numpy import array
A = array([[1, 2, 3], [4, 5, 6]])
print(A)
B = array([[1, 2, 3], [4, 5, 6]])
print(B)
C = A / B
print(C)

# 矩阵相除

from numpy import array

A = array([[1, 2,3], [4, 5, 6]])

print(A)

B = array([[1, 2,3], [4, 5, 6]])

print(B)

C = A / B

print(C)

此示例首先定义两个 2×3 矩阵，然后将第一个矩阵除以第二个矩阵。

运行示例首先打印两个父矩阵，然后将第一个矩阵除以第二个矩阵的结果。

[[1 2 3]
 [4 5 6]]

[[1 2 3]
 [4 5 6]]

[[ 1.  1.  1.]
 [ 1.  1.  1.]]

[[1 2 3]

[4 5 6]]

[[1 2 3]

[4 5 6]]

[[ 1. 1. 1.]

[ 1. 1. 1.]]

矩阵-矩阵乘法（点积）

矩阵乘法，也称为矩阵点积，比之前的操作更复杂，并且涉及一个规则，因为并非所有矩阵都可以相乘。

C = A * B

C = A * B

或者

C = AB

C = AB

矩阵乘法的规则如下：

第一个矩阵 (A) 的列数 (n) 必须等于第二个矩阵 (B) 的行数 (m)。

例如，矩阵 A 的维度为 m 行 n 列，矩阵 B 的维度为 n 行 k 列。A 中的 n 列和 B 中的 n 行相等。结果是一个新的矩阵，具有 m 行 k 列。

C(m,k) = A(m,n) * B(n,k)

1	C(m,k) = A(m,n) * B(n,k)

此规则适用于矩阵乘法链，其中链中一个矩阵的列数必须与链中下一个矩阵的行数匹配。

涉及矩阵的最重要操作之一是两个矩阵的乘法。矩阵 A 和 B 的矩阵乘积是第三个矩阵 C。为了定义此乘积，A 的列数必须与 B 的行数相同。如果 A 的形状为 m × n，B 的形状为 n × p，则 C 的形状为 m × p。

—— 第 34 页，《深度学习》，2016 年。

矩阵乘法的直观理解是，我们正在计算矩阵 A 中的每一行与矩阵 B 中的每一列之间的点积。例如，我们可以沿着 A 列的行向下，并将每一行与 B 中的第 1 列相乘，以得到 C 中第 1 列的标量值。

下面的图片清楚地说明了这一点。

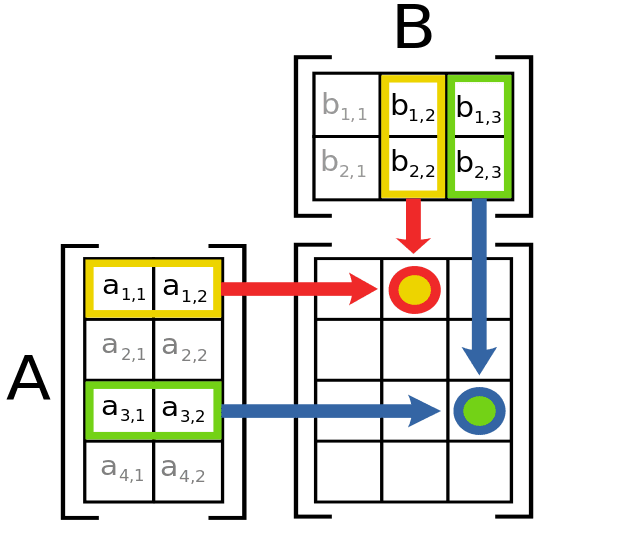
矩阵乘法的示意图，摘自维基百科，保留部分权利。

下面描述了使用矩阵符号的矩阵乘法。

     a11, a12
A = (a21, a22)
     a31, a32

     b11, b12
B = (b21, b22)

     a11 * b11 + a12 * b21, a11 * b12 + a12 * b22
C = (a21 * b11 + a22 * b21, a21 * b12 + a22 * b22)
     a31 * b11 + a32 * b21, a31 * b12 + a32 * b22

a11, a12

A = (a21, a22)

a31, a32

b11, b12

B = (b21, b22)

a11 * b11 + a12 * b21, a11 * b12 + a12 * b22

C = (a21 * b11 + a22 * b21, a21 * b12 + a22 * b22)

a31 * b11 + a32 * b21, a31 * b12 + a32 * b22

这可以通过删除乘法符号来简化，如下所示：

     a11b11 + a12b21, a11b12 + a12b22
C = (a21b11 + a22b21, a21b12 + a22b22)
     a31b11 + a32b21, a31b12 + a32b22

a11b11 + a12b21, a11b12 + a12b22

C = (a21b11 + a22b21, a21b12 + a22b22)

a31b11 + a32b21, a31b12 + a32b22

我们可以使用数组符号来描述矩阵乘法运算。

C[0,0] = A[0,0] * B[0,0] + A[0,1] * B[1,0]
C[1,0] = A[1,0] * B[0,0] + A[1,1] * B[1,0]
C[2,0] = A[2,0] * B[0,0] + A[2,1] * B[1,0]
C[0,1] = A[0,0] * B[0,1] + A[0,1] * B[1,1]
C[1,1] = A[1,0] * B[0,1] + A[1,1] * B[1,1]
C[2,1] = A[2,0] * B[0,1] + A[2,1] * B[1,1]

C[0,0] = A[0,0] * B[0,0] + A[0,1] * B[1,0]

C[1,0] = A[1,0] * B[0,0] + A[1,1] * B[1,0]

C[2,0] = A[2,0] * B[0,0] + A[2,1] * B[1,0]

C[0,1] = A[0,0] * B[0,1] + A[0,1] * B[1,1]

C[1,1] = A[1,0] * B[0,1] + A[1,1] * B[1,1]

C[2,1] = A[2,0] * B[0,1] + A[2,1] * B[1,1]

矩阵乘法运算可以在 NumPy 中使用 dot() 函数实现。

# matrix dot product
from numpy import array
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
B = array([[1, 2], [3, 4]])
print(B)
C = A.dot(B)
print(C)

# 矩阵点积

from numpy import array

A = array([[1, 2], [3, 4], [5, 6]])

print(A)

B = array([[1, 2], [3, 4]])

print(B)

C = A.dot(B)

print(C)

此示例首先定义两个 2×3 矩阵，然后计算它们的点积。

运行示例首先打印两个父矩阵，然后打印点积的结果。

[[1 2]
 [3 4]
 [5 6]]

[[1 2]
 [3 4]]

[[ 7 10]
 [15 22]
 [23 34]]

[[1 2]

[3 4]

[5 6]]

[[1 2]

[3 4]]

[[ 7 10]

[15 22]

[23 34]]

矩阵-向量乘法

只要遵循矩阵乘法的规则，矩阵和向量就可以相乘。

具体来说，矩阵的列数必须等于向量中的元素数量。与矩阵乘法一样，该操作可以使用点符号编写。因为向量只有一列，所以结果总是一个向量。

c = A . v

c = A . v

或者以紧凑形式不带点。

c = Av

c = Av

结果是一个向量，其行数与父矩阵相同。

     a11, a12
A = (a21, a22)
     a31, a32

     v1
v = (v2)

     a11 * v1 + a12 * v2
c = (a21 * v1 + a22 * v2)
     a31 * v1 + a32 * v2

a11, a12

A = (a21, a22)

a31, a32

v = (v2)

a11 * v1 + a12 * v2

c = (a21 * v1 + a22 * v2)

a31 * v1 + a32 * v2

或者，更简洁地。

     a11v1 + a12v2
c = (a21v1 + a22v2)
     a31v1 + a32v2

a11v1 + a12v2

c = (a21v1 + a22v2)

a31v1 + a32v2

矩阵-向量乘法可以在 NumPy 中使用 dot() 函数或 @ 运算符（自 Python 3.5 版本起）实现。

# matrix-vector multiplication
from numpy import array
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
B = array([0.5, 0.5])
print(B)
C = A.dot(B)
print(C)
D = A @ B
print(D)

# 矩阵-向量乘法

from numpy import array

A = array([[1, 2], [3, 4], [5, 6]])

print(A)

B = array([0.5, 0.5])

print(B)

C = A.dot(B)

print(C)

D = A @ B

print(D)

此示例首先定义一个 3×2 矩阵和一个 2 元素向量，然后将它们相乘。

运行示例首先打印父矩阵和向量，然后打印它们相乘的结果。

[[1 2]
 [3 4]
 [5 6]]

[ 0.5  0.5]

[ 1.5  3.5  5.5]

[ 1.5  3.5  5.5]

[[1 2]

[3 4]

[5 6]]

[ 0.5 0.5]

[ 1.5 3.5 5.5]

矩阵-标量乘法

矩阵可以乘以一个标量。

这可以使用矩阵和标量之间的点符号来表示。

C = A . b

C = A . b

或者不带点符号。

C = Ab

C = Ab

结果是一个与父矩阵大小相同的矩阵，其中矩阵的每个元素都乘以标量值。

     a11, a12
A = (a21, a22)
     a31, a32

b

     a11 * b, a12 * b
C = (a21 * b, a22 * b)
     a31 * b, a32 * b

a11, a12

A = (a21, a22)

a31, a32

a11 * b, a12 * b

C = (a21 * b, a22 * b)

a31 * b, a32 * b

或者

     a11b, a12b
C = (a21b, a22b)
     a31b, a32b

a11b, a12b

C = (a21b, a22b)

a31b, a32b

我们也可以用数组表示法来表示这一点。

C[0,0] = A[0,0] * b
C[1,0] = A[1,0] * b
C[2,0] = A[2,0] * b
C[0,1] = A[0,1] * b
C[1,1] = A[1,1] * b
C[2,1] = A[2,1] * b

C[0,0] = A[0,0] * b

C[1,0] = A[1,0] * b

C[2,0] = A[2,0] * b

C[0,1] = A[0,1] * b

C[1,1] = A[1,1] * b

C[2,1] = A[2,1] * b

这可以直接在 NumPy 中使用乘法运算符实现。

# matrix-scalar multiplication
from numpy import array
A = array([[1, 2], [3, 4], [5, 6]])
print(A)
b = 0.5
print(b)
C = A * b
print(C)

# 矩阵-标量乘法

from numpy import array

A = array([[1, 2], [3, 4], [5, 6]])

print(A)

b = 0.5

print(b)

C = A * b

print(C)

此示例首先定义一个 2×3 矩阵和一个标量，然后将它们相乘。

运行示例首先打印父矩阵和标量，然后打印它们相乘的结果。

[[1 2]
 [3 4]
 [5 6]]

0.5

[[ 0.5  1. ]
 [ 1.5  2. ]
 [ 2.5  3. ]]

[[1 2]

[3 4]

[5 6]]

0.5

[[ 0.5 1. ]

[ 1.5 2. ]

[ 2.5 3. ]]

扩展

本节列出了一些您可能希望探索的扩展本教程的想法。

使用您自己的数据，为每个操作创建 5 个示例。
手动实现将矩阵定义为列表的列表的每个矩阵操作。
搜索机器学习论文，并找到每个操作被使用的一个例子。

如果您探索了这些扩展中的任何一个，我很想知道。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

第 2.3 节，矩阵运算。无废话线性代数指南，2017。
第 3.3 节，矩阵乘法。无废话线性代数指南，2017。
第 1.3 节矩阵，《线性代数导论》，第五版，2016。
第 2.4 节矩阵运算规则，《线性代数导论》，第五版，2016。
第 2.1 节标量、向量、矩阵和张量，《深度学习》，2016。
第 2.2 节矩阵和向量乘法，《深度学习》，2016。

API

文章

总结

在本教程中，您学习了线性代数中的矩阵以及如何在 Python 中操作它们。

具体来说，你学到了：

什么是矩阵以及如何在 Python 中使用 NumPy 定义矩阵。
如何执行逐元素操作，如加法、减法和哈达玛乘积。
如何将矩阵相乘以及操作背后的直觉。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

关于此主题的更多信息