1x1 卷积简介以管理模型复杂度

池化可用于对特征图内容进行下采样，在保持其显著特征的同时，减少其宽度和高度。

深度卷积神经网络的一个问题是，特征图的数量通常随网络深度的增加而增加。当使用较大的滤波器尺寸（如 5x5 和 7x7）时，此问题可能导致参数数量和所需计算量急剧增加。

为了解决这个问题，可以使用 1x1 卷积层，它提供通道式池化，通常称为特征图池化或投影层。这种简单的技术可用于降维，减少特征图的数量，同时保留其显著特征。它也可以直接用于创建特征图的一对一投影，以跨通道池化特征，或增加特征图的数量，例如在传统池化层之后。

在本教程中，您将学习如何使用 1x1 滤波器来控制卷积神经网络中特征图的数量。

完成本教程后，您将了解：

• 1x1 滤波器可用于创建特征图堆栈的线性投影。
• 1x1 创建的投影可以充当通道式池化，并用于降维。
• 1x1 创建的投影也可以直接使用，或用于增加模型中特征图的数量。

通过我的新书《计算机视觉深度学习》**启动您的项目**，其中包括*分步教程*和所有示例的 *Python 源代码*文件。

让我们开始吧。

1x1 卷积简介：减少卷积神经网络的复杂性
照片版权，保留部分权利。

教程概述

本教程分为五个部分；它们是：

1. 跨通道卷积
2. 特征图过多问题
3. 使用 1x1 滤波器对特征图进行下采样
4. 如何使用 1x1 卷积的示例
5. CNN 模型架构中 1x1 滤波器的示例

跨通道卷积

回想一下，卷积操作是较小的滤波器对较大输入的线性应用，从而产生输出特征图。

应用于输入图像或输入特征图的滤波器总是产生一个数字。滤波器对输入进行系统地从左到右、从上到下的应用，从而产生二维特征图。一个滤波器创建一个对应的特征图。

滤波器的深度或通道数必须与输入相同，然而，无论输入和滤波器的深度如何，结果输出都是一个数字，一个滤波器创建一个具有单个通道的特征图。

让我们通过一些例子来具体说明这一点。

• 如果输入有一个通道，例如灰度图像，则将以 3x3x1 的块应用 3x3 滤波器。
• 如果输入图像有红色、绿色和蓝色的三个通道，则将以 3x3x3 的块应用 3x3 滤波器。
• 如果输入是来自另一个卷积或池化层的特征图块，深度为 64，则将以 3x3x64 的块应用 3x3 滤波器，以创建构成单个输出特征图的单个值。

一个卷积层的输出深度仅由应用于输入的并行滤波器数量定义。

特征图过多问题

卷积层中使用的输入深度或滤波器数量通常随网络深度的增加而增加，导致结果特征图的数量增加。这是一种常见的模型设计模式。

此外，某些网络架构（例如 Inception 架构）也可能连接多个卷积层的输出特征图，这可能还会急剧增加后续卷积层的输入深度。

卷积神经网络中大量的特征图可能会导致问题，因为卷积操作必须沿着输入深度向下执行。如果执行的卷积操作相对较大，例如 5x5 或 7x7 像素，则这是一个特殊问题，因为它可能导致参数（权重）和执行卷积操作所需的计算量（大的空间和时间复杂度）显著增加。

池化层旨在缩小特征图，并系统地将网络中特征图的宽度和高度减半。然而，池化层不会改变模型中滤波器、深度或通道的数量。

深度卷积神经网络需要一种相应的池化类型层，该层可以对深度或特征图的数量进行下采样或减少。

使用 1x1 滤波器对特征图进行下采样

解决方案是使用 1x1 滤波器对深度或特征图的数量进行下采样。

一个 1x1 滤波器在输入中的每个通道将只有一个参数或权重，并且像任何滤波器的应用一样，会产生一个输出值。这种结构允许 1x1 滤波器像单个神经元一样工作，其输入来自输入中每个特征图的相同位置。然后，这个单个神经元可以系统地以步幅为一的方式，从左到右、从上到下进行应用，无需填充，从而产生一个与输入宽度和高度相同的特征图。

1x1 滤波器非常简单，不涉及输入中的任何相邻像素；它可能不被视为卷积操作。相反，它是对输入的线性加权或投影。此外，与其它卷积层一样，也使用了非线性，从而允许投影对输入特征图执行非平凡的计算。

这个简单的 1x1 滤波器提供了一种有效总结输入特征图的方法。反过来，使用多个 1x1 滤波器允许调整要创建的输入特征图总结的数量，从而有效地根据需要增加或减少特征图的深度。

因此，带有 1x1 滤波器的卷积层可以在卷积神经网络中的任何位置用于控制特征图的数量。因此，它通常被称为投影操作或投影层，甚至特征图或通道池化层。

现在我们知道可以使用 1x1 滤波器控制特征图的数量，让我们通过一些例子来具体说明。

如何使用 1x1 卷积的示例

我们可以通过一些例子来具体说明 1x1 滤波器的使用。

假设我们有一个卷积神经网络，它期望输入颜色图像的方形形状为 256x256x3 像素。

然后，这些图像通过第一个隐藏层，该层有 512 个滤波器，每个滤波器尺寸为 3x3，采用相同填充，然后是ReLU 激活函数。

下面的示例演示了这个简单的模型。

运行示例将创建模型并总结模型架构。

不出所料；第一个隐藏层的输出是一个形状为 256x256x512 的三维特征图块。

投影特征图示例

1x1 滤波器可用于创建特征图的投影。

创建的特征图数量将相同，并且效果可能是对已提取特征的细化。这通常被称为通道式池化，而不是每个通道上的传统特征式池化。它可以按以下方式实现：

我们可以看到，我们使用了相同数量的特征，并且仍然在滤波器应用后使用了修正线性激活函数。

完整的示例如下所示。

运行示例将创建模型并总结其架构。

我们可以看到，特征图的宽度或高度没有改变，并且通过设计，特征图的数量通过简单的投影操作保持不变。

减少特征图的例子

1x1 滤波器可用于减少特征图的数量。

这是这种类型滤波器最常见的应用，因此该层通常被称为特征图池化层。

在这个例子中，我们可以将深度（或通道）从 512 减少到 64。如果我们要添加到模型中的后续层是另一个具有 7x7 滤波器的卷积层，这可能会很有用。这些滤波器将只应用于 64 的深度，而不是 512。

64 个特征图的构成与原始的 512 个不同，但包含一个有用的降维总结，它捕获了显著特征，因此 7x7 操作对 64 个特征图可能与对原始 512 个特征图具有相似的效果。

此外，一个具有 64 个滤波器的 7x7 卷积层，如果应用于第一个隐藏层输出的 512 个特征图，将产生大约一百万个参数（权重）。如果首先使用 1x1 滤波器将特征图的数量减少到 64，那么 7x7 层所需的参数数量大约只有 200,000，这是一个巨大的差异。

使用 1x1 滤波器进行降维的完整示例如下所示。

运行示例将创建模型并总结其结构。

我们可以看到特征图的宽度和高度没有改变，但特征图的数量从 512 减少到 64。

增加特征图的示例

1x1 滤波器可用于增加特征图的数量。

这是在池化层之后、应用另一个卷积层之前使用的常见操作。

滤波器的投影效果可以根据需要多次应用于输入，允许特征图的数量按比例增加，并且其组成仍能捕获原始图像的显著特征。

我们可以将第一个隐藏层输入的特征图数量从 512 增加到 1,024，即两倍。

完整的示例如下所示。

运行示例将创建模型并总结其结构。

我们可以看到，特征图的宽度和高度没有改变，并且特征图的数量从 512 增加到 1,024，即两倍。

现在我们已经熟悉了如何使用 1x1 滤波器，接下来让我们看看一些在卷积神经网络模型架构中使用了 1x1 滤波器的示例。

CNN 模型架构中 1x1 滤波器的示例

在本节中，我们将重点介绍一些重要的示例，其中 1x1 滤波器已成为现代卷积神经网络模型架构的关键元素。

网络中的网络

1x1 滤波器可能最早由 Min Lin 等人在 2013 年发表的论文《Network In Network》中描述和推广。

在论文中，作者提出了对 MLP 卷积层和跨通道池化的需求，以促进跨通道学习。

这种级联的跨通道参数池化结构允许复杂的、可学习的跨通道信息交互。

— 《Network In Network》，2013 年。

他们将 1x1 卷积层描述为跨通道参数池化的一种特定实现，而这正是 1x1 滤波器所实现的。

每个池化层对输入特征图执行加权线性重组，然后通过整流线性单元。 […] 跨通道参数池化层也等同于使用 1x1 卷积核的卷积层。

— 《Network In Network》，2013 年。

Inception 架构

1x1 滤波器被明确用于降维和在池化后增加特征图维度，这在 Christian Szegedy 等人在其 2014 年论文《Going Deeper with Convolutions》中描述的 GoogLeNet 模型中使用的 Inception 模块设计中。

该论文描述了一个“Inception 模块”，其中输入特征图块由不同的卷积层并行处理，每个卷积层使用不同大小的滤波器，其中 1x1 大小滤波器是使用的层之一。

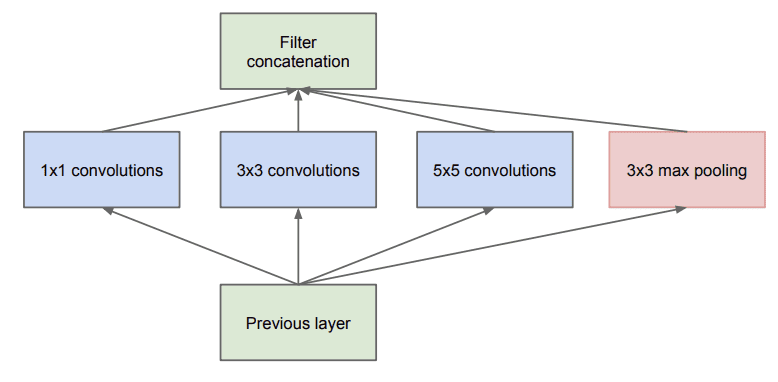
朴素 Inception 模块示例
摘自《Going Deeper with Convolutions》，2014 年。

并行层的输出然后按通道堆叠，导致非常深的卷积层堆栈，由随后的 Inception 模块处理。

池化层输出与卷积层输出的合并将导致阶段之间的输出数量不可避免地增加。即使这种架构可能覆盖最优的稀疏结构，它也会非常低效地实现，导致在几个阶段内计算量爆炸式增长。

— Going Deeper with Convolutions，2014。

然后重新设计 Inception 模块，使用 1x1 滤波器减少特征图数量，然后使用 5x5 和 7x7 大小滤波器的并行卷积层。

这导致了所提出架构的第二个思想：在计算需求过高时，明智地应用降维和投影。 […] 也就是说，在昂贵的 3x3 和 5x5 卷积之前，使用 1x1 卷积进行降维。除了用作降维之外，它们还包括使用整流线性激活，这使它们具有双重目的。

— Going Deeper with Convolutions，2014。

1x1 滤波器还用于在池化后增加特征图的数量，人工创建更多降采样特征图内容的投影。

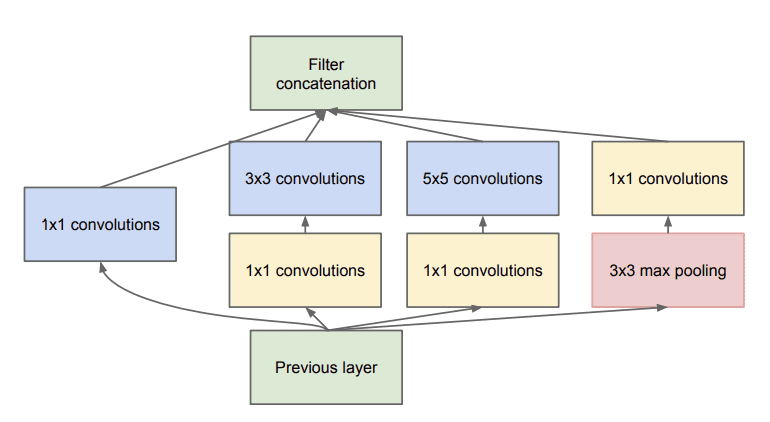
带有降维的 Inception 模块示例
摘自《Going Deeper with Convolutions》，2014 年。

残差架构

1x1 滤波器被用作一种投影技术，以匹配输入滤波器数量与残差模块输出，这在 Kaiming He 等人在其 2015 年论文《Deep Residual Learning for Image Recognition》中设计的残差网络中。

作者描述了一种由“残差模块”组成的架构，其中模块的输入被添加到模块的输出中，这被称为快捷连接。

由于输入被添加到模块的输出中，因此维度必须在宽度、高度和深度方面匹配。宽度和高度可以通过填充来保持，尽管 1x1 滤波器用于根据需要改变输入的深度，以便它可以与模块的输出相加。这种连接被称为投影快捷连接。

此外，残差模块采用瓶颈设计，使用 1x1 滤波器减少特征图数量，以提高计算效率。

这三层是 1x1、3x3 和 1x1 卷积，其中 1x1 层负责减少和增加（恢复）维度，使 3x3 层成为具有较小输入/输出维度的瓶颈。

— 用于图像识别的深度残差学习，2015年。

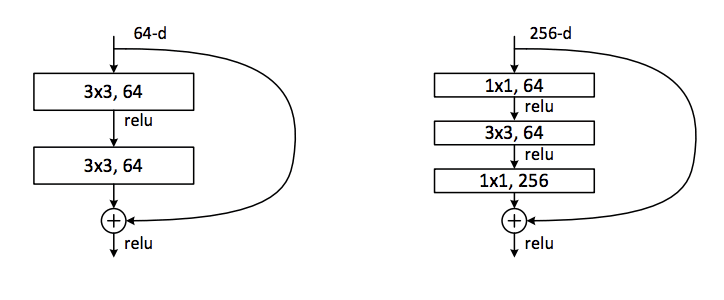
带有快捷连接的普通和瓶颈残差模块示例
摘自《Deep Residual Learning for Image Recognition》，2015 年。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

论文

• 网络中的网络, 2013.
• 使用卷积网络更深入, 2014.
• 用于图像识别的深度残差学习, 2015.

文章

• 1x1 卷积——反直觉的有用, 2016.
• Yann LeCun 关于 CNN 中没有全连接层, 2015.
• Networks in Networks and 1x1 Convolutions，YouTube.

总结

在本教程中，您学习了如何使用 1x1 滤波器来控制卷积神经网络中特征图的数量。

具体来说，你学到了：

• 1x1 滤波器可用于创建特征图堆栈的线性投影。
• 1x1 创建的投影可以充当通道式池化，并用于降维。
• 1x1 创建的投影也可以直接使用，或用于增加模型中特征图的数量。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

立即开发用于视觉的深度学习模型！

在几分钟内开发您自己的视觉模型

...只需几行python代码

在我的新电子书中探索如何实现
用于计算机视觉的深度学习

它提供关于以下主题的自学教程：
分类、物体检测（YOLO和R-CNN）、人脸识别（VGGFace和FaceNet）、数据准备等等……

最终将深度学习引入您的视觉项目

跳过学术理论。只看结果。

查看内容