概率模型可以定义变量之间的关系并用于计算概率。
例如,完全条件模型可能需要海量数据才能涵盖所有可能的情况,而在实践中计算概率可能难以处理。诸如所有随机变量的条件独立性之类的简化假设可能有效,例如朴素贝叶斯的情况,尽管这是一个极大的简化步骤。
另一种方法是开发一个模型,该模型保留随机变量之间已知的条件依赖性以及所有其他情况下的条件独立性。贝叶斯网络是一种概率图模型,它在图模型中通过有向边显式地捕获已知的条件依赖性。所有缺失的连接定义了模型中的条件独立性。
因此,贝叶斯网络提供了一个有用的工具来可视化域的概率模型,回顾随机变量之间的所有关系,并根据可用证据推理场景的因果概率。
在这篇文章中,您将发现对贝叶斯网络的一个简单介绍。
阅读本文后,你将了解:
- 贝叶斯网络是一种由节点和有向边组成的概率图模型。
- 贝叶斯网络模型捕获了随机变量之间条件依赖和条件独立的关系。
- 模型可以由专家准备,也可以从数据中学习,然后用于推理以估计因果事件或后续事件的概率。
启动你的项目,阅读我的新书《机器学习中的概率》,其中包含分步教程和所有示例的Python源代码文件。
让我们开始吧。

贝叶斯信念网络简明入门
照片由 Armin S Kowalski 拍摄,部分权利保留。
概述
本教程分为五个部分;它们是:
- 概率建模的挑战
- 贝叶斯信念网络作为概率模型
- 如何开发和使用贝叶斯网络
- 贝叶斯网络的示例
- Python 中的贝叶斯网络
概率建模的挑战
概率模型的设计和使用可能具有挑战性。
最常见的问题是缺乏关于领域的信息,无法完全指定随机变量之间的条件依赖性。如果可用,计算事件的完全条件概率可能不切实际。
解决此挑战的一种常见方法是添加一些简化假设,例如假设模型中的所有随机变量都是条件独立的。这是一个极端的假设,尽管它在实践中被证明是有用的,为朴素贝叶斯分类算法提供了基础。
另一种方法是开发一个问题的概率模型,其中包含一些条件独立性假设。这提供了介于完全条件模型和完全条件独立模型之间的折衷方法。
贝叶斯信念网络是其中一些变量是条件独立的概率模型的一个示例。
因此,贝叶斯信念网络提供了一种折衷方法,其约束性不如朴素贝叶斯分类器所做的全局条件独立性假设,但比完全避免条件独立性假设更易于处理。
— 第 184 页,机器学习,1997 年。
想学习机器学习概率吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
贝叶斯信念网络作为概率模型
贝叶斯信念网络是一种概率图模型。
概率图模型
概率图模型(Probabilistic Graphical Model, PGM),或简称“图模型”,是一种用图结构表示概率模型的方法。
图中的节点代表随机变量,连接节点的边代表随机变量之间的关系。
图由节点(也称为顶点)和连接它们的链接(也称为边或弧)组成。在概率图模型中,每个节点代表一个随机变量(或一组随机变量),链接表达了这些变量之间的概率关系。
— 第 360 页,模式识别与机器学习,2006 年。
- 节点:图模型中的随机变量。
- 边:图模型中随机变量之间的关系。
有许多不同类型的图模型,尽管最常描述的是隐马尔可夫模型和贝叶斯网络。
隐马尔可夫模型(Hidden Markov Model, HMM)是一种图模型,其中图的边是无向的,意味着图包含环。贝叶斯网络更具限制性,其中图的边是有向的,意味着它们只能沿一个方向导航。这意味着不可能出现环,并且该结构可以更普遍地称为有向无环图(DAG)。
有向图有助于表达随机变量之间的因果关系,而无向图更适合表达随机变量之间的软约束。
— 第 360 页,模式识别与机器学习,2006 年。
贝叶斯信念网络
贝叶斯信念网络(Bayesian Belief Network),或简称“贝叶斯网络”,提供了一种将贝叶斯定理应用于复杂问题的方法。
网络本身并非严格意义上的贝叶斯,尽管由于随机变量(节点)的概率分布和随机变量(边)之间的关系都是主观指定的,因此该模型可以被认为捕获了复杂领域的“信念”。
贝叶斯概率是关于结果的主观概率或信念的研究,与频率学派方法(其中概率纯粹基于事件的过去发生情况)相比。
贝叶斯网络捕获了模型所代表的事件的联合概率。
贝叶斯信念网络描述了一组变量的联合概率分布。
— 第 185 页,机器学习,1997 年。
贝叶斯网络的核心是条件独立性的概念。
独立性指的是不受其他所有变量影响的随机变量。依赖变量是其概率依赖于一个或多个其他随机变量的随机变量。
条件独立性描述了多个随机变量之间的关系,其中一个给定变量可能条件独立于一个或多个其他随机变量。这并不意味着该变量本身就是独立的;相反,它清楚地定义了该变量独立于特定的其他已知随机变量。
像贝叶斯网络这样的概率图模型,通过陈述已知变量的所有条件独立性假设,同时允许存在未知(潜在)变量,提供了一种为复杂问题定义概率模型的方法。
因此,图模型中边的存在和缺失在模型解释中都很重要。
图模型(GM)是通过做出[条件独立性] CI 假设来表示联合分布的一种方式。特别是,图中的节点代表随机变量,(缺乏)边代表 CI 假设。(这些模型的一个更好的名称实际上应该是“独立性图”……
— 第 308 页,机器学习:概率视角,2012 年。
贝叶斯网络作为概率模型提供了有用的好处。
例如
- 可视化。该模型提供了一种直接可视化模型结构并激励新模型设计的方法。
- 关系。深入了解随机变量之间关系的存在和缺失。
- 计算。提供了一种构建复杂概率计算的方法。
如何开发和使用贝叶斯网络
设计贝叶斯网络至少需要定义三件事
- 随机变量。问题中的随机变量是什么?
- 条件关系。变量之间的条件关系是什么?
- 概率分布。每个变量的概率分布是什么?
问题领域的专家可能能够在其模型设计中指定其中一些或所有方面。
在许多情况下,图模型的体系结构或拓扑可以由专家指定,但概率分布必须从该领域的数据中进行估计。
尽管概率分布和图结构本身都可以从数据中估计,但这可能是一个具有挑战性的过程。因此,通常为此目的使用学习算法;例如,假设连续随机变量的高斯分布,使用梯度上升来估计分布参数。
一旦为某个领域准备好贝叶斯网络,就可以将其用于推理,例如做出决策。
推理是通过针对给定情况使用模型进行推断来实现的。例如,已知某些事件的结果并将其插入随机变量。该模型可用于估计事件原因或可能的后续事件的概率。
推理(推断)是通过引入将变量设置为已知状态的证据,然后计算在这些证据条件下感兴趣的概率来完成的。
— 第 13 页,贝叶斯推理与机器学习,2012 年。
在实践中使用贝叶斯网络的实际示例包括医学(症状和疾病)、生物信息学(性状和基因)以及语音识别(话语和时间)。
贝叶斯网络的示例
我们可以通过一个小例子来具体化贝叶斯网络。
考虑一个具有三个随机变量的问题:A、B 和 C。A 依赖于 B,C 依赖于 B。
我们可以如下陈述条件依赖性
- A 条件依赖于 B,例如 P(A|B)
- C 条件依赖于 B,例如 P(C|B)
我们知道 C 和 A 之间没有相互影响。
我们也可以如下陈述条件独立性
- A 条件独立于 C:P(A|B, C)
- C 条件独立于 A:P(C|B, A)
请注意,条件依赖性是在条件独立性存在的情况下陈述的。也就是说,A 条件独立于 C,或者在存在 C 的情况下 A 条件依赖于 B。
我们也可以将 A 给定 C 的条件独立性陈述为 A 给定 B 的条件依赖性,因为 A 不受 C 影响,并且可以仅从 A 给定 B 来计算。
- P(A|C, B) = P(A|B)
我们可以看到 B 不受 A 和 C 的影响,也没有父节点;我们可以简单地将 B 的 A 和 C 的条件独立性陈述为 P(B, P(A|B), P(C|B)) 或 P(B)。
我们也可以将 A 和 C 在给定 B 的联合概率或条件为 B 的联合概率写成两个条件概率的乘积;例如
- P(A, C | B) = P(A|B) * P(C|B)
该模型总结了 A、B、C 的联合概率 P(A, B, C),计算如下
- P(A, B, C) = P(A|B) * P(C|B) * P(B)
我们可以如下绘制图
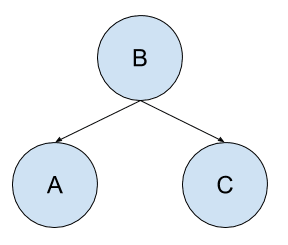
简单贝叶斯网络示例
请注意,随机变量各自被分配了一个节点,条件概率表示为节点之间的有向连接。另外请注意,在图中导航时不可能出现循环,例如,通过边从一个节点导航到另一个节点时不可能出现循环。
同时请注意,即使在此时我们不知道变量的概率分布时,该图也很有用。
您可能想通过为每个随机变量使用人为设计的概率来扩展此示例,并练习一些不同场景的简单推理。
Python 中的贝叶斯网络
可以在 Python 中开发贝叶斯网络并用于推理。
一个流行的库叫做 PyMC,它提供了用于贝叶斯建模的各种工具,包括贝叶斯网络等图模型。
该库的最新版本称为 PyMC3,以 Python 3 版本命名,它构建在 Theano 数学计算库之上,该库提供快速的自动微分。
PyMC3 是一个用 Python 编写的新的开源概率编程框架,它使用 Theano 通过自动微分计算梯度,并即时将概率程序编译为 C 以提高速度。
— 使用 PyMC3 进行 Python 概率编程,2016 年。
更一般地说,在用于推理的计算机软件中使用概率图模型被称为“概率编程”。
这种编程被称为概率编程,[...] 它之所以是概率性的,是因为我们使用编程变量作为模型的组件来创建概率模型。模型组件是 PyMC 框架中的一等公民。
— 黑客的贝叶斯方法:概率编程与贝叶斯推断,2015 年。
要获得有关 PyMC 的贝叶斯方法总体介绍的绝佳资料,请参阅 Cameron Davidson-Pilon 的免费书籍《黑客的贝叶斯方法》。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 贝叶斯推理与机器学习, 2012.
- 黑客的贝叶斯方法:概率编程与贝叶斯推断, 2015.
书籍章节
- 第 6 章:贝叶斯学习,机器学习,1997 年。
- 第 8 章:图模型,模式识别与机器学习,2006 年。
- 第 10 章:有向图模型(贝叶斯网),机器学习:概率视角,2012 年。
- 第 14 章:概率推理,人工智能:一种现代方法,第 3 版,2009 年。
论文
- 使用 PyMC3 的 Python 概率编程, 2016.
代码
文章
总结
在这篇文章中,您了解了贝叶斯网络的一个简单介绍。
具体来说,你学到了:
- 贝叶斯网络是一种由节点和有向边组成的概率图模型。
- 贝叶斯网络模型捕获了随机变量之间条件依赖和条件独立的关系。
- 模型可以由专家准备,也可以从数据中学习,然后用于推理以估计因果事件或后续事件的概率。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。







贝叶斯信念网络和贝叶斯神经网络有什么区别?
BBN 是一种概率图模型。我对贝叶斯神经网络了解不多,抱歉,但它们是神经网络,而不是图模型。
@Leo 实际上,确实存在贝叶斯神经网络,但它们的训练方式与常规神经网络不同。标准神经网络具有固定或常量的参数矩阵。这些参数使用反向传播和梯度下降进行估计。贝叶斯神经网络实际上会估计神经网络矩阵中每个参数或权重的分布。与其说权重是 [1 2 3; 4 5 6],不如说贝叶斯神经网络会为这些参数分配分布,例如 [Normal(1.0, sigma^2) Normal(2.0, sigma^2) Normal(3.0, sigma^2 ...]。
当然,你不能使用标准的反向传播来训练这种模型。你会使用类似变分推断的方法。一种有趣的方法是称为随机梯度 Langevin 梯度下降的方法,这又类似于变分推断。
如果你能提供一些 BN 在 ML 问题陈述中的应用用例,或者提供链接,那就太好了。
感谢您的建议。
如果我想在研究任务中应用 BN,是否必须使用算法?
例如,当我们使用数据挖掘概念时,我们必须根据其技术应用一些算法。
我对这两个概念感到困惑。
请给我一个清晰的解释。
是的,您可以使用库来实现模型,例如 pymc3。
在您的包中进行结构学习需要哪些模型诊断...可能是一致性?
例如,我正在使用以下方法处理一组观察到的二元调查变量的结构学习估计:
I. ML 估计,
II. BIC 拟合优度标准,以及
III. Tabu 优化。
这在 Scutari 的 R 的 bnlearn 包中完成,并且所有操作都在后台进行,解释很少。我对可能在 Python 中重新实现我的工作以练习该主题非常感兴趣。谢谢!
抱歉,我不知道“结构学习”,不确定我能否当场给你好的建议。
在贝叶斯信念网络(BBN)中,有两件事是从数据中学习的:一是网络的结构(即哪些节点连接到哪些节点,但有限制,即没有循环,因为 BBN 是有向无环图 DAG);二是每个节点的节点概率表(NPT),您可能称之为条件概率表(CPT),如果它是子节点或同时是父节点和子节点。对于仅父节点,NPT 不是条件分布。现在,如果像在机器学习中那样,我们通过数据挖掘估计结构和 NPT,则称为全自动化学习。如果结构由主题/领域专家确定,并且 NPT 通过数据挖掘从数据中学习,则称为半自动化学习。如果两者都由领域/主题专家指定,则称为手动学习。网络结构的估计称为结构学习。
我们可以将贝叶斯网络用于图像分类吗?
如果可以,如何做到?
谢谢你
可能不能。在我看来,这听起来不是该技术的合适用途。
在我看来,除非 A 和 C 的所有结果都不相关,否则 A 不会条件独立于 C。它们对 B 的共同依赖性表明,某些 A 和 C 的组合可能比其他组合更有可能。这是否意味着条件独立性并不排除相关性?
相关性不等同于因果关系
感谢您的撰写。请问,我们可以在复杂系统的故障定位中使用 BN 吗?
也许可以尝试一下。
嗨,Jason,
我想请教您对以下场景使用贝叶斯网络的个人意见/建议(附注:如果您能推荐一个程序,我将深表感谢)
收集了约 150 个不同的水生站点,用于收集水生无脊椎动物以及浮游动物和浮游植物,同时收集了水和生态相关的变量(例如,温度、pH 值等)。
我们可以应用 BN 吗?
我暂时不知道,也许可以试试看。
您能否针对时间序列数据(多元)的贝叶斯网络结构学习提供一些思路?我发现很难找到能为这个问题提供良好结果的库。pgmpy 具有高斯变量的结构学习框架,这引出了第二个问题,如果我们采用多元时间序列数据并将其放入将它视为 iid 高斯分布的算法中,准确性会受到多大影响?
抱歉,我不能。
您能否在 Python 中使用贝叶斯网络查找分类数据的概率?
我不确定您的意思。
您可以使用经验分布来估计变量值的概率。无需贝叶斯网络。
> 隐马尔可夫模型(HMM)是一种图模型,其中图的边是无向的,意味着图包含环。贝叶斯网络更具限制性,其中图的边是有向的,意味着它们只能沿一个方向导航。这意味着不可能出现环,并且该结构可以更普遍地称为有向无环图(DAG)。
事情并非如此。仅仅因为一个图是无向的,并不一定意味着它包含一个环。同样,很容易创建一个有向图,它有一个环。环形图仅意味着从任何节点开始,都可以遵循一条路径(在图论的意义上)回到您的原始节点。路径必须由图的顶点子集组成,因此您不能重复使用同一个节点(这就是为什么并非所有无向图都是环形图的原因——从 A 到 B 然后直接返回 A 不算)。
感谢您的反馈 Audemar!
“隐马尔可夫模型(HMM)是一种图模型,其中图的边是无向的,意味着图包含环。”
我认为这个说法是错误的。HMM 在视觉上是两个序列(x_n, y_n),其中观察值 y_n 有一个指向它的箭头来自 x_n。状态 x_n 从前一个状态有一个有向箭头指向它,并发出一个箭头指向下一个状态 x_{n+1}。因此,我看不出边是如何无向的以及图如何包含环。您能解释一下吗?
你好 statstudent... 感谢您的反馈!以下资源可能会有所帮助
https://web.math.princeton.edu/~rvan/orf557/hmm080728.pdf