矩阵分解是一种有用的工具,用于将矩阵分解为其组成部分,以简化一系列更复杂的操作。
也许最常用的矩阵分解类型是特征分解,它将矩阵分解为特征向量和特征值。这种分解在机器学习中使用的方法中也发挥着作用,例如在主成分分析方法或PCA中。
在本教程中,您将了解线性代数中的特征分解、特征向量和特征值。
完成本教程后,您将了解:
- 什么是特征分解以及特征向量和特征值的作用。
- 如何使用 NumPy 在 Python 中计算特征分解。
- 如何确认一个向量是特征向量,以及如何从特征向量和特征值重建矩阵。
通过我的新书《机器学习线性代数》**开启您的项目**,其中包括**逐步教程**和所有示例的**Python 源代码**文件。
让我们开始吧。

机器学习中特征分解、特征值和特征向量的温和介绍
图片由Mathias Appel拍摄,保留部分权利。
教程概述
本教程分为5个部分,它们是:
- 矩阵的特征分解
- 特征向量和特征值
- 特征分解的计算
- 确认特征向量和特征值
- 重建原始矩阵
在机器学习线性代数方面需要帮助吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
矩阵的特征分解
矩阵的特征分解是一种分解类型,它涉及将一个方阵分解成一组特征向量和特征值。
最广泛使用的矩阵分解之一称为特征分解,其中我们将矩阵分解成一组特征向量和特征值。
— 第42页,深度学习,2016。
如果一个向量满足以下方程,它就是矩阵的特征向量。
|
1 |
A . v = lambda . v |
这被称为特征值方程,其中 A 是我们正在分解的父方阵,v 是矩阵的特征向量,lambda 是小写希腊字母,代表特征值标量。
或者没有点符号。
|
1 |
Av = lambdav |
一个矩阵可以为父矩阵的每个维度拥有一个特征向量和特征值。并非所有方阵都可以分解为特征向量和特征值,有些只能以需要复数的方式分解。父矩阵可以表示为特征向量和特征值的乘积。
|
1 |
A = Q . diag(V) . Q^-1 |
或者,不使用点符号。
|
1 |
A = Qdiag(V)Q^-1 |
其中 Q 是由特征向量组成的矩阵,diag(V) 是一个由对角线上的特征值组成的对角矩阵(有时用大写 lambda 表示),Q^-1 是由特征向量组成的矩阵的逆。
然而,我们经常希望将矩阵分解为它的特征值和特征向量。这样做可以帮助我们分析矩阵的某些性质,就像将整数分解为它的素因子可以帮助我们理解该整数的行为一样。
— 第43页,深度学习,2016。
“Eigen”不是一个名字,例如该方法不是以“Eigen”命名的;“eigen”(发音为 eye-gan)是一个德语单词,意思是“自己的”或“固有的”,如同属于父矩阵一样。
分解操作不会导致矩阵的压缩;相反,它将其分解为组成部分,以使对矩阵的某些操作更容易执行。与其他矩阵分解方法一样,特征分解被用作简化其他更复杂矩阵操作计算的元素。
几乎所有向量乘以 A 时都会改变方向。某些特殊向量 x 与 Ax 方向相同。这些是“特征向量”。将特征向量乘以 A,向量 Ax 是数字 lambda 乘以原始 x。[…] 特征值 lambda 告诉我们当特殊向量 x 乘以 A 时,它是否被拉伸、缩小、反转或保持不变。
— 第289页,线性代数导论,第五版,2016。
特征分解还可用于在主成分分析方法或 PCA 中计算矩阵的主成分,该方法可用于降低机器学习中数据的维度。
特征向量和特征值
特征向量是单位向量,这意味着它们的长度或大小等于 1.0。它们通常被称为右向量,这简单地意味着一个列向量(与行向量或左向量相对)。右向量就是我们理解的向量。
特征值是应用于特征向量的系数,它们赋予向量长度或大小。例如,负特征值可能会在缩放特征向量时反转其方向。
只具有正特征值的矩阵被称为正定矩阵,而如果特征值全为负数,则被称为负定矩阵。
将矩阵分解为它的特征值和特征向量,可以为我们提供有关矩阵性质的有价值的见解。当使用矩阵的特征分解时,某些矩阵计算(例如计算矩阵的幂)变得更容易。
— 第262页,线性代数无废话指南,2017
特征分解的计算
特征分解是在一个方阵上使用高效迭代算法计算的,我们不会深入探讨细节。
通常首先找到特征值,然后找到一个特征向量来将方程求解为一组系数。
可以使用 NumPy 中的 eig() 函数计算特征分解。
下面的示例首先定义一个 3×3 方阵。在该矩阵上计算特征分解,返回特征值和特征向量。
|
1 2 3 4 5 6 7 8 9 10 |
# 特征分解 from numpy import array 从 numpy.linalg 导入 eig # 定义矩阵 A = 数组([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print(A) # 计算特征分解 values, vectors = eig(A) 打印(values) 打印(vectors) |
运行示例首先打印定义的矩阵,然后打印特征值和特征向量。更具体地说,特征向量是右手特征向量,并归一化为单位长度。
|
1 2 3 4 5 6 7 8 9 |
[[1 2 3] [4 5 6] [7 8 9]] [ 1.61168440e+01 -1.11684397e+00 -9.75918483e-16] [[-0.23197069 -0.78583024 0.40824829] [-0.52532209 -0.08675134 -0.81649658] [-0.8186735 0.61232756 0.40824829]] |
确认特征向量和特征值
我们可以确认一个向量确实是矩阵的特征向量。
我们通过将候选特征向量乘以特征向量并将其结果与特征值进行比较来完成此操作。
首先,我们将定义一个矩阵,然后计算特征值和特征向量。然后我们将测试第一个向量和值是否实际上是矩阵的特征值和特征向量。我们知道它们是,但这是一个很好的练习。
特征向量以与父矩阵相同维度的矩阵返回,其中每列都是一个特征向量,例如第一个特征向量是 vectors[:, 0]。特征值以列表形式返回,其中返回数组中的值索引与按列索引的特征向量配对,例如 values[0] 处的第一个特征值与 vectors[:, 0] 处的第一个特征向量配对。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
# 确认特征向量 from numpy import array 从 numpy.linalg 导入 eig # 定义矩阵 A = 数组([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # 计算特征分解 values, vectors = eig(A) # 确认第一个特征向量 B = A.dot(vectors[:, 0]) print(B) C = vectors[:, 0] * values[0] print(C) |
该示例将原始矩阵与第一个特征向量相乘,并将其结果与第一个特征向量乘以第一个特征值进行比较。
运行示例会打印这两个乘法的结果,显示相同的最终向量,正如我们所预期的那样。
|
1 2 3 |
[ -3.73863537 -8.46653421 -13.19443305] [ -3.73863537 -8.46653421 -13.19443305] |
重建原始矩阵
我们可以反转过程,仅给定特征向量和特征值来重建原始矩阵。
首先,特征向量列表必须转换为矩阵,其中每个向量成为一行。特征值需要排列成对角矩阵。NumPy 的 diag() 函数可用于此目的。
接下来,我们需要计算特征向量矩阵的逆,这可以通过 inv() NumPy 函数实现。最后,这些元素需要与 dot() 函数一起相乘。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# 重建矩阵 从 numpy 导入 diag 从 numpy 导入 dot 从 numpy.linalg 导入 inv from numpy import array 从 numpy.linalg 导入 eig # 定义矩阵 A = 数组([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print(A) # 计算特征向量和特征值 values, vectors = eig(A) # 从特征向量创建矩阵 Q = vectors # 创建特征向量矩阵的逆 R = inv(Q) # 从特征值创建对角矩阵 L = diag(values) # 重建原始矩阵 B = Q.dot(L).dot(R) print(B) |
该示例再次计算特征值和特征向量,并使用它们重建原始矩阵。
运行示例首先打印原始矩阵,然后打印从特征值和特征向量重建的与原始矩阵匹配的矩阵。
|
1 2 3 4 5 6 7 |
[[1 2 3] [4 5 6] [7 8 9]] [[ 1. 2. 3.] [ 4. 5. 6.] [ 7. 8. 9.]] |
扩展
本节列出了一些您可能希望探索的扩展本教程的想法。
- 使用您自己的数据,为每个操作创建5个示例。
- 手动实现每个矩阵操作,用于定义为列表的列表的矩阵。
- 搜索机器学习论文,并找到每个操作被使用的一个例子。
如果您探索了这些扩展中的任何一个,我很想知道。
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 第6.1节 特征值和特征向量。《线性代数无废话指南》,2017年。
- 第6章 特征值和特征向量,《线性代数导论》,第五版,2016年。
- 第2.7节 特征分解,《深度学习》,2016年。
- 第5章 特征值、特征向量和不变子空间,《线性代数精讲》,第三版,2015年。
- 讲座24,特征值问题,《数值线性代数》,1997年。
API
文章
总结
在本教程中,您学习了线性代数中的特征分解、特征向量和特征值。
具体来说,你学到了:
- 什么是特征分解以及特征向量和特征值的作用。
- 如何使用 NumPy 在 Python 中计算特征分解。
- 如何确认一个向量是特征向量,以及如何从特征向量和特征值重建矩阵。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。




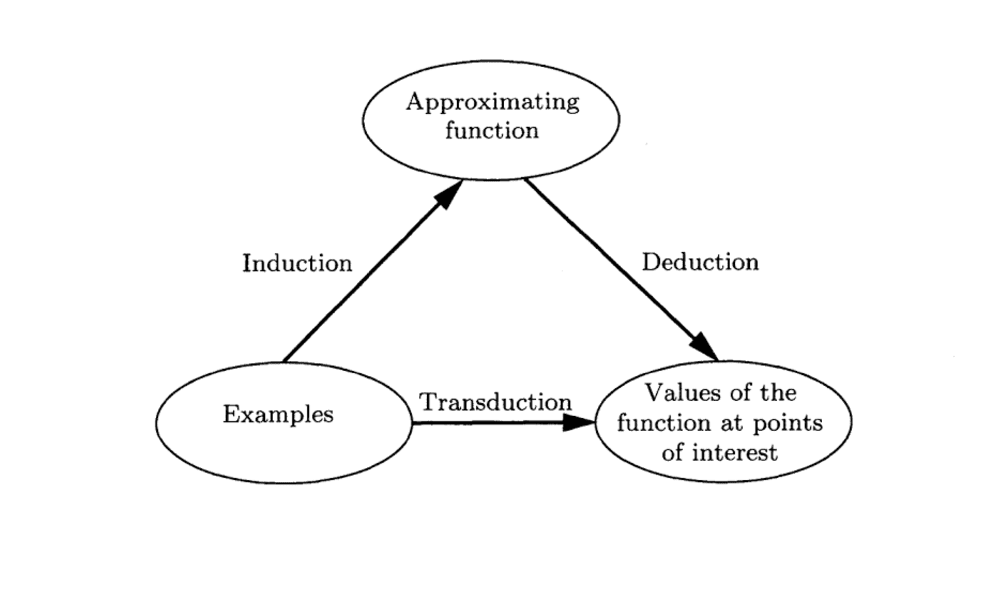

对特征向量、特征值和特征基的用处的直观理解。
3Blue1Brown 的 YouTube 频道 https://www.youtube.com/watch?v=PFDu9oVAE-g 对可视化所有这些内容非常有帮助。
感谢分享,哈维!
嗨,Jason,
我有一个小小的批评:如果有一些好的图片,特别是描述矩阵及其方向的图片,事情会变得更清楚、更快。例如(除了我最终弄明白了这一点),你对右向量和左向量的定义被额外的陈述“右向量就是我们理解的向量”所混淆,因为不是每个人都学习“向量”意味着列向量。这个问题被这样一个事实所困扰:搜索“右向量的定义”几乎除了定义什么都找不到。甚至 David Lay 的《线性代数》在索引中也没有提到右向量(据我所知,正文中也没有)[我查过了]。对于那些对某个细节不清楚但由于某种原因无法直接询问他人的人来说,这令人困惑。简单的图片在使事情更清楚方面大有帮助。公平地说,即使 NIST 的在线统计参考也缺乏图画或图片,而且我认为他们的文本中有一个错误,他们混淆了行和列——在这种情况下,图片会带来清晰度。
我很感谢您为发布这些材料和您的其他文章(比如最初引导我来到这里的 PCA)所做的努力。
很好的建议,谢谢。
我想我不是一个视觉型的人——请注意这个网站上900多篇教程中缺乏图片。
我用代码思考。也许我需要在这方面下功夫。或者,也许这个网站是为像我这样的人准备的。
肯说得对,这个话题值得配上视觉效果。
谢谢。
第117页,《机器学习线性代数》一书
你的书中有一个错误,当你写到父矩阵的特征分解是公式15.3时。第三个元素不是矩阵的转置,而是矩阵的逆。在这个博客中是正确的。
这本书会持续更新以修复问题。
我已将您的购买收据以及最新版本书籍的更新下载链接重新发送给您。
嗨,Jason,
这是一个有趣且基础的教程,用于理解与矩阵(例如,与样本-特征表格数据集操作相关联)相关的特征值和特征向量。我在您的另一个更偏向 PCA 分析的教程“如何从零开始用 Python 计算主成分分析 (PCA)”之后学习了这个教程。
为了将数据集缩减(例如列特征缩减)与此特征值和特征向量“线性代数”工具连接起来,如果您预先创建了您的矩阵“A”,并执行了中心化和协方差矩阵(列或特征的比较),就像您在之前提到的教程中所做的那样,您现在就可以通过特征值和特征向量的应用来缩减数据集了……
无论如何,我仍然缺少对特征值的解释,在之前的教程中,它是作为数据集(样本-特征)问题缩减的标准。也就是说,将最小特征值与忽略特征(相对于最大特征值)联系起来……这样我们最终可以消除与这些被忽略的轴(它们内部没有变化发生!)相关的轴或特征向量或特征……这样我们就得到了我们正在寻找的……通过特征值/特征向量分析来简化数据集或消除机器学习问题中冗余的数据集特征或不重要的特征……
我将继续学习您的其他与特征选择、缩减和重要性评估相关的教程……以便更好地理解其工作原理!
感谢您提供所有这些精彩的教程,杰森!
谢谢,很高兴它有帮助。
在特征值分解中,我感觉应该添加一个虽小但重要的句子——v(特征向量)不能是零向量。
感谢您的反馈,迪皮卡!
在“重建原始矩阵”一节中,代码与所提供的描述不符
> 首先,特征向量列表必须转换为矩阵,其中每个向量成为一行。特征值需要排列成对角矩阵。
代码将特征向量矩阵保持原样,即每个向量作为一列,而不是一行。
感谢您的反馈,桑迪普!