函数优化入门指南

函数优化是一个基础研究领域，其技术几乎应用于所有量化领域。

重要的是，函数优化是几乎所有机器学习算法和预测建模项目的核心。因此，理解函数优化是什么、该领域使用的术语以及构成函数优化问题的要素至关重要。

在本教程中，您将了解函数优化的入门知识。

完成本教程后，您将了解：

• 函数优化的三个要素是候选解、目标函数和成本。
• 函数优化的概念化是导航搜索空间和响应曲面。
• 在解决函数优化问题时，全局最优解和局部最优解的区别。

通过我的新书《机器学习优化》来启动您的项目，其中包括分步教程和所有示例的Python源代码文件。

函数优化入门指南
照片由 USFS, Interior West FIA 提供，保留部分权利。

教程概述

本教程分为四个部分；它们是

1. 函数优化
2. 候选解
3. 目标函数
4. 评估成本

函数优化

函数优化是数学的一个子领域，在现代，它通过数值计算方法来解决。

连续函数优化（在此简称为“函数优化”）属于一个更广泛的研究领域，称为数学优化。

它与其他类型的优化不同，因为它涉及寻找由数字输入变量组成的最佳候选解，而不是由序列或组合组成的候选解（例如组合优化）。

函数优化是一套广泛使用的技术工具包，应用于几乎所有的科学和工程学科。

人们都在进行优化。投资者寻求创建既能避免过度风险又能实现高回报率的投资组合。[…] 优化是决策科学和物理系统分析中的重要工具。

— 第2页，《数值优化》，2006年。

它在机器学习中扮演着核心角色，因为几乎所有的机器学习算法都使用函数优化来将模型拟合到训练数据集。

例如，将一条线拟合到一组点需要解决一个优化问题。将线性回归或神经网络模型拟合到训练数据集也是如此。

通过这种方式，优化提供了一种将通用模型适应特定情况的工具。学习被视为一个优化或搜索问题。

实际上，函数优化描述了一类问题，即找到给定函数的输入，以使该函数的输出结果最小或最大。

目标取决于系统的某些特性，称为变量或未知数。我们的目标是找到能够优化目标的变量值。

— 第2页，《数值优化》，2006年。

函数优化涉及三个要素：函数的输入（例如 x）、目标函数本身（例如 f()）以及函数的输出（例如 成本）。

• 输入 (x): 待评估函数的输入，例如一个候选解。
• 函数 (f()): 用于评估输入的目标函数。
• 成本: 用目标函数评估候选解的结果，需要最小化或最大化。

让我们依次仔细看看每个要素。

候选解

候选解是目标函数的单个输入。

候选解的形式取决于目标函数的具体情况。它可能是一个浮点数、一个数字向量、一个数字矩阵，或者根据特定问题领域的需求而变得复杂。

最常见的是数字向量。对于一个测试问题，向量表示函数每个输入变量的具体值（x = x1, x2, x3, …, xn）。对于机器学习模型，向量可能表示模型系数或权重。

从数学上讲，优化是在其变量受约束的情况下，最小化或最大化一个函数。

— 第2页，《数值优化》，2006年。

问题领域或目标函数可能会对候选解施加约束。这可能包括以下方面：

• 变量的数量（1, 20, 1,000,000 等）
• 变量的数据类型（整数、二进制、实值等）
• 可接受值的范围（0到1之间等）

重要的是，候选解是离散的，并且有很多。

候选解的范围可能非常广阔，大到无法枚举。因此，我们能做的最好方法是在搜索空间中对候选解进行抽样。作为实践者，我们寻求一种优化算法，能够最有效地利用关于问题的可用信息，以便有效地抽样搜索空间并找到一个好的或最佳的候选解。

• 搜索空间：由目标函数可接受输入的数量、类型和范围定义的候选解的集合。

最后，可以根据目标函数的评估结果对候选解进行排序，这意味着有些解比其他的更好。

目标函数

目标函数是特定于问题领域的。

它可能是一个测试函数，例如，一个具有特定数量输入变量的著名方程，其计算结果返回输入的成本。测试函数的最优解是已知的，这使得可以根据算法在搜索空间中有效导航的能力来比较它们。

在机器学习中，目标函数可能涉及将候选解代入模型，并根据一部分训练数据集对其进行评估，而成本可能是一个误差分数，通常称为模型的损失。

目标函数很容易定义，但评估成本很高。函数优化的效率指的是最小化函数评估的总次数。

尽管目标函数很容易定义，但它可能难以优化。目标函数的难度范围可以从能够直接使用微积分或线性代数解析求解函数（简单），到使用局部搜索算法（中等），再到使用全局搜索算法（困难）。

目标函数的难度取决于对该函数的了解程度。这通常不能通过简单地查看评估候选解的方程或代码来确定。相反，它指的是响应曲面的结构。

响应曲面（或搜索景观）是成本相对于候选解搜索空间的几何结构。例如，平滑的响应曲面表明，输入的微小变化（候选解）会导致目标函数输出（成本）的微小变化。

• 响应曲面：目标函数的成本因候选解变化而产生的几何特性。

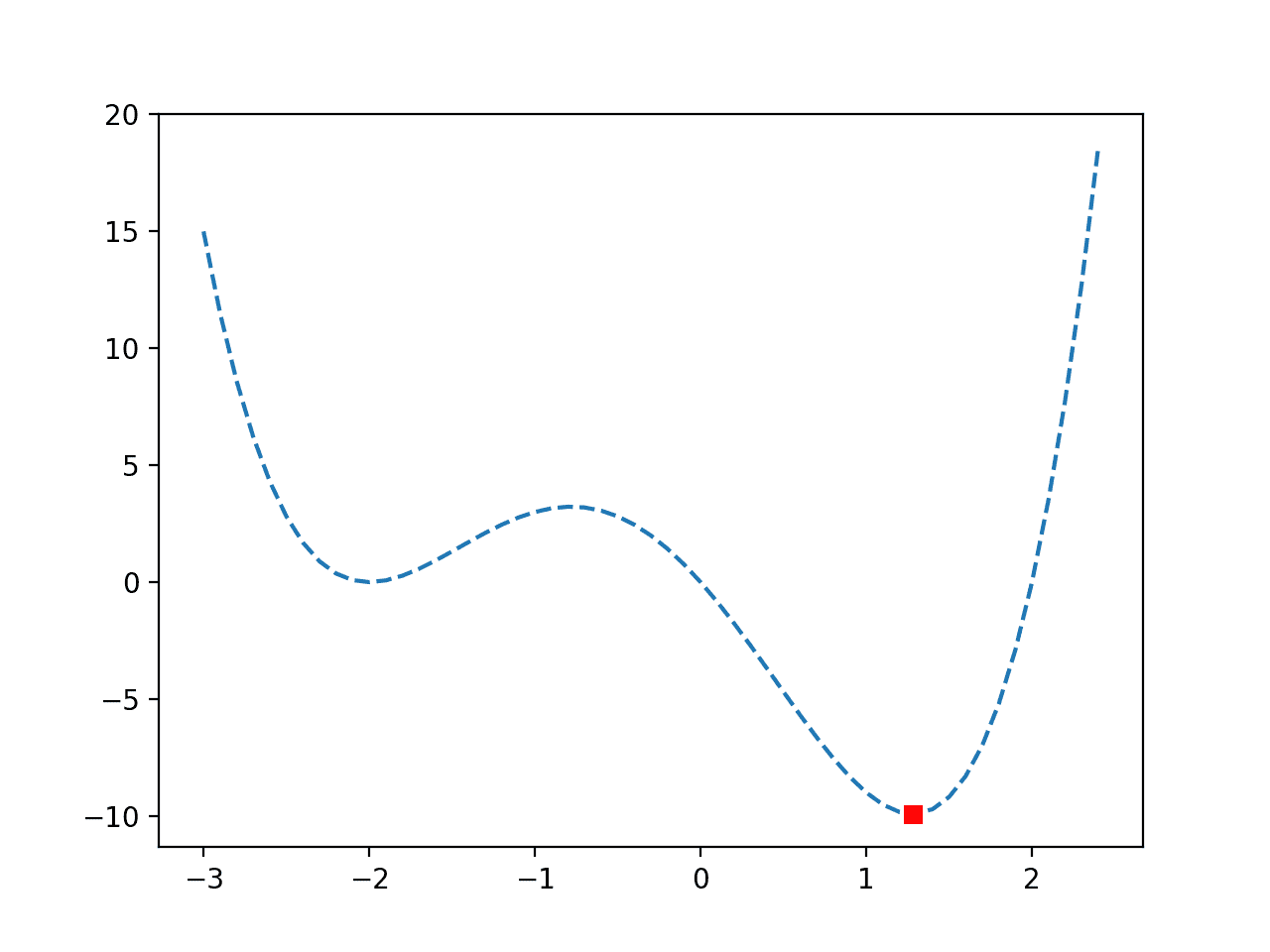
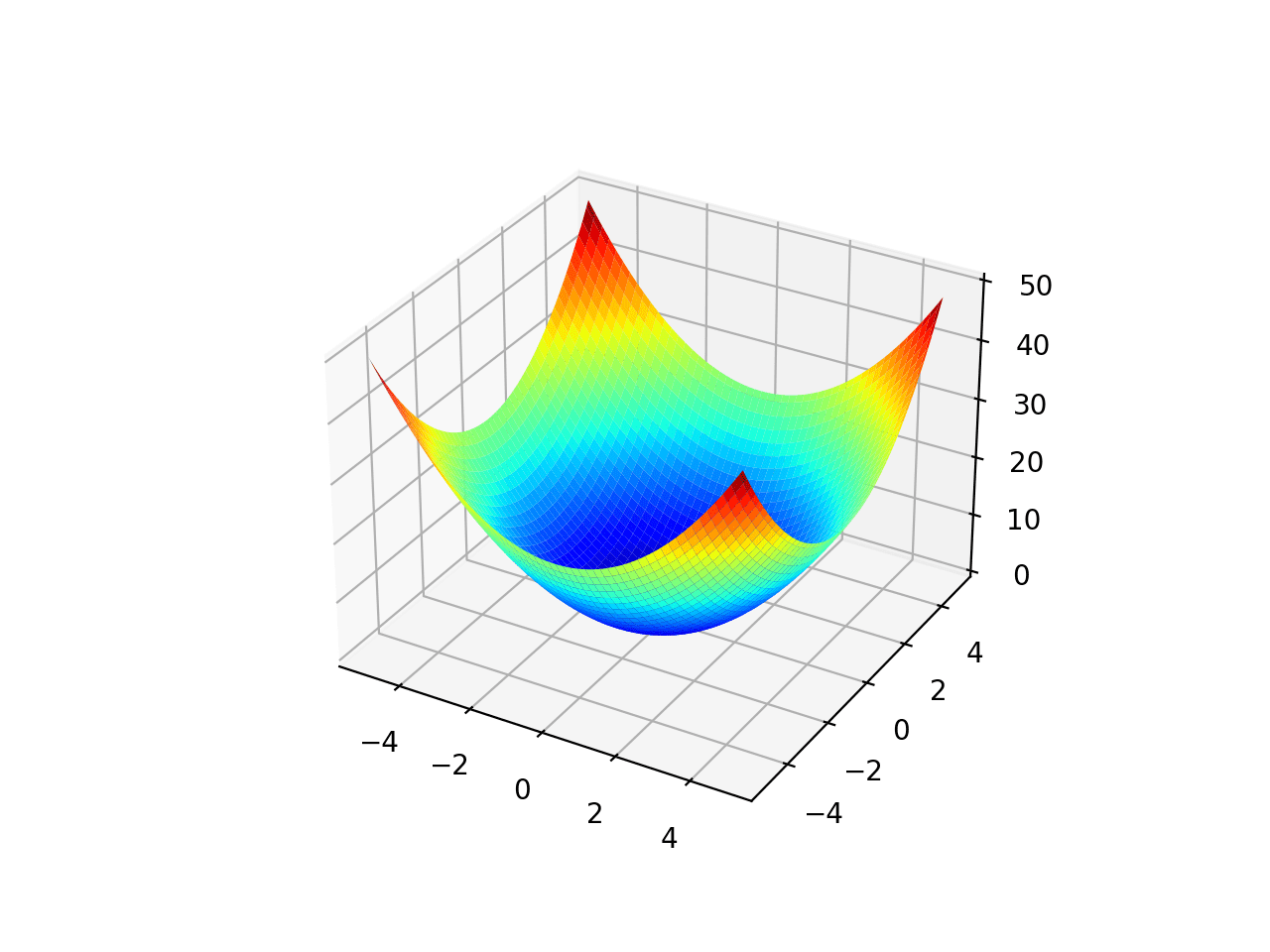
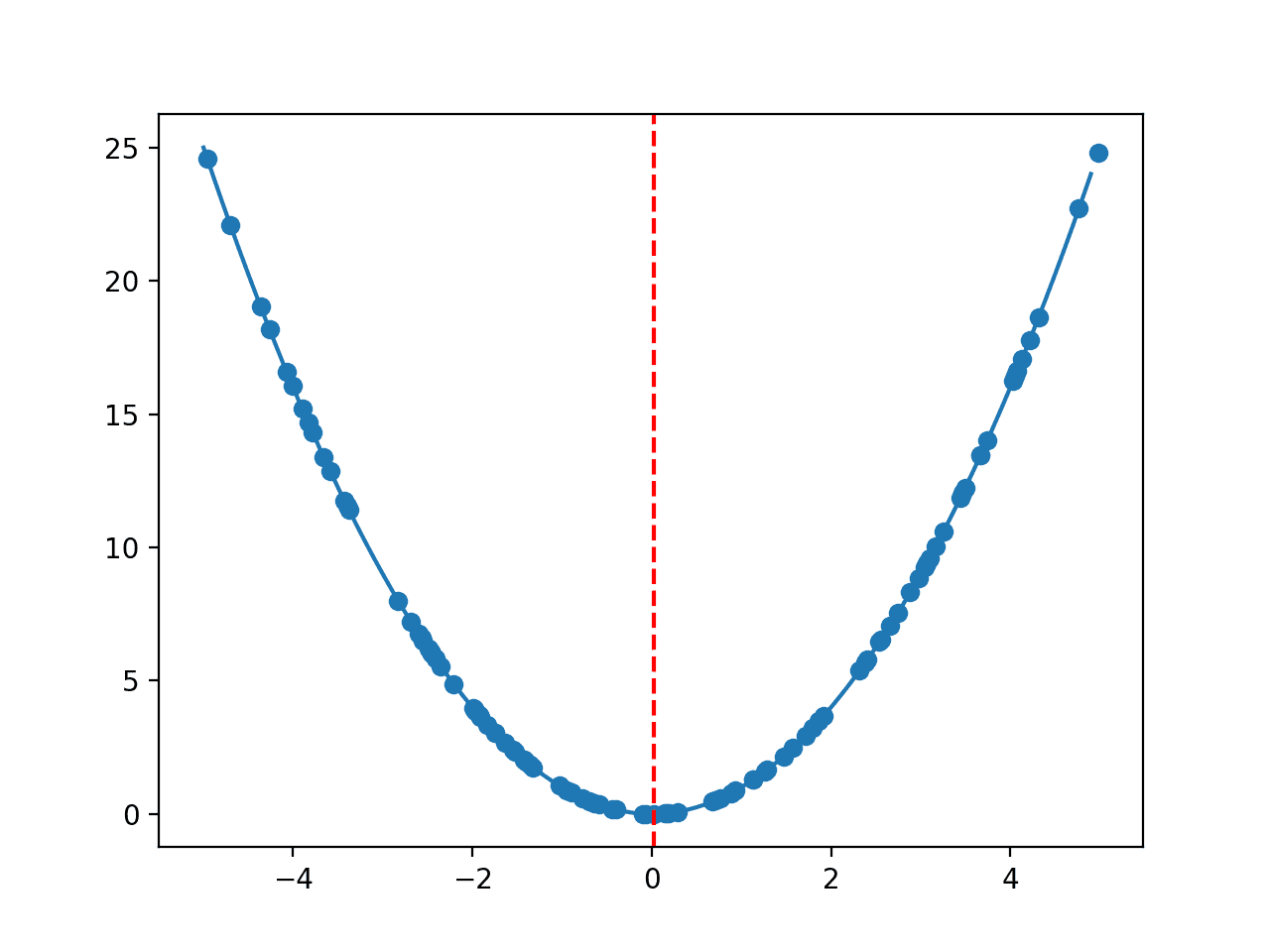
响应曲面可以在低维度下可视化，例如，对于具有一个或两个输入变量的候选解。一维输入可以绘制成二维散点图，x轴为输入值，y轴为成本。二维输入可以绘制成三维曲面图，x轴和y轴为输入变量，曲面的高度代表成本。

在最小化问题中，差的解在响应曲面上表示为山丘，好的解表示为山谷。对于最大化问题，情况则相反。

这个响应曲面的结构和形状决定了算法在导航搜索空间以找到解决方案时将面临的困难。

实际目标函数的复杂性意味着我们无法解析地分析其曲面，而输入的高维度和函数评估的计算成本使得绘制和映射实际目标函数变得不可行。

评估成本

候选解的成本几乎总是一个单一的实数值。

成本值的尺度将根据目标函数的具体情况而变化。通常，成本值的唯一有意义的比较是与由相同目标函数计算出的其他成本值进行比较。

函数的最小或最大输出被称为函数的最优解（optima），通常简化为最小值。任何我们希望最大化的函数，都可以通过在函数返回的成本前加上一个负号来转换为最小化问题。

在全局优化中，会找到优化问题的真正全局解；代价是效率。全局优化方法的最坏情况复杂度会随着问题规模呈指数级增长……

— 第10页，《凸优化》，2004年。

一个目标函数可能只有一个最佳解，称为该目标函数的全局最优解。或者，目标函数可能有多个全局最优解，在这种情况下，我们可能希望找到其中一个或全部。

许多数值优化方法寻求局部最小值。局部最小值是局部最优的，但我们通常不知道一个局部最小值是否是全局最小值。

— 第8页，《优化算法》，2019年。

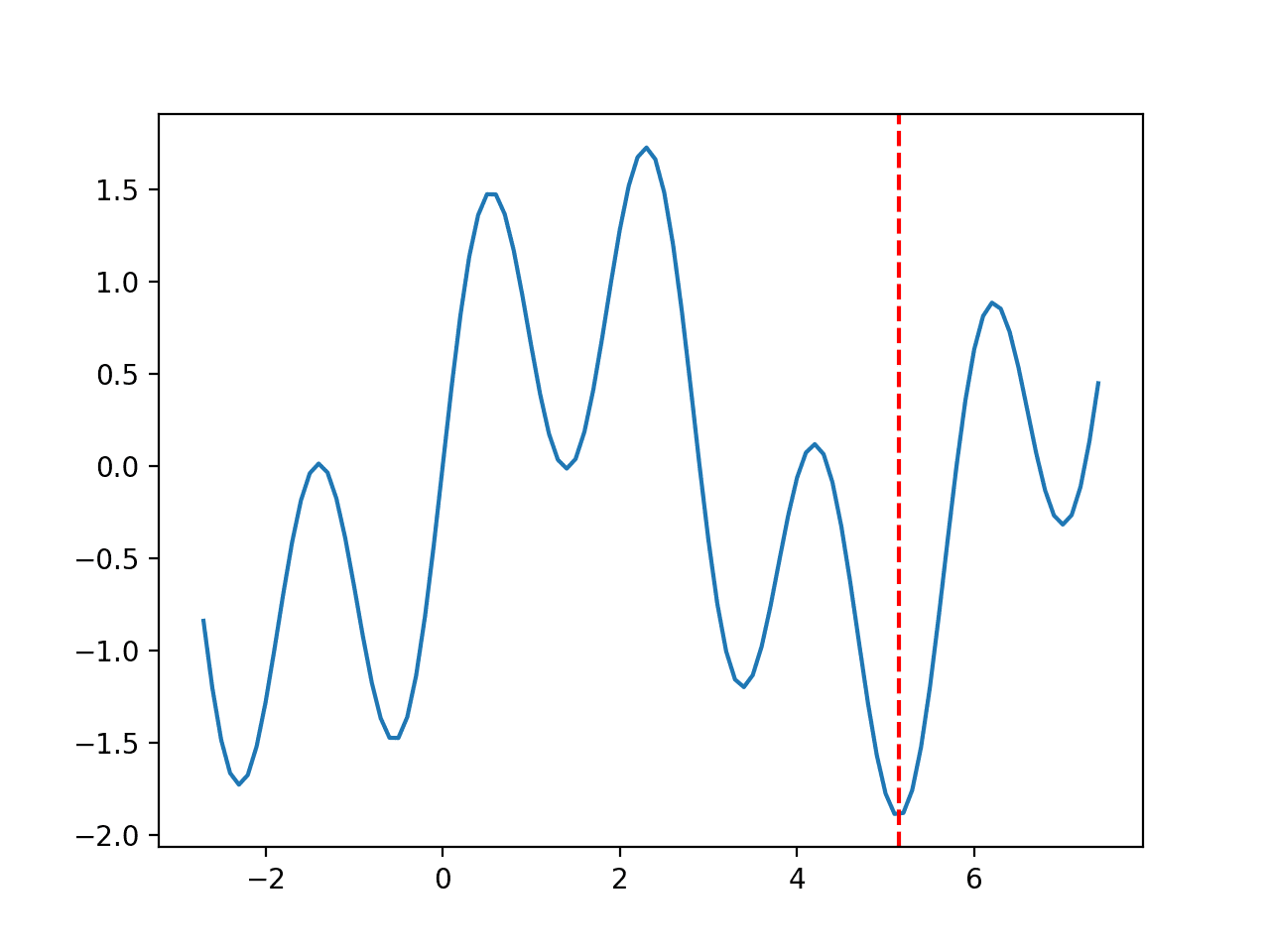
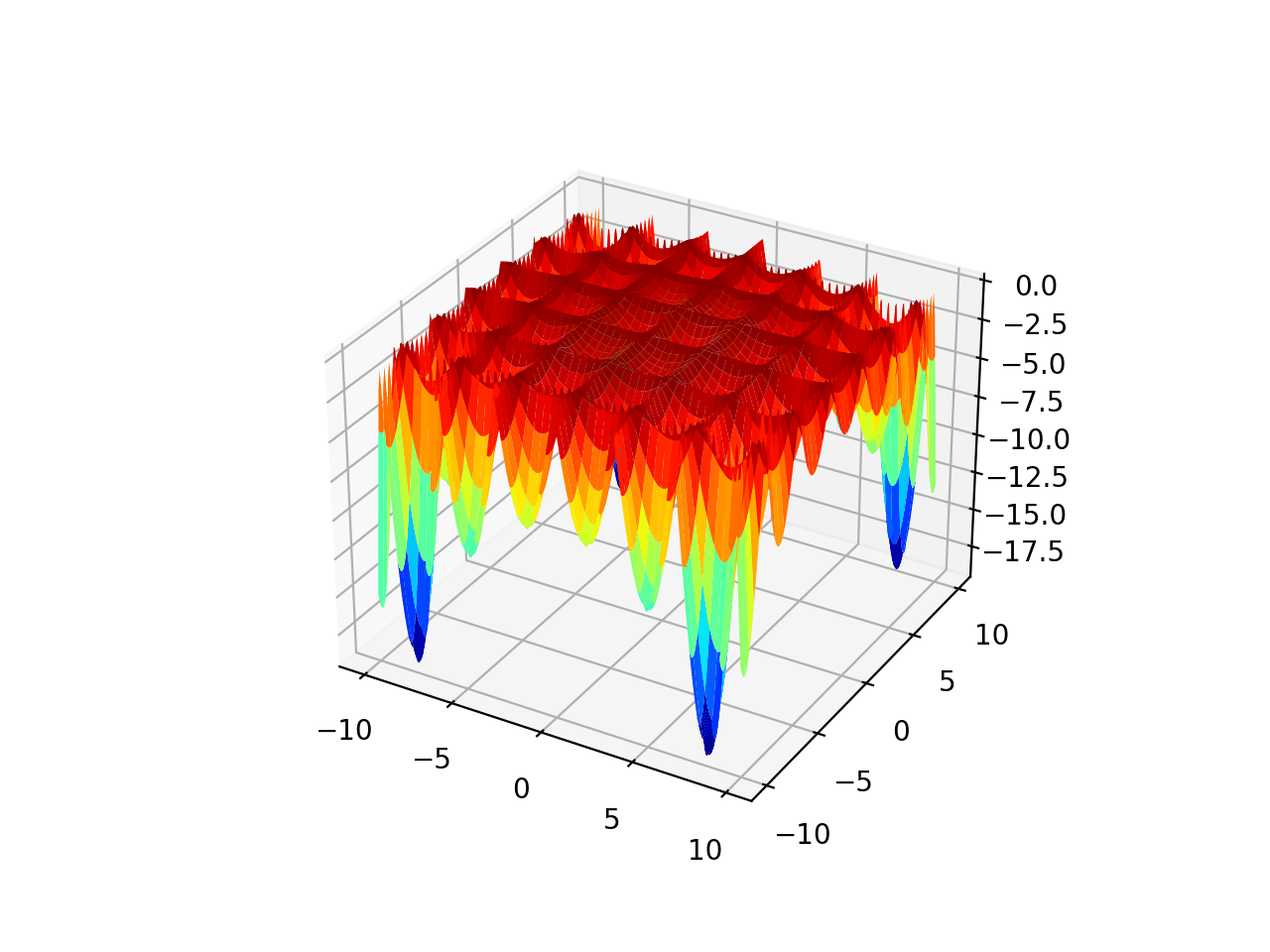
除了全局最优解，一个函数可能还有局部最优解，它们是好的候选解，可能相对容易找到，但不如全局最优解好。局部最优解对搜索算法来说可能看起来像全局最优解，例如，可能位于响应曲面的一个山谷中，在这种情况下，我们可能会称它们为“欺骗性的”，因为算法会很容易找到它们并陷入其中，从而无法找到全局最优解。

• 全局最优解：具有目标函数最佳成本的候选解。
• 局部最优解：好的候选解，但不如全局最优解好。

成本值的相对性意味着，在挑战性问题上，可以使用一个简单的搜索算法（例如随机搜索）来建立性能基准，然后将更复杂的搜索算法找到的最优解的“好坏”与该基准进行比较。

候选解通常描述起来非常简单，构建起来也很容易。函数优化的挑战在于评估候选解。

解决一个函数优化问题或目标函数指的是找到最优解。整个项目的目标是在可用的时间和资源下，找到一个具有良好或最佳成本的特定候选解。在简单和中等难度的问题中，我们或许能够精确地找到最优候选解，并对此有一定信心。

许多非线性优化问题的算法只寻求一个局部解，即目标函数值小于所有其他可行邻近点的点。它们并不总能找到全局解，即在所有可行点中函数值最低的点。在某些应用中需要全局解，但对于许多问题，它们难以识别，更难找到。

— 第6页，《数值优化》，2006年。

在更具挑战性的问题上，考虑到项目可用的时间，我们可能满足于一个相对较好的候选解（例如，足够好）。

进一步阅读

如果您想深入了解，本节提供了更多关于该主题的资源。

书籍

• 优化算法, 2019.
• 凸优化, 2004.
• 数值优化, 2006.

文章

• 数学优化，维基百科.

总结

在本教程中，您了解了函数优化的入门知识。

具体来说，你学到了：

• 函数优化的三个要素是候选解、目标函数和成本。
• 函数优化的概念化是导航搜索空间和响应曲面。
• 在解决函数优化问题时，全局最优解和局部最优解的区别。

你有什么问题吗？
在下面的评论中提出你的问题，我会尽力回答。

掌握现代优化算法！

加深您对优化的理解

...只需几行python代码

在我的新电子书中探索如何实现
机器学习优化

它提供**自学教程**，并附有关于以下内容的**完整工作代码**：
梯度下降、遗传算法、爬山法、曲线拟合、RMSProp、Adam，以及更多...

将现代优化算法应用于
您的机器学习项目

查看内容