迭代局部搜索是一种随机全局优化算法。
它涉及对先前找到的良好解决方案的修改版本反复应用局部搜索算法。这样,它就像是随机重启的随机爬山算法的智能版本。
该算法背后的直觉是,随机重启可以帮助定位问题中的许多局部最优解,而更好的局部最优解通常靠近其他局部最优解。因此,对现有局部最优解进行适度扰动可能会找到优化问题的更好甚至最佳的解决方案。
在本教程中,您将学习如何从头开始实现迭代局部搜索算法。
完成本教程后,您将了解:
- 迭代局部搜索是一种随机全局搜索优化算法,它是随机爬山法加随机重启的更智能版本。
- 如何从头开始实现带有随机重启的随机爬山算法。
- 如何实现迭代局部搜索算法并将其应用于非线性目标函数。
用我的新书《机器学习优化》开启您的项目,书中包含分步教程以及所有示例的Python源代码文件。
让我们开始吧。
从零开始用 Python 实现迭代局部搜索
照片来自 Susanne Nilsson,保留部分权利。
教程概述
本教程分为五个部分;它们是:
- 什么是迭代局部搜索
- Ackley 目标函数
- 随机爬山算法
- 带随机重启的随机爬山算法
- 迭代局部搜索算法
什么是迭代局部搜索
迭代局部搜索,简称 ILS,是一种随机全局搜索优化算法。
它与随机爬山法和带随机重启的随机爬山法相关或为其扩展。
它本质上是带随机重启的爬山法的更智能版本。
— 第 26 页,《元启发式方法要点》,2011 年。
随机爬山法是一种局部搜索算法,它涉及对现有解决方案进行随机修改,并且仅当修改结果比当前工作解决方案更好时才接受该修改。
一般而言,局部搜索算法会陷入局部最优解。解决此问题的一种方法是从新的随机选择的起点重新开始搜索。重启过程可以进行多次,并且可以在固定的函数评估次数后触发,或者如果给定数量的算法迭代没有进一步的改进。此算法称为带随机重启的随机爬山法。
改进局部搜索找到的成本的最简单方法是从另一个起点重复搜索。
— 第 132 页,《元启发式手册》,第三版 2019 年。
迭代局部搜索类似于带随机重启的随机爬山法,不同之处在于,每次重启不是选择一个随机起点,而是根据迄今为止在更广泛搜索中找到的最佳点的修改版本来选择一个点。
对迄今为止最佳解决方案的扰动就像在搜索空间中进行一次大跳跃到一个新区域,而随机爬山算法进行的扰动要小得多,局限于搜索空间的特定区域。
这里的启发式思想是,您通常可以在您当前所在的附近找到更好的局部最优解,而以这种方式从一个局部最优解走到另一个局部最优解,通常优于完全随机地尝试新位置。
— 第 26 页,《元启发式方法要点》,2011 年。
这使得搜索可以在两个级别上进行。爬山算法是用于充分利用特定候选解决方案或搜索空间区域的局部搜索,而重启方法允许探索搜索空间的不同区域。
通过这种方式,迭代局部搜索算法探索搜索空间中的多个局部最优解,增加了找到全局最优解的可能性。
迭代局部搜索是针对组合优化问题提出的,例如旅行商问题(TSP),尽管它可以通过在搜索空间中使用不同的步长来应用于连续函数优化:爬山法使用较小的步长,随机重启使用较大的步长。
现在我们熟悉了迭代局部搜索算法,让我们探讨一下如何从头开始实现该算法。
想要开始学习优化算法吗?
立即参加我为期7天的免费电子邮件速成课程(附示例代码)。
点击注册,同时获得该课程的免费PDF电子书版本。
Ackley 目标函数
首先,让我们将一个挑战性优化问题定义为实现迭代局部搜索算法的基础。
Ackley 函数是多模态目标函数的一个示例,它具有单个全局最优解和多个局部最优解,局部搜索可能会陷入其中。
因此,需要一种全局优化技术。它是一个二维目标函数,在 [0,0] 处有全局最优解,其值为 0.0。
下面的例子实现了 Ackley 函数并创建了一个三维曲面图,显示了全局最优解和多个局部最优解。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
# ackley 多峰函数 from numpy import arange from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy import meshgrid from matplotlib import pyplot from mpl_toolkits.mplot3d import Axes3D # 目标函数 def objective(x, y): return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # 定义输入范围 r_min, r_max = -5.0, 5.0 # 以 0.1 为增量均匀采样输入范围 xaxis = arange(r_min, r_max, 0.1) yaxis = arange(r_min, r_max, 0.1) # 从坐标轴创建网格 x, y = meshgrid(xaxis, yaxis) # 计算目标值 results = objective(x, y) # 使用 jet 配色方案创建曲面图 figure = pyplot.figure() axis = figure.gca(projection='3d') axis.plot_surface(x, y, results, cmap='jet') # 显示绘图 pyplot.show() |
运行该示例会创建 Ackley 函数的曲面图,显示大量的局部最优解。
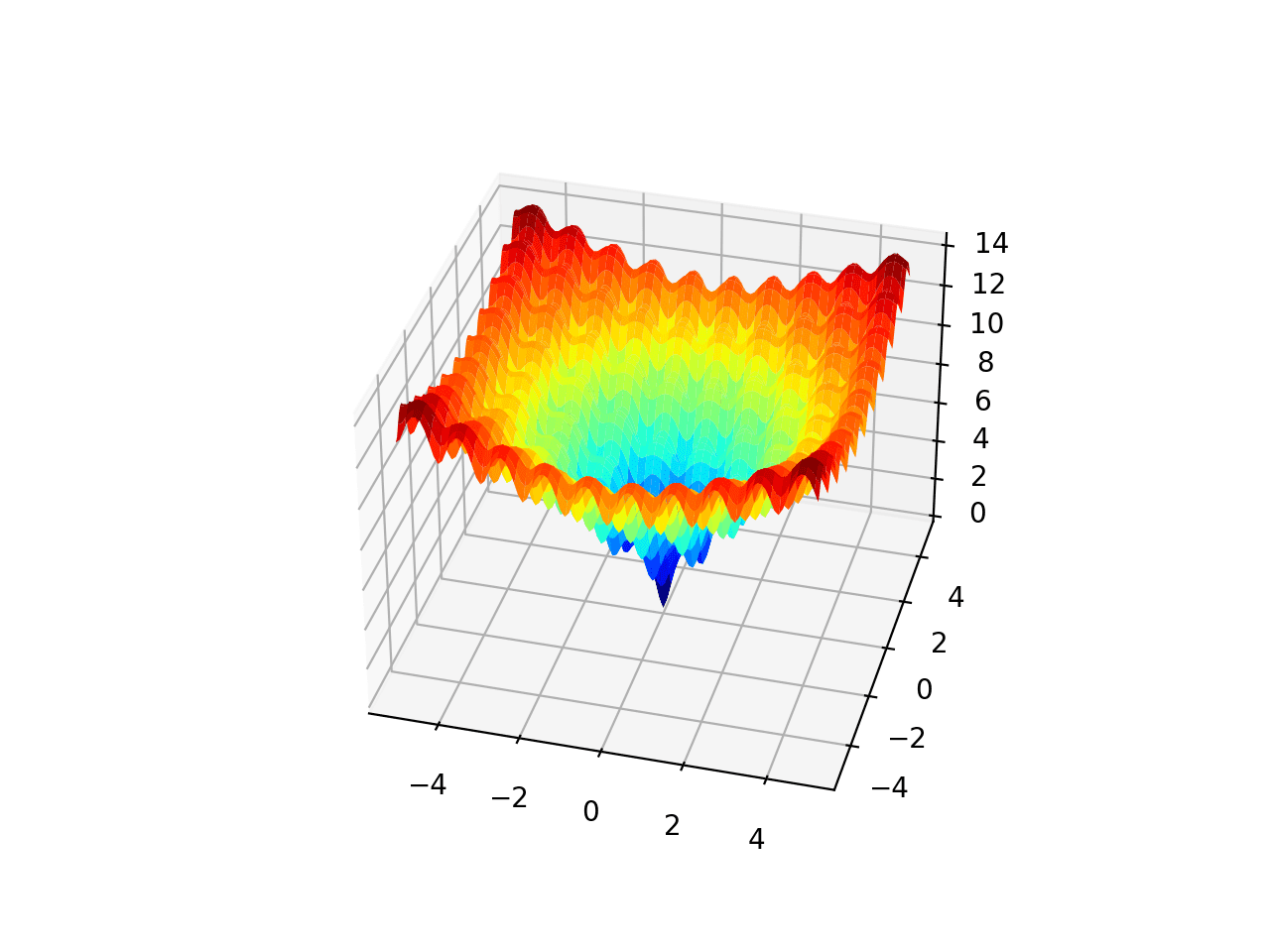
Ackley 多峰函数的三维曲面图
我们将使用它作为实现和比较简单随机爬山算法、带随机重启的随机爬山算法以及最终迭代局部搜索算法的基础。
我们预计随机爬山算法会很容易陷入局部最小值。我们预计带随机重启的随机爬山算法会找到许多局部最小值,并且我们预计迭代局部搜索在适当配置的情况下在该问题上的表现会优于这两种方法。
随机爬山算法
迭代局部搜索算法的核心是局部搜索,在本教程中,我们将为此使用随机爬山算法。
随机爬山算法首先生成一个随机起点和当前工作解决方案,然后生成当前工作解决方案的扰动版本,并在它们比当前工作解决方案更好时接受它们。
鉴于我们正在处理一个连续优化问题,解决方案是需要由目标函数评估的值向量,在这种情况下,是在-5到5之间有界的一维空间中的一个点。
我们可以通过以均匀概率分布采样搜索空间来生成一个随机点。例如
|
1 2 3 |
... # 在搜索空间中生成一个随机点 solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) |
我们可以通过高斯概率分布生成当前工作解决方案的扰动版本,其均值为当前解决方案中的值,标准差由一个超参数控制,该超参数控制搜索允许从当前工作解决方案中探索的距离。
我们将此超参数称为“step_size”(步长),例如
|
1 2 3 |
... # 生成当前工作解决方案的扰动版本 candidate = solution + randn(len(bounds)) * step_size |
重要的是,我们必须检查生成的解决方案是否在搜索空间内。
这可以通过一个名为 in_bounds() 的自定义函数来实现,该函数接受一个候选解决方案和搜索空间的边界,如果该点在搜索空间内则返回 True,否则返回 *False*。
|
1 2 3 4 5 6 7 8 |
# 检查一个点是否在搜索边界内 def in_bounds(point, bounds): # 枚举点的所有维度 for d in range(len(bounds)): # 检查此维度是否超出界限 if point[d] < bounds[d, 0] or point[d] > bounds[d, 1]: return False return True |
此函数随后可以在爬山过程中调用,以确认新点是否在搜索边界内,如果不在,则可以生成新点。
将这些结合起来,下面的 hillclimbing() 函数实现了随机爬山局部搜索算法。它将目标函数名称、问题边界、迭代次数和步长作为参数,并返回最佳解决方案及其评估值。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 爬山局部搜索算法 def hillclimbing(objective, bounds, n_iterations, step_size): # 生成初始点 solution = None while solution is None or not in_bounds(solution, bounds): solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 评估初始点 solution_eval = objective(solution) # 运行爬山算法 for i in range(n_iterations): # 迈出一步 candidate = None while candidate is None or not in_bounds(candidate, bounds): candidate = solution + randn(len(bounds)) * step_size # 评估候选点 candidte_eval = objective(candidate) # 检查是否应该保留新点 if candidte_eval <= solution_eval: # 存储新点 solution, solution_eval = candidate, candidte_eval # 报告进度 print('>%d f(%s) = %.5f' % (i, solution, solution_eval)) return [solution, solution_eval] |
我们可以对 Ackley 函数测试此算法。
我们将固定伪随机数生成器的种子,以确保每次运行代码时都能获得相同的结果。
该算法将运行 1,000 次迭代,步长为 0.05 个单位;这两个超参数都是经过一些试错后选择的。
在运行结束时,我们将报告找到的最佳解决方案。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
... # 播种伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-5.0, 5.0], [-5.0, 5.0]]) # 定义总迭代次数 n_iterations = 1000 # 定义最大步长 step_size = 0.05 # 执行爬山搜索 best, score = hillclimbing(objective, bounds, n_iterations, step_size) print('Done!') print('f(%s) = %f' % (best, score)) |
将这些结合起来,下面列出了将随机爬山算法应用于 Ackley 目标函数的完整示例。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
# 爬山搜索 Ackley 目标函数 from numpy import asarray from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy.random import randn from numpy.random import rand from numpy.random import seed # 目标函数 def objective(v): x, y = v return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # 检查一个点是否在搜索边界内 def in_bounds(point, bounds): # 枚举点的所有维度 for d in range(len(bounds)): # 检查此维度是否超出界限 if point[d] < bounds[d, 0] or point[d] > bounds[d, 1]: return False return True # 爬山局部搜索算法 def hillclimbing(objective, bounds, n_iterations, step_size): # 生成初始点 solution = None while solution is None or not in_bounds(solution, bounds): solution = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 评估初始点 solution_eval = objective(solution) # 运行爬山算法 for i in range(n_iterations): # 迈出一步 candidate = None while candidate is None or not in_bounds(candidate, bounds): candidate = solution + randn(len(bounds)) * step_size # 评估候选点 candidte_eval = objective(candidate) # 检查是否应该保留新点 if candidte_eval <= solution_eval: # 存储新点 solution, solution_eval = candidate, candidte_eval # 报告进度 print('>%d f(%s) = %.5f' % (i, solution, solution_eval)) return [solution, solution_eval] # 播种伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-5.0, 5.0], [-5.0, 5.0]]) # 定义总迭代次数 n_iterations = 1000 # 定义最大步长 step_size = 0.05 # 执行爬山搜索 best, score = hillclimbing(objective, bounds, n_iterations, step_size) print('Done!') print('f(%s) = %f' % (best, score)) |
运行示例将在目标函数上执行随机爬山搜索。将报告搜索过程中找到的每一次改进,并在搜索结束时报告最佳解决方案。
注意:由于算法或评估程序的随机性,或数值精度的差异,您的结果可能有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以在搜索过程中看到大约 13 次改进,最终解决方案约为 f(-0.981, 1.965),评估值为 5.381 左右,这与 f(0.0, 0.0) = 0 相差甚远。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
>0 f([-0.85618854 2.1495965 ]) = 6.46986 >1 f([-0.81291816 2.03451957]) = 6.07149 >5 f([-0.82903902 2.01531685]) = 5.93526 >7 f([-0.83766043 1.97142393]) = 5.82047 >9 f([-0.89269139 2.02866012]) = 5.68283 >12 f([-0.8988359 1.98187164]) = 5.55899 >13 f([-0.9122303 2.00838942]) = 5.55566 >14 f([-0.94681334 1.98855174]) = 5.43024 >15 f([-0.98117198 1.94629146]) = 5.39010 >23 f([-0.97516403 1.97715161]) = 5.38735 >39 f([-0.98628044 1.96711371]) = 5.38241 >362 f([-0.9808789 1.96858459]) = 5.38233 >629 f([-0.98102417 1.96555308]) = 5.38194 完成! f([-0.98102417 1.96555308]) = 5.381939 |
接下来,我们将修改该算法以执行随机重启,看看是否能获得更好的结果。
带随机重启的随机爬山算法
带随机重启的随机爬山算法涉及重复运行随机爬山算法并跟踪找到的最佳解决方案。
首先,让我们修改 hillclimbing() 函数,使其接受搜索的起始点,而不是随机生成它。这将在我们稍后实现迭代局部搜索算法时有所帮助。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 爬山局部搜索算法 def hillclimbing(objective, bounds, n_iterations, step_size, start_pt): # 存储初始点 solution = start_pt # 评估初始点 solution_eval = objective(solution) # 运行爬山算法 for i in range(n_iterations): # 迈出一步 candidate = None while candidate is None or not in_bounds(candidate, bounds): candidate = solution + randn(len(bounds)) * step_size # 评估候选点 candidte_eval = objective(candidate) # 检查是否应该保留新点 if candidte_eval <= solution_eval: # 存储新点 solution, solution_eval = candidate, candidte_eval return [solution, solution_eval] |
接下来,我们可以通过多次调用 hillclimbing() 函数来实现随机重启算法。
每次调用,我们都将为爬山搜索生成一个新的随机选择的起点。
|
1 2 3 4 5 6 7 |
... # 为搜索生成一个随机初始点 start_pt = None while start_pt is None or not in_bounds(start_pt, bounds): start_pt = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 执行随机爬山搜索 solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt) |
然后,我们可以检查结果,如果它比我们迄今为止搜索过的任何结果都好,就保留它。
|
1 2 3 4 5 |
... # 检查新最佳 if solution_eval < best_eval: 最佳, best_eval = solution, solution_eval print('重启 %d, 最佳: f(%s) = %.5f' % (n, best, best_eval)) |
总而言之,random_restarts() 函数实现了带有随机重启的随机爬山算法。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 带有随机重启的爬山算法 def random_restarts(objective, bounds, n_iter, step_size, n_restarts): best, best_eval = None, 1e+10 # 枚举重启 for n in range(n_restarts): # 为搜索生成一个随机初始点 start_pt = None while start_pt is None or not in_bounds(start_pt, bounds): start_pt = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 执行随机爬山搜索 solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt) # 检查是否为新的最佳 if solution_eval < best_eval: 最佳, best_eval = solution, solution_eval print('重启 %d, 最佳: f(%s) = %.5f' % (n, best, best_eval)) return [best, best_eval] |
然后,我们可以将此算法应用于 Ackley 目标函数。在这种情况下,我们将随机重启次数限制为 30 次,这是任意选择的。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
# 带有随机重启的 Ackley 目标函数的爬山搜索 from numpy import asarray from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy.random import randn from numpy.random import rand from numpy.random import seed # 目标函数 def objective(v): x, y = v return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # 检查一个点是否在搜索边界内 def in_bounds(point, bounds): # 枚举点的所有维度 for d in range(len(bounds)): # 检查此维度是否超出界限 if point[d] < bounds[d, 0] or point[d] > bounds[d, 1]: return False return True # 爬山局部搜索算法 def hillclimbing(objective, bounds, n_iterations, step_size, start_pt): # 存储初始点 solution = start_pt # 评估初始点 solution_eval = objective(solution) # 运行爬山算法 for i in range(n_iterations): # 迈出一步 candidate = None while candidate is None or not in_bounds(candidate, bounds): candidate = solution + randn(len(bounds)) * step_size # 评估候选点 candidte_eval = objective(candidate) # 检查是否应该保留新点 if candidte_eval <= solution_eval: # 存储新点 solution, solution_eval = candidate, candidte_eval return [solution, solution_eval] # 带有随机重启的爬山算法 def random_restarts(objective, bounds, n_iter, step_size, n_restarts): best, best_eval = None, 1e+10 # 枚举重启 for n in range(n_restarts): # 为搜索生成一个随机初始点 start_pt = None while start_pt is None or not in_bounds(start_pt, bounds): start_pt = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 执行随机爬山搜索 solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt) # 检查是否为新的最佳 if solution_eval < best_eval: 最佳, best_eval = solution, solution_eval print('重启 %d, 最佳: f(%s) = %.5f' % (n, best, best_eval)) return [best, best_eval] # 播种伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-5.0, 5.0], [-5.0, 5.0]]) # 定义总迭代次数 n_iter = 1000 # 定义最大步长 step_size = 0.05 # 总随机重启次数 n_restarts = 30 # 执行爬山搜索 best, score = random_restarts(objective, bounds, n_iter, step_size, n_restarts) print('Done!') print('f(%s) = %f' % (best, score)) |
运行示例将对 Ackley 目标函数执行带有随机重启的随机爬山搜索。每次发现改进的总体解决方案时,都会报告该解决方案,并在搜索结束时总结找到的最佳解决方案。
注意:由于算法或评估程序的随机性,或数值精度的差异,您的结果可能有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以在搜索过程中看到三次改进,并且找到的最佳解决方案大约是 f(0.002, 0.002),其评估值为 0.009 左右,这比单次运行爬山算法要好得多。
|
1 2 3 4 5 |
Restart 0, best: f([-0.98102417 1.96555308]) = 5.38194 Restart 2, best: f([1.96522236 0.98120013]) = 5.38191 Restart 4, best: f([0.00223194 0.00258853]) = 0.00998 完成! f([0.00223194 0.00258853]) = 0.009978 |
接下来,让我们看看如何实现迭代局部搜索算法。
迭代局部搜索算法
迭代局部搜索算法是带有随机重启的随机爬山算法的一个修改版本。
重要的区别在于,每次应用随机爬山算法的起始点是迄今为止找到的最佳点的扰动版本。
我们可以使用random_restarts() 函数作为起点来实现此算法。在每次重启迭代中,我们可以生成迄今为止找到的最佳解决方案的修改版本,而不是随机的起始点。
这可以通过使用步长超参数来实现,就像在随机爬山算法中使用的一样。在这种情况下,将使用更大的步长值,因为搜索空间需要更大的扰动。
|
1 2 3 4 5 |
... # 生成一个初始点,作为上一个最佳点的扰动版本 start_pt = None while start_pt is None or not in_bounds(start_pt, bounds): start_pt = best + randn(len(bounds)) * p_size |
总而言之,下面定义了iterated_local_search() 函数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
# 迭代局部搜索算法 def iterated_local_search(objective, bounds, n_iter, step_size, n_restarts, p_size): # 定义起始点 best = None while best is None or not in_bounds(best, bounds): best = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 评估当前最佳点 best_eval = objective(best) # 枚举重启 for n in range(n_restarts): # 生成一个初始点,作为上一个最佳点的扰动版本 start_pt = None while start_pt is None or not in_bounds(start_pt, bounds): start_pt = best + randn(len(bounds)) * p_size # 执行随机爬山搜索 solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt) # 检查是否为新的最佳 if solution_eval < best_eval: 最佳, best_eval = solution, solution_eval print('重启 %d, 最佳: f(%s) = %.5f' % (n, best, best_eval)) return [best, best_eval] |
然后,我们可以将该算法应用于 Ackley 目标函数。在这种情况下,我们将为随机重启使用更大的步长值 1.0,这是经过一些试错后选择的。
完整的示例如下所示。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
# Ackley 目标函数的迭代局部搜索 from numpy import asarray from numpy import exp from numpy import sqrt from numpy import cos from numpy import e from numpy import pi from numpy.random import randn from numpy.random import rand from numpy.random import seed # 目标函数 def objective(v): x, y = v return -20.0 * exp(-0.2 * sqrt(0.5 * (x**2 + y**2))) - exp(0.5 * (cos(2 * pi * x) + cos(2 * pi * y))) + e + 20 # 检查一个点是否在搜索边界内 def in_bounds(point, bounds): # 枚举点的所有维度 for d in range(len(bounds)): # 检查此维度是否超出界限 if point[d] < bounds[d, 0] or point[d] > bounds[d, 1]: return False return True # 爬山局部搜索算法 def hillclimbing(objective, bounds, n_iterations, step_size, start_pt): # 存储初始点 solution = start_pt # 评估初始点 solution_eval = objective(solution) # 运行爬山算法 for i in range(n_iterations): # 迈出一步 candidate = None while candidate is None or not in_bounds(candidate, bounds): candidate = solution + randn(len(bounds)) * step_size # 评估候选点 candidte_eval = objective(candidate) # 检查是否应该保留新点 if candidte_eval <= solution_eval: # 存储新点 solution, solution_eval = candidate, candidte_eval return [solution, solution_eval] # 迭代局部搜索算法 def iterated_local_search(objective, bounds, n_iter, step_size, n_restarts, p_size): # 定义起始点 best = None while best is None or not in_bounds(best, bounds): best = bounds[:, 0] + rand(len(bounds)) * (bounds[:, 1] - bounds[:, 0]) # 评估当前最佳点 best_eval = objective(best) # 枚举重启 for n in range(n_restarts): # 生成一个初始点,作为上一个最佳点的扰动版本 start_pt = None while start_pt is None or not in_bounds(start_pt, bounds): start_pt = best + randn(len(bounds)) * p_size # 执行随机爬山搜索 solution, solution_eval = hillclimbing(objective, bounds, n_iter, step_size, start_pt) # 检查是否为新的最佳 if solution_eval < best_eval: 最佳, best_eval = solution, solution_eval print('重启 %d, 最佳: f(%s) = %.5f' % (n, best, best_eval)) return [best, best_eval] # 播种伪随机数生成器 seed(1) # 定义输入范围 bounds = asarray([[-5.0, 5.0], [-5.0, 5.0]]) # 定义总迭代次数 n_iter = 1000 # 定义最大步长 s_size = 0.05 # 总随机重启次数 n_restarts = 30 # 扰动步长 p_size = 1.0 # 执行爬山搜索 best, score = iterated_local_search(objective, bounds, n_iter, s_size, n_restarts, p_size) print('Done!') print('f(%s) = %f' % (best, score)) |
运行示例将执行 Ackley 目标函数的迭代局部搜索。
每次发现改进的总体解决方案时,都会报告该解决方案,并在运行结束时总结搜索找到的最终最佳解决方案。
注意:由于算法或评估程序的随机性,或数值精度的差异,您的结果可能有所不同。考虑多次运行示例并比较平均结果。
在这种情况下,我们可以在搜索过程中看到四次改进,并且找到的最佳解决方案是两个非常小的接近零的输入,其评估值约为 0.0003,这优于单次爬山运行或带重启的爬山运行。
|
1 2 3 4 5 6 |
Restart 0, best: f([-0.96775653 0.96853129]) = 3.57447 Restart 3, best: f([-4.50618519e-04 9.51020713e-01]) = 2.57996 Restart 5, best: f([ 0.00137423 -0.00047059]) = 0.00416 Restart 22, best: f([ 1.16431936e-04 -3.31358206e-06]) = 0.00033 完成! f([ 1.16431936e-04 -3.31358206e-06]) = 0.000330 |
进一步阅读
如果您想深入了解,本节提供了更多关于该主题的资源。
书籍
- 元启发式算法精要, 2011.
- Handbook of Metaheuristics, 3rd edition 2019.
文章
总结
在本教程中,您学习了如何从头开始实现迭代局部搜索算法。
具体来说,你学到了:
- 迭代局部搜索是一种随机全局搜索优化算法,它是随机爬山法加随机重启的更智能版本。
- 如何从头开始实现带有随机重启的随机爬山算法。
- 如何实现迭代局部搜索算法并将其应用于非线性目标函数。
你有什么问题吗?
在下面的评论中提出你的问题,我会尽力回答。





哈喽 杰森,
我有一个关于 Facebook Prophet 的问题。
是否可以使用 Prophet 来预测工作(即有多少工作岗位可用)?(例如)明年(给定历史数据框)。
同样,预测明年(或未来几年)有多少人会获得特定学位是否也可能?
有什么建议吗?
谢谢
当然可以。
试试看吧。
你好 Jason,
我还有最后一个问题,
我看到(在您的示例中)您使用了 from sklearn.metrics import mean_absolute_error 来获取 MAE,更普遍地说,我看到有很多
示例使用 sklearn.metrics 来获取指标。
但是我也在 https://fbdocs.cn/prophet/docs/diagnostics.html#cross-validation 上看到,可以使用 prophet.diagnostics 来获取指标(即 mse、rmse、mae)。
使用 sklearn.metrics 和 prophet.diagnostics 有什么区别?哪种更有效?
谢谢,
Marco
我预计它们会计算相同的东西。
选择一个指标,然后评估您的模型。
很有用的帖子,迭代局部搜索算法肯定能提高性能。谢谢
不客气。
我非常感谢您这篇清晰而有用的帖子!