在之前的教程中，我们探讨了将 k-means 聚类算法作为一种无监督机器学习技术，该技术旨在将相似数据分组到不同的簇中，以发现数据中的模式。
到目前为止，我们已经看到了如何将 k-means 聚类算法应用于包含不同簇的简单二维数据集以及图像颜色量化问题。
在本教程中，您将学习如何应用 OpenCV 的 k-means 聚类算法进行图像分类。
完成本教程后，您将了解：
- 为什么 k-means 聚类可以应用于图像分类。
- 将 k-means 聚类算法应用于 OpenCV 中的数字数据集进行图像分类。
- 如何减少由于倾斜导致的数字变化，以提高 k-means 聚类算法在图像分类中的准确性。
通过我的书《OpenCV 机器学习》启动您的项目。它提供了带有可用代码的自学教程。
让我们开始吧。
使用 OpenCV 进行图像分类的 K-均值聚类
图片由 Jeremy Thomas 拍摄，保留部分权利。
教程概述
本教程分为两部分；它们是
- 作为无监督机器学习技术的 k-Means 聚类回顾
- 将 k-Means 聚类应用于图像分类
作为无监督机器学习技术的 k-Means 聚类回顾
在之前的教程中，我们介绍了 k-means 聚类作为一种无监督学习技术。
我们已经看到，这种技术涉及将数据自动分组到不同的组（或簇）中，其中每个簇内的数据彼此相似，但与其他簇中的数据不同。它旨在发现聚类之前可能不明显的数据模式。
我们已将 k-means 聚类算法应用于包含五个簇的简单二维数据集，以相应地标记属于每个簇的数据点，随后应用于颜色量化任务，我们使用此算法来减少表示图像的不同颜色的数量。
在本教程中，我们将再次利用 k-means 聚类的强大功能，通过将其应用于图像分类任务来发现数据中的隐藏结构。
对于此类任务，我们将使用之前教程中介绍的 OpenCV 数字数据集，我们将尝试以无监督方式（即不使用真实标签信息）对相似手写数字图像进行分组。
将 k-Means 聚类应用于图像分类
我们首先需要加载 OpenCV 数字图像，将其分成许多子图像，这些子图像包含从 0 到 9 的手写数字，并创建相应的真实标签，这将使我们能够稍后量化 k-means 聚类算法的性能。
|
1 2 3 4 5 |
# 加载数字图像并将其分成子图像 img, sub_imgs = split_images('Images/digits.png', 20) # 创建真实标签 imgs, labels_true, _, _ = split_data(20, sub_imgs, 1.0) |
返回的 imgs 数组包含 5,000 个子图像，按行组织成扁平的一维向量形式，每个向量包含 400 个像素。
|
1 2 |
# 检查“imgs”数组的形状 print(imgs.shape) |
|
1 |
(5000, 400) |
随后可以为 k-means 算法提供与我们用于颜色量化示例的输入参数相同的输入参数，唯一的例外是我们需要将 imgs 数组作为输入数据传递，并且我们将把 K 簇的值设置为 10（即我们可用的数字数量）。
|
1 2 3 4 5 |
# 指定算法的终止条件 criteria = (TERM_CRITERIA_MAX_ITER + TERM_CRITERIA_EPS, 10, 1.0) # 对图像数据运行 k-means 聚类算法 compactness, clusters, centers = kmeans(data=imgs.astype(float32), K=10, bestLabels=None, criteria=criteria, attempts=10, flags=KMEANS_RANDOM_CENTERS) |
kmeans 函数返回一个 centers 数组，该数组应包含每个簇的代表性图像。返回的 centers 数组的形状为 10×400，这意味着我们需要先将其重塑回 20×20 像素图像，然后才能进行可视化。
|
1 2 3 4 5 6 7 8 9 10 |
# 将数组重塑为 20x20 图像 imgs_centers = centers.reshape(-1, 20, 20) # 可视化聚类中心 fig, ax = subplots(2, 5) for i, center in zip(ax.flat, imgs_centers): i.imshow(center) show() |
聚类中心的代表性图像如下所示：
k-Means 算法发现的聚类中心的代表性图像
值得注意的是，k-means 算法生成的聚类中心确实与 OpenCV 数字数据集中包含的手写数字相似。
您可能还会注意到，聚类中心的顺序不一定遵循数字 0 到 9 的顺序。这是因为 k-means 算法可以将相似数据聚类在一起，但对其顺序没有概念。然而，这在比较预测标签和真实标签时也会产生问题。这是因为真实标签已生成以对应图像中显示的数字。但是，k-means 算法生成的聚类标签不一定遵循相同的约定。为了解决这个问题，我们需要*重新排序*聚类标签。
|
1 2 3 4 5 6 7 8 9 |
# 找到的聚类标签 labels = array([2, 0, 7, 5, 1, 4, 6, 9, 3, 8]) labels_pred = zeros(labels_true.shape, dtype='int') # 重新排序聚类标签 for i in range(10): mask = clusters.ravel() == i labels_pred[mask] = labels[i] |
现在我们准备好计算算法的准确性，通过查找与真实值对应的预测标签的百分比。
|
1 2 3 4 5 |
# 计算算法的准确性 accuracy = (sum(labels_true == labels_pred) / labels_true.size) * 100 # 打印准确性 print("准确性: {0:.2f}%".format(accuracy[0])) |
|
1 |
准确性：54.80% |
到此为止的完整代码如下：
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
from cv2 import kmeans, TERM_CRITERIA_MAX_ITER, TERM_CRITERIA_EPS, KMEANS_RANDOM_CENTERS from numpy import float32, array, zeros from matplotlib.pyplot import show, imshow, subplots from digits_dataset import split_images, split_data # 加载数字图像并将其分成子图像 img, sub_imgs = split_images('Images/digits.png', 20) # 创建真实标签 imgs, labels_true, _, _ = split_data(20, sub_imgs, 1.0) # 检查“imgs”数组的形状 print(imgs.shape) # 指定算法的终止条件 criteria = (TERM_CRITERIA_MAX_ITER + TERM_CRITERIA_EPS, 10, 1.0) # 对图像数据运行 k-means 聚类算法 compactness, clusters, centers = kmeans(data=imgs.astype(float32), K=10, bestLabels=None, criteria=criteria, attempts=10, flags=KMEANS_RANDOM_CENTERS) # 将数组重塑为 20x20 图像 imgs_centers = centers.reshape(-1, 20, 20) # 可视化聚类中心 fig, ax = subplots(2, 5) for i, center in zip(ax.flat, imgs_centers): i.imshow(center) show() # 聚类标签 labels = array([2, 0, 7, 5, 1, 4, 6, 9, 3, 8]) labels_pred = zeros(labels_true.shape, dtype='int') # 重新排序聚类标签 for i in range(10): mask = clusters.ravel() == i labels_pred[mask] = labels[i] # 计算算法的准确性 accuracy = (sum(labels_true == labels_pred) / labels_true.size) * 100 |
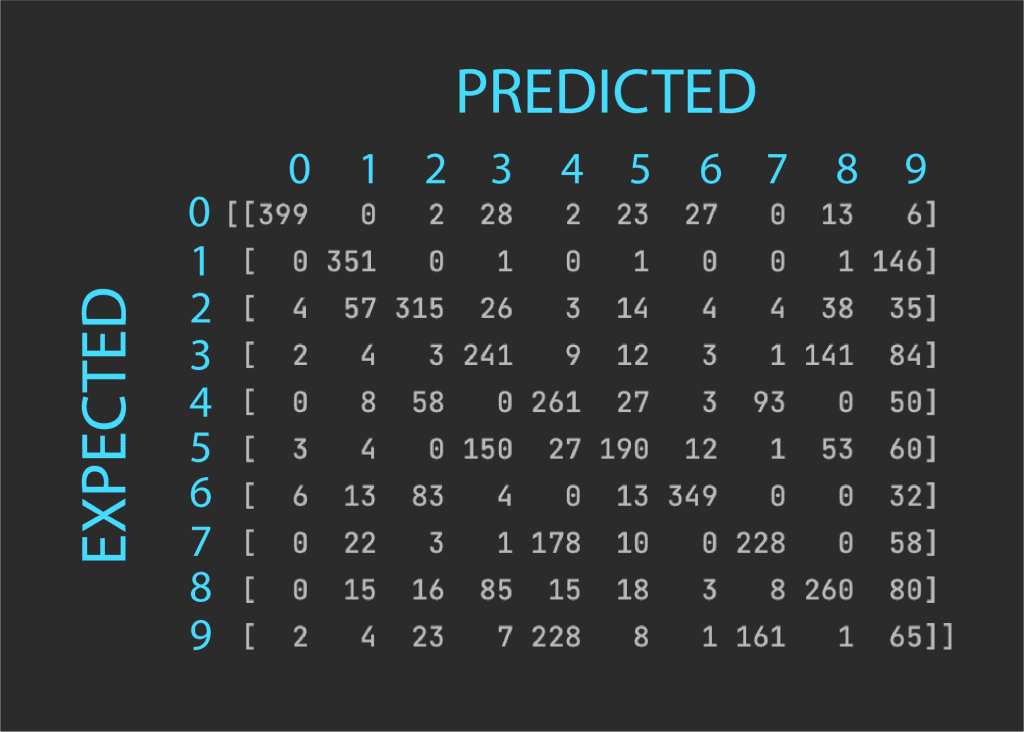
现在，让我们打印出混淆矩阵，以更深入地了解哪些数字被误认为是其他数字。
|
1 2 3 4 |
from sklearn.metrics import confusion_matrix # 打印混淆矩阵 print(confusion_matrix(labels_true, labels_pred)) |
|
1 2 3 4 5 6 7 8 9 10 |
[[399 0 2 28 2 23 27 0 13 6] [ 0 351 0 1 0 1 0 0 1 146] [ 4 57 315 26 3 14 4 4 38 35] [ 2 4 3 241 9 12 3 1 141 84] [ 0 8 58 0 261 27 3 93 0 50] [ 3 4 0 150 27 190 12 1 53 60] [ 6 13 83 4 0 13 349 0 0 32] [ 0 22 3 1 178 10 0 228 0 58] [ 0 15 16 85 15 18 3 8 260 80] [ 2 4 23 7 228 8 1 161 1 65]] |
混淆矩阵应按以下方式解释：
解释混淆矩阵
对角线上的值表示正确预测的数字数量，而对角线外的值表示每个数字的错误分类。我们可以看到，性能最好的数字是*0*，对角线值最高，误分类非常少。性能最差的数字是*9*，因为它与许多其他数字（主要是 4）的误分类数量最多。我们还可以看到，*7* 主要被误认为是 4，而*8* 主要被误认为是*3*。
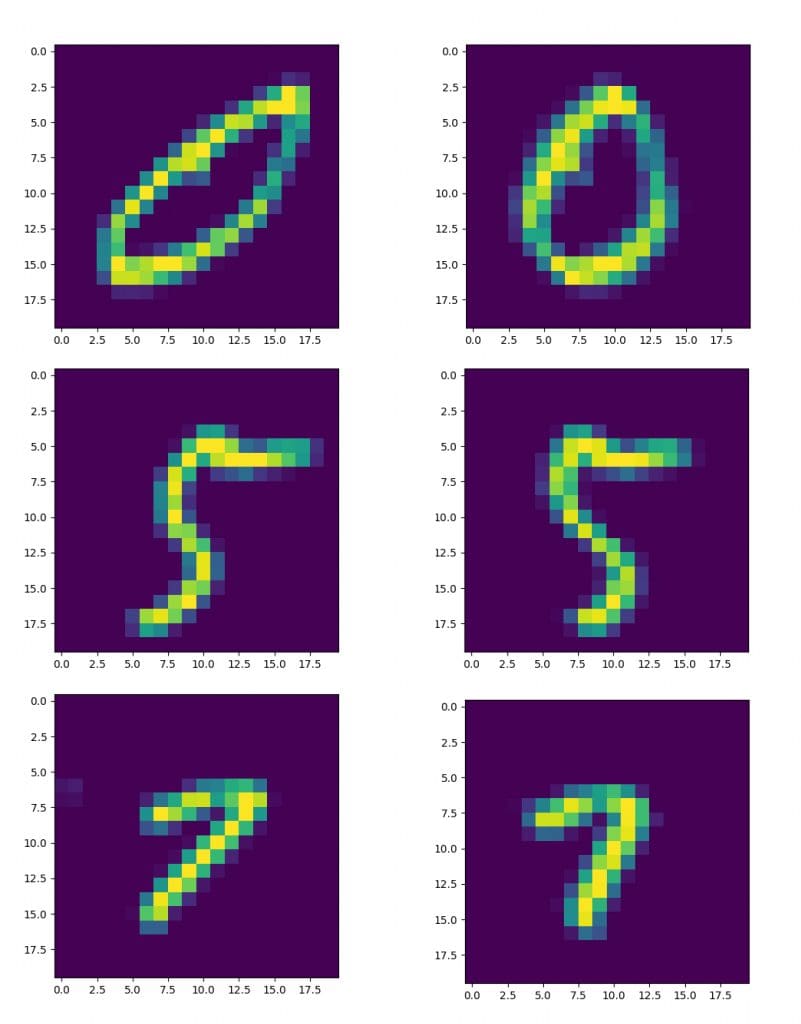
这些结果并不令人意外，因为如果我们查看数据集中的数字，我们会发现几个不同数字的曲线和倾斜导致它们彼此相似。为了研究减少数字变化的效果，让我们引入一个函数 deskew_image()，它根据从图像矩计算的倾斜度量对图像应用仿射变换。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
from cv2 import (kmeans, TERM_CRITERIA_MAX_ITER, TERM_CRITERIA_EPS, KMEANS_RANDOM_CENTERS, moments, warpAffine, INTER_CUBIC, WARP_INVERSE_MAP) from numpy import float32, array, zeros from matplotlib.pyplot import show, imshow, subplots from digits_dataset import split_images, split_data from sklearn.metrics import confusion_matrix # 加载数字图像并将其分成子图像 img, sub_imgs = split_images('Images/digits.png', 20) # 创建真实标签 imgs, labels_true, _, _ = split_data(20, sub_imgs, 1.0) # 消除所有数据集图像的倾斜 imgs_deskewed = zeros(imgs.shape) for i in range(imgs_deskewed.shape[0]): new = deskew_image(imgs[i, :].reshape(20, 20)) imgs_deskewed[i, :] = new.reshape(1, -1) # 指定算法的终止条件 criteria = (TERM_CRITERIA_MAX_ITER + TERM_CRITERIA_EPS, 10, 1.0) # 对去倾斜的图像数据运行 k-means 聚类算法 compactness, clusters, centers = kmeans(data=imgs_deskewed.astype(float32), K=10, bestLabels=None, criteria=criteria, attempts=10, flags=KMEANS_RANDOM_CENTERS) # 将数组重塑为 20x20 图像 imgs_centers = centers.reshape(-1, 20, 20) # 可视化聚类中心 fig, ax = subplots(2, 5) for i, center in zip(ax.flat, imgs_centers): i.imshow(center) show() # 聚类标签 labels = array([9, 5, 6, 4, 2, 3, 7, 8, 1, 0]) labels_pred = zeros(labels_true.shape, dtype='int') # 重新排序聚类标签 for i in range(10): mask = clusters.ravel() == i labels_pred[mask] = labels[i] # 计算算法的准确性 accuracy = (sum(labels_true == labels_pred) / labels_true.size) * 100 # 打印准确性 print("准确性: {0:.2f}%".format(accuracy[0])) # 打印混淆矩阵 print(confusion_matrix(labels_true, labels_pred)) def deskew_image(img): # 计算图像矩 img_moments = moments(img) # 矩 m02 表示像素强度沿垂直轴的分布程度 if abs(img_moments['mu02']) > 1e-2: # 计算图像倾斜 img_skew = (img_moments['mu11'] / img_moments['mu02']) # 生成变换矩阵 # (我们在这里通过使用一个 # 缩放因子 0.6 稍微调整了倾斜引起的垂直平移近似值，因为我们凭经验发现这个值对于此应用程序效果更好) m = float32([[1, img_skew, -0.6 * img.shape[0] * img_skew], [0, 1, 0]]) # 将变换矩阵应用于图像 img_deskew = warpAffine(src=img, M=m, dsize=img.shape, flags=INTER_CUBIC | WARP_INVERSE_MAP) else: # 如果像素强度的垂直分布很小，则返回原始图像的副本 img_deskew = img.copy() return img_deskew |
|
1 2 3 4 5 6 7 8 9 10 11 12 |
准确性：70.92% [[400 1 5 1 2 58 27 1 1 4] [ 0 490 1 1 0 1 2 0 1 4] [ 5 27 379 28 10 2 3 4 30 12] [ 1 27 7 360 7 44 2 9 31 12] [ 1 29 3 0 225 0 13 1 0 228] [ 5 12 1 14 24 270 11 0 7 156] [ 8 40 6 0 6 8 431 0 0 1] [ 0 39 2 0 48 0 0 377 4 30] [ 2 32 3 21 8 77 2 0 332 23] [ 5 13 1 5 158 5 2 28 1 282]] |
去倾斜功能对某些数字有以下影响：
第一列显示原始数据集图像，第二列显示经过倾斜校正的图像
值得注意的是，当数字的倾斜度降低时，准确性提高到 70.92%，同时聚类中心更能代表数据集中的数字。
k-Means 算法发现的聚类中心的代表性图像
该结果表明，倾斜是导致我们在未进行校正时准确性下降的一个重要因素。
您还能想到哪些可以提高准确性的预处理步骤？
想开始学习 OpenCV 机器学习吗？
立即参加我的免费电子邮件速成课程（附示例代码）。
点击注册，同时获得该课程的免费PDF电子书版本。
进一步阅读
如果您想深入了解此主题，本节提供了更多资源。
书籍
- OpenCV 机器学习, 2017.
- 使用 Python 精通 OpenCV 4, 2019.
网站
- 10 种使用 Python 的聚类算法，https://machinelearning.org.cn/clustering-algorithms-with-python/
- OpenCV 中的 K-Means 聚类，https://docs.opencv.ac.cn/3.4/d1/d5c/tutorial_py_kmeans_opencv.html
- k-means 聚类，https://en.wikipedia.org/wiki/K-means_clustering
总结
在本教程中，您学习了如何将 OpenCV 的 k-means 聚类算法应用于图像分类。
具体来说，你学到了：
- 为什么 k-means 聚类可以应用于图像分类。
- 将 k-means 聚类算法应用于 OpenCV 中的数字数据集进行图像分类。
- 如何减少由于倾斜导致的数字变化，以提高 k-means 聚类算法在图像分类中的准确性。
你有什么问题吗？
在下面的评论中提出您的问题，我将尽力回答。
开始使用 OpenCV 进行机器学习！
学习如何在图像处理项目中使用机器学习技术
...以高级方式使用 OpenCV，超越像素处理
在我的新电子书中探索如何实现
OpenCV 机器学习
它提供带有所有可用 Python 代码的自学教程，让您从新手成长为专家。它为您提供了
逻辑回归、随机森林、支持向量机、k 均值聚类、神经网络等等……所有这些都使用 OpenCV 中的机器学习模块
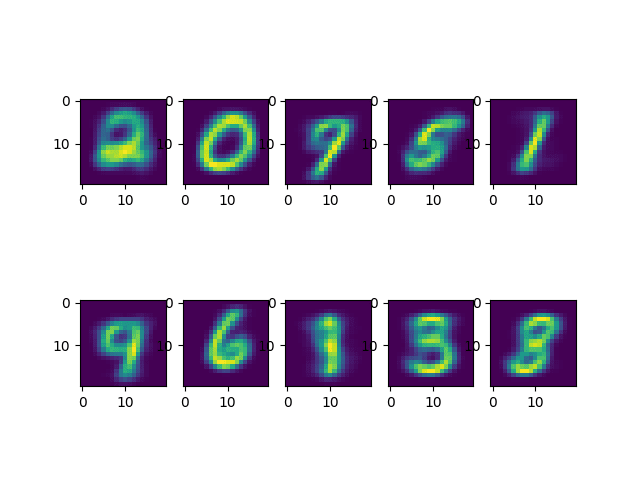
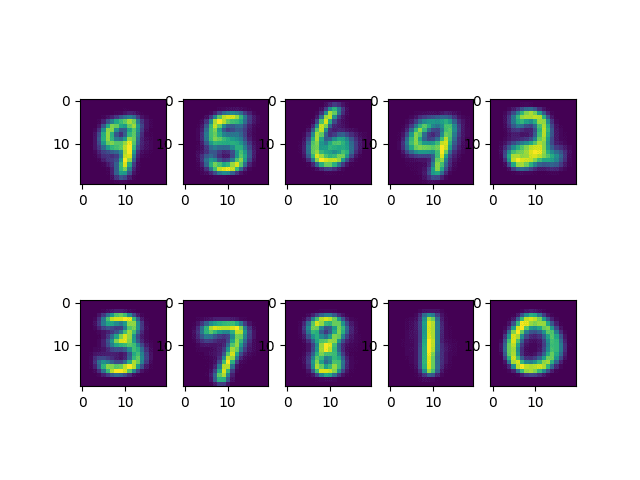
对于此类任务，我们将使用“之前的教程”中介绍的 OpenCV 数字数据集。
“之前的教程”中嵌入的链接无效。
感谢您的反馈，shincheng！