
Python 机器学习中的核方法
图片来源:编辑 | Midjourney
引言
核方法是一类强大的机器学习算法,它允许我们对数据进行复杂的非线性变换,而无需显式计算变换后的特征空间。当处理高维数据或特征之间的关系是非线性时,这些方法特别有用。
核方法依赖于**核函数**的概念,核函数在不显式执行变换的情况下计算两个向量在变换后的特征空间中的点积。这被称为**核技巧**。核技巧允许我们高效地在高维空间中工作,从而使解决否则在计算上不可行的问题成为可能。
我们为什么要使用核方法?
- 非线性:核方法可以通过将数据映射到可以应用线性方法的更高维空间来捕获数据中的非线性关系
- 效率:通过使用核技巧,我们避免了显式转换数据的计算成本
- 多功能性:核方法可以应用于各种任务,包括分类、回归和降维
在本教程中,我们将探讨核方法的基础知识,重点关注以下主题
- **核技巧**:理解核方法的数学基础
- **支持向量机 (SVM)**:使用核函数进行分类的 SVM
- **核 PCA**:使用核 PCA 进行降维
- **实际示例**:在 Python 中实现 SVM 和核 PCA
核技巧
核技巧是一种数学技术,它允许我们在不显式将向量映射到该空间的情况下,计算高维空间中两个向量的点积。当向高维空间的变换计算成本很高甚至无法直接计算时,这特别有用。
**核函数** \( K(x, y) \) 计算变换后的特征空间中两个向量 \( x \) 和 \( y \) 的点积
\[
K(x, y) = \phi(x) \cdot \phi(y)
\]
这里,\( \phi(x) \) 是从原始特征空间到更高维空间的映射。核函数允许我们直接在原始空间中计算这个点积。
常见的核函数包括
- **线性核**:\( K(x, y) = x \cdot y \)
- **多项式核**:\( K(x, y) = (x \cdot y + c)^d \)
- **径向基函数 (RBF) 核**:\( K(x, y) = \exp(-\gamma \|x – y\|^2) \)
核函数的选择取决于手头的问题。例如,当数据不是线性可分时,通常使用 RBF 核。
带核函数的支持向量机 (SVM)
**支持向量机 (SVM)** 是一种用于分类和回归任务的监督学习算法。SVM 的目标是找到能够最好地将数据分离成不同类别的超平面。当数据不是线性可分时,我们可以使用核函数将数据映射到更高维空间,使其变得可分。
让我们使用 **scikit-learn** 库实现一个核 SVM。我们将使用著名的 Iris 数据集进行分类。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn.svm import SVC from sklearn.metrics import accuracy_score # 加载 Iris 数据集 iris = datasets.load_iris() X = iris.data[:, :2] # 我们只使用前两个特征进行可视化 y = iris.target # 将数据拆分为训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # 使用 RBF 核创建 SVM 分类器 svm = SVC(kernel='rbf', gamma=0.7, C=1.0) # 训练 SVM svm.fit(X_train, y_train) # 进行预测 y_pred = svm.predict(X_test) # 评估模型 accuracy = accuracy_score(y_test, y_pred) print(f"Accuracy: {accuracy:.2f}") # 绘制决策边界 def plot_decision_boundary(X, y, model): h = .02 # 网格中的步长 x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1 y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) Z = model.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.contourf(xx, yy, Z, alpha=0.8) plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o') plt.xlabel('Sepal length') plt.ylabel('Sepal width') plt.title('SVM Decision Boundary with RBF Kernel') plt.show() plot_decision_boundary(X_train, y_train, svm) |
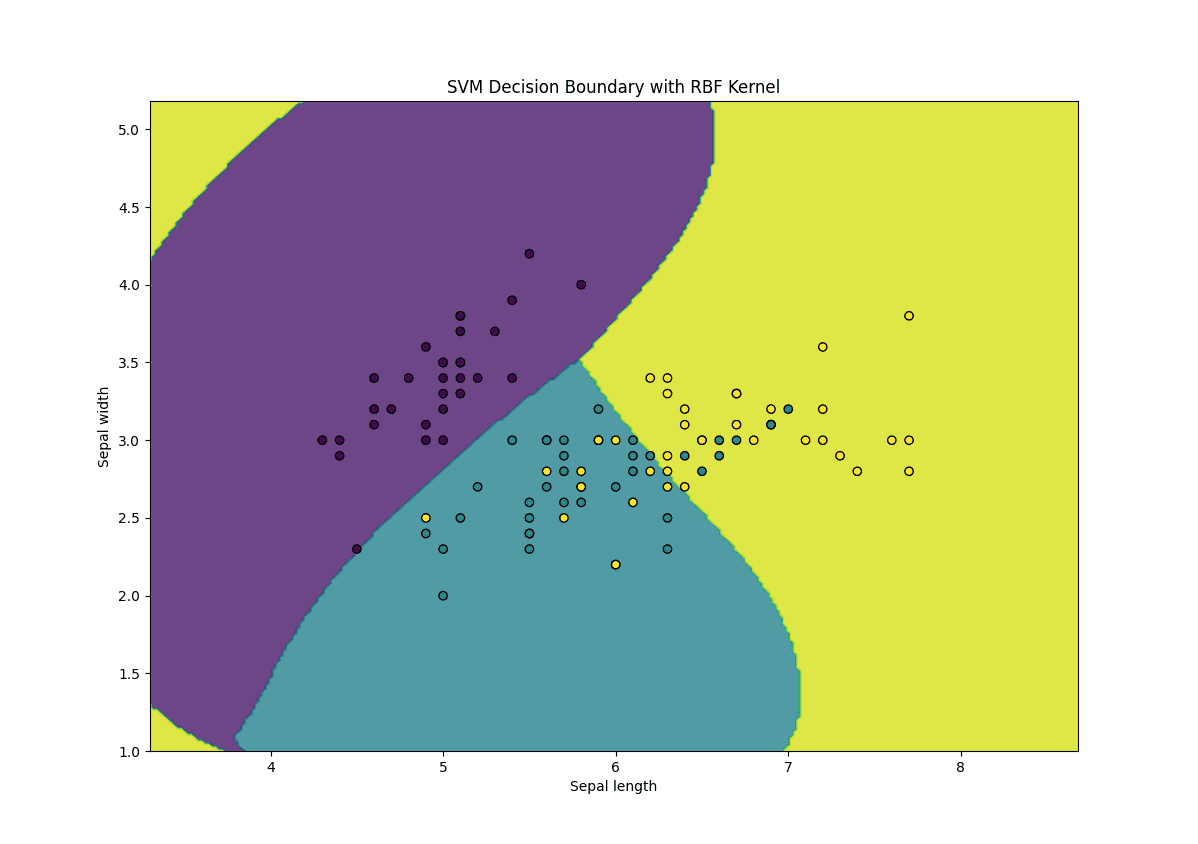
以下是上述代码的解释
- **核选择**:我们使用 RBF 核(**kernel='rbf'**)来处理非线性数据
- **Gamma 参数**:**gamma** 参数控制每个训练示例的影响,其中 gamma 值越高,决策边界越复杂
- **C 参数**:**C** 参数控制实现低训练误差和低测试误差之间的权衡
核主成分分析 (Kernel PCA)
**主成分分析 (PCA)** 是一种降维技术,它将数据投影到较低维空间,同时尽可能多地保留方差。然而,标准 PCA 仅限于线性变换。**核 PCA** 通过使用核函数执行非线性降维来扩展 PCA。
让我们使用 **scikit-learn** 实现核 PCA,并将其应用于非线性数据集。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
from sklearn.decomposition import KernelPCA from sklearn.datasets import make_moons # 生成非线性数据集 X, y = make_moons(n_samples=100, noise=0.1, random_state=42) # 应用带有 RBF 核的核 PCA kpca = KernelPCA(kernel='rbf', gamma=15, n_components=2) X_kpca = kpca.fit_transform(X) # 绘制原始数据和转换后的数据 plt.figure(figsize=(12, 5)) plt.subplot(1, 2, 1) plt.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o') plt.title('Original Data') plt.subplot(1, 2, 2) plt.scatter(X_kpca[:, 0], X_kpca[:, 1], c=y, edgecolors='k', marker='o') plt.title('Kernel PCA Transformed Data') plt.show() |
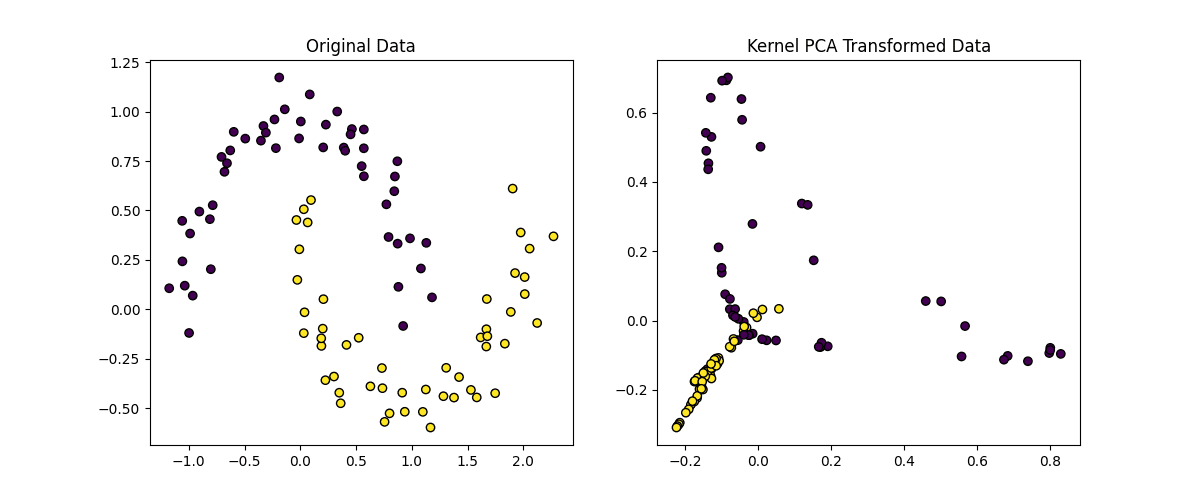
以下是上述代码的解释
- **核选择**:我们使用 RBF 核(**kernel='rbf'**)来捕获数据中的非线性关系
- **Gamma 参数**:**gamma** 参数控制每个数据点的影响,其中 gamma 值越高,转换越复杂
- **组件数量**:我们将数据降维到 2 维(**n_components=2**)用于可视化
从零开始实现核技巧
快速提醒:核技巧允许我们在不显式将向量映射到高维空间的情况下计算高维空间中两个向量的点积。这是通过**核函数**直接在变换后的空间中计算点积来实现的。
让我们从零开始实现**径向基函数 (RBF) 核**,并使用它来计算数据集的核矩阵。RBF 核定义为
\[
K(x, y) = \exp\left(-\gamma \|x – y\|^2\right)
\]
其中
- \( x \) 和 \( y \) 是数据点
- \( \gamma \) 是一个控制每个数据点影响的参数,我们将其称为 **gamma**
- \( \|x – y\|^2 \) 是 \( x \) 和 \( y \) 之间的平方欧几里得距离
第 1 步:定义 RBF 核函数
让我们从 RBF 核函数开始。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import numpy as np def rbf_kernel(x1, x2, gamma=1.0): """ 计算两个向量 x1 和 x2 之间的 RBF 核。 参数 - x1, x2:输入向量。 - gamma:核参数。 返回 - 核值(标量)。 """ squared_distance = np.sum((x1 - x2) ** 2) return np.exp(-gamma * squared_distance) |
第 2 步:计算核矩阵
**核矩阵**(或 Gram 矩阵)是一个矩阵,其中每个元素 \( K_{ij} \) 是第 \( i \) 个和第 \( j \) 个数据点之间的核值。让我们计算数据集的核矩阵。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
def compute_kernel_matrix(X, kernel_function, gamma=1.0): """ 使用给定核函数计算数据集 X 的核矩阵。 参数 - X:输入数据集 (n_samples, n_features)。 - kernel_function:要使用的核函数。 - gamma:核参数。 返回 - 核矩阵 (n_samples, n_samples)。 """ n_samples = X.shape[0] kernel_matrix = np.zeros((n_samples, n_samples)) for i in range(n_samples): for j in range(n_samples): kernel_matrix[i, j] = kernel_function(X[i], X[j], gamma) return kernel_matrix |
第 3 步:将核技巧应用于简单数据集
让我们生成一个简单的 2D 数据集,并使用 RBF 核计算其核矩阵。
|
1 2 3 4 5 6 7 8 9 |
# 生成一个简单的 2D 数据集 X = np.array([[1, 2], [2, 3], [3, 4], [4, 5]]) # 使用 RBF 核计算核矩阵 gamma = 0.1 kernel_matrix = compute_kernel_matrix(X, rbf_kernel, gamma) print("Kernel Matrix (RBF Kernel):") print(kernel_matrix) |
核矩阵将如下所示
|
1 2 3 4 5 |
Kernel Matrix (RBF Kernel): [[1. 0.81873075 0.44932896 0.16529889] [0.81873075 1. 0.81873075 0.44932896] [0.44932896 0.81873075 1. 0.81873075] [0.16529889 0.44932896 0.81873075 1. ]] |
第 4 步:在核化算法中使用核矩阵
现在我们有了核矩阵,我们可以在核化算法中使用它,例如核 SVM。然而,从零开始实现一个完整的核 SVM 是复杂的,所以我们将使用核矩阵来演示这个概念。
例如,在核 SVM 中,新数据点 \( x \) 的决策函数计算为
\[
f(x) = \sum_{i=1}^n \alpha_i y_i K(x, x_i) + b
\]
其中
- \( \alpha_i \) 是拉格朗日乘数(在训练期间学习)。
- \( y_i \) 是训练数据的标签。
- \( K(x, x_i) \) 是 \( x \) 和第 \( i \) 个训练点之间的核值。
- \( b \) 是偏置项。
虽然我们不会在这里实现完整的 SVM,但核矩阵是核化算法的关键组成部分。
以下是核技巧实现的总结
- 我们从零开始实现了 RBF 核函数
- 我们使用 RBF 核计算了数据集的核矩阵
- 核矩阵可以用于核 SVM 或核 PCA 等核化算法
此实现演示了核技巧的核心思想:在不显式转换数据的情况下在高维空间中工作。您可以扩展此方法以实现其他核函数(例如,多项式核)或在自定义核化算法中使用核矩阵。
核技巧与显式转换的优点
那么,为什么我们使用核技巧而不是显式转换呢?
显式转换
假设我们有一个 2D 数据集 \( X = [x_1, x_2] \),我们想使用多项式转换将其转换到更高维空间。为简单起见,我们考虑一个二次转换
\[
\phi(x) = [x_1, x_2, x_1^2, x_2^2, x_1 x_2]
\]
这里,\( \phi(x) \) 将原始 2D 数据映射到 5D 空间。如果我们有 \( n \) 个数据点,我们需要为每个点计算此转换,从而生成一个 \( n \times 5 \) 矩阵。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
import numpy as np # 原始 2D 数据 X = np.array([[1, 2], [2, 3], [3, 4]]) # 显式转换为 5D 空间 def explicit_transformation(X): x1 = X[:, 0] x2 = X[:, 1] return np.column_stack((x1, x2, x1**2, x2**2, x1 * x2)) # 应用转换 X_transformed = explicit_transformation(X) print("Explicitly Transformed Data:") print(X_transformed) |
以上代码的输出将是
|
1 2 3 4 |
Explicitly Transformed Data: [[ 1 2 1 4 2] [ 2 3 4 9 6] [ 3 4 9 16 12]] |
在这里,我们明确地计算了5D空间中的新特征。这对于小型数据集和低维转换来说效果很好,但对于以下情况就会出现问题:
- 高维数据:如果原始数据有许多特征,转换后的空间大小会呈指数级增长。
- 复杂转换:某些转换(例如RBF)将数据映射到无限维空间,这是无法明确计算的。
现在,让我们将其与核技巧进行对比。
核技巧
核技巧通过使用核函数 \( K(x, y) \) 直接计算转换空间中的点积 \( \phi(x) \cdot \phi(y) \) 来避免明确计算 \( \phi(x) \)。例如,RBF核隐式地将数据映射到无限维空间,但我们从不直接计算 \( \phi(x) \)。
|
1 2 3 4 5 6 7 8 9 |
# 核技巧:在不进行显式转换的情况下计算转换空间中的点积 def rbf_kernel(x1, x2, gamma=1.0): squared_distance = np.sum((x1 - x2) ** 2) return np.exp(-gamma * squared_distance) # 计算核矩阵 kernel_matrix = compute_kernel_matrix(X, rbf_kernel, gamma=1.0) print("Kernel Matrix (RBF Kernel):") print(kernel_matrix) |
输出结果:
|
1 2 3 4 5 |
Kernel Matrix (RBF Kernel): [[1.00000000e+00 1.35335283e-01 3.35462628e-04 1.52299797e-08] [1.35335283e-01 1.00000000e+00 1.35335283e-01 3.35462628e-04] [3.35462628e-04 1.35335283e-01 1.00000000e+00 1.35335283e-01] [1.52299797e-08 3.35462628e-04 1.35335283e-01 1.00000000e+00]] |
在这里,我们从未明确计算 \( \phi(x) \)。相反,我们使用核函数直接计算转换空间中的点积。
方法对比
以下是显式转换存在问题的原因:
- 计算成本:将数据显式转换为高维空间需要计算和存储新特征,这可能计算成本高昂。
- 无限维度:某些转换(例如RBF)将数据映射到无限维空间,这是不可能明确计算的。
- 内存使用:存储转换后的数据可能需要大量内存,特别是对于大型数据集。
显式转换一句话总结:直接计算更高维空间中的转换特征 \( \phi(x) \)。这对于简单的低维转换是可行的,但对于复杂或高维转换则变得不切实际。
相反,核技巧在以下情况下特别有用:
- 转换后的特征空间是超高维或无限维的。
- 您想避免显式转换数据的计算成本。
- 您正在使用支持向量机 (SVM)、核主成分分析 (Kernel PCA) 或高斯过程等核化算法。
核技巧一句话总结:通过使用核函数直接计算点积 \( \phi(x) \cdot \phi(y) \) 来避免显式转换。这既高效又适用于无限维空间。核技巧是一个巧妙的数学捷径,它允许我们在高维空间中工作,而无需承担显式转换的计算负担。
结论
核方法是机器学习中一个强大的工具,使我们能够有效地处理非线性数据。在本教程中,我们探讨了核技巧、核 SVM 和核 PCA,并提供了实用的 Python 示例,帮助您开始使用这些技术。
通过掌握核方法,您可以更灵活、高效地解决各种机器学习问题,从分类到降维。




暂无评论。